Intelligent Energy Management in a Prosumer Community Considering the Load Factor Enhancement
Abstract
1. Introduction
1.1. Overview
- Proposing a computationally efficient MILP model to improve the value of LF related to the consumption profile of prosumers while taking into account the efficient scheduling of technologies such as SBs and shared PV generation.
- Investigating the intelligent management of an energy community by improving an indicator of the rational usage of energy.
- Establishing the management of household appliances (including the EV) to avoid their coincident consumption, especially those with higher average power, to mitigate the occurrence of peak consumption in off-peak periods and/or with insufficient levels of solar irradiation.
- Contributing to reducing the dependence on fossil fuels to meet the energy of domestic customers aiming at a sustainability context.
1.2. Literature Review
2. Simulation Setup
2.1. Hypotheses
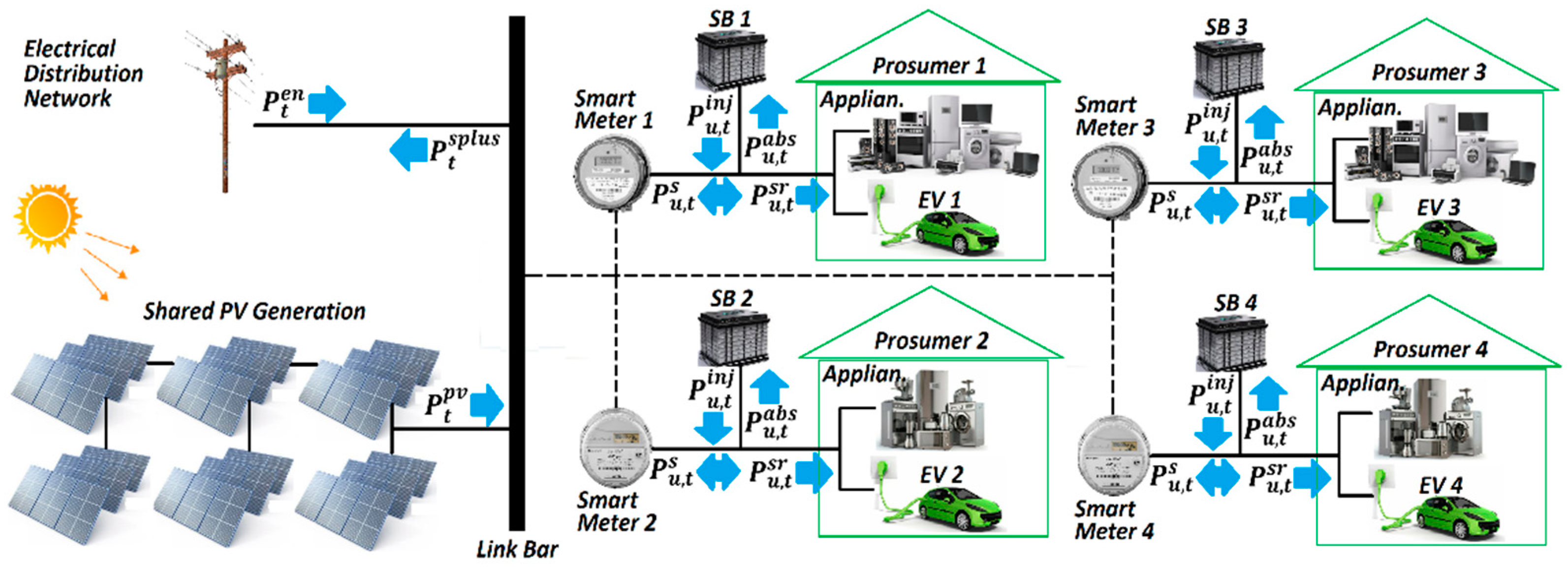
- The research is carried out in the SG environment depicted in Figure 1, which highlights the bidirectional flows between various technologies.
- Considering that household income is proportional to the number of appliances present at home, it is assumed that all consumers have the same household income taking into account the appliances reported in Table 1 and Table 2 including the presence of a single EV (to be charged within each household) according to Table 3.
- The habitual consumption of each appliance (including the EV) for each period of the day is obtained using the Monte Carlo simulation algorithm.
- The study horizon considers one day, which is divided into 24 hourly periods.
- A tariff structure is divided into three levels (peak, intermediate, and off-peak) to efficiently schedule the consumption periods of household appliances and the EV charging.
- The PV plant is shared by the community of prosumers. The PV panels operate in a horizontal position and at the point of maximum power.
- The effect of the presence of clouds on the yield of the PV plant is not considered.
2.2. Shared PV Plant and Prosumers Community Operation
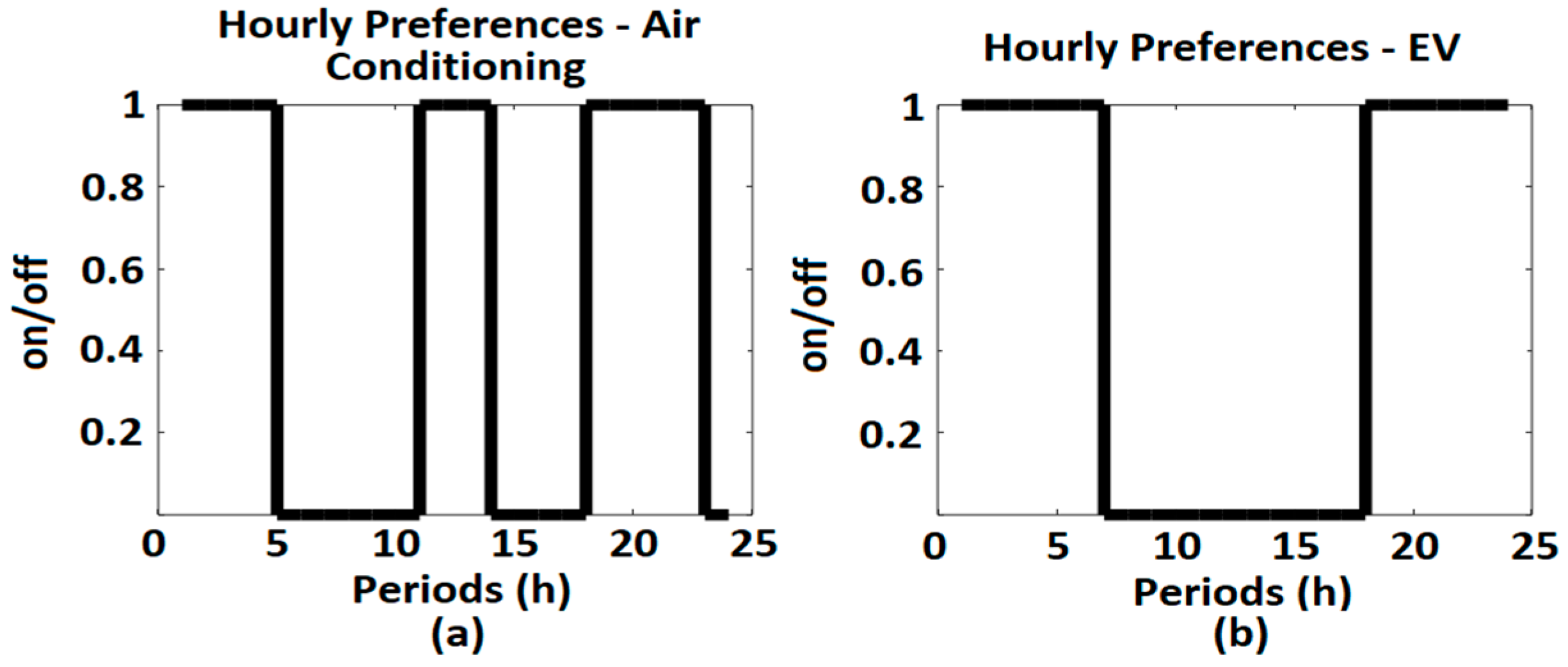
2.3. Habitual Consumption Profile and Hourly Preferences
| Algorithm 1. Simulation of uncertainties in household appliances usage. |
 |
3. Mathematical Model
3.1. Objective Function
3.2. Constraints
3.2.1. Home Appliances Constraints
3.2.2. Power Balance Constraints
3.2.3. Energy Storage Constraints
3.3. Linearization
3.4. Linearized Model
4. Results and Discussion
4.1. Basic Data
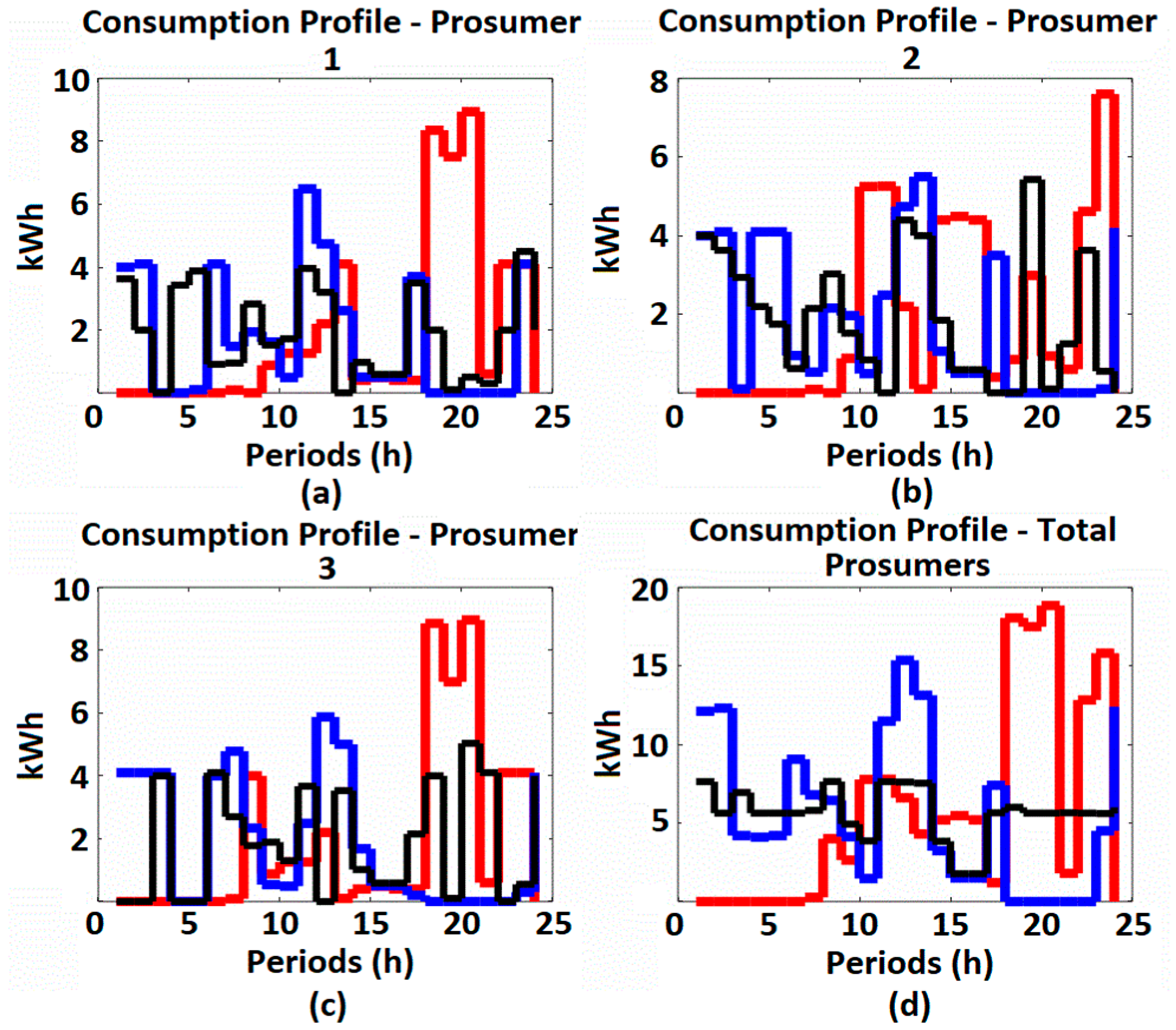
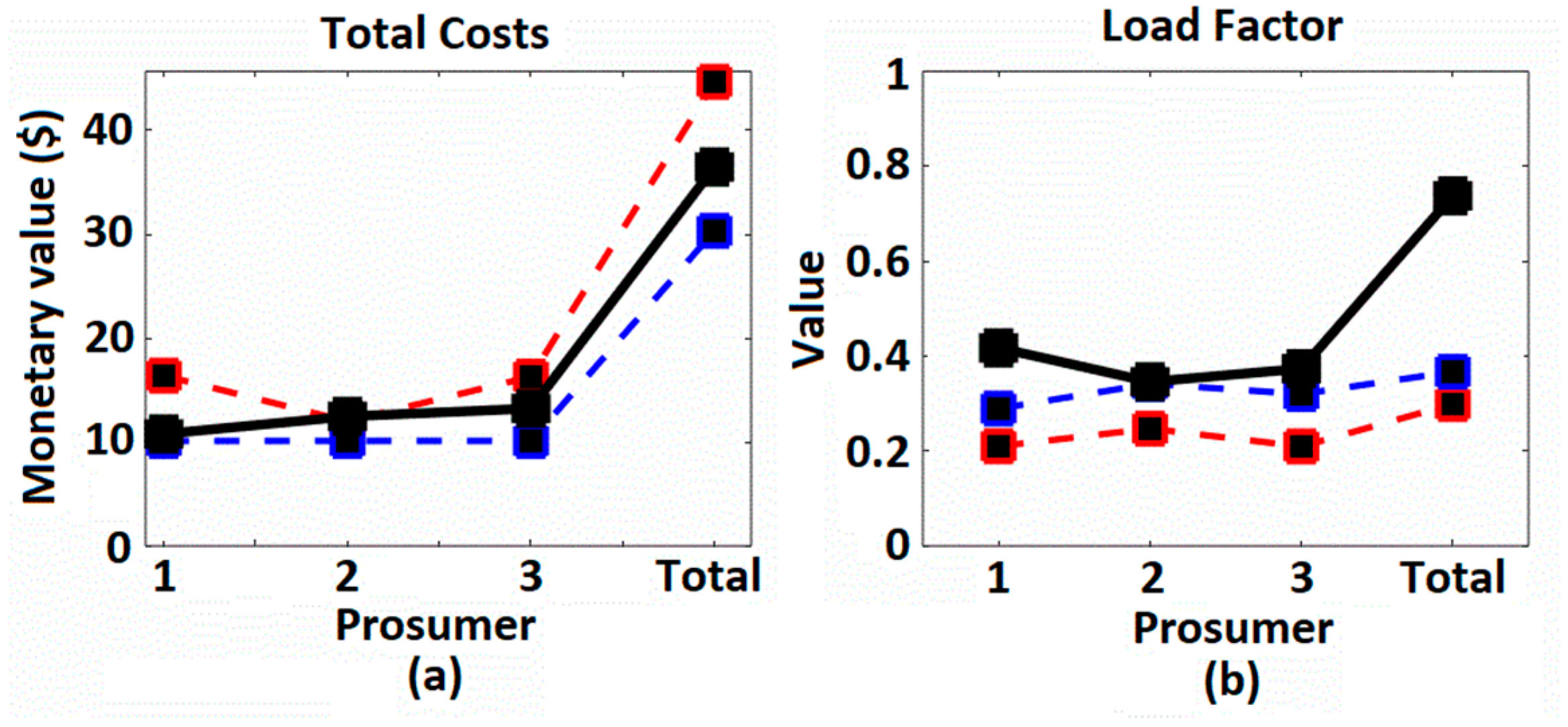
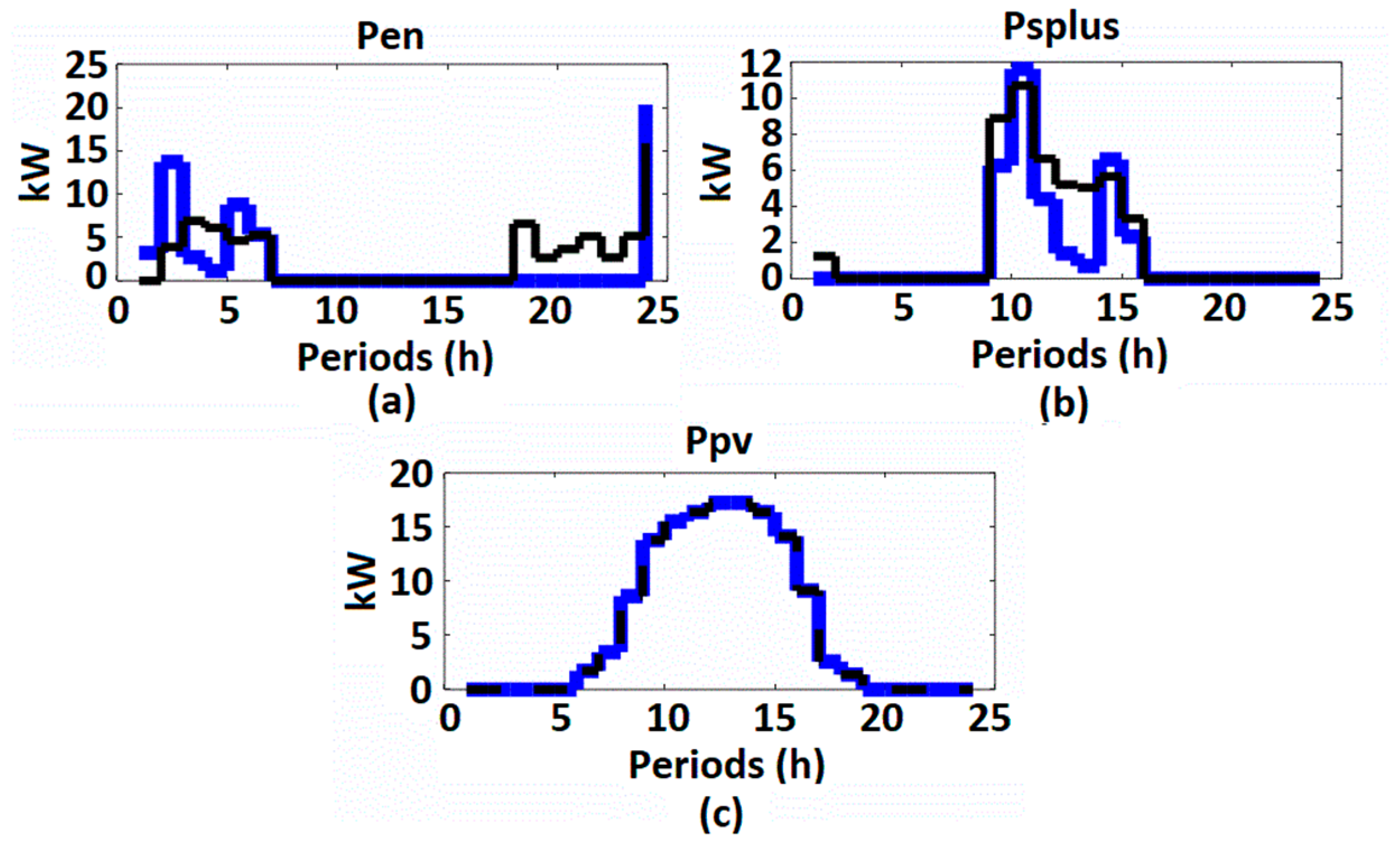
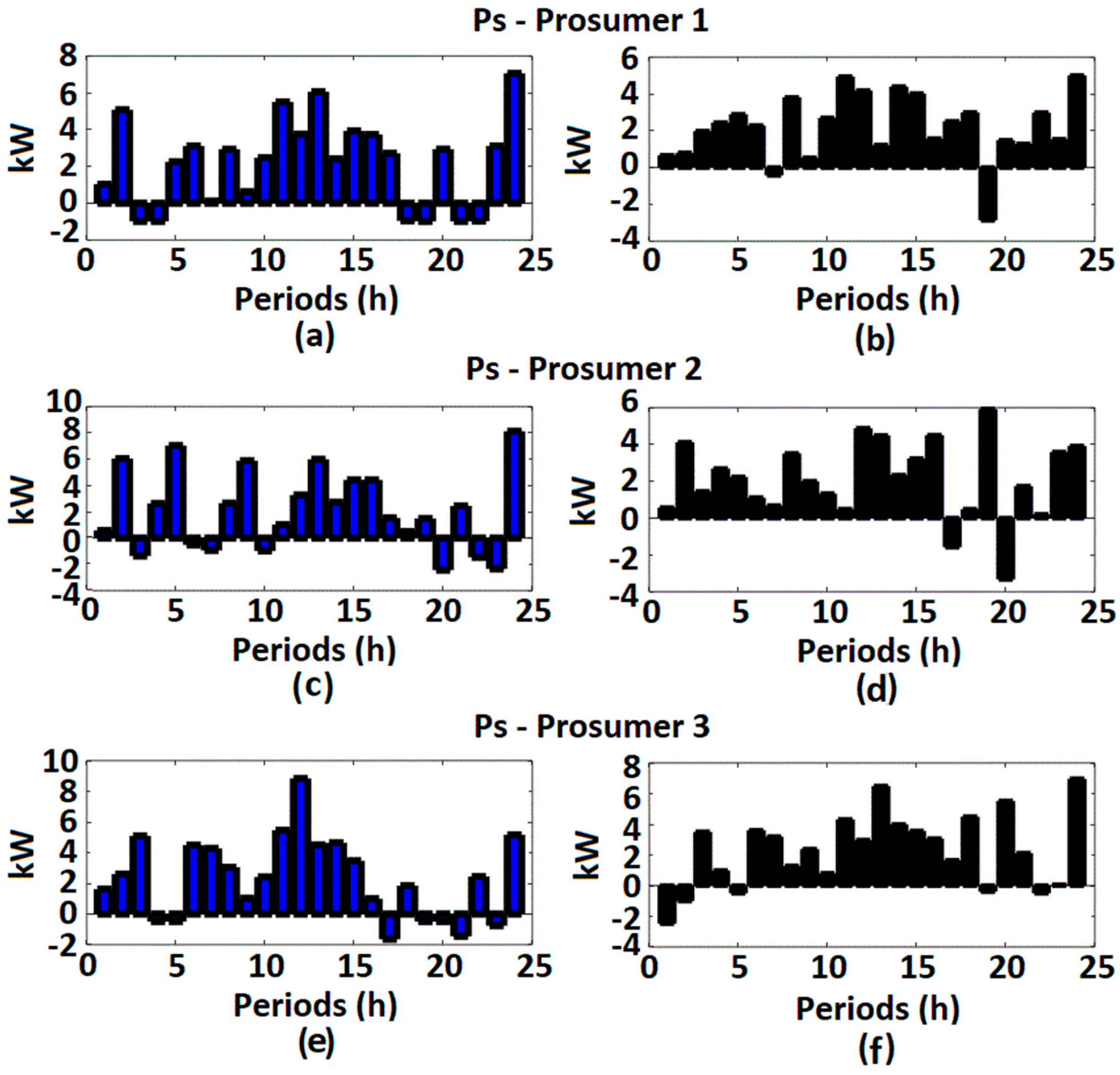
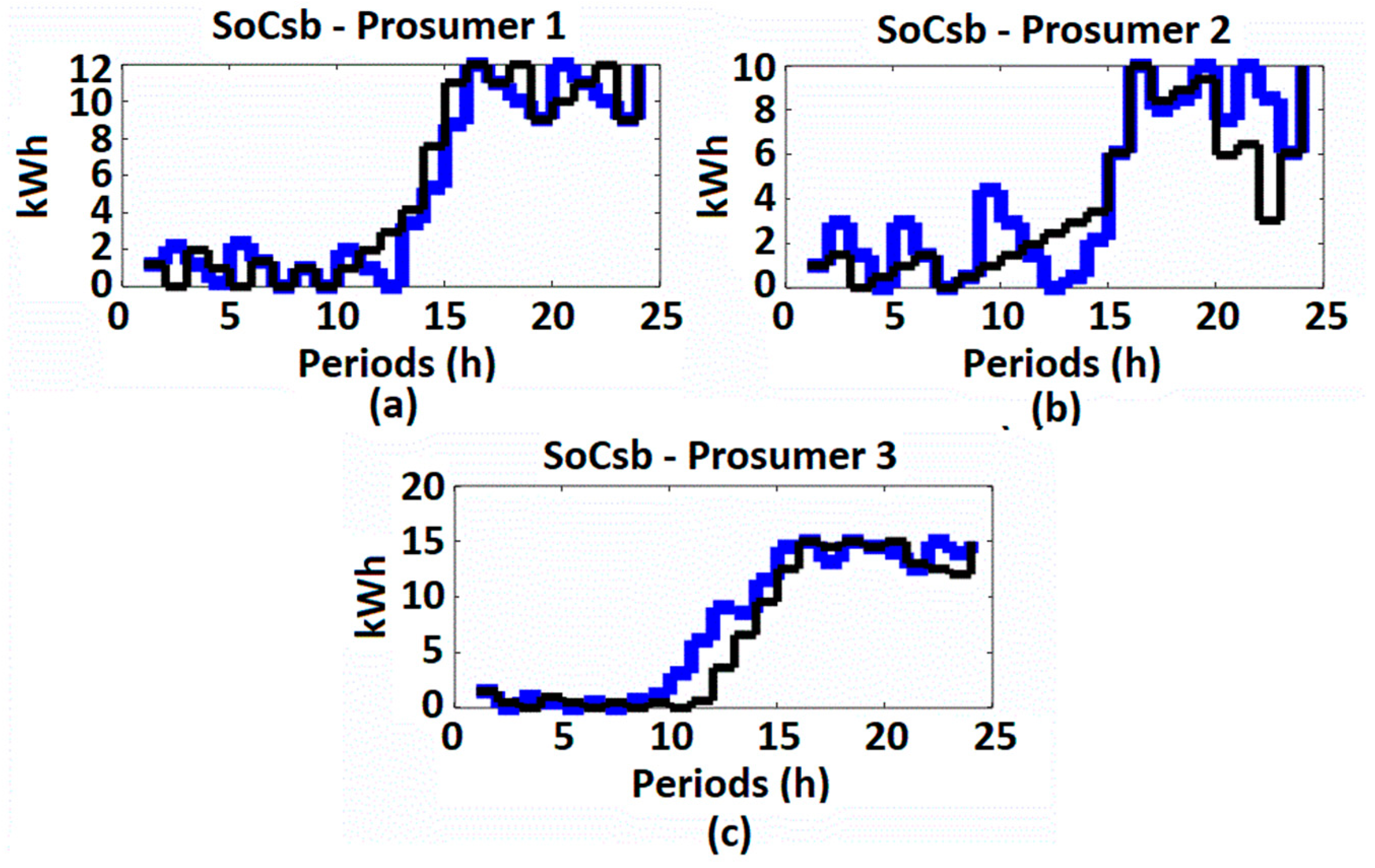
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Functions | |
| Cost function related to the optimal consumption profile of prosumers, appliances with higher average power, and the surplus power to be injected into the electric network of the energy company. | |
| Cost function related to the load factor of prosumers. | |
| Indexes | |
| u | Index for prosumers. |
| a | Index for home appliances. |
| t | Index for periods. |
| y | Index for discrete blocks. |
| Sets | |
| U | Set of prosumers u |
| A | Set of home appliances a |
| T | Set of periods t |
| Y | Set of discrete blocks y |
| Parameters | |
| Energy price in period t [$/kWh]. | |
| Average power of appliance a [kW]. | |
| Represents the type of appliance a: −1: EV; 0: appliance a with working hours greater than or equal to 1 h; and 1: appliance a with working hours less than 1 h. | |
| Binary parameter that adopts 1 for appliances with power higher than average. Otherwise, adopts 0. | |
| Usage probability of a given appliance a in period t. | |
| Accumulated probability related to the usage of a given appliance a in period t. | |
| Time duration of each period t [h]. | |
| Average value of usage time for the appliance a [h]. | |
| Minimum number of times that appliance a with = 1 is utilized. | |
| Maximum number of times that appliance a with = 1 is utilized. | |
| Minimum usage time of appliance a with = 1 [h]. | |
| Maximum usage time of appliance a with = 1 [h]. | |
| Average value related to the number of times the appliance a with = 0 [kW]. | |
| Binary matrix related to . Indicates for each prosumer u, the usage state of appliance a in each period t. | |
| Continuous values matrix. Indicates for each prosumer u, the habitual energy consumption of each appliance a in period t [kWh]. | |
| Big value related to the linearization process. | |
| EV charging rate [kW]. | |
| Minimum charging time of the EV related to prosumer u [h]. | |
| Maximum charging time of the EV related to prosumer u [h]. | |
| Minimum number of times the battery of the EV related to prosumer u can be charged. | |
| Maximum number of times the battery of the EV related to prosumer u can be charged. | |
| Initial state of charge related to EV battery of prosumer u [kWh]. | |
| Energy storage capacity of the EV battery related to prosumer u [kWh]. | |
| Percentage value related to . | |
| Hourly preferences. Indicates flexibility in the periods t when prosumer u can usage the home appliance a without creating discomfort. | |
| Maximum value related to the variable . | |
| Inclination value related to the discrete block y at period t. | |
| Minimum value of power absorbed by the SB related to prosumer u [kW]. | |
| Maximum value of power absorbed by the SB related to prosumer u [kW]. | |
| Minimum value of power injected by the storage battery related to prosumer u [kW]. | |
| Maximum value of power injected by the SB related to prosumer u [kW]. | |
| Efficiency in power absorption by the SB related to prosumer u. | |
| Efficiency in power injection by the SB related to prosumer u. | |
| SB capacity related to prosumer u [kWh]. | |
| Percentage value related to . | |
| Power supplied by the photovoltaic plant in each period t [kW]. | |
| k | Accumulator. |
| Maximum value of the local solar radiation [kW/m2]. | |
| Local solar radiation in each period t [kW/m2]. | |
| Standard solar radiation profile per unit. | |
| Photovoltaic area [m2]. | |
| Reduction factor due to production tolerance. | |
| Reduction factor due to temperature increase. | |
| Reduction factor due to the presence of dirt and dust. | |
| Reduction factor due to mismatch and wiring losses. | |
| Reduction factor due to DC to AC conversion losses. | |
| Weighted weight related to the first component of function . | |
| Weighted weight related to the second component of function . | |
| Weighted weight related to the third component of function . | |
| Weighted weight related to single component of function . | |
| Variables | |
| Binary matrix related to . Indicates for each prosumer u, the usage state of the appliance a in each period t. | |
| Continuous values matrix. Indicates for each prosumer u, the optimal energy consumption of each appliance a in period t [kWh]. | |
| Represents for the prosumer u, the time of usage of the appliance a in period t [h]. | |
| Coincidence factor. Indicates for the prosumer u, the number of appliances that are utilized at the same period t. | |
| Indicates for the prosumer u, the state of charge of the EV battery in each period t [kWh]. | |
| Represents for the prosumer u, the EV battery charging time in period t [h]. | |
| Indicates for the prosumer u, the total energy stored in the EV battery [kWh]. | |
| Linearization variable related to . | |
| Linearization variable related to . | |
| Indicates for each period t, the power related to the total number of prosumers [kW]. | |
| Average value of [kW]. | |
| Represents the difference between and at period t [kW]. | |
| Auxiliary variable to be used in the objective function discretization process. | |
| Auxiliary variable to be used in the objective function discretization process. | |
| Auxiliary variable to be used in the square of discretization process. | |
| Power supplied by the electricity distribution company in each period t [kW]. | |
| Surplus power sent to the electricity distribution network in each period t [kW]. | |
| Indicate for the prosumer u, the bidirectional power measured by the smart meter in each period t [kW]. | |
| Power injected by SB related to the prosumer u in period t [kW]. | |
| Indicates for the prosumer u, the power injected in each period t [kW]. | |
| Indicates for the prosumer u, the power absorbed in each period t [kW]. | |
| Binary variable that determines for the prosumer u the injection status of the SB in each period t. | |
| Binary variable that determines for the prosumer u the absorption status of the SB in each period t. | |
| Indicates for the prosumer u, the state of charge of the SB in each period t [kWh]. | |
References
- Rawlings, J.; Coker, P.; Doak, J.; Burfoot, B. Do smart grids offer a new incentive for SME carbon reduction? Sustain. Cities Soc. 2014, 10, 245–250. [Google Scholar] [CrossRef]
- Abujubbeh, M.; Al-Turjman, F.; Fahrioglu, M. Software-defined wireless sensor networks in smart grid: An overview. Sustain. Cities Soc. 2019, 51, 101754. [Google Scholar] [CrossRef]
- Joseph, A.; Balachandra, P. Energy internet, the future electricity system: Overview, concept, model structure, and mechanism. Energies 2020, 13, 4242. [Google Scholar] [CrossRef]
- Yu, D.; Xu, X.; Dong, M.; Nojavan, S.; Jermsittiparsert, K.; Abdollahi, A.; Allah Aalami, H.; Pashaei-Didani, H. Modeling and prioritizing dynamic demand response programs in the electricity markets. Sustain. Cities Soc. 2020, 53, 101921. [Google Scholar] [CrossRef]
- Pourakbari-Kasmaei, M.; Asensio, M.; Lehtonen, M.; Contreras, J. Trilateral Planning Model for Integrated Community Energy Systems and PV-Based Prosumers—A Bilevel Stochastic Programming Approach. IEEE Trans. Power Syst. 2020. [Google Scholar] [CrossRef]
- Miller, W.; Senadeera, M. Social transition from energy consumers to prosumers: Rethinking the purpose and functionality of eco-feedback technologies. Sustain. Cities Soc. 2017, 35, 615–625. [Google Scholar] [CrossRef]
- Strielkowski, W.; Streimikiene, D.; Fomina, A.; Semenova, E. Internet of energy (IoE) and high-renewables eletricity systems market design. Energies 2019, 12, 4790. [Google Scholar] [CrossRef]
- Espe, E.; Potdar, V.; Chang, E. Prosumer communities and relationships in smart grids: A literature review, evolution and future directions. Energies 2018, 11, 2528. [Google Scholar] [CrossRef]
- Li, L.; Yu, S. Optimal management of multi-stakeholder distributed energy systems in low-carbon communities considering demand response resources ans carbon tax. Sustain. Cities Soc. 2020, 61, 102230. [Google Scholar] [CrossRef]
- Guichi, A.; Talha, A.; Madjid Berkouk, E.; Mekhilef, S. Energy management and performance evaluation of grid connected PV-battery hybrid system with inherent control scheme. Sustain. Cities Soc. 2018, 41, 490–504. [Google Scholar] [CrossRef]
- Tascikaraoglu, A. Economic and operational benefits of energy storage sharing for a neighborhood of prosumers in a dynamic pricing environment. Sustain. Cities Soc. 2018, 38, 219–229. [Google Scholar] [CrossRef]
- Rahman, M.; Arefi, A.; Shafiullah, G.; Hettiwatte, S. A new approach to voltage management in unbalanced low voltage network using demand response and OLTC considering consumer preference. Int. J. Elec. Power. 2018, 99, 11–27. [Google Scholar] [CrossRef]
- Morteza Ghorashi, S.; Rastergar, M.; Senemmar, S.; Reza Seifi, A. Optimal design of reward-penalty demand response programs in smart power grids. Sustain. Cities Soc. 2020, 60, 102150. [Google Scholar] [CrossRef]
- European Comission–Gfk Belgium Consortium. Study on Residential Prosumers in the European Energy Union. Available online: https://ec.europa.eu/commission/sites/beta-political/files/study-residential-prosumers-energy-union_en.pdf (accessed on 23 December 2020).
- Nuchprayoon, S. Calculation and allocation of load losses in distribution system using load research data and load factor method. In Proceedings of the 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Batu Ferringhi, Malaysia, 25–27 November 2016; pp. 85–90. [Google Scholar]
- Saikira, B.; Manas, M.; Baruah, D. Distribution loss reduction in a university of north east india through load factor improvement. In Proceedings of the 2015 International Conference on Energy Systems and Applications, Pune, India, 30 October–1 November 2015; pp. 203–208. [Google Scholar]
- Surai, J.; Surapatana, V. Load factor improvement in industrial sector load duration curves. In Proceedings of the 2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014; pp. 1–4. [Google Scholar]
- Cerna, F.V.; Contreras, J. A MILP model to relieve the occurrence of new demand peaks by improving the load factor in smart homes. Sustain. Cities Soc. 2021, 71. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.M.; Kernighan, B.W. AMPL: A Modeling Language for Mathematical Programming, 2nd ed.; Duxbury Press/Brooks/Cole Publishing Company: Boston MA, USA, 2001; Available online: https://ampl.com/resources/the-ampl-book/ (accessed on 17 March 2020). [CrossRef]
- IBM ILOG CPLEX Optimization Studio CPLEX User’s Manual–Version 12 Release 8. Available online: https://www.ibm.com/support/knowledgecenter/SSSA5P_12.8.0/ilog.odms.studio.help/pdf/usrcplex.pdf (accessed on 20 October 2020).
- AssLiu, X.; Wang, S.; Sun, J. Energy management for community energy network with CHP based on cooperative game. Energies 2018, 11, 1066. [Google Scholar] [CrossRef]
- Radl, J.; Fleischhacker, A.; Huglen Revheim, F.; Lettner, G.; Auer, H. Comparison of profitability of PV electricity sharing in renewable energy communities in selected european countries. Energies 2020, 13, 2644. [Google Scholar] [CrossRef]
- De la Hoz, J.; Alonso, A.; Coronas, S.; Martin, H.; Matas, J. Impact of different regulatory structures on the management of energy communities. Energies 2020, 13, 2892. [Google Scholar] [CrossRef]
- Marangoni, F.; Magatão, L.; Ramos de Arruda, L. Demand response optimization model to energy and power expenses analysis and contract revision. Energies 2020, 13, 2803. [Google Scholar] [CrossRef]
- Wang, J.; Garifi, K.; Baker, K.; Zou, W.; Zhang, Y.; Huang, S.; Vrabie, D. Optimal renewable resource allocation and load scheduling of resilient communities. Energies 2020, 13, 5683. [Google Scholar] [CrossRef]
- Ghosh, A.; Aggarwai, V. Penalty based control mechanism for strategic prosumers in a distribution network. Energies 2020, 13, 452. [Google Scholar] [CrossRef]
- Correa-Florez, C.; Michiorri, A.; Kariniotakis, G. Comparative analysis of adjustable robust optimization alternatives for the participation of aggregated residential prosumers in eletricity markets. Energies 2019, 12, 1019. [Google Scholar] [CrossRef]
- Ur Rashid, M.; Granelli, F.; Hossain, A.; Alam, S.; Saleh Al-Ismail, F.; Kumar Karmaker, A.; Rahaman, M. Development of home energy management scheme for a smart grid community. Energies 2020, 13, 4288. [Google Scholar] [CrossRef]
- Alabdullatif, A.; Gerding, E.; Perez Diaz, A. Market design and trading strategies for community energy markets with storage and renewable supply. Energies 2020, 13, 972. [Google Scholar] [CrossRef]
- Li, L. Optimal coordination strategies for load service entity and community energy systems based on centralized and decentralized approaches. Energies 2020, 13, 3202. [Google Scholar] [CrossRef]
- Bukhsh, R.; Umar Javed, M.; Fatima, A.; Javaid, N.; Shafiq, M.; Ghoo Choi, J. Cost efficient real time electricity management services for green community using fog. Energies 2020, 13, 3164. [Google Scholar] [CrossRef]
- Kuruseelan, S.; Vaithilingam, C. Peer-to-peer energy trading of a community connected with an ac and dc microgrid. Energies 2019, 12, 3709. [Google Scholar] [CrossRef]
- González-Romera, E.; Ruiz-Cortés, M.; Milanés-Montero, M.; Barrero-Gonzáles, F.; Romero-Cadaval, E.; Amaral Lopes, R.; Martins, J. Advantages of minimizing energy exchange instead of energy cost in prosumer microgrids. Energies 2019, 12, 719. [Google Scholar] [CrossRef]
- Shin, I. Approximation algorithm-based prosumer scheduling for microgrids. Energies 2020, 13, 5853. [Google Scholar] [CrossRef]
- Achiluzzi, E.; Kobikrishna, K.; Sivabalan, A.; Sabillon, C.; Venkatesh, B. Optimal asset planning for prosumers considering energy storage and photovoltaic (PV) units: A stochastic approach. Energies 2020, 13, 1813. [Google Scholar] [CrossRef]
- Toquica, D.; Agbossou, K.; Malhamé, R.; Henao, N.; Kelouwani, S.; Cardenas, A. Adaptive machine learning for automated modeling of residential prosumer agents. Energies 2020, 13, 2250. [Google Scholar] [CrossRef]
- De Greve, Z.; Bottieau, J.; Vangulick, D.; Wautier, A.; David Dapoz, P.; Arrigo, A.; Toubeau, J.; Vallée, F. Machine learning techniques for improving self-consumption in renewable energy communities. Energies 2020, 13, 4892. [Google Scholar] [CrossRef]
- García-Villalobos, J.; Zamora, I.; Eguia, P.; Torres, E.; Etxegarai, A.; San Martin, J.I. Optimization of load factor in distribution networks with high share of plug-in electric vehicles and photovoltaic generation. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; pp. 1–6. [Google Scholar]
- Trongwanichnam, K.; Thitapars, S.; Leeprechanon, N. Impact of plug-in electrici vehicles load planning to load factor and total generation cost in a power system. In Proceedings of the 2019 IEEE PES GTD Grand international and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 599–604. [Google Scholar]
- Mohg Ali, S.B.; Hasanuzzaman, A.; Rahim, N. Investigation on the load factor performance at Wisma R&D universiti Malaya building. In Proceedings of the 5th IET International Conference on Clean Energy and Technology (CEAT2018), Kuala Lumpur, Malaysia, 5–6 September 2018; pp. 1–6. [Google Scholar]
- Chiu, W.Y.; Hsieh, J.T.; Chen, C.M. Pareto optimal demand response based on energy costs and load factor in smart grid. IEEE Trans. Ind. Inform. 2020. [Google Scholar] [CrossRef]
- Al Fardan, A.S.; Al Gahtani, K.S.; Asif, M. Demand side management solution through new tariff structure to minimize excessive load growth and improve system load factor by improving commercial buildings energy performance in Saudi Arabia. In Proceedings of the 2017 IEEE International Conference on Smart Energy Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 308–320. [Google Scholar]
- Lorestani, A.; Aghaee, S.S.; Gharehpetian, G.B.; Ardehali, M.M. Energy management in smart home including PV panel, battery, electric heater with integration of plug-in electric vehicle. In Proceedings of the 2017 Smart Grid Conference (SGC), Tehran, Iran, 20–21 December 2017; pp. 1–7. [Google Scholar]
- Cho, D.; Valenzuela, J. Optimization of residential off-grid PV-battery systems. Sol. Energy 2020, 28, 647–653. [Google Scholar] [CrossRef]
- Liu, N.; Wang, J.; Yu, X.; Ma, L. Hybrid energy sharing for smart building cluster with CHP system and PV prosumers: A coalitional game approach. IEEE Access 2018. [Google Scholar] [CrossRef]
- Muqeet, H.A.U.; Ahmad, A. Optimal scheduling for campus prosumer microgrid considering price based demand response. IEEE Access. 2020. [Google Scholar] [CrossRef]
- Barnes, A.K.; Balda, J.C.; Hayes, J.K.; Modelling, P.V. Clouding Effects Using a Semi-Markov Process with Application to Energy Storage. IFAC Proc. Vol. 2014, 47, 9444–9449. [Google Scholar] [CrossRef]
- Lappalainen, K.; Valkealahti, S. Effects of PV array layout, electrical configuration and geographic orientation on mismatch losses caused by moving clouds. Solar Energy 2017, 144, 548–555. [Google Scholar] [CrossRef]
- Lappalainen, K.; Valkealahti, S. Photovoltaic mismatch losses caused by moving clouds. Solar Energy 2017, 158, 455–561. [Google Scholar] [CrossRef]
- Element Energy, Further Analysis of the Household Electricity Use Survey–Electrical Appliances at Home: Tuning in to Energy Saving. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/275484/electricity_survey_2_tuning_in_to_energy_saving.pdf (accessed on 10 December 2020).
- UNDP CEDRO Project, Energy Efficient Home Appliances: Perspctives from Lebanese Consumers. Available online: https://www.undp.org/content/dam/lebanon/docs/Energy%20and%20Environment/Publications/CEDRO%20_%20Energy%20Efficient%20Home%20Appliances.pdf (accessed on 15 November 2020).
- Robert, P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2004; p. 157. [Google Scholar] [CrossRef]
- US Department of Energy. Appliance & Equipment Standards/Standards and Test Procedures. Available online: https://www.energy.gov/eere/buildings/standards-and-test-procedures (accessed on 20 December 2020).
- Data. Available online: https://drive.google.com/file/d/1i50a68nRO2zEl8pjPIwlOYKEmOWdMnhS/view?usp=sharing (accessed on 2 January 2021).
- Yahia, Z.; Pradhan, A. Multi-objective optimization of household appliance scheduling problem considering consumer preference and peak load reduction. Sustain. Cities Soc. 2020, 55. [Google Scholar] [CrossRef]
- Cerna, F.V.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Contreras, J. Efficient automation of an HEV heterogeneous fleet using a two-stage methodology. IEEE Trans. Veh. Technol. 2019. [Google Scholar] [CrossRef]
- Borges, M.C.O.; Franco, J.F.; Rider, M.J. Optimal reconfiguration of electrical distribution systems using mathematical programming. J. Control. Autom. Electr. Syst. 2014, 25. [Google Scholar] [CrossRef]
- Gonçalves, R.R.; Alves, R.P.; Franco, J.F. Operation planning of electrical distribution systems using a mixed integer linear model. J. Control. Autom. Electr. Syst. 2013, 24. [Google Scholar] [CrossRef]
- National Electric Energy Agency (ANEEL), Normative Resolution n°. 733–White Tariff (2016). Available online: https://www.aneel.gov.br/tarifa-branca (accessed on 10 July 2020).
- Binkley, A. Solar Technology Reference Guide. NAIOP Research Foundation. Available online: File:///C:/Users/Samsung/Downloads/solartechrefguide.pdf (accessed on 15 July 2020).
- Goodrich, A.; James, T.; Woodhouse, M. Residential, Commercial, and Utility-Scale Photovoltaic (PV) Systems Prices in the United States: Current Drivers and Cost-Reduction Opportunities, Technical Report NREL/TP-6 A20-53347. Available online: https://www.nrel.gov/docs/fy12osti/53347.pdf (accessed on 25 October 2020).
- Xie, H.; Teng, X.; Xu, Y.; Wang, Y. Optimal energy storage sizing for networked microgrids considering reliability and resilience. IEEE Access. 2019. [Google Scholar] [CrossRef]
- Asian Development Bank. Handbook on Battery Energy Storage System; 6 ADB: Mandaluyong City, Manila, Philippines, 2018; p. 157. [Google Scholar] [CrossRef]
- Digital Atlas-Solar Radiation (W/m2)–April 2020. Available online: https://www.cnpma.embrapa.br/climapest/atlasdigital/radiacao_solar/2020/html/MED_RAD_SOLAR_2020_A2_ABR.html (accessed on 10 May 2020).
- Melhem, F.Y.; Grunder, O.; Hammoudan, Z.; Moubayed, N. Energy management in electrical smart grid environment using robust optimization algorithm. IEEE Trans. Ind. Appl. 2018. [Google Scholar] [CrossRef]
- SUNTECH–330 Watt Polycrystalline Solar Module. Available online: http://www.get-systems.com/productsfiles/solarcells/AU_STP330_VfwMC4_330_325_320_1500V.pdf (accessed on 15 June 2020).

| a | Appliances | ||||||
|---|---|---|---|---|---|---|---|
| 1 | Air Conditioner | 4.00 | 2 | 2 | 0.25 | - | 1 |
| 2 | Freezer | 0.40 | 10 | 10 | 0.50 | - | 0 |
| 3 | Clothes Dryer | 3.50 | 1 | 1 | 0.50 | - | 1 |
| 4 | Computer | 0.25 | 2 | 2 | 0.50 | - | 0 |
| 5 | Incand. light | 0.10 | 5 | 5 | 0.25 | - | 0 |
| 6 | TV | 0.09 | 5 | 5 | 0.50 | - | 0 |
| 7 | Electric Iron | 1.00 | 1 | 1 | 0.25 | - | 1 |
| 8 | Fan | 0.10 | 4 | 4 | 0.50 | - | 0 |
| 9 | DVD Player | 0.025 | 2 | 2 | 0.25 | - | 0 |
| 10 | Stereo | 0.020 | 2 | 2 | 0.25 | - | 0 |
| a | Appliances | ||||||
|---|---|---|---|---|---|---|---|
| 11 | Electric Faucet | 3.50 | 0.50 | 1 | - | 1 | 1 |
| 12 | Dishwasher | 1.50 | 0.75 | 1 | - | 1 | 1 |
| 13 | Coffee Maker | 1.00 | 0.50 | 1 | - | 1 | 0 |
| 14 | Resistance Oven | 1.50 | 0.50 | 1 | - | 1 | 0 |
| 15 | Electric Shower | 3.50 | 0.15 | 1 | - | 1 | 1 |
| 16 | Microwave | 1.30 | 0.33 | 1 | - | 1 | 0 |
| 17 | Washing Machine | 1.50 | 0.50 | 1 | - | 1 | 0 |
| 18 | Vacuum Cleaner | 1.00 | 0.33 | 1 | - | 1 | 0 |
| 19 | Hair Dryer | 0.70 | 0.50 | 1 | - | 1 | 0 |
| 20 | Toaster | 0.80 | 0.16 | 1 | - | 1 | 0 |
| a | Appliances | |||||
|---|---|---|---|---|---|---|
| 21 | EV 1, 2, 3 | 4.00 | 20.0 | 0.5 | 5.00 | 1 |
| t | Periods | (p.u.) | t | Periods | (p.u.) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 01:00–02:00 h | 0.22419 | 0.00 | 0.00 | 13 | 13:00–14:00 h | 0.22419 | 1.00 | 0.220 |
| 2 | 02:00–03:00 h | 0.22419 | 0.00 | 0.00 | 14 | 14:00–15:00 h | 0.22419 | 0.95 | 0.209 |
| 3 | 03:00–04:00 h | 0.22419 | 0.00 | 0.00 | 15 | 15:00–16:00 h | 0.22419 | 0.82 | 0.180 |
| 4 | 04:00–05:00 h | 0.22419 | 0.00 | 0.00 | 16 | 16:00–17:00 h | 0.22419 | 0.53 | 0.117 |
| 5 | 05:00–06:00 h | 0.22419 | 0.00 | 0.00 | 17 | 17:00–18:00 h | 0.22419 | 0.15 | 0.033 |
| 6 | 06:00–07:00 h | 0.22419 | 0.10 | 0.022 | 18 | 18:00–19:00 h | 0.32629 | 0.08 | 0.018 |
| 7 | 07:00–08:00 h | 0.22419 | 0.20 | 0.044 | 19 | 19:00–20:00 h | 0.51792 | 0.00 | 0.00 |
| 8 | 08:00–09:00 h | 0.22419 | 0.50 | 0.11 | 20 | 20:00–21:00 h | 0.51792 | 0.00 | 0.00 |
| 9 | 09:00–10:00 h | 0.22419 | 0.80 | 0.176 | 21 | 21:00–22:00 h | 0.51792 | 0.00 | 0.00 |
| 10 | 10:00–11:00 h | 0.22419 | 0.90 | 0.198 | 22 | 22:00–23:00 h | 0.32629 | 0.00 | 0.00 |
| 11 | 11:00–12:00 h | 0.22419 | 0.95 | 0.209 | 23 | 23:00–24:00 h | 0.22419 | 0.00 | 0.00 |
| 12 | 12:00–13:00 h | 0.22419 | 1.00 | 0.220 | 24 | 24:00–01:00 h | 0.22419 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerna, F.V.; Pourakbari-Kasmaei, M.; Pinheiro, L.S.S.; Naderi, E.; Lehtonen, M.; Contreras, J. Intelligent Energy Management in a Prosumer Community Considering the Load Factor Enhancement. Energies 2021, 14, 3624. https://doi.org/10.3390/en14123624
Cerna FV, Pourakbari-Kasmaei M, Pinheiro LSS, Naderi E, Lehtonen M, Contreras J. Intelligent Energy Management in a Prosumer Community Considering the Load Factor Enhancement. Energies. 2021; 14(12):3624. https://doi.org/10.3390/en14123624
Chicago/Turabian StyleCerna, Fernando V., Mahdi Pourakbari-Kasmaei, Luizalba S. S. Pinheiro, Ehsan Naderi, Matti Lehtonen, and Javier Contreras. 2021. "Intelligent Energy Management in a Prosumer Community Considering the Load Factor Enhancement" Energies 14, no. 12: 3624. https://doi.org/10.3390/en14123624
APA StyleCerna, F. V., Pourakbari-Kasmaei, M., Pinheiro, L. S. S., Naderi, E., Lehtonen, M., & Contreras, J. (2021). Intelligent Energy Management in a Prosumer Community Considering the Load Factor Enhancement. Energies, 14(12), 3624. https://doi.org/10.3390/en14123624










