Analysis of the Velocity Distribution in the Plenum Box with Various Entries
Abstract
:1. Introduction
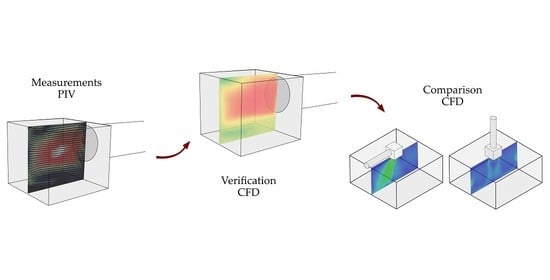
2. Materials and Methods
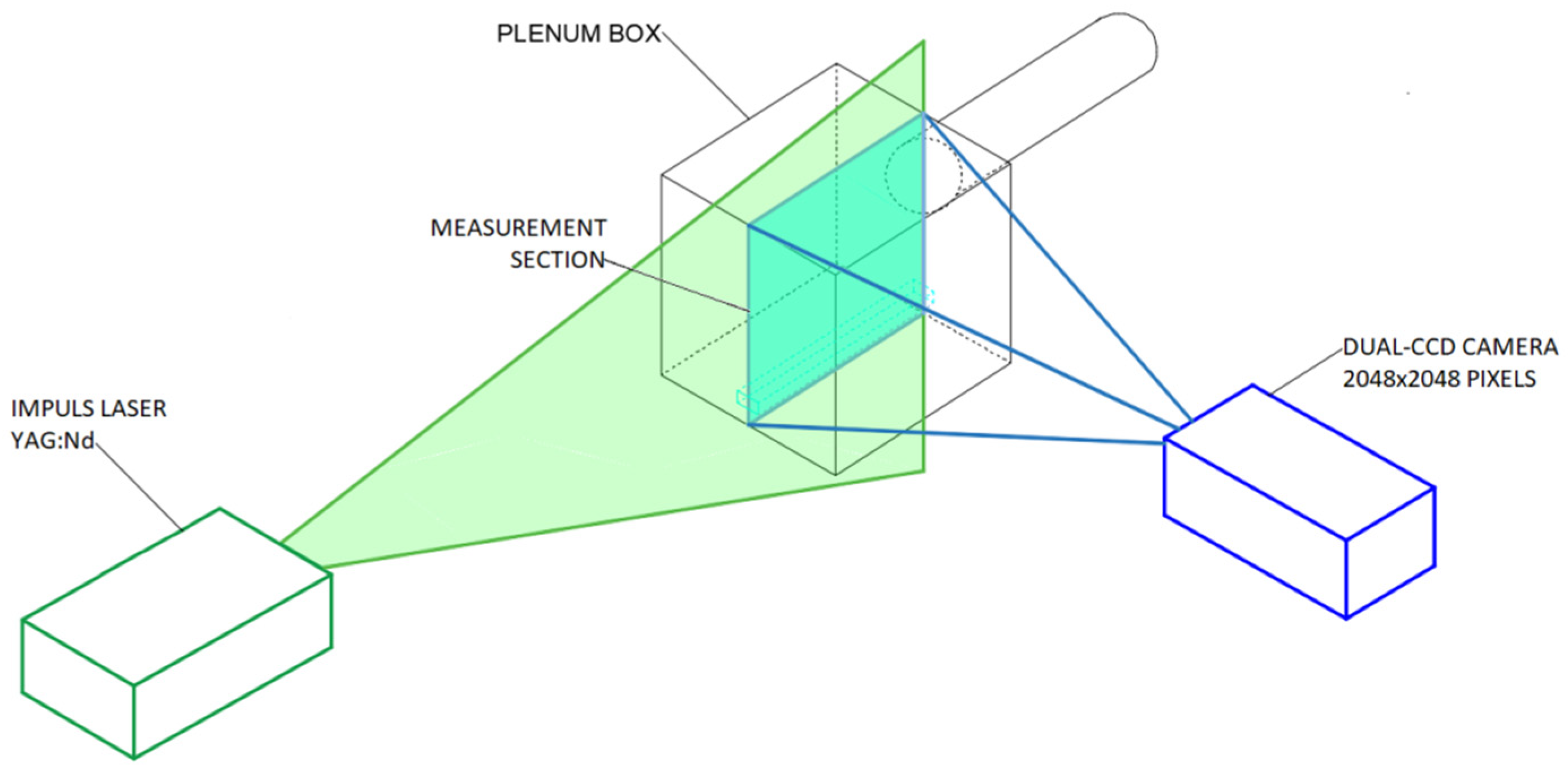
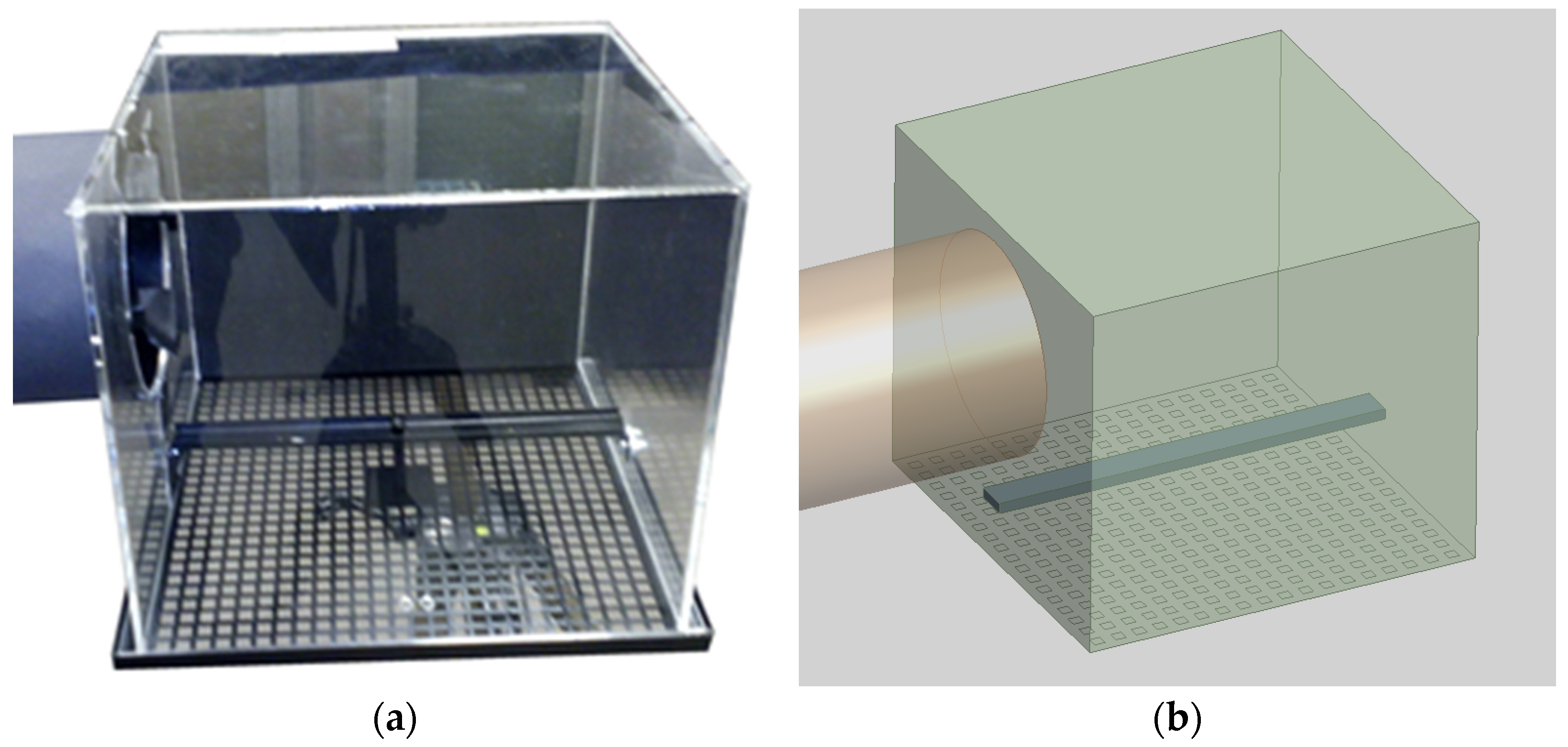
2.1. Experimental Measurement
2.2. Numerical Analyses
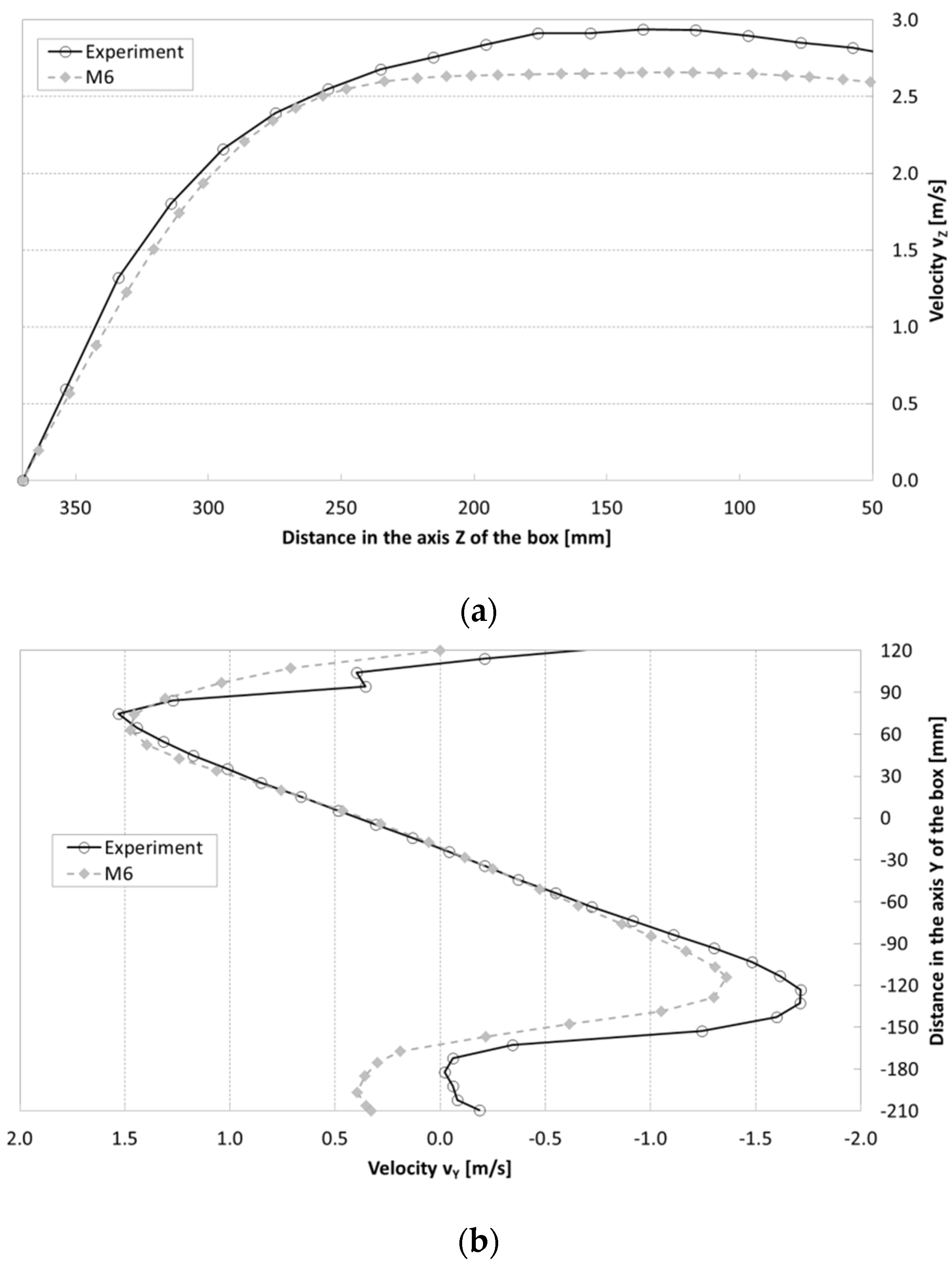
2.2.1. Verification of Computational Models
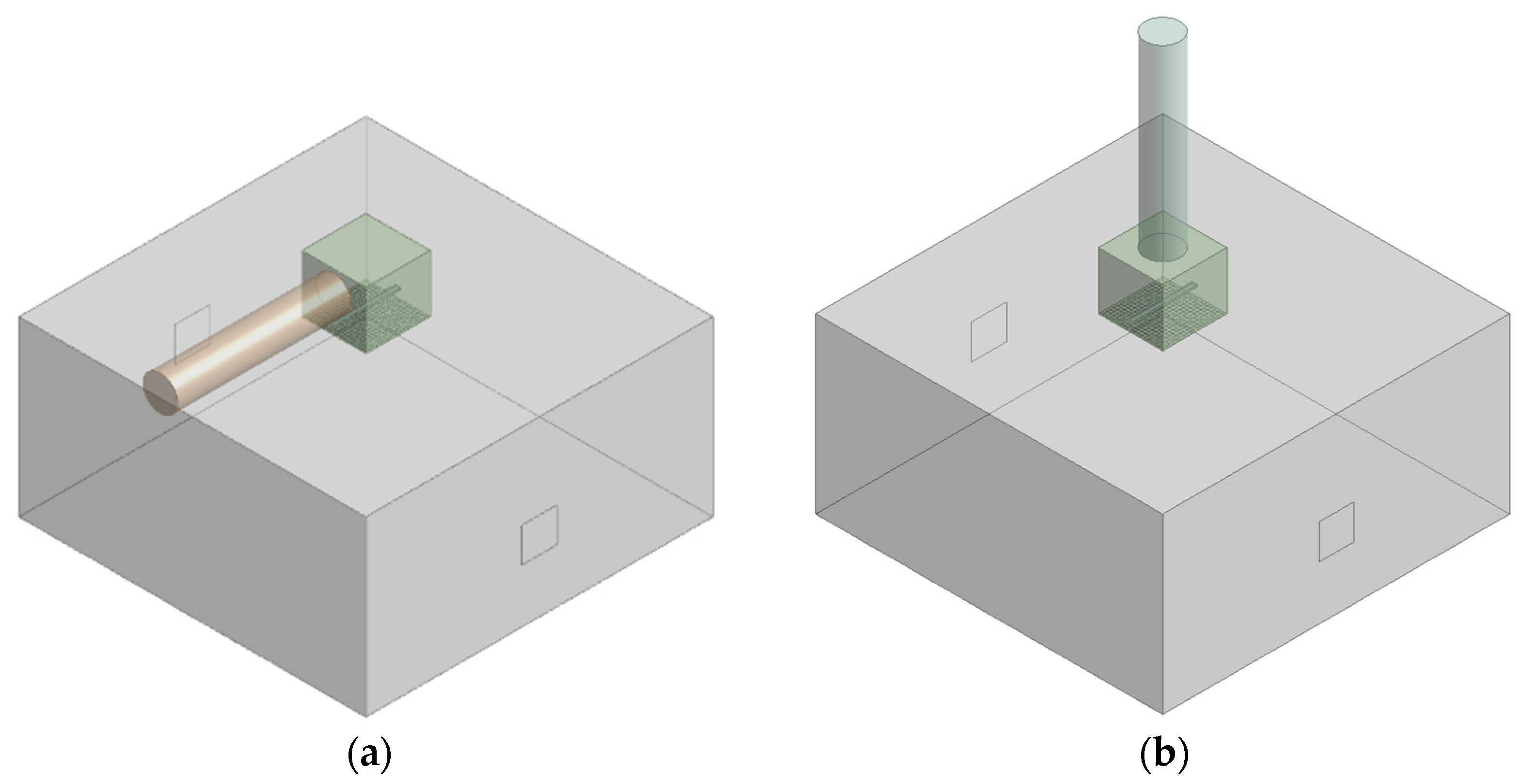
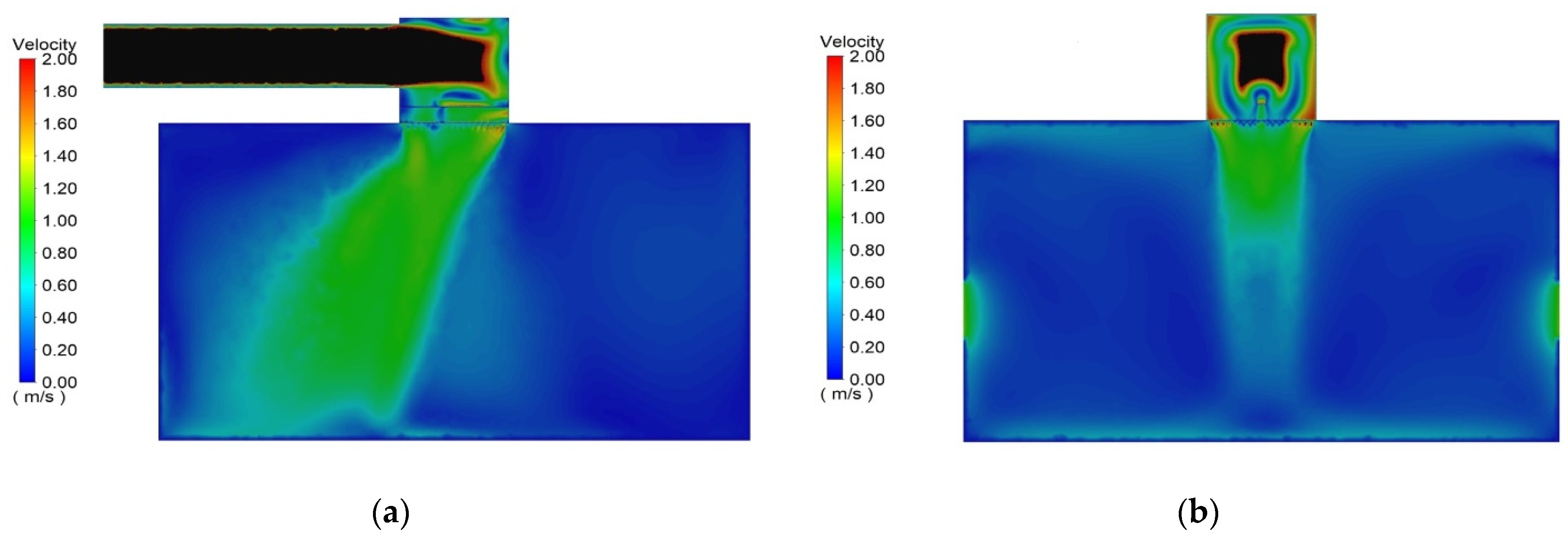
2.2.2. Comparative Analysis for Plenum Box with Side and Top Entry
3. Results
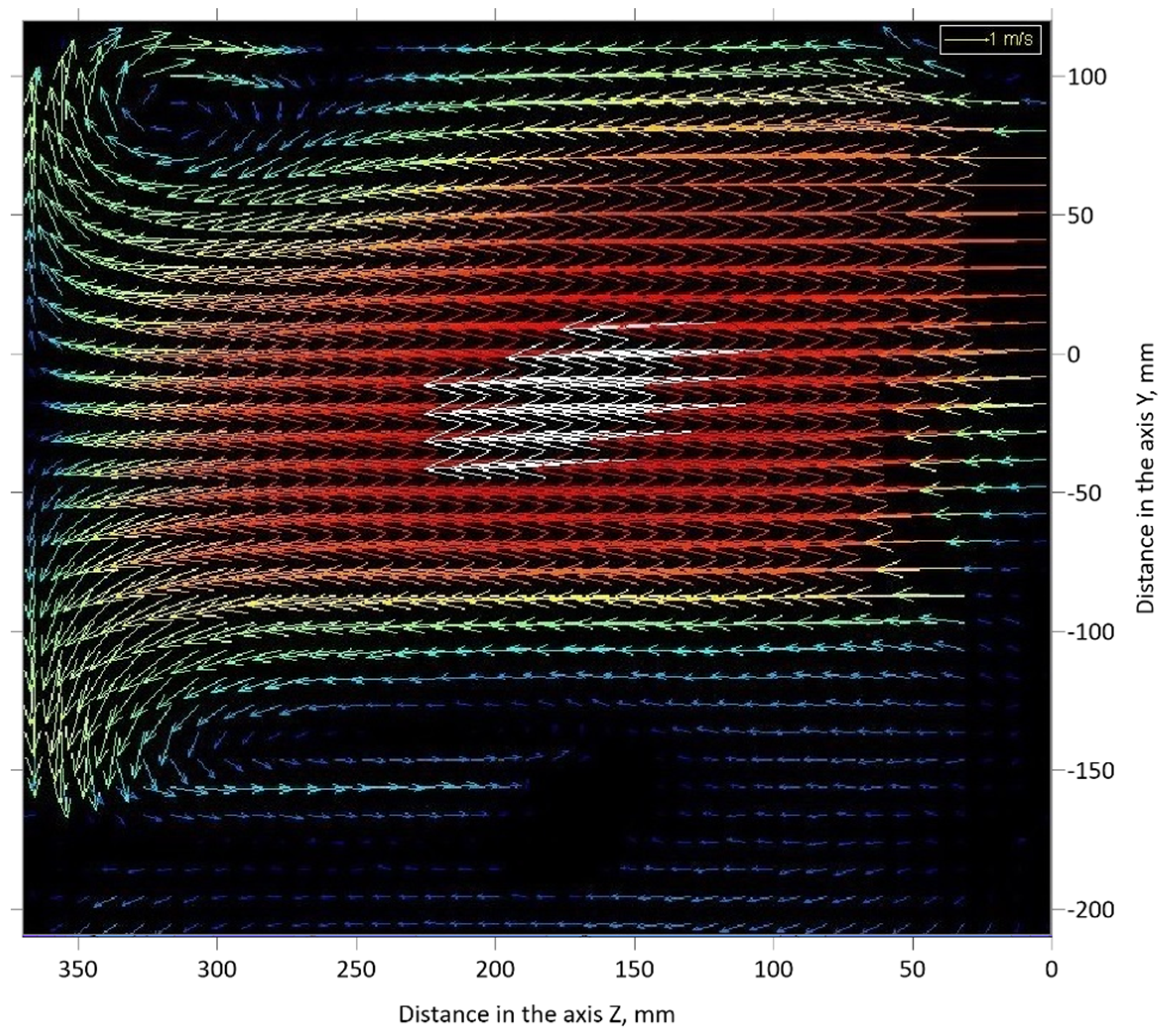
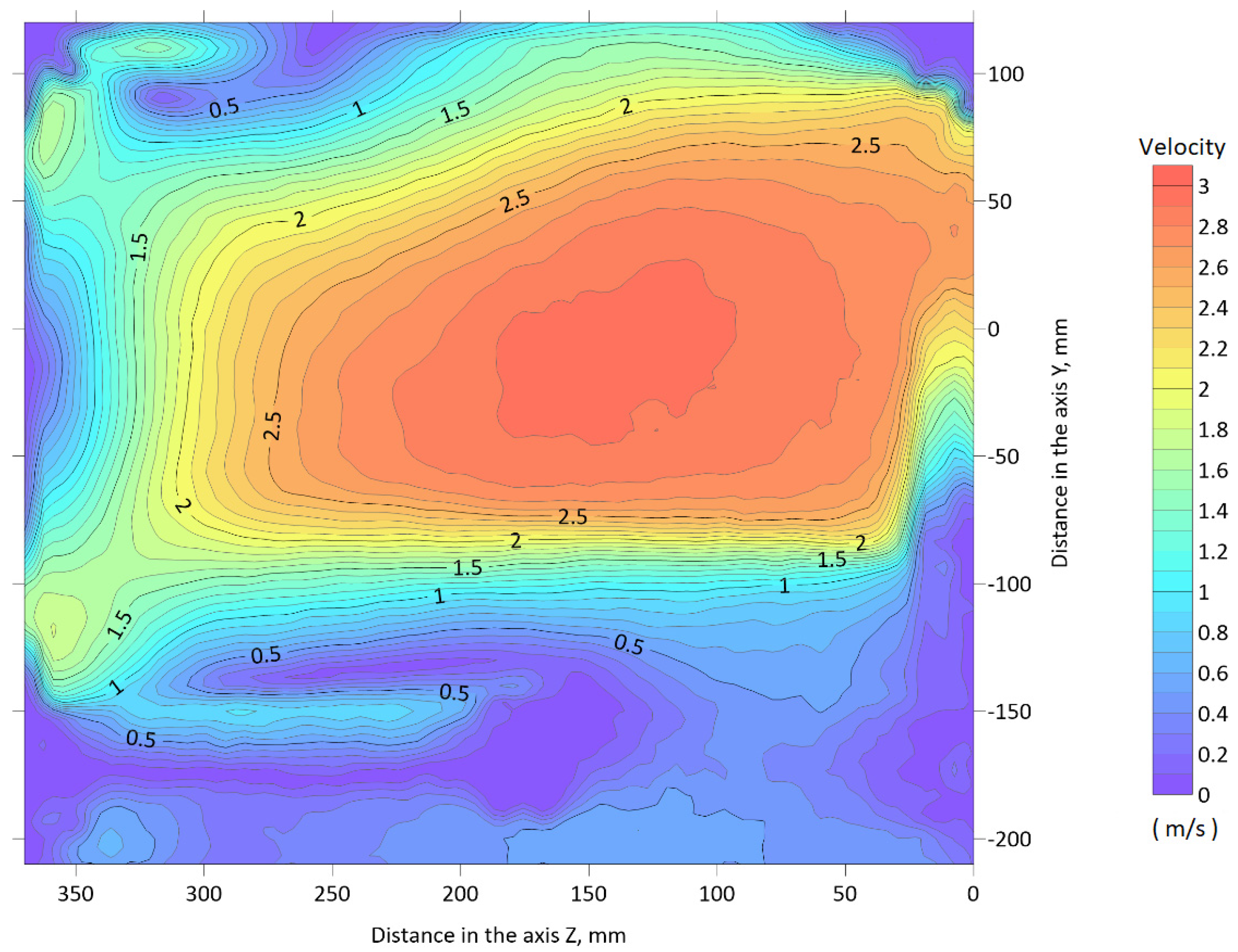
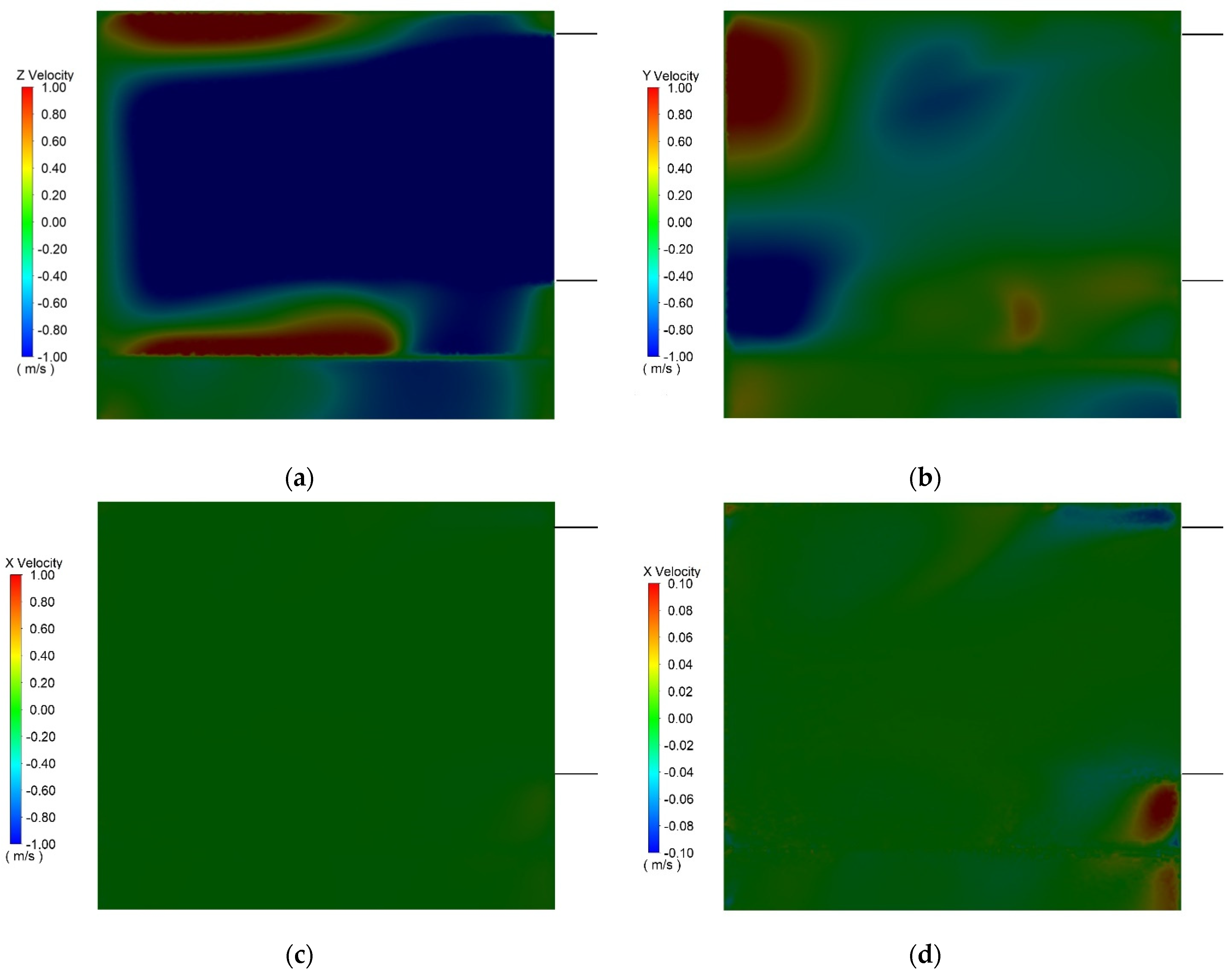
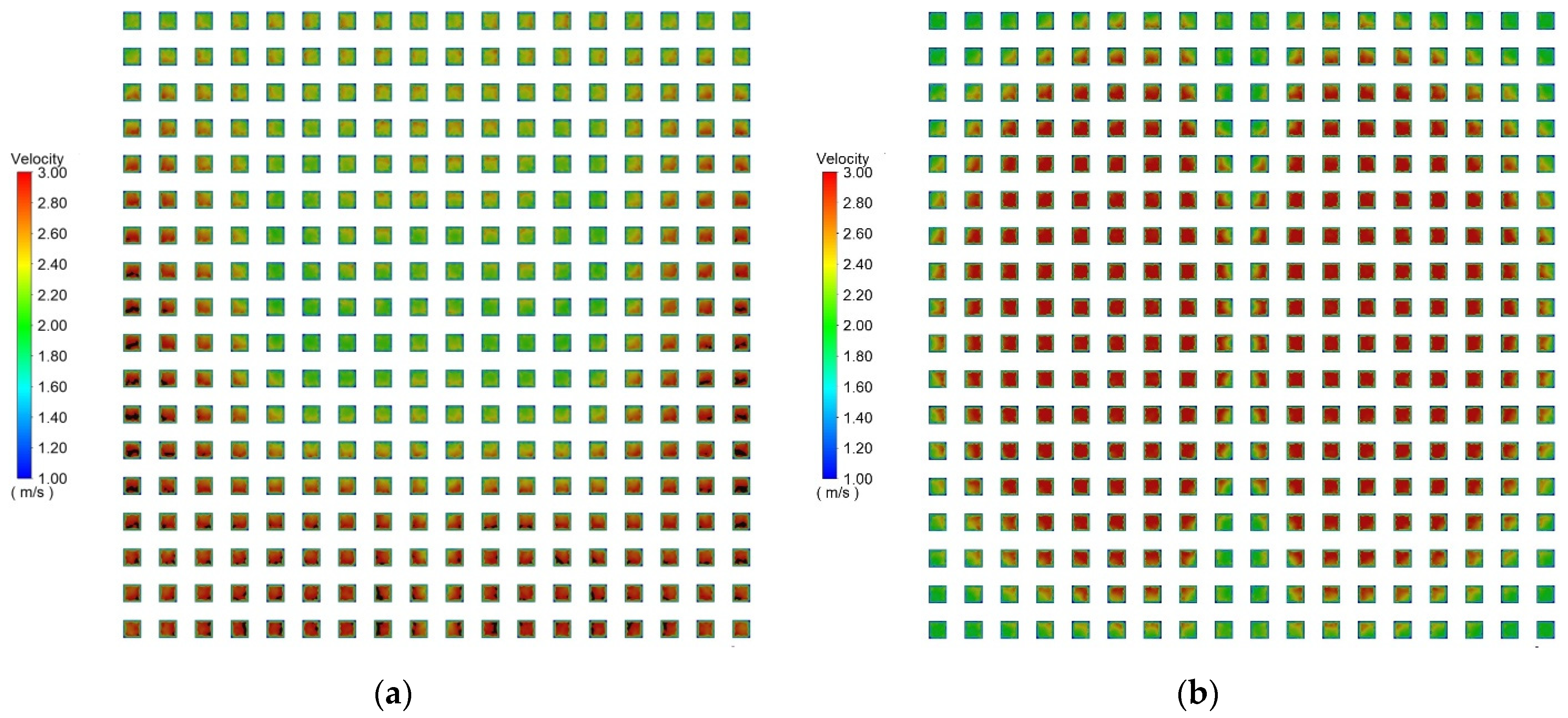
3.1. Experimental Results
3.2. Numerical Analyses
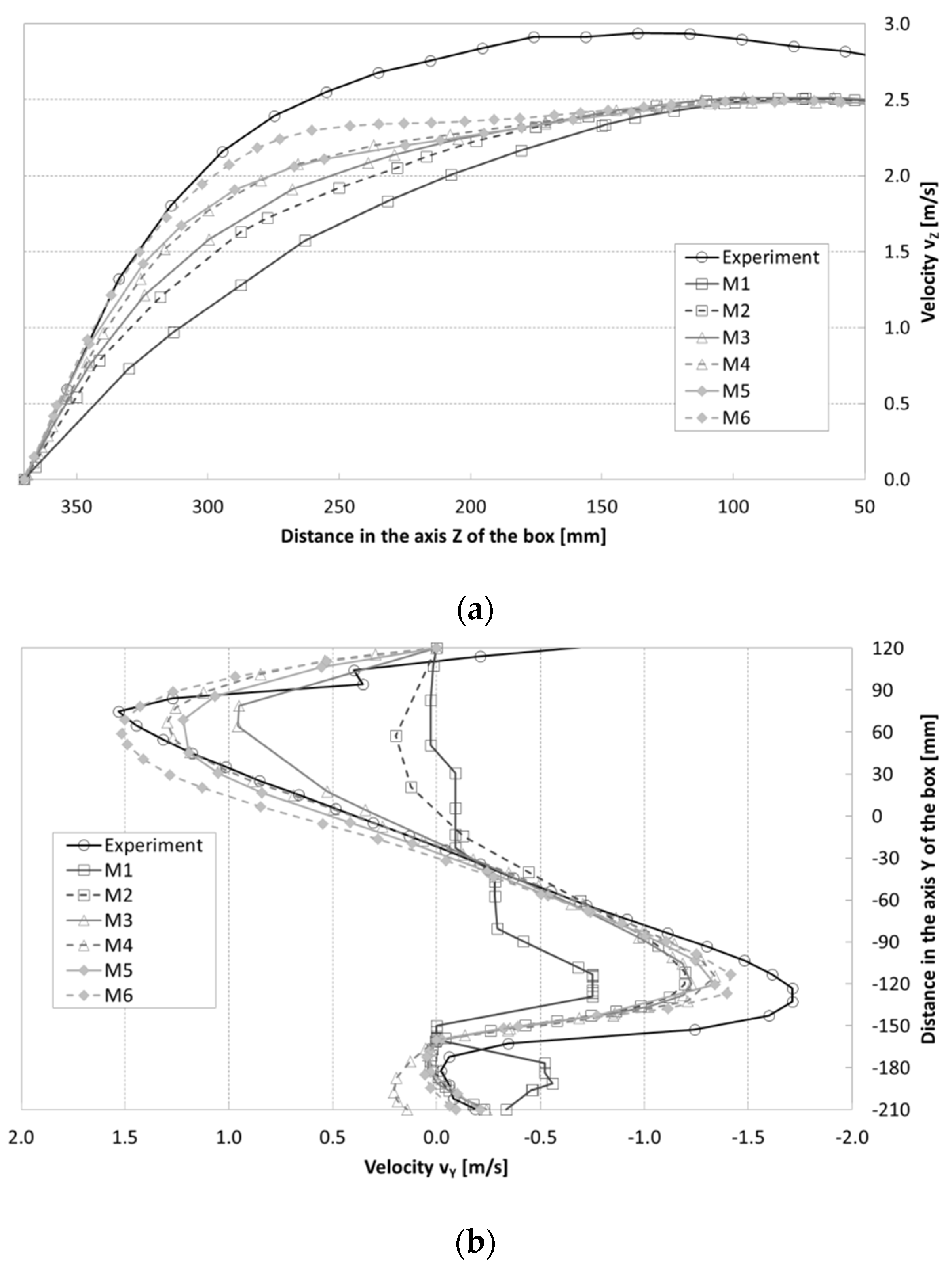
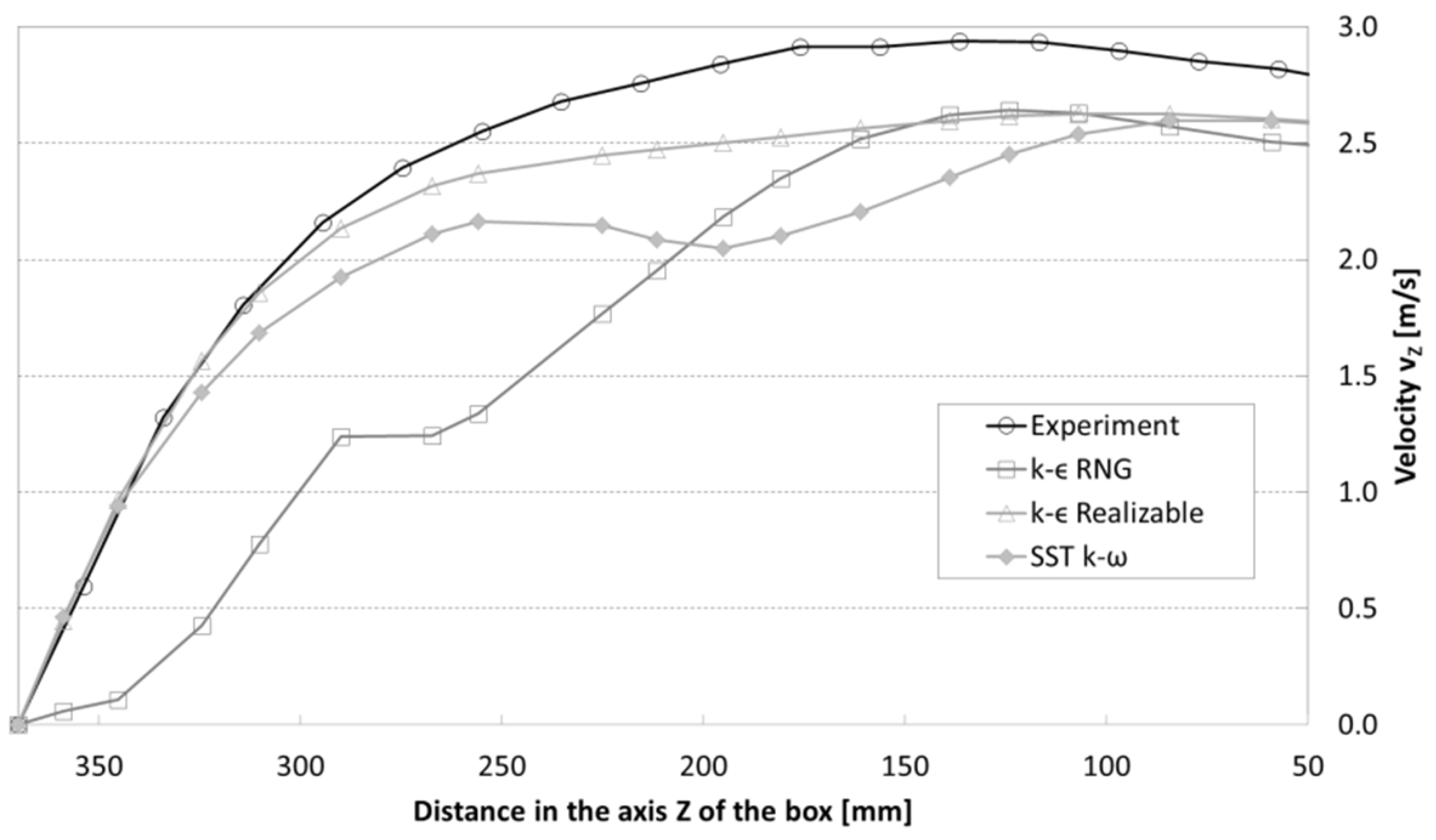
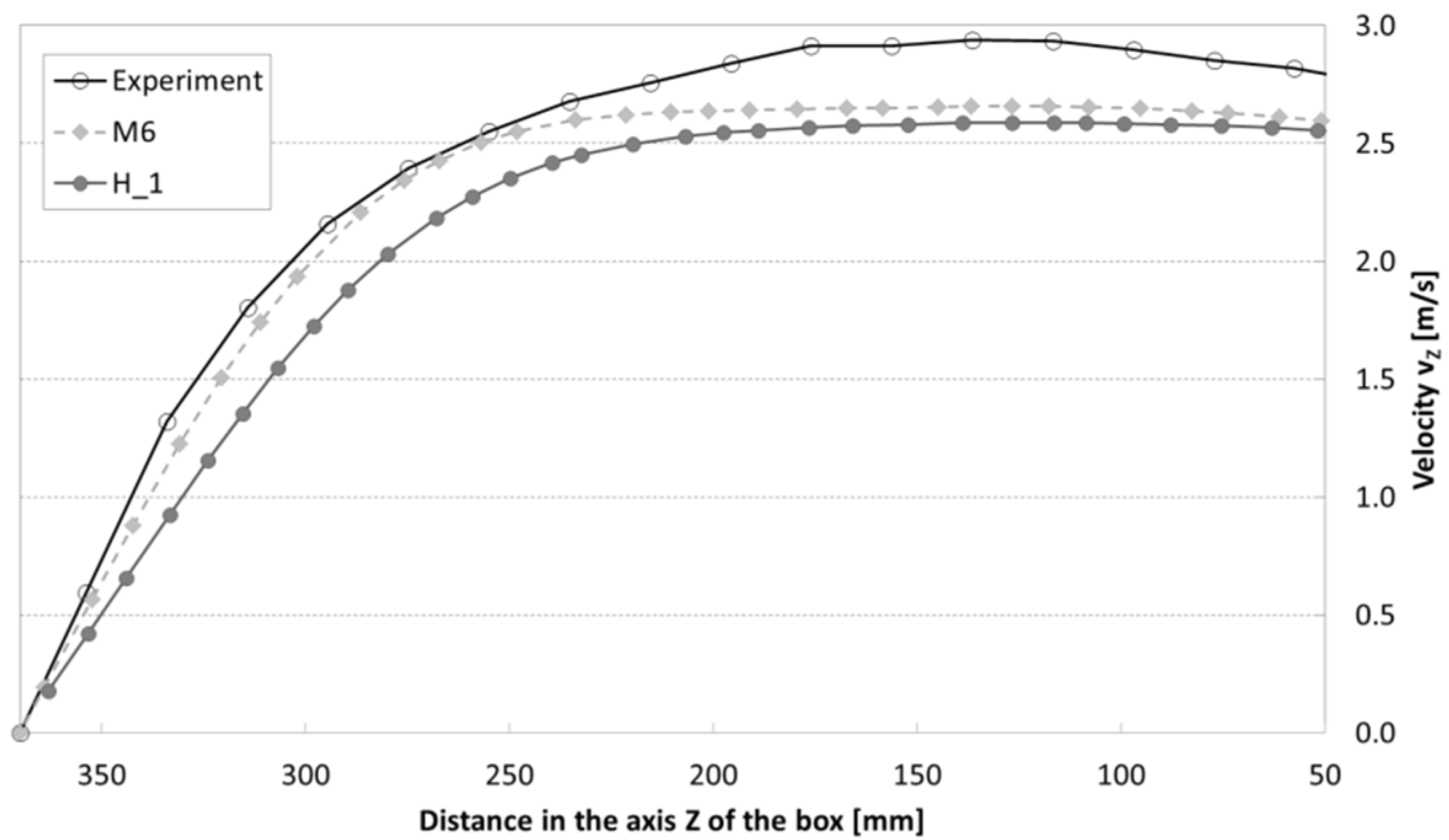
3.2.1. Verification of Computational Models
3.2.2. Comparative Analysis for Plenum Box with Side and Top Entry
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ANSI/ASHRAE. Thermal Environmental Conditions for Human Occupancy. In Refrigerating and Air-Conditioning Engineers; Standard 55 2017; American Society of Heating: Atlanta, GA, USA, 2017. [Google Scholar]
- ISO 7730. EN ISO 7730: 2005 Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria; International Standardisation Organisation: Geneve, Switzerland, 2005. [Google Scholar]
- Jones, W.P. Air Conditioning Engineering, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2001; pp. 80–103. [Google Scholar]
- Khalil, E.E. Air Distribution in Buildings; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–20. [Google Scholar]
- Navvab, M. HVAC ventylation strategies: The contribution for thermal comfort, energy efficiency, and indoor air quality. Green Build. 2007, 2, 131–150. [Google Scholar] [CrossRef]
- American Society of Heating Refrigerating and Air-Conditioning Engineers, Inc. ASHRAE Handbook—Heating, Ventilating, and Air-Conditioning Applications, SI ed.; American Society of Heating Refrigerating and Air-Conditioning Engineers, Inc.: Washington, DC, USA, 2015. [Google Scholar]
- Li, A.; Yang, C.; Ren, T.; Bao, X.; Qin, E.; Gao, R. PIV experiment and evaluation of air flow performance of swirl diffuser mounted on the floor. Energy Build. 2017, 156, 58–69. [Google Scholar] [CrossRef]
- Hurnik, M.; Kaczmarczyk, J.; Popiolek, Z. Study of Radial Wall Jets from Ceiling Diffusers at Variable Air Volume. Energies 2021, 14, 240. [Google Scholar] [CrossRef]
- Jaszczur, M.; Madejski, P.; Kleszcz, S.; Zych, M.; Palej, P. Numerical and experimental analysis of the air stream generated by square ceiling diffusers. E3S Web Conf. 2019, 128, 08003. [Google Scholar] [CrossRef]
- Szczepanik-Scislo, N.; Antonowicz, A.; Scislo, L. PIV measurement and CFD simulations of an air terminal device with a dynamically adapting geometry. SN Appl. Sci. 2019, 1, 370. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Lin, Z. An experimental and numerical study on the effect of air terminal types on the performance of stratum ventilation. Build. Environ. 2014, 82, 431–441. [Google Scholar] [CrossRef]
- Martinez-Almansa, J.J.; Fernandez-Gutierrez, A.; Parras, L.; del Pino, C. Numerical and experimental study of a HVAC wall diffuser. Build. Environ. 2014, 80, 1–10. [Google Scholar] [CrossRef]
- Nocente, A.; Arslan, T.; Grynning, S.; Goia, F. CFD Study of Diffuse Ceiling Ventilation through Perforated Ceiling Panels. Energies 2020, 13, 1995. [Google Scholar] [CrossRef]
- Jaszczur, M.; Madejski, P.; Borowski, M.; Karch, M. Experimental analysis of the air stream generated by square ceiling diffusers to reduce energy consumption and improve thermal comfort. Heat Transfer. Eng. 2021. [Google Scholar] [CrossRef]
- Aziz, M.A.; Gad, I.A.M.; Mohammed, E.S.F.A.; Mohammed, R.H. Experimental and numerical study of influence of air ceiling diffusers on room air flow characteristics. Energy Build. 2012, 55, 738–746. [Google Scholar] [CrossRef]
- Chen, Q.; Srebric, J. Simplified Diffuser Boundary Conditions for Numerical Room Airflow Models; Final Report for ASHRAE RP-1009; ASHRAE: Atlanta, GA, USA, 2000; pp. 96–107. [Google Scholar]
- Shakerin, S.; Miller, P. Experimental study of Vortex Diffusers. ASHRAE Trans. 1996, 102, 340–346. [Google Scholar]
- Borowski, M.; Jaszczur, M.; Branny, M.; Karch, M. Experimental analysis of the velocity field of the air flowing through the swirl diffusers. In Proceedings of the 7th European Thermal-Sciences Conference, Kraków, Poland, 19–23 June 2016. [Google Scholar]
- Borowski, M.; Karch, M.; Łuczak, R.; Życzkowski, P.; Jaszczur, M. Numerical and experimental analysis of the velocity field of air flowing through swirl diffusers. E3S Web Conf. 2019, 128, 05003. [Google Scholar] [CrossRef]
- Sajadi, B.; Saidi, M.H.; Mohebbian, A. Numerical investigation of the swirling air diffuser: Parametric study and optimization. Energy Build. 2011, 43, 1329–1333. [Google Scholar] [CrossRef]
- Hongze, R.; Bin, Z.; Xianting, L.; Hongming, F.; Xudong, Y. Influence of Diffuser Jet Characteristics on Indoor Air Distribution under Actual Connecting conditions. J. Archit. Eng. 2003, 9, 141–144. [Google Scholar]
- Villafruela, J.M.; Sierra-Pallares, J.B.; Castro, F.; Álvaro, A.; Santiago-Casado, P. Experimental and numerical study of the influence of the plenum box on the airflow pattern generated by a swirl air diffuser. Exp. Therm. Fluid Sci. 2018, 99, 547–557. [Google Scholar] [CrossRef] [Green Version]
- Smoljan, D.; Balen, I. Influence of a Plenum Box Design on Uniformity of the Radial Air Jet Issuing from a Vortex Diffuser. Strojarstvo 2010, 52, 379–386. [Google Scholar]
- Vasic, M.; Stevanovic, V.D.; Zivkovic, B. Uniformity of air flow from the ceiling diffuser by an advanced design of the equalizing element in the plenum box with side entry. Sci. Technol. Built Environ. 2020, 26, 676–686. [Google Scholar] [CrossRef]
- Product Manual for DaVis 7.2; La Vision GmbH: Gottingen, Germany, 2011.
- Abdulwahab, M.R.; Ali, H.Y.; Habeeb, F.J.; Borhana, A.A.; Abdelrhman, A.M.; Al-Obaidi, S.M.A. A review in particle image velocimetry techniques (developments and applications). J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 65, 213–229. [Google Scholar]
- Ferziger, J.H. Large Eddy Simulation. In Simulation and Modeling of Turbulent Flows; Gatski, T.B., Hussaini, M.Y., Lumley, J.L., Eds.; Oxford University Press: New York, NY, USA, 1996; pp. 109–116. [Google Scholar]
- Gunzburger, M.D. Navier-Stokes equations for incompressible flows: Finite-element methods. In Handbook of Computational Fluid Mechanics; Peyret, R., Ed.; Academic Press: London, UK, 1996; pp. 28–35. [Google Scholar]
- Argyropoulosa, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2001; pp. 358–385. [Google Scholar]






| Sign | Number of Cells | Plenum Box | Entourage |
|---|---|---|---|
| M1 | 65,948 | Body size 0.100 m | Body size 0.100 m |
| M2 | 423,068 | Body size 0.050 m, face size on the cross bar 0.002 m | Body size 0.050 m |
| M3 | 966,655 | Body size 0.025 m, face size on the cross bar 0.002 m | Body size 0.025 m |
| M4 | 5,081,680 | Body size 0.025 m, face size on the cross bar and wall 0.002 m | Body size 0.025 m |
| M5 | 1,285,344 | Body size 0.010 m, face size on the cross bar 0.002 m, and wall 0.005 m | Body size 0.025 m |
| M6 | 3,679,285 | Body size 0.005 m, face size on the cross bar 0.002 m, and wall 0.005 m | Body size 0.025 m |
| Parameter | Selection |
|---|---|
| Solver | Pressure based Steady-state simulations |
| Fluid material | Air, Viscosity 1.7894−5 kg/(m∙s), Density 1.225 kg/m3 |
| Solution Methods | Scheme: SIMPLE Gradient: least squares cell-based Pressure: second order Momentum: second order |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halibart, J.; Zwolińska, K.; Borowski, M.; Jaszczur, M. Analysis of the Velocity Distribution in the Plenum Box with Various Entries. Energies 2021, 14, 3630. https://doi.org/10.3390/en14123630
Halibart J, Zwolińska K, Borowski M, Jaszczur M. Analysis of the Velocity Distribution in the Plenum Box with Various Entries. Energies. 2021; 14(12):3630. https://doi.org/10.3390/en14123630
Chicago/Turabian StyleHalibart, Joanna, Klaudia Zwolińska, Marek Borowski, and Marek Jaszczur. 2021. "Analysis of the Velocity Distribution in the Plenum Box with Various Entries" Energies 14, no. 12: 3630. https://doi.org/10.3390/en14123630
APA StyleHalibart, J., Zwolińska, K., Borowski, M., & Jaszczur, M. (2021). Analysis of the Velocity Distribution in the Plenum Box with Various Entries. Energies, 14(12), 3630. https://doi.org/10.3390/en14123630