A Mathematical Model for the Analysis of Jet Engine Fuel Consumption during Aircraft Cruise

Abstract

In this paper we propose a mathematical model for the fuel consumption analysis during aircraft cruise. A closed-form formula that expresses the aircraft’s weight variation over time, and hence, the fuel flow rate, is obtained as a result. Furthermore, a closed-form expression of the aircraft’s main performance parameters is also obtained. We compare the values of such parameters computed by using the Piano-X software and computed by using our mathematical model. Simulation results confirm that our mathematical model provides results very close to reality. Finally, the closed-form formula of the fuel flow rate provided by our model is used to improve the calculation of the carbon dioxide emissions for four example routes, which, unlike here, are usually obtained under the assumption of a constant value of the fuel flow rate.

1. Introduction

Flight dynamics is a discipline that studies the performance of an aircraft flying. Among other topics, it studies the influence of aerodynamic, propulsive and gravitational forces on an aircraft. One of its main purposes is to provide mathematical models of the aircraft’s state variables as a function of time during the different flight phases, with applications such as fuel consumption analysis.

Fuel consumption has been a critical issue of aircraft design and performance since the early days of modern aviation. Flight planning is concerned with the estimation of the trip fuel required for a certain mission profile and the fulfillment of the standards established by safety and regulatory agencies (EASA, FAA, ICAO, etc.), along with the requirements of Air Traffic Control (ATC) in order to guarantee the optimal and safest route to the destination airport. The mission profile is defined for a specific distance and payload, and the fuel required for each of the mission’s segments is usually estimated through iterative computational procedures which depend on the aircraft’s take-off weight, performance characteristics and atmospheric conditions ([1], pp. 411–419). Common methods for the fuel economy analysis of an aircraft include the study of parameters such as fuel burn and fuel efficiency per seat, both of them determined by the interior configuration of the aircraft and the trip distance. As an example, the Boeing 767-300ER has an average fuel burn of 5.51 kg/km and a fuel efficiency of 2.56 L/100 km per passenger for a trip distance of 3000 nautical miles (nmi) and a 269-passenger configuration [2].

In general terms, the usefulness of such parameters relies in their effectiveness on estimating fuel costs for a certain aircraft type and route. These estimations serve as indices that reflect if fuel saving strategies are being implemented successfully. Since modern air transport has been, and remains, a continuously growing industry, it has brought with it a great concern about fuel combustion emissions and climate change. Consequently, the safety and regulatory agencies have developed strict standards regarding this matter, encouraging airlines around the globe to improve their fuel saving strategies and, hence, search for more efficient ways to mitigate atmospheric pollution. As of 2019, jet fuel combustion in the aviation industry amounted to 915 million tons of CO${}_2$, corresponding to a 2% of all human-induced CO${}_2$ emissions and a 12% of the general transport emissions [3].

Airlines are continuously faced with the need of finding an equilibrium point between their operational costs associated to the fuel saving strategies and the developing climate policies. Engine manufacturers give special aid in this matter, since they seek to design and adapt more fuel-efficient engines, helping airlines reduce both operational costs and greenhouse gas emissions.

Several known software modules and manuals are widely used in the field for aircraft preliminary design, stability and control and mission performance analysis (PIANO, ACSYNT, FLOPS, DATCOM, BADA, ESDU) [4] (pp. 9–10). Regarding mission performance analysis, this software is based either on the numerical resolution of the differential equations of motion or on the application of energy balance methods for each flight phase. Since early stages, the refinement of such software has enabled very accurate simulations of aircraft performance. In addition, previous studies have been carried out with the objective of analyzing the aircraft’s fuel consumption during the different flight phases by means of energy balance methods [5,6] (pp. 11–15), or statistical models [7,8,9,10,11,12,13]. Other recent studies such as [14,15,16] propose some frameworks in which aircraft performance models (which are based on some of the abovementioned softwares), fleet data sets and route data sets are integrated into unique tools where statistical techniques such as regression analysis are applied in order to estimate fuel consumption and emissions during the different flight phases and at a global scale. In addition, aircraft emission inventories have been developed throughout the years based on historical fuel burn data [17,18,19] or on other methodologies [20] and enhanced by a more accurate estimation of the pollutant emission indices [21].

However, the numerical solution of the differential equations of motion, energy balance methods and statistical models, although being very reliable, do not provide a complete understanding of the performance of the physical system described by the differential equations of motion. Obtaining closed-form (non-numerical) solutions of the differential equations of motion is very difficult in general. However, such a closed-form solution would instead enable a complete understanding of the system since it allows identifying the critical variables of the model and how they influence the system. Closed-form formulae not only provide the possibility of applying analytical (ideal) optimization techniques but also the knowledge of the fundamental limits of such optimization problem, that is, what is possible to achieve and what is not.

The focus of this study is the fuel consumption of a jet engine aircraft during the cruising flight phase. This phase is the dominant flight phase both in duration and in fuel consumption.

Specifically, in this paper, a closed-form formula for the aircraft’s weight as a function of time during the cruising flight phase is presented. To obtain such formula, the equations of motion for this flight phase are considered along with the fuel consumption relationship. The formula obtained in this paper is a closed-form solution of a certain differential equation.

The resolution of this problem opens a wide range of possible applications such as:

• Calculation of pollutant emissions (carbon dioxide (CO${}_2$), hydrocarbons (HC), nitrogen oxides (NO${}_x$) and similar) by means of the aircraft’s fuel flow rate closed-form formula and validated emissions indices.
• Knowing the fuel fraction that has been invested during the cruising flight phase and the aircraft’s weight at any moment in time.
• Knowing the closed-form formula of the relationship between the aircraft’s weight and the engine’s fuel consumption.
• Performance analysis with different types of jet fuel.
• Optimal aircraft selection for a certain route in terms of fuel consumption.
• Optimal engine selection for a certain aircraft type and route in terms of fuel consumption.

In this paper, we focus on the first application, that is, we calculate the pollutant emissions by means of the closed-form formula of the aircraft’s fuel flow rate. Such emissions, unlike here, are usually obtained under the assumption of a constant value of the fuel flow rate.

The rest of the paper is organized as follows: Section 2 states the problem. Section 3 presents the closed-form formulae for both the aircraft’s weight as a function of time and the aircraft’s fuel flow rate. Section 4 compares the values of the aircraft’s main performance parameters provided by our mathematical model and by the Piano-X software. Section 5 is dedicated to the application of the mathematical model for the calculation of carbon dioxide (CO${}_2$) emissions for four example routes. Finally, Section 6 concludes the paper, giving some insight on future work.

2. Problem Statement

The physical system under consideration resembles that of a modern jet engine aircraft during the cruising flight phase. We seek to address the analysis of fuel consumption for such physical system. To that end, we combine the fuel consumption relationship along with the equations of motion and the aerodynamic expressions of lift, drag and drag polar of the aircraft during the cruising flight phase. These equations can be considered under the following flight configurations, as stated by [4] (pp. 342–343):

(a)

Constant altitude and Mach number.

(b)

Constant altitude and lift coefficient.

(c)

Constant Mach number and lift coefficient.

In this paper, we propose the mathematical model for flight configuration (a), that is, cruise at constant altitude and Mach number.

The following assumptions are made in order to obtain the mathematical model:

(1)

The aircraft is considered a variable-mass system: fuel is being consumed along time and weight varies consequently.

(2)

Fuel consumption is only considered for the aircraft’s engines and under ideal conditions, i.e., engines consume equal fuel quantity and their degradation effects are not taken into account.

(3)

Static atmosphere and ideal gas conditions enable thermodynamic parameters such as pressure, temperature and air density to be expressed only as a function of altitude.

(4)

Regarding aircraft flight mechanics:

• The aircraft is considered as a physical system that follows a rectilinear trajectory contained in a horizontal plane, meaning that its velocity vector remains constant both in magnitude and direction.
• A vertical mass symmetry plane exists along the longitudinal axis and all the interacting forces are contained in the same plane, including the aircraft’s velocity vector.
• Wind effects are not taken into account.

(5)

Regarding the aircraft performance parameters:

• The thrust specific fuel consumption (TSFC) is considered a constant parameter [22], since the flight configuration studied implies constant altitude and Mach number, and the parabolic drag polar approach is employed.

As it will be shown later in Section 4, despite the assumptions made, the results provided by our mathematical model turn out to be very close to the results given by the Piano-X software. Since the Piano-X software results are proven to be close to reality, we will conclude that our mathematical model also provides results close to reality.

Equations for the Mathematical Model

The aircraft’s total weight $W\left(t\right)$ is presented as a sum of a fixed and a time-varying term, as established by [23] (p. 406):

$$W\left(t\right)=W_0+W_f\left(t\right),$$

(1)

where the fixed term $W_0$ includes, in the general case, the operating empty and payload weights. The time-varying term $W_f\left(t\right)$ refers to the fuel weight, which is the fuel mass $m_f\left(t\right)$ multiplied by the gravitational acceleration g, i.e., $W_f\left(t\right)=m_f\left(t\right)g$.

Fuel mass variation, also known as fuel flow rate, is described by the fuel consumption relationship for a jet engine aircraft [24] (p. 29):

$$\frac{d{m}_f}{dt}=-c_{j}F\left(t\right),$$

(2)

being $d{m}_f/dt$ the fuel flow rate, $c_j$ the thrust specific fuel consumption and $F\left(t\right)$ the aircraft’s thrust. Hence, a direct relationship can be obtained between Equations (1) and (2), taking the time derivative of (1)

$$\frac{dW}{dt}=\frac{d{m}_f}{dt}g=-c_{j}F\left(t\right)g.$$

(3)

The objective of this study is to determine whether it is possible to integrate, and thereby find a closed-form solution of Equation (3), under the constraints established by the equations of motion of the cruising flight phase.

It is known from [25] (pp. 178–180) that the equations of motion for the flight configuration considered can be reduced to the following expressions

$$W\left(t\right)=L\left(t\right)$$

(4)

$$F\left(t\right)=D\left(t\right)$$

(5)

where the aerodynamic forces, lift ($L\left(t\right)$) and drag ($D\left(t\right)$), are defined by

$$L\left(t\right)=qA{c}_L\left(t\right)$$

(6)

$$D\left(t\right)=qA{c}_D\left(t\right)$$

(7)

being q the dynamic pressure defined as $q=(1/2)\rho v^2$, in which $\rho$ is the density of air and v the aircraft’s true airspeed. The total wing area A is a known geometric parameter, $c_L\left(t\right)$ is the lift coefficient and the drag coefficient $c_D\left(t\right)$ is defined through the parabolic drag polar

$$c_D\left(t\right)=c_{D,0}+k{c}_L{\left(t\right)}^2$$

(8)

where $c_{D,0}>0$ is the zero-lift drag coefficient and $k>0$ is the induced drag factor. The latter is a function of the Oswald efficiency factor e and the aircraft’s aspect ratio $AR$, i.e., $k=1/\left(\pi ARe\right)$, and the aspect ratio is defined as the squared term of the aircraft’s wingspan $b^2$ divided by A.

3. Closed-Form Solution of the Fuel Consumption for the Cruising Flight Phase

In the following section we derive the closed-form expression of the aircraft’s weight as a function of time with $t\in [0,t_{cr}]$, where $t=0$ and $t=t_{cr}$ are the initial and final time instants of the cruising flight phase, respectively.

From (5) and (7) we have

$$F\left(t\right)=qA{c}_D\left(t\right).$$

By combining (4), (6) and (8) we obtain

$$c_D\left(t\right)=c_{D,0}+k{\left(\frac{W\left(t\right)}{qA}\right)}^2,$$

(9)

and hence

$$F\left(t\right)=qA{c}_{D,0}+\frac{k}{qA}{\left(W\left(t\right)\right)}^2.$$

(10)

Equation (10) expresses the aircraft’s thrust as a function of weight. Therefore, the following differential equation is obtained from (3)

$$\frac{dW}{dt}=-c_{j}g\left(qA{c}_{D,0}+\frac{k}{qA}{\left(W\left(t\right)\right)}^2\right)=k_1+k_2{\left(W\left(t\right)\right)}^2$$

(11)

where $k_1$, $k_2$ are constant parameters defined as

$$\begin{array}{ccc}\hfill k_1=-c_{j}gqA{c}_{D,0}& \hfill & \hfill k_2=-c_{j}g\frac{k}{qA}.\end{array}$$

(12)

Observe that, $k_1\ne 0$ and $k_2/k_1>0$.

Integrating (11) leads to

$$\int \frac{W^{\prime }\left(t\right)dt}{1+(k_2/k_1){\left(W\left(t\right)\right)}^2}=k_1\int dt$$

whose solution is given by

$$\sqrt{\frac{k_1}{k_2}}arctan\left(\sqrt{\frac{k_2}{k_1}}W\left(t\right)\right)=k_{1}t+C$$

(13)

where C is an arbitrary constant.

Reordering terms

$$arctan\left(\sqrt{\frac{k_2}{k_1}}W\left(t\right)\right)=k_1\sqrt{\frac{k_2}{k_1}}t+C^{\prime }.$$

(14)

Since $W\left(0\right)$ is the initial cruise weight,

$$C^{\prime }=arctan\left(\sqrt{\frac{k_2}{k_1}}W\left(0\right)\right),$$

(15)

we obtain the implicit formula

$$arctan\left(\sqrt{\frac{k_2}{k_1}}W\left(t\right)\right)-arctan\left(\sqrt{\frac{k_2}{k_1}}W\left(0\right)\right)=k_1\sqrt{\frac{k_2}{k_1}}t.$$

(16)

Applying the rule of a tangent of a sum (see, e.g., [26] (p. 59)), Equation (16) can be written as

$$\frac{\sqrt{k_2/k_1}\left(W\left(t\right)-W\left(0\right)\right)}{1+(k_2/k_1)W\left(t\right)W\left(0\right)}=tan\left(k_1\sqrt{\frac{k_2}{k_1}}t\right),$$

(17)

or equivalently,

$$W\left(t\right)\left(\sqrt{\frac{k_2}{k_1}}-\frac{k_2}{k_1}W\left(0\right)tan\left(k_1\sqrt{\frac{k_2}{k_1}}t\right)\right)=W\left(0\right)\sqrt{\frac{k_2}{k_1}}+tan\left(k_1\sqrt{\frac{k_2}{k_1}}t\right).$$

(18)

Let

$$\beta =W\left(0\right)\sqrt{\frac{k_2}{k_1}}=\frac{W\left(0\right)}{qA}\sqrt{\frac{k}{c_{D,0}}}.$$

(19)

Combining Equations (12), (18) and (19) yields the explicit formula

$$W\left(t\right)=W\left(0\right)\frac{1-(1/\beta )tan\left(c_{j}g\sqrt{c_{D,0}k}t\right)}{1+\beta tan\left(c_{j}g\sqrt{c_{D,0}k}t\right)}.$$

(20)

Equation (20) provides the sought closed-form expression of the aircraft’s weight as a function of time.

From (2) and (10) we obtain

$$\frac{d{m}_f}{dt}=-c_{j}qA{c}_{D,0}\left(1+{\left(\frac{W\left(t\right)}{qA}\sqrt{\frac{k}{c_{D,0}}}\right)}^2\right)=-c_{j}qA{c}_{D,0}\left(1+{\left(\frac{W\left(t\right)}{W\left(0\right)}\beta \right)}^2\right).$$

(21)

Substituting (20) in (21) brings

$$\frac{d{m}_f}{dt}=-c_{j}qA{c}_{D,0}\frac{(1+{\beta }^2)(1+{tan}^2\left(c_{j}g\sqrt{c_{D,0}k}t\right))}{{(1+\beta tan\left(c_{j}g\sqrt{c_{D,0}k}t\right))}^2}.$$

(22)

Equation (22) represents the closed-form formula of the aircraft’s fuel flow rate, which enables further optimization and sensibility analyses in order to evaluate the dependence on aerodynamic and engine parameters, with the objective of reaching a more efficient aircraft performance. Note that the negative sign means that fuel is consumed in $t\in [0,t_{cr}]$.

4. Example Case: Validation and Discussion

The objective of this section is the validation of our mathematical model for the jet engine aircraft performance during the cruising flight phase. We compare the values of the aircraft main performance parameters computed by using Piano-X Aircraft Emissions and Performance software [27] and our mathematical model. One of the Piano-X’s freely available database aircraft models is used. An example route is taken for the aforementioned aircraft model from FlightRadar24 [28], where the chosen route has a range of 2145 nautical miles (nmi) and a cruise altitude ($h_{cr}$) of 10,668 meters (m), i.e., flight level 350 (FL350).

Table 1. Table of input data.

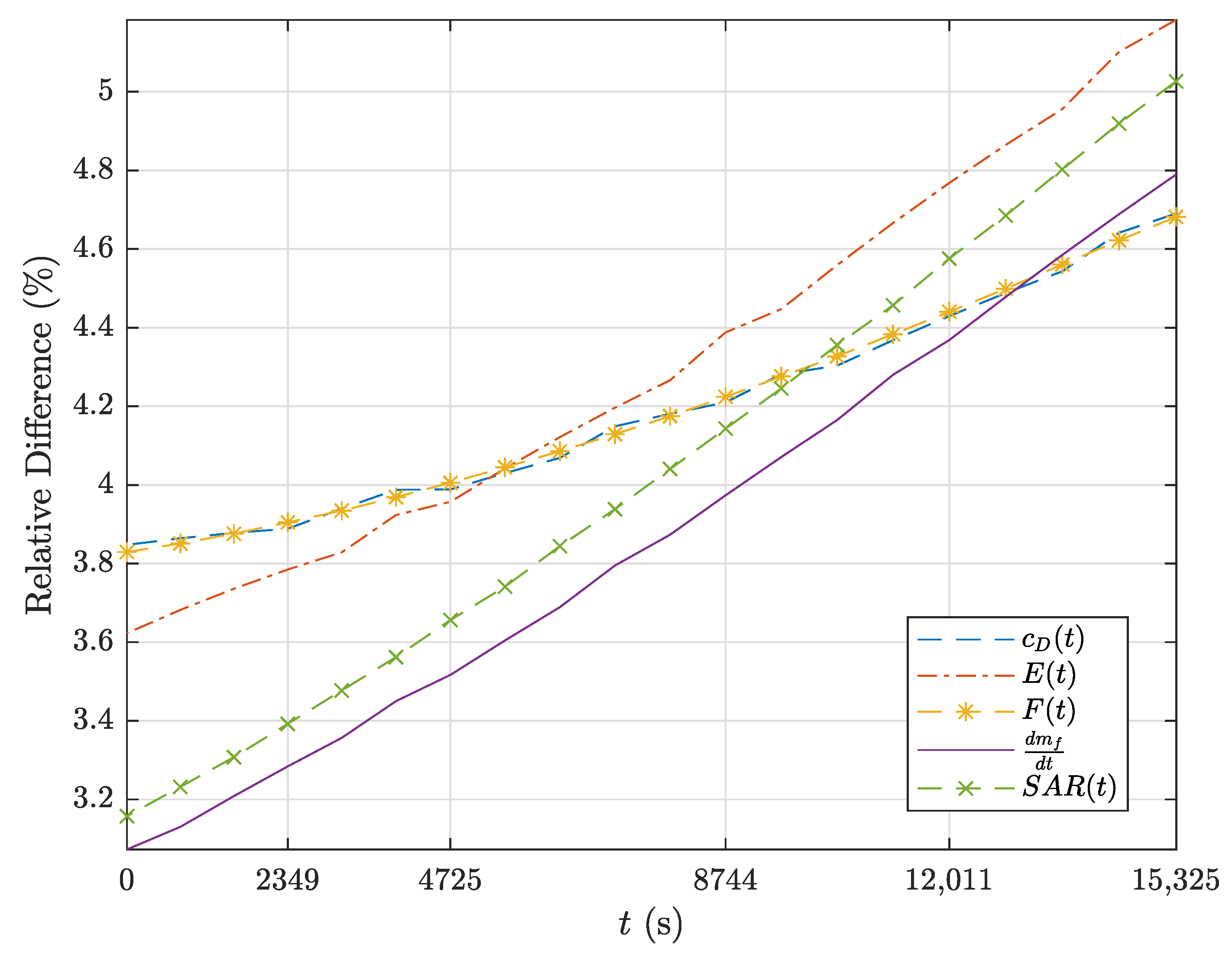
Aircraft Model	Range (nmi)	${\mathit{M}}_{\mathit{c}\mathit{r}}$ (-)	${\mathit{h}}_{\mathit{c}\mathit{r}}$ (FL)	${\mathit{W}}_0$ (N)	${\mathit{t}}_{\mathit{c}\mathit{r}}$ (s)	${\mathit{m}}_{\mathit{f}}\left(0\right)$ (kg)
B767-300ER	2145	0.8	350	1,045,232	15,325	22,227

$M_{cr}$ is the cruise Mach number, defined as $v_{cr}/a_{cr}$, being $v_{cr}$ the aircraft’s true airspeed at cruise and $a_{cr}$ the speed of sound at the cruising altitude.

presents a summary of the parameters for the considered example flight. In Appendix A, we provide further details on the particular configuration used in Piano-X,

Table 2. Performance parameters computed by using Piano-X and our mathematical model.

t (s)	Performance Parameter	Mathematical Model	Piano-X	Relative Difference
$t=0$	$W\left(t\right)·{10}^6$ (N)	1.26049	1.26049	0%
	$c_L\left(t\right)$ (-)	0.4164	0.418	0.3659%
	$c_D\left(t\right)$ (-)	0.02135	0.02221	3.84%
	$E\left(t\right)$ (-)	19.5	18.82	3.62%
	$F\left(t\right)$ (N)	64,634	67,208	3.83%
	$d{m}_f/dt$ (kg/s)	1.12	1.15	3.07%
	$SAR\left(t\right)$ (nmi/kg)	0.1143	0.1108	3.15%
$t=2349$	$W\left(t\right)·{10}^6$ (N)	1.23495	1.23410	0.07%
	$c_L\left(t\right)$ (-)	0.408	0.409	0.23%
	$c_D\left(t\right)$ (-)	0.02105	0.02191	3.88%
	$E\left(t\right)$ (-)	19.37	18.67	3.78%
	$F\left(t\right)$ (N)	63,734	66,324	3.9%
	$d{m}_f/dt$ (kg/s)	1.10	1.14	3.28%
	$SAR\left(t\right)$ (nmi/kg)	0.1159	0.1121	3.4%
$t=4725$	$W\left(t\right)·{10}^6$ (N)	1.20947	1.20771	0.14%
	$c_L\left(t\right)$ (-)	0.3996	0.4	0.0965%
	$c_D\left(t\right)$ (-)	0.02076	0.02163	3.98%
	$E\left(t\right)$ (-)	19.24	18.51	3.95%
	$F\left(t\right)$ (N)	62,854	65,477	4%
	$d{m}_f/dt$ (kg/s)	1.09	1.13	3.51%
	$SAR\left(t\right)$ (nmi/kg)	0.1175	0.1134	3.65%
$t=8744$	$W\left(t\right)·{10}^6$ (N)	1.16715	1.16372	0.3%
	$c_L\left(t\right)$ (-)	0.3856	0.3860	0.0953%
	$c_D\left(t\right)$ (-)	0.0203	0.02119	4.2%
	$E\left(t\right)$ (-)	18.9	18.2	4.38%
	$F\left(t\right)$ (N)	61,433	64,143	4.2%
	$d{m}_f/dt$ (kg/s)	1.06	1.10	3.97%
	$SAR\left(t\right)$ (nmi/kg)	0.1202	0.1154	4.14%
t = 12,011	$W\left(t\right)·{10}^6$ (N)	1.13345	1.12854	0.43%
	$c_L\left(t\right)$ (-)	0.3745	0.3740	0.13%
	$c_D\left(t\right)$ (-)	0.01993	0.02086	4.43%
	$E\left(t\right)$ (-)	18.78	17.93	4.76%
	$F\left(t\right)$ (N)	60,338	63,142	4.4%
	$d{m}_f/dt$ (kg/s)	1.04	1.09	4.36%
	$SAR\left(t\right)$ (nmi/kg)	0.1224	0.1170	4.57%
t = 15,325	$W\left(t\right)·{10}^6$ (N)	1.09988	1.09335	0.6%
	$c_L\left(t\right)$ (-)	0.3634	0.362	0.38%
	$c_D\left(t\right)$ (-)	0.01958	0.02055	4.7%
	$E\left(t\right)$ (-)	18.55	17.64	5.18%
	$F\left(t\right)$ (N)	59,279	62,191	4.68%
	$d{m}_f/dt$ (kg/s)	1.02	1.08	4.79%
	$SAR\left(t\right)$ (nmi/kg)	0.1246	0.11867	5.02%

presents the values of the aircraft’s main performance parameters when they are computed using Piano-X or using our mathematical model. These parameters are the aircraft’s weight ($W\left(t\right)$), lift coefficient ($c_L\left(t\right)$), drag coefficient ($c_D\left(t\right)$), lift-to-drag ratio ($E\left(t\right)$), thrust ($F\left(t\right)$), fuel flow rate ($d{m}_f/dt$) and specific air range ($SAR\left(t\right)$), where,

$$E\left(t\right)=\frac{L\left(t\right)}{D\left(t\right)},SAR\left(t\right)=\frac{v_{cr}}{d{m}_f/dt}.$$

Necessary data from the Boeing 767-300ER was retrieved from [29,30].

It is interesting to note that at time instant $t_{cr}=$ 15,325 s of the cruising flight phase, that is, after 4 h and 15 min, the greatest relative difference values amid the performance parameters are between 4.7% and 5.02%. From this, one can conclude that, despite the assumptions made to obtain our mathematical model, its results are very close to the results provided by the Piano-X software. Since the Piano-X software results are proven to be close to reality, we conclude that our mathematical model also provides results close to reality.

In fact, considering the assumptions made in Section 2, it can be intuited that the difference between the values provided by our mathematical model and the values provided by Piano-X values arise from two main sources:

(a)

We have assumed the thrust specific fuel consumption to be constant, but it actually varies simultaneously with the aircraft’s thrust.

(b)

For the drag polar presented in Equation (8), we only included the zero-lift drag coefficient and the induced drag coefficient. Other phenomena such as the compressibility and trim effects need to be considered.

Figure 1 shows the evolution of the relative difference over the cruising time for the performance parameters considered in Table 2. It can be noticed that, although having an initial relative difference at $t=0$ s, the increase of this relative difference for the analyzed parameters from $t=0$ s to $t_{cr}$ = 15,325 s is relatively small. For the drag coefficient ($c_D\left(t\right)$), this increase corresponds to 0.84%, for the lift-to-drag coefficient ($E\left(t\right)$) the increase is of 1.56%; the aircraft’s thrust ($F\left(t\right)$) has a 0.85% increase, followed by a 1.71% from the fuel flow rate ($d{m}_f/dt$) and finally, the specific air range ($SAR\left(t\right)$) presents the highest increase with a 1.87%. Note that the aircraft’s weight ($W\left(t\right)$) and the lift coefficient ($c_L\left(t\right)$) were not included in Figure 1 due to their low relative difference.

The estimation of the fuel consumed during the total cruising time is presented in Figure 2. It is important to observe how the relative difference between both values increases from $t=0$ s until $t_{cr}$ = 15,325 s, reaching its maximum value at the latter. The result given by Piano-X at $t=t_{cr}$ is 17,115 kg, whereas the result given by our mathematical model at $t=t_{cr}$ is 16,435 kg. This means that the maximum relative difference in the fuel consumption calculation is 3.8%.

We conclude that our mathematical model turns out to be not only a useful tool for the fuel consumption calculation but also a comprehensive tool for the performance analysis of a jet engine aircraft during the cruising flight phase.

5. Application: Pollutant Emissions Calculation

In this section we use our mathematical model to obtain a closed-form expression for the amount of pollutant emissions of an aircraft during cruising time. Knowing the emitted pollutants during the cruising flight phase, along with its associated cost index, would enable the estimation of the Green Direct Operating Cost (GDOC), as proposed by [31]. Observe that in [31], unlike here, the calculation of the GDOC is based on a constant value of the fuel flow rate. Considering such parameter as a fixed value entails a loss of accuracy in the calculation of the pollutant mass emitted. Hence, we propose a closed-form expression, based on Equations (1) and (20), that provides a more accurate value of the pollutant mass emitted. This closed-form expression is as follows,

$$\begin{array}{cc}\hfill p_i& =E{I}_i{\int }_0^{t_{cr}}\left(-\frac{d{m}_f}{dt}\right)dt=E{I}_i[m_f\left(0\right)-m_f\left(t_{cr}\right)]\hfill \\ \hfill & =E{I}_i\frac{W\left(0\right)}{g}\left(1-\frac{1-(1/\beta )tan\left(c_{j}g\sqrt{c_{D,0}k}{t}_{cr}\right)}{1+\beta tan\left(c_{j}g\sqrt{c_{D,0}k}{t}_{cr}\right)}\right),\hfill \end{array}$$

where $p_i$ is the total emitted pollutant mass, $E{I}_i$ the emission index and i the chemical component analyzed.

The closed-form expression given in Equation (22) of the fuel flow rate for an aircraft during the cruising flight phase also provides the closed-form formula for the engine fuel flow rate proposed in [32] (p. 5). Hence, it would help tools like the Boeing Fuel Flow Method2 (BFFM2) in addressing the estimation of emissions indices for pollutants such as nitrogen oxides (NO${}_x$) and carbon monoxide (CO) at different cruising altitudes.

We next present an example where the emissions calculation procedure takes place as follows: in the first place, we observe four example routes for the selected aircraft model in the FlightRadar24 platform in order to obtain the range and the number of cruise segments for each route. The information collected from each of the cruise segments are the cruising altitude ($h_{cr}$) and its respective time duration ($t_{cr}$). The latter information is taken as input data, along with the emission index for CO${}_2$, which is of 3159 [31]. The emission index has units of grams of pollutant per kilograms of fuel burned, i.e., g/kg.

The example route data and the total CO${}_2$ emissions results are presented in

Table 3. Carbon dioxide emissions for four example routes.

Route	${\mathit{n}}_{\mathit{c}\mathit{r}}$	${\mathit{h}}_{\mathit{c}\mathit{r}}$	${\mathit{t}}_{\mathit{c}\mathit{r}}$ (s)	${\mathit{m}}_{\mathit{f}}\left(0\right)-{\mathit{m}}_{\mathit{f}}\left({\mathit{t}}_{\mathit{c}\mathit{r}}\right)$ (kg)	${\mathit{p}}_{{\mathbf{CO}}_2}$ (kg)
A	1	FL350	11,280	12,566	39,696
B	2	FL310	3000	3632	11,473
		FL370	9600	10,220	32,285
C	3	FL360	2040	2435	7692
		FL370	9180	10,444	32,992
		FL390	8160	8620	27,230
D	4	FL340	3240	4063	12,835
		FL360	3540	4272	13,495
		FL370	9540	10,914	34,477
		FL390	6660	7073	22,343

, where the following parameters appear: route designation, number of cruise segments ($n_{cr}$), cruise altitude for each segment ($h_{cr}$), cruise time duration for each segment ($t_{cr}$), the total fuel consumed ($m_f\left(0\right)-m_f\left(t_{cr}\right)$) and the respective pollutant mass emissions ($p_i$). We assume that for each of the cruise segments, the aircraft has a constant Mach number of 0.8 and the thrust specific fuel consumption is calculated with the formula proposed by [33] (p. 75). For the example routes with more than one cruise segment, i.e., $n_{cr}\ge 2$, the fuel consumed during the stepped cruise phase, that is, the transition from one cruise flight level to another, is neglected. We also assume that 11% of the total fuel load has been consumed during the taxi-out, take-off and climbing phases.

6. Conclusions and Future Work

From the mathematical model of flight configuration (a) presented in Section 2, the aircraft’s weight is expressed as a function of time by means of a closed-form formula. Consequently, a closed-form formula for the aircraft’s fuel flow rate is obtained. The latter represents a formula based on elementary functions in which critical performance and design parameters appear. Such parameters are the thrust specific fuel consumption ($c_j$), zero-lift drag coefficient ($c_{D,0}$), induced drag factor (k), dynamic pressure (q) and the wing area (A).

It is interesting to observe that, besides the dependency of the fuel flow rate on performance and design parameters, the same closed-form formula exhibits a dependency on the aircraft’s weight. Meaning that a same aircraft type, flying the same route, may not have the same cruise fuel consumption, since the latter depends on how much payload and fuel weight the aircraft has prior to take-off and how much fuel is burned in the flight phases prior to the cruising flight phase, i.e., taxi-out, take-off and climbing.

In order to validate our mathematical model, an example route was chosen. The calculation during the cruising flight phase of the aircraft’s weight ($W\left(t\right)$), the lift ($c_L\left(t\right)$) and drag ($c_D\left(t\right)$) coefficients, lift-to-drag ratio ($E\left(t\right)$), aircraft’s thrust ($F\left(t\right)$), fuel flow rate ($d{m}_f/dt$), specific air range ($SAR\left(t\right)$) and total fuel consumed ($m_f\left(0\right)-m_f\left(t\right)$) are computed with our model and are contrasted with the results provided by the Piano-X software. The relative difference obtained for all of the above performance parameters is very low. Since the Piano-X software results are proven to be close to reality, we conclude that our mathematical model also provides results close to reality.

As an application, our closed-form formula was used to obtain a closed-form expression for the pollutant emissions during the cruising flight phase. Our closed-form formula is of great aid as an estimation of pollutant emissions since it can provide an accurate prediction just by knowing the aircraft’s initial weight, its performance and design parameters and the cruise flight segments.

Finally, further research will be focused on developing a mathematical model for the aircraft’s fuel consumption during cruise in flight configuration (b), that is, constant altitude and constant lift coefficient. Other flight phases such as take-off and climbing will also be addressed in order to obtain a closed-form formula of the aircraft’s weight variation over time for the analysis of the fuel consumption and the aircraft performance.