The Effect of Ceiling Heating and Mechanical Ventilation on Thermal Comfort
Abstract
:1. Introduction
- -
- If PPD < 6%, radiant temperature asymmetry varies in an interval of 5–15 °C and draught rate is DR = 15% or DR = 25%, then are AMV and PMV values the same or are they significantly different?
- -
- If the value of the AMV is different, is it lower or higher than the PMV?
- -
- If the PMV value is constant, does the change in radiant temperature asymmetry relevantly influence the AMV value?
- -
- If the AMV changes with the radiant temperature asymmetry, to what extent does it change?
- -
- By increasing the draught rate from DR = 15% to DR = 25%: is the AMV value effected significantly?
2. Methods
2.1. Methodology
- -
- Determining the surface temperature of the delimiting surfaces—this step allows the desired radiant temperature asymmetry to be set;
- -
- Specifying the temperature of the inlet air—the temperature and the volume of the inlet air ensure the thermally stationary state of the measuring chamber; at the same time, both of them influence the forecast draught rate;
- -
- Fine-tuning of the the air flow in the measuring chamber, with the aim of identifying and maintaining the desired draught rate.
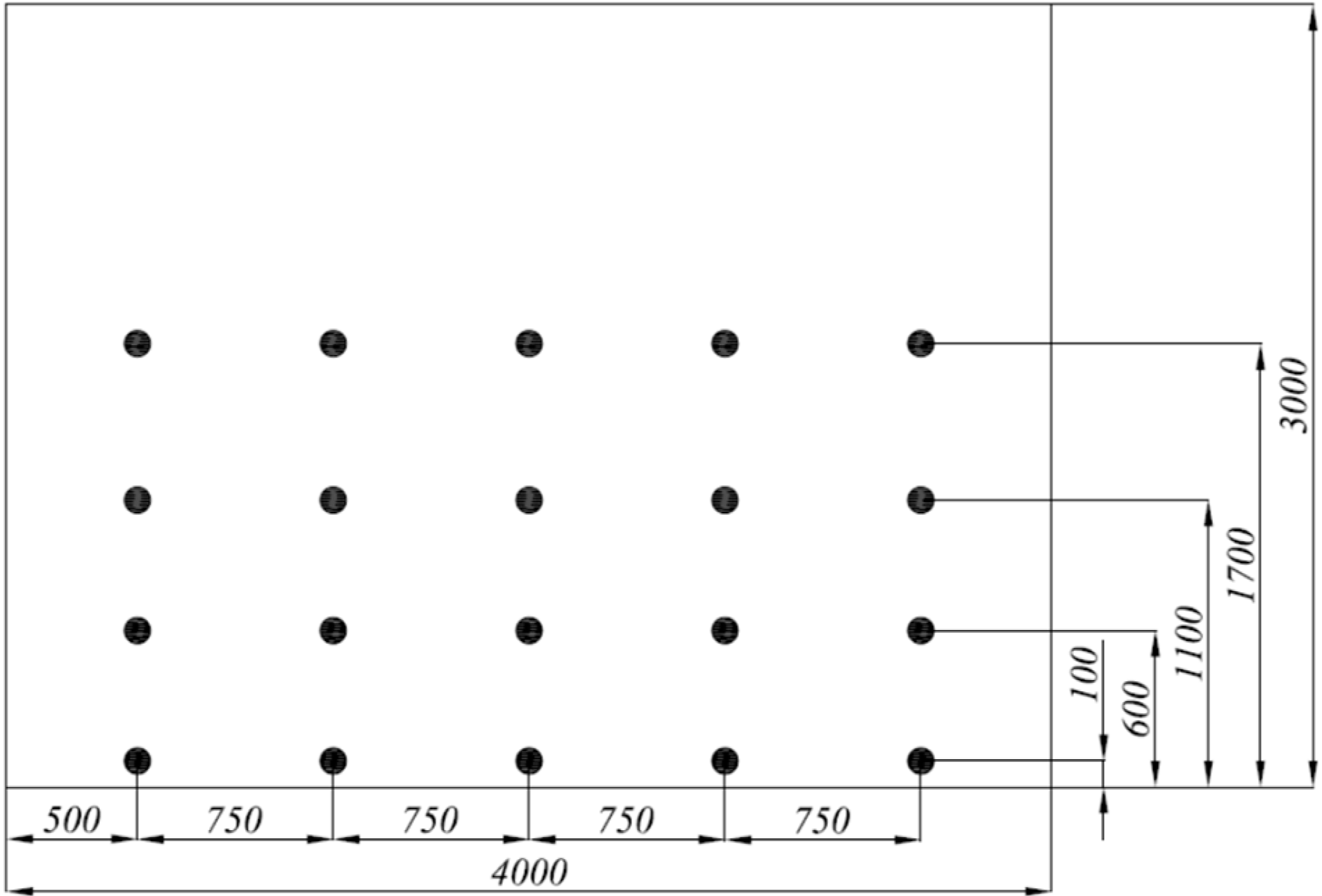
2.2. Human Subject Measurements
- -
- radiant temperature asymmetry: 5 °C, 7 °C, 10 °C 12 °C, 15 °C;
- -
- draught rate: 15% and 25%.
2.3. Methodology of Evaluation
- H0: sub>0: The expected values of X and Y random variable are equal;
- H1: The expected values of X and Y random variable are not equal [30].
- H0: sub>0: F1 = F2;
- H1: F1≠F2. [31].
3. Results
- -
- AMV as a function of radiant temperature asymmetry, in women, DR = 15% draught rate;
- -
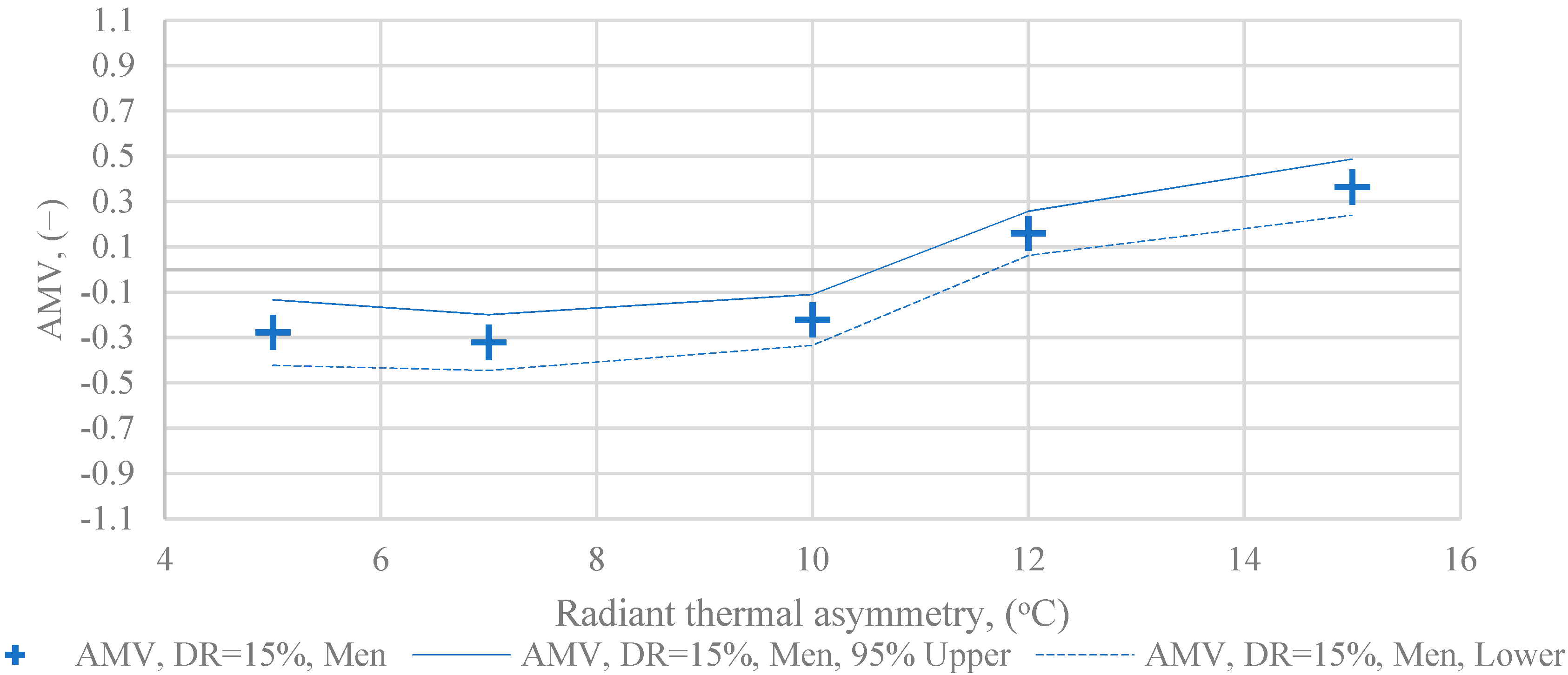
- AMV as a function of radiant temperature asymmetry, in men, with DR = 15% draught rate;
- -
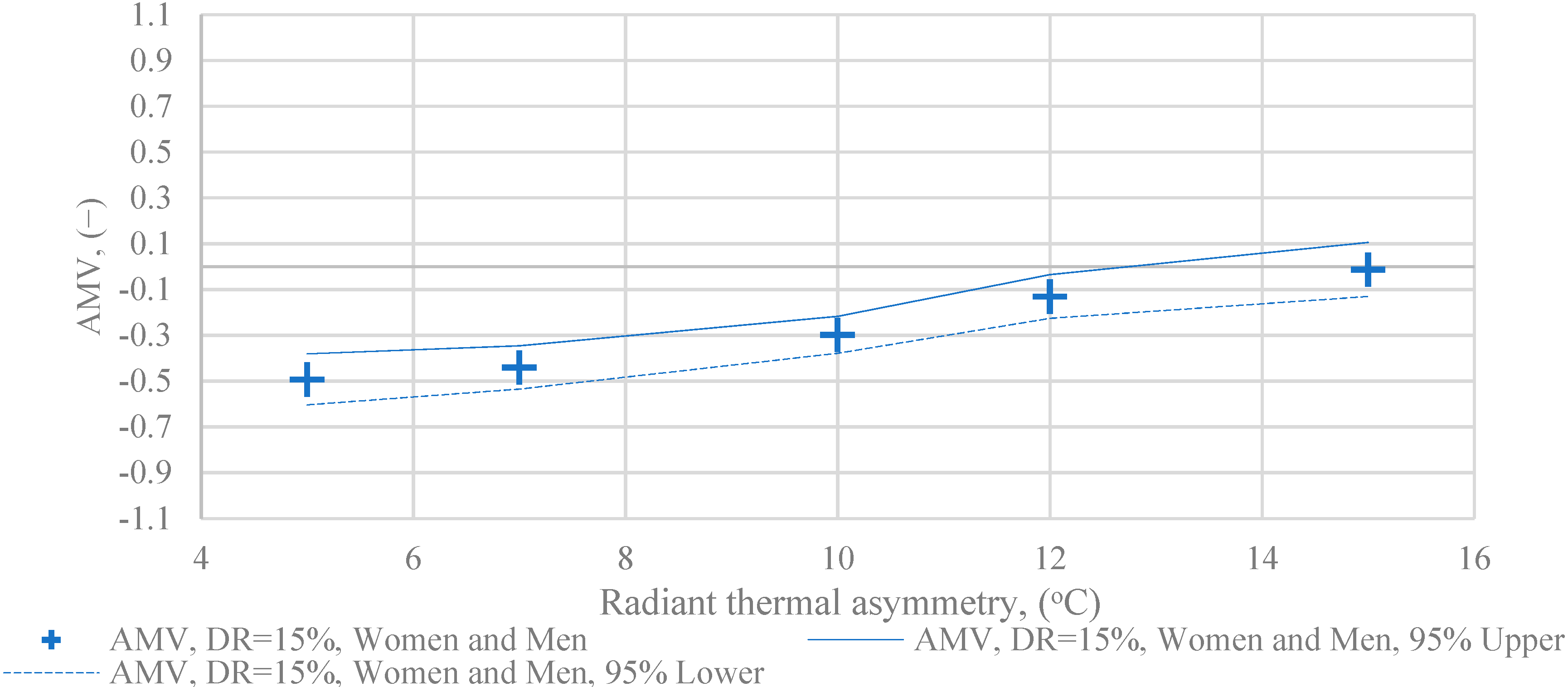
- AMV as a function of radiant temperature asymmetry, for women and men, with DR = 15% draught rate;
- -
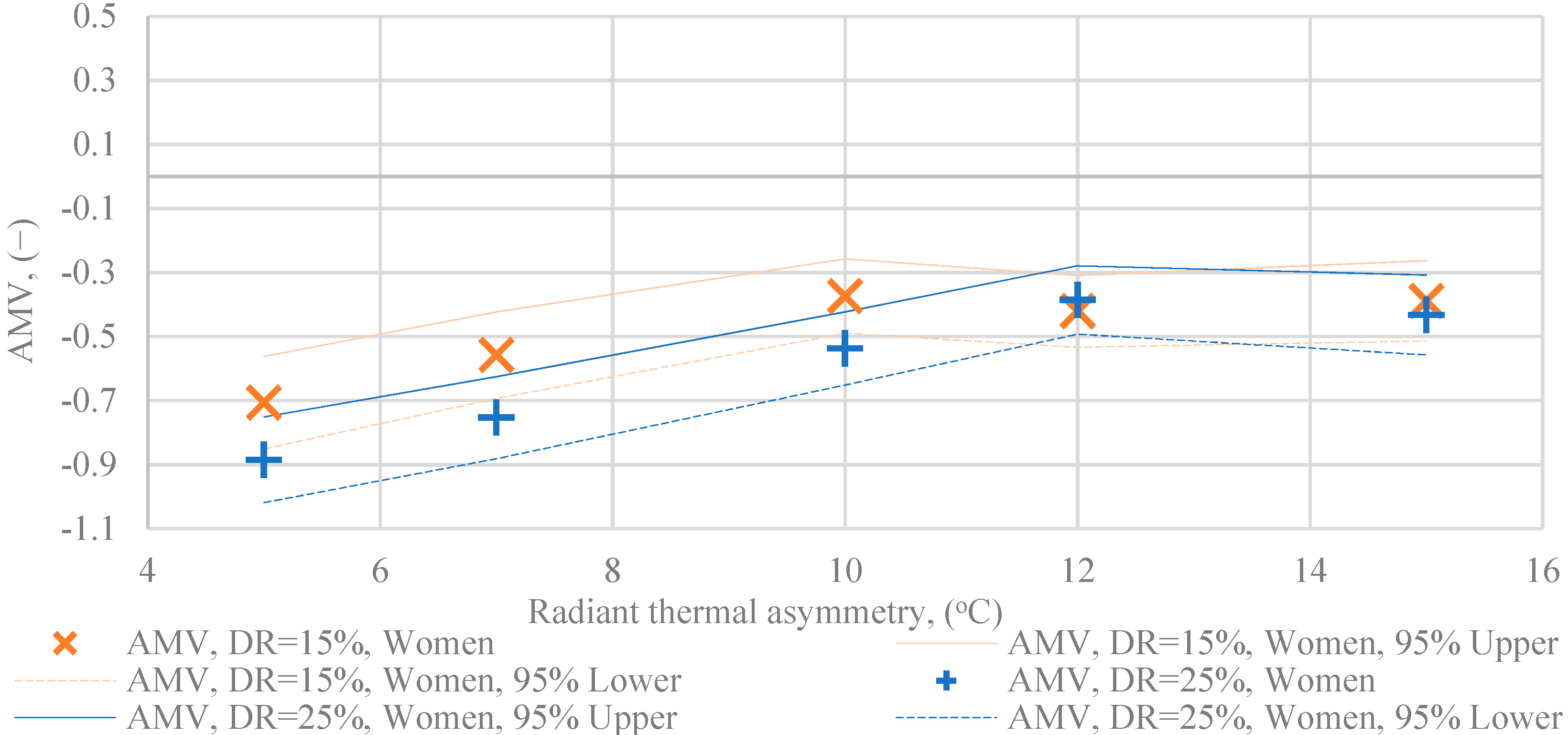
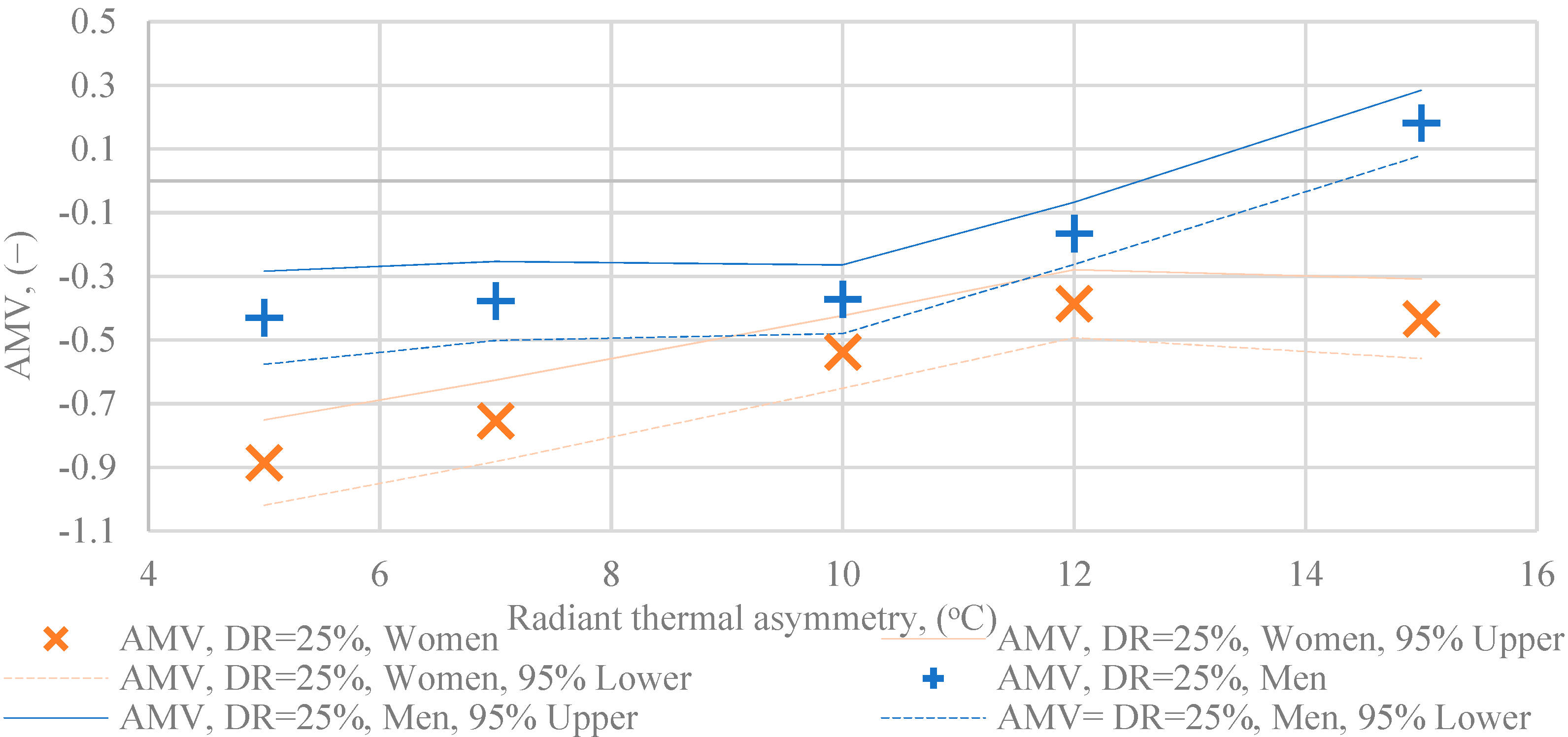
- AMV as a function of radiant temperature asymmetry, in women, DR = 25% draught rate;
- -
- AMV as a function of radiant temperature asymmetry, in men, DR = 25% draught rate;
- -
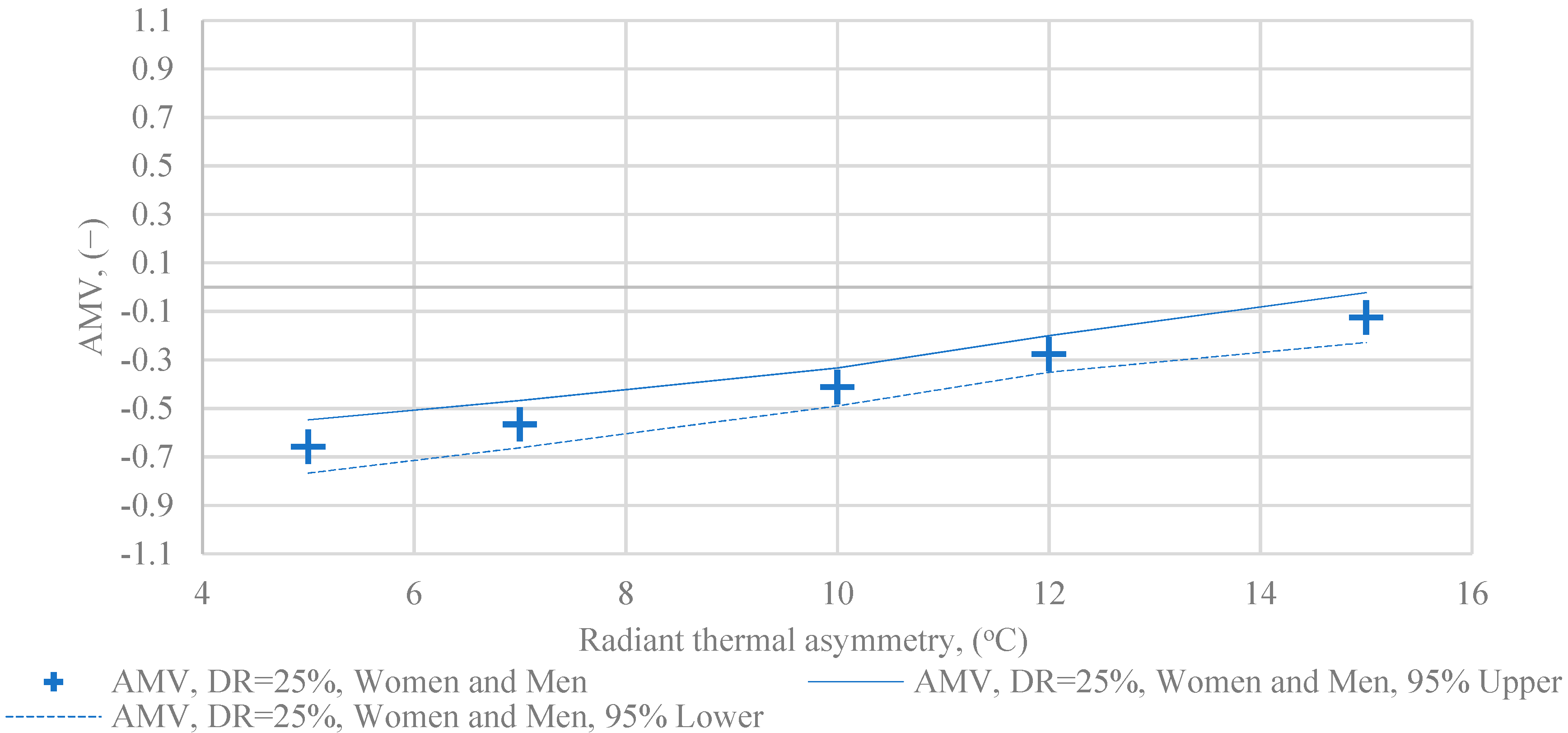
- AMV as a function of radiant temperature asymmetry, for women and men, with DR = 25% draught rate;
4. Discussion
4.1. Evaluation of the Results
- -
- the effect of the increase in draught on the AMV value in the interval between 5–15 °C;
- -
- a description of the differences between women’s and men’s votes;
- -
- change in AMV with increasing the radiant temperature asymmetry.
- -
- in all cases, the value of the AMV differs significantly from the value of the PMV;
- -
- at DR = 15%, if all votes are taken into account: the AMV value surges alongside with the increase of the radiation temperature asymmetry, remaining below 0 for the whole interval;
- -
- at DR = 15%, considering women´s votes: the AMV value increases with increasing radiation temperature asymmetry, remaining below 0 for the entire interval;
- -
- at DR = 15%, considering the votes of men: the AMV value is constant in the range of 5–10 °C; then it increases, reaching a positive value at 15 °C asymmetry
- -
- the trends are similar also at a draught effect of DR = 25%.
4.2. Usability of the Results
5. Conclusions
- -
- if PPD < 6%, the radiant temperature asymmetry varies in the range of 5–15 °C and the draught is DR = 15% or DR = 25%, then the AMV and PMV values are significantly different;
- -
- the AMV value is lower in all cases, with the exception of male votes DR = 15%, AS = 12 and 15 °C, and DR = 25%, AS = 15 °C;
- -
- for an approximately constant PMV value, a change in radiant temperature asymmetry significantly affects the AMV value;
- -
- when considering the votes of all human subjects: increasing DR = 15% to DR = 25% has a significant effect on AMV;
- -
- there is a significant difference between the women’s and men’s AMV votes in both DR = 15% and DR = 25%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Meaning | Dimension |
| AMV | Actual Mean Vote | - |
| DR | Draught rate | % |
| f | Degrees of freedom | - |
| F1 | Distribution function—first sample | - |
| F2 | Distribution function—second sample | - |
| H0 | Null hypothesis | - |
| H1 | Alternative hypothesis | - |
| m | First sample size | - |
| n | Second sample size | - |
| PMV | Predicted Mean Vote | - |
| PPD | Predicted Percentage of Dissatisfied | % |
| sx | Standard deviation of the first sample | Variable |
| sy | Standard deviation of the second sample | Variable |
| Tu | Turbulence intensity | % |
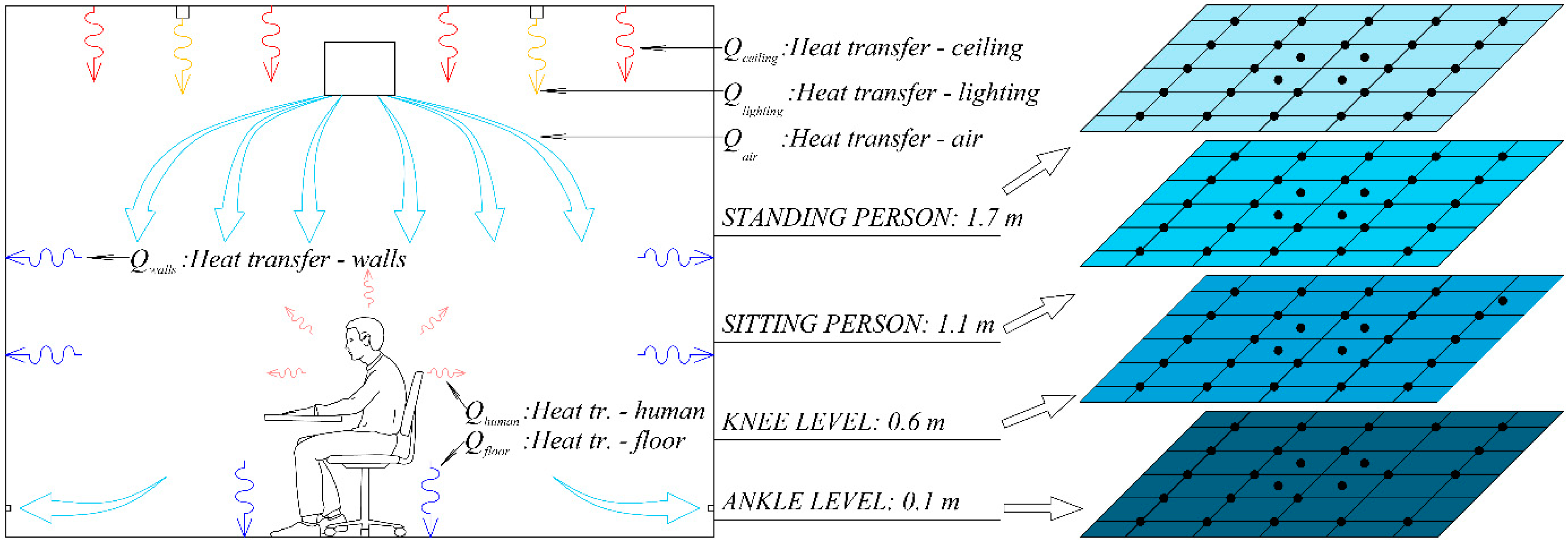
| Qair | Heat transfer from the chamber to the air | W |
| Qceiling | Heat transfer from the ceiling to the chamber | W |
| Qfloor | Heat transfer from the chamber to the floor | W |
| Qhuman | Heat transfer from the human to the chamber | W |
| Qlighting | Heat transfer from the lighting to the chamber | W |
| Qwalls | Heat transfer from the chamber to the walls | W |
| x | Mean value of the first sample | Variable |
| X | First random variable | Variable |
| y | Mean value of the second sample | Variable |
| Y | Second random variable | Variable |
References
- Energy Performance of Buildings Directive, 2002/91/EC. Available online: https://ec.europa.eu/energy/topics/energy-efficiency/energy-efficient-buildings/energy-performance-buildings-directive_en (accessed on 30 April 2021).
- Ren, J.; Zhu, L.; Wang, Y.; Wang, C.; Xiong, W. Very low temperature radiant heating/cooling indoor end system for efficient use of renewable energies. Sol. Energy 2010, 84, 1072–1083. [Google Scholar] [CrossRef]
- Olesen, B.W. Radiant heating in theory and practice. Ashrae J. 2008, 50, 16–22. [Google Scholar]
- Rhee, K.-N.; Kim, K.W. A 50 year review of basic and applied research in radiant heating and cooling systems for the built environment. Build. Environ. 2015, 91, 166–190. [Google Scholar] [CrossRef]
- Self, S.J.; Reddy, B.V.; Rosen, M. Geothermal heat pump system: Status review and comparison with other heating options. Appl. Energy 2013, 101, 341–348. [Google Scholar] [CrossRef]
- Wargocki, P.; Wyon, P.D. Ten questions concerning thermal and indoor air quality effects on the performance of office work and schoolwork. Build. Environ. 2003, 51, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Wargocki, P.; Wyon, P.D. Providing better thermal and air quality conditions in school classrooms would be cost-effective. Build. Environ. 2013, 59, 581–589. [Google Scholar] [CrossRef]
- Fanger, P.O.; Christensen, N.K. Perception of draught in ventilated spaces. Ergonomics 2003, 2, 215–235. [Google Scholar] [CrossRef]
- Fanger, P.O.; Melinkov, A.; Hanzawa, H. Air turbulence and sensation of draught. Energy Build. 1988, 12, 21–39. [Google Scholar] [CrossRef]
- Toftum, J.; Nielsen, R. Draught sensitivity is influenced by general thermal sensation. Ind. Ergon. 1996, 18, 295–305. [Google Scholar] [CrossRef]
- Gagge, A. The linearity criterion as applied to partitional calorimetry. Am. J. Phisyol. 1936, 116, 656–668. [Google Scholar] [CrossRef]
- MacPherson, R. The assessment of the thermal environment. A review. Br. J. Ind. Med. 1962, 19, 115–164. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort; Danish Technical Press: Copenhagen, The Netherlands, 1970. [Google Scholar]
- Fanger, P.O.; Ipsen, G.; Langkilde, G.; Olesen, B.W.; Christensen, N.K.; Tanabe, S. Comfort limits for asymmetric radiation. Energy Build. 1985, 8, 225–236. [Google Scholar] [CrossRef]
- ISO 7730. Energonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the Pmv and Ppd Indices and Local Thermal Comfort Criteria; International Organization for Standardization: Geneva, Switzerland, 2005. [Google Scholar]
- ASHRAE Standard 55. Thermal Environment Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2020. [Google Scholar]
- Bartal, I. Joint Impact of Cold Wall and Airflow. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2012. [Google Scholar]
- Barna, E.; Bánhidi, L. Combined effect of two local discomfort parameters studied with a thermal manekin and human subjects. Energy Build. 2012, 112, 359–365. [Google Scholar]
- Toftum, J.; Nielsen, R. Impact of metabolic rate on human response to air movements during work in cool environments. Ind. Ergon. 1996, 18, 307–316. [Google Scholar] [CrossRef]
- Arens, E.; Zhang, H.; Huizenga, C. Partial- and whole-body thermal sensation and comfort—Part I: Uniform environmental conditions. J. Od Therm. Biol. 2006, 31, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Huizenga, C.; Zhang, H.; Arens, E.; Wang, D. Skin and core temperature response to partial– and whole–body heating and cooling. J. Therm. Biol. 2004, 29, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; He, Y.; Hou, J.; Jiang, L. Human skin temperature and thermal response in asymmetrical cold radiation environments. Build. Environ. 2013, 67, 217–223. [Google Scholar] [CrossRef]
- Fang, Z.; Liu, H.; Li, B.; Tan, M.; Olaide, O. Experimental investigation on thermal comfort model between local thermal sensation and overall thermal sensation. Energy Build. 2018, 158, 1286–1295. [Google Scholar] [CrossRef] [Green Version]
- Schellen, L. The influence of local effects on thermal sensation under non-uniform environmental conditions—Gender differences in thermophysiology, thermal comfort and productivity during convective and radiant cooling. Physiol. Behav. 2012, 107, 252–261. [Google Scholar] [CrossRef] [PubMed]
- Kalmár, F.; Kalmár, T. Study of human response in conditions of surface heating, asymmetric radiation and variable air jet direction. Energy Build. 2018, 179, 133–143. [Google Scholar] [CrossRef]
- Boerstra, A.; Kulde, M.; Toftum, J. Comfort and performance impact of personal control over thermal environment in summer: Result from laboratory study. Build. Environ. 2015, 87, 315–326. [Google Scholar] [CrossRef]
- Wyon, D.P. Methodology for indoor environment research. Magy. Épületgépészet 2018, 181, 38–49. [Google Scholar]
- Zhang, F.; de Dear, R.; Hancock, P. Effects of moderate thermal environments on cognitive performance: A multidisciplinary review. Appl. Energy 2019, 236, 760–777. [Google Scholar] [CrossRef]
- Wim, Z.; Gert, B. Effect of thermal activated building systems in schools on thermal comfort in winter. Build. Environ. 2009, 11, 2308–2317. [Google Scholar]
- Fazekas, I. Bevezetés a Matematikai Statisztikába; Kossuth Egyetemi Kiadó: Debrecen, Hungary, 2000. [Google Scholar]
- Ketskeméty, L.; Izsó, L.; Könyves, T.E. Bevezetés az IBM SPSS Statisztikai programrendszerbe; Artéria Stúdió: Budapest, Hungary, 2001. [Google Scholar]
- Humphreys, M.; Nicol, F. The validity of ISO-PMV for predicting comfort votes in every-day thermal environments. Energy Build. 2002, 34, 667–684. [Google Scholar] [CrossRef]









| Parameter | Measured/Calculated | Measurement Errors |
|---|---|---|
| Air and mean radiant temperature | Measured | 0.1 °C |
| Air velocity | Measured | 0.03 m/s + 0.04 Measured value |
| Relative humidity | Measured | 1.8%+ 0.007 Measured value |
| Thermal insulation of the clothing | Calculated | - |
| Metabolic rate | Calculated | - |
| Turbulence intensity | Calculated | - |
| DR | Calculated | - |
| PMV | Calculated | - |
| PPD | Calculated | - |
| Boundaries | |
|---|---|
| 1 | Number of healthy subjects: 20—10 women and 10 men |
| 2 | Length of exposure: 180 min + acclimatisation prior to the measurements |
| 3 | Number of parameter groups: 10 (5 radiant thermal asyymetries and 2 draught rates) |
| 4 | During one measurement session, the subjects were exposed to only 1 thermal comfort environment |
| 5 | Only one subject at a time participates in the experiment |
| 6 | The occurrence of parameter groups is random |
| 7 | The thermal comfort chamber was thermally stationary during the entire measurement |
| 8 | Acoustic and visual disturbances were ruled out |
| 9 | Due to the high volume of air flow, the indoor air quality is ideal |
| 10 | The thermal insulation capacity of the clothing is 1 clo |
| 11 | Breakfast is mandatory, meals are adapted to the individual’s daily routine |
| 12 | Using the lavatory before starting the experiment is ideal |
| 13 | Water can be brought into the measuring chamber, all other food is forbidden |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
András-Tövissi, B.; Kajtár, L.; Nyers, Á. The Effect of Ceiling Heating and Mechanical Ventilation on Thermal Comfort. Energies 2021, 14, 3712. https://doi.org/10.3390/en14123712
András-Tövissi B, Kajtár L, Nyers Á. The Effect of Ceiling Heating and Mechanical Ventilation on Thermal Comfort. Energies. 2021; 14(12):3712. https://doi.org/10.3390/en14123712
Chicago/Turabian StyleAndrás-Tövissi, Balázs, László Kajtár, and Árpád Nyers. 2021. "The Effect of Ceiling Heating and Mechanical Ventilation on Thermal Comfort" Energies 14, no. 12: 3712. https://doi.org/10.3390/en14123712
APA StyleAndrás-Tövissi, B., Kajtár, L., & Nyers, Á. (2021). The Effect of Ceiling Heating and Mechanical Ventilation on Thermal Comfort. Energies, 14(12), 3712. https://doi.org/10.3390/en14123712





