Improvements and Spatial Dependencies in Energy Transition Measures
Abstract
:1. Introduction
2. Energy Transition Index—Composition and Methodology
3. Materials and Methods
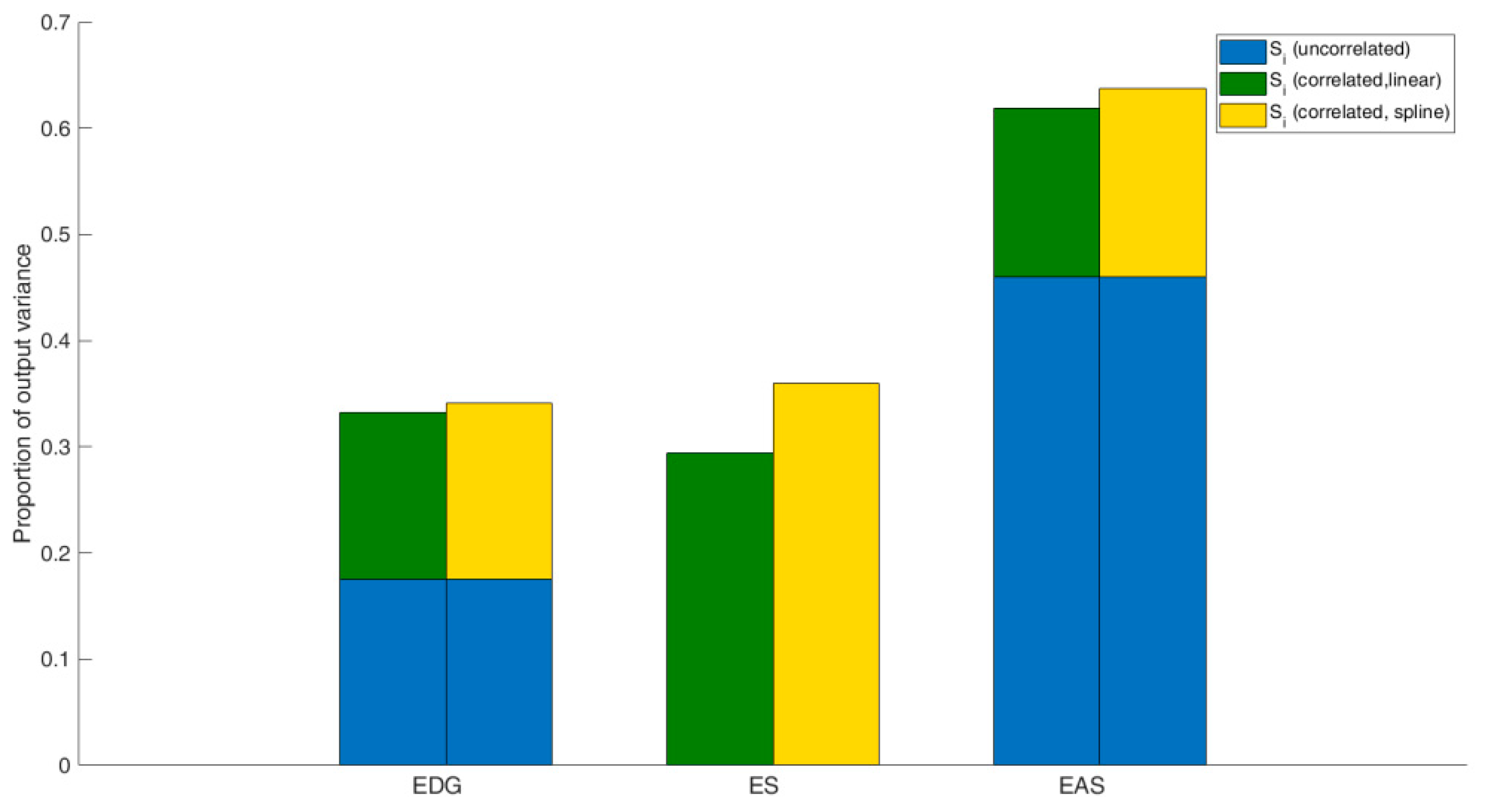
3.1. Sensitivity-Based Approach
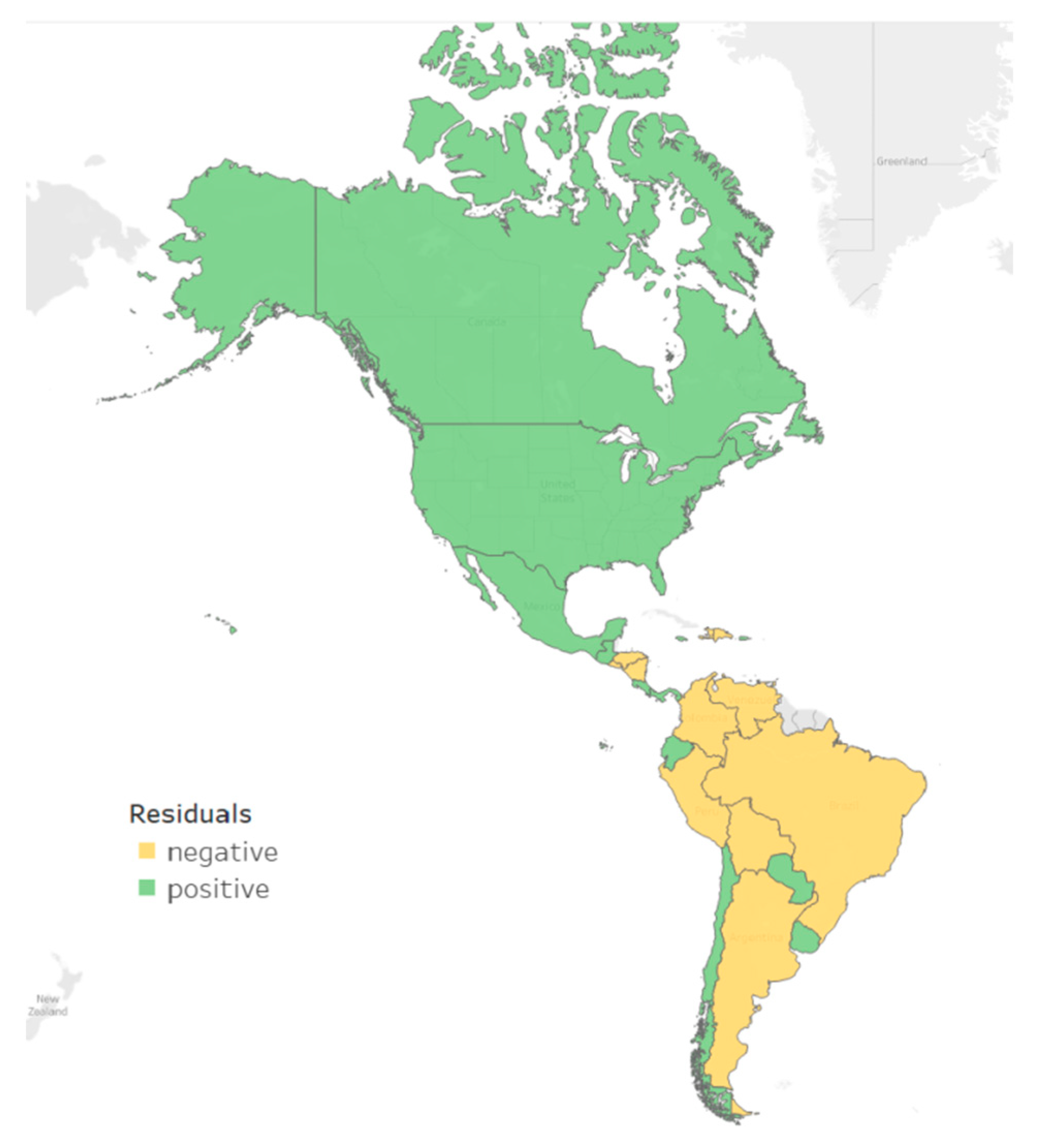
3.2. Spatial Modelling
4. Results
4.1. Optimisation of ETI Weights
4.2. Spatial Models
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- AlKhars, M.; Miah, F.; Qudrat-Ullah, H.; Kayal, A. A Systematic Review of the Relationship between Energy Consumption and Economic Growth in GCC Countries. Sustainability 2020, 12, 3845. [Google Scholar] [CrossRef]
- Ha, N.M.; Ngoc, B.H. Revisiting the relationship between energy consumption and economic growth nexus in Vietnam: New evidence by asymmetric ARDL cointegration. Appl. Econ. Lett. 2020, 1–7. [Google Scholar] [CrossRef]
- Humbatova, S.I.; Ahmadov, F.S.; Seyfullayev, I.Z.; Hajiyev, N.G.-O. The relationship between electricity consumption and economic growth: Evidence from Azerbaijan. Int. J. Energy Econ. Policy 2020, 10, 436–455. [Google Scholar] [CrossRef]
- Chen, C.; Pinar, M.; Stengos, T. Renewable energy consumption and economic growth nexus: Evidence from a threshold model. Energy Policy 2020, 139, 111295. [Google Scholar] [CrossRef]
- Filimonova, I.; Komarova, A.; Mishenin, M. Impact of the global green factor on the capitalization of oil companies in Russia. Oecon. Copernic. 2020, 11, 309–324. [Google Scholar] [CrossRef]
- International Monetary Fund (IMF). World Economic Outlook. 2021. Available online: https://www.imf.org/en/Publications/WEO/Issues/2021/03/23/world-economic-outlook-april-2021 (accessed on 12 January 2021).
- International Energy Agency. Global Energy Review 2020; OECD Publishing: Paris, France, 2020. [CrossRef]
- Ritchie, H.; Roser, M. Energy. Available online: https://ourworldindata.org/energy (accessed on 4 February 2021).
- Araújo, K. The emerging field of energy transitions: Progress, challenges, and opportunities. Energy Res. Soc. Sci. 2014, 1, 112–121. [Google Scholar] [CrossRef]
- Hirsh, R.F.; Jones, C.F. History’s contributions to energy research and policy. Energy Res. Soc. Sci. 2014, 1, 106–111. [Google Scholar] [CrossRef]
- Jonek-Kowalska, I. Transformation of energy balances with dominant coal consumption in European economies and Turkey in the years 1990–2017. Oecon. Copernic. 2019, 10, 627–647. [Google Scholar] [CrossRef] [Green Version]
- Czech, A. Economic dimension of Polish energy security. Oecon. Copernic. 2017, 8, 383–399. [Google Scholar] [CrossRef]
- Miller, C.A.; Richter, J.; O’Leary, J. Socio-energy systems design: A policy framework for energy transitions. Energy Res. Soc. Sci. 2015, 6, 29–40. [Google Scholar] [CrossRef] [Green Version]
- World Economic Forum (WEF). Fostering Effective Energy Transition 2019 Edition; World Economic Forum: Geneva, Switzerland, 2019. [Google Scholar]
- Strunz, S. The German energy transition as a regime shift. Ecol. Econ. 2014, 100, 150–158. [Google Scholar] [CrossRef] [Green Version]
- Chovancová, J.; Tej, J. Decoupling economic growth from greenhouse gas emissions: The case of the energy sector in V4 countries. Equilib. Q. J. Econ. Econ. Policy 2020, 15, 235–251. [Google Scholar] [CrossRef]
- Fischer, J.; Alimi, D.; Knieling, J.; Camara, C. Stakeholder Collaboration in Energy Transition: Experiences from Urban Testbeds in the Baltic Sea Region. Sustainability 2020, 12, 9645. [Google Scholar] [CrossRef]
- Höfer, T.; Madlener, R. A participatory stakeholder process for evaluating sustainable energy transition scenarios. Energy Policy 2020, 139, 111277. [Google Scholar] [CrossRef] [Green Version]
- Falcone, P.M. Analysing stakeholders’ perspectives towards a socio-technical change: The energy transition journey in Gela Municipality. AIMS Energy 2018, 6, 645–657. [Google Scholar] [CrossRef]
- Graff, M.; Carley, S.; Konisky, D.M. Stakeholder perceptions of the United States energy transition: Local-level dynamics and community responses to national politics and policy. Energy Res. Soc. Sci. 2018, 43, 144–157. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015.
- Iddrisu, I.; Bhattacharyya, S.C. Sustainable Energy Development Index: A multi-dimensional indicator for measuring sustainable energy development. Renew. Sustain. Energy Rev. 2015, 50, 513–530. [Google Scholar] [CrossRef] [Green Version]
- Global Energy Institute (GEI). International Index of Energy Security Index. Assessing Risk in a Global Energy Market; Global Energy Instinute: Washington, DC, USA, 2020. [Google Scholar]
- Nussbaumer, P.; Bazilian, M.; Modi, V. Measuring energy poverty: Focusing on what matters. Renew. Sustain. Energy Rev. 2012, 16, 231–243. [Google Scholar] [CrossRef] [Green Version]
- World Energy Council (WEC). World Energy Trilemma Index 2020; World Energy Council: London, UK, 2020. [Google Scholar]
- Broto, V.C.; Baker, L. Spatial adventures in energy studies: An introduction to the special issue. Energy Res. Soc. Sci. 2018, 36, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bridge, G. The map is not the territory: A sympathetic critique of energy research’s spatial turn. Energy Res. Soc. Sci. 2018, 36, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Bridge, G.; Barr, S.; Bouzarovski, S.; Bradshaw, M.; Brown, E.; Bulkeley, H.; Walker, G. Energy and Society: A Critical Perspective; Routledge: Abingdon-on-Thames, UK, 2018. [Google Scholar]
- Wang, Z.; Zhu, Y. Do energy technology innovations contribute to CO2 emissions abatement? A spatial perspective. Sci. Total. Environ. 2020, 726, 138574. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Fang, L.; He, L. The impact of energy price on CO2 emissions in China: A spatial econometric analysis. Sci. Total Environ. 2020, 706, 135942. [Google Scholar] [CrossRef] [PubMed]
- Gailing, L.; Bues, A.; Kern, K.; Röhring, A. Socio-spatial dimensions in energy transitions: Applying the TPSN framework to case studies in Germany. Environ. Plan. A Econ. Space 2019, 52, 1112–1130. [Google Scholar] [CrossRef] [Green Version]
- World Economic Forum. Fostering Effective Energy Transition: A Fact-Based Framework to Support Decision-Making; World Economic Forum: Geneva, Switzerland, 2018. [Google Scholar]
- Singh, H.V.; Bocca, R.; Gomez, P.; Dahlke, S.; Bazilian, M. The energy transitions index: An analytic framework for understanding the evolving global energy system. Energy Strategy Rev. 2019, 26. [Google Scholar] [CrossRef]
- Becker, W.; Paruolo, P.; Saisana, M.; Saltelli, A. Weights and Importance in Composite Indicators: Mind the Gap. In Handbook of Uncertainty Quantification; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2015; pp. 1–30. [Google Scholar]
- Gómez-Limón, J.; Arriaza, M.; Guerrero-Baena, M. Building a Composite Indicator to Measure Environmental Sustainability Using Alternative Weighting Methods. Sustainability 2020, 12, 4398. [Google Scholar] [CrossRef]
- Fostering Effective Energy Transition. 2019. Available online: https://www.weforum.org/reports/fostering-effective-energy-transition-2019 (accessed on 27 March 2021).
- Lindén, D.; Cinelli, M.; Spada, M.; Becker, W.; Burgherr, P. Composite Indicator Analysis and Optimisation (CIAO) Tool. 2021, Volume 2. Available online: https://www.researchgate.net/publication/348186561_Composite_Indicator_Analysis_and_Optimization_CIAO_Tool_v2 (accessed on 15 February 2021). [CrossRef]
- Böhringer, C.; Jochem, P.E. Measuring the immeasurable—A survey of sustainability indices. Ecol. Econ. 2007, 63, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Greco, S.; Ishizaka, A.; Tasiou, M.; Torrisi, G. On the Methodological Framework of Composite Indices: A Review of the Issues of Weighting, Aggregation, and Robustness. Soc. Indic. Res. 2019, 141, 61–94. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A. Composite indicators between analysis and advocacy. Soc. Indic. Res. 2007, 81, 65–77. [Google Scholar] [CrossRef]
- Gnaldi, M.; Del Sarto, S. Variable Weighting via Multidimensional IRT Models in Composite Indicators Construction. Soc. Indic. Res. 2018, 136, 1139–1156. [Google Scholar] [CrossRef]
- Cinelli, M.; Spada, M.; Kim, W.; Zhang, Y.; Burgherr, P. MCDA Index Tool: An interactive software to develop indices and rankings. Environ. Syst. Decis. 2021, 41, 82–109. [Google Scholar] [CrossRef]
- Kuc-Czarnecka, M.; Piano, S.L.; Saltelli, A. Quantitative Storytelling in the Making of a Composite Indicator. Soc. Indic. Res. 2020, 149, 775–802. [Google Scholar] [CrossRef] [Green Version]
- Saltelii, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modelling. Stat. Sci. 2000, 15, 377–395. [Google Scholar]
- Saisana, M.; Saltelli, A.; Tarantola, S. Uncertainty and sensitivity analysis techniques as tools for the quality assessment of composite indicators. J. R. Stat. Soc. Ser. A Stat. Soc. 2005, 168, 307–323. [Google Scholar] [CrossRef]
- Paruolo, P.; Saisana, M.; Saltelli, A. Ratings and rankings: Voodoo or science? J. R. Stat. Soc. Ser. A Stat. Soc. 2012, 176, 609–634. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Tarantola, S. On the Relative Importance of Input Factors in Mathematical Models. J. Am. Stat. Assoc. 2002, 97, 702–709. [Google Scholar] [CrossRef]
- Becker, W.; Saisana, M.; Paruolo, P.; Vandecasteele, I. Weights and importance in composite indicators: Closing the gap. Ecol. Indic. 2017, 80, 12–22. [Google Scholar] [CrossRef]
- Harezlak, J.; Ruppert, D.; Wand, M.P. Penalized Splines. In Data Manipulation with R; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 15–70. [Google Scholar]
- Nelder, J.A.; Mead, R. Simplex method for function minimisation. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Buccellato, T. Convergence across Russian Regions: A spatial econometrics approach. Econ. Work. Pap. 2007, 72, 1–24. [Google Scholar]
- Pietrzak, M.B.; Balcerzak, A.P. A regional scale analysis of economic convergence in Poland in the Years 2004–2012. In Regional Studies on Economic Growth, Financial Economics and Management; Springer: Cham, Switzerland, 2017; pp. 257–268. [Google Scholar] [CrossRef]
- Griffith, D.A. Some guidelines for specifying the geographic weights matrix contained in spatial statistical models 1. In Practical Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Moran, P.A.P. Notes on continuous stochastic phenomenon. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Vavrek, R.; Kovářová, E. Assessment of the social exclusion at the regional level using multi-criteria approach: Evidence from the Czech Republic. Equilib. Q. J. Econ. Econ. Policy 2021, 16, 75–102. [Google Scholar] [CrossRef]
- Anselin, L.; Rey, S.J. Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL; GeoDa Press LLC: Chicago, IL, USA, 2014. [Google Scholar]
- Larch, M.; Walde, J. Lag or Error?—Detecting the Nature of Spatial Correlation. In Data Science; Springer: Berlin/Heidelberg, Germany, 2008; pp. 301–308. [Google Scholar] [CrossRef]
- Fischer, M.M.; Wang, J. Modelling Area Data. In Spatial Data Analysis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 31–44. [Google Scholar] [CrossRef]
- Davoudabadi, R.; Mousavi, S.M.; Sharifi, E. An integrated weighting and ranking model based on entropy, DEA and PCA considering two aggregation approaches for resilient supplier selection problem. J. Comput. Sci. 2020, 40. [Google Scholar] [CrossRef]
- Falcone, P.M.; Sica, E. Assessing the Opportunities and Challenges of Green Finance in Italy: An Analysis of the Biomass Production Sector. Sustainability 2019, 11, 517. [Google Scholar] [CrossRef] [Green Version]
- Falcone, P.M. Environmental regulation and green investments: The role of green finance. Int. J. Green Econ. 2020, 14, 159. [Google Scholar] [CrossRef]
- Van De Putte, A.; Campbell-Holt, A.; Littlejohn, G. Financing the Sustainable Energy Transition. In The Geopolitics of the Global Energy Transition; Springer: Cham, Switzerland, 2020; pp. 257–277. [Google Scholar]
- Przychodzen, W.; Przychodzen, J. Determinants of renewable energy production in transition economies: A panel data approach. Energy 2020, 191, 116583. [Google Scholar] [CrossRef]
- Balash, V.; Balash, O.; Faizliev, A.; Chistopolskaya, E. Economic Growth Patterns: Spatial Econometric Analysis for Russian Regions. Information 2020, 11, 289. [Google Scholar] [CrossRef]
- European Commission. COM(2014) 15 Final: A Policy Framework for Climate and Energy in the Period from 2020 to 2030; European Commission: Brussels, Belgium, 2014; pp. 1–18.
- Dialga, I. Evaluating Normandy’s sustainable development and energy transition policies. J. Clean. Prod. 2021, 305, 127096. [Google Scholar] [CrossRef]










| Variable | Description |
|---|---|
| ETI | The logarithm of the Energy Transition Index value |
| HEP | The logarithm of household electricity prices (PPP USDc/kWh) |
| CO2 | The logarithm of CO2 emissions per capita (tonnes per capita) |
| RCB | The logarithm of renewable capacity buildout (% of installed capacity) |
| JLCI | The logarithm of share of renewable energy jobs as part of countries total workforce |
| POP | The logarithm of population size |
| UR | The logarithm of urban population as % of the total population |
| EM | The logarithm of employment in manufacturing as % of total employment |
| Dimension | Original Weight | Optimal Weight | Direction |
|---|---|---|---|
| System performance | 0.50 | 0.5249 | Underestimated |
| Environmental sustainability | 0.33 | 0.3612 | Underestimated |
| Particular matter concentration | 0.25 | 0.0833 | Overestimated |
| Energy intensity | 0.25 | 0.0260 | Overestimated |
| CO2 emission per capita | 0.25 | 0.5075 | Underestimated |
| CO2 emission per TPES | 0.25 | 0.3779 | Underestimated |
| Top Countries | Bottom Countries | ||
|---|---|---|---|
| Original ETI | Optimised ETI | Original ETI | Optimised ETI |
| Sweden | Sweden | Mozambique | Benin |
| Switzerland | Finland | Venezuela | Mozambique |
| Norway | Switzerland | Zimbabwe | Botswana |
| Finland | Norway | South Africa | Zimbabwe |
| Denmark | United States | Haiti | Haiti |
| Most Significant | Least Significant |
|---|---|
| CO2 per capita | RISE access score |
| Household electricity prices | Quality of transportation infrastructure |
| CO2 per TPES | Energy Intensity |
| Renewable capacity buildout | Share of global fossil-fuel reserves |
| Jobs in low-carbon industries | Transparency |
| Variable | Original ETI | Optimal ETI | ||||
|---|---|---|---|---|---|---|
| America | Asia | Europe | America | Asia | Europe | |
| - | - | 0.659 (0.0001) | - | - | 0.769 | |
| HEP | 0.088 (0.086) | 0.014 (0.478) | −0.015 (0.655) | 0.013 (0.741) | 0.020 (0.220) | −0.045 (0.087) |
| CO2 | 0.047 (0.241) | 0.001 (0.981) | −0.055 (0.106) | 0.109 (0.003) | 0.086 (0.009) | 0.014 (0.601) |
| RCB | −0.149 (0.798) | −0.324 (0.442) | 0.331 (0.456) | 0.234 (0.610) | −0.489 (0.114) | 0.028 (0.933) |
| JLCI | 4.337 (0.148) | 5.665 (0.153) | 2.217 (0.055) | 3.318 (0.159) | 4.321 (0.161) | 2.477 (0.006) |
| POP | −0.013 (0.626) | −0.005 (0.767) | −0.003 (0.808) | 0.013 (0.541) | 0.016 (0.261) | 0.005 (0.632) |
| UR | 0.280 (0.148) | 0.058 (0.532) | 0.065 (0.524) | 0.131 (0.379) | −0.033 (0.649) | 0.100 (0.218) |
| EM | 0.269 (0.040) | −0.135 (0.178) | −0.110 (0.170) | 0.028 (0.767) | −0.101 (0.191) | −0.005 (0.930) |
| R2 | 0.602 | 0.258 | 0.642 | 0.742 | 0.621 | 0.781 |
| Moran’s I (error) | (0.118) | (0.617) | (0.044) | (0.128) | (0.491) | (0.012) |
| LM (lag) | (0.226) | (0.182) | (0.117) | (0.882) | (0.483) | (0.056) |
| LM (lag) robust | (0.270) | (0.180) | (0.089) | (0.857) | (0.369) | (0.566) |
| LM (error) | (0.345) | (0.896) | (0.073) | (0.369) | (0.388) | (0.002) |
| LM (error) robust | (0.422) | (0.805) | (0.047) | (0.366) | (0.303) | (0.011) |
| Variable | Original SP | Optimal SP | ||||
|---|---|---|---|---|---|---|
| America | Asia | Europe | America | Asia | Europe | |
| 0.617 (0.001) | - | 0.563 (0.0001) | - | - | 0.572 (0.0001) | |
| HEP | 0.043 (0.232) | 0.028 (0.288) | −0.009 (0.812) | −0.114 (0.083) | 0.038 (0.146) | −0.046 (0.276) |
| CO2 | −0.024 (0.538) | 0.026 (0.586) | −0.081 (0.021) | 0.063 (0.220) | 0.199 (0.0001) | 0.022 (0.600) |
| RCB | −0.317 (0.502) | −0.690 (0.186) | −0.110 (0.814) | −0.380 (0.611) | −0.311 (0.548) | −0.813 (0.140) |
| JLCI | 2.226 (0.301) | 3.537 (0.456) | 1.293 (0.274) | 1.971 (0.597) | 0.100 (0.983) | 0.279 (0.841) |
| POP | −0.015 (0.520) | −0.001 (0.985) | 0.004 (0.751) | −0.007 (0.847) | 0.012 (0.572) | 0.0126 (0.439) |
| UR | 0.344 (0.030) | 0.011 (0.924) | 0.083 (0.433) | 0.422 (0.093) | −0.183 (0.116) | 0.234 (0.061) |
| EM | 0.356 (0.004) | −0.214 (0.082) | −0.144 (0.084) | −0.060 (0.703) | −0.194 (0.116) | 0.017 (0.864) |
| R2 | 0.722 | 0.254 | 0.518 | 0.682 | 0.598 | 0.549 |
| Moran’s I (error) | (0.019) | (0.133) | (0.047) | (0.371) | (0.278) | (0.004) |
| LM (lag) | (0.378) | (0.408) | (0.207) | (0.272) | (0.722) | (0.023) |
| LM (lag) robust | (0.495) | (0.364) | (0.120) | (0.275) | (0.815) | (0.187) |
| LM (error) | (0.036) | (0.331) | (0.093) | (0.811) | (0.535) | (0.008) |
| LM(error) robust | (0.160) | (0.298) | (0.049) | (0.837) | (0.576) | (0.060) |
| Variable | Original TR | Optimal TR | ||||
|---|---|---|---|---|---|---|
| America | Asia | Europe | America | Asia | Europe | |
| - | - | 0.670 (0.0001) | - | - | 0.806 (0.0001) | |
| HEP | 0.170 (0.005) | 0.001 (0.946) | −0.019 (0.622) | 0.101 (0.060) | 0.013 | 0.011 (0.118) |
| CO2 | 0.105 (0.021) | −0.033 (0.432) | −0.022 (0.570) | 0.136 (0.004) | 0.038 (0.447) | 0.424 (0.645) |
| RCB | 0.058 (0.925) | 0.112 (0.780) | 0.847 (0.087) | 0.312 (0.604) | −0.531 (0.249) | 3.611 (0.173) |
| JLCI | 4.775 (0.139) | 8.043 (0.059) | 3.577 (0.006) | 4.266 (0.166) | 6.172 (0.136) | 0.001 (0.0001) |
| POP | −0.016 (0.578) | −0.011 (0.554) | −0.012 (0.443) | 0.017 (0.526) | 0.017 (0.065) | 0.058 (0.911) |
| UR | 0.124 (0.538) | 0.124 (0.209) | 0.088 (0.421) | 0.021 (0.912) | 0.035 (0.256) | −0.016 (0.453) |
| EM | 0.189 (0.162) | −0.040 (0.691) | −0.072 (0.447) | 0.095 (0.453) | −0.060 (0.653) | 0.011 (0.788) |
| R2 | 0.631 | 0.274 | 0.712 | 0.652 | 0.536 | 0.822 |
| Moran’s I (error) | (0.520) | (0.680) | (0.092) | (0.347) | (0.295) | (0.073) |
| LM (lag) | (0.117) | (0.218) | (0.571) | (0.836) | (0.516) | (0.218) |
| LM (lag) robust | (0.114) | (0.220) | (0.485) | (0.654) | (0.262) | (0.354) |
| LM (error) | (0.979) | (0.519) | (0.094) | (0.776) | (0.245) | (0.001) |
| LM(error) robust | (0.849) | (0.634) | (0.043) | (0.626) | (0.139) | (0.001) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuc-Czarnecka, M.E.; Olczyk, M.; Zinecker, M. Improvements and Spatial Dependencies in Energy Transition Measures. Energies 2021, 14, 3802. https://doi.org/10.3390/en14133802
Kuc-Czarnecka ME, Olczyk M, Zinecker M. Improvements and Spatial Dependencies in Energy Transition Measures. Energies. 2021; 14(13):3802. https://doi.org/10.3390/en14133802
Chicago/Turabian StyleKuc-Czarnecka, Marta Ewa, Magdalena Olczyk, and Marek Zinecker. 2021. "Improvements and Spatial Dependencies in Energy Transition Measures" Energies 14, no. 13: 3802. https://doi.org/10.3390/en14133802
APA StyleKuc-Czarnecka, M. E., Olczyk, M., & Zinecker, M. (2021). Improvements and Spatial Dependencies in Energy Transition Measures. Energies, 14(13), 3802. https://doi.org/10.3390/en14133802







