Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race
Abstract
:1. Introduction
2. Numerical Method
2.1. Vortex Particle Method
- A rotational velocity component accounting for particle–particle interaction, the core of any Lagrangian Vortex method. The component is the discrete solution of the continuous equation:obtained by introducing the Helmholtz decomposition (Equation (5)) into the definition of vorticity. The solution for this Equation (6) is given at any point M of the fluid domain by the Biot and Savart law [37,39,46,47]:This formulation is desingularised using a regularisation parameter , as described by Winckelmans and Leonard [47]. Additional developments are carried out in the numerical implementation of this formulation, such as a Treecode type acceleration algorithm (see Lindsay and Krasny [48]) and particles redistribution algorithms (see Cottet and Koumoutsakos [39]), as well as time stepping procedures.
- A potential velocity component , representing the influence of a solid body. There are many applications for the use of such a component, such as the simulation of the nozzle of jet [49], of a sail [50], or of a monofin [51]. In the present study, the potential velocity component represents the influence of the rotor of a turbine [9], as will be demonstrated in the following sections. This velocity component derives from a scalar potential , which must satisfy:Equation (8) is obtained by introducing the velocity decomposition Equation (5) into the continuity Equation (1). The latest developments on this aspect of the software are detailed by Carlier et al. [52] as well as Mycek et al. [35].
- A velocity component representing the upstream velocity field at infinity, generally treated as a constant vector. The focus of this paper will be to adapt the upstream velocity component in order to account for ambient turbulence in the surrounding flow.
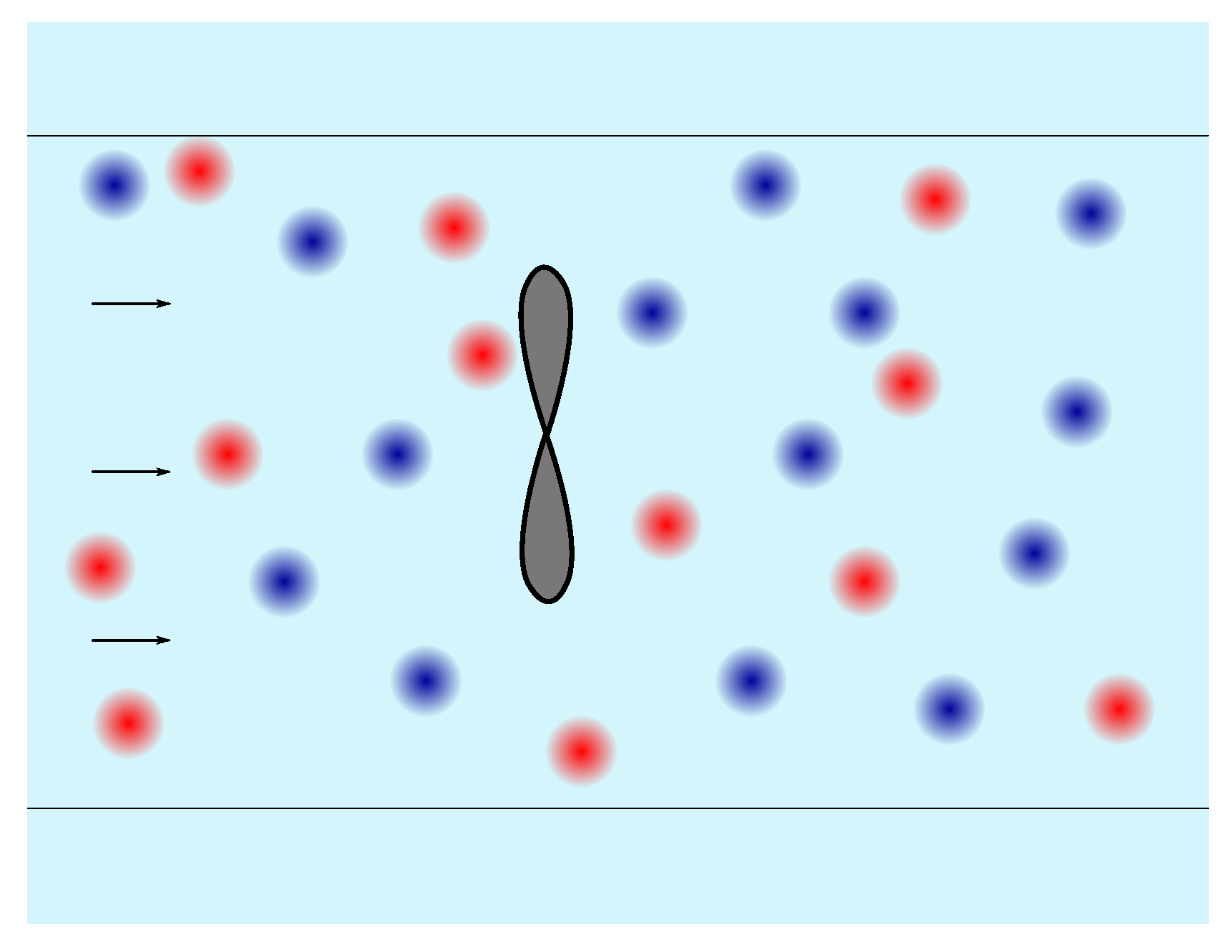
2.2. Synthetic Eddy Method
2.3. Numerical Parameters
3. Computation of a Single Tidal Turbine
3.1. Numerical Set-Up and Tested Configurations
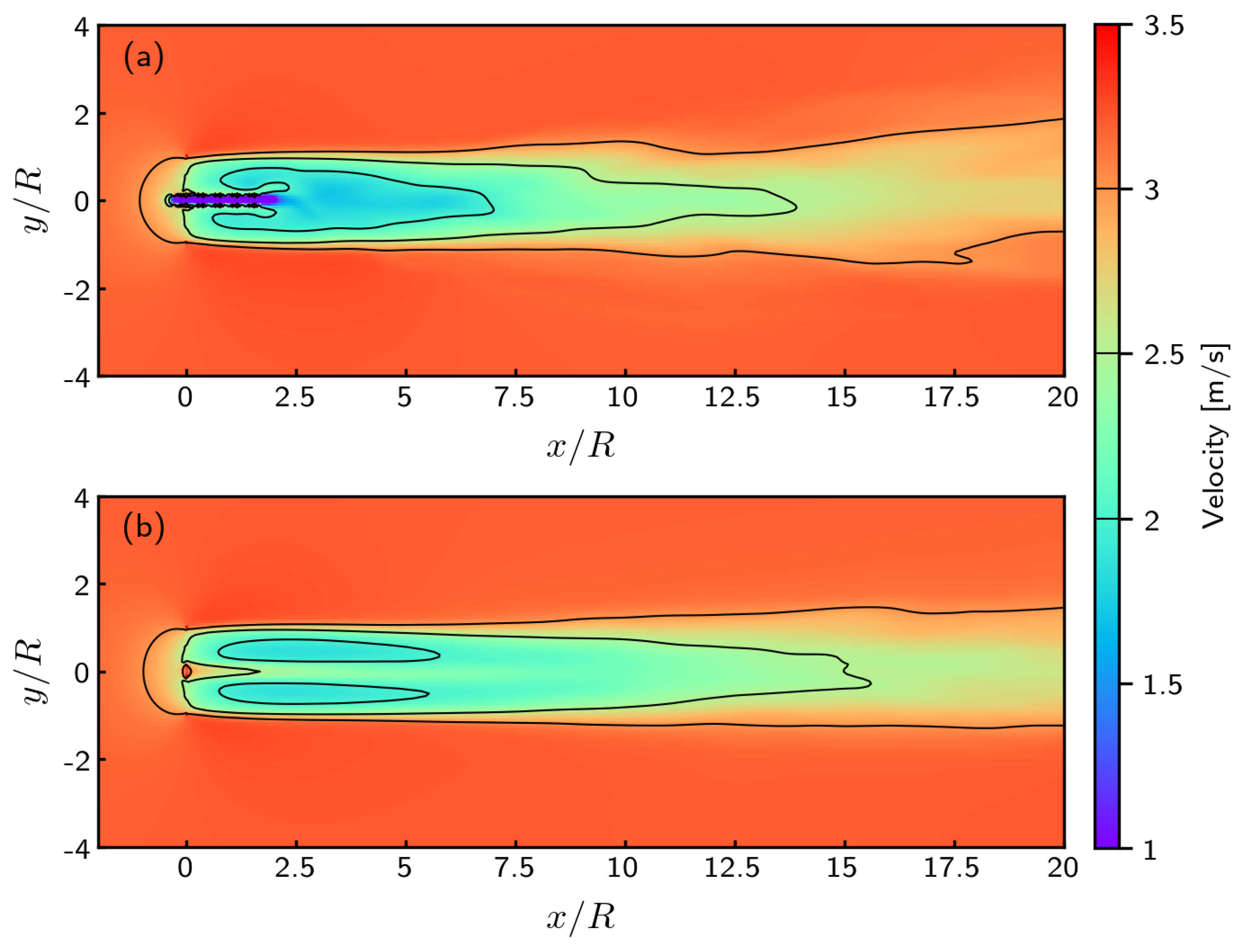
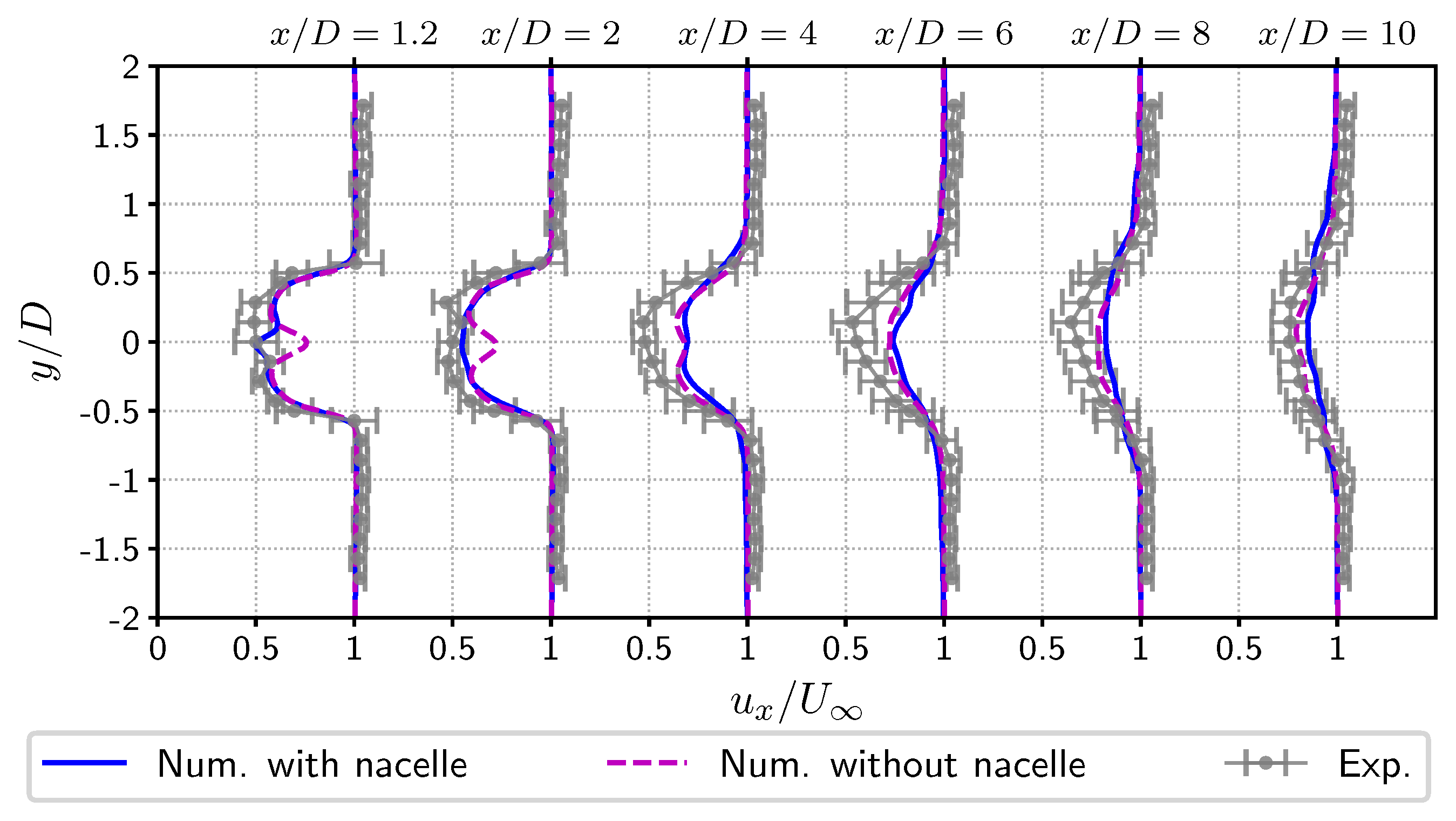
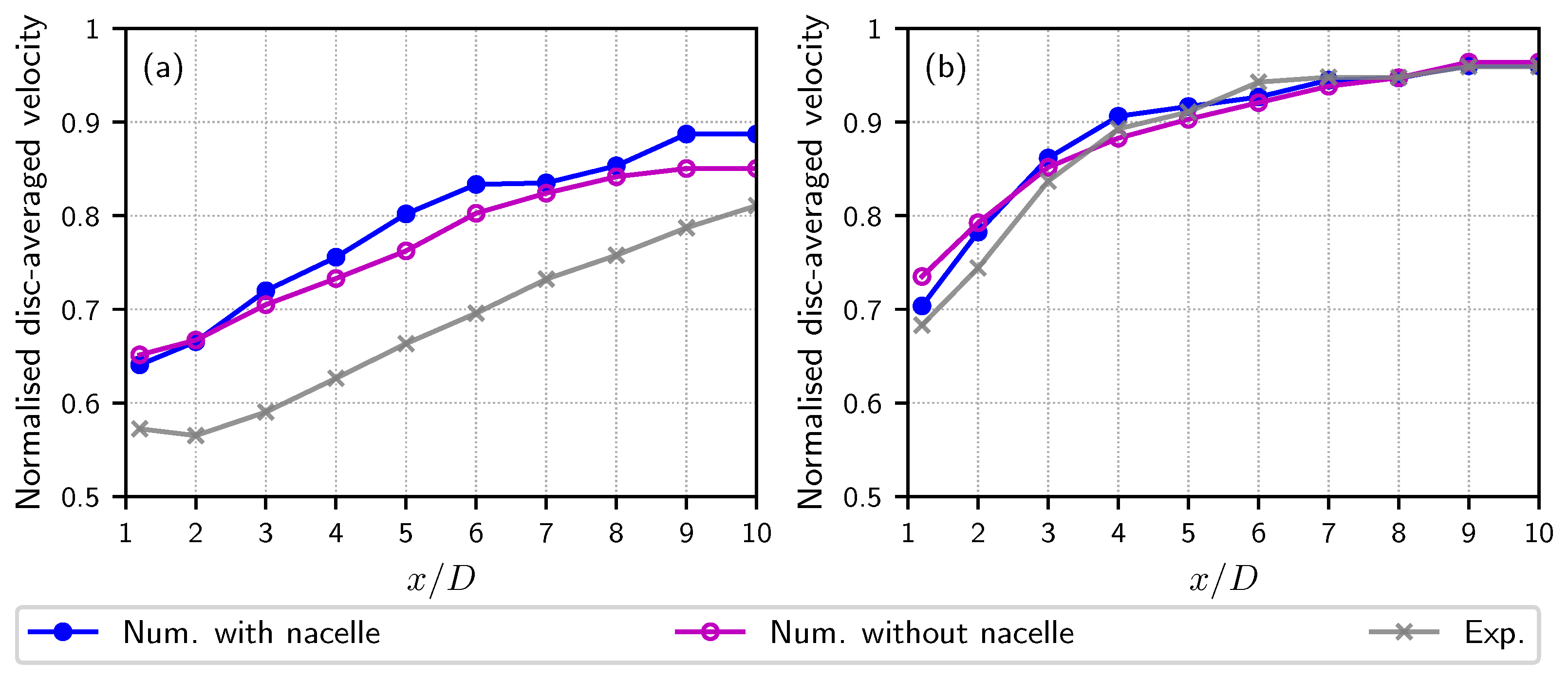
3.2. Taking into Account the Nacelle
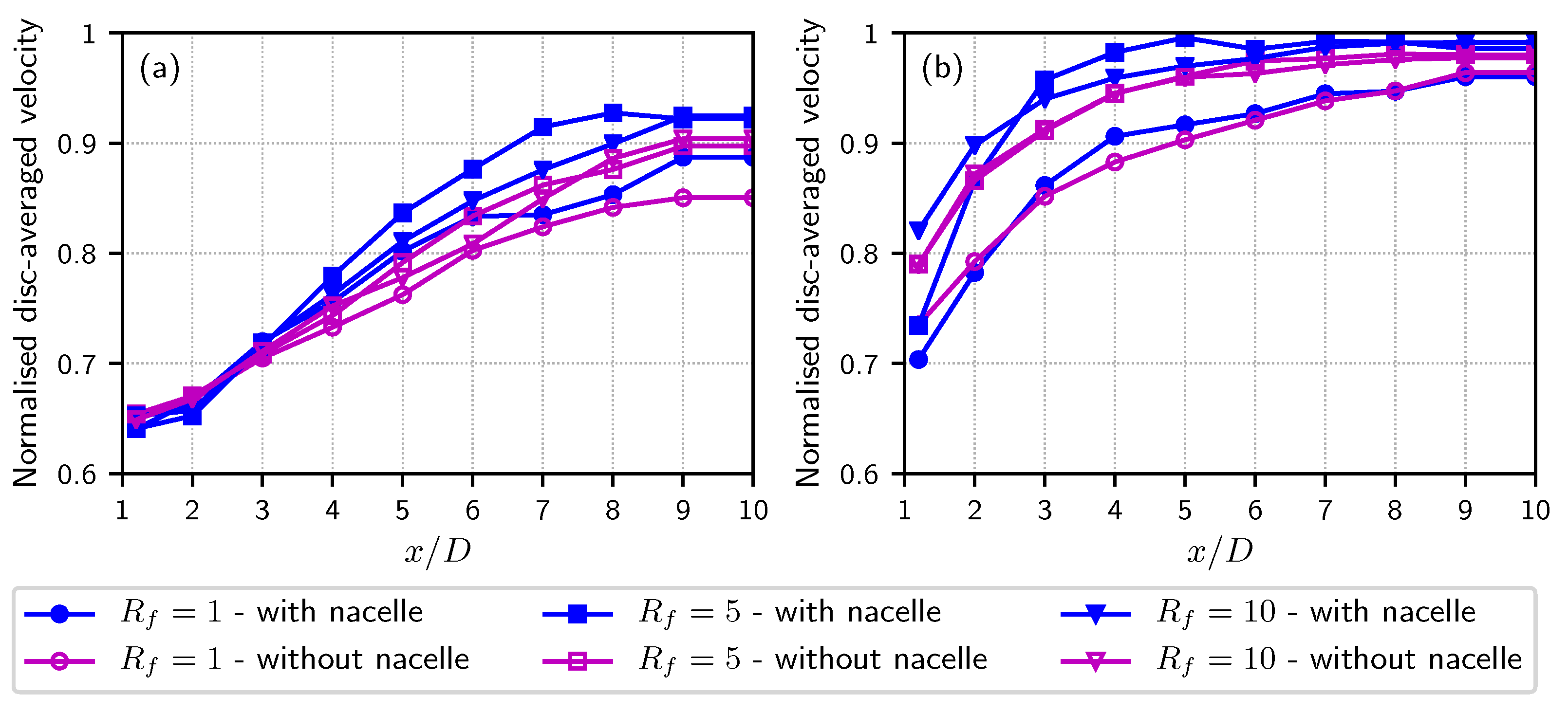
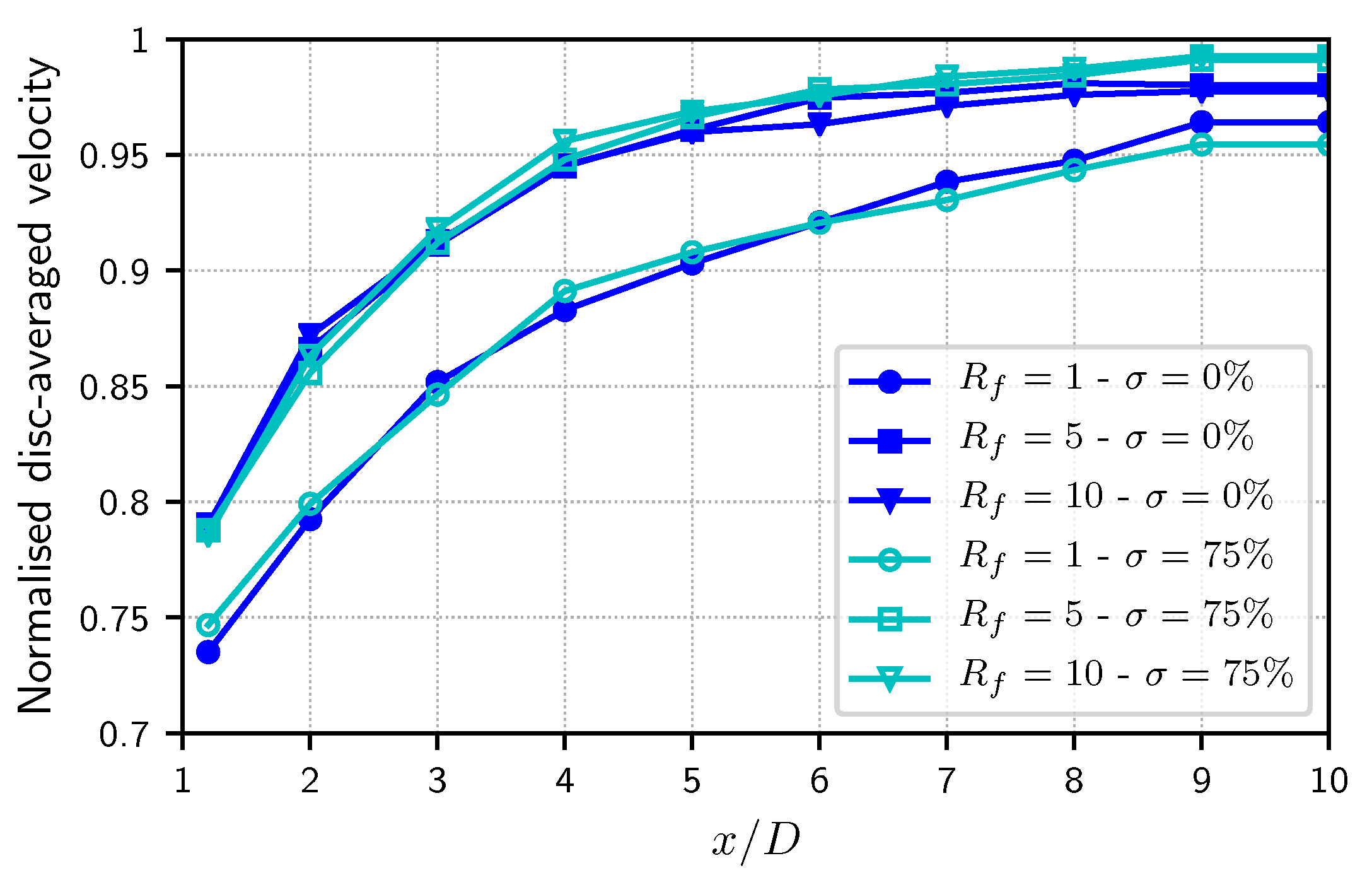
3.3. Influence of the Filling Ratio Rf
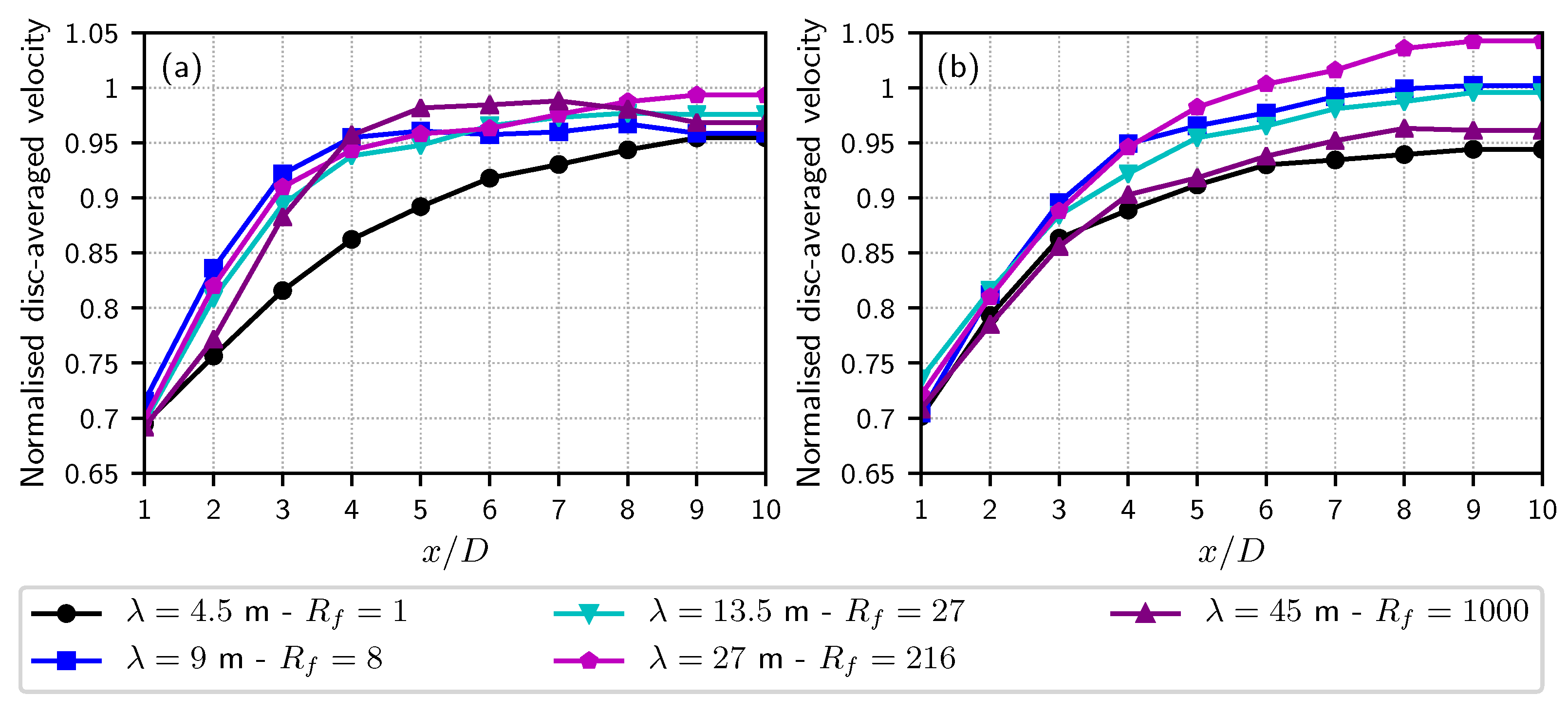
3.4. Influence of the Turbulent Structure Size λ
4. Four Tidal Turbine Array: The NEPTHYD Layout
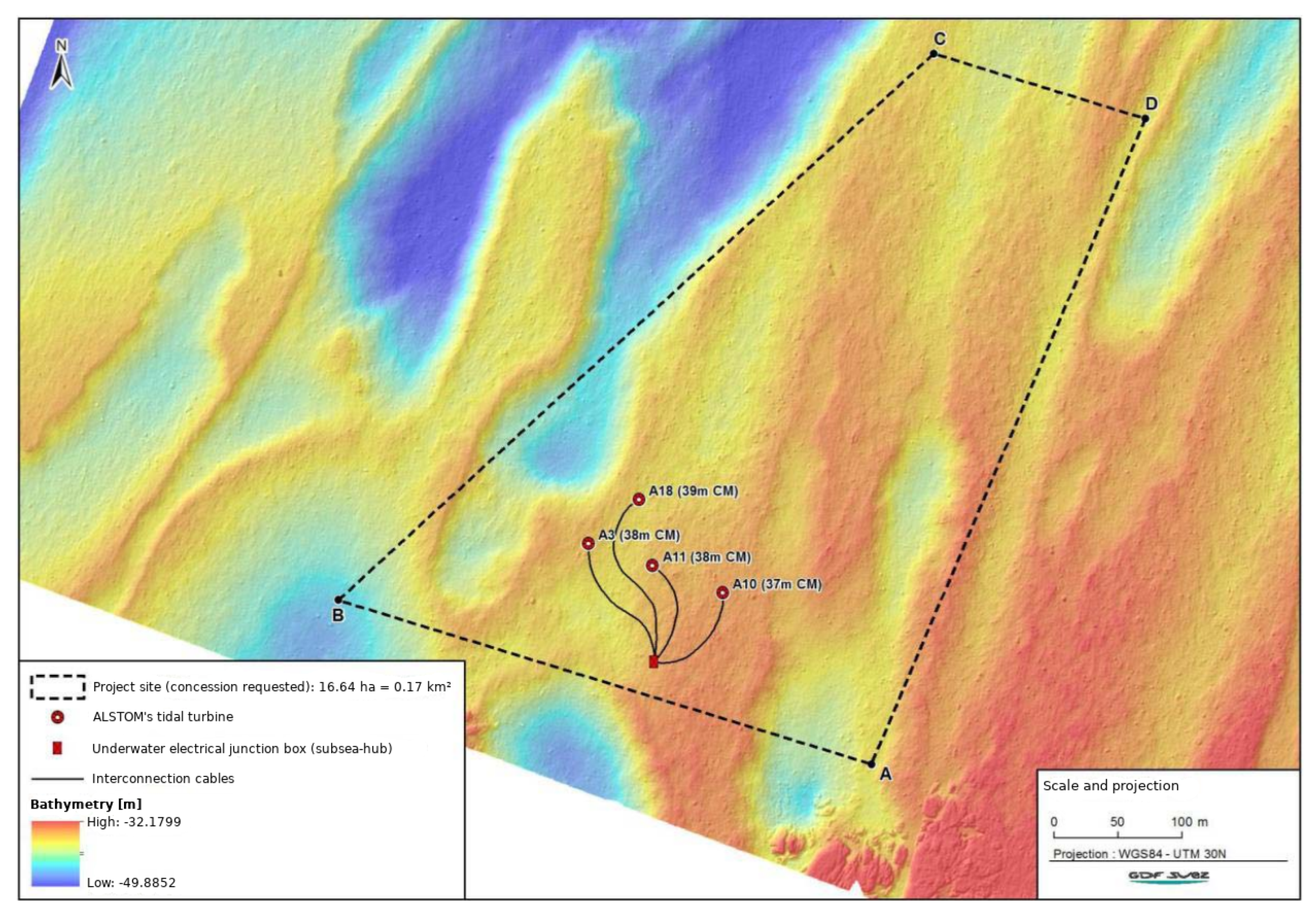
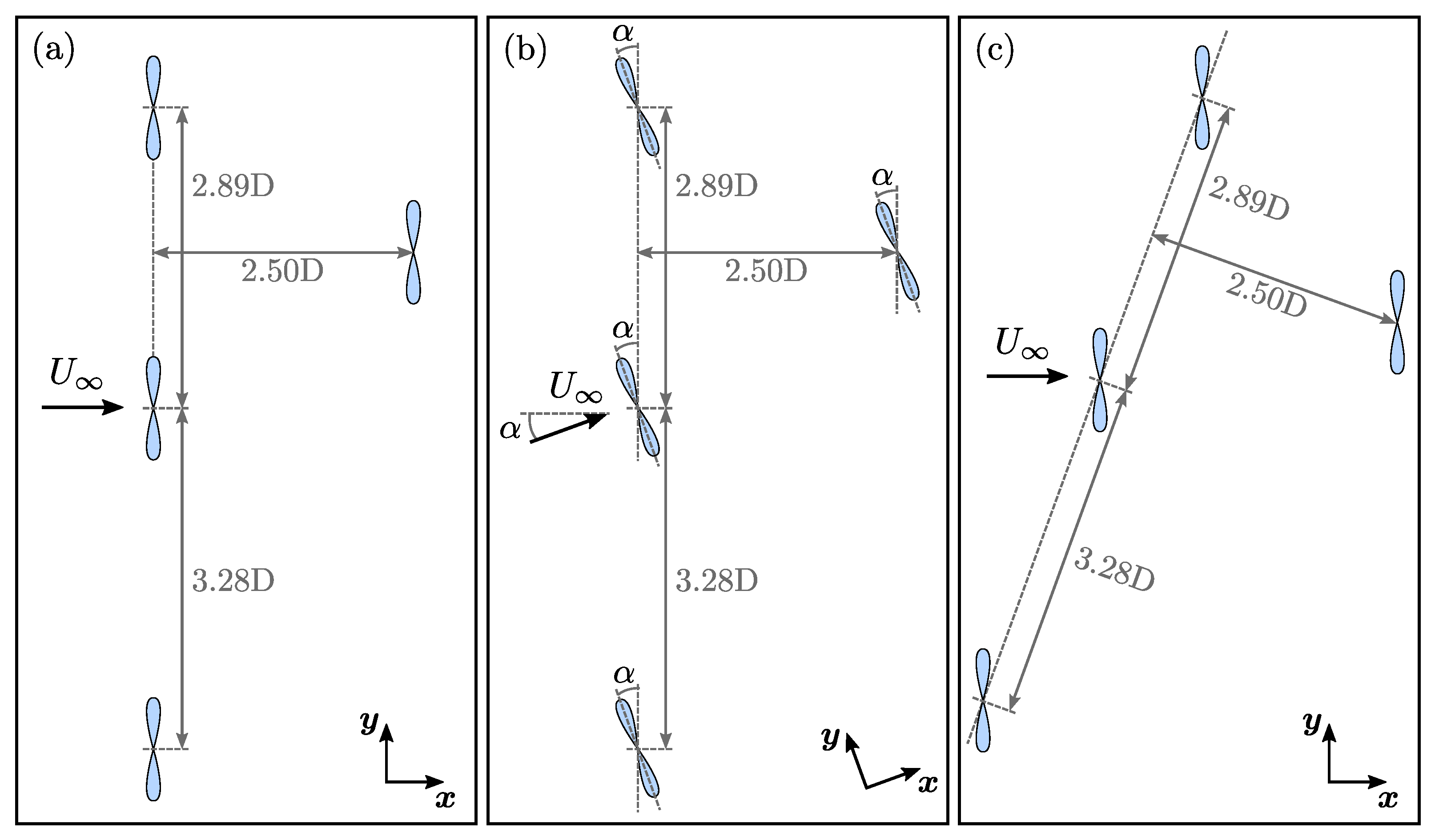
4.1. Description of the Selected Configuration: The NEPTHYD Project
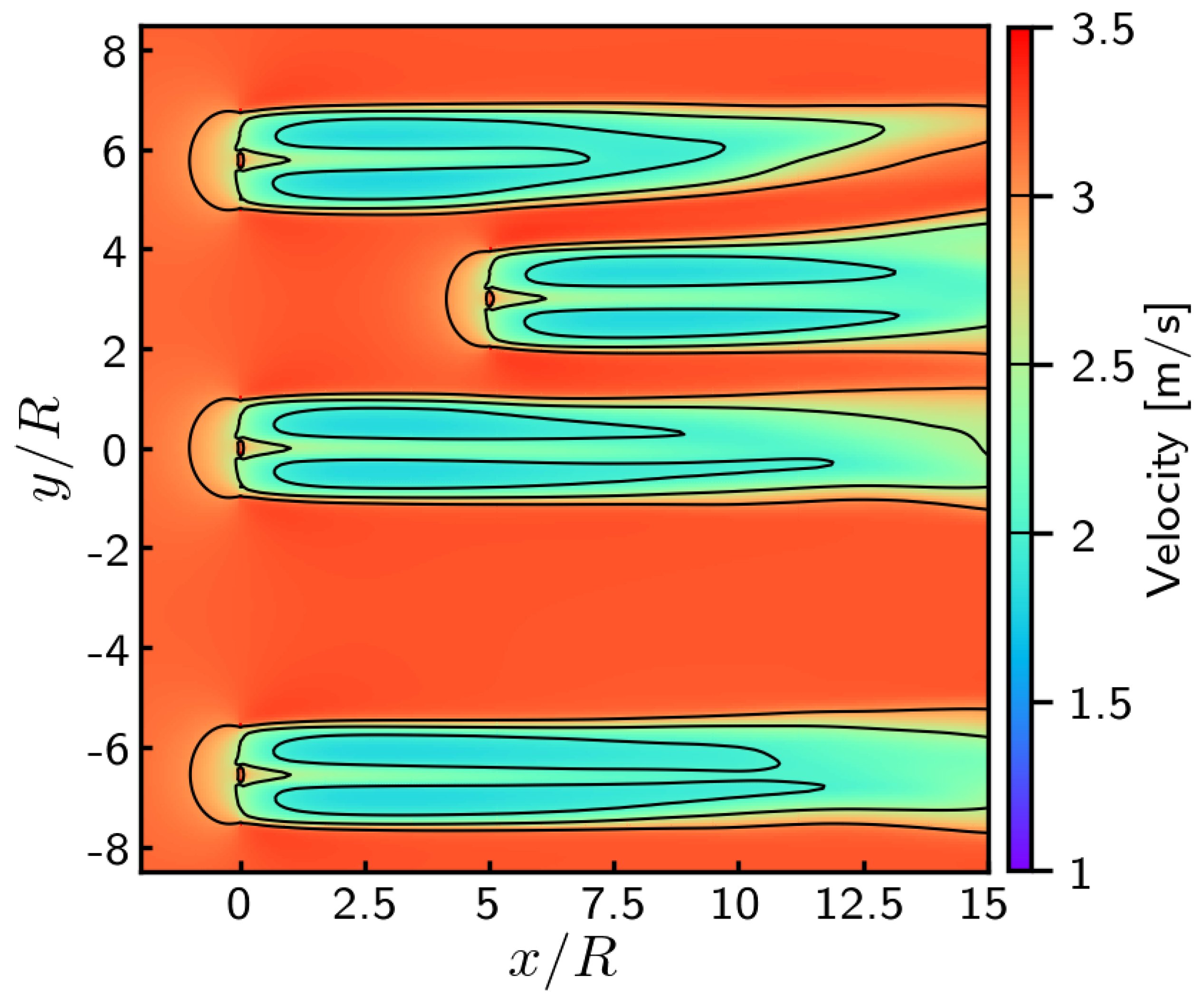
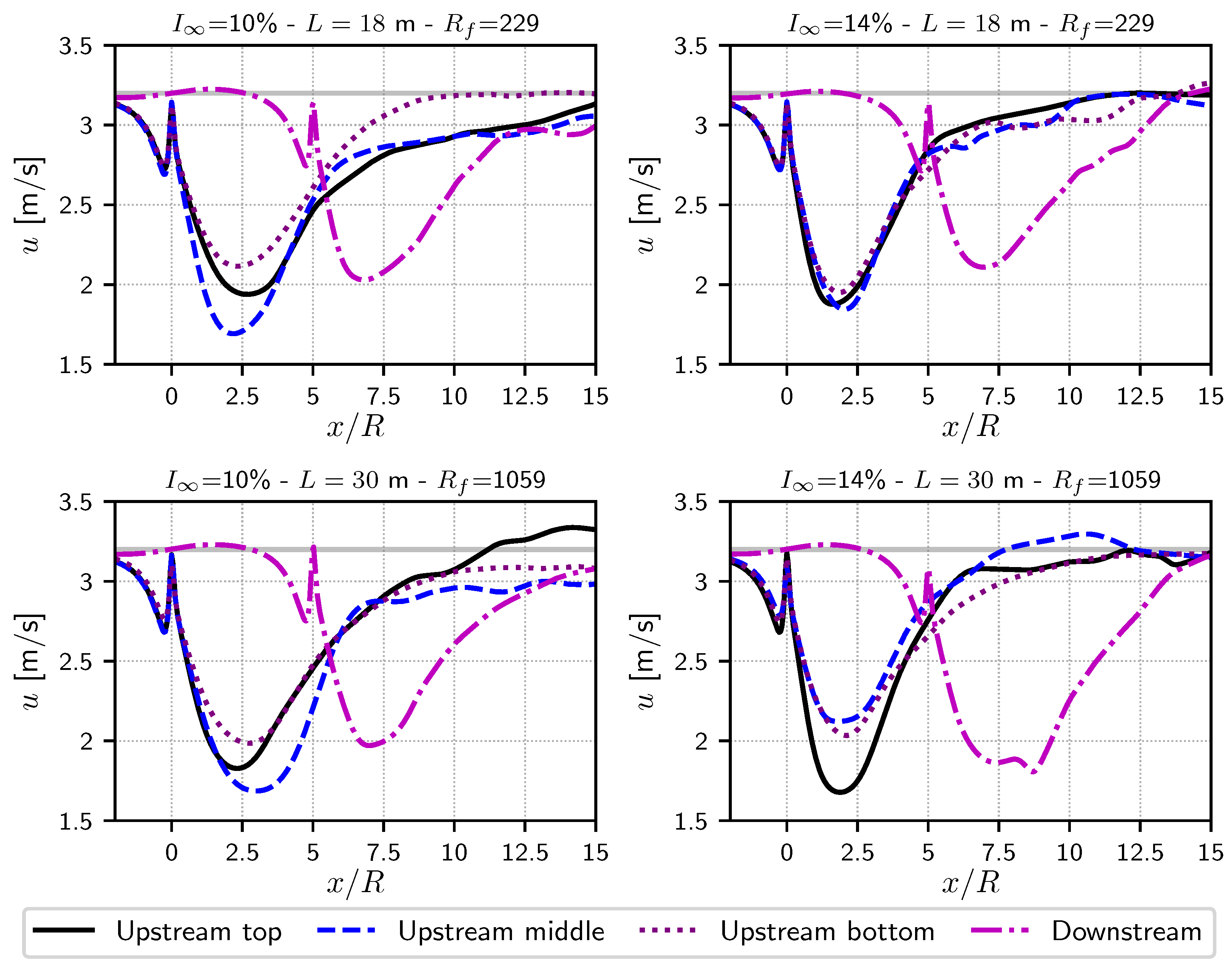
4.2. Initial Configuration
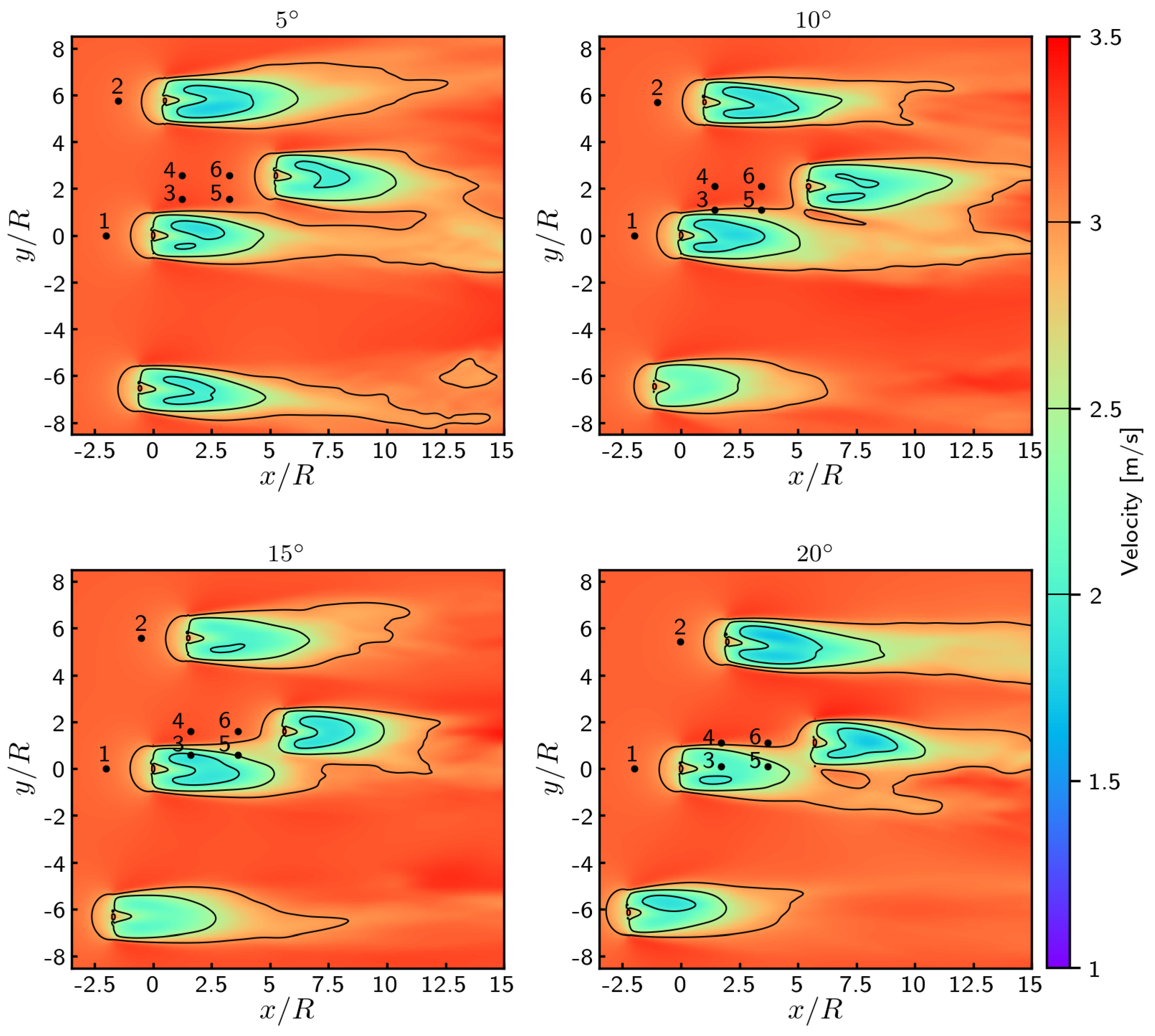
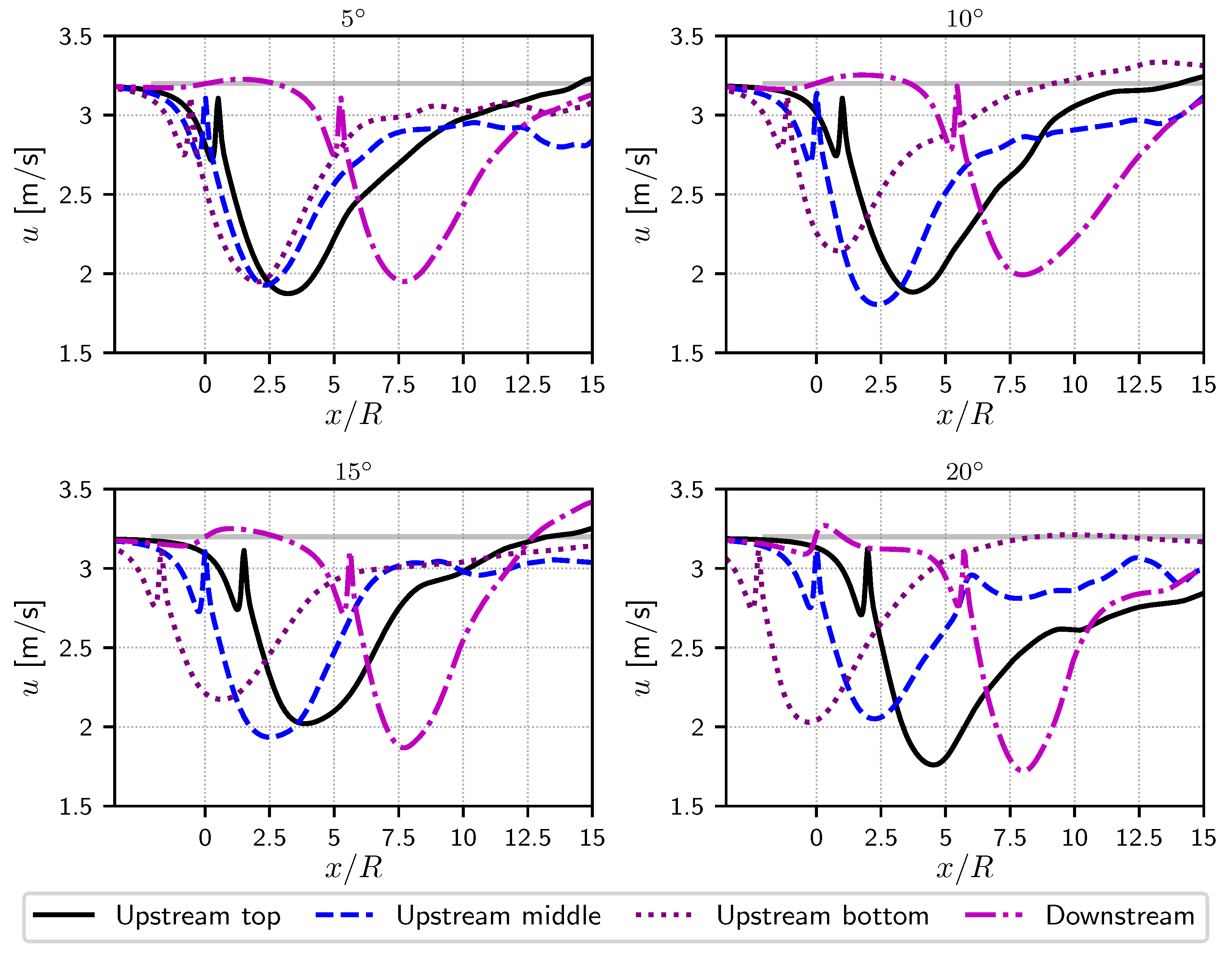
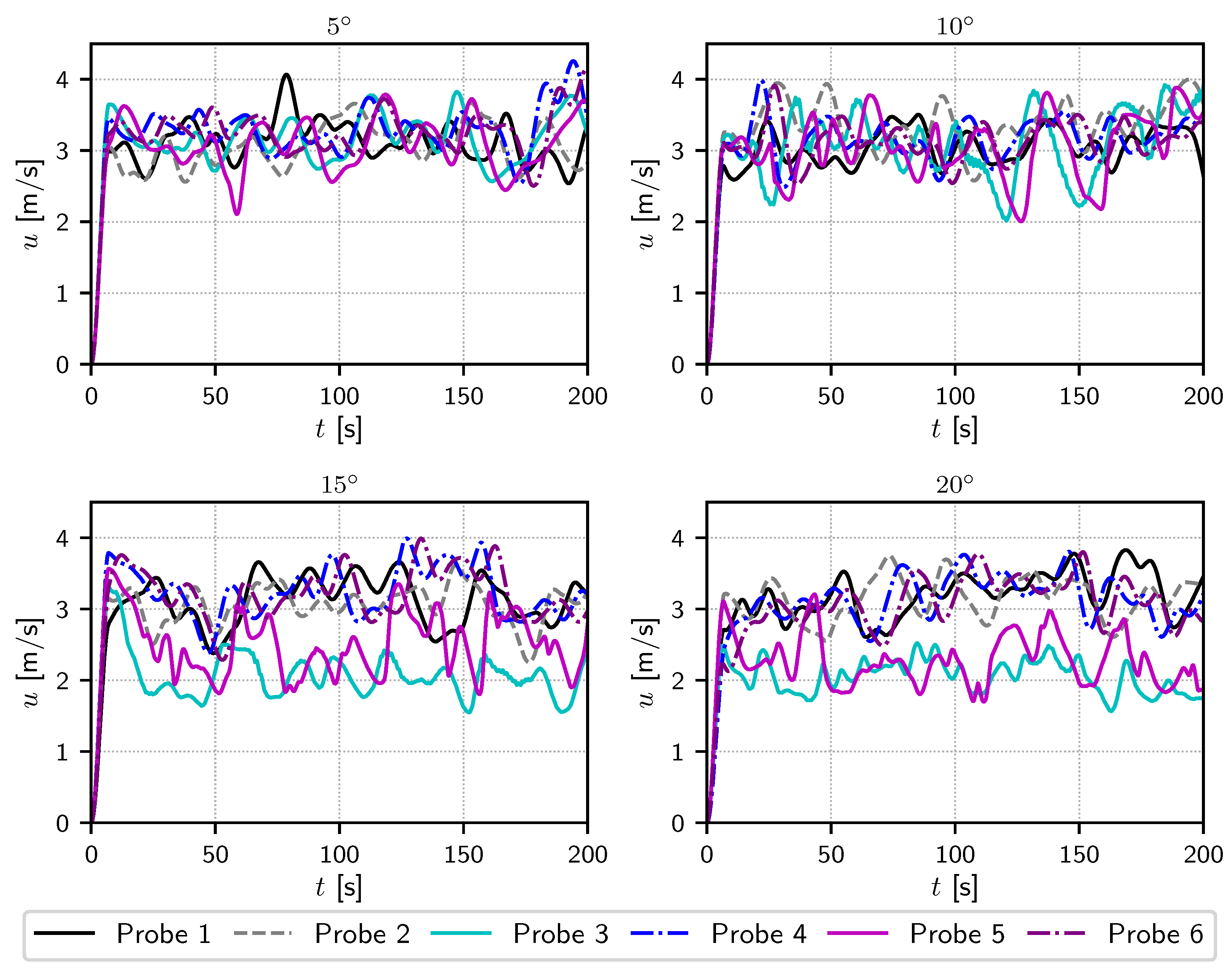
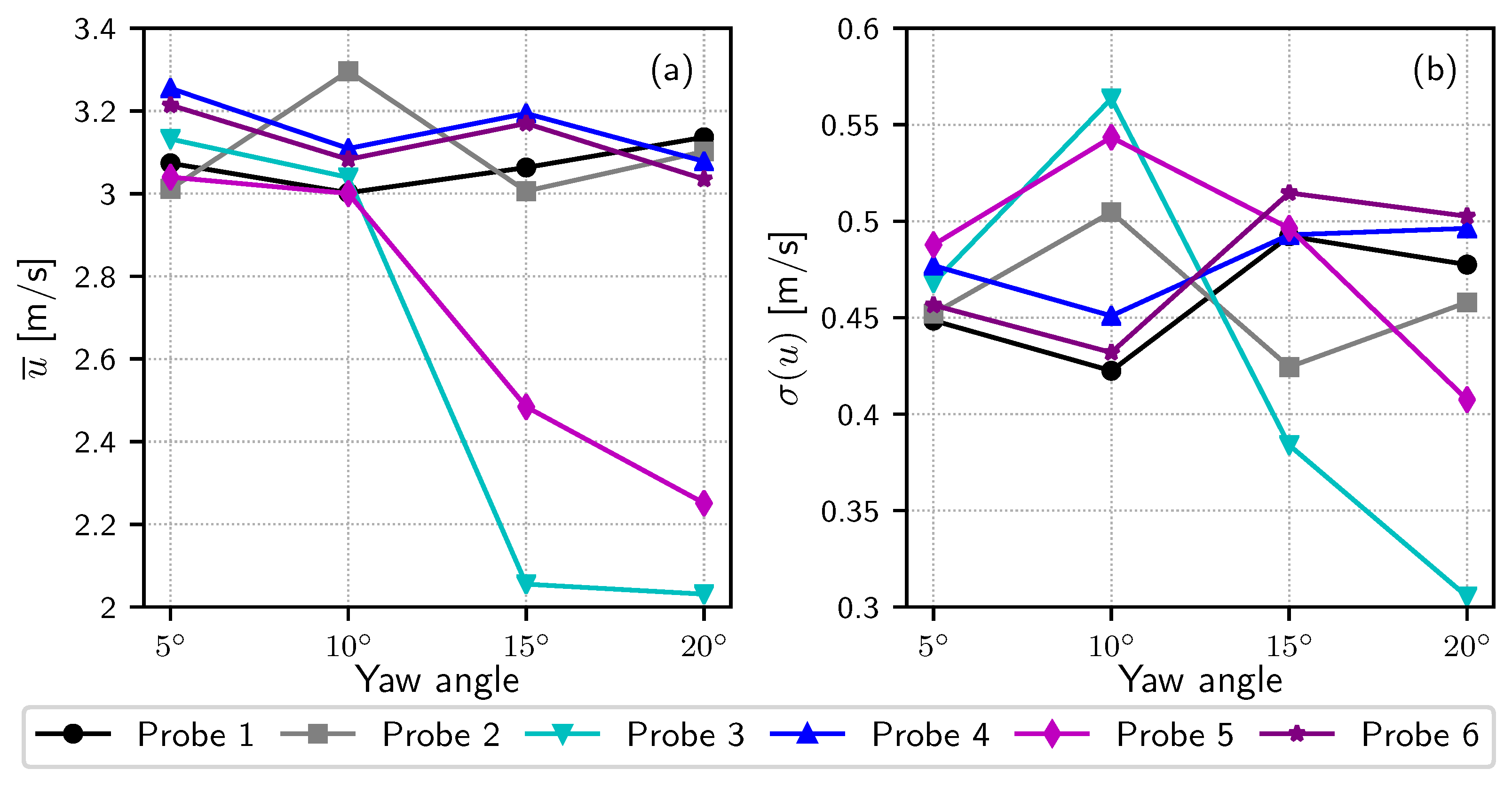
4.3. Yawed Flows
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LES | Large Eddy Simulation |
| PSE | Particle Strength Exchange |
| SEM | Synthetic Eddy Method |
| TSR | Tip Speed Ratio |
References
- EnFAIT. Enabling Future Arrays in Tidal. Available online: https://www.enfait.eu/ (accessed on 14 June 2021).
- SIMEC Atlantis Energy. Tidal Stream Projects MeyGen. Available online: https://simecatlantis.com/projects/meygen/ (accessed on 14 June 2021).
- Karsten, R.; Swan, A.; Culina, J. Assessment of arrays of in-stream tidal turbines in the Bay of Fundy. Philos. Trans. R. Soc. A Math. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [Green Version]
- Divett, T.; Vennell, R.; Stevens, C. Optimization of multiple turbine arrays in a channel with tidally reversing flow by numerical modelling with adaptive mesh. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef]
- Gerris Flow Solver. Available online: http://gfs.sourceforge.net/wiki/index.php/Main_Page (accessed on 14 June 2021).
- Churchfield, M.J.; Li, Y.; Moriarty, P.J. A large-eddy simulation study of wake propagation and power production in an array of tidal-current turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [Green Version]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part II: Two interacting turbines. Renew. Energy 2014, 68, 876–892. [Google Scholar] [CrossRef] [Green Version]
- Mycek, P. Étude Numérique et Expérimentale du Comportement d’Hydroliennes. Ph.D. Thesis, Université du Havre, Le Havre, France, 2013. [Google Scholar]
- Pinon, G.; Mycek, P.; Germain, G.; Rivoalen, E. Numerical simulation of the wake of marine current turbines with a particle method. Renew. Energy 2012, 46, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Osalusi, E.; Side, J.; Harris, R. Structure of turbulent flow in EMEC’s tidal energy test site. Int. Commun. Heat Mass Transf. 2009, 36, 422–431. [Google Scholar] [CrossRef]
- Osalusi, E.; Side, J.; Harris, R. Reynolds stress and turbulence estimates in bottom boundary layer of Fall of Warness. Int. Commun. Heat Mass Transf. 2009, 36, 412–421. [Google Scholar] [CrossRef]
- Thomson, J.; Polagye, B.; Durgesh, V.; Richmond, M. Measurements of Turbulence at Two Tidal Energy Sites in Puget Sound, WA. IEEE J. Ocean. Eng. 2012, 37, 363–374. [Google Scholar] [CrossRef]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.J.; Bickerton, S. Characteristics of the turbulence in the flow at a tidal stream power site. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef] [PubMed]
- McCaffrey, K.; Fox-Kemper, B.; Hamlington, P.E.; Thomson, J. Characterization of turbulence anisotropy, coherence, and intermittency at a prospective tidal energy site: Observational data analysis. Renew. Energy 2015, 76, 441–453. [Google Scholar] [CrossRef] [Green Version]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Chaplain, N.; Guillou, S. A comprehensive assessment of turbulence at a tidal-stream energy site influenced by wind-generated ocean waves. Energy 2020, 191, 116550. [Google Scholar] [CrossRef]
- Sentchev, A.; Thiébaut, M.; Guillou, S. Turbulence characterization at tidal-stream energy site in Alderney Race. In Developments in Renewable Energies Offshore; Soares, C.G., Ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Mercier, P.; Thiébaut, M.; Guillou, S.; Maisondieu, C.; Poizot, E.; Pieterse, A.; Thiébot, J.; Filipot, J.F.; Grondeau, M. Turbulence measurements: An assessment of Acoustic Doppler Current Profiler accuracy in rough environment. Ocean Eng. 2021, 226, 108819. [Google Scholar] [CrossRef]
- Furgerot, L.; Sentchev, A.; Bailly du Bois, P.; Lopez, G.; Morillon, M.; Poizot, E.; Méar, Y.; Bennis, A.C. One year of measurements in Alderney Race: Preliminary results from database analysis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef] [PubMed]
- Sentchev, A.; Nguyen, T.D.; Furgerot, L.; Bailly du Bois, P. Underway velocity measurements in the Alderney Race: Towards a three-dimensional representation of tidal motions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef] [PubMed]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Jochum, C.; Kilcher, L.F.; Guillou, S. Characterization of the vertical evolution of the three-dimensional turbulence for fatigue design of tidal turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef] [PubMed]
- Thiébaut, M.; Filipot, J.F.; Maisondieu, C.; Damblans, G.; Duarte, R.; Droniou, E.; Guillou, S. Assessing the turbulent kinetic energy budget in an energetic tidal flow from measurements of coupled ADCPs. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef]
- Bourgoin, A.C.L.; Guillou, S.S.; Thiébot, J.; Ata, R. Turbulence characterization at a tidal energy site using large-eddy simulations: Case of the Alderney Race. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef]
- Guillou, N.; Neill, S.P.; Thiébot, J. Spatio-temporal variability of tidal-stream energy in north-western Europe. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef] [PubMed]
- Lopez, G.; Bennis, A.C.; Barbin, Y.; Sentchev, A.; Benoit, L.; Marié, L. Surface currents in the Alderney Race from high-frequency radar measurements and three-dimensional modelling. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef]
- Bailly du Bois, P.; Dumas, F.; Morillon, M.; Furgerot, L.; Voiseux, C.; Poizot, E.; Méar, Y.; Bennis, A.C. The Alderney Race: General hydrodynamic and particular features. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A Synthetic-Eddy-Method for Generating Inflow Conditions for Large-Eddy Simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, B.J.; Kilcher, L. TurbSim User’s Guide: Version 1.06.00 (Draft Version); Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2012.
- Bernard, P.; Viré, A.; Moureau, V.; Lartigue, G.; Beaudet, L.; Deglaire, P.; Bricteux, L. Large-Eddy Simulation of wind turbines wakes including geometrical effects. Comput. Fluids 2018, 173, 133–139. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.; Afgan, I.; Stallard, T.; Stansby, P. Fluctuating loads on a tidal turbine due to velocity shear and turbulence: Comparison of CFD with field data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Mercier, P.; Grondeau, M.; Guillou, S.; Thiébot, J.; Poizot, E. Numerical study of the turbulent eddies generated by the seabed roughness. Case study at a tidal power site. Appl. Ocean Res. 2020, 97, 102082. [Google Scholar] [CrossRef]
- Pinon, G.; Carlier, C.; Fur, A.; Gaurier, B.; Germain, G.; Rivoalen, E. Account of ambient turbulence for turbine wakes using a Synthetic-Eddy-Method. J. Phys. Conf. Ser. 2017, 854, 012016. [Google Scholar] [CrossRef] [Green Version]
- Choma Bex, C.; Carlier, C.; Fur, A.; Pinon, G.; Germain, G.; Rivoalen, É. A stochastic method to account for the ambient turbulence in Lagrangian Vortex computations. Appl. Math. Model. 2020, 88, 38–54. [Google Scholar] [CrossRef]
- Chatelain, P.; Backaert, S.; Winckelmans, G.; Kern, S. Large Eddy Simulation of Wind Turbine Wakes. Flow Turbul. Combust. 2013, 91, 587–605. [Google Scholar] [CrossRef]
- Bossy, M.; Espina, J.; Moricel, J.; Paris, C.; Rousseau, A. Modeling the wind circulation around mills with a Lagrangian stochastic approach. SMAI J. Comput. Math. 2016, 2, 177–214. [Google Scholar] [CrossRef] [Green Version]
- Mycek, P.; Pinon, G.; Lothodé, C.; Dezotti, A.; Carlier, C. Iterative solver approach for turbine interactions: Application to wind or marine current turbine farms. Appl. Math. Model. 2017, 41, 331–349. [Google Scholar] [CrossRef] [Green Version]
- Autorité Environnementale. Projet Nepthyd. Technical report, Conseil Général de l’environement et du développement durable. Available online: http://www.cgedd.developpement-durable.gouv.fr/IMG/pdf/160406_-_Hydroliennes_Raz_Blanchard_-_Nepthyd_50_-_delibere_cle05849f.pdf (accessed on 9 March 2021).
- Rehbach, C. Calcul numérique d’écoulements tridimensionnels instationnaires avec nappes tourbillonaires. La Rech. Aérosp. 1977, 5, 289–298. [Google Scholar]
- Lewis, R. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Cottet, G.; Koumoutsakos, P. Vortex Methods: Theory and Practice; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Degond, P.; Mas-Gallic, S. The weighted particle method for convection-diffusion equations. Part I: The case of an isotropic viscosity. Math. Comp. 1989, 53, 485–507. [Google Scholar] [CrossRef]
- Choquin, J.; Huberson, S. Particles simulation of viscous flow. Comput. Fluids 1989, 17, 397–410. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Scientific Computation; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Mansour, N.; Ferziger, J.; Reynolds, W. Large-Eddy Simulation of a Turbulent Mixing Layer; Technical Report, Report TF-11; Thermosciences Div., Dept. of Mech. Eng., Stanford University: Stanford, CA, USA, 1978. [Google Scholar]
- Ogami, Y.; Akamatsu, T. Viscous flow simulation using the discrete vortex model—The diffusion velocity method. Comput. Fluids 1991, 19, 433–441. [Google Scholar] [CrossRef]
- Mycek, P.; Pinon, G.; Germain, G.; Rivoalen, E. Formulation and analysis of a diffusion-velocity particle model for transport-dispersion equations. Comput. Appl. Math. 2016, 35, 447–473. [Google Scholar] [CrossRef]
- Leonard, A. Vortex methods for flow simulation. J. Comput. Phys. 1980, 37, 289–335. [Google Scholar] [CrossRef]
- Winckelmans, G.S.; Leonard, A. Contributions to Vortex Particle Methods for the Computation of Three-Dimensional Incompressible Unsteady Flows. J. Comput. Phys. 1993, 109, 247–273. [Google Scholar] [CrossRef]
- Lindsay, K.; Krasny, R. A particle method and adaptive treecode for vortex sheet motion in three-dimensional flow. J. Comput. Phys. 2001, 172, 879–907. [Google Scholar] [CrossRef] [Green Version]
- Pinon, G.; Bratec, H.; Huberson, S.; Pignot, G.; Rivoalen, E. Vortex method for simulation of a 3D round jet in a cross-stream. J. Turbul. 2005, 6, 1–25. [Google Scholar] [CrossRef]
- Hauville, F.; Roux, Y. Réglage Dynamique d’une Voile par une Méthode d’Intéraction Fluide/Structure. 9èmes Journées de l’Hydrodynamique. 2003. Available online: http://website.ec-nantes.fr/actesjh/images/9JH/Annexe/16-04-05.pdf (accessed on 23 June 2021).
- Luersen, M.; Le Riche, R.; Lemosse, D.; Le Maître, O. A computationally efficient approach to swimming monofin optimization. Struct. Multidiscip. Optim. 2006, 31, 488–496. [Google Scholar] [CrossRef]
- Carlier, C.; Pinon, G.; Gaurier, B.; Germain, G.; Rivoalen, E. Numerical and experimental study of elementary interactions in marine current turbines array. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar]
- Lund, T.S.; Wu, X.; Squires, K.D. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef] [Green Version]
- Jarrin, N. Synthetic Inflow Boundary Conditions for the Numerical Simulation of Turbulence. Ph.D. Thesis, University of Manchester, Manchester, UK, 2008. [Google Scholar]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef] [Green Version]
- Choma Bex, C.; Pinon, G.; Slama, M.; Gaston, B.; Germain, G.; Rivoalen, E. Lagrangian Vortex computations of turbine wakes: Recent improvements using Poletto’s Synthetic Eddy Method (SEM) to account for ambient turbulence. J. Phys. Conf. Ser. 2020, 1618, 062028. [Google Scholar] [CrossRef]
- Maganga, F.; Germain, G.; King, J.; Pinon, G.; Rivoalen, E. Experimental characterisation of flow effects on marine current turbine behaviour and on its wake properties. IET Renew. Power Gener. 2010, 4, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Harding, S.; Bryden, I. Directionality in prospective Northern UK tidal current energy deployment sites. Renew. Energy 2012, 44, 474–477. [Google Scholar] [CrossRef]
- Frost, C.H.; Evans, P.S.; Harrold, M.J.; Mason-Jones, A.; O’Doherty, T.; O’Doherty, D.M. The impact of axial flow misalignment on a tidal turbine. Renew. Energy 2017, 113, 1333–1344. [Google Scholar] [CrossRef]
- Maslov, N.; Charpentier, J.F.; Claramunt, C. A modelling approach for a cost-based evaluation of the energy produced by a marine energy farm. Int. J. Mar. Energy 2015, 9, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Guillou, N.; Neill, S.P.; Robins, P.E. Characterising the tidal stream power resource around France using a high-resolution harmonic database. Renew. Energy 2018, 123, 706–718. [Google Scholar] [CrossRef] [Green Version]
- Baltazar, J.; Falcão de Campos, J.A.C. Hydrodynamic Analysis of a Horizontal Axis Marine Current Turbine With a Boundary Element Method. In Proceedings of the ASME 27th Conference on Offshore Mechanics and Arctic Engineering (OMAE), Estoril, Portugal, 15–20 June 2008; pp. 883–893. [Google Scholar] [CrossRef]
- Baltazar, J.; Falcão de Campos, J. An iteratively coupled solution of the cavitating flow on marine propellers using BEM. J. Hydrodyn. Ser. B 2010, 22, 838–843. [Google Scholar] [CrossRef]
- Boujleben, A.; Ibrahimbegovic, A.; Lefrançois, E. An efficient computational model for fluid-structure interaction in application to large overall motion of wind turbine with flexible blades. Appl. Math. Model. 2020, 77, 392–407. [Google Scholar] [CrossRef]
- Riziotis, V.A.; Voutsinas, S.G. Dynamic stall modelling on airfoils based on strong viscous–inviscid interaction coupling. Int. J. Numer. Methods Fluids 2008, 56, 185–208. [Google Scholar] [CrossRef]
- Zanon, A.; Giannattasio, P.; Simão Ferreira, C. A vortex panel model for the simulation of the wake flow past a vertical axis wind turbine in dynamic stall. Wind Energy 2013, 16, 661–680. [Google Scholar] [CrossRef]
- Salvatore, F.; Sarichloo, Z.; Calcagni, D. Marine Turbine Hydrodynamics by a Boundary Element Method with Viscous Flow Correction. J. Mar. Sci. Eng. 2018, 6, 53. [Google Scholar] [CrossRef] [Green Version]
- Togneri, M.; Pinon, G.; Carlier, C.; Choma Bex, C.; Masters, I. Comparison of synthetic turbulence approaches for blade element momentum theory prediction of tidal turbine performance and loads. Renew. Energy 2020, 145, 408–418. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slama, M.; Choma Bex, C.; Pinon, G.; Togneri, M.; Evans, I. Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race. Energies 2021, 14, 3826. https://doi.org/10.3390/en14133826
Slama M, Choma Bex C, Pinon G, Togneri M, Evans I. Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race. Energies. 2021; 14(13):3826. https://doi.org/10.3390/en14133826
Chicago/Turabian StyleSlama, Myriam, Camille Choma Bex, Grégory Pinon, Michael Togneri, and Iestyn Evans. 2021. "Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race" Energies 14, no. 13: 3826. https://doi.org/10.3390/en14133826
APA StyleSlama, M., Choma Bex, C., Pinon, G., Togneri, M., & Evans, I. (2021). Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race. Energies, 14(13), 3826. https://doi.org/10.3390/en14133826





