Photovoltaic Maximum Penetration Limits on Medium Voltage Overhead and Underground Cable Distribution Feeders: A Comparative Study

Abstract

This paper investigates the maximum photovoltaic (PV) penetration limits on both overhead lines and underground cables medium voltage radial distribution system. The maximum PV penetration limit is estimated considering both bus voltage limit (1.05 p.u.) and feeder current ampacity (1 p.u.). All factors affect the max PV penetration limit are investigated in detail. Substation voltage, load percentage, load power factor, and power system frequency (50 Hz or 60 Hz) are analyzed. The maximum PV penetration limit associated with overhead lines is usually higher than the value associated with the underground cables for high substation voltage (substation voltage = 1.05 and 1.04 p.u.). The maximum PV penetration limit decreases dramatically with low load percentage for both feeder types but still the overhead lines accept PV plant higher than the underground cables. Conversely, the maximum PV penetration increases with load power factor decreasing and the overhead lines capability for hosting PV plant remains higher than the capability of the underground cables. This paper proved that the capability of the 60-Hz power system for hosting the PV plant is higher than the capability of 50 Hz power system. MATLAB software has been employed to obtain all results in this paper. The Newton-Raphson iterative method was the used method to solve the power flow of the investigated systems.

1. Introduction

The need for affordable and accessible renewable energy sources (RESs) is, without a doubt, one of the key challenges facing the world. Access to energy is important to the development of any community. Therefore, the United Nations (UN) has included clean and affordable energy as one of the 2030 Sustainable Development Goals (SDGs). In this worldwide accepted resolution, goal seven aims to ensure access to affordable, reliable, sustainable, and modern energy for all [1,2]. In most typical electrical power grids, the generation units use fossil fuels to produce electricity. Burning fossil fuels creates several environmental problems such as climate change, global warming pollution, and ocean acidification. In fact, around 40% of global greenhouse gas emissions is related to electricity generation from burning fossil fuels [2]. Further, fossil fuels are nonrenewable resources and hence by definition are limited in supply. These reasons and more are what drive countries and utilities toward renewable energies.

One of the leading sources of the renewable energies is solar photovoltaic (PV) system. Using of this technology has been increasing rapidly in the last decade. As seen in Figure 1, in 2010, the solar PV contributed to around 3.3% of MW capacity of renewable energy worldwide, whereas it reached a little over 25% in 2020. In fact, the solar energy has now reached about the same level as the wind energy capacity [3]. This is due to many reasons such as the support of governments and environmental organizations to encourage utilities and consumers to shift toward cleaner and renewable energy sources. Further, the sharp decline of cost in manufacturing the PV panels is a big factor in increasing the presence of the solar PV systems around the world. In the last decade, the global weighted-average levelized cost of electricity (LCOE) of new utility-scale solar PV projects fell 82% [4]. In fact, a recent report [5] has found that the levelized cost of building large solar PV plants in many Asian countries is close to, or even lower than, building new thermal power plants with the same MW capacity. Hence, the cost of new solar PV projects is continuously decreasing. Case in point, UAE’s 1.5 GW tender, which drew world record for solar power price ($0.0135/kWh) back in April 2020, was trumped the following year by Saudi Arabia’s 600 MW second PV tender with a bid of $0.0104/kWh [6,7]. The capacity of installation in MW and GW represents the rating (peak power) of the PV plant at standard conditions (solar irradiance of 1000 W/m² and temperature = 25 °C). On the other hand, the $/kWh represents the price of every kWh of the produced energy by the PV plant.

However, this rise of solar PV is not without its own concerns. Due to the intermittent nature of RESs, especially solar PV, integration to existing distribution power systems could cause issues with stability and reliability of the power system [8,9]. It may cause problems with system voltage, nominal frequency, operations of capacitors and under-load tap changing transformers (LTC) [10]. This problem is more obvious in distribution systems since they tend to be radial, operate unbalanced, connected to dynamic consumer loads, and have high R/X ratios [11]. Hence, various research, summarized in reference [12], have been conducted on the effects of the high solar PV penetration. For example, reference [13] concluded that voltage is the limiting factor in reaching the maximum PV penetration limit, while reference [14] concluded that both the voltage and the harmonics affect the PV grid integration. Furthermore, reference [15] identified that the presence of unbalanced voltage conditions is a major concern. Moreover, other research have focused on providing solutions to mitigate the effects of high PV penetration and limit the issues that rise with integrating RESs with existing power systems especially distribution low voltage networks [16,17,18].

One of the research papers that discussed solar PV penetration and its effects on voltage limitations in distribution power networks is [19]. The authors in reference [19] studied the effects of the solar PV penetration on two major points: (1) limitation of receiving-end load voltage (${\mathrm{V}}_{\mathrm{L}}$) and (2) the feeder current ampacity. They concluded that when the sending-voltage of the distribution substation (${\mathrm{V}}_{\mathrm{S}}$) is lower than the upper voltage limit (105%), the feeder ampacity plays a role in limiting the solar PV power injected in the receiving-side of the feeder (at load). However, this paper and others, such as [20,21], focused only on the overhead lines (OHL). There are major known differences between the overhead lines and the underground cables (UGC). Aside from the cost [22] and reliability issues [23], there are electrical differences. A main difference is that the underground cables (UGC) have a much higher shunt capacitance per km than the overhead lines (OHL) [24].

Our study addresses this important difference by simulating a radial distribution system using underground cables. Since radial distribution feeders are almost all exclusively short lines (less than 80 km), we will not use the universally accepted approximation method of neglecting the capacitance C, as illustrated in many textbooks [25,26,27,28,29]. While this method is widely accepted, it defeats the purpose of our research since it will diminish the differences between the underground cables (UGC) and the overhead lines (OHL). Rather, we will simulate the UGC using the accurate modified π circuit, which is typically reserved for the long transmission lines (longer than 240 km). This method offers a better analysis and representation of the underground cables. Concurrently, many countries, such as the state of Kuwait (case study), primarily use underground cables for their distribution system. This paper moves to study the underground cables using the accurate modified π circuit to eliminate any approximation. Moreover, when a more accurate representation of the feeder as a real underground cable is employed, the feeder’s length can be adjusted to be a truer representation of a distribution system.

Moreover, most research has focused on PV penetration limitations considering voltage rise only. Though this is a major factor, it is not the only one. Feeder ampacity is a factor too. This paper examines these two stability limiters by combining them. It will be shown that most of the times, specifically for low sending-end voltage (${\mathrm{V}}_{\mathrm{S}}$), the feeder ampacity will be the effective limiting factor. Finally, this paper examines PV penetration under different operating conditions, such as: (1) changing sending-end voltage, (2) changing load percentage, (3) changing load power factor, and (4) changing operating system frequency (50 Hz or 60 Hz).

To summarize, the objectives of this paper are:

• Considering both voltage and current simultaneously as PV penetration limiters;
• Comparing the PV penetration limits on OHL and UGC;
• Modelling the UGC using the accurate modified π circuit;
• Investigating the system under different operating conditions especially the power system frequency (50–60 Hz).

This paper is divided into six sections. Section 2 provides a detailed description of the investigated radial distribution system along with parameters of the used feeders (both OHL and UGC). Section 3 provides the mathematical analysis and the employed methodologies. It also examines the effect of PV penetration on both types (OHL and UGC) of the feeder. The results and discussions are explored in Section 4. There, results show the effects of changing operation conditions on PV maximum penetration limits. Section 5 compares Thumb rule of determining maximum PV penetration limit to the more accurate calculated method. The paper is, finally, concluded in Section 6.

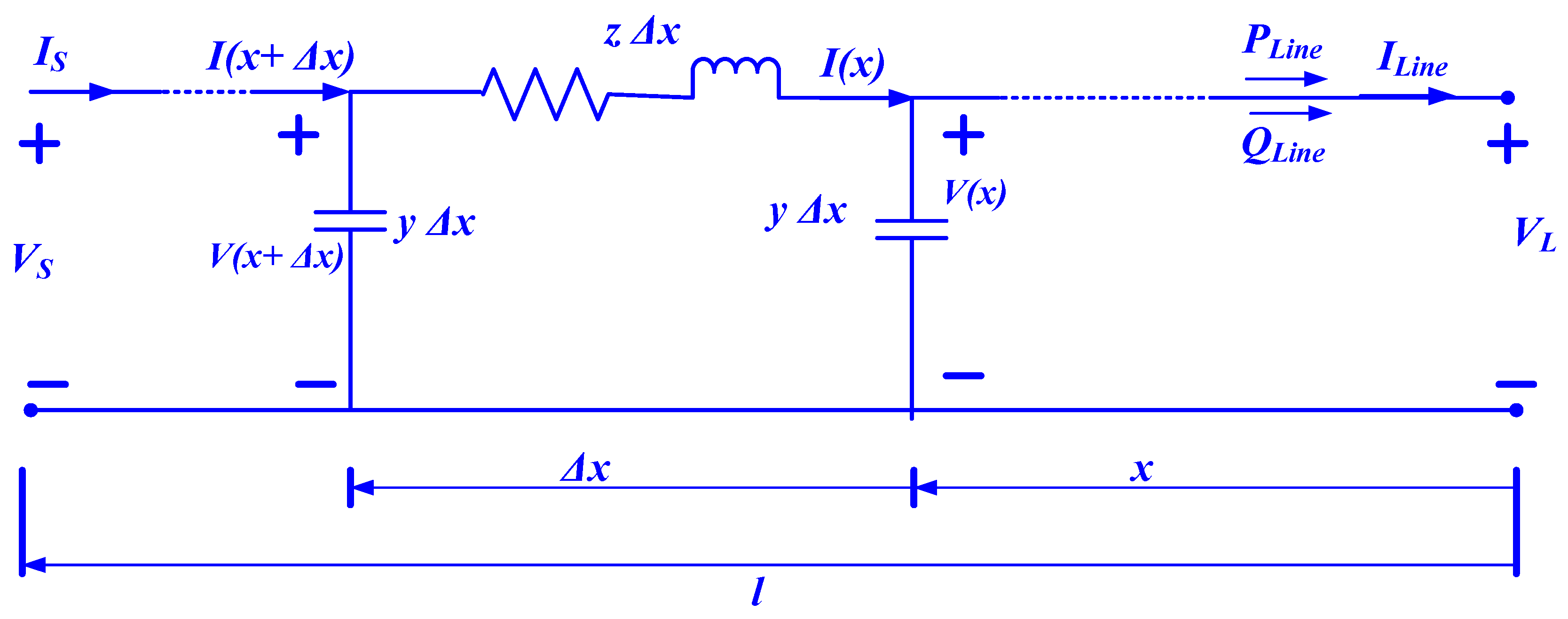
2. Description of the Investigated Overhead Lines (OHL) and Underground Cables (UGC) Distribution Systems

The investigated system in this paper is a medium-voltage (MV) radial distribution feeder as shown in Figure 2. The feeder supplies its rated load at the end of the feeder. The proposed PV plant is shunted at the load bus as shown in Figure 2. As mentioned in the introduction, most researchers focused on the maximum PV penetration limit for the OHL. For many countries, such as the state of Kuwait (case study), nearly all MV distribution systems are UGC. Based on this fact, this manuscript investigates three distribution feeders as follows:

2.1. Overhead Medium Voltage (MV) Distribution Overhead Line (OHL)

The overhead line (OHL) represents the reference case which is described in detail in [19]. The studied line is three phase balanced radial line. It compromised of aluminum conductor with parameters and rated values as reported in

Table 1. Parameters and rated values of the studied Overhead Lines (OHL) [19].

Type	Voltage ${\mathbf{V}}_{\mathbf{Rated}}$	Current ${\mathbf{I}}_{\mathbf{Rated}}$	Complex Power ${\mathbf{S}}_{\mathbf{Rated}}$	Frequency $\mathit{f}$	Power Factor pf	Resistance $\mathit{r}$	Reactance $\mathit{x}$	Capacitance $\mathit{c}$
OHL	13.8 kV	314 A	7.5 MVA	50 Hz	0.92 lagging	0.3 Ω/km	0.409 Ω/km	0 µF/km

. The investigated OHL data in Table 1 and detailed information are available in reference [19].

For calculating the length of the OHL, maintain a voltage drop $\Delta \mathrm{V}=5\%$ of the nominal operating voltage at rated load. Feeder length is calculated using the approximate method of voltage drop where:

$$\Delta V=\left|IZ\right|=\left|I\right|\left(R\cos \theta +X\sin \theta \right)=\left|I\right|\left(r\times l\cos \theta +x\times l\sin \theta \right)$$

(1)

From Equation (1), the line length can be calculated as follows:

$$\mathrm{Line\; Length}=l=\frac{\Delta V}{\left|I\right|\left(r\cos \theta +x\sin \theta \right)}$$

where cos(θ) is the load power factor.

Considering the distribution feeder as an overhead line (OHL) with the parameter in Table 1 [19]:

$$l=\frac{0.05\left(\raisebox{1ex}{$13.8$}\!\left/ \!\raisebox{-1ex}{$\sqrt{3}$}\right.\mathrm{kV}\right)}{314\mathrm{A}\left(0.300\left[\frac{\Omega }{\mathrm{km}}\right]\times \cos 23.073°+0.409\left[\frac{\Omega }{\mathrm{km}}\right]\times \sin 23.073°\right)}=2.91\mathrm{km}$$

However, we used 2.85 km to be consistent with the reference paper [19].

2.2. Underground Cable—Long (UGCL)

To make a comparison between the capability of the OHL and the UGC for hosting new PV plant, this study considered UGC to nearly has the same rating of the OHL. This cable is used in the Kuwait MV distribution system. The cable parameters and rated values are reported in

Table 2. Underground Cable (UGC) parameters and rated values.

Type	$\mathbf{Voltage} {\mathbf{V}}_{\mathbf{Rated}}$	$\mathbf{Current} {\mathbf{I}}_{\mathbf{Rated}}$	$\mathbf{Complex} \mathbf{Power} {\mathbf{S}}_{\mathbf{Rated}}$	Frequency $\mathit{f}$	Power Factor pf	Resistance $\mathit{r}$	Reactance $\mathit{x}$	Capacitance $\mathit{c}$
UGC	13.8 kV	320 A	7.648 MVA	50 Hz	0.92 lagging	0.247 Ω/km	0.132 Ω/km	0.259 µF/km

. Detailed information about the used cable can be found in Reference [30].

To calculate the feeder maximum length ($\Delta \mathrm{V}=5\%$), using Equation (1) and cable parameters in Table 2, the UGC length can be calculated as follows:

$$l=\frac{0.05\left(\raisebox{1ex}{$13.8$}\!\left/ \!\raisebox{-1ex}{$\sqrt{3}$}\right.\mathrm{kV}\right)}{320\mathrm{A}\left(0.247\left[\frac{\Omega }{\mathrm{km}}\right]\times \cos 23.073°+0.132\left[\frac{\Omega }{\mathrm{km}}\right]\times \sin 23.073°\right)}=4.46\mathrm{km}$$

As shown, the UGC (4.46 km) is longer than the same rating OHL (2.85 km). Due to this fact, this cable will be called UGC long (UGCL).

2.3. Underground Cable (UGC) with Same Length of the Overhead Lines (OHL)

For the purpose of comparison, this study investigated UGC with the parameters and rated values exist in Table 2, but the cable will be assigned the same length of the OHL (2.85 km). This cable will be called UGC.

3. Effect of Photovoltaic (PV) Penetration on Both Overhead Lines (OHL) and Underground Cable (UGC) Feeders: Mathematical Analysis and Modeling

Connecting PV plant to the radial distribution feeder (OHL or UGC) affects the receiving-end voltage (load bus voltage) and the feeder current. The following subsections describe how the voltage and the current of the OHL and the UGC distribution feeders will be affected by the PV penetration.

3.1. Effect of Photovoltaic (PV) Penetration in the Overhead Lines (OHL)

3.1.1. Effect of Photovoltaic (PV) Plant on Feeder end Voltage (Load Bus Voltage)

From single line diagram in Figure 3, the voltage-drop ($\Delta V$) across the OHL can be calculated as follows:

$$\Delta \mathrm{V}=V_S-V_L=\frac{\left(P_{line}{R}_{line}+Q_{line}{X}_{line}\right)}{V_L}$$

(2)

$$P_{line}=\left(P_{Load}-P_{PV}\right)$$

(3)

The injected reactive power by the PV inverter ($Q_{PV}$) is equal to zero (the PV plant operates at unity power factor):

$$Q_{PV}=0$$

(4)

The reactive power flow through the line is:

$$Q_{line}=Q_{Load}$$

(5)

From Equations (2) to (5), the voltage drop across the OHL is given by:

$$\Delta V=\frac{\left[R_{line}\left(P_{load}-P_{PV}\right)+X_{line}{Q}_{load}\right]}{V_L}$$

(6)

From Equation (6), as the PV power ($P_{PV}$) increases, the voltage drop across the OHL ($\Delta V$) decreases and the load voltage $V_L$ increases. If the generated power by PV plant $\left(P_{PV}\right)$ is equal to the power consumed by the load ($P_{load}$), only the reactive power absorbed by load ($Q_{Load}$) flows through the feeder. If the $P_{PV}$ exceeds the load power, the first term in Equation (6) ($R_{line}\left(P_{load}-P_{PV}\right)$) becomes negative.

For the following condition,

$$\frac{\left(P_{load}-P_{PV}\right)}{Q_{load}}=\frac{X_{line}}{R_{line}}$$

(7)

The voltage-drop over the OHL ($\Delta V$) is equal to zero, and the load voltage ($V_L$) is equal to the substation voltage ($V_S$).

If the PV power ($P_{PV}$) continues to increase, the voltage-drop across the feeder $\left(\Delta V\right)$ will be negative, which means that the load voltage $\left(V_L\right)$ is higher than the substation voltage $\left(V_S\right)$.

The PV maximum penetration limit can be defined as the value forces the load voltage $\left(V_L\right)$ to reach the upper limit voltage ($V_{L-upper}=1.05\mathrm{p.u.}$). This rating of PV plant power ($P_{PV}$) represents the maximum PV penetration on OHL limited by the load bus voltage.

3.1.2. Effect of Photovoltaic (PV) Penetration on Overhead Lines (OHL) Current

From Figure 3, the feeder or line current ($I_{line}$) can be calculated as follows:

$$\left|I_{line}\right|=\frac{\left|S_{line}\right|}{\left|V_L\right|}$$

(8)

$$S_{line}=P_{line}+j{Q}_{line}=\left(P_{load}-P_{PV}\right)+j{Q}_{load}$$

(9)

$$\left|S_{line}\right|=\sqrt{{\left(P_{load}-P_{PV}\right)}^2+Q_{load}^2}$$

(10)

From Equations (8) and (10), the magnitude of the feeder current ($\left|I_{line}\right|$) can be expressed as:

$$\left|I_{line}\right|=\frac{\sqrt{{\left(P_{load}-P_{PV}\right)}^2+Q_{load}^2}}{\left|V_L\right|}$$

(11)

From Equation (11), for zero PV power $P_{PV}=0$, (No PV plant or during the night), the feeder current is equal to the load current as follows:

$$\left|I_{line}\right|=\frac{\sqrt{P_{load}^2+Q_{load}^2}}{\left|V_L\right|}$$

(12)

When the PV plant injects active power, the line current starts to decrease. If the PV plant power equal to the load power ($P_{PV}=P_{load}$), the feeder current is at its minimum value (only the load reactive power flow in line), and can be calculated as follows:

$$\min \left|I_{line}\right|=\frac{\left|Q_{load}\right|}{\left|V_L\right|}$$

(13)

If the PV active power exceeds than the load demand (active power reverse), the feeder current increases again. The feeder current continues to increase until it reaches the feeder rated current (feeder ampacity, $\left|I_{line}\right|=1\mathrm{p.u.}$). The value of the PV power at this condition is equal to the maximum PV penetration on OHL limited by the feeder ampacity (line current) and can be calculated as follows:

$$\max \left|I_{line}\right|=1 \mathrm{p.u}.=\frac{\sqrt{{\left(P_{load}-P_{PV,max}\right)}^2+Q_{load}^2}}{\left|V_L\right|}$$

(14)

From Equation (14), the PV maximum power ($P_{PV,max}$) limited by the line current (feeder ampacity) can be estimated as:

$$P_{PV,max}=P_{load}-\sqrt{{\left(V_L\right)}^2-Q_{load}^2}$$

(15)

3.2. Effect of Photovoltaic (PV) Penetration on the Underground Cable (UGC)

The maximum PV power limited by the voltage and current of the OHL has been described in Section 3.1. As shown in Figure 3, the capacitance of OHL is neglected. This is because the line voltage is a medium voltage (13.8 kV) and the line length is very short (2.85 km). For UGC, the cable has a considerable capacitance (Table 2) and cannot be ignored. In this study, the exact equivalent circuit of the UGC with distributed parameters (Figure 4) is considered [27,28].

Assuming $z=r+j\omega L$ is the series impedance of the cable per unit length, and $y=g+j\omega C$ is the parallel admittance of the cable per unit length. After writing and solving the differential equation of the UGC equivalent circuit in Figure 4 [27,28], the following equations can be obtained:

$$V_S=\cosh \left(\gamma l\right)V_L+Z_C\sinh \left(\gamma l\right)I_{line}$$

(16)

$$I_S=\frac{1}{Z_C}\sinh \left(\gamma l\right)V_L+\cosh \left(\gamma l\right)I_{line}$$

(17)

where $Z_C$ is the characteristics impedance and can be given by:

$$Z_C=\sqrt{\frac{z}{y}}$$

(18)

where $\gamma$ is the propagation constant of the waveform and can be calculated as:

$$\gamma =\sqrt{zy}=\sqrt{\left(r+j\omega L\right)\left(g+j\omega C\right)}$$

(19)

We can find an accurate π model (Figure 5) of the UGC using these steps. The following equations are the basis for the π model of the UGC [27,28]:

$$V_S=\left(1+\frac{Z^{-}{Y}^{-}}{2}\right)V_L+Z^{-}{I}_{line}$$

(20)

$$I_S=\left(1+\frac{Z^{-}{Y}^{-}}{4}\right)V_L+\left(1+\frac{Z^{-}{Y}^{-}}{2}\right)I_{line}$$

(21)

The parameters of the accurate π model of the UGC can be defined as follows [27,28]:

$$Z^{-}=Z_C\sinh \left(\gamma l\right)=Z\frac{\sinh \left(\gamma l\right)}{\left(\gamma l\right)}$$

(22)

$$\frac{Y^{-}}{2}=\frac{1}{Z_C}\tanh \left(\frac{\gamma l}{2}\right)=\frac{Y}{2}\frac{\tanh \left(\gamma l/2\right)}{\left(\gamma l/2\right)}$$

(23)

The line current in Equation (20) can be written as follows:

$$I_{line}=\frac{S_{line}^{*}}{V_L^{*}}=\frac{\left(P_{load}-P_{PV}\right)-j{Q}_{load}}{V_L^{*}}$$

(24)

From Equations (20) and (24), the following equation can be obtained:

$$V_S=\left(1+\frac{Z^{-}{Y}^{-}}{2}\right)V_L+Z^{-}\frac{\left(P_{load}-P_{PV}\right)-j{Q}_{load}}{V_L^{*}}$$

(25)

This equation is a nonlinear equation and can be solved by one of the iterative methods, such as Gauss–Seidel and Newton-Raphson. Due to its fast conversion, this paper used the Newton-Raphson method. MATLAB codes have been developed by authors to solve the nonlinear equation according to the Newton-Raphson method iterative method. For every value of $P_{PV}$, the load voltage ($V_L$) can be estimated. The value of $P_{PV}$ that forces the load voltage $V_L$ to its upper limit value (1.05 p.u.) represents the maximum PV penetration on the UGC limited by load bus voltage.

From Equation (24), as the $P_{PV}$ increases, the line current ($I_{line}$) decreases until it reaches the minimum value when the $P_{PV}=P_{load}$. If the $P_{PV}$ exceeds the load demand, the line current ($I_{line}$) increases again. Value of the $P_{PV}$ that forces the line current ($I_{line}$) to be equal to the feeder ampacity (1 p.u.) represents the maximum $P_{PV}$ penetration on UGC limited by feeder ampacity (line current). The following flowchart describes in detail the steps of the employed methods (Figure 6).

4. Results and Discussions

The following results show how the maximum PV penetration limit for different types of radial distribution feeders (OHL, UGC, and the longer UGCL) can be affected by substation voltage, load percentage, load power factor, and system frequency (50 or 60 Hz). For each one of the previous factors, the PV maximum penetration limit and the limiting factor (feeder ampacity or bus voltage) are decided. Additionally, the increasing or decreasing percentages of the PV maximum penetration limit for the three feeder types are estimated for each case.

4.1. Effects of Substation Voltage

Usually, the MV transformer substation is equipped with a transformer tab changer (Figure 2). The tab changer is responsible for the voltage regulation at different load conditions [31,32,33]. In this study, the transformer substation voltage ($V_S$) varies from 1.05 p.u. (at heavy loads) to 1 p.u. at (light loads).

4.1.1. PV Maximum Penetration Limited by Voltage Only for Different Feeders

In this case, the maximum PV penetration limits for different feeders are estimated while only the voltage upper limit ($V_L=1.05\mathrm{p.u}.$) is considered and the feeders ampacities are ignored. The purpose of studying this case is to prove that the feeder ampacity is the limiting factor not the bus voltage during several conditions. As mentioned before, most literature which deals with the maximum PV penetration limit only considers the voltage rise and ignores the feeder ampacity. The following table and figure show that the current limiting is more important than the voltage limiting in several cases.

As indicated in

Table 3. Changing the substation voltage ($V_S$) for the different feeders (limited by voltage only).

VS. $(\mathbf{p}.\mathbf{u}.)$	VL $(\mathbf{p}.\mathbf{u}.)$			ILine $(\mathbf{p}.\mathbf{u}.)$			PPV $(\mathbf{p}.\mathbf{u}.)$			Change in % PPV from the OHL
	OHL	UGC	UGCL	OHL	UGC	UGCL	OHL	UGC	UGCL	UGC	UGCL
1.05	1.05	1.05	1.05	0.65	0.42	0.42	1.474	1.131	1.131	−23.3%	−23.3%
1.04	1.05	1.05	1.05	0.92	0.67	0.57	1.805	1.505	1.371	−16.6%	−24.0%
1.03	1.05	1.05	1.05	1.22	0.99	0.76	2.142	1.880	1.612	−12.2%	−24.8%
1.02	1.05	1.05	1.05	1.54	1.33	0.96	2.489	2.258	1.854	−9.3%	−25.5%
1.01	1.05	1.05	1.05	1.87	1.68	1.18	2.845	2.636	2.096	−7.3%	−26.3%
1.00	1.05	1.05	1.05	2.21	2.03	1.40	3.211	3.015	2.340	−6.1%	−27.1%

, all currents with shaded cells cannot be achieved in the practical situation. These results indicate that the most important limiting factor is the feeder current ampacity not the voltage rise, as most researchers have claimed.

Figure 7 shows the maximum PV penetration limit considering the voltage limit only (for ${\mathrm{V}}_{\mathrm{S}}=1\mathrm{p.u}.$). As shown, the current for all feeders reached very high unacceptable values. For OHL, the current reached 2.21 p.u. which means the feeder is more than 120% overload. For UGC, the current value reached 2.03 p.u. which is also an unacceptable value.

4.1.2. PV Maximum Penetration Limited by Both Voltage and Current (Practical Case)

Table 4. Changing the substation voltage ($V_S$) for the different feeders (limited by both voltage and current).

VS. $(\mathbf{p}.\mathbf{u}.)$	VL $(\mathbf{p}.\mathbf{u}.)$			ILine $(\mathbf{p}.\mathbf{u}.)$			PPV $(\mathbf{p}.\mathbf{u}.)$			Change in % PPV from the OHL
	OHL	UGC	UGCL	OHL	UGC	UGCL	OHL	UGC	UGCL	UGC	UGCL
1.05	1.05	1.05	1.05	0.65	0.42	0.42	1.474	1.131	1.131	−23.3%	−23.3%
1.04	1.05	1.05	1.05	0.92	0.67	0.57	1.805	1.505	1.371	−16.6%	−24.0%
1.03	1.04	1.05	1.05	1.00	0.99	0.76	1.885	1.880	1.612	−0.30%	−14.5%
1.02	1.03	1.04	1.05	1.00	1.00	0.96	1.875	1.883	1.854	0.40%	−1.10%
1.01	1.02	1.03	1.04	1.00	1.00	1.00	1.863	1.872	1.884	0.50%	1.10%
1.00	1.01	1.02	1.03	1.00	1.00	1.00	1.852	1.860	1.874	0.50%	1.20%

shows the maximum PV penetration limited by both voltage and current for different feeders and different substation voltages. As shown in Table 4, for high substation voltages ($V_S=1.05$ or $1.04\mathrm{p.u}.$), the load bus voltage is the limiting factor for the three feeder types (Figure 8). On the other side, for low substation voltages ($V_S=1.01$ or $1\mathrm{p.u}.$), the feeder ampacity is the limiting factor. For $V_S=1.03\mathrm{p.u}.$, the maximum PV penetration is limited by feeder ampacity of the OHL while it is limited by bus voltage for both UGC and UGCL. If $V_S=1.02\mathrm{p.u}.$, the maximum PV penetration is limited by feeder current for both the OHL and the UGC while limited by voltage for the UGCL.

As shown in Table 4, for the high substation voltage ($V_S=1.05$ or $1.04\mathrm{p.u}.$), the load bus voltage is the limiting factor for the three feeder types (Figure 8). On the other side, for the low substation voltage ($V_S=1.01$ or $1\mathrm{p.u}.$), the feeder ampacity is the limiting factor. For $V_S=1.03\mathrm{p.u}.$, the maximum PV penetration is limited by feeder ampacity of the OHL and limited by bus voltage for both the UGC and the UGCL. If $V_S=1.02\mathrm{p.u}.$, the maximum PV penetration is limited by current for both the OHL and the UGC while limited by voltage for the UGCL.

The difference between maximum PV penetration limit for the OHL and the UGC decreases as the substation voltage decreases. For $V_S=1.05\mathrm{p.u}.$, both the UGC and the UGCL can host PV plants with a rating 23.3% lower than what can be hosted by the OHL. For $V_S=1.01\mathrm{p.u}.$, there is no considerable difference between the maximum PV penetration limits of the three different feeders (0.5% and 1.1%).

4.2. Effects of Load Percentage

Table 5. Changing the load percentage for the different feeders (Substation voltage $V_S=1.05\mathrm{p.u}.$).

% of Rated Load	VL $(\mathbf{p}.\mathbf{u}.)$			ILine $(\mathbf{p}.\mathbf{u}.)$			PPV $(\mathbf{p}.\mathbf{u}.)$			Change in % PPV from OHL
	OHL	UGC	UGCL	OHL	UGC	UGCL	OHL	UGC	UGCL	UGC	UGCL
100	1.05	1.05	1.05	0.646	0.424	0.424	1.474	1.131	1.131	−23.3%	−23.3%
90	1.05	1.05	1.05	0.580	0.381	0.381	1.324	1.017	1.017	−23.2%	−23.2%
80	1.05	1.05	1.05	0.514	0.339	0.339	1.175	0.903	0.903	−23.1%	−23.1%
70	1.05	1.05	1.05	0.449	0.296	0.296	1.027	0.79	0.79	−23.1%	−23.1%
60	1.05	1.05	1.05	0.384	0.253	0.253	0.879	0.676	0.676	−23.1%	−23.1%
50	1.05	1.05	1.05	0.319	0.211	0.210	0.731	0.563	0.562	−23.0%	−23.1%
40	1.05	1.05	1.05	0.254	0.168	0.168	0.584	0.45	0.45	−22.9%	−22.9%
30	1.05	1.05	1.05	0.190	0.126	0.126	0.437	0.337	0.336	−22.8%	−23.1%
20	1.05	1.05	1.05	0.126	0.084	0.083	0.29	0.224	0.222	−23.0%	−23.5%
10	1.05	1.05	1.05	0.063	0.042	0.041	0.145	0.111	0.11	−23.5%	−24.4%

summarizes the maximum PV penetration limits for the different feeders under different load percentage and constant substation voltage ($V_S=1.05\mathrm{p.u}.$) As shown in Figure 2, the transformer substation feeds several feeders beside the feeder which the PV is connected. Many loads are constant power loads [34]. If those loads are supplied with voltage less than the rated voltage, they will draw overload current. For example, if the load voltage $V_L=0.95\mathrm{p.u}.$ (lower limit), the load current will be $\left(1/0.95\right)=1.0526\mathrm{p.u}.$ (overloaded). Based on this fact, the transformer substation voltage is maintained at higher value ($V_S=1.05,1.04,$ or $1.03\mathrm{p.u}.$) when the substation supplies many feeders to keep the voltage at the end of the most feeders near to the rated value.

As shown in Table 5, for all feeders, the maximum PV penetration limit falls with load decreasing. For light load, the bus voltage is the limiting factor. This is because the voltage-drop over the feeder resistance and reactance is small at light loads and the bus voltage reaches the upper limit. Furthermore, the light loads will be supplied by the PV plant. Only the reactive power flows through the line because the PV inverter operates at unity power factor (i.e., no reactive power is injected by the PV inverter).

As shown in Table 5 and Figure 9, the UGC feeder can host PV plant nearly 23% lower than the OHL for any load percentage.

4.3. Effects of Load Power Factor

Table 6. Changing the load power factor for the different feeders (Substation voltage $V_S=1.05\mathrm{p.u}.$).

Load pf (lag)	VL $(\mathbf{p}.\mathbf{u}.)$			ILine $\left(\mathbf{p.u.}\right)$			PPV $(\mathbf{p}.\mathbf{u}.)$			Change in % PPV from OHL
	OHL	UGC	UGCL	OHL	UGC	UGCL	OHL	UGC	UGCL	UGC	UGCL
1.0	1.05	1.05	1.05	0.00	0.002	0.004	0.999	0.998	0.996	−0.20%	−0.30%
0.9	1.05	1.05	1.05	0.72	0.472	0.472	1.519	1.135	1.136	−25.3%	−25.2%
0.8	1.05	1.05	1.05	1.00	0.650	0.652	1.661	1.126	1.13	−32.2%	−32%
0.7	1.04	1.05	1.05	1.00	0.775	0.778	1.458	1.09	1.096	−25.2%	−24.8%
0.6	1.03	1.05	1.05	1.00	0.869	0.872	1.255	1.039	1.046	−17.2%	−16.7%
0.5	1.03	1.05	1.05	1.00	0.941	0.945	1.054	0.977	0.984	−7.30%	−6.60%
0.4	1.02	1.05	1.05	1.00	0.997	1.00	0.853	0.906	0.911	6.30%	6.90%
0.3	1.02	1.05	1.05	1.00	1.00	1.00	0.654	0.732	0.727	11.9%	11.1%
0.2	1.01	1.05	1.04	1.00	1.00	1.00	0.457	0.563	0.553	23.3%	21.0%
0.1	1.01	1.04	1.04	1.00	1.00	1.00	0.27	0.414	0.399	53.2%	47.4%

shows effects of changing the load power factor on PV maximum penetration limit for the three feeders. For the OHL, the load bus voltage is the limiting factor for high load power factor (pf = $0.8$ to $1.0$), while the feeder current is the limiting factor for low load power factor (pf = $0.1$ to $0.7$). On the other side, for the UGC, the voltage is the limiting factor for most values of the load power factor (pf = $0.2$ to $1.0$). The UGC can host PV plant lower than the PV plant which can be hosted by the OHL for high load power factor ($0.5–1.0$) cases (the practical cases). However, for low load power factor ($0.1–0.4$) (rarely cases), the UGC can host PV plant higher than the OHL.

As shown in Figure 10, for 0.7 load power factor (lagging), the OHL can host $1.458\mathrm{p.u}.$ and the limiting factor is the feeder ampacity. At the same load power factor, the UGC and the UGCL can host PV plants with rating $1.09$ and $1.096\mathrm{p.u}.$, respectively. Here the bus voltage is the limiting factor.

4.4. Effects of Power Systems Frequency (50 Hz–60 Hz)

As known, there are two frequencies in the power systems: 50 Hz (Europe, China, middle east, etc.) and 60 Hz (USA, KSA, etc.). The following subsections explore how the power system frequency can affect the maximum PV penetration limit of all feeders (OHL, UGC, and UGCL).

4.4.1. Effect of Frequency on the OHL Maximum PV Penetration Limit

Table 7. Effect of system frequency on maximum PV penetration limit for the OHL.

${\mathbf{V}}_{\mathbf{S}}.$ (p.u.)	${\mathbf{V}}_{\mathbf{L}}$ (p.u.) $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{I}}_{\mathbf{Line}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=50 \mathbf{Hz}$	$\mathbf{Change} \mathbf{in} {\mathbf{P}}_{\mathbf{PV}}\mathbf{from}$ $\mathit{f}=50 \mathbf{Hz}$
1.05	1.050	0.74	1.595	1.474	8.2%
1.04	1.050	1.00	1.892	1.805	4.8%
1.03	1.040	1.00	1.881	1.885	−0.2%
1.02	1.030	1.00	1.869	1.875	−0.3%
1.01	1.020	1.00	1.859	1.863	−0.2%
1.00	1.010	1.00	1.848	1.852	−0.2%

and Figure 11 show how the frequency can affect the OHL maximum PV penetration limit. For high substation voltage ($V_S=1.05\mathrm{p.u}.$ and $1.04\mathrm{p.u}.$), the 60 Hz OHL can accept PV plant higher than the 50 Hz OHL. However, for low substation voltage ($V_S=1.0\mathrm{p.u}.$ to $1.03\mathrm{p.u}.$), the difference between 50 Hz and 60 Hz is negligible. It is noted that, the feeder current is the limiting factor for most cases especially at low substation voltage.

4.4.2. Effect of Frequency on the UGC Maximum PV Penetration Limit

Table 8. Effect of system frequency on maximum PV penetration limit for the UGC.

${\mathbf{V}}_{\mathbf{S}}.$ (p.u.)	${\mathbf{V}}_{\mathbf{L}}$ (p.u.) $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{I}}_{\mathbf{Line}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=50 \mathbf{Hz}$	$\mathbf{Change} \mathbf{in} {\mathbf{P}}_{\mathbf{PV}}\mathbf{from}$ $\mathit{f}=50 \mathbf{Hz}$
1.05	1.050	0.44	1.171	1.131	3.6%
1.04	1.050	0.70	1.548	1.505	2.9%
1.03	1.050	1.00	1.893	1.880	0.7%
1.02	1.040	1.00	1.881	1.883	−0.1%
1.01	1.030	1.00	1.871	1.872	−0.1%
1.00	1.020	1.00	1.859	1.860	−0.1%

and Figure 12 show how the frequency can affect the UGC maximum PV penetration limit. For high substation voltage ($V_S=1.05$ to $1.03\mathrm{p.u}.$), the UGC exists in the 60 Hz power system can accept PV plant higher than the same UGC exists in the 50 Hz power system. However, for low substation voltage ($V_S=1\mathrm{p.u}.$ to $1.02\mathrm{p.u}.$), there is no considerable difference in the maximum PV penetration limit between the 50 Hz and the 60 Hz UGC. It is noted that, the feeder current is the limiting factor for low substation voltage while the bus voltage is the limiting factor for high substation voltage.

4.4.3. Effect of Frequency on the UGCL Maximum PV Penetration Limit

Table 9. Effect of system frequency on maximum PV penetration limit for the UGCL.

${\mathbf{V}}_{\mathbf{S}}.$ (p.u.)	${\mathbf{V}}_{\mathbf{L}}$ (p.u.) $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{I}}_{\mathbf{Line}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=60 \mathbf{Hz}$	${\mathbf{P}}_{\mathbf{PV}} (\mathbf{p}.\mathbf{u}.)$ $\mathit{f}=50 \mathbf{Hz}$	$\mathbf{Change} \mathbf{in} {\mathbf{P}}_{\mathbf{PV}}\mathbf{from}$ $\mathit{f}=50 \mathbf{Hz}$
1.05	1.050	0.44	1.173	1.131	3.7%
1.04	1.050	0.61	1.422	1.371	3.7%
1.03	1.050	0.81	1.673	1.612	3.8%
1.02	1.050	1.00	1.892	1.854	2.0%
1.01	1.040	1.00	1.881	1.884	−0.1%
1.00	1.030	1.00	1.870	1.874	−0.2%

and Figure 13 show how the power system frequency can affect the UGCL maximum PV penetration limit. For high substation voltage ($V_S=1.05$ to $1.02\mathrm{p.u}.$), the installed UGCL in the 60 Hz power system can accept PV plant nearly 3.7% higher than the existing UGCL in the 50 Hz power system. However, for low substation voltage ($V_S=1$ to $1.01\mathrm{p.u}.$), the effect of power system frequency on UGCL maximum PV penetration limit is negligible. It is noted that the line current (feeder ampacity) is the limiting factor for low substation voltage while the load bus voltage is the limiting factor for high substation voltage.

5. Comparison between Thumb Rule and Accurate Calculated Method

Several studies used an approximate equation (empirical equation) to calculate the maximum PV penetration limit [19]. This empirical equation is based on the fact that “the value of PV power must be enough to supply the load demand (active power) and export an equal quantity to the system. It also must compensate for any differences at the line if the load demand is below the rated value”. In mathematical terms, the following empirical equation is used [19]:

$$P_{PV}=2P_{\mathrm{load}}+\left(1-\left|S_{\mathrm{load}}\right|\right)$$

(26)

Table 10. Maximum PV penetration comparison between calculated values and approximate values.

Factor	${\mathbf{V}}_{\mathbf{S}}$ (p.u.)	% Load	Load pf	${\mathbf{S}}_{\mathbf{load}}$ (p.u.)	PPV $\mathbf{Approx}.$ Eqn.	OHL			UGC			UGCL
						PPV $\mathbf{Calc}.$	Error (%)	Limiting Factor	PPV $\mathbf{Calc}.$	Error (%)	Limiting Factor	PPV $\mathbf{Calc}.$	Error (%)	Limiting Factor
Effect of Supply Voltage	1.05	100	0.92	1.0	1.84	1.474	24.8%	Voltage	1.131	62.68%	Voltage	1.131	62.68%	Voltage
	1.04	100	0.92	1.0	1.84	1.805	1.93%	Voltage	1.505	22.25%	Voltage	1.371	34.2%	Voltage
	1.03	100	0.92	1.0	1.84	1.885	−2.38%	Current	1.88	−2.12%	Voltage	1.612	14.14%	Voltage
	1.02	100	0.92	1.0	1.84	1.875	−1.86%	Current	1.883	−2.28%	Current	1.854	−0.75%	Voltage
	1.01	100	0.92	1.0	1.84	1.863	−1.23%	Current	1.872	−1.7%	Current	1.884	−2.33%	Current
	1.00	100	0.92	1.0	1.84	1.852	−0.64 %	Current	1.86	−1.07%	Current	1.874	−1.81%	Current
Effect of Load Percent.	1.05	90	0.92	0.9	1.756	1.324	32.6%	Voltage	1.017	72.66%	Voltage	1.017	72.66%	Voltage
	1.05	80	0.92	0.8	1.672	1.175	42.29%	Voltage	0.903	85.16%	Voltage	0.903	85.16%	Voltage
	1.05	70	0.92	0.7	1.588	1.027	54.62%	Voltage	0.79	101%	Voltage	0.790	101%	Voltage
	1.05	60	0.92	0.6	1.504	0.879	71%	Voltage	0.676	122.4%	Voltage	0.676	122.4%	Voltage
	1.05	50	0.92	0.5	1.42	0.731	94.25%	Voltage	0.563	152.2%	Voltage	0.562	152.6%	Voltage
	1.05	40	0.92	0.4	1.336	0.584	128.7%	Voltage	0.45	196.9%	Voltage	0.450	196.8%	Voltage
	1.05	30	0.92	0.3	1.252	0.437	186.4%	Voltage	0.337	271.5%	Voltage	0.336	272.6%	Voltage
	1.05	20	0.92	0.2	1.168	0.29	302.7%	Voltage	0.224	421.4%	Voltage	0.222	426.1%	Voltage
	1.05	10	0.92	0.1	1.08	0.145	644.8%	Voltage	0.111	872.9%	Voltage	0.110	881.8%	Voltage
Effect of load Power Factor	1.05	100	1.0	1.0	2.0	0.999	100.2%	Voltage	0.998	100.4%	Voltage	0.996	100.8%	Voltage
	1.05	100	0.9	1.0	1.8	1.519	18.5%	Voltage	1.135	58.6%	Voltage	1.136	58.45%	Voltage
	1.05	100	0.8	1.0	1.6	1.661	−3.67%	Voltage	1.126	42.1%	Voltage	1.130	41.59%	Voltage
	1.05	100	0.7	1.0	1.4	1.458	−3.97%	Current	1.090	28.44%	Voltage	1.096	27.73%	Voltage
	1.05	100	0.6	1.0	1.2	1.255	−4.38%	Current	1.039	15.49%	Voltage	1.046	14.72%	Voltage
	1.05	100	0.5	1.0	1.0	1.054	−5.12%	Current	0.977	2.35%	Voltage	0.984	1.62%	Voltage
	1.05	100	0.4	1.0	0.8	0.853	−6.2%	Current	0.906	−11.69%	Voltage	0.911	−12.1%	Voltage
	1.05	100	0.3	1.0	0.6	0.654	−8.25%	Current	0.732	−18%	Current	0.727	−17.4%	Voltage
	1.05	100	0.2	1.0	0.4	0.457	−12.47%	Current	0.563	−28.95%	Current	0.553	−27.6%	Current
	1.05	100	0.1	1.0	0.2	0.270	−25.9%	Current	0.414	−51.69%	Current	0.399	−49.8%	Current

summarizes all results with different feeders and compares the results with the results yield by approximate Equation (26).

The empirical equation gives an acceptable accuracy for low substation voltage ($V_S=1$, $1.01$, and $1.02\mathrm{p.u.}$). For high substation voltage ($V_S=1.05$ and $1.04\mathrm{p.u}.$), the error between approximate (empirical) method and accurate calculated method is very high and cannot be acceptable. Moreover, the empirical method is not accurate for low load percentage (Table 10). The errors between the accurate calculated method and the empirical method for UGC are higher than the corresponding values in the OHL (Table 10). Based on those results, the empirical method is not recommended, especially for the UGC and high substation voltage.

As shown in Table 10, the empirical approximate equation can be used and give acceptable results for different feeders (OHL, UGC, and UGCL) for low substation voltage only. For instance, at substation voltage = 1 p.u., the empirical method gives results with error less than 1% for OHL (−0.64%). For the same low substation voltage (1 p.u.), the difference between the empirical method and accurate calculated method is −1.07% and −1.81% for UGC and UGCL, respectively. On the other side, for high substation voltage (1.05 p.u.), the errors between empirical method and accurate calculated method are 24.8% and 62.68% for OHL and UGC, respectively. Those values of errors are not acceptable at all.

The errors between the empirical method and accurate calculated method increases with decreasing the load percentage. For instance, at 90% load percentage, the errors between the empirical method and the accurate calculated method are 32.6% and 72.66% for the OHL and UGC, respectively. If the load percentage decreases from 90% to 50%, the errors increase to 94.45% and 152% for OHL and UGC, respectively. Those value of errors cannot be acceptable at all.

As the load power factor decreases from unity (resistive load) to 0.6 lagging power factor load, the error between the empirical method and calculated method decreases from 100.2% to −4.38% for OHL, and the error decreases from 100.4% to 15.49% for the UGC as shown in Table 10. If the load power factor decreases from 0.5 lagging to 0.1 lagging, the error between the empirical method and accurate calculated method increases from −5.12% to −25.9% for the OHL and increases from 2.35% to −51.69% for the UGC as reported in Table 10. The limiting factor for every investigated case is decided and exist in separate column in Table 10 for OHL, UGC, and UGCL.

6. Conclusions

This paper presented a comparative study about the maximum PV penetration limit in different types of MV distribution feeders (OHL and UGC). It is found that; the maximum PV penetration limit in the OHL is higher than the value accompanied with the UGC. When the substation voltage is equal to $1.05\mathrm{p.u}.$, the UGC can accept PV plant 23.3% less than the accepted value by the OHL. This percentage decreased to 16.6% if the substation voltage is equal to $1.04\mathrm{p.u}.$. When the feeder load decreases, the PV maximum limit will also decrease for the same feeder type. The PV penetration limit is maximum at rated load for both feeder type (OHL and UGC). The OHL accepts high PV plant for light loads if it is compared with the corresponding UGC. When the feeder load power factor decreases, the maximum PV plant with each feeder type will increase until the power factor reaches to 0.7 lagging. If the feeder power factor decreases than the 0.7 lagging, the maximum allowed PV penetration begins to fall. When the load power factor is higher than 0.5 lagging, the OHL accepts higher PV plant compared to the UGC. In contrary, if the load power factor is lower than 0.5 lagging (rare cases), the UGC can accept PV plant higher than the OHL.

Furthermore, this paper investigated the effect of the power system frequency on the maximum PV penetration for all feeder types. For high substation voltage ($V_S=1.05$ and $1.04\mathrm{p.u}.$), the power system with the 60 Hz frequency allows higher rating PV plants than the 50 Hz power system with value 8.2% and 3.6% for OHL and UGC, respectively. For low substation voltage ($V_S=1$ to $1.02\mathrm{p.u}.$), both the 50 Hz and the 60 Hz power systems approximately have the same performance with PV maximum penetration limit.

A comparison between values of the maximum PV penetration obtained by approximate method and accurate calculated method is performed in this paper. Errors between the two methods are acceptable for low substation voltage only.