Assessment of Sensitivity to Evaluate the Impact of Operating Parameters on Stability and Performance in Proton Exchange Membrane Fuel Cells
Abstract
:1. Introduction
- To make the obtained sensitivity indexes comparable, this paper combined with the actual operating conditions to uniformly delineate the calibration parameters and their fluctuation ranges before starting the sensitivity analysis. Moreover, a reliable parameter sensitivity assessment method was designed.
- The Monte Carlo method was adopted to quantitatively analyze the parameters, which have little effect on the output performance (failed to judge by the deviation percentages) under calibration conditions. The parameter sensitivity rankings under specific current density were obtained.
- In addition to determining the impact of single parameter fluctuations on the output voltage, the water content distribution cloud maps of the contact surface between anode side catalyst layer (CL) and membrane are used to prove the improvement/deterioration of PEMFC performance, which can intuitively explain the phenomena.
2. Description of Model
2.1. Governing Equation
2.2. Electrochemical Reaction Model
2.3. Membrane Electrode Water Transport Model
2.4. Boundary Conditions and Material Properties
- (1)
- Anode/cathode adopted mass flow inlet (AMFR/CMFR): was used to define the mass fraction of each component of the reaction gas at the inlet.
- (2)
- Channel outlet employed pressure outlet: was used to define the anode and cathode pressures, respectively. Moreover, anode operating pressure (AOP) and cathode operating pressure (COP) are usually controlled by back pressure of PEMFC.
- (3)
- The voltage or current density of the fuel cell model was set at the bipolar plate surface; the potential on the surface of the end plate of the anode and cathode bipolar plates can be expressed as .
- (4)
- The no-slip wall boundary was applied to the wall interface between the fluid and solid computing domains.
- (5)
- (1)
- Stoichiometric ratio of hydrogen to air (excess coefficient):
- (2)
- Relative humidity:
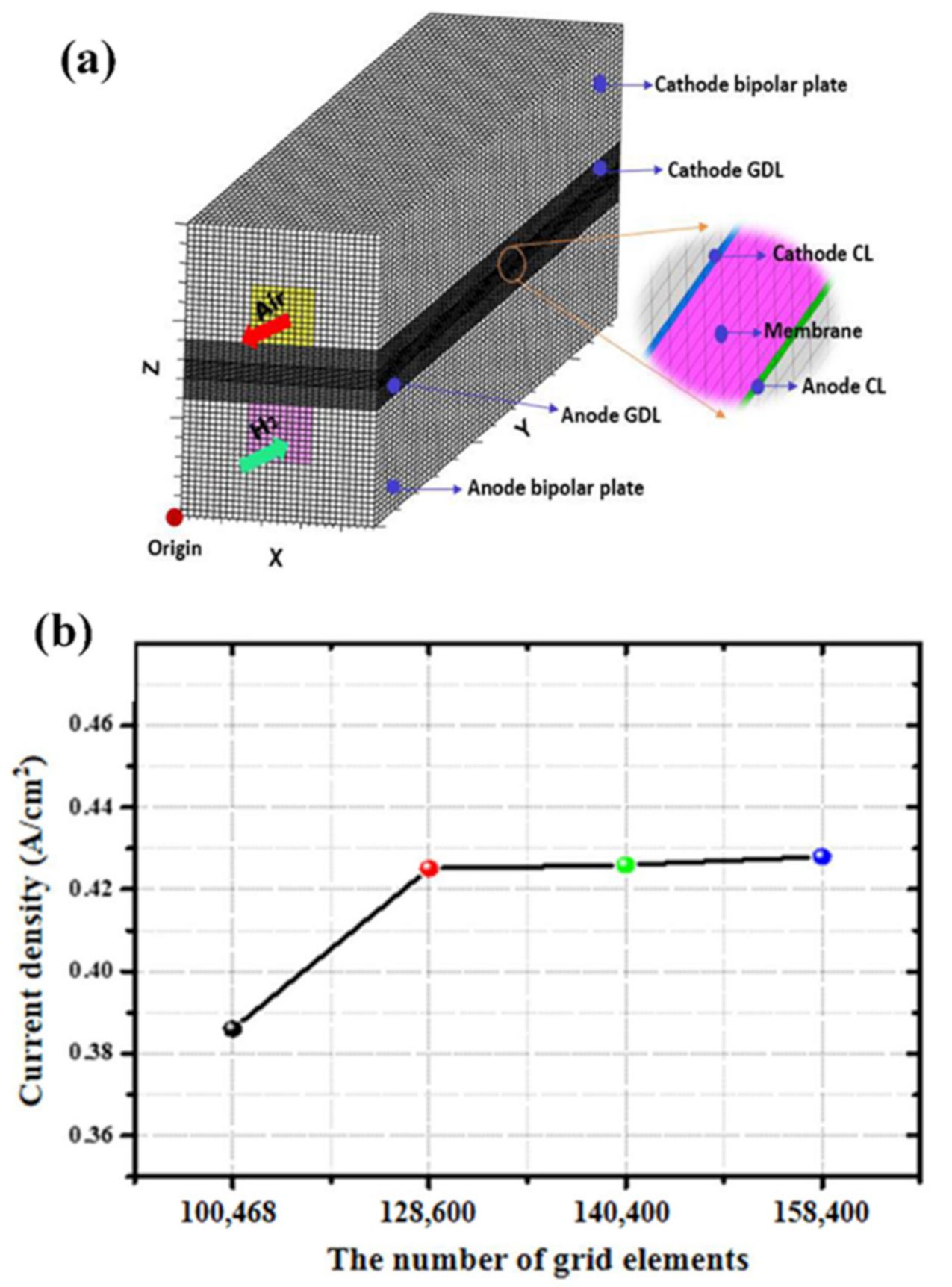
2.5. Geometric Model and Meshing
3. Results and Discussion
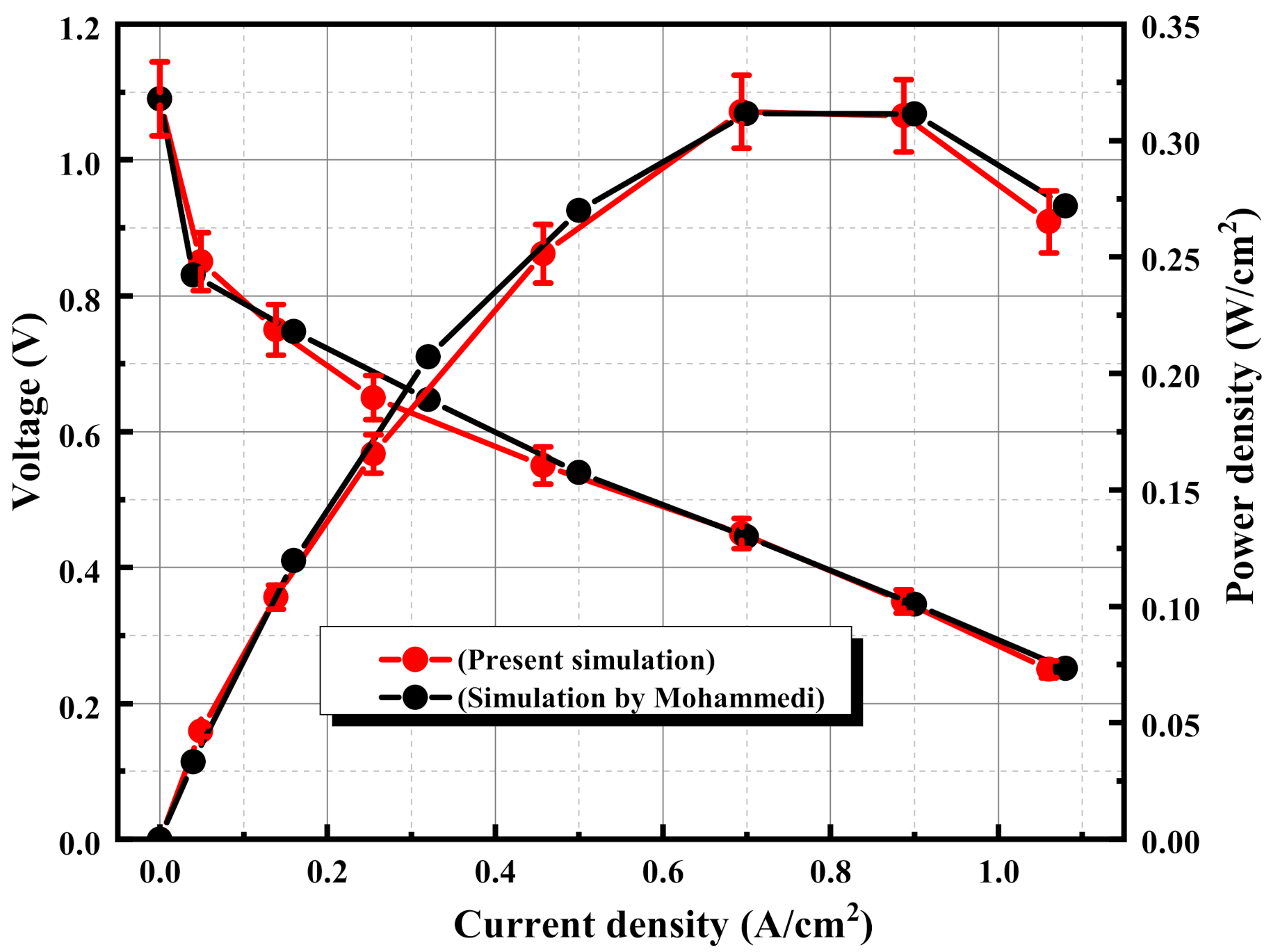
3.1. Model Validation
3.2. Parameter Setting
3.3. Simulation Results
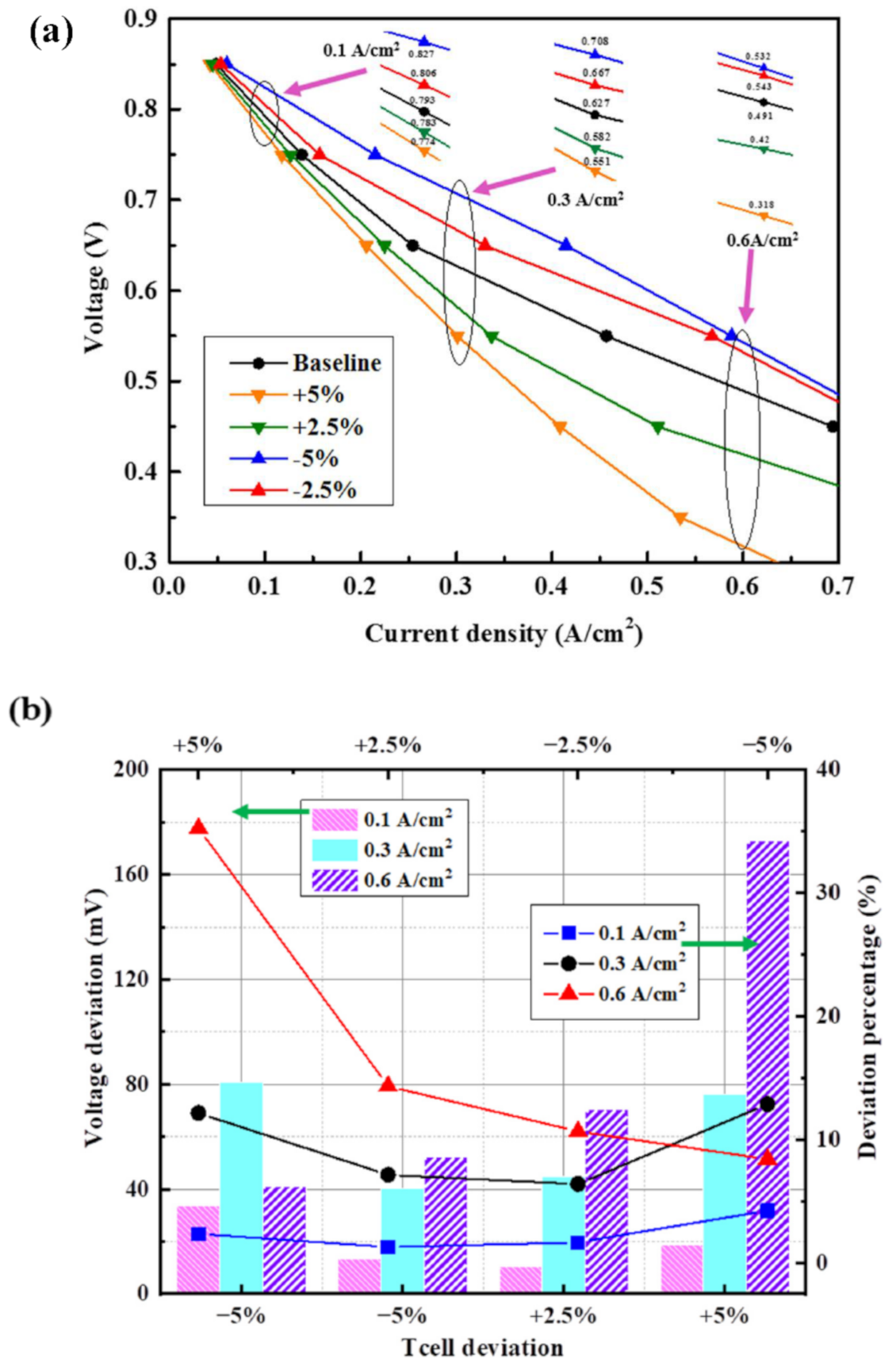
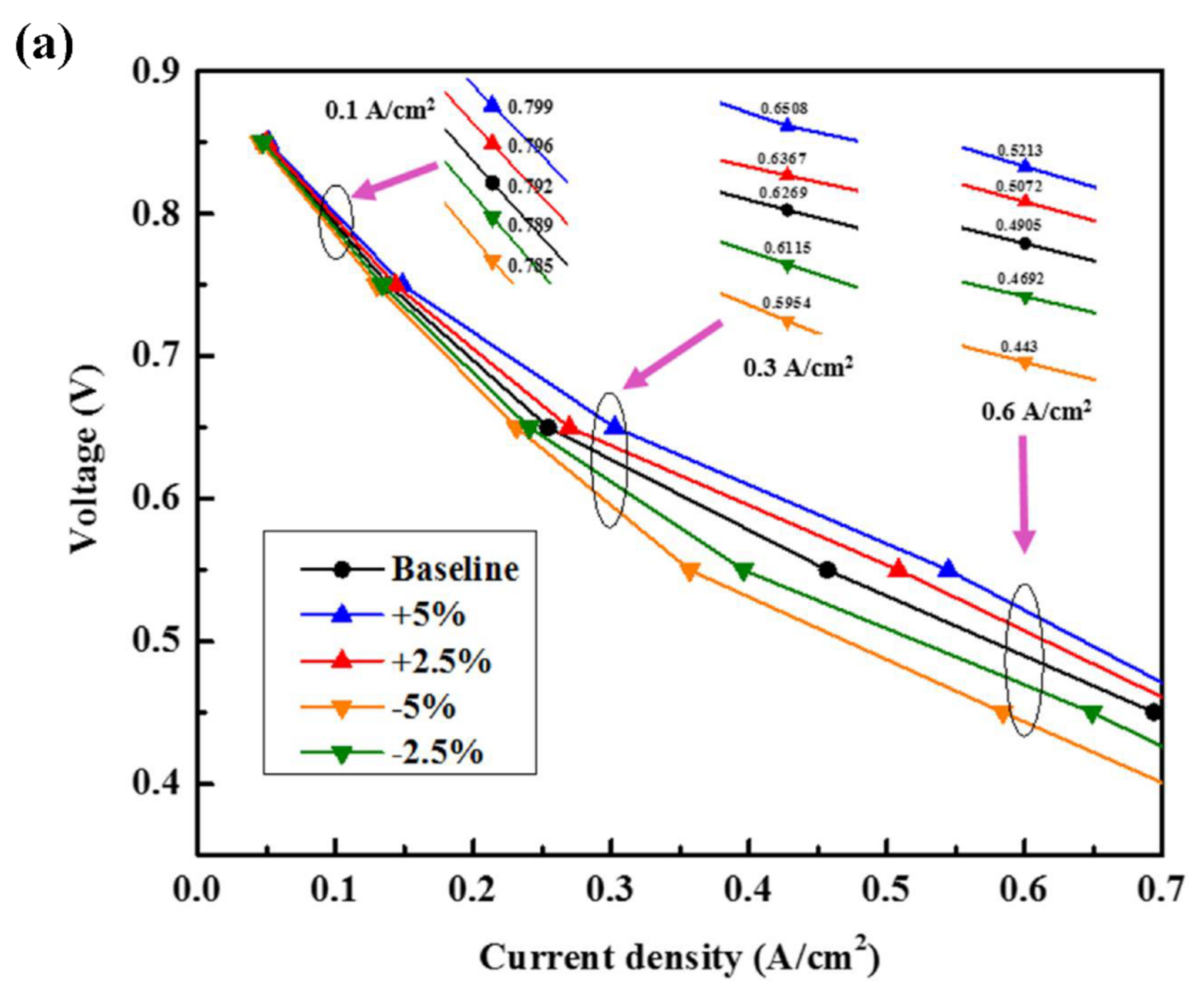
3.3.1. Deviation of Cell Operating Temperature
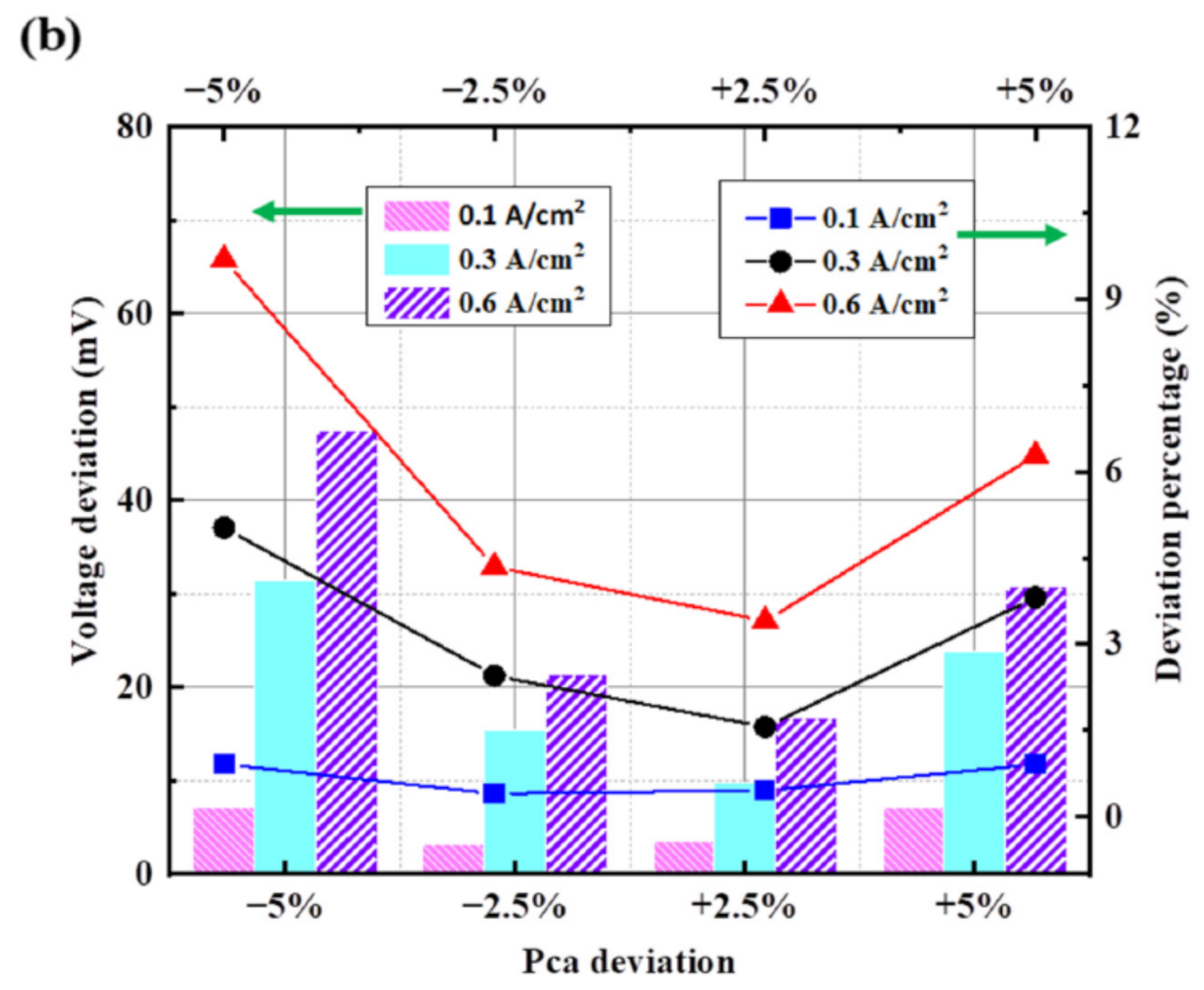
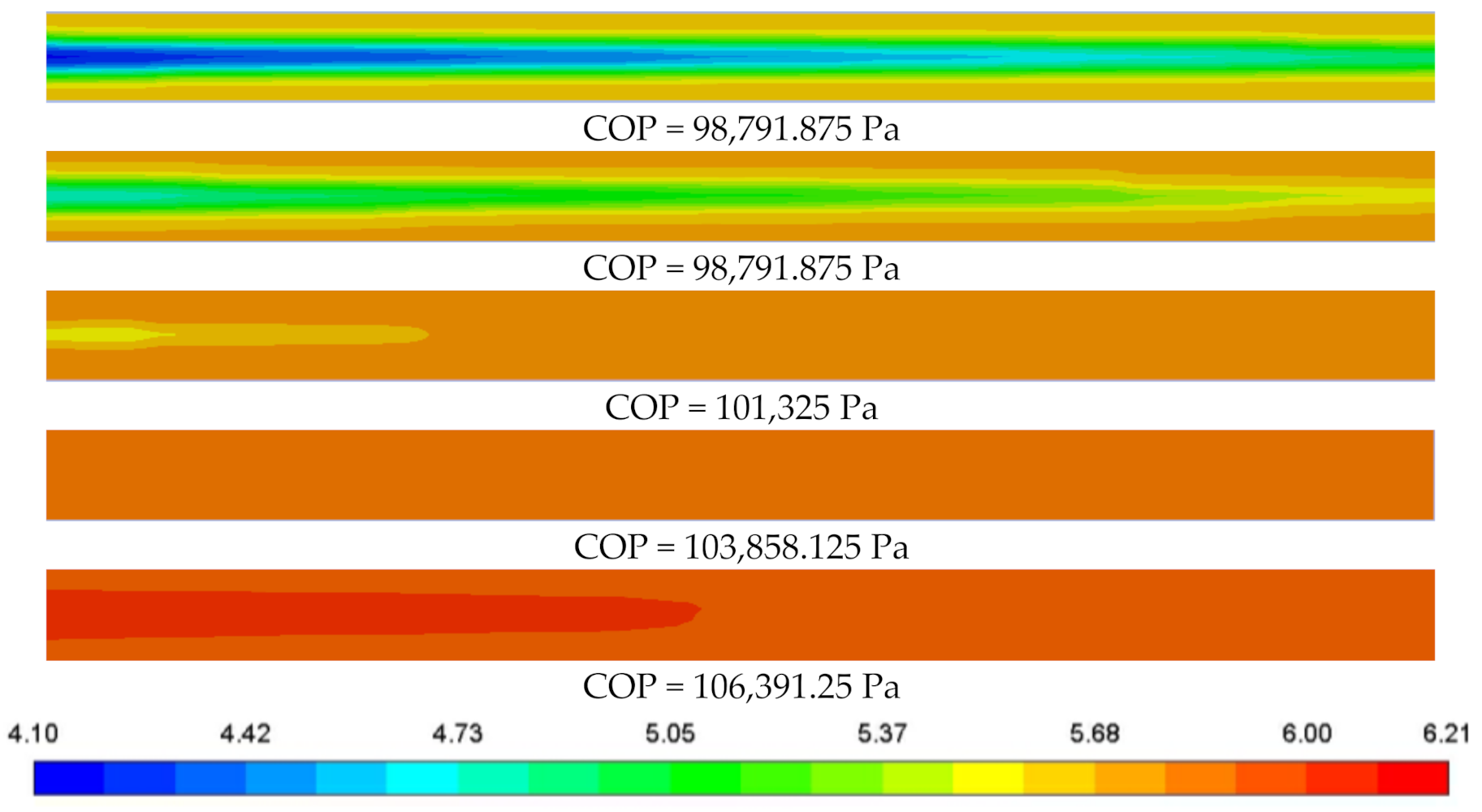
3.3.2. Deviation of Cathode Operating Pressure
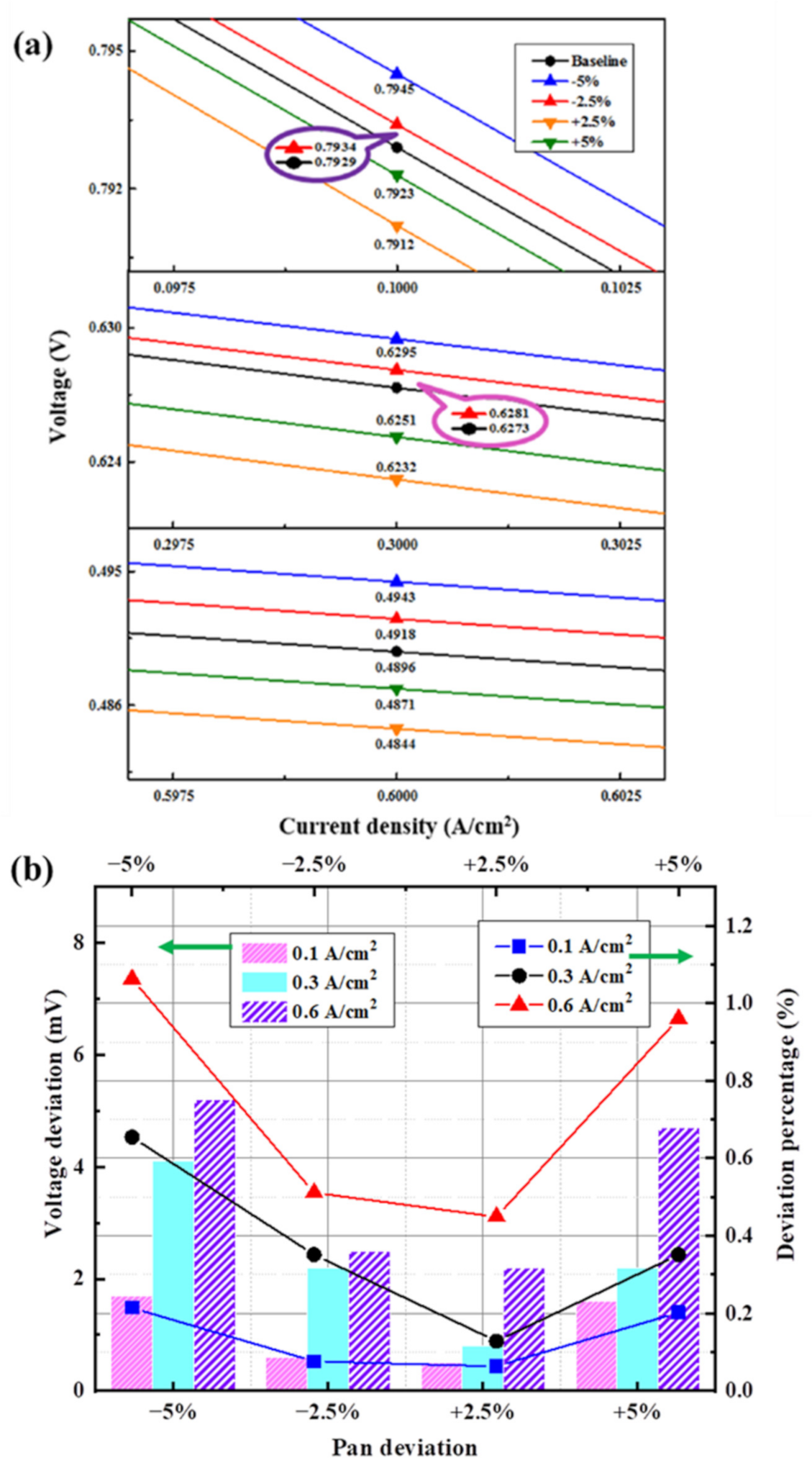
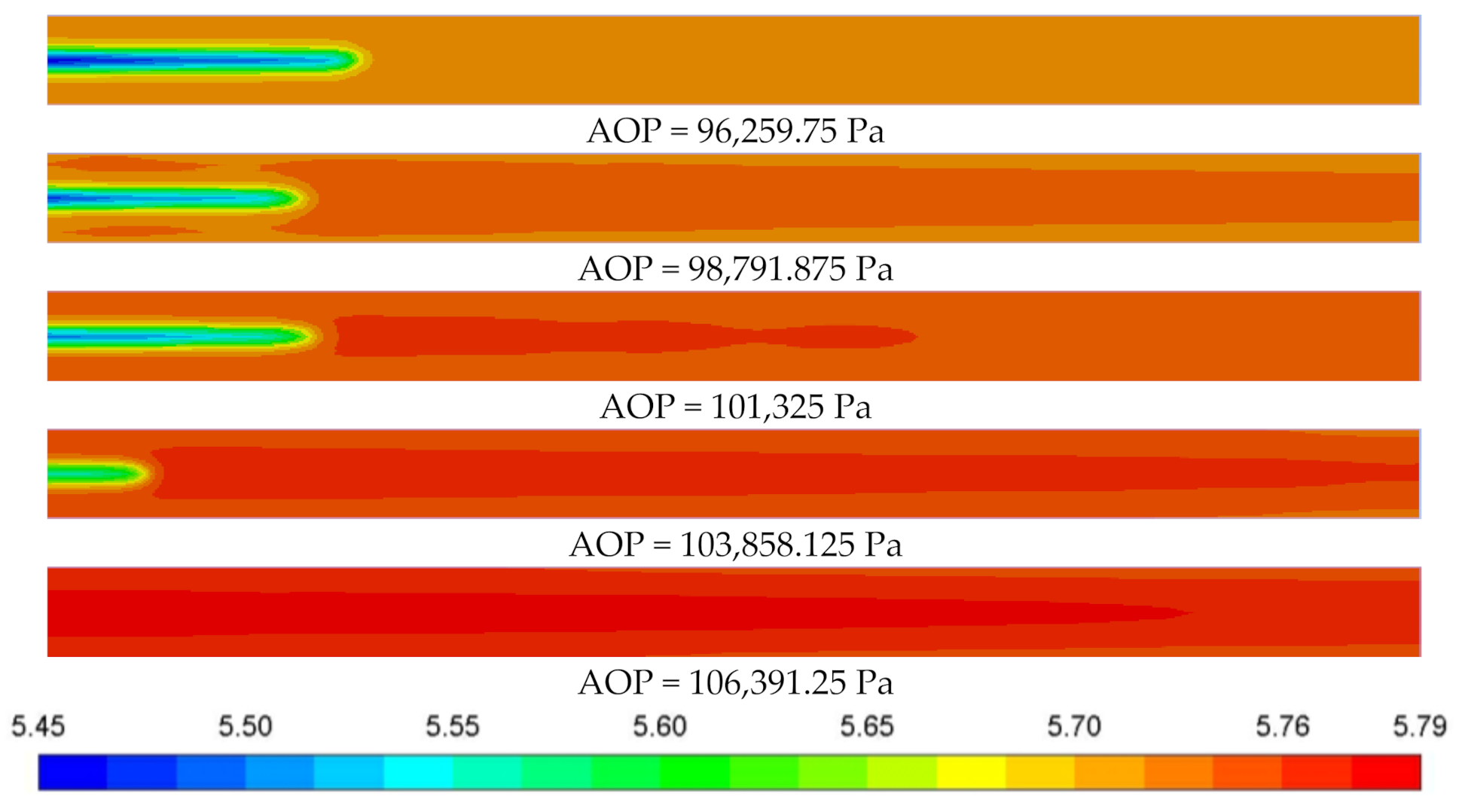
3.3.3. Deviation of Anode Pressure
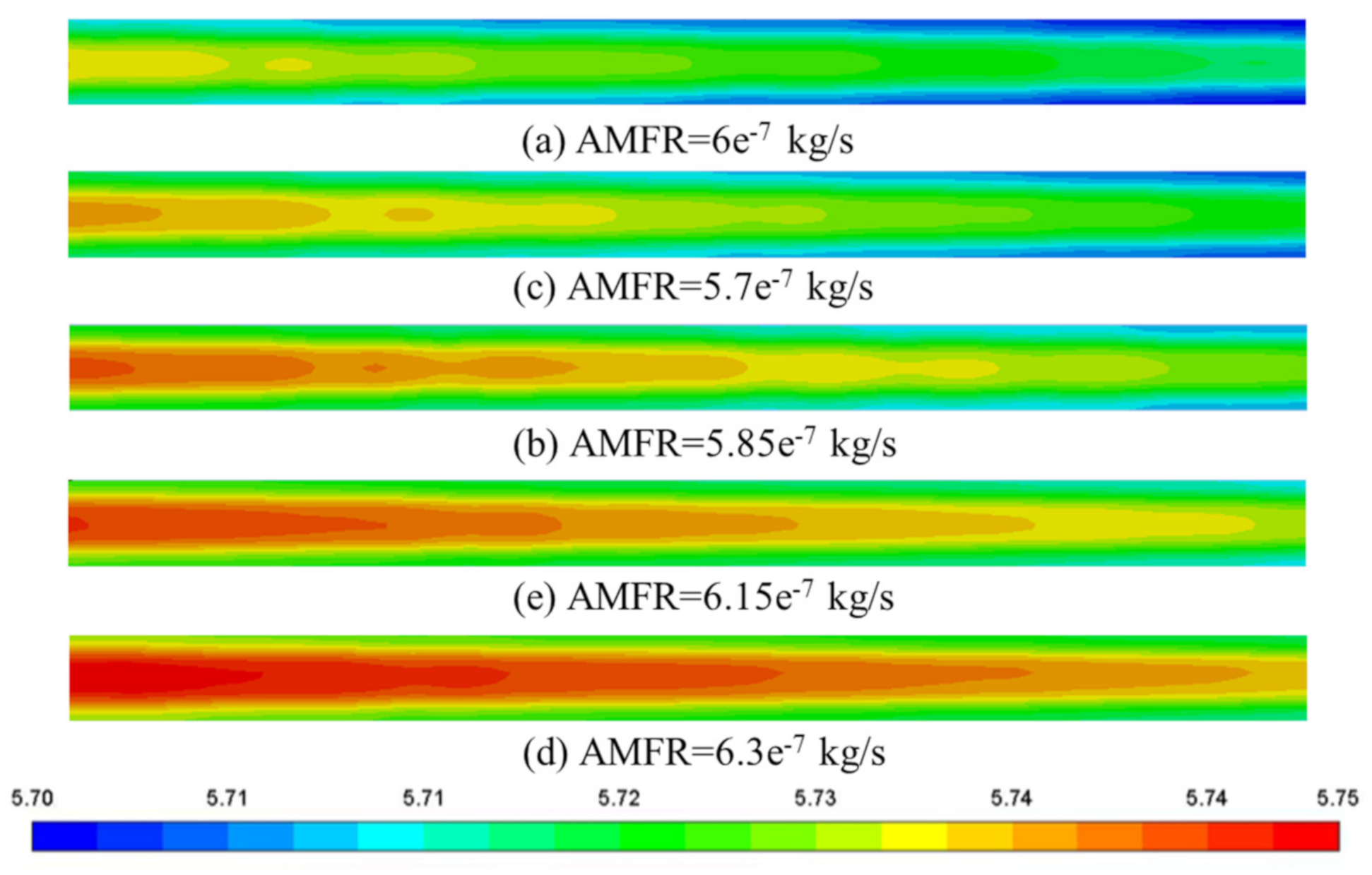
3.3.4. Deviation of Anode Mass Flow Rate
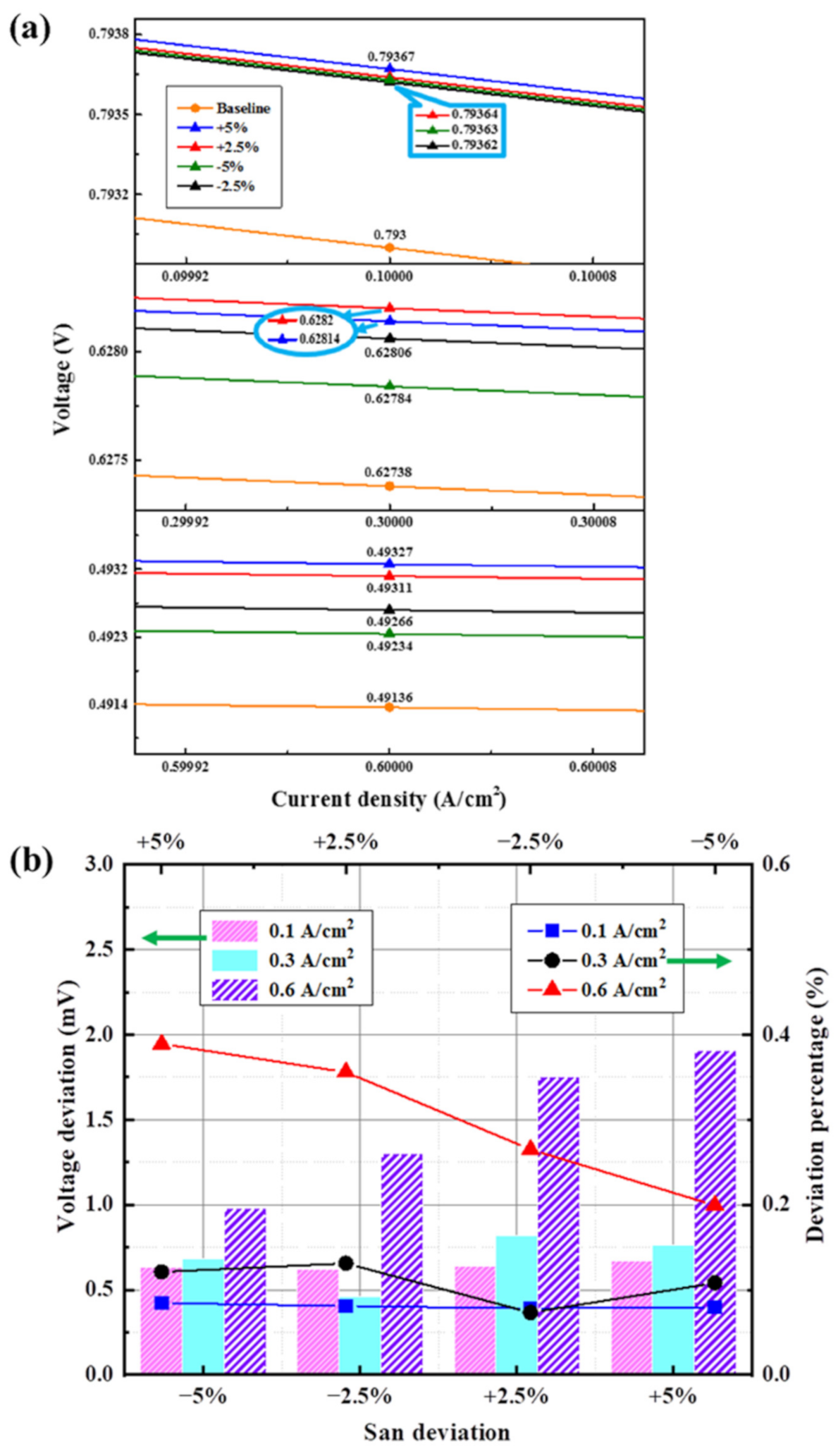
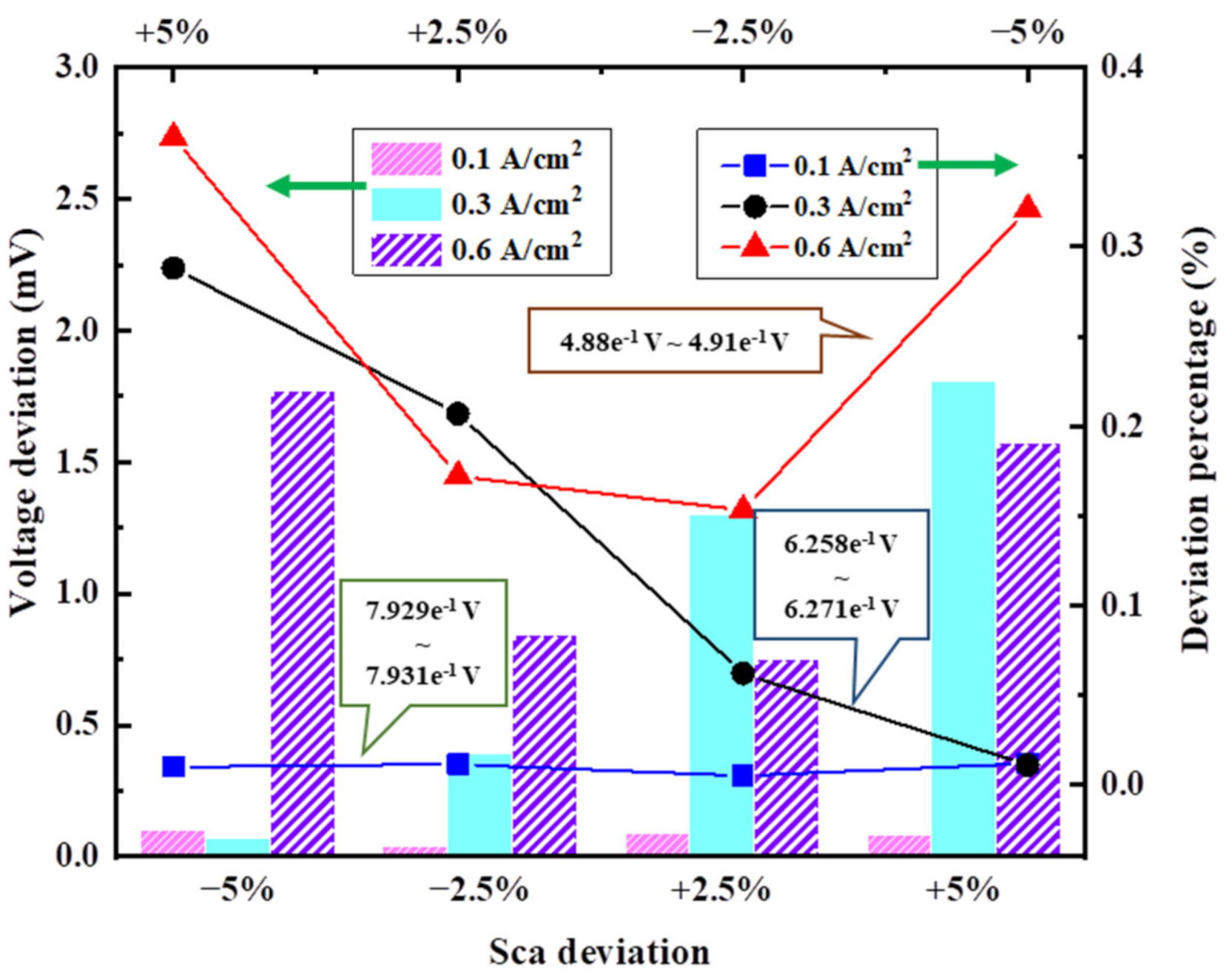
3.3.5. Deviation of Cathode Mass Flow Rate
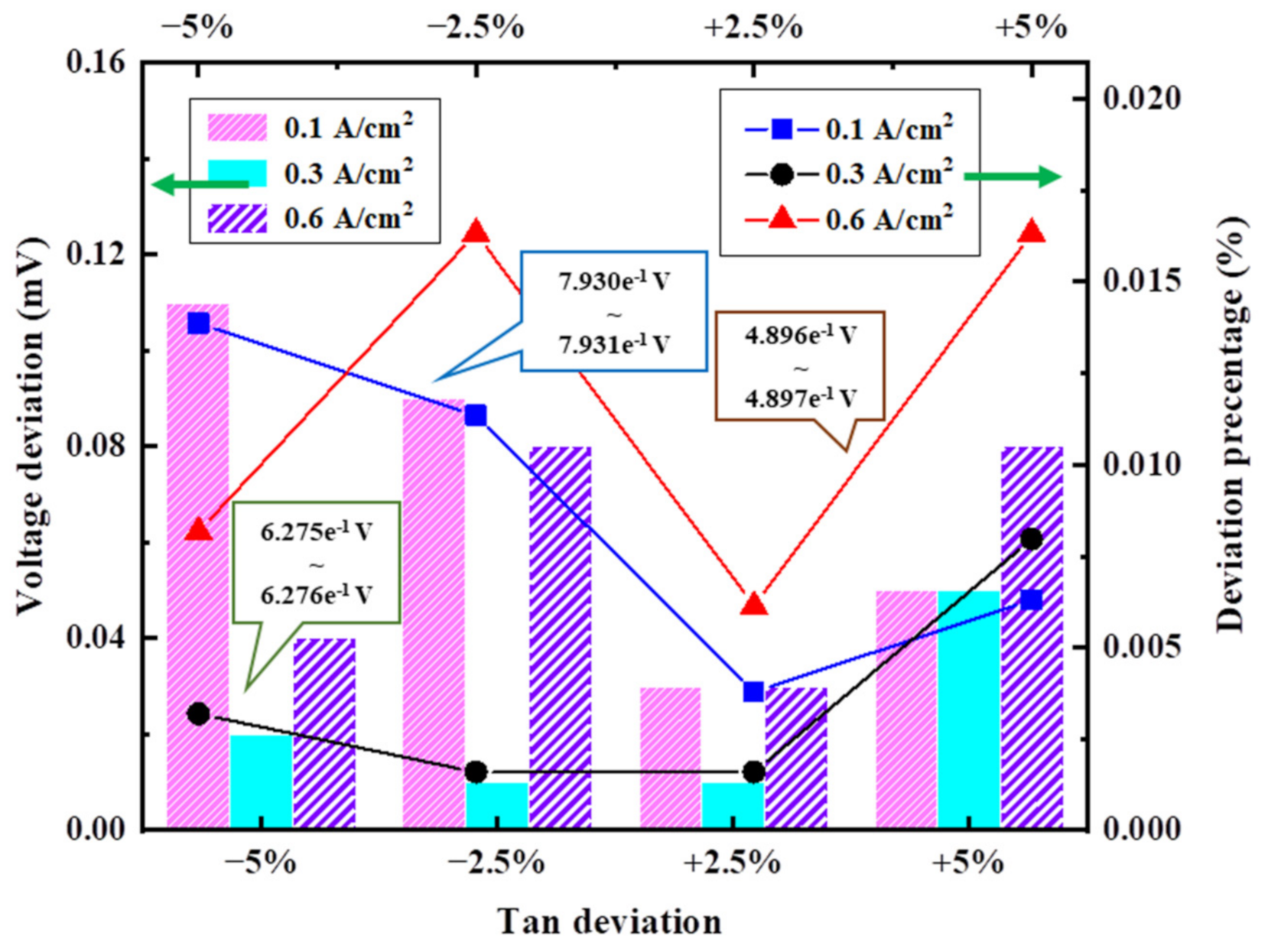
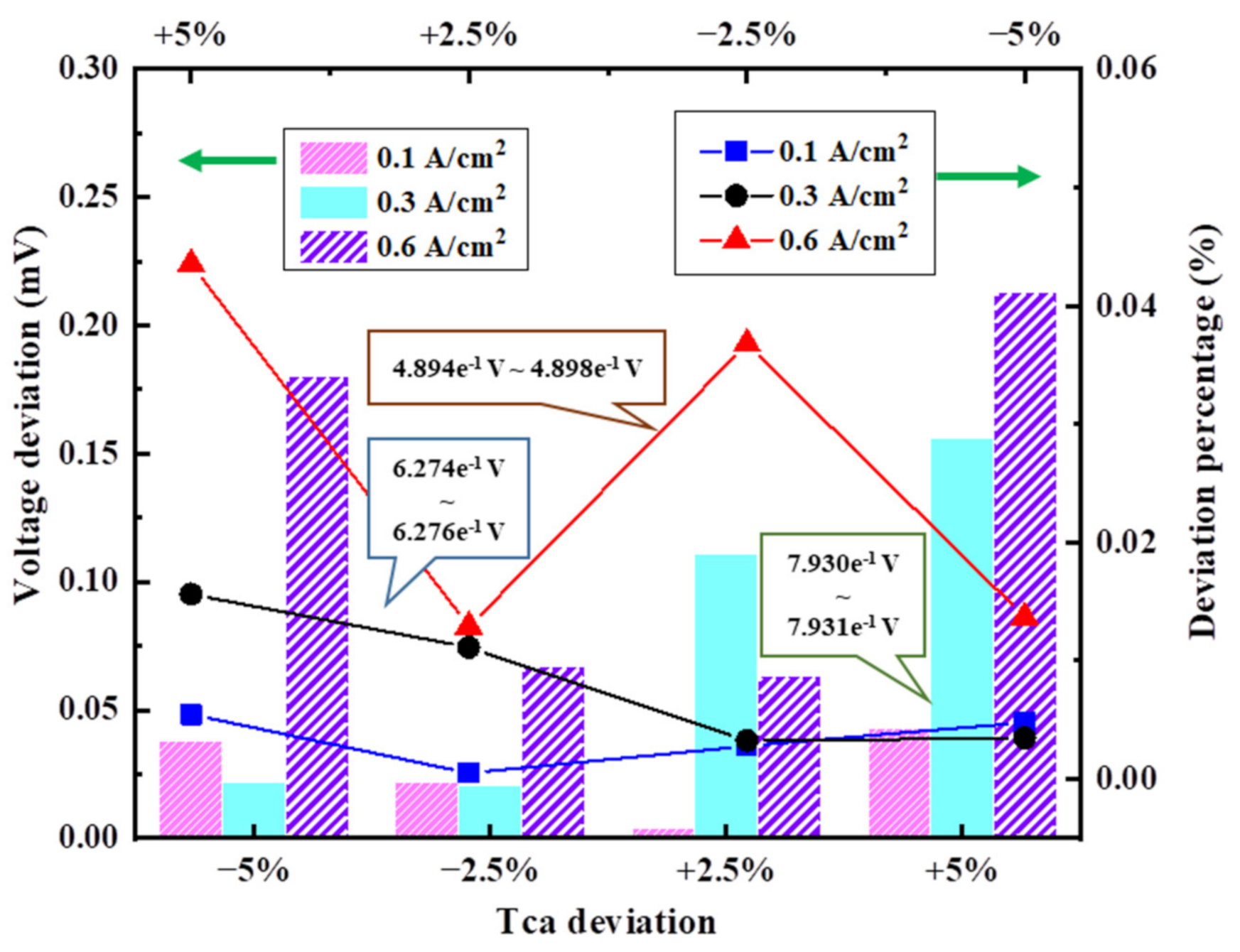
3.3.6. Deviation of Anode/Cathode Inlet Temperature
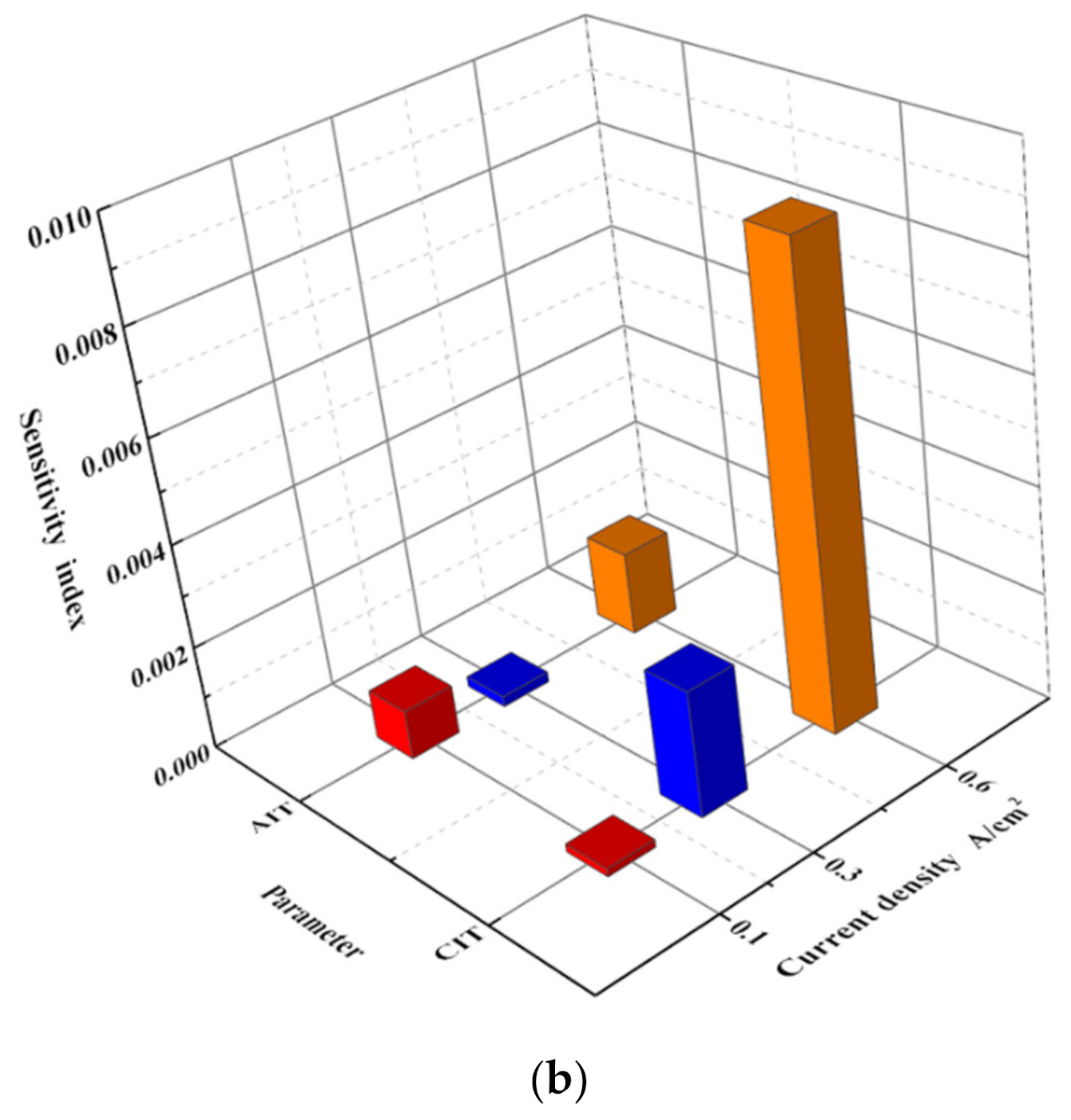
3.4. Sensitivity Analysis
3.4.1. Process of Sensitivity Analysis
- (1)
- Determining the insensitive parameters: , as seen in Table 4, and defining the deviation range of the standard value as .
- (2)
- Randomly generating 12 sets of uniform operating parameter values within the range of positive and negative deviation of each parameter, then bringing in the calculated model and obtaining the voltage, which corresponds to the current density as 0.1 A/cm2, 0.3 A/cm2, 0.6 A/cm2, respectively.
- (3)
- Substituting the output voltage from step 2) into the function. Finally, the sensitivity of static evaluation parameters was obtained from Equation (19).
- (4)
- where , , , and represent the sum of the output voltage deviation, the parameter sensitivities, the reference voltage, and calculated voltage, respectively, when the current density is . k is the zoom factor and n refers to the number of simulation times when the current density is i.
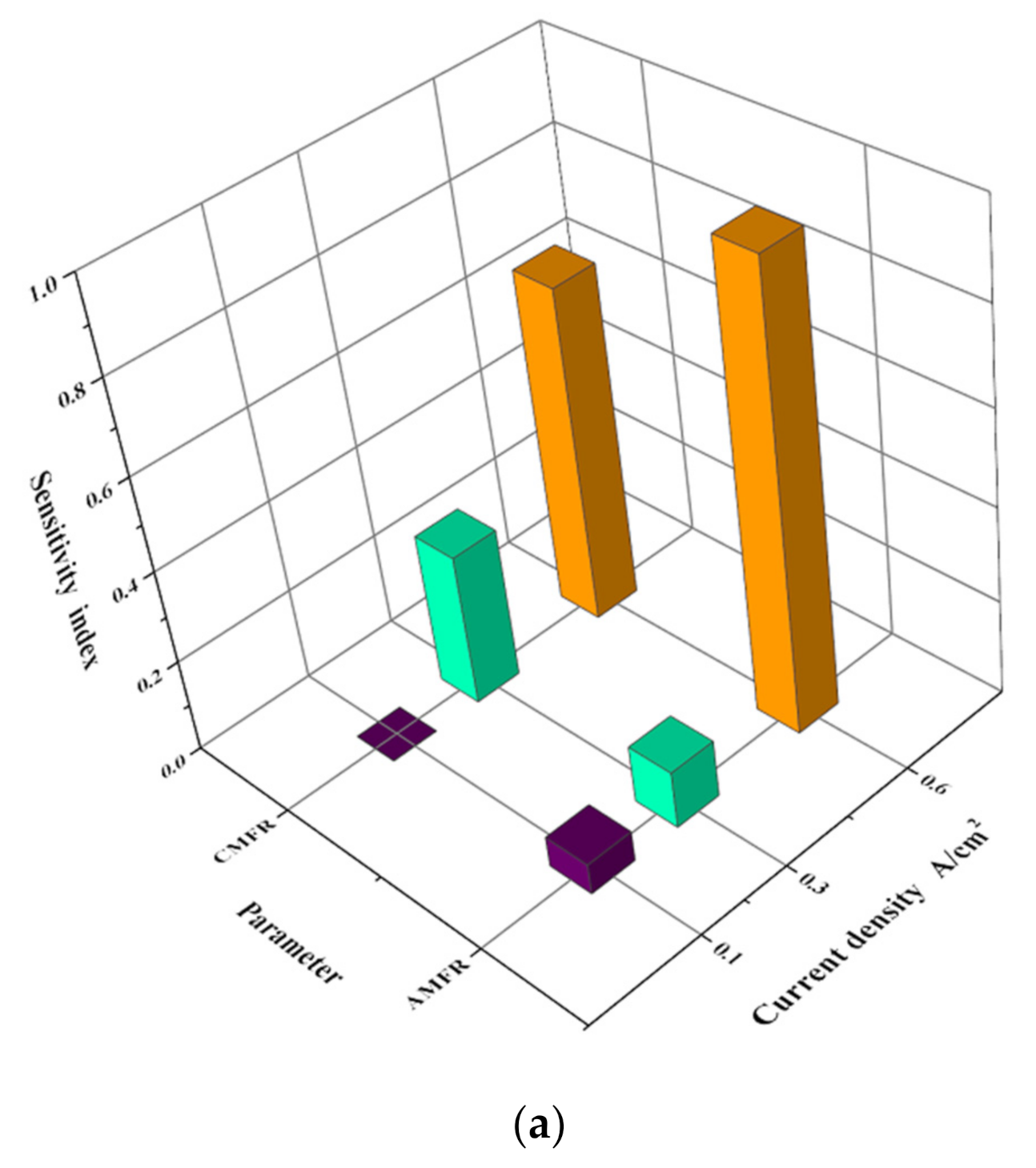
3.4.2. Results of Analysis
3.5. Cloud Maps Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviation
| List of Symbols | |
| Cp | Specific heat capacity of mixture |
| D | Diffusion coefficient of gas |
| Dc | Capillary diffusion coefficient of liquid water |
| Dm | Diffusion coefficient of water molecules |
| Dp | Pressure transfer coefficient |
| F | Faraday constant |
| j | Exchange current density per unit area (A/cm2) |
| Pc | Capillary pressure (bar) |
| Ran | Anode current density (A/cm2) |
| Rca | Cathode current density (A/cm2) |
| Voc | Open circuit voltage (V) |
| Source Term | |
| Sm | Source term of mass conservation control equation |
| Su | Source term of momentum equation |
| ST | Source term of energy equation |
| Si | Source term of components conservation |
| Sl | Source term of transfer current |
| Greek Symbols | |
| porosity | |
| eff | Effective dynamic viscosity |
| Overpotential of anode surface | |
| Overpotential of cathode surface | |
| i | Proton membrane conductivity (S/cm) |
| eff | Effective thermal conductivity |
| Activation area ratio (1/m) | |
| i | Membrane phase voltage (V) |
| Potential on the end plate surface of anode bipolar plates (V) | |
| Potential on the end plate surface of cathode bipolar plates (V) | |
| Anode charge transfer coefficient of reduction reaction | |
| Cathode charge transfer coefficient of reduction reaction | |
| Cathode charge transfer coefficient of oxidation reaction | |
| Anode charge transfer coefficient of oxidation reaction | |
| Gaseous water density | |
| Liquid water density | |
| Abbreviation | |
| COT | Cell operating temperature |
| AIT | Anode inlet temperature |
| CIT | Cathode inlet temperature |
| AMFR | Anode mass flow rate |
| CMFR | Cathode mass flow rate |
| AOP | Anode operating pressure |
| COP | Cathode operating pressure |
References
- Shahgaldi, S.; Alaefour, I.; Zhao, J.; Li, X. Impact of ionomer in the catalyst layers on proton exchange membrane fuel cell performance under different reactant flows and pressures. Fuel 2018, 227, 35–41. [Google Scholar] [CrossRef]
- Truc, N.T.; Ito, S.; Fushinobu, K. Numerical and experimental investigation on the reactant gas crossover in a PEM fuel cell. Int. J. Heat Mass Tran. 2018, 127, 447–456. [Google Scholar] [CrossRef]
- Meidanshahi, V.; Karimi, G. Dynamic modeling, optimization and control of power density in a PEM fuel cell. Appl. Energ. 2012, 93, 98–105. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Alaswad, A.; Omran, A.; Sodre, J.; Wilberforce Awotwe, T.; Pignatelli, G.; Dassisti, M.; Baroutaji, A.; Olabi, A.G. Technical and Commercial Challenges of Proton-Exchange Membrane (PEM) Fuel Cells. Energies 2020, 14, 144. [Google Scholar] [CrossRef]
- Movahedi, M.; Ramiar, A.; Ranjber, A.A. 3D numerical investigation of clamping pressure effect on the performance of Proton Exchange Membrane fuel cell with interdigitated flow field. Energy 2018, 142, 617–632. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, L.; Li, J.; Ouyang, M. Performance prediction of proton exchange membrane fuel cell engine thermal management system using 1D and 3D integrating numerical simulation. Int. J. Hydrogen Energ. 2018, 43, 1736–1748. [Google Scholar] [CrossRef]
- Yang, Z.; Du, Q.; Jia, Z.; Yang, C.; Jiao, K. Effects of operating conditions on water and heat management by a transient multi-dimensional PEMFC system model. Energy 2019, 183, 462–476. [Google Scholar] [CrossRef]
- Mohammedi, A.; Sahli, Y.; Moussa, H.B. 3D investigation of the channel cross-section configuration effect on the power delivered by PEMFCs with straight channels. Fuel 2020, 263, 116713. [Google Scholar] [CrossRef]
- Zhao, J.; Shahgaldi, S.; Alaefour, I.; Yang, S.; Li, X. Pore structure and effective diffusion coefficient of catalyzed electrodes in polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energ. 2018, 43, 3776–3785. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X. Oxygen transport in polymer electrolyte membrane fuel cells based on measured electrode pore structure and mass transport properties. Energ. Convers. Manag. 2019, 186, 570–585. [Google Scholar] [CrossRef]
- Qin, Y.; Du, Q.; Fan, M.; Chang, Y.; Yin, Y. Study on the operating pressure effect on the performance of a proton exchange membrane fuel cell power system. Energ. Convers. Manag. 2017, 142, 357–365. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.; Kang, T.; Sohn, Y.; Song, T.; Choi, K.H. Degradation modeling and operational optimization for improving the lifetime of high-temperature PEM (proton exchange membrane) fuel cells. Energy 2014, 66, 41–49. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, R.; Técher, L.; Cui, X. Experimental study of variable operating parameters effects on overall PEMFC performance and spatial performance distribution. Energy 2016, 115, 550–560. [Google Scholar] [CrossRef]
- Chavan, S.; Talange, D. Modeling and Performance Evaluation of PEM Fuel Cell by Controlling its Input Parameters. Energy 2017, 138, 437–445. [Google Scholar] [CrossRef]
- Yan, W.; Chen, C.; Mei, S.; Soong, C.; Chen, F. Effects of operating conditions on cell performance of PEM fuel cells with conventional or interdigitated flow field. J. Power Sources 2006, 162, 1157–1164. [Google Scholar] [CrossRef]
- Abdin, Z.; Webb, C.J.; Gray, E.M. PEM fuel cell model and simulation in Matlab–Simulink based on physical parameters. Energy 2016, 116, 1131–1144. [Google Scholar] [CrossRef]
- Wu, H.; Shih, G.; Chen, Y. Effect of operational parameters on transport and performance of a PEM fuel cell with the best protrusive gas diffusion layer arrangement. Appl. Energ. 2018, 220, 47–58. [Google Scholar] [CrossRef]
- Belkhiri, Z.; Zeroual, M.; Ben Moussa, H.; Zereg, M.; Zitouni, B. Numerical simulation of exchange membrane fuel cells in different operating conditions. Int. J. Hydrogen Energ. 2012, 37, 5444–5451. [Google Scholar] [CrossRef]
- Ghasabehi, M.; Ashrafi, M.; Shams, M. Performance analysis of an innovative parallel flow field design of proton exchange membrane fuel cells using multiphysics simulation. Fuel 2021, 285, 119194. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, R.; Pan, R.; Cao, G. Disclosure of the internal transport phenomena in an air-cooled proton exchange membrane fuel cell— part II: Parameter sensitivity analysis. Int. J. Hydrogen. Energ. 2021, 46, 18589–18603. [Google Scholar] [CrossRef]
- Kamal, R.; Chan, S.H. Sensitivity analysis of anode overpotential during start-up process of a high temperature proton exchange membrane fuel cell. Electrochim. Acta 2015, 176, 965–975. [Google Scholar] [CrossRef]
- Zhou, D.; Trang Nguyen, T.; Breaz, E.; Zhao, D.; Clénet, S.; Gao, F. Global parameters sensitivity analysis and development of a two-dimensional real-time model of proton-exchange-membrane fuel cells. Energ. Convers. Manag. 2018, 162, 276–292. [Google Scholar] [CrossRef] [Green Version]
- Vetter, R.; Schumacher, J.O. Experimental parameter uncertainty in proton exchange membrane fuel cell modeling. Part II: Sensitivity analysis and importance ranking. J. Power Sources 2019, 439, 126529. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Wang, X.; Zhu, J.; Wang, C.; Zhou, T.; Zhang, X. Sensitivity analysis of proton exchange membrane fuel cell performance to operating parameters and its applicability assessment under different conditions. Energ. Convers. Manag. 2021, 228, 113727. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.; Hirano, S.; Ersal, T. Effective Parameterization of PEM Fuel Cell Models—Part I: Sensitivity Analysis and Parameter Identifiability. J. Electrochem. Soc. 2020, 167, 044504. [Google Scholar] [CrossRef]
- Kannan, V.; Xue, H.; Raman, K.; Chen, J.; Fisher, A.; Birgersson, E. Quantifying operating uncertainties of a PEMFC—Monte Carlo-machine learning based approach. Renew Energ. 2020, 158, 343–359. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Lee, D. Parameter sensitivity examination for a complete three-dimensional, two-phase, non-isothermal model of polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energ. 2012, 37, 15766–15777. [Google Scholar] [CrossRef]
- Min, C.H.; He, Y.L.; Liu, X.L.; Yin, B.H.; Jiang, W.; Tao, W.Q. Parameter sensitivity examination and discussion of PEM fuel cell simulation model validation. J. Power Sources 2006, 160, 374–385. [Google Scholar] [CrossRef]
- Elsawwaf, M.; Willems, P.; Feyen, J. Assessment of the sensitivity and prediction uncertainty of evaporation models applied to Nasser Lake. Egypt. J. Hydrol. 2010, 395, 10–22. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simulat. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Zhao, D.; Dou, M.; Zhou, D.; Gao, F. Study of the modeling parameter effects on the polarization characteristics of the PEM fuel cell. Int. J. Hydrogen Energ. 2016, 41, 22316–22327. [Google Scholar] [CrossRef]
- Chen, H.; Liu, B.; Zhang, T.; Pei, P. Influencing sensitivities of critical operating parameters on PEMFC output performance and gas distribution quality under different electrical load conditions. Appl. Energ. 2019, 255, 113849. [Google Scholar] [CrossRef]
- Oldham, K.; Myland, J. Fundamentals of Electrochemical Science; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Dickinson, E.J.; Hinds, G. The Butler-Volmer equation for polymer electrolyte membrane fuel cell (PEMFC) electrode kinetics: A critical discussion. J. Electrochem. Soc. 2019, 166, F221. [Google Scholar] [CrossRef]
- Ko, D.; Doh, S.; Park, H.S.; Kim, M.H. Investigation of the effect of operating pressure on the performance of proton exchange membrane fuel cell: In the aspect of water distribution. Renew Energy. 2018, 115, 896–907. [Google Scholar] [CrossRef]
- Zhan, Z.; Zhao, H.; Sui, P.C.; Jiang, P.; Pan, M.; Djilali, N. Numerical analysis of ice-induced stresses in the membrane electrode assembly of a PEM fuel cell under sub-freezing operating conditions. Int. J. Hydrogen Energ. 2018, 43, 4563–4582. [Google Scholar] [CrossRef]
- Husar, A.; Higier, A.; Liu, H. In situ measurements of water transfer due to different mechanisms in a proton exchange membrane fuel cell. J. Power Sources 2008, 183, 240–246. [Google Scholar] [CrossRef]
- Heidary, H.; Kermani, M.J.; Dabir, B. Influences of bipolar plate channel blockages on PEM fuel cell performances. Energ. Convers. Manag. 2016, 124, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Hayre, R.; Cha, S.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Ogungbemi, E.; Wilberforce, T.; Ijaodola, O.; Thompson, J.; Olabi, A.G. Review of operating condition, design parameters and material properties for proton exchange membrane fuel cells. Int. J. Energ. Res. 2021, 45, 1227–1245. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Academic Press: New York, NY, USA, 2012. [Google Scholar]

| Mass | Momentum | Energy | Species | Charges | |
|---|---|---|---|---|---|
| 1 | T | ||||
| 0 | |||||
| Γϕ | 0 | ||||
| 0 | 0 | 0 | 0 |
| Computational Domain | Source Term | |||||
|---|---|---|---|---|---|---|
| Mass | Momentum | Energy | Species | Potential | ||
| Sm | Su | ST | Si | Sele | Sion | |
| Bipolar plate | 0 | 0 | 0 | 0 | 0 | |
| Flow channel | 0 | 0 | 0 | 0 | 0 | 0 |
| Gas diffusive layer | 0 | 0 | 0 | 0 | ||
| Anode catalyst layer | Ra | −Ra | ||||
| Cathode catalystlayer | −Rc | Rc | ||||
| Proton exchangemembrane | 0 | 0 | 0 | 0 | 0 | |
| Compute Domain Name | X(mm)/NGE | Y(mm)/NGE | Z(mm)/NGE |
|---|---|---|---|
| 45,000 Bipolar plate | 2.4/25 | 100/60 | 2/15 |
| 8400 Flow channel | 0.8/10 | 100/60 | 0.8/7 |
| 30,000 Gas diffusive layer | 2.4/25 | 100/60 | 0.25/10 |
| 15,000 Catalyst layer | 2.4/25 | 100/60 | 0.014/3 |
| 42,000 Proton exchange membrane | 2.4/25 | 100/60 | 0.23/14 |
| Operating Parameters | Symbol | Calibration Value (Unit) | Range |
|---|---|---|---|
| COT | Tcell | 70 (°C) | 66.5 ~ 73.5 (±5%) |
| AOP | Pan | 1 (atm) | 0.95 ~ 1.5(±5%) |
| COP | Pca | 1 (atm) | 0.95 ~ 1.5 (±5%) |
| AIT | Tan | 70 (°C) | 66.5 ~ 73.5(±5%) |
| CIT | Tca | 70 (°C) | 66.5 ~ 73.5 (±5%) |
| AMFR | 6 × 10−7 (kg/s) | 5.7 × 10−7 ~ 6.3 × 10−7 (±5%) | |
| CMFR | 5 × 10−6 (kg/s) | 4.75 × 10−6 ~ 5.25 × 10−6 (±5%) |
| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| Open circuit voltage (E) | 1.09 | V | CL viscous resistance () | 1.76 × 1011 | 1/m2 |
| Anode reference current density (jan(T)) | 71.7 | A/m2 | Anode/cathode CL surface to volume ratio () | 1.127 × 107 | 1/m |
| Cathode reference current density (jca(T)) | 7.17 × 10−4 | A/m2 | Membrane equivalent weight (EW) | 1100 | kg/kmol |
| Anode/cathode reference concentration ([A]ref/[C]ref) | 1 | kmol/m3 | GDL viscous resistance () | 1.76 × 1011 | 1/m2 |
| Anode concentration exponent () | 0.5 | - | Membrane density () | 1980 | kg/m3 |
| Cathode concentration exponent () | 1 | - | Ionic conductivity () | 9 | S/m |
| Anode/cathode exchange coefficient of reduction reaction () | 1.5 | - | Electrical conductivity () | 1000 | S/m |
| Anode/cathode exchange coefficient of oxidation reaction () | 2 | - | Specific heat capacity of the membrane; CL; GDL; BP; H2; O2 (Cp) | 833; 3300; 568; 871; 14,283; 919 | J/(kg•K) |
| H2 diffusivity () | 2.25 × 10−5 | m2/s | |||
| O2 diffusivity () | 1.13 × 10−5 | m2/s | |||
| H2O diffusivity () | 1.35 × 10−5 | m2/s | ) | 0.4 | |
| Relative humidity (RH) | 100% | ) | 0.6 |
| Operating Conditions | Rankings |
|---|---|
| Idle condition | Tcell > Pca > Pan > San > Sca > Tan > Tca |
| Intermediate condition | Tcell > Pca > Pan > Sca > San > Tca > Tan |
| Rated condition | Tcell > Pca > Pan > San > Sca > Tca > Tan |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, M.; Pan, C.; Liao, J.; Li, C.; Huang, R.; Wang, Q. Assessment of Sensitivity to Evaluate the Impact of Operating Parameters on Stability and Performance in Proton Exchange Membrane Fuel Cells. Energies 2021, 14, 4069. https://doi.org/10.3390/en14144069
Pan M, Pan C, Liao J, Li C, Huang R, Wang Q. Assessment of Sensitivity to Evaluate the Impact of Operating Parameters on Stability and Performance in Proton Exchange Membrane Fuel Cells. Energies. 2021; 14(14):4069. https://doi.org/10.3390/en14144069
Chicago/Turabian StylePan, Mingzhang, Chengjie Pan, Jinyang Liao, Chao Li, Rong Huang, and Qiwei Wang. 2021. "Assessment of Sensitivity to Evaluate the Impact of Operating Parameters on Stability and Performance in Proton Exchange Membrane Fuel Cells" Energies 14, no. 14: 4069. https://doi.org/10.3390/en14144069
APA StylePan, M., Pan, C., Liao, J., Li, C., Huang, R., & Wang, Q. (2021). Assessment of Sensitivity to Evaluate the Impact of Operating Parameters on Stability and Performance in Proton Exchange Membrane Fuel Cells. Energies, 14(14), 4069. https://doi.org/10.3390/en14144069






