Optimization of an Energy Storage System for Electric Bus Fast-Charging Station
Abstract
:1. Introduction
2. Modeling of the Electric Bus Fast-Charging Station with ESS
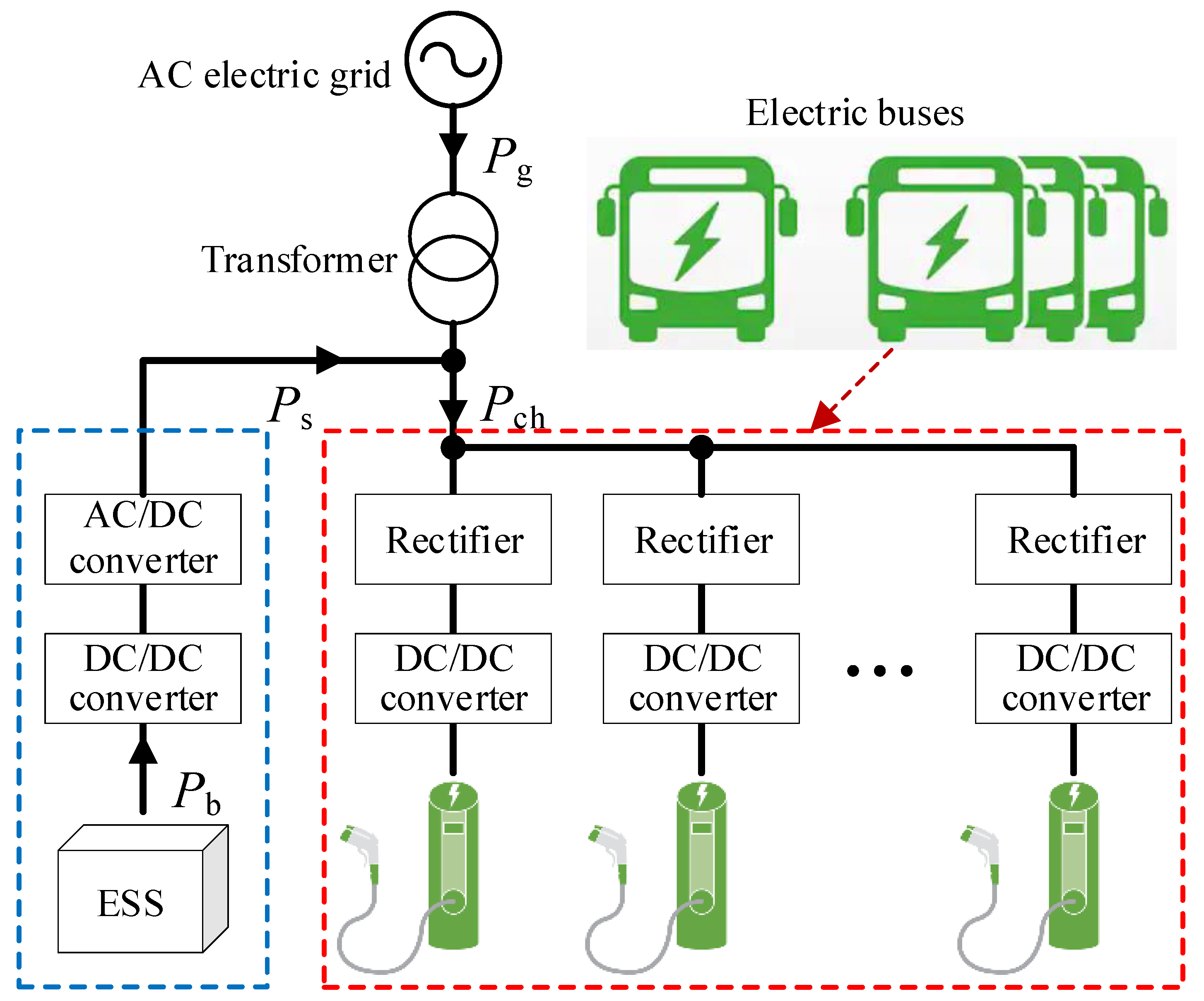
2.1. Topology of the Electric Bus Fast-Charging Station
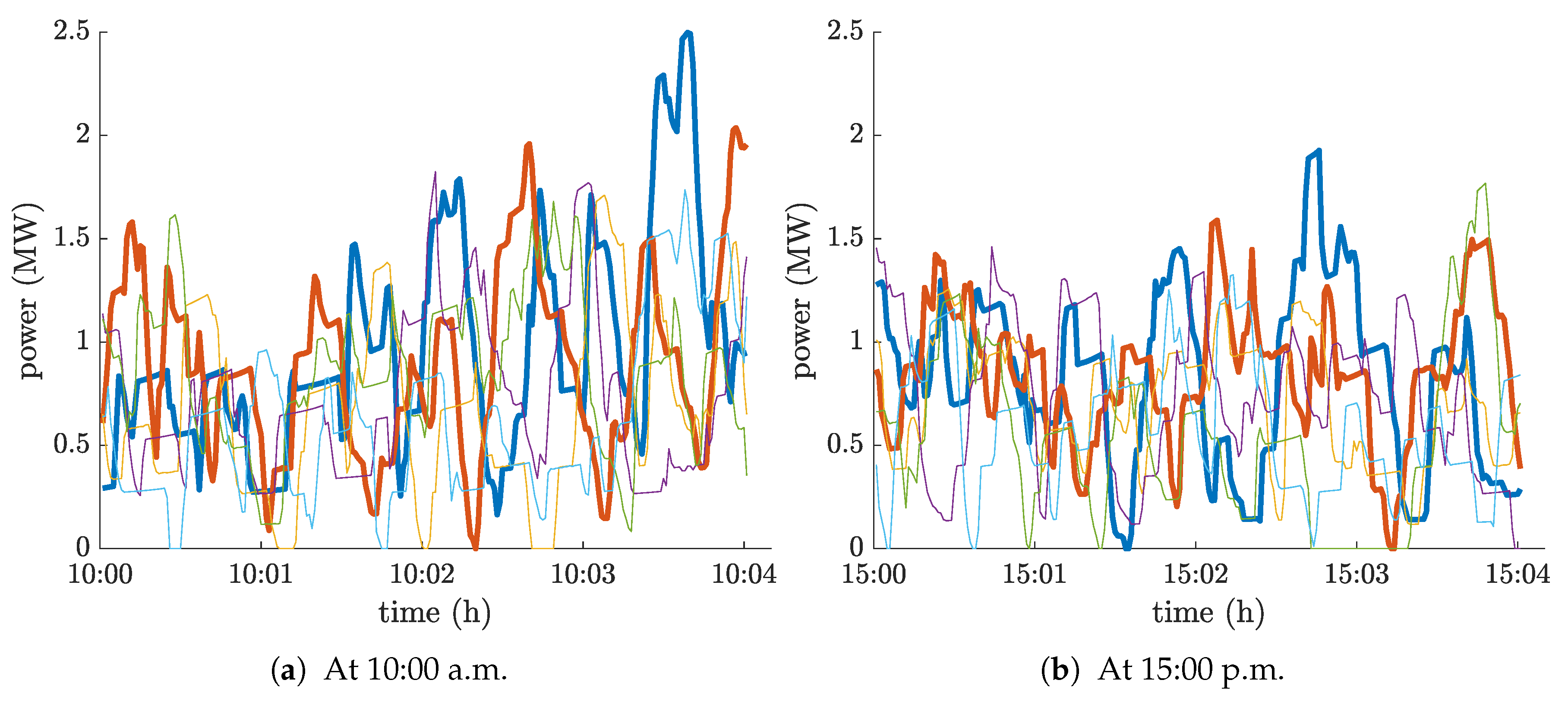
2.2. Charging Demands of the Electric Bus Fast-Charging Station
2.3. ESS Modeling
3. Problem Formulation
3.1. Objective Function: A Daily Average Cost
3.2. Chance-Constrained Programming for ESS Optimization
4. Convex Modeling
5. Case Study
5.1. Parameters Selection
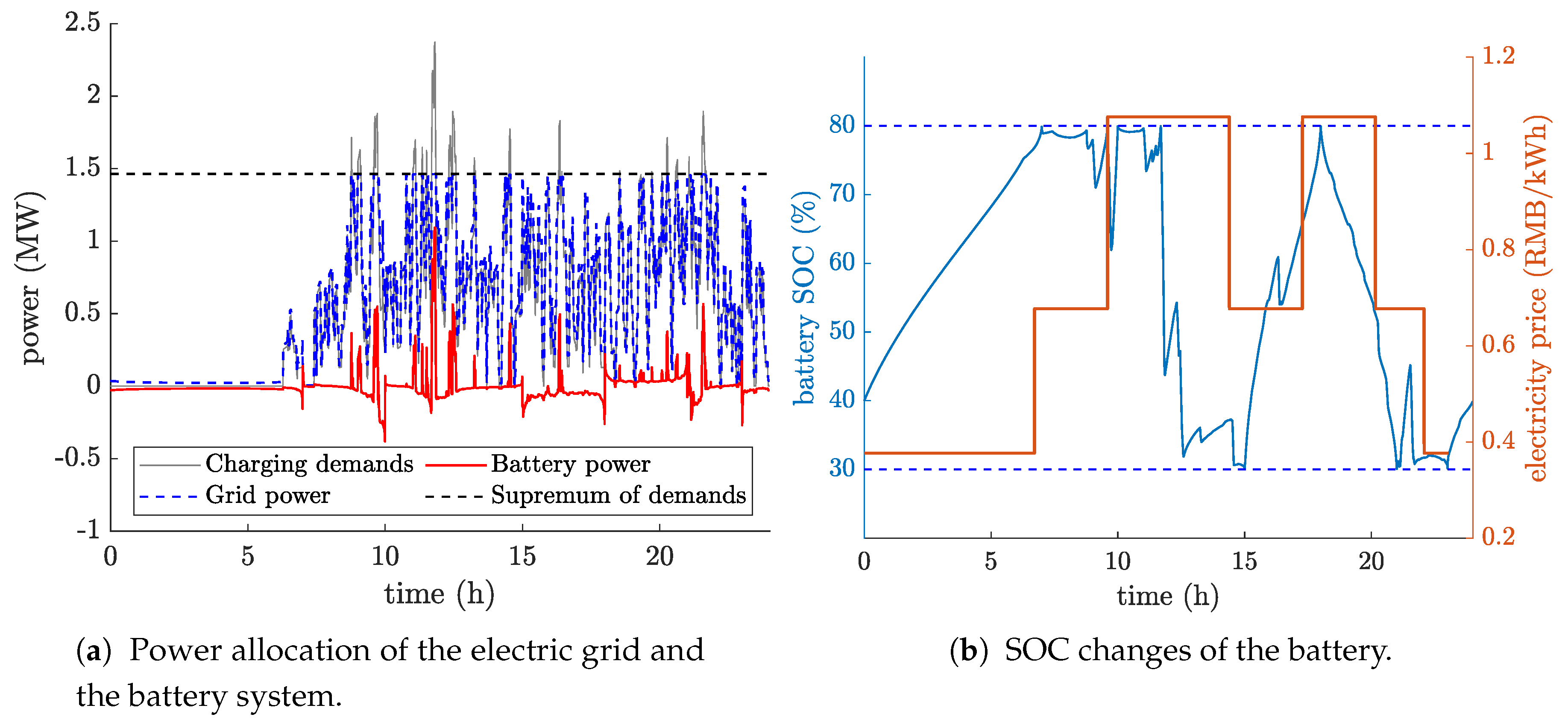
5.2. Optimization Results
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- García-Trivińo, P.; Torreglosa, J.P.; Fernández-Ramírez, L.M.; Jurado, F. Control and operation of power sources in a medium-voltage direct-current microgrid for an electric vehicle fast charging station with a photovoltaic and a battery energy storage system. Energy 2016, 115, 38–48. [Google Scholar] [CrossRef]
- Ayetor, G.K.; Mbonigaba, I.; Sunnu, A.K.; Nyantekyi-Kwakye, B. Impact of replacing ICE bus fleet with electric bus fleet in Africa: A lifetime assessment. Energy 2021, 221, 119852. [Google Scholar] [CrossRef]
- Cempírek, V.; Glock, C.H. Development of electromobility in terms of freight transport. LOGI-Sci. J. Transp. Logist. 2019, 10, 23–32. [Google Scholar] [CrossRef] [Green Version]
- Tomáš, S.; Martin, K.; Ondrej, S.; Saxsxa, M.; Tomasz, F.; Csaba, C. Impact of the electric mobility implementation on the greenhouse gases production in central european countries. Sustainability 2019, 11, 4948. [Google Scholar]
- Nyaki, P.S.; Bwire, H.; Mushule, N.K.; Nyaki, S. Travel time reliability of bus operation in heterogeneous traffic conditions of Dar es Salaam City, Tanzania. LOGI J. Transp. Logist. 2020, 11, 44–55. [Google Scholar] [CrossRef]
- Stopka, O.; Stopkova, M.; Lizbetin, J.; Soviar, J. Development trends of electric vehicles in the context of road passenger and freight transport. In Proceedings of the 12th International Science-Technical Conference Automotive Safety, Kielce, Poland, 21–23 October 2020. [Google Scholar]
- Małek, A.; Caban, J.; Wojciechowski, L. Charging electric cars as a way to increase the use of energy produced from RES. Open Eng. 2020, 10, 98–104. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Miao, R.; Wu, X.; Liu, X. Examining influential factors on the energy consumption of electric and diesel buses: A data-driven analysis of large-scale public transit network in Beijing. Energy 2021, 216, 119196. [Google Scholar] [CrossRef]
- Weitzel, T.; Glock, C.H. Energy management for stationary electric energy storage systems: A systematic literature review. Eur. J. Oper. Res. 2018, 264, 831–845. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, Y.; Song, Z. A cost-competitiveness analysis of charging infrastructure for electric bus operations. Transp. Res. Part C 2018, 93, 351–366. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Qureshi, F.A.; Bitlislioglu, A.; Poland, J.; Zanarini, A.; Mercangoez, M.; Jones, C. Ancillary services provision utilizing a network of fast-charging stations for electrical buses. IEEE Trans. Smart Grid 2020, 11, 665–672. [Google Scholar] [CrossRef]
- He, Y.; Song, Z.; Liu, Z. Fast-charging station deployment for battery electric bus systems considering electricity demand charges. Sustain. Cities Soc. 2019, 48, 101530. [Google Scholar] [CrossRef] [Green Version]
- Teichert, O.; Chang, F.; Ongel, A.; Lienkamp, M. Joint optimization of vehicle battery pack capacity and charging infrastructure for electrified public bus systems. IEEE Trans. Transp. Electrif. 2019, 5, 672–682. [Google Scholar] [CrossRef]
- Chen, H.; Hu, Z.; Zhang, H.; Luo, H. Coordinated Charging and Discharging Strategies for Plug-in Electric Bus Fast Charging Station with Energy Storage System. IET Gener. Transm. Distrib. 2018, 12, 2019–2028. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Hu, Z.; Song, Y. Value of the energy storage system in an electric bus fast charging station. Appl. Energy 2015, 157, 630–639. [Google Scholar] [CrossRef]
- Wei, S.; Jiang, J.; Murgovski, N.; Sjöberg, J.; Zhang, W.; Zhang, C.; Hu, X. Optimisation of a catenary-free tramline equipped with stationary energy storage systems. IEEE Trans. Veh. Technol. 2020, 69, 2449–2462. [Google Scholar] [CrossRef]
- Uslu, T.; Kaya, O. Location and capacity decisions for electric bus charging stations considering waiting times. Transp. Res. Part D 2021, 90, 102645. [Google Scholar] [CrossRef]
- Ro, L.; Je, H. Optimal charging schedule planning and economic analysis for electric bus charging stations. Energies 2017, 10, 483. [Google Scholar]
- He, Y.; Liu, Z.; Song, Z. Optimal charging scheduling and management for a fast-charging battery electric bus system. Transp. Res. Part E 2020, 142, 102056. [Google Scholar] [CrossRef]
- Chen, L.; Qin, M.; Xia, Y.; Qian, K.; Xu, X. A configuration-control integrated strategy for electric bus charging station with echelon battery system. IEEE Trans. Ind. Appl. 2020, 56, 6019–6028. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Wang, X.; Wang, Y.; Fang, C.; Xue, H.; Fang, C. Modeling of fast charging station equipped with energy storage. Glob. Energy Interconnect. 2018, 1, 145–152. [Google Scholar]
- Arif, S.M.; Lie, T.T.; Seet, B.C.; Ahsan, S.M.; Khan, H.A. Plug-in electric bus depot charging with PV and ESS and their impact on LV feeder. Energies 2020, 13, 2139. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.; Jiang, J.; Zhang, W.; Bao, Y.; Huang, M. Research on configuration methods of battery energy storage system for pure electric bus fast charging station. Energies 2019, 12, 558. [Google Scholar] [CrossRef] [Green Version]
- Trocker, F.; Teichert, O.; Gallet, M.; Ongel, A.; Lienkamp, M. City-scale assessment of stationary energy storage supporting end-station fast charging for different bus-fleet electrification levels. J. Energy Storage 2020, 32, 101794. [Google Scholar] [CrossRef]
- Aghapour, R.; Sepasian, M.S.; Arasteh, H.; Vahidinasab, V.; Catalão, J.P. Probabilistic planning of electric vehicles charging stations in an integrated electricity-transport system. Electr. Power Syst. Res. 2020, 189, 106698. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Abedini, M.; Rezaei, M.M.; Nasri, M. Optimum design of a multi-form energy in the presence of electric vehicle charging station and renewable resources considering uncertainty. Sustain. Energy Grids Netw. 2020, 23, 100375. [Google Scholar] [CrossRef]
- Yang, D.; Sarma, N.J.S.; Hyland, M.F.; Jayakrishnan, R. Dynamic modeling and real-time management of a system of EV fast-charging stations. Transp. Res. Part C Emerg. Technol. 2021, 128, 103186. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Q.; Bai, C.; Lai, C.S.; Ji, Y.; Lai, L.L. A novel fast-charging stations locational planning model for electric bus transit system. Energy 2021, 224, 120106. [Google Scholar] [CrossRef]
- Pamuła, T.; Pamuła, W. Estimation of the energy consumption of battery electric buses for public transport networks using real-world data and deep learning. Energies 2020, 13, 2340. [Google Scholar] [CrossRef]
- An, K. Battery electric bus infrastructure planning under demand uncertainty. Transp. Res. Part C 2020, 111, 572–587. [Google Scholar] [CrossRef]
- Liu, X.; Feng, T. Energy-storage configuration for EV fast charging stations considering characteristics of charging load and wind-power fluctuation. Renew. Sustain. Energy Rev. 2021, 4, 48–57. [Google Scholar]
- Toshiba. Product Specification. Available online: https://www.scib.jp/en/product/cell.htm (accessed on 1 May 2021).
- Herrera, V.; Milo, A.; Gaztanaga, H.; Etxeberria-Otadui, I.; Villarreal, I.; Camblong, H. Adaptive energy management strategy and optimal sizing applied on a battery-supercapacitor based tramway. Appl. Energy 2016, 169, 831–845. [Google Scholar] [CrossRef]
- Takami, N.; Inagaki, H.; Tatebayashi, Y.; Saruwatari, H.; Honda, K.; Egusa, S. High-power and long-life lithium-ion batteries using lithium titanium oxide anode for automotive and stationary power applications. J. Power Sources 2013, 244, 469–475. [Google Scholar] [CrossRef]
- Beijing Municipal Commission of Development and Reform. Electricity Price List of Beijing. 2021. Available online: http://fgw.beijing.gov.cn/bmcx/djcx/jzldj/202003/P020200331428682714728.pdf (accessed on 1 May 2021).
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2019. Available online: http://cvxr.com/cvx (accessed on 1 May 2021).





| Variable | Symbol | Value |
|---|---|---|
| Rated voltage | V | |
| Rated capacitance | 20 Ah | |
| Rated energy | 46 Wh | |
| Maximum current | 100 A | |
| Minimum current | −100 A | |
| Internal resistance | ||
| Maximum SOC | 80 % | |
| Minimum SOC | 30 % | |
| Pack price | 40 RMB/Wh | |
| Cost for ESS installation | 40,000 RMB |
| Day Hour [h] | [10, 15], [18, 21] | [7, 10], [15, 18], [21, 23] | [23, 7] |
|---|---|---|---|
| ( RMB/kWh) |
| Problem Parameter | Optimization with Different | ||
|---|---|---|---|
| Number of constraint | 1,048,377 | 1,048,377 | 1,048,377 |
| Number of scalar variable | 1,451,581 | 1,451,581 | 1,451,581 |
| Number of integer variable | 1 | 1 | 1 |
| Computational time | 683 s | 711 s | 829 s |
| Variables | Without ESS () | With ESS | ||
|---|---|---|---|---|
| Supremum of demands, | 2498 | 1463 | 1171 | 1014 |
| Maximum operating capacity of grid, | 2629 | 1540 | 1233 | 1067 |
| Installation flag, b | 0 | 1 | 1 | 1 |
| Rated energy of ESS, | 0 | 325 | 1214 | 1889 |
| Rated capacity of charging equipment, | 0 | 1190 | 1498 | 1677 |
| Initial cost of ESS, ( RMB/day) | 0 | 5038 | 17,765 | 27,408 |
| Electricity cost of grid, ( RMB/day) | 10,698 | 10,617 | 10,311 | 10,170 |
| Maximum operating capacity cost, ( RMB/day) | 2805 | 1643 | 1315 | 1138 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Zhang, W.; Wei, S.; Wang, Z. Optimization of an Energy Storage System for Electric Bus Fast-Charging Station. Energies 2021, 14, 4143. https://doi.org/10.3390/en14144143
Ding X, Zhang W, Wei S, Wang Z. Optimization of an Energy Storage System for Electric Bus Fast-Charging Station. Energies. 2021; 14(14):4143. https://doi.org/10.3390/en14144143
Chicago/Turabian StyleDing, Xiaowei, Weige Zhang, Shaoyuan Wei, and Zhenpo Wang. 2021. "Optimization of an Energy Storage System for Electric Bus Fast-Charging Station" Energies 14, no. 14: 4143. https://doi.org/10.3390/en14144143





