Modeling and Analysis of Heat Dissipation for Liquid Cooling Lithium-Ion Batteries
Abstract
:1. Introduction
2. Modeling and Numerical Methodology
2.1. Arrangement and Geometry of the Batteries and Cooling Plates to Be Modeled
2.2. Mathematical Equations and Modeling Method for BTMS
2.2.1. The Governing Equations
2.2.2. Battery Heat Generation Model
2.2.3. Physical and Thermal Properties
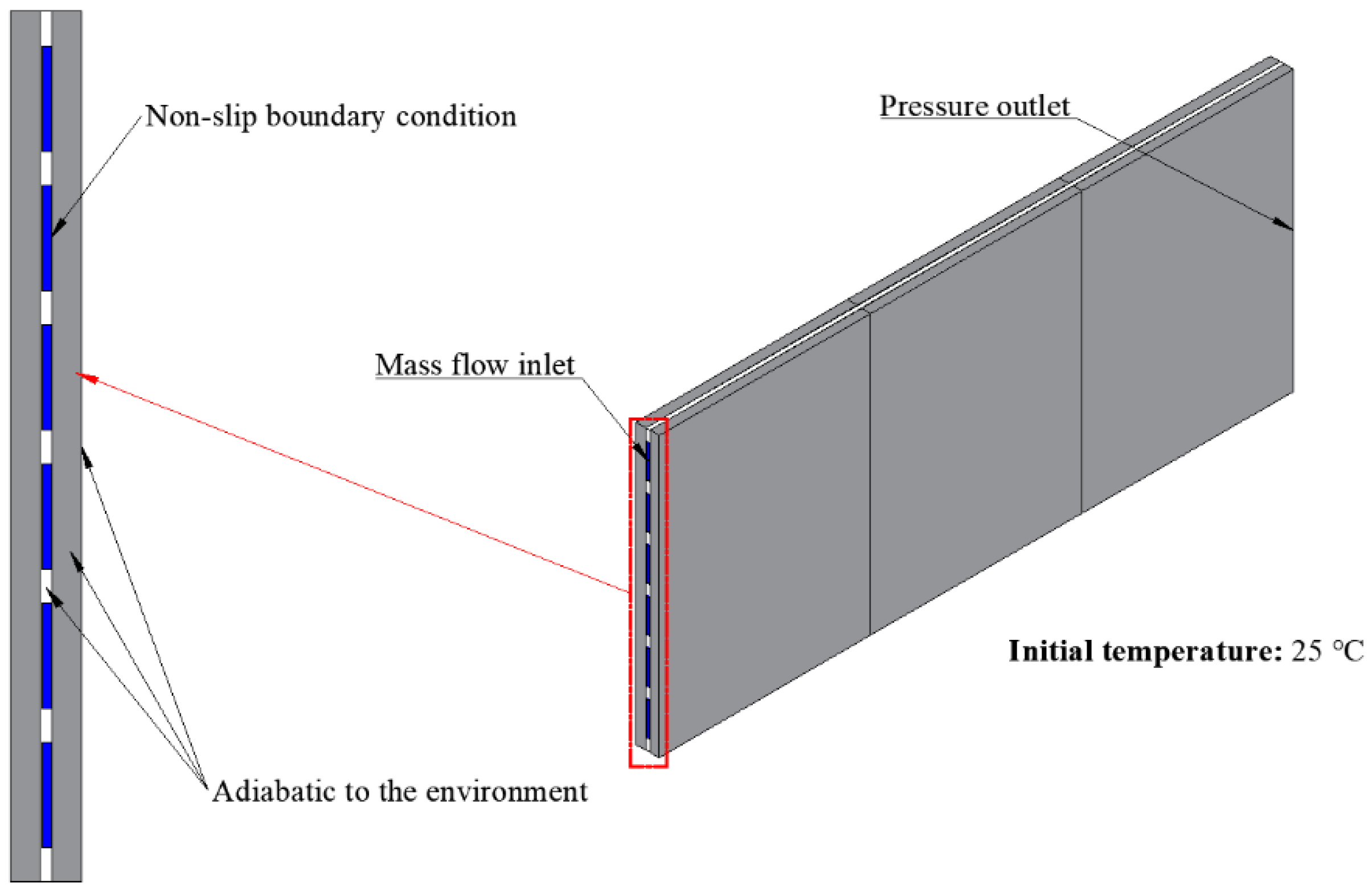
2.2.4. Initial and Boundary Conditions
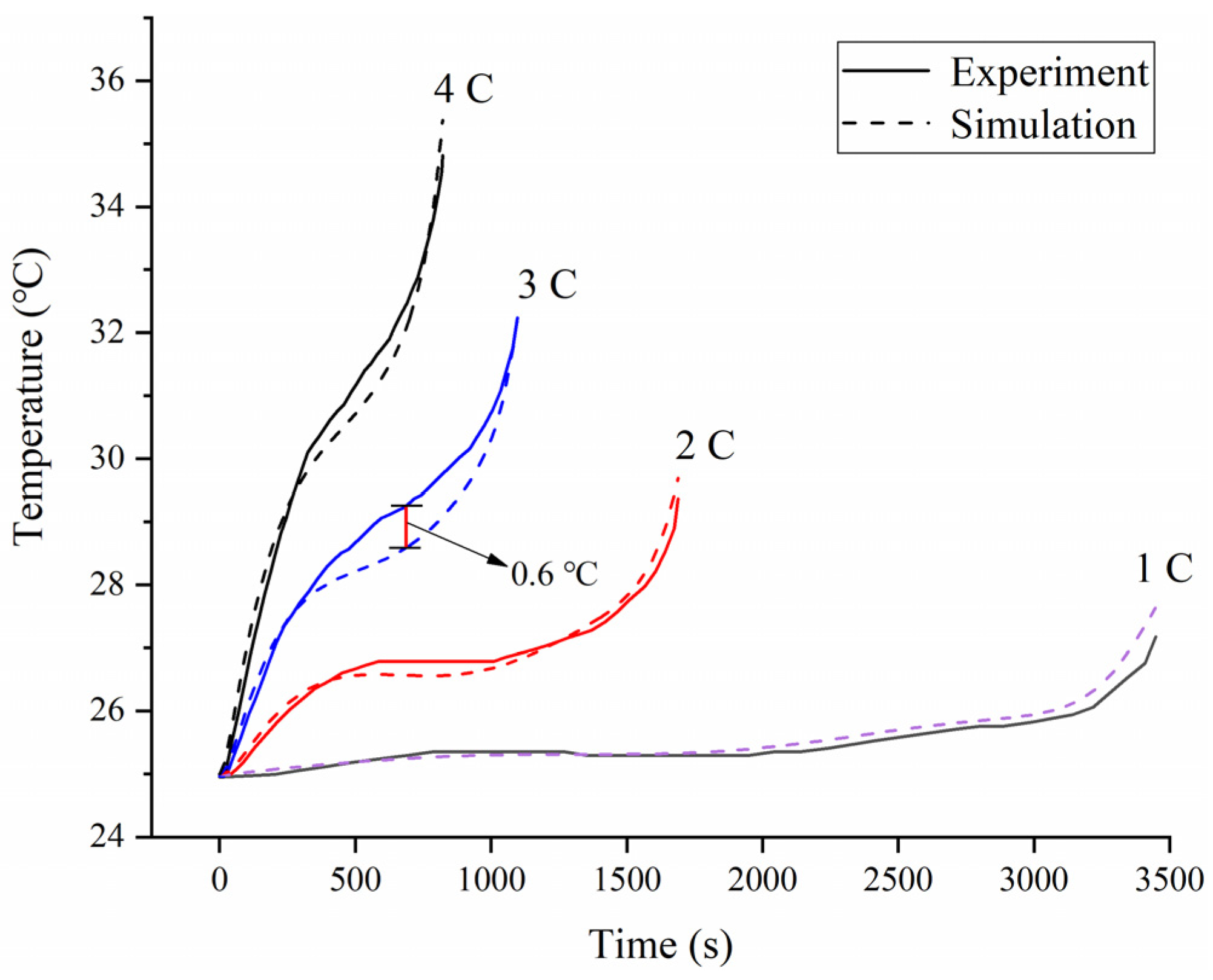
2.2.5. Implementation Method and Validation of the Model
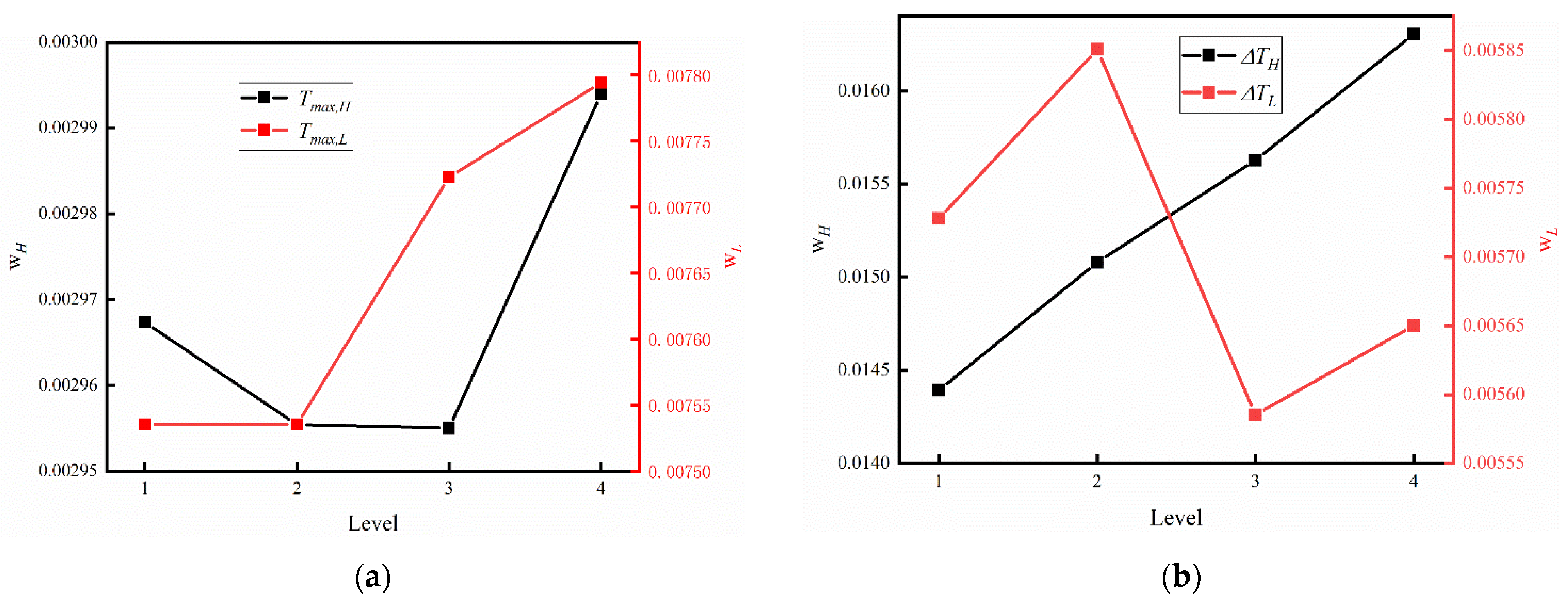
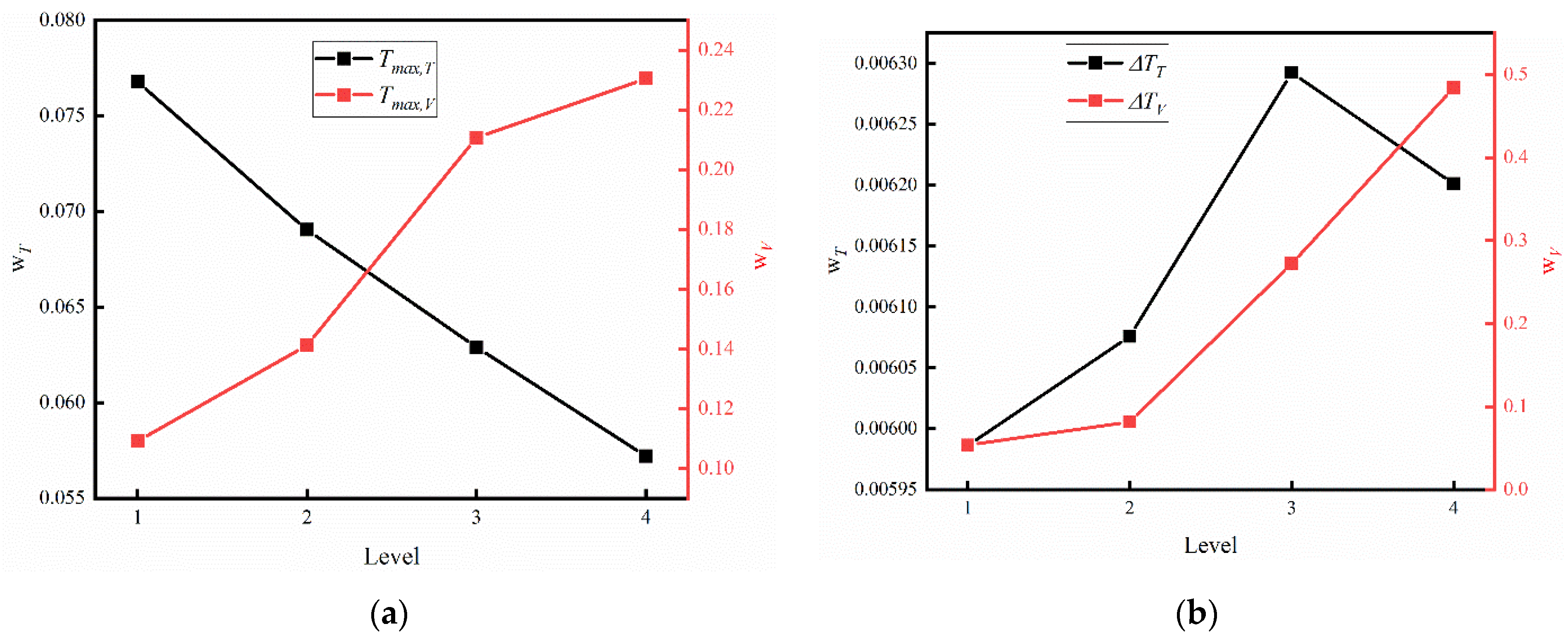
2.3. Orthogonal Design Method for BTMS and Its Matrix Analysis
3. Results and Discussion
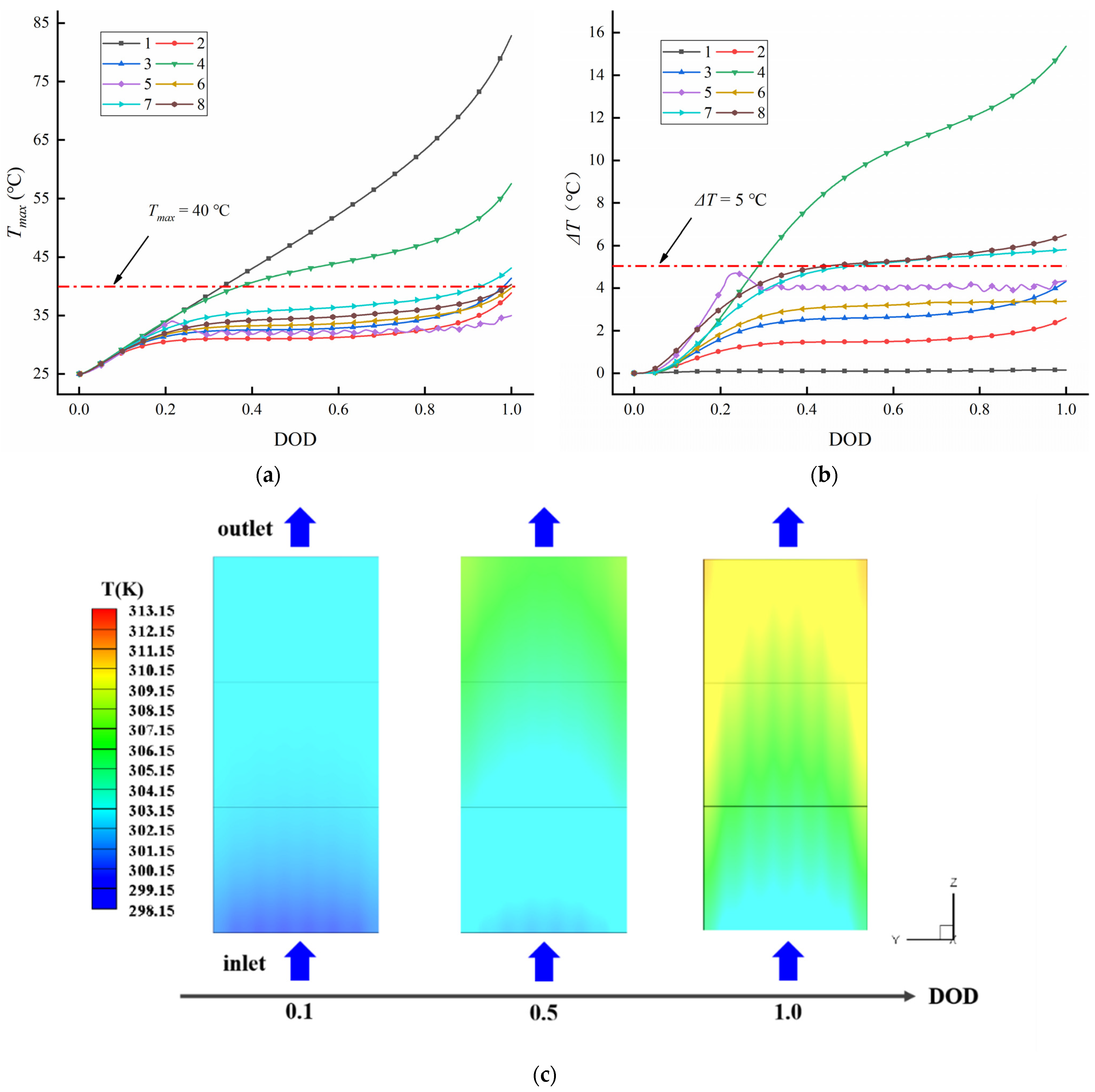
3.1. The Influence of Channel Size
3.2. The Influence of Inlet Temperature and Flow Rate
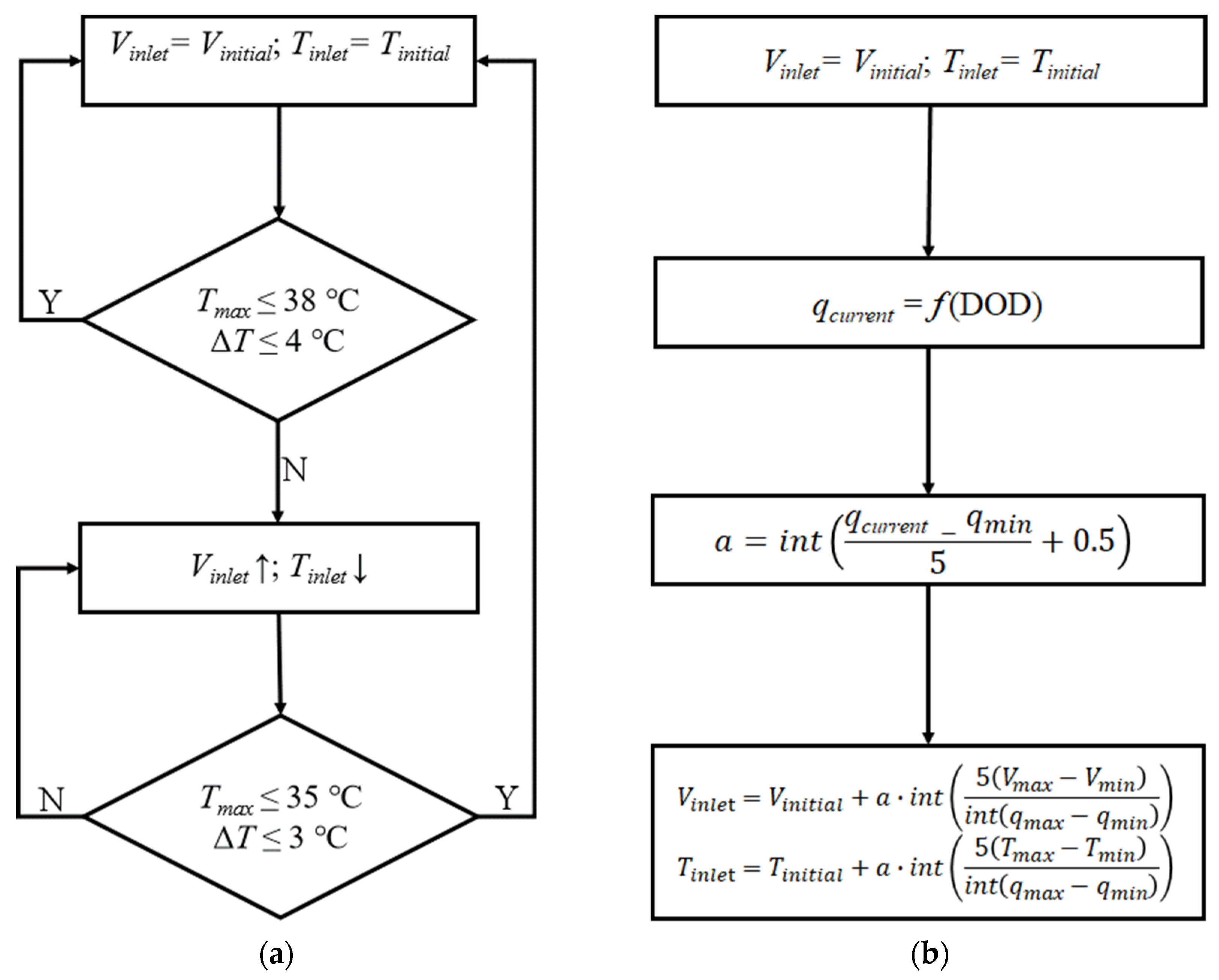
3.3. Evaluation of Various Temperature Control Strategies
4. Conclusions
- (1)
- Thermal contact resistance between the direct contacting interface between the battery and cooling plate surfaces is significant and needs to be considered in the modelling of the temperature distribution.
- (2)
- For the rectangular channels in the cooling plates, the inlet flow rate has the most significant impact on the temperature distribution in the battery module. In addition, increasing channel height can effectively decrease the parasitic energy consumption of the BTMS.
- (3)
- Among the eight temperature control schemes, Scheme 5 adjusting the inlet flow rate can maintain a reasonable temperature distribution range in the module and has a lower energy consumption, which is considered as the better temperature control scheme for the specific BTMS in this work. In addition, for Strategy (a), the response time of BTMS is only affected by the temperature distribution, not by the discharging/charging time of the battery.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables | Greek Symbols | ||
| C | specific heat (J/kg·K) | δ | thickness (m) |
| d | the equivalent diameter of the channel (m) | molecular viscosity (kg/m·s) | |
| H | height of fluid channel (mm) | λ | thermal conductivity (W/m·K) |
| j | heat transfer factor | η | ratio of energy consumption of a certain Scheme to that of Scheme 2 |
| k | rate of temperature change | ||
| L | width of fluid channel (mm) | density (kg/m3) | |
| P | static pressure (Pa) | the stress tensor | |
| Pr | Prandtl number | ||
| ΔP | pressure drop (Pa) | Subscripts | |
| qc | heat exchange between the battery and the coolant (W) | b | battery |
| c | coolant | ||
| heat generation rate per unit volume (W/m3) | env | environment | |
| R | contact thermal resistance | max | maximum |
| Re | Reynolds number | sen | sensible |
| St | Stanton number | ||
| T | temperature (°C) | Acronyms | |
| t | time(s) | BMS | Battery management system |
| ΔT | temperature difference (°C) | BTMS | Battery thermal management system |
| velocity vector | CFD | Computational fluid dynamics | |
| V | mass flow rate (kg/s) | DOD | Depth of discharge |
| Vb | battery volume (m3) | EER | Energy efficiency ratio |
| EV | Electric vehicle | ||
| HEV | Hybrid electric vehicle | ||
| PCM | Phase change material | ||
| SOC | State of charge | ||
| UDF | User defined function | ||
References
- Alptekin, E. Emission, injection and combustion characteristics of biodiesel and oxygenated fuel blends in a common rail diesel engine. Energy 2017, 119, 44–52. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Kukay, A.; Sahore, R.; Parejiya, A.; Blake Hawley, W.; Li, J.; Wood, D.L. Aqueous Ni-rich-cathode dispersions processed with phosphoric acid for lithium-ion batteries with ultra-thick electrodes. J. Colloid Interface Sci. 2021, 581, 635–643. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Noise-Immune Model Identification and State-of-Charge Estimation for Lithium-Ion Battery Using Bilinear Parameterization. IEEE Trans. Ind. Electron 2021, 68, 312–323. [Google Scholar] [CrossRef]
- Yamada, Y. Concentrated battery electrolytes: Developing new functions by manipulating the coordination states. Bull. Chem. Soc. Jpn. 2020, 93, 109–118. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.; Rao, Z. Thermal performance of lithium-ion battery thermal management system by using mini-channel cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Rao, Z.; Zhang, X. Investigation on thermal management performance of wedge-shaped microchannels for rectangular Li-ion batteries. Int. J. Energy Res. 2019, 43, 3876–3890. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part II. Capacity fade analysis. J. Power Sources 2002, 112, 614–620. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Pesaran, A.A.; Burch, S.; Keyser, M. An Approach for Designing Thermal Management Systems for Electric and Hybrid Vehicle Battery Packs. In Proceedings of the Fourth Vehicle Thermal Management Systems Conference and Exhibition; London, UK, 24–27 May 1999. Available online: http://www.doe.gov/bridge/home.html (accessed on 9 July 2021).
- Al Hallaj, S.; Selman, J.R. A Novel Thermal Management System for Electric Vehicle Batteries Using Phase-Change Material. J. Electrochem. Soc 2000, 147, 3231. [Google Scholar] [CrossRef]
- Choudhari, V.G.; Dhoble, A.S.; Panchal, S. Numerical analysis of different fin structures in phase change material module for battery thermal management system and its optimization. Int. J. Heat Mass Transf. 2020, 163, 120434. [Google Scholar] [CrossRef]
- Lv, P.; Liu, C.; Rao, Z. Review on clay mineral-based form-stable phase change materials: Preparation, characterization and applications. Renew. Sustain. Energy Rev. 2017, 68, 707–726. [Google Scholar] [CrossRef]
- Wu, M.S.; Liu, K.H.; Wang, Y.Y.; Wan, C.C. Heat dissipation design for lithium-ion batteries. J. Power Sources 2002, 109, 160–166. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Li, Y. Investigation on the thermal performance of a battery thermal management system using heat pipe under different ambient temperatures. Energy Convers. Manag. 2018, 155, 1–9. [Google Scholar] [CrossRef]
- Jaguemont, J.; Van Mierlo, J. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage 2020, 31, 101551. [Google Scholar] [CrossRef]
- Panchal, S.; Gudlanarva, K.; Tran, M.; Fraser, R. High Reynold’s Number Turbulent Model for Micro-Channel Cold Plate Using Reverse Engineering Approach for Water-Cooled Battery in Electric Vehicles. Energies 2020, 13, 1638. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, W.; Xu, X.; Tong, G. Heat dissipation analysis of different flow path for parallel liquid cooling battery thermal management system. Int. J. Energy Res. 2020, 44, 5165–5176. [Google Scholar] [CrossRef]
- Zhao, C.; Cao, W.; Dong, T.; Jiang, F. Thermal behavior study of discharging/charging cylindrical lithium-ion battery module cooled by channeled liquid flow. Int. J. Heat Mass Transf. 2018, 120, 751–762. [Google Scholar] [CrossRef]
- Xu, X.; Tong, G.; Li, R. Numerical study and optimizing on cold plate splitter for lithium battery thermal management system. Appl. Therm. Eng. 2020, 167, 114787. [Google Scholar] [CrossRef]
- Deng, T.; Zhang, G.; Ran, Y. Study on thermal management of rectangular Li-ion battery with serpentine-channel cold plate. Int. J. Heat Mass Transf. 2018, 125, 143–152. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Panchal, S.; Jee, S.W.; Lee, M.Y. Investigation on thermal performance of water-cooled Li-ion pouch cell and pack at high discharge rate with U-turn type microchannel cold plate. Int. J. Heat Mass Transf. 2020, 155, 119728. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, Q.; Wang, G.; Gu, Y.; Wang, Y.; Bao, W.; Zhang, D. Investigation on the promotion of temperature uniformity for the designed battery pack with liquid flow in cooling process. Appl. Therm. Eng. 2017, 116, 655–662. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, S.; Lu, Y.; Huang, R.; Yu, X. Study on a liquid cooled battery thermal management system pertaining to the transient regime. Appl. Therm. Eng. 2020, 180, 115793. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Panchal, S.; Lee, M.Y. Numerical study on sensitivity analysis of factors influencing liquid cooling with double cold-plate for lithium-ion pouch cell. Int. J. Energy Res. 2021, 45, 2533–2559. [Google Scholar] [CrossRef]
- Huo, Y.; Rao, Z.; Liu, X.; Zhao, J. Investigation of power battery thermal management by using mini-channel cold plate. Energy Convers. Manag. 2015, 89, 387–395. [Google Scholar] [CrossRef]
- Wang, F.; Cao, J.; Ling, Z.; Zhang, Z.; Fang, X. Experimental and simulative investigations on a phase change material nano-emulsion-based liquid cooling thermal management system for a lithium-ion battery pack. Energy 2020, 207, 118215. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Experimental and theoretical investigations of heat generation rates for a water cooled LiFePO4 battery. Int. J. Heat Mass Transf. 2016, 101, 1093–1102. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Panchal, S.; Science, A. Experimental Investigation and Modeling of Lithium-Ion Battery Cells and Packs for Electric Vehicles. Ph.D. Thesis, Faculty of Engineering and Applied Science, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2016. Available online: http://hdl.handle.net/10155/747 (accessed on 9 July 2021).
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal design and simulation of mini-channel cold plate for water cooled large sized prismatic lithium-ion battery. Appl. Therm. Eng. 2017, 122, 80–90. [Google Scholar] [CrossRef]
- Zhou, Y. A Matrix Analysis of Orthogonal Design. Math. Pract. Theory 2009, 29, 202–207. (in Chinese). Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2009&filename=SSJS200902033&v=uGgOHP8P%25mmd2FYysaiZRLyVk%25mmd2FzUxqHzvuZSmDhqAuE83FhFGqZnLR9pqyfkBcCOO4vLo (accessed on 9 July 2021).
- Jin, X.; Duan, X.; Jiang, W.; Wang, Y.; Zou, Y.; Lei, W.; Sun, L.; Ma, Z. Structural design of a composite board/heat pipe based on the coupled electro-chemical-thermal model in battery thermal management system. Energy 2021, 216, 119234. [Google Scholar] [CrossRef]




| Material | ρ (kg/m3) | C (J/kg·K) | λ (W/m·K) | μ (kg/m·s) |
|---|---|---|---|---|
| Battery | 2092 | 678 | 18.2 | - |
| Water | 998.2 | 4128 | 0.6 | 0.001001 |
| Aluminum | 2719 | 871 | 202.4 | - |
| Level | Factors | |||
|---|---|---|---|---|
| H (mm) | L (mm) | V (kg/s) | T (°C) | |
| 1 | 0.5 | 10 | 0.0005 | 20 |
| 2 | 1.0 | 15 | 0.001 | 25 |
| 3 | 1.5 | 20 | 0.005 | 30 |
| 4 | 2.0 | 25 | 0.01 | 35 |
| Number | Factor | Evaluation Index | |||||
|---|---|---|---|---|---|---|---|
| H | L | T | V | Tmax (°C) | ΔT (°C) | ΔP (Pa) | |
| 1 | 1 | 1 | 1 | 1 | 67.29 | 29.25 | 1770.11 |
| 2 | 1 | 2 | 2 | 2 | 54.36 | 19.21 | 3525.29 |
| 3 | 1 | 3 | 3 | 3 | 39.52 | 5.95 | 6776.63 |
| 4 | 1 | 4 | 4 | 4 | 40.78 | 3.36 | 12,198.85 |
| 5 | 2 | 1 | 2 | 3 | 36.00 | 5.18 | 1789.54 |
| 6 | 2 | 2 | 1 | 4 | 26.93 | 2.96 | 2129.14 |
| 7 | 2 | 3 | 4 | 1 | 81.08 | 28.39 | 166.21 |
| 8 | 2 | 4 | 3 | 2 | 58.76 | 18.62 | 265.14 |
| 9 | 3 | 1 | 3 | 4 | 38.64 | 2.80 | 924.58 |
| 10 | 3 | 2 | 4 | 3 | 45.83 | 5.16 | 391.45 |
| 11 | 3 | 3 | 1 | 2 | 48.55 | 17.94 | 99.27 |
| 12 | 3 | 4 | 2 | 1 | 69.77 | 27.31 | 39.52 |
| 13 | 4 | 1 | 4 | 2 | 64.21 | 16.81 | 84.95 |
| 14 | 4 | 2 | 3 | 1 | 73.97 | 25.57 | 29.93 |
| 15 | 4 | 3 | 2 | 4 | 31.99 | 3.13 | 348.67 |
| 16 | 4 | 4 | 1 | 3 | 29.98 | 5.49 | 149.66 |
| Scheme | Vinlet (kg/s) | Tinlet (°C) | Tmax < 40 (°C) | ΔT < 5 (°C) | η | Strategy |
|---|---|---|---|---|---|---|
| 1 | 0.01 | Tinlet = Toutlet | × | × | — | — |
| 2 | 0.01 | 25 | √ | √ | 100% | Constant |
| 3 | 0.005 | 25 | × | √ | 25% | Constant |
| 4 | 0.001 | 25 | × | × | 1% | Constant |
| 5 | 0.001–0.01 | 25 | √ | √ | 20% | Strategy (a) |
| 6 | 0.001–0.01 | 25 | √ | √ | 24% | Strategy (b) |
| 7 | 0.001–0.005 | 25 | × | × | 7% | Strategy (b) |
| 8 | 0.001–0.005 | 25–20 | √ | × | Strategy (b) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Zhao, J.; Li, X.; Panchal, S.; Yuan, J.; Fraser, R.; Fowler, M. Modeling and Analysis of Heat Dissipation for Liquid Cooling Lithium-Ion Batteries. Energies 2021, 14, 4187. https://doi.org/10.3390/en14144187
Duan J, Zhao J, Li X, Panchal S, Yuan J, Fraser R, Fowler M. Modeling and Analysis of Heat Dissipation for Liquid Cooling Lithium-Ion Batteries. Energies. 2021; 14(14):4187. https://doi.org/10.3390/en14144187
Chicago/Turabian StyleDuan, Jiabin, Jiapei Zhao, Xinke Li, Satyam Panchal, Jinliang Yuan, Roydon Fraser, and Michael Fowler. 2021. "Modeling and Analysis of Heat Dissipation for Liquid Cooling Lithium-Ion Batteries" Energies 14, no. 14: 4187. https://doi.org/10.3390/en14144187
APA StyleDuan, J., Zhao, J., Li, X., Panchal, S., Yuan, J., Fraser, R., & Fowler, M. (2021). Modeling and Analysis of Heat Dissipation for Liquid Cooling Lithium-Ion Batteries. Energies, 14(14), 4187. https://doi.org/10.3390/en14144187









