Influence of Heavy Weight Drill Pipe Material and Drill Bit Manufacturing Errors on Stress State of Steel Blades
Abstract
:1. Introduction
- −
- to develop a mathematical model of drill bit rock interaction taking into account manufacturing errors.
- −
- to investigate the influence of the mechanical properties of different classes of drill pipe materials on the additional force that clamps the drill bit to the well wall and the level of stresses in the metal bit.
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhironkin, S.; Demchenko, S.; Kayachev, G.; Taran, E.; Zhironkina, O. Convergent and nature-like technologies as the basis for sustainable development in the 21st Century. E3S Web Conf. 2019, 105, 03008. [Google Scholar] [CrossRef]
- Ursul, A.; Ursul, T.; Dugarova, M. Towards a global sustainable future. Philos. Cosmol. 2017, 15, 37–50. [Google Scholar]
- Zhironkin, S.; Khloptsov, D.; Skrylnikova, N.; Petinenko, I.; Zhironkina, O. Economic principles of mining region sustainable development. E3S Web Conf. 2018, 41, 04010. [Google Scholar] [CrossRef]
- Rozin, V. From engineering and technological process to post-cultural technology. Future Hum. Image 2020, 15, 99–109. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook. Flagship Report—2019; International Energy Agency: Paris, France, 2019; Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 20 May 2021).
- Krichevskiy, S. Evolution of technologies, “green” development and grounds of the general theory of technologies. Philos. Cosmol. 2015, 14, 120–139. [Google Scholar]
- Falshtynskyi, V.; Saik, P.; Lozynskyi, V.; Dychkovskyi, R.; Petlovanyi, M. Innovative aspects of underground coal gasification technology in mine conditions. Min. Miner. Depos. 2018, 12, 68–75. [Google Scholar] [CrossRef]
- Lozynskyi, V.; Medianyk, V.; Saik, P.; Rysbekov, K.; Demydov, M. Multivariance solutions for designing new levels of coal mines. Rud. Geol. Naft. Zb. 2020, 35, 23–31. [Google Scholar] [CrossRef]
- Le Billon, P.; Kristoffersen, B. Just cuts for fossil fuels? Supply-side carbon constraints and energy transition. Environ. Plan. A Econ. Space 2020, 52, 1072–1092. [Google Scholar] [CrossRef]
- Bazaluk, O.; Slabyi, O.; Vekeryk, V.; Velychkovych, A.; Ropyak, L.; Lozynskyi, V. A technology of hydrocarbon fluid production intensification by productive stratum drainage zone reaming. Energies 2021, 14, 3514. [Google Scholar] [CrossRef]
- Svyrydenko, D.; Mozgin, W. The soft power of the state as a dialectic of contemporary dependencies in the international arena. Ukrainian Policymaker 2019, 5, 89–97. [Google Scholar] [CrossRef]
- Olovyannyy, A.; Chantsev, V. Numerical experiments concerning long-term deformation of rock samples. Min. Miner. Depos. 2019, 13, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Babets, D.V.; Sdvyzhkova, O.O.; Larionov, M.H.; Tereshchuk, R.M. Estimation of rock mass stability based on probability approach and rating systems. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2017, 2, 58–64. [Google Scholar]
- Gorova, A.; Pavlychenko, A.; Borysovs’ka, O. The study of ecological state of waste disposal areas of energy and mining companies. In Annual Scientific-Technical Colletion—Mining of Mineral Deposits; CRC Press: Boca Raton, FL, USA, 2013; pp. 169–172. [Google Scholar] [CrossRef]
- Khomenko, O.; Barna, T. Zonal-and-wave structure of open systems on micro, mega- and macrolevels of the universe. Philos. Cosmol. 2019, 22, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Haeri, H.; Marji, M.F. Simulating the crack propagation and cracks coalescence underneath TBM disc cutters. Arab. J. Geosci. 2016, 9, 124. [Google Scholar] [CrossRef]
- Marji, M.F. Modeling of Cracks in Rock Fragmentation with a Higher Order Displacement Discontinuity Method. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 1996. [Google Scholar]
- Marji, M.F. Simulation of crack coalescence mechanism underneath single and double disc cutters by higher order displacement discontinuity method. J. Cent. South Univ. 2015, 22, 1045–1054. [Google Scholar] [CrossRef]
- Behnia, M.; Goshtasbi, K.; Marji, M.F.; Golshani, A. Numerical simulation of crack propagation in layered formations. Arab. J. Geosci. 2013, 7, 2729–2737. [Google Scholar] [CrossRef]
- Bondarenko, V.; Kovalevs’ka, I.; Ganushevych, K. Progressive Technologies of Coal, Coalbed Methane, and Ores Mining; CRC Press: London, UK, 2014; 523p. [Google Scholar] [CrossRef]
- Dreus, A.Y.; Sudakov, A.K.; Kozhevnikov, A.A.; Vakhalin, Y.N. Study on thermal strength reduction of rock formation in the diamond core drilling process using pulse flushing mode. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2016, 3, 5–10. [Google Scholar]
- Sobko, B.; Lozhnikov, O.; Levytskyi, V.; Skyba, G. Conceptual development of the transition from drill and blast excavation to non-blasting methods for the preparation of mined rock in surface mining. Rud. Geol. Naft. Zb. 2019, 34, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Moisyshyn, V.; Voyevidko, I.; Tokaruk, V. Design of bottom hole assemblies with two rock cutting tools for drilling wells of large diameter. Min. Miner. Depos. 2020, 14, 128–133. [Google Scholar] [CrossRef]
- Araujo, A.C.; Landon, Y.; Lagarrigue, P. Smart drilling for Aerospace Industry: State of art in research and education. Procedia CIRP 2021, 99, 387–391. [Google Scholar] [CrossRef]
- Dychkovskyi, R.O.; Lozynskyi, V.H.; Saik, P.B.; Petlovanyi, M.V.; Malanchuk, Y.Z.; Malanchuk, Z.R. Modeling of the disjunctive geological fault influence on the exploitation wells stability during underground coal gasification. Arch. Civ. Mech. Eng. 2018, 18, 1183–1197. [Google Scholar] [CrossRef]
- Falshtynskyi, V.S.; Dychkovskyi, R.O.; Lozynskyi, V.G.; Saik, P.B. Determination of the technological parameters of borehole underground coal gasification for thin coal seams. J. Sustain. Min. 2013, 12, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Bazaluk, O.; Sai, K.; Lozynskyi, V.; Petlovanyi, M.; Saik, P. Research into dissociation zones of gas hydrate deposits with a heterogeneous structure in the Black Sea. Energies 2021, 14, 1345. [Google Scholar] [CrossRef]
- Onysko, O.R.; Kopey, V.B.; Panchuk, V.G. Theoretical investigation of the tapered thread joint surface contact pressure in the dependence on the profile and the geometric parameters of the threading turning tool. IOP Conf. Ser. Mater. Sci. Eng. 2020, 749, 012007. [Google Scholar] [CrossRef]
- Onysko, O.; Borushchak, L.; Kopei, V.; Lukan, T.; Medvid, I.; Vryukalo, V. Computer studies of the tightness of the drill string connector depending on the profile of its tapered thread. Lect. Notes Netw. Syst. 2020, 128, 720–729. [Google Scholar] [CrossRef]
- Onysko, O.; Kopei, V.; Medvid, I.; Pituley, L.; Lukan, T. Influence of the Thread Profile Accuracy on Contact Pressure in Oil and Gas Pipes Connectors. Lect. Notes Mech. Eng. 2020, 432–441. [Google Scholar] [CrossRef]
- Shatskyi, I.; Ropyak, L.; Velychkovych, A. Model of contact interaction in threaded joint equipped with spring-loaded collet. Eng. Solid Mech. 2020, 8, 301–312. [Google Scholar] [CrossRef]
- Striletskyi, Y.Y.; Melnychuk, S.I.; Gryga, V.M.; Pashkevych, O.P. Using broadband signals for structural change detection in metal details. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2020, 3, 19–26. [Google Scholar] [CrossRef]
- Saakiyan, L.S.; Efremov, A.P.; Ropyak, L.Y.; Gorbatskii, A.V. A method of microelectrochemical investigations. Sov. Mater. Sci. 1987, 23, 267–269. [Google Scholar] [CrossRef]
- Saakiyan, L.S.; Efremov, A.P.; Ropyak, L.Y. Effect of stress on the microelectrochemical heterogeneity of steel. Prot. Met. 1989, 25, 185–189. [Google Scholar]
- Chudyk, I.; Poberezhny, L.; Hrysanchuk, A.; Poberezhna, L. Corrosion of drill pipes in high mineralized produced waters. Procedia Struct. Integr. 2019, 16, 260–264. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Contact interaction of crack lips in shallow shells in bending with tension. Mater. Sci. 2005, 41, 486–494. [Google Scholar] [CrossRef]
- Guillal, A.; Abdelbaki, N.; Bensghier, M.E.A.; Betayeb, M.; Kopei, B. Effect of shape factor on structural reliability analysis of a surface cracked pipeline-parametric study. Frat. Integrita Strutt. 2019, 13, 341–349. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Equilibrium of cracked shell with flexible coating. In Proceedings of the 11th International Conference on Shell Structures: Theory and Applications, Gdansk, Poland, 11–13 October 2017; pp. 165–168. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Influence of a flexible coating on the strength of a shallow cylindrical shell with longitudinal crack. J. Math. Sci. 2019, 238, 165–173. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Perepichka, V.V.; Ropyak, L.Y. On the influence of facing on strength of solids with surface defects. Metallofiz. Noveishie Tekhnologii 2020, 42, 69–76. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Makoviichuk, M.V.; Shatskyi, I.P.; Pritula, I.M.; Gryn, L.O.; Belyakovskyi, V.O. Stressed state of laminated interference-absorption filter under local loading. Funct. Mater. 2020, 27, 638–642. [Google Scholar] [CrossRef]
- Mandryk, O.; Artym, V.; Shtohry, M.; Zaytsev, V. Scientific Rationale for the Movable Pipeline Technology for Transporting CNG by Sea. Manag. Syst. Prod. Eng. 2020, 28, 168–177. [Google Scholar] [CrossRef]
- Yakym, R.S.; Petryna, D.Y. Analysis of causes and preventing ways of early workability loss of three-cone rock bit cutters. Metallofiz. Noveishie Tekhnologii 2020, 42, 731–751. [Google Scholar] [CrossRef]
- Vytyaz, O.; Chudyk, I.; Mykhailiuk, V. Study of the effects of drilling string eccentricity in the borehole on the quality of its cleaning. New Dev. Min. Eng. 2015, 591–595. [Google Scholar]
- Krol, R.; Kawalec, W.; Gladysiewicz, L. An effective belt conveyor for underground ore transportation systems. IOP Conf.Ser. Earth Environ.Sci. 2017, 95, 042047. [Google Scholar] [CrossRef]
- Król, R. Studies of the durability of belt conveyor idlers with working loads taken into account. IOP Conf. Ser. Earth Environ. Sci. 2017, 95. [Google Scholar] [CrossRef] [Green Version]
- Król, R.; Kisielewski, W. Research of loading carrying idlers used in belt conveyor-practical applications. Diagnostyka 2014, 15, 67–74. [Google Scholar]
- Ropyak, L.Y.; Pryhorovska, T.O.; Levchuk, K.H. Analysis of Materials and Modern Technologies for PDC Drill Bit Manufacturing. Prog. Phys. Met. 2020, 21, 274–301. [Google Scholar] [CrossRef]
- Nurpeissova, M.; Bekbassarov, S.; Bek, A.; Kyrgizbaeva, G.; Turisbekov, S.; Ormanbekova, A. The geodetic monitoring of the engineering structures stability conditions. J. Eng. Appl. Sci. 2020, 12, 9151–9163. [Google Scholar] [CrossRef]
- Onysko, O.; Panchuk, V.; Kopei, V.; Havryliv, Y.; Schuliar, I. Investigation of the influence of the cutter-tool rake angle on the accuracy of the conical helix in the tapered thread machining. J. Phys. Conf. Ser. 2021, 1781, 012028. [Google Scholar] [CrossRef]
- Medvid, I.; Onysko, O.; Panchuk, V.; Pituley, L.; Schuliar, I. Kinematics of the Tapered Thread Machining by Lathe: Analytical Study. Lect. Notes Mech. Eng. 2021, 555–565. [Google Scholar] [CrossRef]
- Danil’chenko, Y.M. Increasing the accuracy of rotation of high-speed spindle units on anti-friction bearings. Sov. Eng. Res. 1987, 7, 61–63. [Google Scholar]
- Muthukumaran, G.; Dinesh Babu, P. Laser transformation hardening of various steel grades using different laser types. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–529. [Google Scholar] [CrossRef]
- Ropyak, L.Y.; Vytvytskyi, V.S.; Velychkovych, A.S.; Pryhorovska, T.O.; Shovkoplias, M.V. Study on grinding mode effect on external conical thread quality. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1018, 012014. [Google Scholar] [CrossRef]
- Ostapovets, A.; Molnár, P.; Jäger, A. Visco-plastic self-consistent modelling of a grain boundary misorientation distribution after equal-channel angular pressing in an AZ31 magnesium alloy. J. Mater. Sci. 2013, 48, 2123–2134. [Google Scholar] [CrossRef]
- Kuanyshbekovna, M.M.; Krupnik, L.; Koptileuovich, Y.K.; Mukhtar, E.; Roza, A. The system is “roof bolting-mountain”. Int. J. Appl. Eng. Res. 2016, 11, 10454–10457. [Google Scholar]
- Zeynullin, A.A.; Abeuov, E.A.; Demin, V.F.; Aliev, S.B.; Kaynazarova, A.S.; Kaynazarov, A.S. Estimation of ways to maintain mining works based on the application of anchor anchoring in the mines of the Karaganda coal basin. Ugol 2021, 2, 4–9. [Google Scholar] [CrossRef]
- Tatarenko, V.A.; Radchenko, T.M.; Nadutov, V.M. Parameters of Interatomic Interaction in a Substitutional Alloy F.C.C. Ni-Fe According to Experimental Data about the Magnetic Characteristics and Equilibrium Values of Intensity of a Diffuse Scattering of Radiations. Metallofiz. Noveishie Tekhnologii 2003, 25, 1303–1319. [Google Scholar]
- Radchenko, T.M.; Tatarenko, V.A.; Bokoch, S.M. Diffusivities and kinetics of short-range and long-range orderings in Ni-Fe permalloys. Metallofiz. Noveishie Tekhnologii 2006, 28, 1699–1720. [Google Scholar]
- Levchuk, K.H.; Radchenko, T.M.; Tatarenko, V.A. High-Temperature Entropy Effects in Tetragonality of the Ordering Interstitial–Substitutional Solution Based on Body-Centred Tetragonal Metal. Metallofiz. Noveishie Tekhnologii 2021, 43, 1–26. [Google Scholar] [CrossRef]
- Tarel’nik, V.B.; Konoplyanchenko, E.V.; Kosenko, P.V.; Martsinkovskii, V.S. Problems and Solutions in Renovation of the Rotors of Screw Compressors by Combined Technologies. Chem. Pet. Eng. 2017, 53, 540–546. [Google Scholar] [CrossRef]
- Tarelnik, V.B.; Gaponova, O.P.; Konoplyantschenko, E.V.; Yevtushenko, N.S.; Gerasimenko, V.A. Analysis of the structural state of the surface layer after electro-erosive alloying. II. Peculiarities of the formation of electroerosive coatings on special steels and stops by hard wear-resistant and soft antifriction materials. Metallofiz. Noveishie Tekhnologii 2018, 11, 795–815. [Google Scholar] [CrossRef]
- Tarelnyk, V.B.; Gaponova, O.P.; Konoplianchenko, Y.V.; Martsynkovskyy, V.S.; Tarelnyk, N.V.; Vasylenko, O.O. Improvement of quality of the surface electroerosive alloyed layers by the combined coatings and the surface plastic deformation. I. Features of formation of the combined electroerosive coatings on special steels and alloys. Metallofiz. Noveishie Tekhnologii 2019, 41, 47–69. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, O.; Prysyazhnyuk, P.; Lutsak, D.; Matviienkiv, O.; Aulin, V. Improvement of Abrasion Resistance of Production Equipment Wear Parts by Hardfacing with Flux-Cored Wires Containing Boron Carbide/Metal Powder Reaction Mixtures. Manag. Syst. Prod. Eng. 2020, 28, 178–183. [Google Scholar] [CrossRef]
- Cizek, J.; Dlouhy, I.; Siska, F.; Khor, K.A. Modification of Plasma-sprayed TiO2 Coatings Characteristics via Controlling the In-flight Temperature and Velocity of the Powder Particles. J. Therm. Spray Technol. 2014, 23, 1339–1349. [Google Scholar] [CrossRef] [Green Version]
- Duryahina, Z.A.; Kovbasyuk, T.M.; Bespalov, S.A.; Pidkova, V.Y. Micromechanical and Electrophysical Properties of Al2O3 Nanostructured Dielectric Coatings on Plane Heating Elements. Mater. Sci. 2016, 52, 50–55. [Google Scholar] [CrossRef]
- Matei, A.A.; Pencea, I.; Stanciu, S.G.; Hristu, R.; Antoniac, I.; Ciovica, E.; Sfat, C.E.; Stanciu, G.A. Structural characterization and adhesion appraisal of TiN and TiCN coatings deposited by CAE-PVD technique on a new carbide composite cutting tool. J. Adhes. Sci. Technol. 2015, 29, 2576–2589. [Google Scholar] [CrossRef]
- Prysyazhnyuk, P.; Lutsak, D.; Shlapak, L.; Aulin, V.; Lutsak, L.; Borushchak, L.; Shihab, T.A. Development of the composite material and coatings based on niobium carbide. East. Eur. J. Enterp. Technol. 2018, 6, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Duryagina, Z.A.; Bespalov, S.A.; Pidkova, V.Y.; Polockyj, D.Y. Examination of the dielectric layers on the structural materials formed by hybrid ion-plasma discharge system. Metallofiz. Noveishie Tekhnologii 2011, 33, 393–400. [Google Scholar]
- Pashechko, M.; Montusiewicz, J.; Dziedzic, K.; Jozwik, J. Multicriterion Assessment of Wear Resistance of Fe–Mn–C–B Eutectic Coatings Alloyed with Si, Ni, and Cr. Powder Metall. Met. Ceram. 2017, 56, 316–322. [Google Scholar] [CrossRef]
- Pashechko, M.I.; Dziedzic, K.; Mendyk, E.; Jozwik, J. Chemical and Phase Composition of the Friction Surfaces Fe-Mn-C-B-Si-Ni-Cr Hardfacing Coatings. J. Tribol. 2018, 140, 021302. [Google Scholar] [CrossRef]
- Chudyk, I.; Raiter, P.; Grydzhuk, Y.; Yurych, L. Mathematical model of oscillations of a drill tool with a drill bit of cutting-scraping type. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2020, 1, 52–57. [Google Scholar] [CrossRef]
- Pryhorovska, T. Rock heterogeneity numerical simulation as a factor of drill bit instability. Eng. Solid Mech. 2018, 6, 315–330. [Google Scholar] [CrossRef]
- Pryhorovska, T.O. Study on rock reaction force depending on PDC cutter placement. Mach. Sci. Technol. 2017, 21, 37–66. [Google Scholar] [CrossRef]
- Pryhorovska, T.A.; Chaplinskiy, S.S. Finite element modeling of rock mass cutting by cutters for PDC drill bits. Neftyanoe Khozyaystvo-Oil Ind. 2018, 1, 38–41. [Google Scholar] [CrossRef]
- Pryhorovska, T.O.; Chaplinskyy, S.S. Probabilistic estimate of pdc drill bit wear rate. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu 2014, 5, 39–45. [Google Scholar]
- Tatsii, R.M.; Pazen, O.Y. Direct (Classical) Method of Calculation of the Temperature Field in a Hollow Multilayer Cylinder. J. Eng. Phys. Thermophys. 2018, 91, 1373–1384. [Google Scholar] [CrossRef]
- Tatsiy, R.M.; Pazen, O.Y.; Vovk, S.Y.; Ropyak, L.Y.; Pryhorovska, T.O. Numerical study on heat transfer in multilayered structures of main geometric forms made of different materials. J. Serb. Soc. Comput. Mech. 2019, 13, 36–55. [Google Scholar] [CrossRef] [Green Version]
- Tatsiy, R.M.; Pazen, O.Y.; Vovk, S.Y.; Kharyshyn, D.V. Direct method of studying heat exchange in multilayered bodies of basic geometric forms with imperfect heat contact. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu 2021, 60–67. [Google Scholar] [CrossRef]
- Kopei, V.B.; Onysko, O.R.; Panchuk, V.G. Principles of development of product lifecycle management system for threaded connections based on the Python programming language. J. Phys. Conf. Ser. 2020, 1426, 012033. [Google Scholar] [CrossRef]
- Levchuk, K.G.; Moisyshyn, V.M.; Tsidylo, I.V. Influence of mechanical properties of a material on dynamics of the stuck drilling pipes. Metallofiz. Noveishie Tekhnologii 2016, 38, 1655–1668. [Google Scholar] [CrossRef] [Green Version]
- Petlovanyi, M.; Lozynskyi, V.; Saik, P.; Sai, K. Predicting the producing well stability in the place of its curving at the underground coal seams gasification. E3S Web Conf. 2019, 123, 01019. [Google Scholar] [CrossRef] [Green Version]
- Velichkovich, A.; Dalyak, T.; Petryk, I. Slotted shell resilient elements for drilling shock absorbers. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2018, 73, 34. [Google Scholar] [CrossRef] [Green Version]
- Moisyshyn, V.M.; Lyskanych, M.V.; Borysevych, L.V.; Kolych, N.B.; Zhovniruk, R.A. Integral Indicators of Change of Drilling Column Vibration-Criterion for Assessing of Roller Cone Bit Wear. Metallofiz. Noveishie Tekhnologii 2019, 41, 1087–1102. [Google Scholar] [CrossRef] [Green Version]
- Mikhlin, Y.V.; Zhupiev, A.L. An application of the ince algebraization to the stability of non-linear normal vibration modes. Int. J. Non-Linear Mech. 1997, 32, 393–409. [Google Scholar] [CrossRef] [Green Version]
- Grydzhuk, J.; Chudyk, I.; Velychkovych, A.; Andrusyak, A. Analytical estimation of inertial properties of the curved rotating section in a drill string. East. Eur. J. Enterp. Technol. 2019, 1, 6–14. [Google Scholar] [CrossRef] [Green Version]
- Dutkiewicz, M.; Gołębiowska, I.; Shatskyi, I.; Shopa, V.; Velychkovych, A. Some aspects of design and application of inertial dampers. MATEC Web of Conf. 2018, 178, 06010. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A. Increase of compliance of shock absorbers with cut shells. IOP Conf.Ser. Mater. Sci. Eng. 2019, 564, 012072. [Google Scholar] [CrossRef]
- Velychkovych, A.; Petryk, I.; Ropyak, L. Analytical study of operational properties of a plate shock absorber of a sucker-rod string. Shock Vib. 2020, 3292713. [Google Scholar] [CrossRef]
- Shatskyi, I.; Popadyuk, I.; Velychkovych, A. Hysteretic Properties of Shell Dampers. Springer Proc. Math. Stat. 2018, 249, 343–350. [Google Scholar] [CrossRef]
- Bulbuk, O.; Velychkovych, A.; Mazurenko, V.; Ropyak, L.; Pryhorovska, T. Analytical estimation of tooth strength, restored by direct or indirect restorations. Eng. Solid Mech. 2019, 7, 193–204. [Google Scholar] [CrossRef]
- Velichkovich, A.S.; Dalyak, T.M. Assessment of stressed state and performance characteristics of jacketed spring with a cut for drill shock absorber. Chem. Pet. Eng. 2015, 51, 188–193. [Google Scholar] [CrossRef]
- Levchuk, K.G. Investigation of the vibration transfer process to a stuck drill string. SOCAR Proc. 2017, 2, 23–33. [Google Scholar] [CrossRef]
- Moisyshyn, V.; Levchuk, K. Investigation on Releasing of a Stuck Drill String by Means of a Mechanical Jar. Oil Gas Sci. Technol. 2017, 72, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Levchuk, K.G. Diagnosis of catches of metal drill pipes by their stress-strain state in a sloping well. Metallofiz. Noveishie Tekhnologii 2018, 40, 701–712. [Google Scholar] [CrossRef] [Green Version]
- Shatskyi, I.; Perepichka, V. Problem of Dynamics of an Elastic Rod with Decreasing Function of Elastic-Plastic External Resistance. Springer Proc. Math. Stat. 2018, 249, 335–342. [Google Scholar] [CrossRef]
- Shatskyi, I.; Vytvytskyi, I.; Senyushkovych, M.; Velychkovych, A. Modelling and improvement of the design of hinged centralizer for casing. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 12073. [Google Scholar] [CrossRef]
- Velychkovych, A.S.; Andrusyak, A.V.; Pryhorovska, T.O.; Ropyak, L.Y. Analytical model of oil pipeline overground transitions, laid in mountain areas. Oil Gas Sci. Technol. 2019, 74, 65. [Google Scholar] [CrossRef] [Green Version]
- Tyrlych, V.; Moisyshyn, V. Predicting remaining lifetime of drill pipes basing upon the fatigue crack kinetics within a pre-critical period. Min. Miner. Depos. 2019, 13, 127–133. [Google Scholar] [CrossRef]
- Vytvytskyi, I.I.; Seniushkovych, M.V.; Shatskyi, I.P. Calculation of distance between elastic-rigid centralizers of casing. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2017, 5, 28–35. [Google Scholar]
- Shatskyi, I.; Velychkovych, A.; Vytvytskyi, I.; Seniushkovych, M. Analytical models of contact interaction of casing centralizers with well wall. Eng. Solid Mech. 2019, 7, 355–366. [Google Scholar] [CrossRef]
- Jiang, K.; Xie, R.; Yun, H. Lightweight drill pipe based on composite carbon fiber material. J. Phys. Conf. Ser. 2020, 1549, 032113. [Google Scholar] [CrossRef]
- Benyahia, H.; Tarfaoui, M.; El Moumen, A.; Ouinas, D. Prediction of notched strength for cylindrical composites pipes under tensile loading conditions. Compos. Part B Eng. 2018, 150, 104–114. [Google Scholar] [CrossRef]
- Fyk, M.; Biletskyi, V.; Abbood, M.; Al-Sultan, M.; Abbood, M.; Abdullatif, H.; Shapchenko, Y. Modeling of the lifting of a heat transfer agent in a geothermal well of a gas condensate deposit. Min. Miner. Depos. 2020, 14, 66–74. [Google Scholar] [CrossRef]
- Kolosov, D.; Snihur, V.; Pysmenkova, T. Stress-strain state of rubber-cable tractive element of tubular shape. Rozrob. Rodov. 2020, 14, 43–52. [Google Scholar]
- Galiyev, D.A.; Uteshov, E.T.; Tekenova, A.T. Digitalization of technological and organizational processes of mining operations due to the implementation of the installation system and accounting the key indicators. News Natl. Acad. Sci. Repub. Kazakhstan Ser. Geol. Tech. Sci. 2020, 5, 47–53. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, J.J.; Zhao, J.P.; Ma, T.J. Mechanical Study of Carbon Fiber Reinforced Plastic and Thin-walled Metal Liner in Bi-Material COPV Based on Grid Theory Optimization. Mater. Sci. Forum 2021, 1027, 15–21. [Google Scholar] [CrossRef]
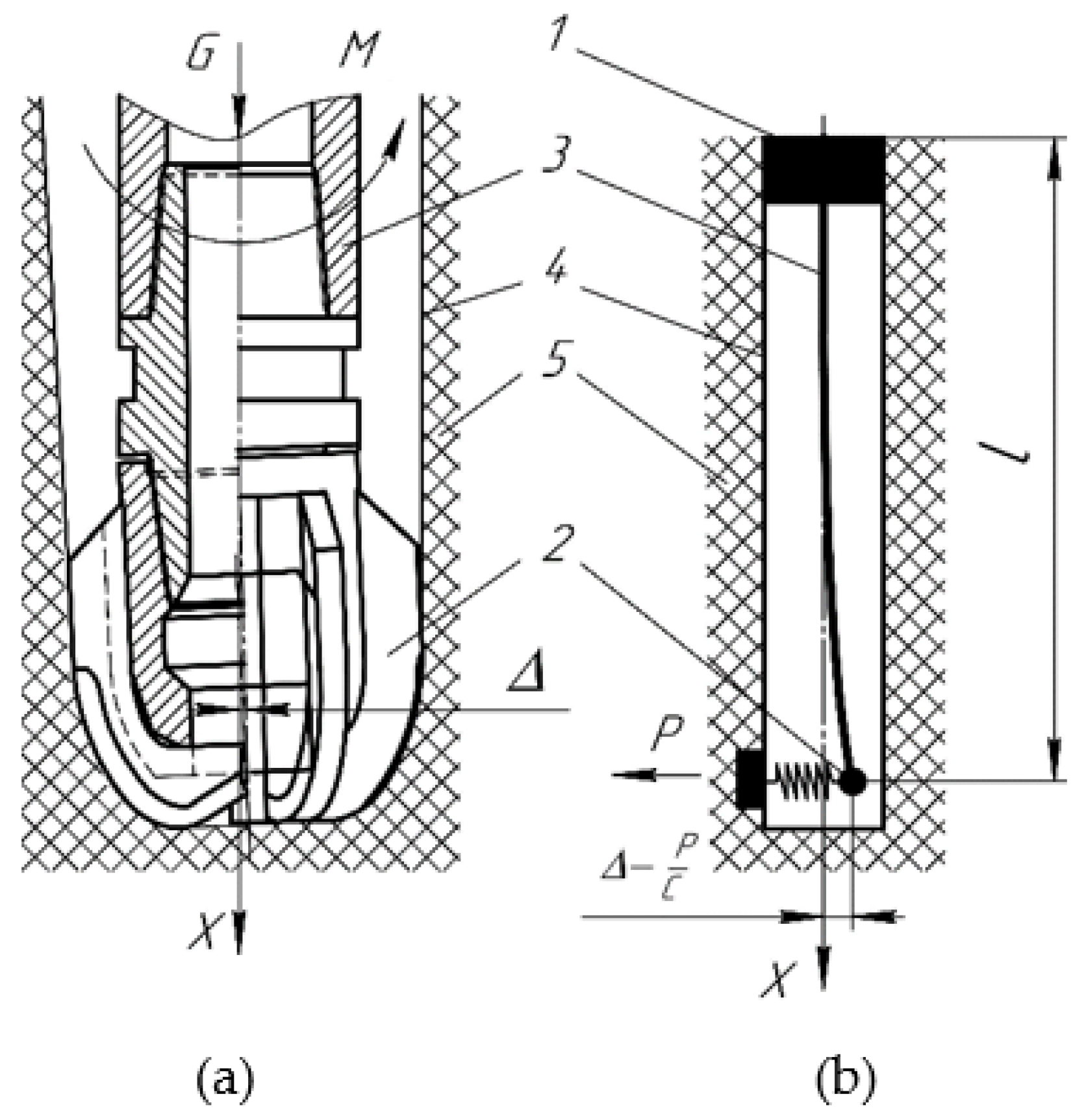
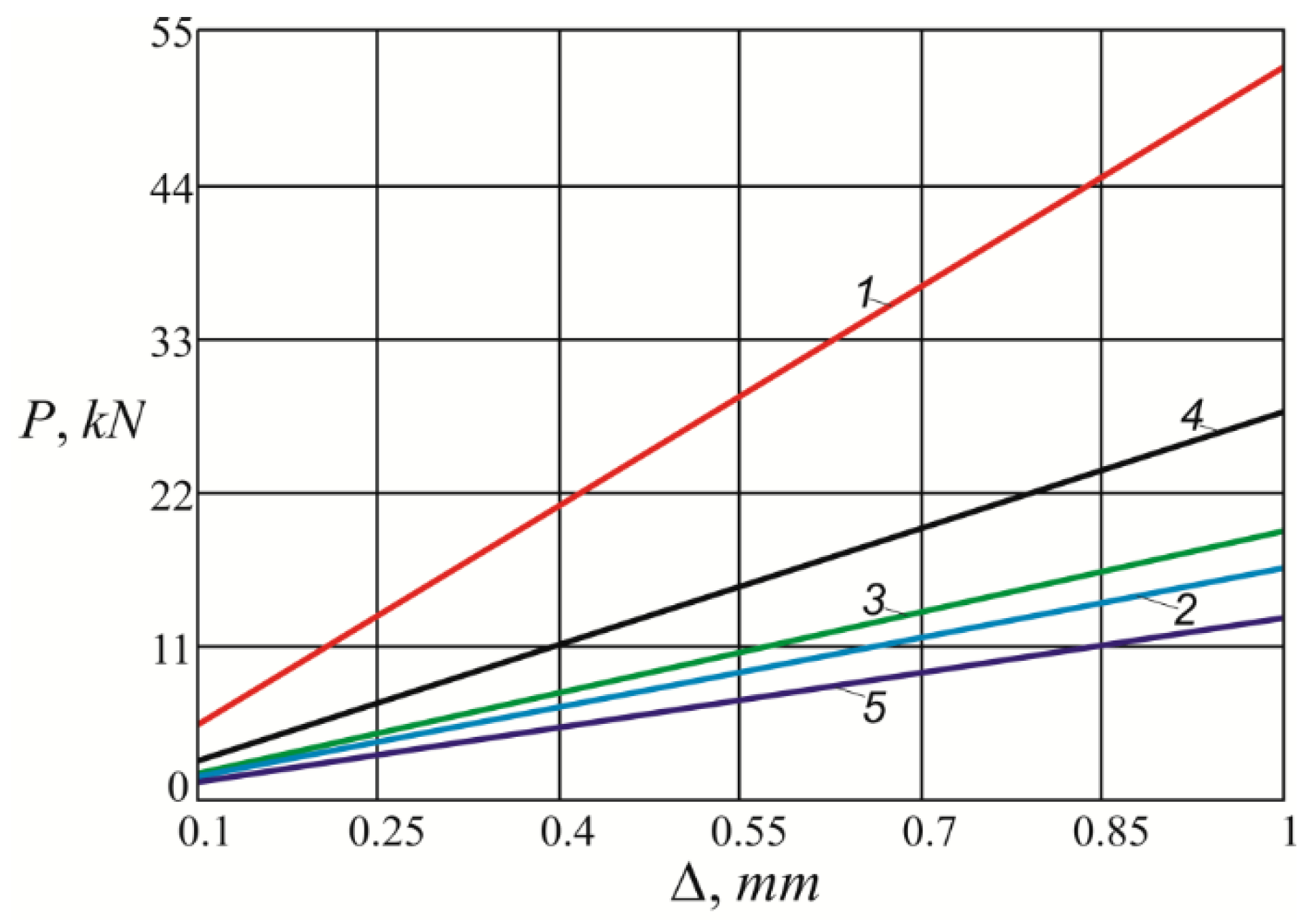
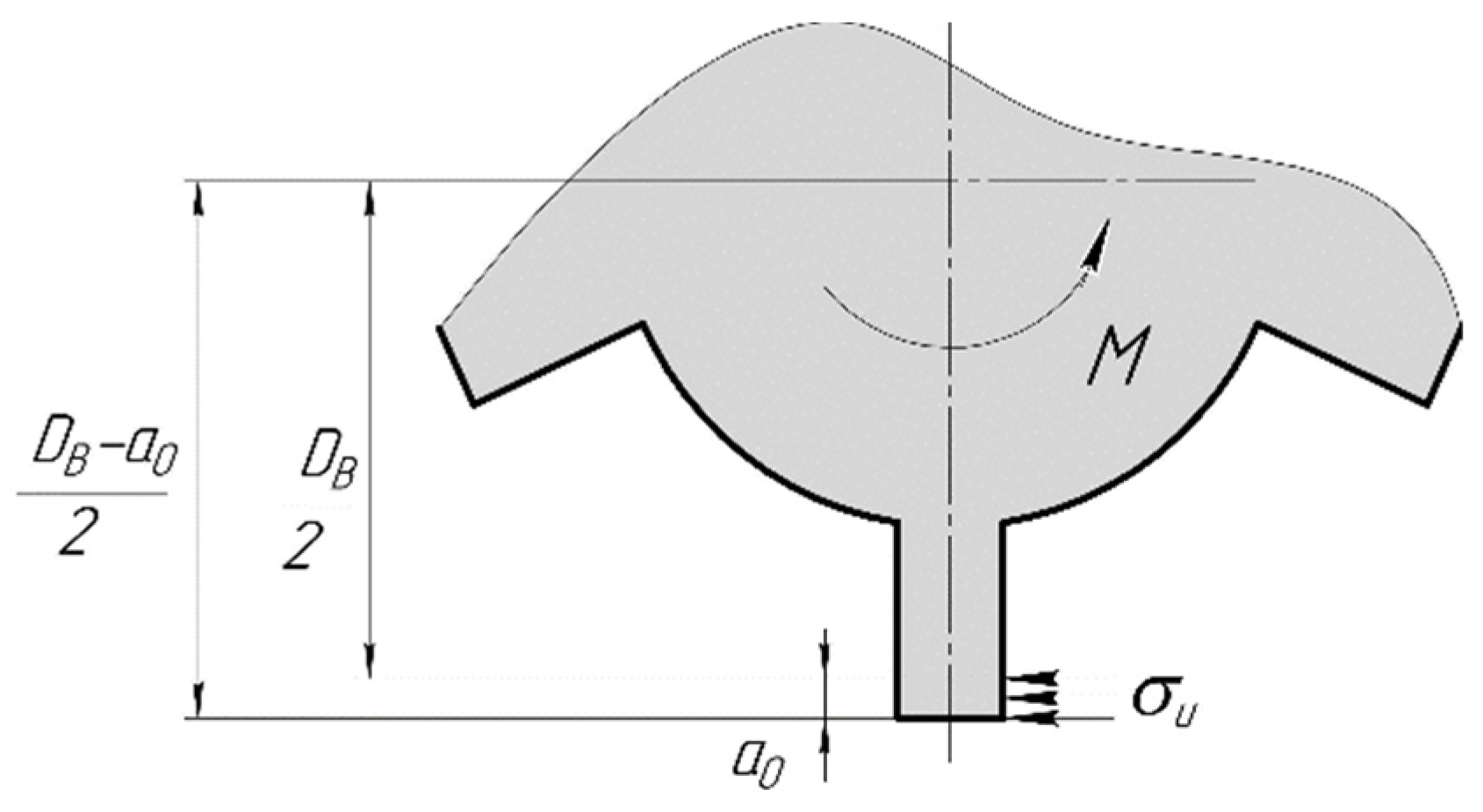
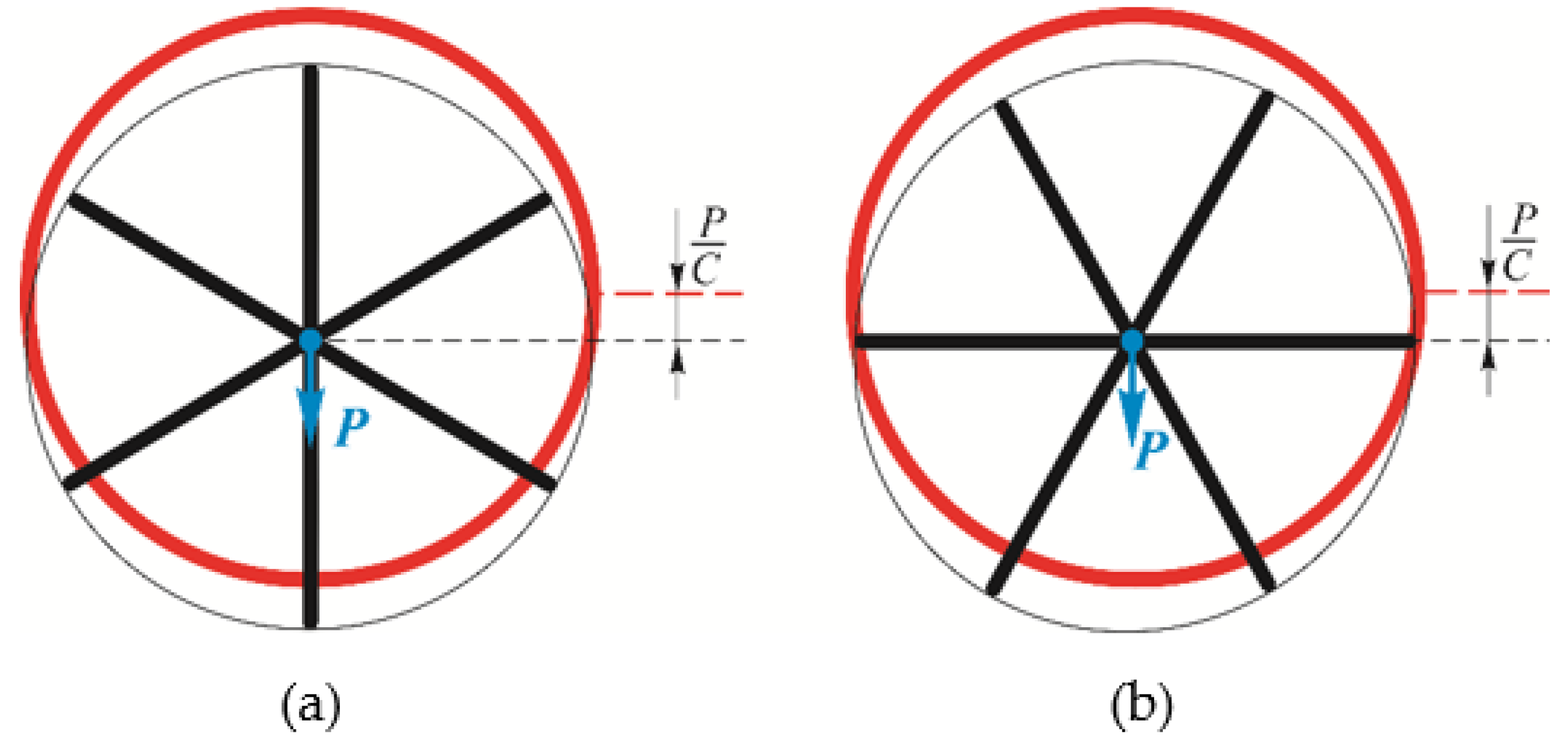
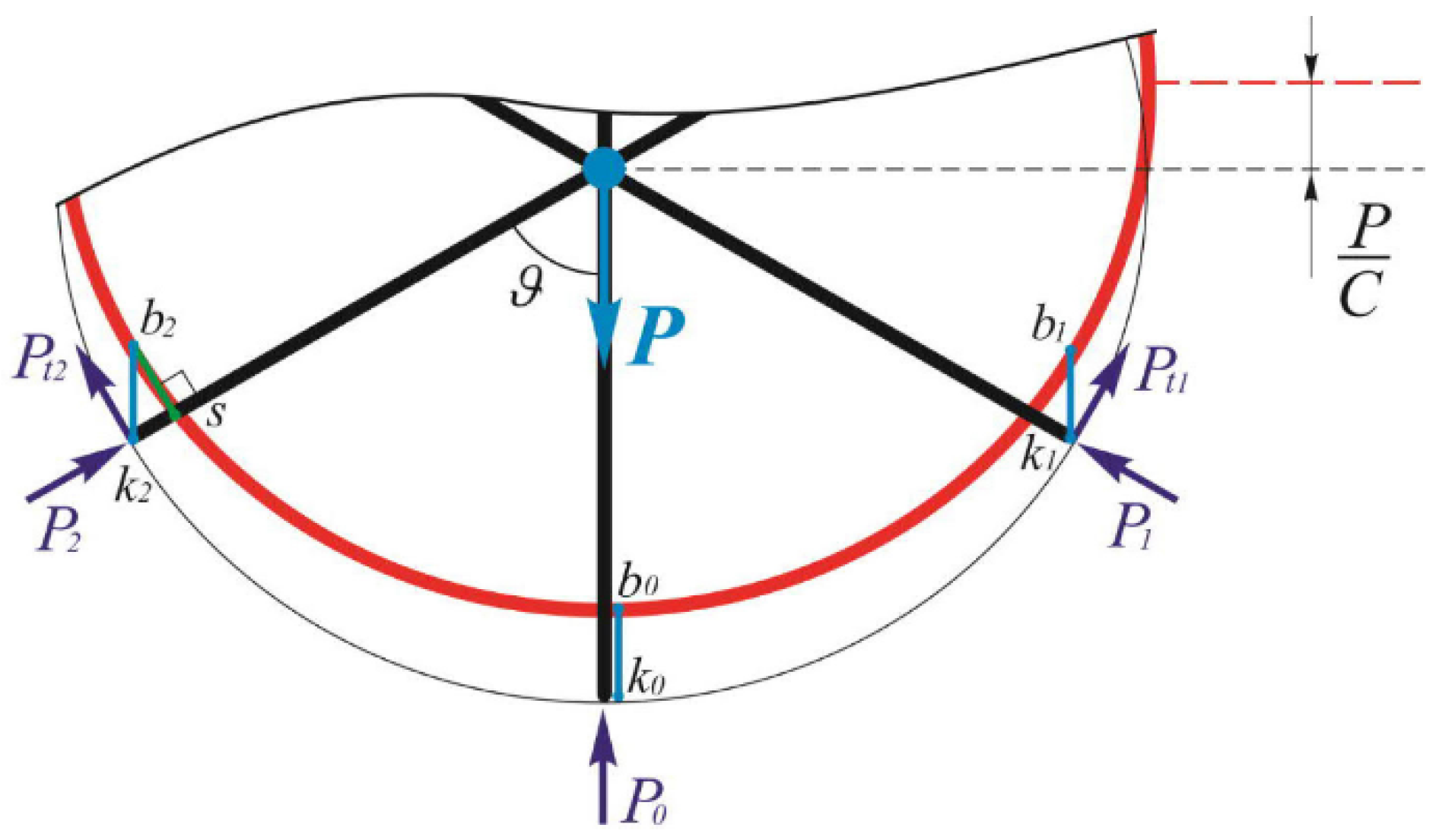
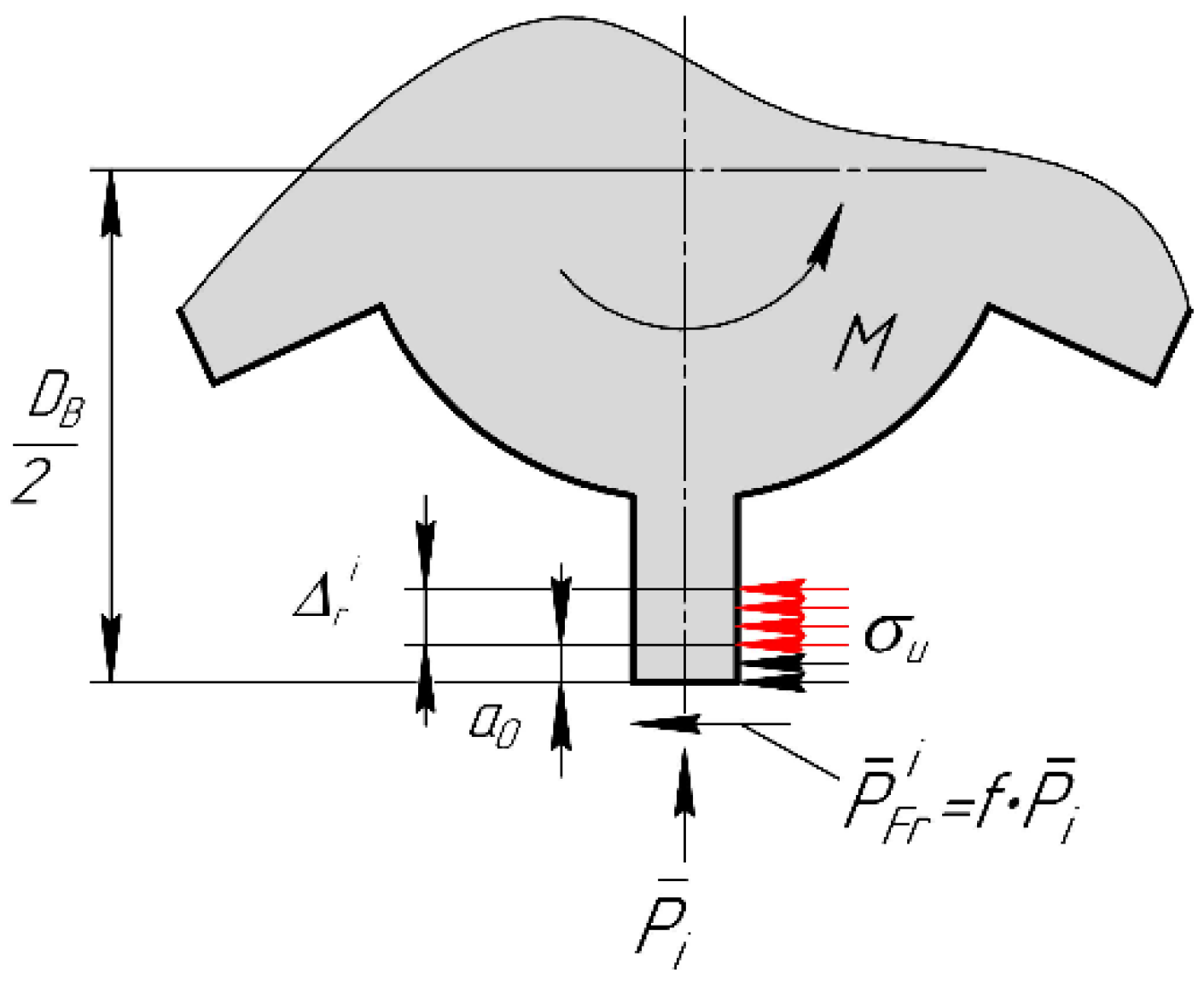
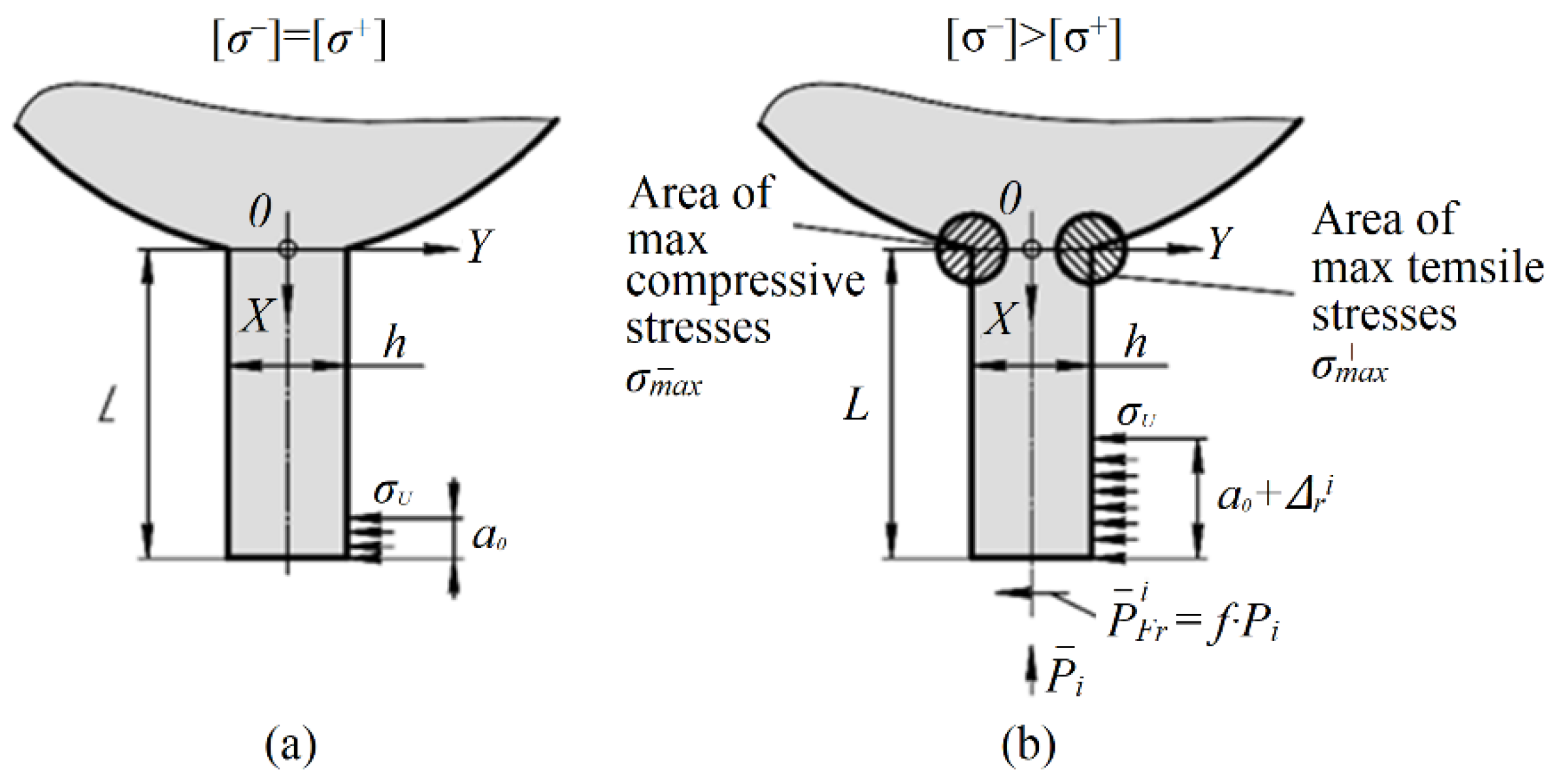
| Parameters | Misalignment Δ, mm | ||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| Additional transverse clamping force P, kN | 1.45 | 2.89 | 4.33 | 5.78 | 7.22 |
| Additional radial recess ∆r, mm | 0.146 | 0.292 | 0.438 | 0.584 | 0.730 |
| Radial force caused by misalignment, P0, kN | 0.48 | 0.96 | 1.44 | 1.92 | 2.41 |
| Radial force caused by the misalignment | 202.2 | 233.5 | 264.8 | 296.2 | 327.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazaluk, O.; Velychkovych, A.; Ropyak, L.; Pashechko, M.; Pryhorovska, T.; Lozynskyi, V. Influence of Heavy Weight Drill Pipe Material and Drill Bit Manufacturing Errors on Stress State of Steel Blades. Energies 2021, 14, 4198. https://doi.org/10.3390/en14144198
Bazaluk O, Velychkovych A, Ropyak L, Pashechko M, Pryhorovska T, Lozynskyi V. Influence of Heavy Weight Drill Pipe Material and Drill Bit Manufacturing Errors on Stress State of Steel Blades. Energies. 2021; 14(14):4198. https://doi.org/10.3390/en14144198
Chicago/Turabian StyleBazaluk, Oleg, Andrii Velychkovych, Liubomyr Ropyak, Mykhailo Pashechko, Tetiana Pryhorovska, and Vasyl Lozynskyi. 2021. "Influence of Heavy Weight Drill Pipe Material and Drill Bit Manufacturing Errors on Stress State of Steel Blades" Energies 14, no. 14: 4198. https://doi.org/10.3390/en14144198
APA StyleBazaluk, O., Velychkovych, A., Ropyak, L., Pashechko, M., Pryhorovska, T., & Lozynskyi, V. (2021). Influence of Heavy Weight Drill Pipe Material and Drill Bit Manufacturing Errors on Stress State of Steel Blades. Energies, 14(14), 4198. https://doi.org/10.3390/en14144198










