Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study
Abstract
:1. Introduction
- ▪
- ▪
- The wind turbine’s design such as rotor´s diameter, blade geometry, and wind tower´s height—the fundamentals of aerodynamics have been decisive for the advance of wind turbines [18]. A number of numerical modelling challenges are present in the design of wind turbines, with respect to the aerodynamics of the rotor and blades and stability of the tower under wind gusts and oscillations [17,19]. Depending on the type of turbine, its performance is influenced by other design parameters such as the number of blades and rotor orientation [14,20,21,22].
- ▪
- The wind farm layout such as the site´s topographic conditions, the distance between two consecutive turbines, and the erection layout (linear or scattered)—depending on the local wind conditions of the wind site, the design can lead to power loss due to wake effect on the wind farm. Wind turbines’ wake effects significantly reduce the performance of downstream wind turbines [7,23,24,25,26]. With the increase in the number of turbines downstream, the influence of the wake effect and load of airflow generated tends to be more significant [7,27].
2. Performance Analysis of Wind Technology Aerodynamics
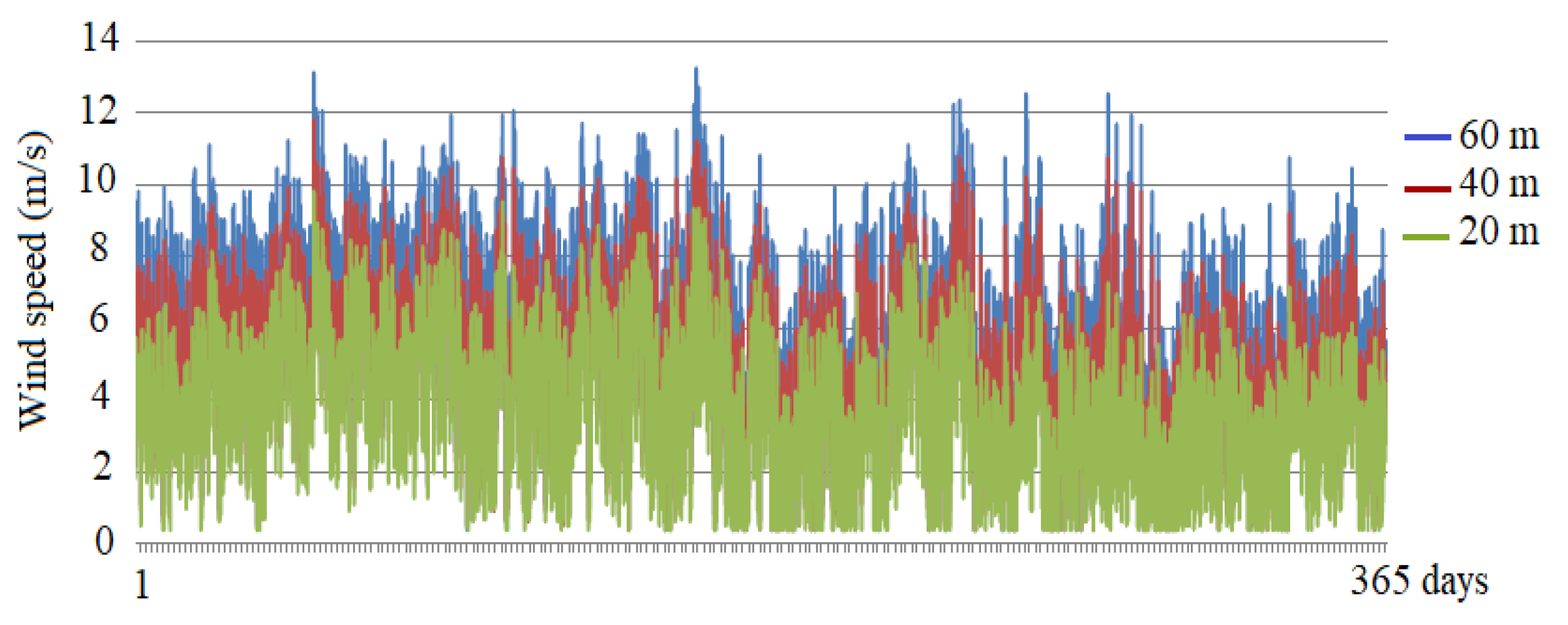
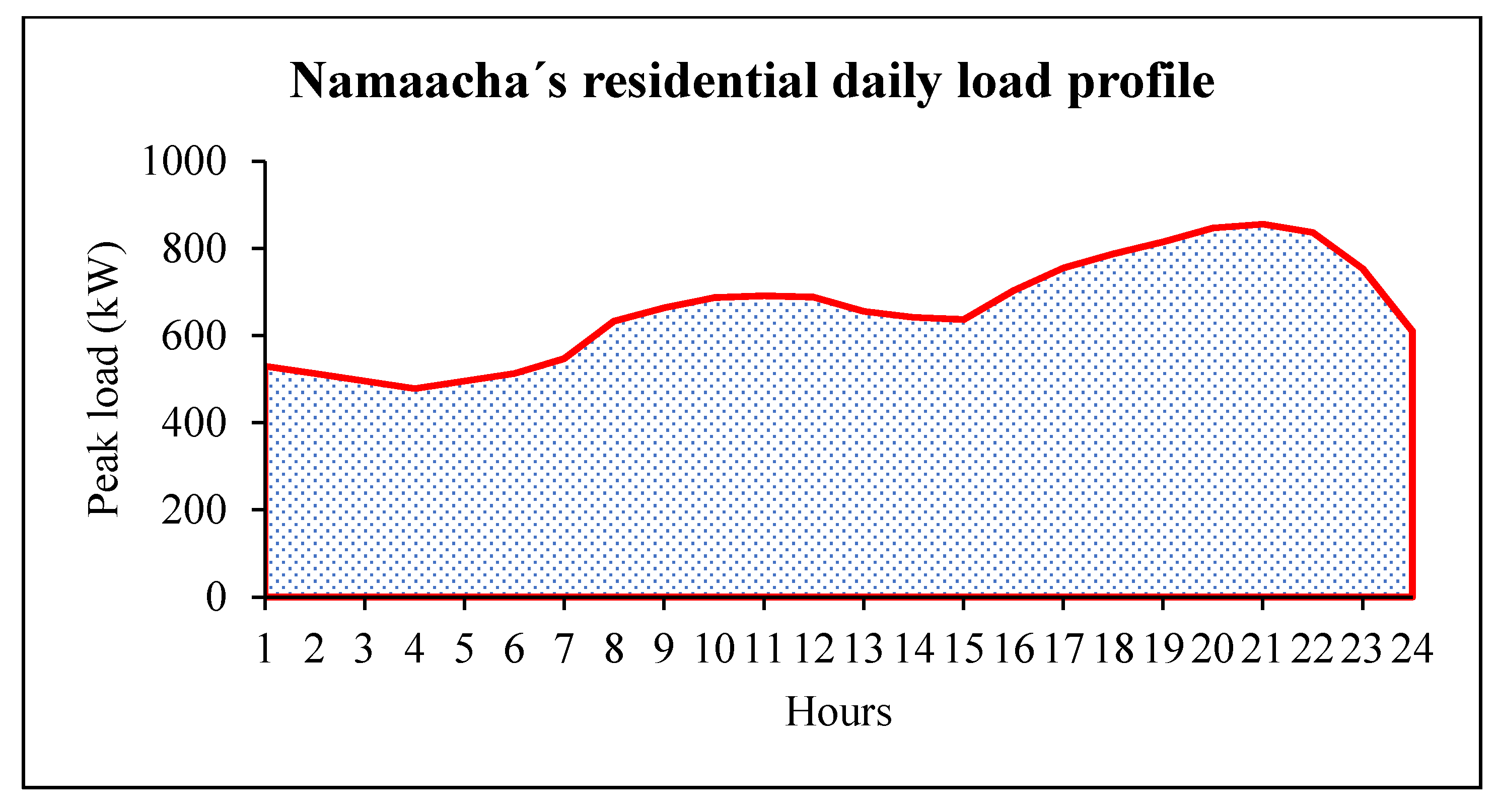
3. Namaacha District Renewable Power Potential Overview
4. Model Application and Assessment of Wake Effect on Turbine Performance
- ▪
- Simple wake model—applies a thrust coefficient to calculate the wind speed deficit in each turbine due to the wake effect of the upwind turbines;
- ▪
- Wind resources assessment, siting, and energy model (WAsP model)—uses a decline constant to estimate the wind speed deficit behind each turbine and computes the overlap of that wake profile with the downwind turbine to calculate the wind speed at the downwind turbine;
- ▪
- Eddy–viscosity—is analogous to the WAsP model, and besides that, the wind speed shortage behind each turbine is presumed to have a Gaussian shape;
- ▪
- Constant loss—estimates wake loss as a constant percentage reduction in the wind farm output.
- ▪
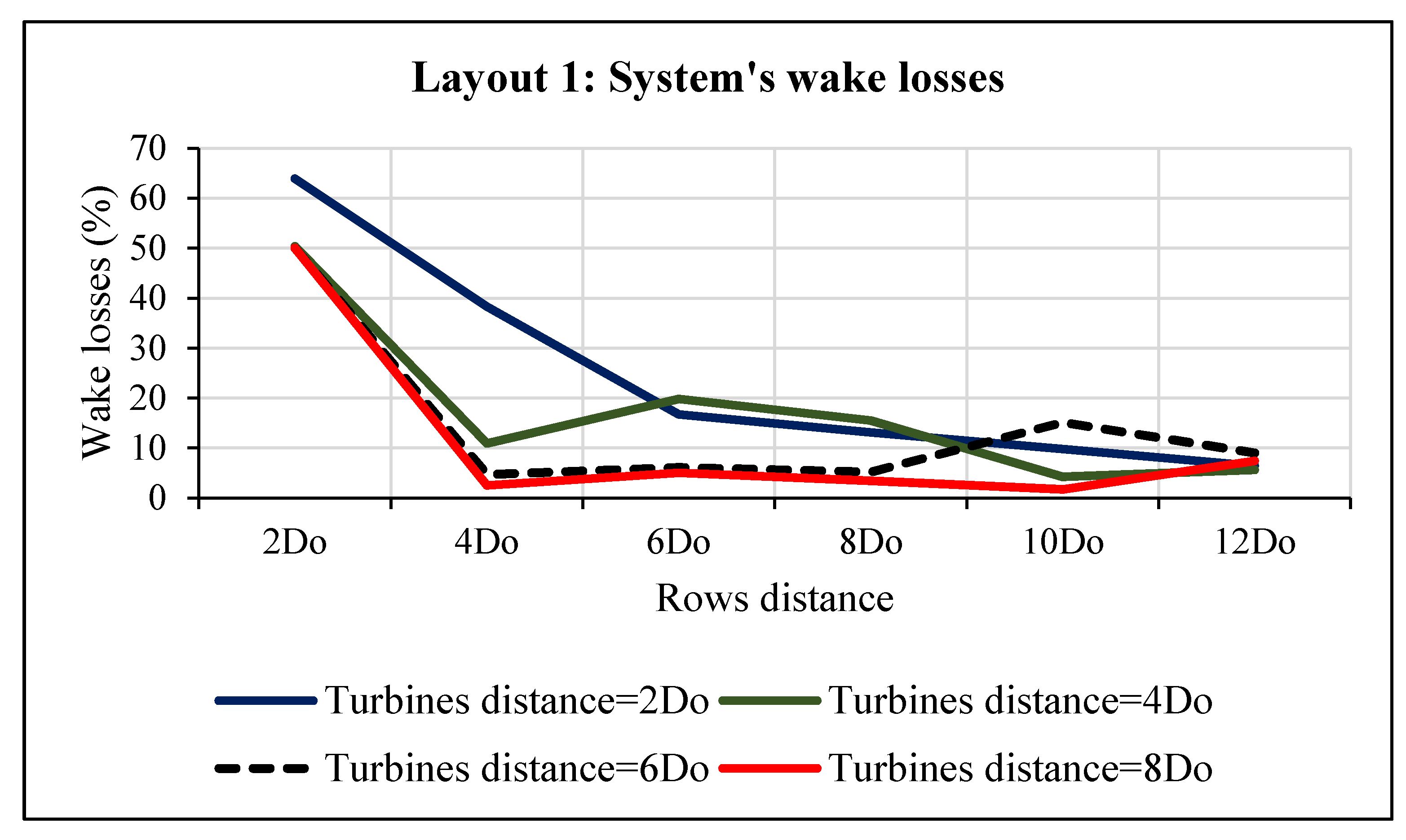
- Layout 1: examined the influence of the increased distance between turbines and the spacing between lines. The distances between turbines used were 2Do, 4Do, 6Do, and 8Do, while the spacing between rows used was 2Do, 4Do, 6Do, 8Do, 10Do, and 12Do. In this layout, in addition to varying the distance between turbines and lines, the wind direction varied from 0° to 60°. SAM considers wind direction equal to 0° when the wind blows from north to south. Row orientation angle and row offset was maintained as β = 0° and L = 0, respectively.
- ▪
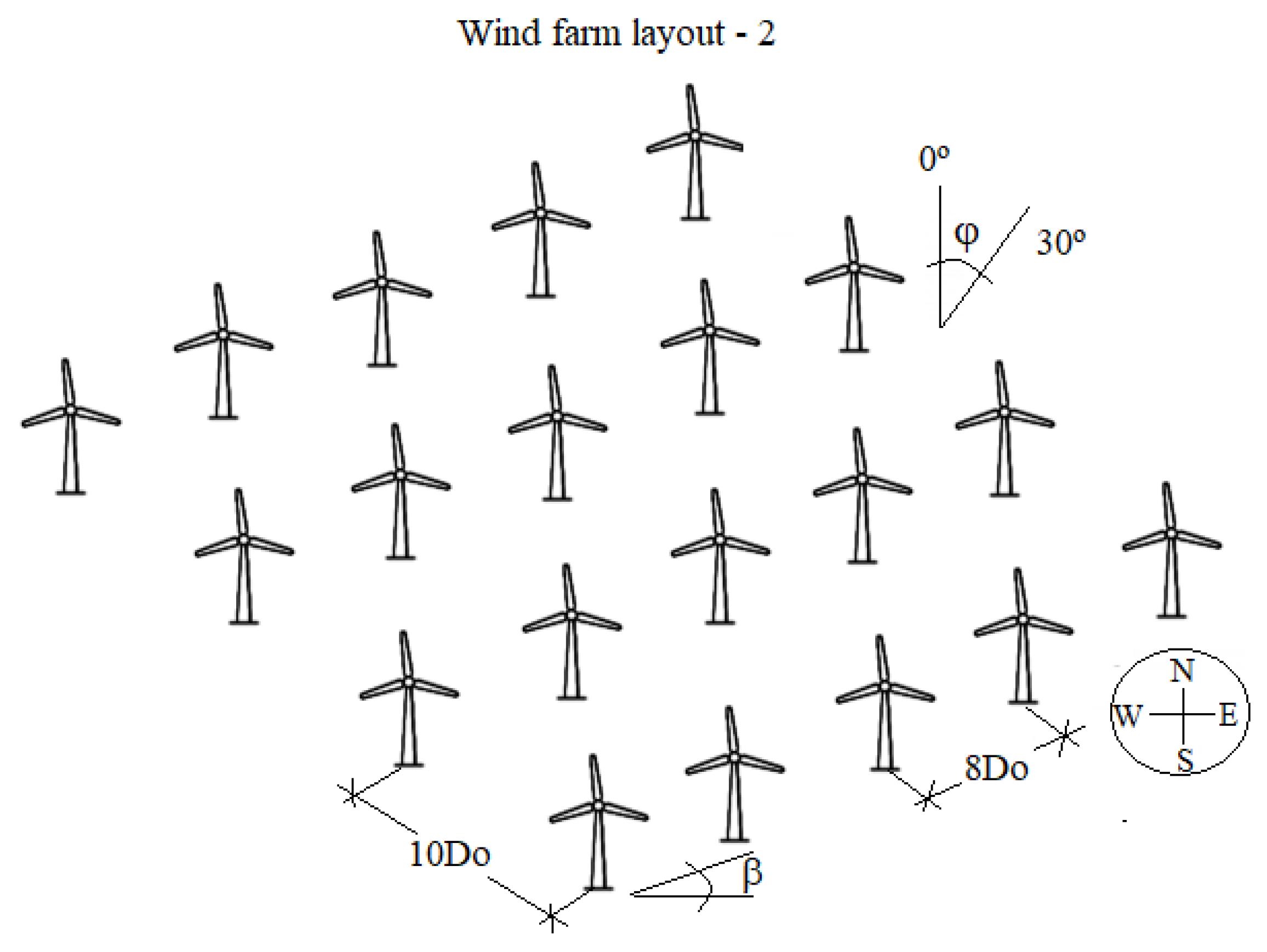
- Layout 2: examined the influence of changing the row orientation angle. The following angles were used: 5°, 10°, 15°, 20°, 25°, and 30°. The optimal distance between the turbines and the rows, as well as the wind direction, was maintained at 8Do, 10Do, and 30°, respectively.
- ▪
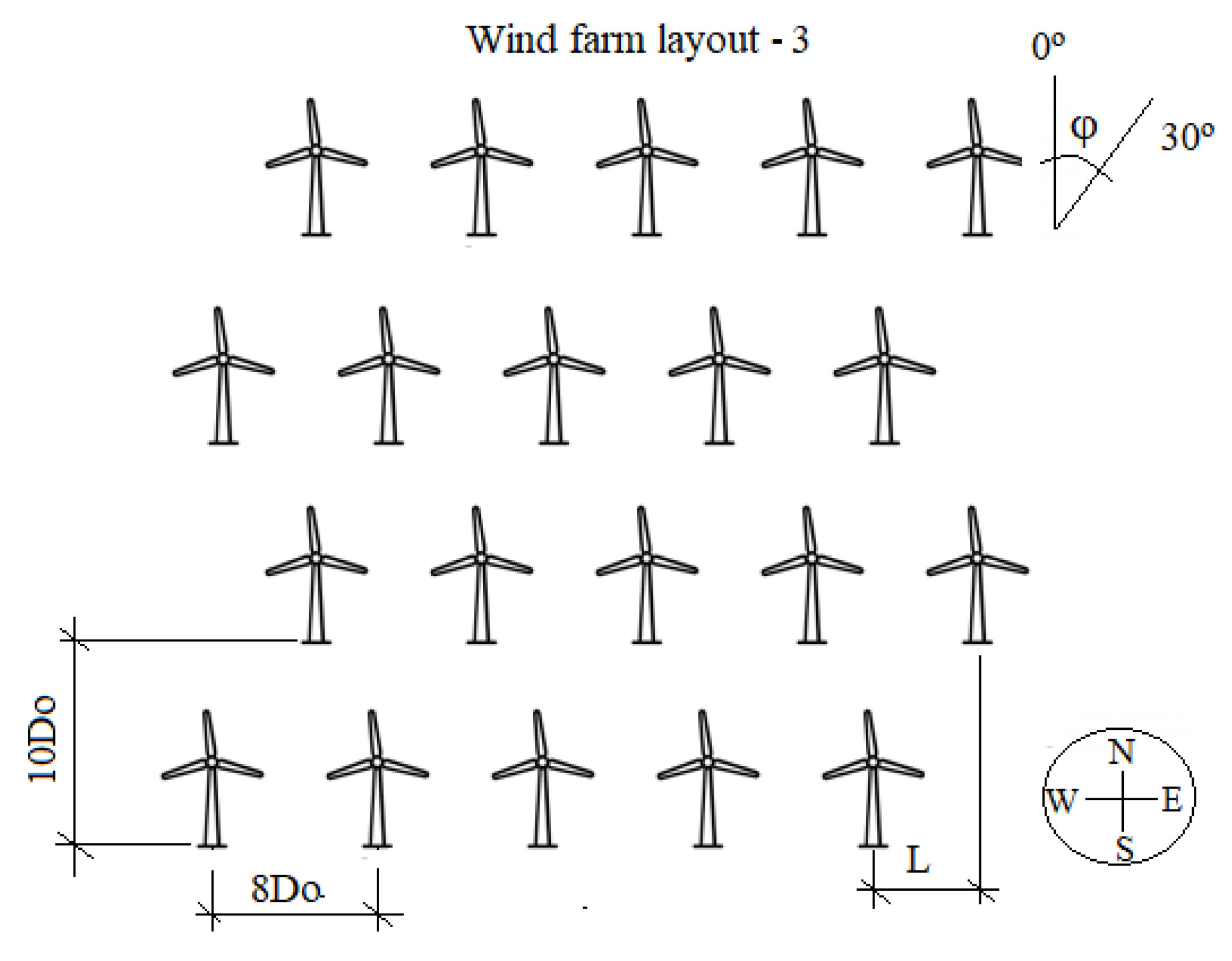
- Layout 3: examined the influence of increased scattering of the turbines by changing the row offset. The following offset rows were used: 0, 0.5Do, Do 1.5Do, 2Do, 2.5Do, and 3Do. The optimal distance between the turbines and the rows, as well as the wind direction, was maintained at 8Do, 10Do, and 30°, respectively.
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
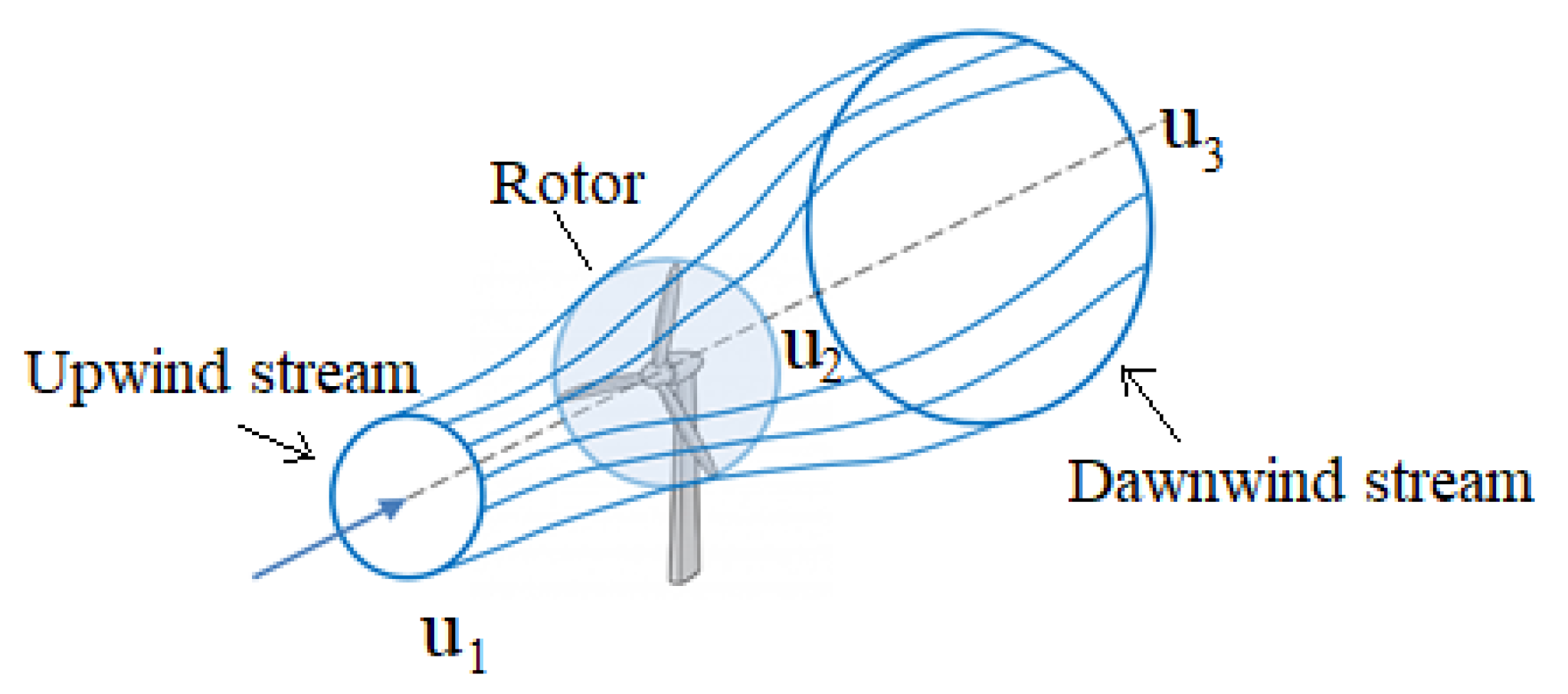
| Upstream wind speed approaching the turbine [m/s] | |
| Wind speed at the rotor [m/s] | |
| Downstream wind speed [m/s] | |
| Air mass flow rate [kg/s] | |
| Force on the turbine resulting from the air mass flow [N] | |
| Power extracted by the turbine [W] | |
| Energy extracted from the wind [W] | |
| Air density [kg/m3] | |
| Swept area of the blades [m2] | |
| Overlapped area of the swept area of the rotors [m2] | |
| Interference factor | |
| Power of the undisturbed upstream air mass | |
| Power coefficient | |
| Shape factor | |
| Scale factor | |
| Wind speed at the hub height of the turbine [m/s] | |
| Wind speed at the anemometer height [m/s] | |
| Hub height of the turbine [m] | |
| Anemometer height [m] | |
| Surface roughness length [m] | |
| Power law exponent | |
| Turbine power output at standard temperature and pressure conditions [W] | |
| Air density at standard temperature and pressure conditions [kg/m3] | |
| Thrust coefficient | |
| Rotor radius [m] | |
| Decay coefficient | |
| Downwind distance between two consecutive wind turbines [m] | |
| Crosswind distance between two consecutive wind turbines [m] | |
| Local turbulence coefficient | |
| Wake wide [m] | |
| Wind direction [°] | |
| Turbines row orientation angle [°] | |
| Rotor diameter [m] | |
| Row offset distance [m] |
References
- Moussa, M.O. Experimental and numerical performances analysis of a small three blades wind turbine. Energy 2020, 203, 117807. [Google Scholar] [CrossRef]
- Wilkie, D.; Galasso, C. Impact of climate-change scenarios on offshore wind turbine structural performance. Renew. Sustain. Energy Rev. 2020, 134, 110323. [Google Scholar] [CrossRef]
- Nazir, M.S.; Alturise, F.; Alshmrany, S.; Nazir, H.M.J.; Bilal, M.; Abdalla, A.N.; Sanjeevikumar, P.; Ali, Z.M. Wind generation forecasting methods and proliferation of artificial neural network: A review of five years research trend. Sustainability 2020, 12, 3778. [Google Scholar] [CrossRef]
- Ulazia, A.; Ibarra-Berastegi, G.; Sáenz, J.; Carreno-Madinabeitia, S.; González-Rojí, S.J. Seasonal Correction of Offshore Wind Energy Potential due to Air Density: Case of the Iberian Peninsula. Sustainability 2019, 11, 3648. [Google Scholar] [CrossRef] [Green Version]
- Guo, P.; Chen, S.; Chu, J.; Infield, D. Wind direction fluctuation analysis for wind turbines. Renew. Energy 2020, 162, 1026–1035. [Google Scholar] [CrossRef]
- Urabe, C.T.; Saitou, T.; Kataoka, K.; Ikegami, T.; Ogimoto, K. Positive Correlations between Short-Term and Average Long-Term Fluctuations in Wind Power Output. Energies 2021, 14, 1861. [Google Scholar] [CrossRef]
- Sun, H.; Gao, X.; Yang, H. A review of full-scale wind-field measurements of the wind-turbine wake effect and a measurement of the wake-interaction effect. Renew. Sustain. Energy Rev. 2020, 132, 110042. [Google Scholar] [CrossRef]
- Veludurthi, A.; Bolleddu, V. Experimental buckling analysis of NACA 63415 aerofoil wind turbine blade. Mater. Today Proc. 2021, 46, 205–211. [Google Scholar] [CrossRef]
- Rahgozar, S.; Pourrajabian, A.; Kazmi, S.A.A. Performance analysis of a small horizontal axis wind turbine under the use of linear/nonlinear distributions for the chord and twist angle. Energy Sustain. Dev. 2020, 58, 42–49. [Google Scholar] [CrossRef]
- Fant, C.; Gunturu, B.; Schlosser, A. Characterizing wind power resource reliability in southern Africa. Appl. Energy 2016, 161, 565–573. [Google Scholar] [CrossRef] [Green Version]
- Jin, G.; Zong, Z.; Jiang, Y.; Zou, L. Aerodynamic analysis of side-by-side placed twin vertical-axis wind turbines. Ocean Eng. 2020, 209, 107296. [Google Scholar] [CrossRef]
- Leelakrishnan, E.; Kumar, M.S.; Selvaraj, S.D.; Vignesh, N.S.; Raja, T.A. Numerical evaluation of optimum tip speed ratio for darrieus type vertical axis wind turbine. Mater. Today Proc. 2020, 33, 4719–4722. [Google Scholar] [CrossRef]
- Vergaerde, A.; De Troyer, T.; Muggiasca, S.; Bayati, I.; Belloli, M.; Kluczewska-Bordier, J.; Parneix, N.; Silvert, F.; Runacres, M.C. Experimental characterisation of the wake behind paired vertical-axis wind turbines. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104353. [Google Scholar] [CrossRef]
- Boudounit, H.; Tarfaoui, M.; Saifaoui, D. Modal analysis for optimal design of offshore wind turbine blades. Mater. Today Proc. 2020, 30, 998–1004. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Sacile, R.; Mimet, A. Monthly and seasonal assessment of wind energy characteristics at four monitored locations in Liguria region (Italy). Renew. Sustain. Energy Rev. 2010, 14, 1959–1968. [Google Scholar] [CrossRef]
- Feroz, R.M.A.; Javed, A.; Syed, A.H.; Kazmi, S.A.A.; Uddin, E. Wind speed and power forecasting of a utility-scale wind farm with inter-farm wake interference and seasonal variation. Sustain. Energy Technol. Assess. 2020, 42, 100882. [Google Scholar] [CrossRef]
- Longo, R.; Nicastro, P.; Natalini, M.; Schito, P.; Mereu, R.; Parente, A. Impact of urban environment on Savonius wind turbine performance: A numerical perspective. Renew. Energy 2020, 156, 407–422. [Google Scholar] [CrossRef]
- Regodeseves, P.G.; Morros, C.S. Unsteady numerical investigation of the full geometry of a horizontal axis wind turbine: Flow through the rotor and wake. Energy 2020, 202, 117674. [Google Scholar] [CrossRef]
- Ali, Q.S.; Kim, M.H. Unsteady aerodynamic performance analysis of an airborne wind turbine under load varying conditions at high altitude. Energy Convers. Manag. 2020, 210, 112696. [Google Scholar] [CrossRef]
- Hohman, T.; Martinelli, L.; Smits, A. The effect of blade geometry on the structure of vertical axis wind turbine wakes. J. Wind. Eng. Ind. Aerodyn. 2020, 207, 104328. [Google Scholar] [CrossRef]
- Pallotta, A.; Pietrogiacomi, D.; Romano, G. HYBRI—A combined Savonius-Darrieus wind turbine: Performances and flow fields. Energy 2020, 191, 116433. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Ren, J.; Meng, X.; Wu, Y. Model experiment study for ventilation performance improvement of the Wind Energy Fan system by optimizing wind turbines. Sustain. Cities Soc. 2020, 60, 102212. [Google Scholar] [CrossRef]
- Fei, Z.; Tengyuan, W.; Xiaoxia, G.; Haiying, S.; Hongxing, Y.; Zhonghe, H.; Yu, W.; Xiaoxun, Z. Experimental study on wake interactions and performance of the turbines with different rotor-diameters in adjacent area of large-scale wind farm. Energy 2020, 199, 117416. [Google Scholar] [CrossRef]
- Abraham, A.; Hong, J. Dynamic wake modulation induced by utility-scale wind turbine operation. Appl. Energy 2020, 257, 114003. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Foley, A.M. Bilateral Gaussian Wake Model Formulation for Wind Farms: A Forecasting Based Approach. Renew. Sustain. Energy Rev. 2020, 127, 109873. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, S.; Meng, H.; Ma, H. Study on interaction between the wind-turbine wake and the urban district model by large eddy simulation. Renew. Energy 2020, 157, 941–950. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Feijóo, A.; Zheng, G.; Zhou, J. Wind farm layout optimization with a three-dimensional Gaussian wake model. Renew. Energy 2020, 159, 553–569. [Google Scholar] [CrossRef]
- Saad, A.S.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance enhancement of twisted-bladed Savonius vertical axis wind turbines. Energy Convers. Manag. 2020, 209, 112673. [Google Scholar] [CrossRef]
- Dorel, S.F.; Mihai, G.A.; Nicusor, D. Review of Specific Performance Parameters of Vertical Wind Turbine Rotors Based on the SAVONIUS Type. Energies 2021, 14, 1962. [Google Scholar] [CrossRef]
- Sedighi, H.; Akbarzadeh, P.; Salavatipour, A. Aerodynamic performance enhancement of horizontal axis wind turbines by dimples on blades: Numerical investigation. Energy 2020, 195, 117056. [Google Scholar] [CrossRef]
- Twidell, J.; Weir, T. Renewable Energy Resources, 2nd ed.; Renewable Energy Resources in ASEAN; Taylor and Francis: 2018. pp. 4–10. Available online: http://www.uobabylon.edu.iq/eprints/publication_4_10679_78.pdf (accessed on 14 July 2020).
- Fundo Nacional de Energia. Renewable Energy Atlas of Mozambique; Gesto Energia S.A.: Maputo, Mozambique, 2014. [Google Scholar]
- Minister of Energy Mozambique, Riso National Laboratoty-Denmark. Support for Wind Power Development in Mozambique Final Report (Draft) June 2008; DNER Risø Danida: Copenhagen, Denmark, 2008. [Google Scholar]
- Mokveld, K.; von Eije, S. Final Energy Report Mozambique; Netherlands Enterprise Agency: Assen, The Netherlands, 2018; pp. 1–43. [Google Scholar]
- EDM. Annual Statistical Report 2016; EDM: Maputo, Mozambique, 2016. [Google Scholar]
- Chaouachi, A.; Covrig, C.F.; Ardelean, M. Multi-criteria selection of offshore wind farms: Case study for the Baltic States. Energy Policy 2017, 103, 179–192. [Google Scholar] [CrossRef]
- Veena, R.; Manuel, S.; Mathew, S.; Petra, I. Parametric Models for Predicting the Performance of Wind Turbines. Mater. Today Proc. 2020, 24, 1795–1803. [Google Scholar] [CrossRef]
- Sun, H.; Yang, H. Numerical investigation of the average wind speed of a single wind turbine and development of a novel three-dimensional multiple wind turbine wake model. Renew. Energy 2020, 147, 192–203. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, Y.; Li, L.; Han, S.; Liu, Y. Multiple Wind Turbine Wakes Modeling Considering the Faster Wake Recovery in Overlapped Wakes. Energies 2019, 12, 680. [Google Scholar] [CrossRef] [Green Version]
- Dhiman, H.S.; Deb, D.; Balas, V.E. Supervised learning for forecasting in presence of wind wakes. In Supervised Machine Learning in Wind Forecasting and Ramp Event Prediction; Academic Press: Cambridge, MA, USA, 2020; pp. 141–169. [Google Scholar]
- International Renewable Energy Agency. Renewable Power Generation Costs in 2017; IRENA: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- International Renewable Energy Agency. Electricity Storage and Renewables: Costs and Markets to 2030; IRENA: Abu Dhabi, United Arab Emirates, 2017. [Google Scholar]
- DMazzeo, D.; Baglivo, C.; Matera, N.; De Luca, P.; Congedo, P.M.; Oliveti, G. Energy and economic dataset of the worldwide optimal photovoltaic-wind hybrid renewable energy systems. Data Brief 2020, 33, 106476. [Google Scholar] [CrossRef]
- Farahmand, H.; Warland, L.; Huertas-Hernando, D. The Impact of Active Power Losses on the Wind Energy Exploitation of the North Sea. Energy Procedia 2014, 53, 70–85. [Google Scholar] [CrossRef] [Green Version]
- Turkia, V.; Huttunen, S.; Wallenius, T. Method for Estimating Wind Turbine Production Losses due to Icing; VTT Technical Research Centre of Finland: Espoo, Finland, 2013. [Google Scholar]
- Colmenar-Santos, A.; Campíñez-Romero, S.; Enríquez-Garcia, L.A.; Pérez-Molina, C. Simplified analysis of the electric power losses for on-shore wind farms considering weibull distribution parameters. Energies 2014, 7, 6856–6885. [Google Scholar] [CrossRef] [Green Version]
- Byrne, R.; Astolfi, D.; Castellani, F.; Hewitt, N.J. A Study of Wind Turbine Performance Decline with Age through Operation Data Analysis. Energies 2020, 13, 2086. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.; Chen, Q.; Fu, Y.; Chung, C.Y.; Mi, Y. Optimization of maintenance scheduling for offshore wind turbines considering the wake effect of arbitrary wind direction. Electr. Power Syst. Res. 2020, 184, 106298. [Google Scholar] [CrossRef]
- Premkumar, P.S.; Nadaraja P., S.; Arunvinthan, S.; Sivaraja, S.; Vinayagamurthy, G.V.; Peradotto, E.; Panunzio, A.M.; Salles, L.; Schwingshackl, C.; Bacharoudis, K.C.; et al. Uncertainty and Risk Assessment in the Design Process for Wind. J. Adv. Res. Dyn. Control Syst. 2015, 9, V07AT30A013. [Google Scholar]






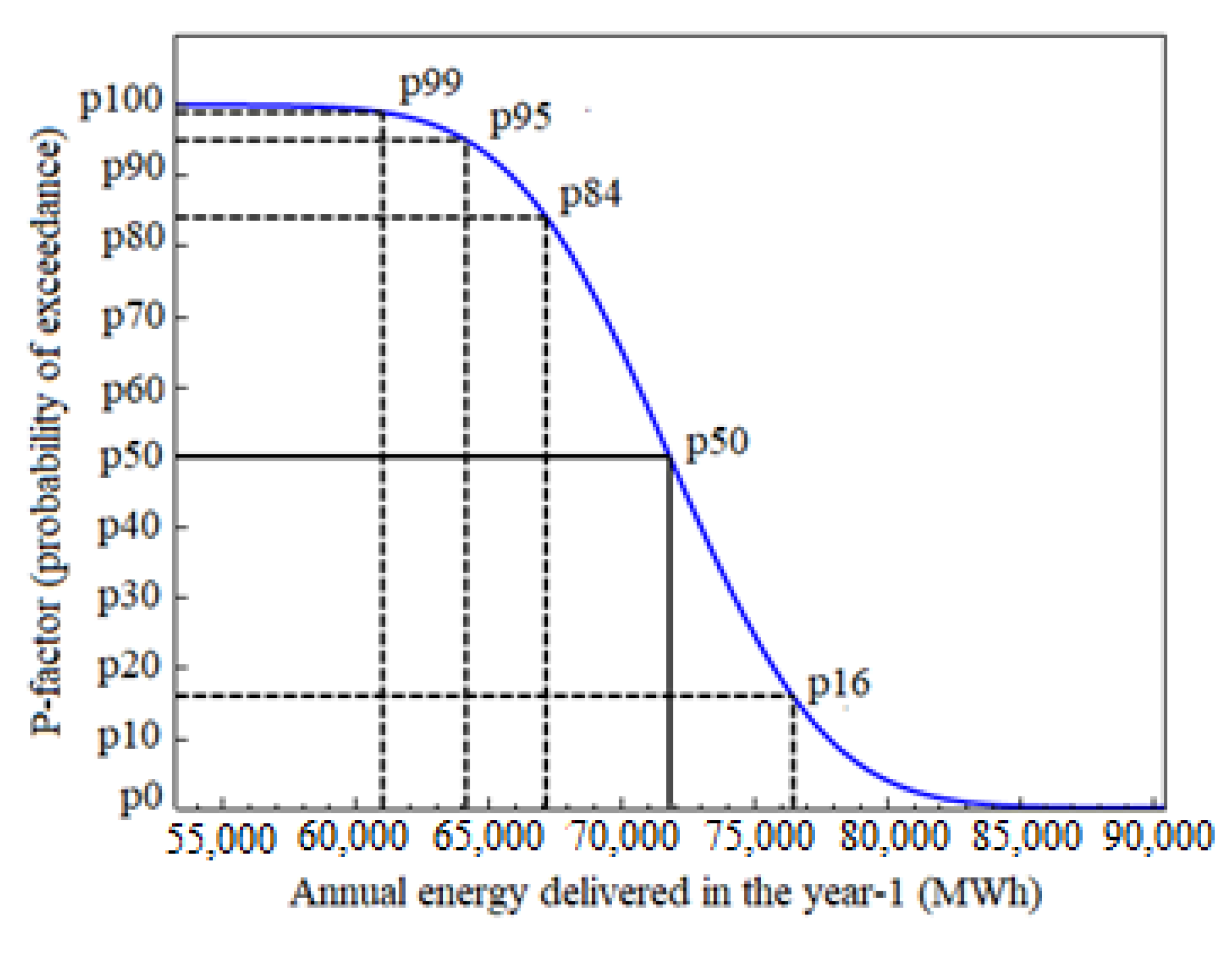

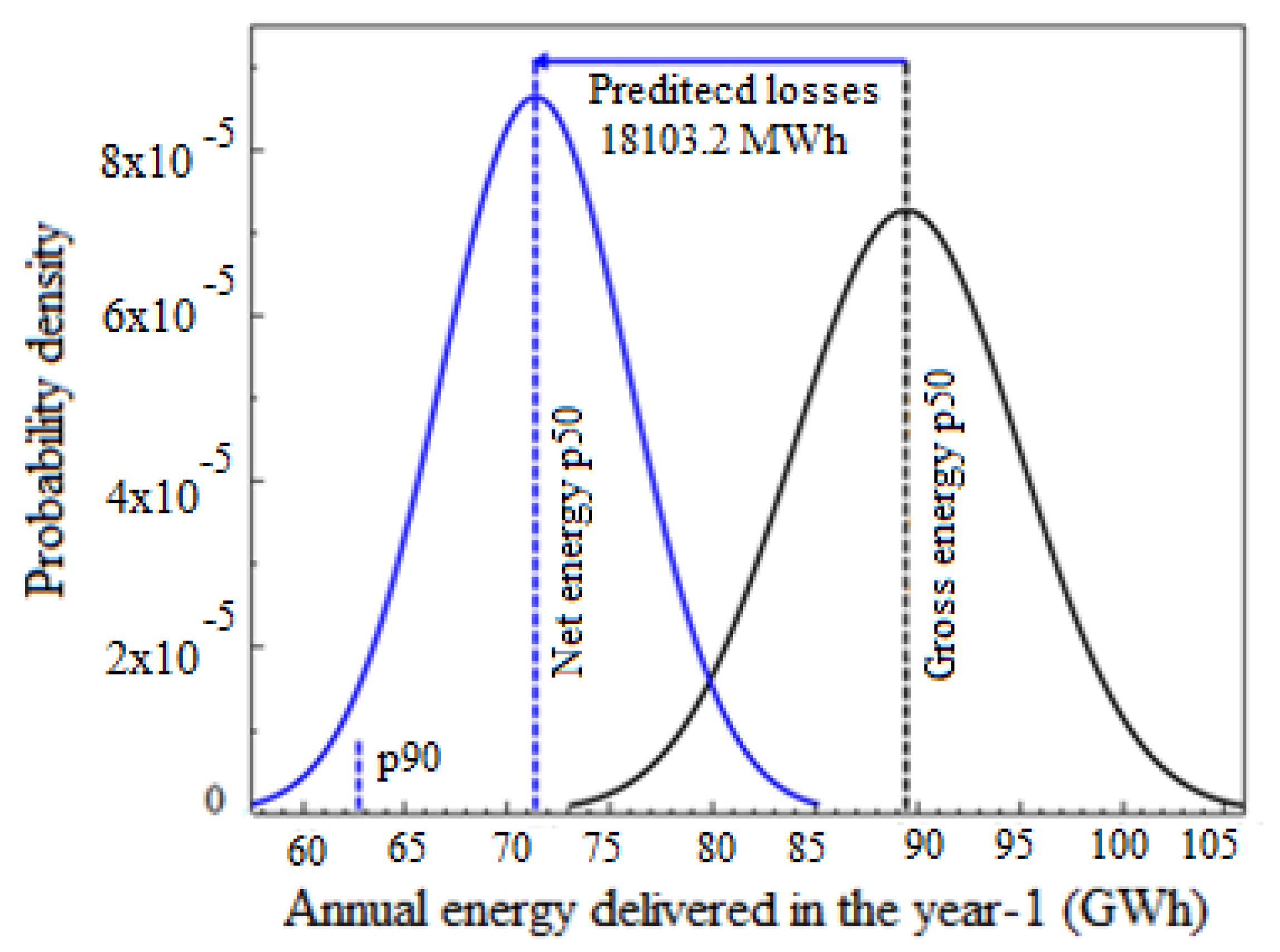
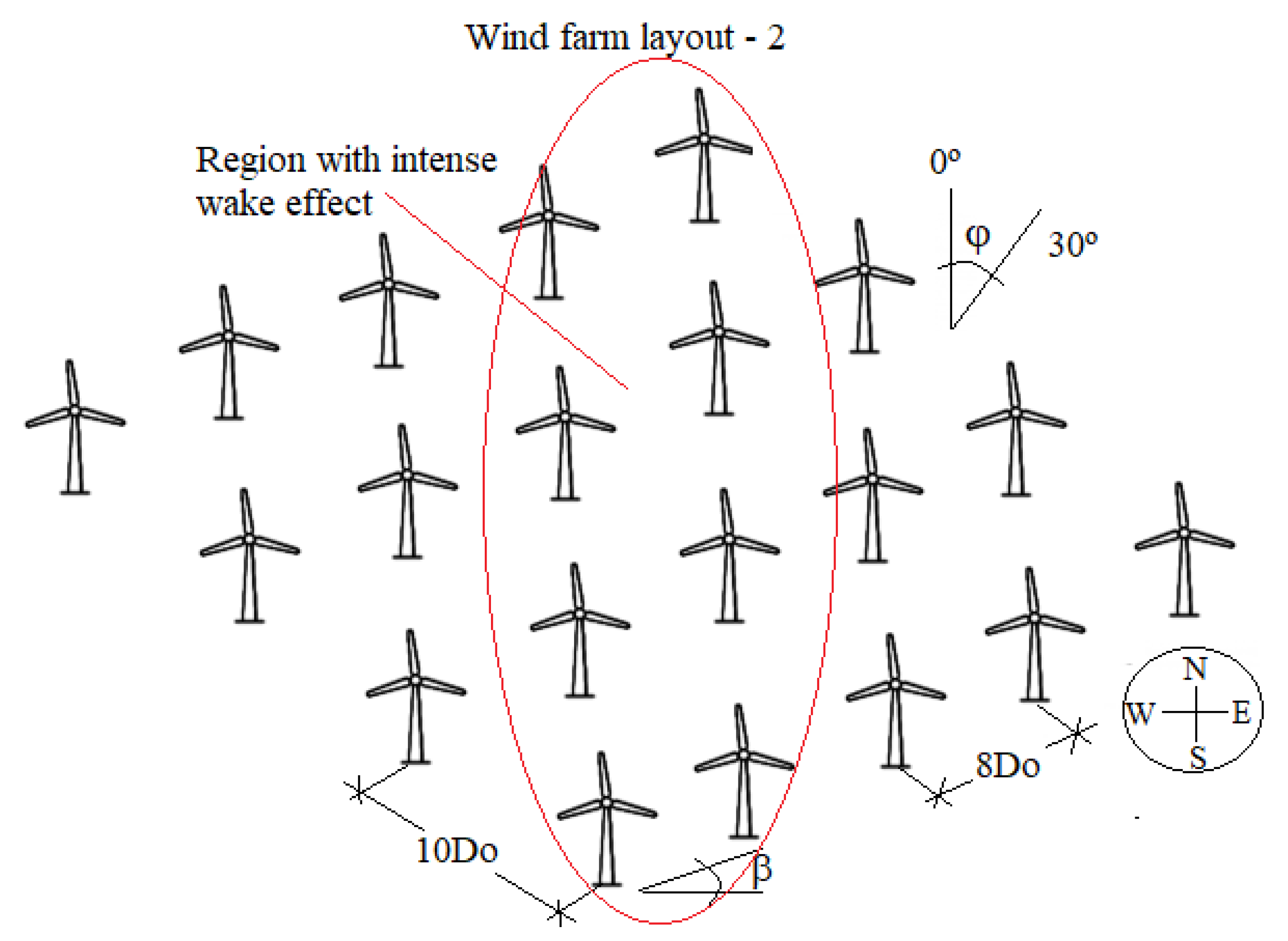
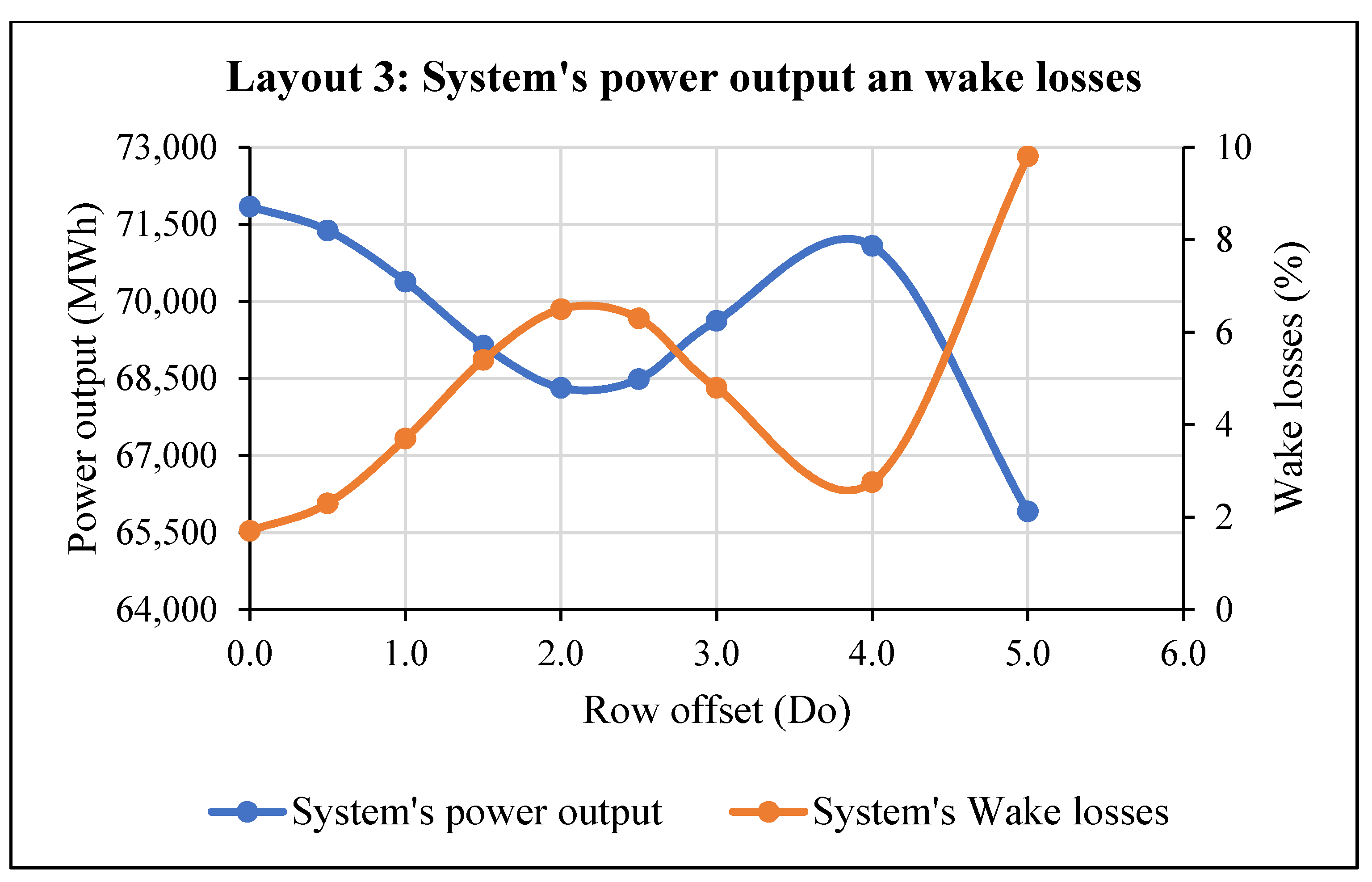
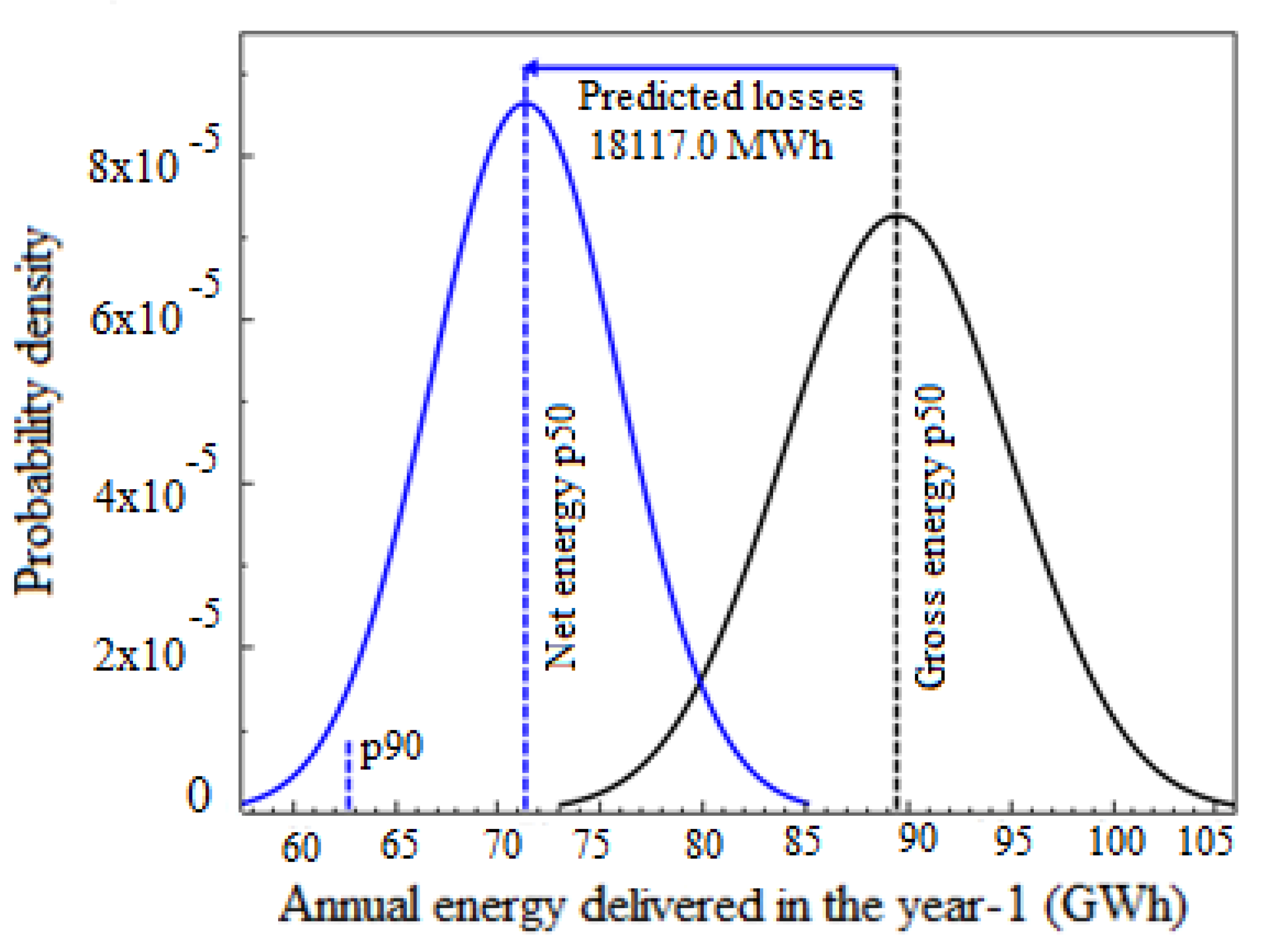
| Parameter | Value |
|---|---|
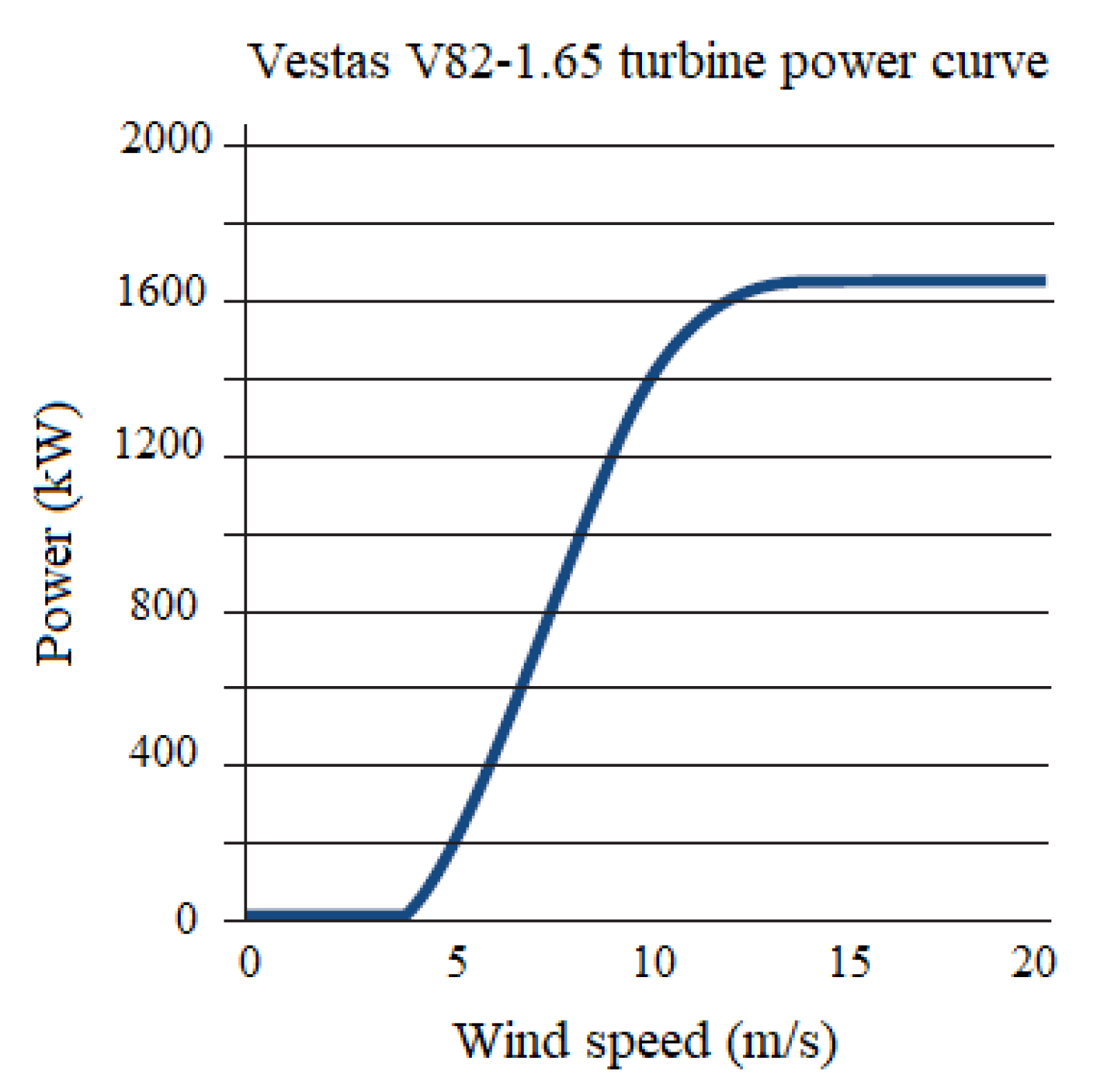
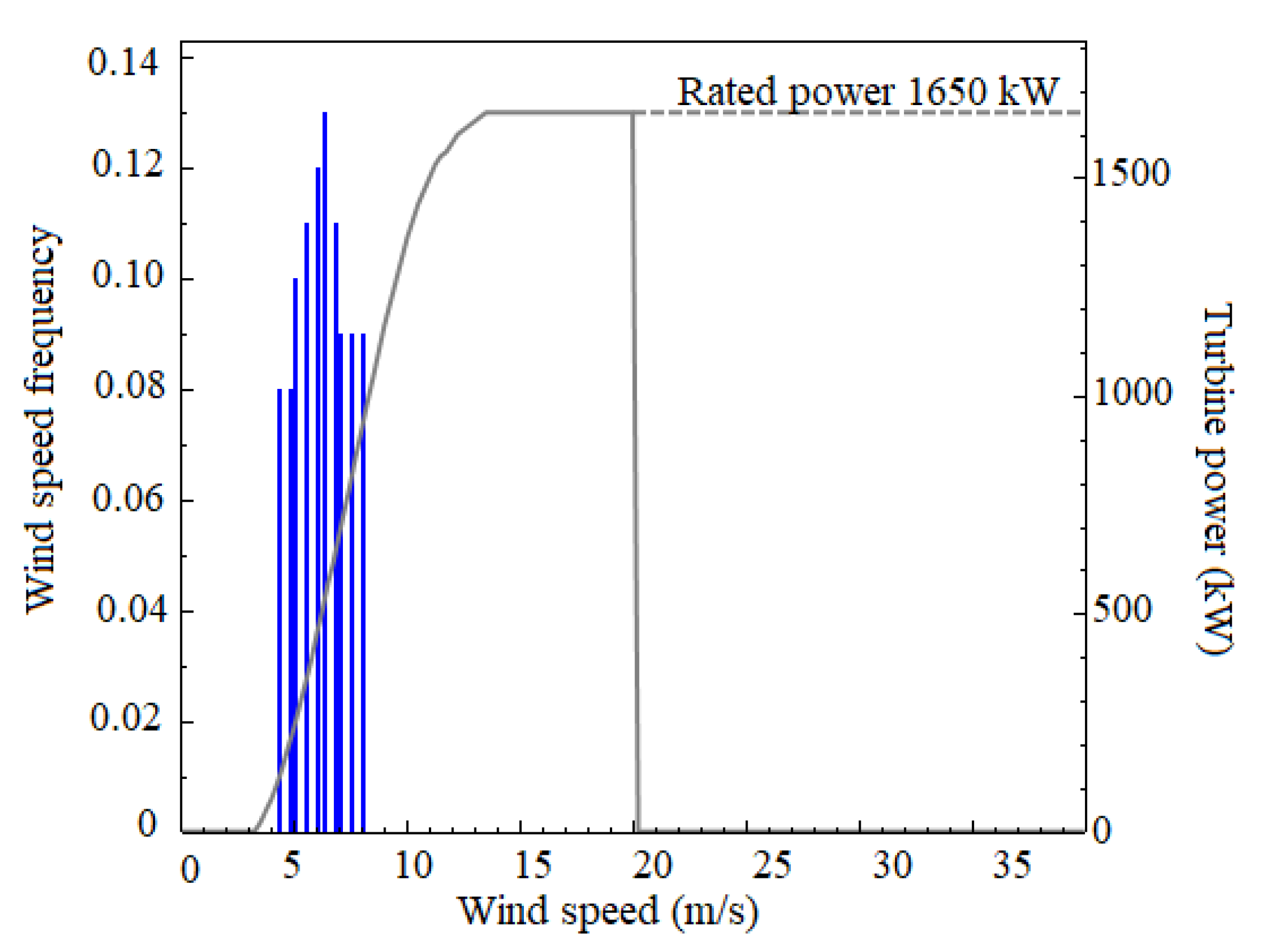
| Cut-in wind speed: | 3.5 m/s |
| Nominal wind speed: | 13 m/s |
| Cut-out wind speed | 20 m/s |
| Hub height (50 Hz, 230 V) | 78 m |
| Designation | Estimated Value (%) |
|---|---|
| Turbine’s availability losses | 5.0 |
| Electrical losses | 3.0 |
| Turbine performance losses | 4.0 |
| Environmental losses | 2.5 |
| Operational strategies losses | 2.0 |
| Operating system uncertainties | 7.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roque, P.M.J.; Chowdhury, S.P.; Huan, Z. Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study. Energies 2021, 14, 4291. https://doi.org/10.3390/en14144291
Roque PMJ, Chowdhury SP, Huan Z. Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study. Energies. 2021; 14(14):4291. https://doi.org/10.3390/en14144291
Chicago/Turabian StyleRoque, Paxis Marques João, Shyama Pada Chowdhury, and Zhongjie Huan. 2021. "Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study" Energies 14, no. 14: 4291. https://doi.org/10.3390/en14144291
APA StyleRoque, P. M. J., Chowdhury, S. P., & Huan, Z. (2021). Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study. Energies, 14(14), 4291. https://doi.org/10.3390/en14144291






