Abstract
In recent years, the evaluation of several energy sources is an extremely significant issue that affects socio-environmental development and techno-economic growth in different sectors. To tackle this concern, many researchers have concentrated on preferring desirable energy sources and adopting multi-criteria group decision-making (MCGDM) approaches for only a single type of user (e.g., agricultural, industrial, tourism, or domestic users). However, every energy user plays an important role in shaping energy policy. In fact, for sustainable energy, it is important to include all main energy users at the same time in energy decision-making. The main objective of this work was to propose a fuzzy MCGDM approach to evaluate and prioritize energy sources in Tunisia from various sectors’ point of views. Many criteria are combined, including the following: technical, economic, social, political and environmental. After applying the fuzzy Delphi method, the proposed approach consists of applying a fuzzy TOPSIS method as a multi-criteria approach. Finally, a sensitivity analysis is performed to evaluate the results of the proposed approach and to study how the optimal solution is affected by the objective function coefficients.
1. Introduction
1.1. Background and Research Motivation
Energy is an important resource for all user sectors in the world. The energy extraction process is characterized by several different practices, techniques, and impacts. However, despite the economic importance of these resources in several countries, and their social and political benefits, these resources cause various economic, environmental, and social impacts in terms of pollution, human health, etc. [1]. These criteria impacts vary mainly due to the practices and techniques used in energy extraction. From this perspective, sustainability studies on energy are vital. Indeed, the aim of sustainable development is to meet industrial, agricultural, domestic, and tourism energy needs, and therefore prosperity for this and future generations, according to various criteria. Generally, the inefficient use of resources and the unbalanced income reparation seem to be problematic for the relative size of sectoral energy source selection. Fulfilling energy requirements is a critical issue for the development of different sectors. Meeting the multiple demands of the industrial, agricultural, domestic, and tourism sectors has the potential to lead to intense energy conflicts. In fact, this has provided a new dimension to existing energy conflicts in addition to an already rising number of inter-state energy disputes. Though several countries’ policies indicate the priorities to be followed in the selection of energy sources for different sectors, they fall short of indicating the mechanism to decide the competing demand among the different sectors simultaneously. These requirements give rise to an energy source selection problem compared to previous studies.
1.2. Literature Overview
From the end of the Second World War, energy problems have affected sustainable development across all sectors. In recent times, various researchers have converged upon the best energy source selection methods for given sectors. The optimization of energy source selection against various criteria could help managers make decisions about their energy consumption, supply, and production [1]. In this regard, multi-criteria group decision-making (MCGDM) methods have been observed as one of the most suitable applications to real world problems [2]. The best energy source selection can be described as a MCGDM problem, where multi-criteria decision analysis can evaluate a set of energy sources according to their relative criteria priorities [3].
There are different multi-criteria decision analyses that have been applied within energy management, i.e., the analytic hierarchy process (AHP) method, the ELimination and Choice Translating REality (ELECTRE) method, the stochastic multi-criteria acceptability analysis (SMAA) method, the analytic network process (ANP) method, the technique for order preference by similarity to ideal solution (TOPSI) method, the preference ranking organization method for enrichment and evaluations (PROMETHEE) method, the VIKOR method, the data envelopment analysis (DEA) method, the additive ratio assessment (ARAS) method, the geographic information system (GIS) method, the multi-actor multi-criteria analysis (MAMCA), and additional extensions of these methods by combining them with fuzzy theory.
Based on the AHP method, the weights of the different energy sources are calculated based on the comparison of all energy sources with each evaluation criterion. Several researchers have applied the AHP method to evaluate a finite set of energy sources according to each criterion, such as in [4,5,6,7,8,9]. For example, Ramanathan and Ganesh [4], Kablan [5], and Garni et al. [9] mentioned that the photovoltaic is the best source of energy for the domestic sector using the AHP method. In contrast, Chatzimouratidis et al. [6] proposed the geothermal source for the same sector. The study of Chinese et al. [7] showed that natural gas is the best energy source for the industrial sector using the AHP method. Ahmad and Tahar [8] proposed the photovoltaic source for the industrial sector according to the AHP analysis.
Another multicriteria hierarchical method is the ANP, which definite the priorities of energy sources to rank them in final decision. Several studies have discus the energy sources selection problems based on the ANP method, such as in [10,11]. In addition, the ELECTRE method determined the outranking relations to rank a set of energy sources. Multiple authors applied the ELECTRE method to evaluate a finite set of energy sources based on various quantitative and qualitative criteria, such as in [12,13]. Beccali et al. [12] selected the geothermal source for the agricultural sector and Catalina et al. [13] proposed the biomass source for the domestic sector based on the ELECTRE method. With the TOPSIS method, we can find a solution of the shortest distance from the ideal solution and the farthest distance from the negative-ideal solution for each energy source, such as in [14,15]). Kaya and Kahraman [14] ranked wind power as the best source for the domestic sector in Turkey. Talukdar et al. [15] selected the solar photovoltaic source for the domestic sector in Bangladesh, according to the TOPSIS method.
Another distance-based analysis is the PROMETHEE method, which performs comparison of energy sources for the ranking based a finite set of criteria. Some researchers utilized the PROMETHEE method to compare various energy sources for the ranking on a given number of criteria such as in [16,17,18]). Haralambopoulos and Polatidis [16] proposed the geothermal source for the tourism sector. Diakoulaki and Karangelis [17] proposed natural gas for the industrial sector in Greece, based on the PROMETHEE methods. Barragán et al. [18] showed that the solar photovoltaic is the best energy source for the domestic sector in Cuenca using the PROMETHEE method.
According to the VIKOR method, we can establish a compromise ranking list and a compromise solution obtained on the criteria priorities. Some authors have applied the VIKOR method to solve the energy source selection problems, such as in [19]. With the DEA method, we can compare the different energy sources to determine their efficiencies based on various criteria. In the stochastic or fuzzy MCGDM method literature, there is a long history of methodologies that allow decision aiding under uncertain and/or imprecise information. The SMAA is an MCGDM method to assess energy sources while taking into account inaccurate, uncertain, or missing information [20]. On the other hand, fuzzy MCGDM methods enable to us model uncertainties in human judgments while analyzing energy source selection problems [21,22,23]. This study presents MCGDM methods that can be used to optimize the selection of energy by various users with different priorities of criteria levels in a given system. The MCGDM methods were widely utilized to evaluate various energy sources in several countries. However, the utilization of MCGDM methods is almost at a domestic, industrial, agricultural, or tourism scale. Table 1 presents an important list of studies that were used for the energy source selections.

Table 1.
Literature review on energy source selection.
In 1995, Ramanathan and Ganesh [4] applied the AHP and goal programming methods to select an energy source for the domestic sector in India. In 2003, Beccali et al. applied the ELECTRE-III method to evaluate a set of renewable energy sources for the agricultural sector in Italy. Haralambopoulos and Polatidis [16] evaluated a set of energy sources using the PROMETHEE method in Greece for the tourism sector. In 2004, Kablan [5] used the AHP method to rank energy sources for the domestic sector in Jordan. In 2007, Diakoulaki and Karangelis used the PROMETHEE method to select the best renewable energy source for the industrial sector in Greece. In 2008, Chatzimouratidis et al. [6] applied the AHP approach to rank several energy sources for the domestic sector in Greece. In the same context, Jaber et al. [24] evaluated various energy sources using the AHP method for the domestic sector in Jordan. Önüt et al. [10] applied the ANP method to rank energy sources for the manufacturing industry in Turkey. In 2009, Ren el al. [25] used the AHP-PROMETHEE methods to determine the best energy source selection for the domestic sector in Japan. In the study of Daim et al. [26], various energy sources were compared using the AHP method for the industrial sector in the USA. Furthermore, Theodorou et al. [27] applied the AHP approach to rank the energy sources for the industrial sector in Cyprus. Kaya et al. [14] used a combinatorial approach based on the VIKOR and AHP methods to find the best renewable energy sources for the industrial sector in Turkey. In 2011, the AHP method was used by Chinese et al. [7] for the industrial sector in Italy. Kaya and Kahraman [23] applied the TOPSIS method to rank a set of energy sources for the domestic sector in Turkey. Catalina et al. [13] applied the ELECTRE III method for the selection of the best combination of energy sources for the domestic sector in France. In 2014, Ahmed and Tahar [8] used the AHP method for the selection of energy sources for the industrial sector in Malaysia. In 2015, Rojas-Zerpa, and Yusta [28] applied the AHP-VIKOR methods to determine the best energy source for the agricultural sector in the Venezuelan Andes. Kontu et al. [20] applied the SMAA method to select the best energy systems for a new sustainable residential area in Finland. Streimikienė et al. [29] used the AHP-ARAS methods for the selection of electricity generation technologies in Lithuania. Garni el al. [9] applied the AHP method to rank the energy sources for the domestic sector in Saudi Arabia. Çelikbilek et al. [30] applied the ANP-VIKOR methods to rank the different renewable energy sources for the industrial sector in Turkey. Jung et al. [31] used the SMAA method to identify the best renewable energy sources for the tourism sector in Helsinki, Finland. Barragán et al. [18] used the PROMETHEE method to determine the best energy sources for the domestic sector in the city of Cuenca. Talukdar et al. [15] used the TOPSIS method to identify the best renewable energy source for the domestic sector in Dhaka, Bangladesh. Strantzali et al. [32] applied the PROMETHEE method to find the best renewable energy sources for the tourism sector in Greece. Kausika et al. [33] applied the GIS-AHP methods to rank energy sources for the domestic sector of the city of Apeldoorn in the Netherlands. Haddad et al. [34] applied the AHP method to evaluate energy sources for the domestic sector in Algeria. Wu et al. [35] used the PROMETHEE-ANP methods to determine the best energy sources for remote areas. Kumar and Samuel [19] utilized the VIKOR method to rank renewable energy sources for the industrial sector in India. Aboushal [36] used the GIS method to rank a set of renewable energy sources for the domestic sector in Egypt. Rathore and Singh [37] used the ARAS method to select an optimal renewable energy source for the agricultural sector in India. In addition, Taskin Gumus et al. [21], Colak et al. [22], and Kaya et al. [14] applied a combined fuzzy MCDM for energy source selection in Turkey. Pratibha et al. [38] applied the TOPSIS method to evaluate the energy source in India for a domestic sector. Liu et al. [39] applied a hybrid approach based on the ANP and VIKOR methods to select the best renewable energy sources for the domestic sector in China.
1.3. Objective of the Study
The recent literature on the subject includes a number of studies that implement the MCGDM method to select a sustainable energy source for a given user (industrial, domestic, agricultural, or tourism). However, the objectives of this paper are to apply a fuzzy MCGDM approach to determine the criteria and energy source selection for multiple users. The contributions of this paper are to determine the priorities of users according to various criteria in the energetic field and to prepare the energy users list for each energy source. Therefore, the fuzzy MCGDM approach is applied to energy field. The procedure consists of evaluating criteria based on energy experts’ opinions (fuzzy Delphi method) and the sectoral rankings of energy sources (fuzzy TOPSIS method).
In the next section we present the sectoral energy source selection problems. After that, we give a description of the proposed approach. The results of the proposed approach are presented at the end of this study.
2. Materials and Methods
2.1. Study Area
Each country should study their sectoral energy source selection as a specific case study. Although Tunisia is a fossil fuel producing country and its climate is conducive to the production of renewable energies, in Tunisia, energy studies are very limited. Energy transitions bring about fundamental changes at various levels in Tunisia, thus it needs broad, all-sector support. To design an accepted energy transition that is sustainable and socially compatible, it must aim at compromises in balancing differing sectoral interests through inclusive processes and fairly distributed outcomes. Tunisia suffers from an energy shortage due to the increased demand for energy that has exceeded the demand for national production. According to the Tunisian Ministry of Energy, over the past few years, primary energy resources have been declining by about 6% per year. This loss is mostly due to the natural degradation of fossil fuels. Moreover, Tunisia’s primary energy needs have increased by more than 2% per year [40]. On the other hand, policy makers are well advised to consult energy specialists from all levels and sectors of society to manage the complexity and contingency of energy transitions. In this paper, the prioritization of each criterium is estimated in each sector using experts’ opinions through the fuzzy Delphi method. The industrial, agricultural, domestic, and tourism sectors are defined, and comparisons from one to another are regarded as a sectoral energy transaction. This approach is adopted as a convenient way to gauge sectoral energy source selection.
2.2. The Proposed Approach
Energy source selection usually involves economic and political influences as well as social and environmental analyses. These interdependent impacts among competing sectors, especially the uncertainty related to energy availability, make the problem rather complex and uncertain. However, a new integrated methodological framework with a fuzzy MCGDM approach is proposed as a decision-making model to solve the multiple users and energy source selection problems. The proposed approach is shown in Figure 1.
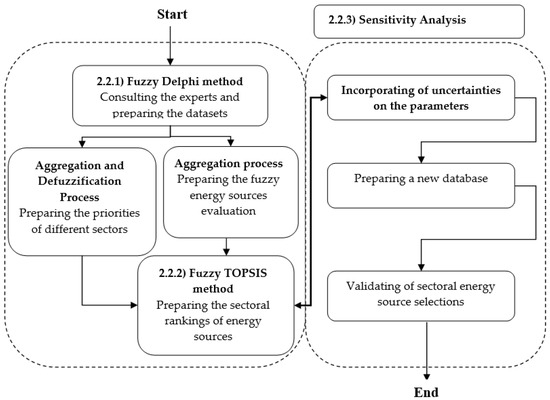
Figure 1.
Flowchart of the proposed approach.
This paper used a new approach to evaluate the different energy sources for various sectors. Firstly, the fuzzy Delphi method is used to consult the experts and to prepare the necessary datasets. Next, the best non-fuzzy performance technique is used to prepare the priorities of different sectors based on the fuzzy Delphi datasets. After that, the fuzzy TOPSIS method is applied for the sectoral rankings of energy sources according to the final results of the fuzzy AHP and Delphi methods. Finally, the fuzzy MCGDM approach is validated with uncertain parameter values by a sensitivity analysis.
2.2.1. Fuzzy Delphi Method
The Delphi method was proposed by Norman and Olaf [41] to collect datasets with a group of decision makers. The main steps of the fuzzy Delphi method are illustrated as follows:
- -
- Step 1. Assume that K energy experts are invited to propose the lists of evaluation criteria, energy sources, and the main energy consumable sectors.
- -
- Step 2. The experts are invited to get the importance of the evaluation sources with respect to different criteria using linguistic variables. For each criterion of energy source , an expert is consulted to assign a score. This score can be seen as the expression of his opinion with respect to the preference of criterion by energy sources.
- -
- Step 3. The same experts are invited to get the importance of the evaluation main energy consumable sectors with respect to various criteria using linguistic variables.
- -
- Step 4. Convert the linguistic variables into triangular fuzzy numbers for criterion and energy source by expert or for criterion and sector ).
- -
- Step 5. Determine of the consensus index of each expert relative to other experts using the similarity measure function. The energy experts consulted were asked to give their opinion on the evaluation matrices. This process was repeated several times until a consensus emerged. In this step, a new consensus index algorithm is proposed as mentioned in Figure 2.
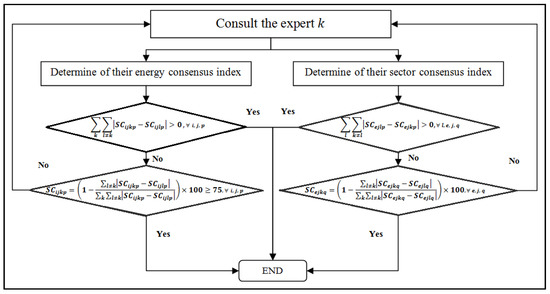 Figure 2. Consensus index algorithm.
Figure 2. Consensus index algorithm.
Each expert prepares two matrices (energy source evaluation matrix and sector evaluation matrix). The consensus algorithm performs the two activities “determining their energy consensus index” and “determining their sector consensus index” in parallel to check the degree of consensus of each matrix. Using the proposed consensus algorithm, the energy consensus index or the sector consensus index can be calculated for each tour () and for each energy expert .
Rules have been introduced into the proposed algorithm. First, a rule has been proposed to calculate the sum of the rank of expert k and its relative compatibility with other experts. If the value of this rule is 0, the consensus index is 100%. Subsequently, an average degree of agreement or , was introduced; when or , the degree of expert consensus is accepted, otherwise, the algorithm forces another round of consultation.
- -
- Step 6. Aggregate the fuzzy evaluations by , whose main target is to aggregate the evaluation matrices experts to a single matrix, where
- -
- Step 7. Defuzzification of the fuzzy sector decision matrix () based on best non-fuzzy performance (BNP) which is expressed in Equation (3).
Therefore, the final results of the fuzzy Delphi method are the fuzzy energy sources evaluation and the priorities of different sectors , which will be the main inputs of the fuzzy TOPSIS method.
2.2.2. Fuzzy TOPSIS Method
The TOPSIS approach was developed by Hwang and Yoon [42] for ranking the alternatives according to various criteria in several fields. In this paper, the fuzzy TOPSIS approach is applied in the energy field to rank the best sectoral energy sources. The process of the fuzzy TOPSIS approach is illustrated as follows:
Equation (4) normalizes the benefit criteria decision matrices. Equation (5) normalizes the cost criteria decision matrices. Equation (6) determines the weighted normalized fuzzy decision matrices . Equation (7) specifies the positive ideal solutions ( for each sector . Equation (8) specifies the negative ideal solutions ( for each sector . Equation (9) determines the distances from the positive ideal solutions ( for each sector . Equation (10) determines the distances from the negative ideal solutions ( for each sector . Equation (11) computes the closeness coefficient () for each energy source and for each sector . The water resource with the highest value represents the best energy sources for sector . According to the fuzzy MCGDM approach, the sectoral rankings of energy sources are shown.
2.2.3. Sensitivity Analysis of FMCGDM Approach
A sensitivity analysis of FMCGDM results is applied to assess how the optimal solution is affected by the coefficients of the objective function. For sensitivity analysis of the fuzzy MCGDM approach, we propose a new linear model. This model is based on the assumption that the objective function seeks to maximize the closeness coefficient () for each energy source and for each sector .
Subject to:
Equation (13) ensures that the three best energy sources are selected for each sector. Equation (14) introduces binary variables to the problem.
3. Results
The proposed approach is based on three input types, including the following: (1) four energy experts; (2) the different criteria observed in Tunisian energy; (3) the evaluations of the different user energy sectors according to the different criteria using the results of energy expert consultations.
3.1. Consulting the Experts and Preparing the Datasets
In this study, we consulted four energy experts to propose the lists of evaluation criteria, energy sources, and the main energy consumable sectors. Table 2 presents the list of evaluation criteria, Table 3 presents the list of energy sources, and Table 4 presents the list of energy consumable sectors.

Table 2.
List of evaluation criteria.

Table 3.
List of energy sources.

Table 4.
List of energy consuming sectors.
In this study, in order to be able to obtain the triangular fuzzy matrices, we utilized the fuzzy linguistic variables presented in Table 5.

Table 5.
Fuzzy linguistic scale.
The calculus detail is given in the Supplementary Materials. For each criterion of energy source , an expert is consulted to assign a score. This score can be seen as the expression of his opinion with respect to the preference of criterion by energy sources. All scores are presented in Table S1. After that, the experts consulted prepared an evaluation of the main energy consuming sectors with respect to various criteria using linguistic variables. Table S2 presents all theses decision opinions on sectors. Next, the consensus index is calculated based on the proposed consensus algorithm. The algorithm has ensured that the degrees of consensus are greater than 75% based on the different scores ( or presented in Table S1. Then, the aggregation of energy source decision matrices is determined according to Equation (1) in Table S3. The aggregation of sector decision matrices is determined according to Equation (2) in Table S4.
In this study, the defuzzification of the fuzzy sector decision matrix () is obtained with the BNP technique according to Equation (3). The results obtained are normalized () and they are presented in Table 6.

Table 6.
Decision sectors defuzzification.
Next, the final results of the fuzzy Delphi method are the fuzzy energy sources evaluation and the priorities of different sectors , which will be the main inputs of the fuzzy TOPSIS method.
3.2. Preparing the Sectoral Rankings of Energy Sources
According the fuzzy TOPSIS method, the sectoral rankings of energy sources are shown in Table 7.

Table 7.
Sectoral rankings of energy sources.
The calculation of the closeness coefficient sectoral rankings of energy sources is done according to Equations (4)–(11), and the results of this step are given in Table 7. Finally, the rankings of the energy sources of each user sector are determined.
3.3. Sensitivity Analysis of FMCGDM Approach
Sensitivity Analysis of FMCGDM results is applied to assess how the optimal solution is affected by the coefficients of the objective function. For sensitivity analysis of the fuzzy MCGDM approach, we applied the linear proposed model according to Equations (12)–(14). Using LINDO software, the sensitivity report for this problem appears in Figure 3.
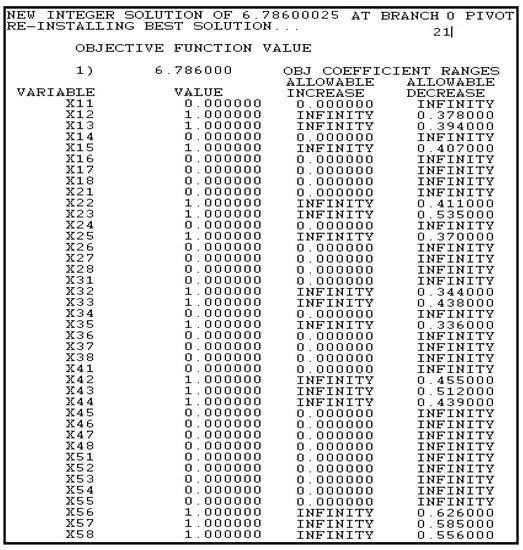
Figure 3.
Sensitivity analysis reports.
In addition, a sensitivity analysis is the study of how the uncertainty in the output of a mathematical model can be divided between various uncertainties in its inputs.
4. Discussion
The discussion section follows a comparison of the results obtained with the results of previous research in the field. From several previous studies, a gap was found in the research because researchers rank the energy sources for a single energy user sector.
For example, Garni el al. [9] mentioned that the photovoltaic is the best source of energy for the domestic sector in Saudi Arabia, using the AHP method. In contrast, Chatzimouratidis et al. [6] proposed the geothermal source for the same sector in Greece. In Italy, the study of Chinese et al. [7] showed that natural gas is the best energy source for the industrial sector using the AHP method and Beccali et al. [12] selected the geothermal source for the agricultural sector based on ELECTRE methods. In addition, the study of Kaya and Kahraman [14] ranked wind power as the best source for the domestic sector in Turkey and the study of Talukdar et al. [15] selected the solar photovoltaic source for the domestic sector in Bangladesh, according to the TOPSIS method.
In this paper, multi-sector energy ranking is discussed. Table 7 shows the final sectoral energy sources ranking of the proposed approach. The results show that:
- -
- Biomass energy is ranked first, followed by wind energy, and solar energy is ranked third for the agricultural sector. These energy sources are the best solutions to ensure a sustainable energy source selection for the agricultural sector in the long term. According to the consulted experts, biomass energy is very profitable in agricultural areas.
- -
- Wind, solar, and biomass energies are successively the best energy sources for the domestic sector. These energy sources are the best solutions to ensure a sustainable energy source selection for the domestic sector in the long term.
- -
- For the industrial sector, the first three energy sources are wind, solar, and biomass energies. These energy sources are the best solutions to ensure a sustainable energy source selection for the industrial sector in the long term.
- -
- Wind energy is ranked first, followed by solar energy and then hydraulic energy for the tourism sector. These energy sources are the best solutions to ensure sustainable energy source selection for the tourism sector in the long term. According to the consulted experts, hydraulic energy is very profitable for tourism in coastal areas.
- -
- For the transport sector, natural gas energy is ranked first, followed by oil energy, and coal energy is ranked third. These energy sources are the best solutions to ensure a sustainable energy source selection for the transport sector in the long term. According to the experts consulted, fossil fuels are the most profitable sources for the transport sector at the present time.
In addition, Figure 3 indicates the amounts by which the objective function coefficients can be changed unilaterally without affecting the character of the optimal solution. The allowable increase/decrease associated with the original coefficient of a decision variable tells us the range within which the coefficient of a given decision variable in the objective function may be increased/decreased without changing the optimal solution, where all other data are fixed.
5. Conclusions
This paper applies a fuzzy MCGDM approach to evaluate and prioritize energy sources for various sectors based on technical, economic, environmental, social, and political criteria. A sensitivity analysis of the FMCGDM results is used to see how the optimal solution is affected by the objective function coefficients and to see how the optimal value is affected by the right-hand side values.
Sectoral energy sources ranking is obtained using the FMCGDM method. The priorities of criteria are estimated in each sector using experts’ opinions through the fuzzy Delphi method. The industrial, agricultural, domestic, and tourism sectors are defined, and comparisons from one to another is regarded as a sectoral energy transaction. This approach is adopted as a convenient way to gauge sectoral energy source selections. The proposed approach is useful to be applied for other problems containing multiple objectives, sources, and users.
Every study has limitations that should be addressed in future research. In this regard, we will consult a large number of national experts as well as international experts. As a future research suggestion, different optimization models can be utilized to solve the sectoral or intersectoral energy source selection problem and the results can be compared with this study. Furthermore, different extensions of MCGDM or MAMCA methods can be applied to these problems. Finally, robustness analyses based on mathematical programs can be realized.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/en14144313/s1, Table S1: Decision matrices of energy sources, Table S2: Decision opinions of sectors, Table S3: Aggregate matrix of decision energy sources, Table S4: Aggregate matrix of decision sectors.
Author Contributions
Conceptualization, M.A.E., M.M., A.F. and W.H.; methodology, M.A.E., M.M., W.H., M.A. and A.M.A.; validation, W.H., M.A. and A.M.A.; formal analysis, M.A.E., M.M., A.F. and W.H.; investigation, M.A.E. and M.M.; resources, M.A.E. and M.M.; data curation, A.F., M.A. and W.H.; writing—original draft preparation, M.A.E., M.M. and A.F.; writing—review and editing, M.A., W.H. and A.M.A.; visualization, M.A., A.F., A.M.A.; supervision, A.F. and W.H.; project administration, W.H. and A.M.A.; funding acquisition, A.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported and funded by Taif University Researchers Supporting Project number (TURSP-2020/229), Taif University, Taif, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research was supported by Taif University Researchers Supporting Project number (TURSP-2020/229), Taif University, Taif, Saudi Arabia. Firstly, the authors are grateful for this financial support. Secondly, the authors would like to thank the four following experts: Ahmed Kammoun, director of SPECTRA company; Rami Gharsallah, director of Joule Energy Company; Ahmed Naifar, Director of Nour Energy Company; and Ridha Elleuch, Doctor in physics and renewable energy. Finally, the authors thank the editor and the anonymous referees for their valuable comments on an earlier version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following acronyms and notations are used in this manuscript:
| : Index of each energy source; | |
| : Index of each criteria; | |
| : Index of each energy user sector; | |
| : Index of each energy expert; | |
| : Set of energy sources; | |
| : Set of criteria; | |
| : Set of energy experts; | |
| : Set of energy user sectors; | |
| : Energy experts; | |
| : Sectors; | |
| : Criteria | |
| : Energy consumable sectors; | |
| : Triangular fuzzy numbers for criterion and energy source by expert ; | |
| : Triangular fuzzy numbers for criterion and user sector by expert ; | |
| : Energy consensus index; | |
| : Sector consensus index; | |
| : Aggregated Triangular fuzzy numbers for criterion and energy source by expert ; | |
| : Aggregated Triangular fuzzy numbers for criterion j and user sector by expert ; | |
| : Best Non-fuzzy Performance numbers for criterion and user sector ; | |
| : Normalized the criteria decision matrices; | |
| : Weighted normalized fuzzy decision matrices; | |
| : Positive ideal solutions for each sector ; | |
| : Negative ideal solutions for each sector ; | |
| : Positive ideal solutions for each sector e | |
| : Distances from the negative ideal solutions for each sector ; | |
| : Closeness coefficient for each energy source and for each sector ; | |
| : Energy sources are selected for each sector e |
References
- Krishankumar, R.; Nimmagadda, S.; Rani, P.; Mishra, A.R.; Ravichandran, K.S.; Gandomi, A.H. Solving renewable energy source selection problems using a q-rung orthopair fuzzy-based integrated decision-making approach. J. Clean. Prod. 2021, 279, 123329. [Google Scholar] [CrossRef]
- Gao, J.; Men, H.; Guo, F.; Liu, H.; Li, X.; Huang, X.; Gao, J.; Men, H.; Guo, F.; Liu, H.; et al. A multi-criteria decision-making framework for compressed air energy storage power site selection based on the probabilistic language term sets and regret theory. J. Energy Storage 2021, 37, 102473. [Google Scholar] [CrossRef]
- Riberio, F.; Ferreira, P.; Araújo, M. Evaluating future scenarios for the power generation sector using a Multi-Criteria Decisions Analysis (MCDA) tool: The Portuguese case. Energy 2013, 52, 126–136. [Google Scholar] [CrossRef] [Green Version]
- Ramanathan, R.; Ganesh, L. Energy resource allocation incorporating qualitative and quantitative criteria: An integrated model using goal programming and AHP. Socio-Econ. Plan. Sci. 1995, 29, 197–218. [Google Scholar] [CrossRef]
- Kablan, M. Decision support for energy conservation promotion: An analytic hierarchy process approach. Energy Policy 2004, 32, 1151–1158. [Google Scholar] [CrossRef]
- Chatzimouratidis, A.I.; Pilavachi, P.A. Multicriteria evaluation of power plants impact on the living standard using the analytic hierarchy process. Energy Policy 2008, 36, 1074–1089. [Google Scholar] [CrossRef]
- Chinese, D.; Nardin, G.; Saro, O. Multi-criteria analysis for the selection of space heating systems in an industrial building. Energy 2011, 36, 556–565. [Google Scholar] [CrossRef]
- Ahmad, S.; Tahar, R.M. Selection of renewable energy sources for sustainable development of electricity generation system using analytic hierarchy process: A case of Malaysia. Renew. Energy 2014, 63, 458–466. [Google Scholar] [CrossRef]
- Al Garni, H.; Kassem, A.; Awasthi, A.; Komljenovic, D.; Al-Haddad, K. A multicriteria decision making approach for evaluating renewable power generation sources in Saudi Arabia. Sustain. Energy Technol. Assess. 2016, 16, 137–150. [Google Scholar] [CrossRef]
- Önüt, S.; Tuzkaya, U.R.; Saadet, N. Multiple criteria evaluation of current energy resources for Turkish manufacturing in-dustry. Energy Convers. Manag. 2008, 49, 1480–1492. [Google Scholar] [CrossRef]
- Serhan, H.; Ozlem, S.; Ozalp, V. Selection of optimal renewable energy investment project via fuzzy anp. J. Econ. Financ. Account. 2018, 5, 224–233. [Google Scholar]
- Beccali, M.; Cellura, M.; Mistretta, M. Decision-making in energy planning: Application of the ELECTRE method at regional level for the diffusion of renewable energy technology. Renew. Energy 2003, 28, 2063–2087. [Google Scholar] [CrossRef]
- Catalina, T.; Virgone, J.; Blanco, E. Multi-source energy systems analysis using a multi-criteria decision aid methodology. Renew. Energy 2011, 36, 2245–2252. [Google Scholar] [CrossRef]
- Kaya, I.; Kahraman, C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS Methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Talukdar, A.; Rahman, H.; Sarker, P.C. Multi criteria Decision Analysis Algorithm based Optimal Selection of PV Panel for Grid-tie PV Electricity Generation System in context of Dhaka, Bangladesh. IJIREEICE 2017, 5, 68–80. [Google Scholar] [CrossRef]
- Haralambopoulos, D.; Polatidis, H. Renewable energy projects: Structuring a multi-criteria group decision-making framework. Renew. Energy 2003, 28, 961–973. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Karangelis, F. Multi-criteria decision analysis and cost–benefit analysis of alternative scenarios for the power generation sector in Greece. Renew. Sustain. Energy Rev. 2007, 11, 716–727. [Google Scholar] [CrossRef]
- Barragán, A.; Arias, P.; Terrados, J. Renewable Energy Generation Technologies on Urban Scale. Renew. Energy Power Qual. J. 2017, 1, 681–685. [Google Scholar] [CrossRef]
- Kumar, M.; Samuel, C. Selection of Best Renewable Energy Source by Using VIKOR Method. Technol. Econ. Smart Grids Sustain. Energy 2017, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Kontu, K.; Rinne, S.; Olkkonen, V.; Lahdelma, R.; Salminen, P. Multicriteria evaluation of heating choices for a new sustainable residential area. Energy Build. 2015, 93, 169–179. [Google Scholar] [CrossRef]
- Taskin, G.; Yayla, A.; Celik, A.Y.E.; Yildiz, A. A combined fuzzy-AHP and Fuzzy-GRA methodology for hydrogen energy storage method selection in Turkey. Energies 2013, 6, 3017–3032. [Google Scholar]
- Çolak, M.; Kaya, I. Prioritization of renewable energy alternatives by using an integrated fuzzy MCDM model: A real case application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Kaya, I.; Colak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Jaber, J.O.; Jaber, Q.M.; Sawalha, S.A.; Mohsen, M.S. Evaluation of conventional and renewable energy sources for space heat-ing in the household sector. Renew. Sustain. Energy Rev. 2008, 12, 278–289. [Google Scholar] [CrossRef]
- Ren, H.; Gao, W.; Zhou, W.; Nakagami, K. Multi-criteria evaluation for the optimal adoption of distributed residential energy systems in Japan. Energy Policy 2009, 37, 5484–5493. [Google Scholar] [CrossRef]
- Daim, T.; Yates, D.; Peng, Y.; Jimenez, B. Technology assessment for clean energy technologies: The case of the Pacific North-west. Technol. Soc. 2009, 31, 232–243. [Google Scholar] [CrossRef]
- Theodorou, S.; Florides, G.; Tassou, S. The use of multiple criteria decision making methodologies for the promotion of RES through funding schemes in Cyprus, a review. Energy Policy 2010, 38, 7783–7792. [Google Scholar] [CrossRef]
- Rojas-Zerpa, J.C.; Yusta, J.M. Application of multicriteria decision methods for electric supply planning in rural and remote areas. Renew. Sustain. Energy Rev. 2015, 52, 557–571. [Google Scholar] [CrossRef]
- Streimikiene, D.; Šliogerienė, J.; Turskis, Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy 2016, 85, 148–156. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An integrated grey based multi-criteria decision-making approach for the evaluation of renewable energy sources. Energy 2016, 115, 1246–1258. [Google Scholar] [CrossRef]
- Jung, N.; Moula, M.E.; Fang, T.; Hamdy, M.; Lahdelma, R. Social acceptance of renewable energy technologies for buildings in the Helsinki Metropolitan Area of Finland. Renew. Energy 2016, 99, 813–824. [Google Scholar] [CrossRef]
- Strantzali, E.; Aravossis, K.; Livanos, G.A. Evaluation of future sustainable electricity generation alternatives: The case of a Greek island. Renew. Sustain. Energy Rev. 2017, 76, 775–787. [Google Scholar] [CrossRef]
- Kausika, B.B.; Dolla, O.; van Sark, W. Assessment of policy based residential solar PV potential using GIS-based multicriteria decision analysis: A case study of Apeldoorn, The Netherlands. Energy Procedia 2017, 134, 110–120. [Google Scholar] [CrossRef]
- Haddad, B.; Liazid, A.; Ferreira, P. A multi-criteria approach to rank renewables for the Algerian electricity system. Renew. Energy 2017, 107, 462–472. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y.; Chen, K.; Xu, C.; Li, L. Social sustainability assessment of small hydropower with hesitant PROMETHEE method. Sustain. Cities Soc. 2017, 35, 522–537. [Google Scholar] [CrossRef]
- Aboushal, E. Applying GIS Technology for optimum selection of Photovoltaic Panels “Spatially at Defined Urban Area in Alexandria, Egypt”. Alex. Eng. J. 2018, 57, 4167–4176. [Google Scholar] [CrossRef]
- Rathore, N.; Singh, M. Selection of Optimal Renewable Energy Resources in Uncertain Environment Using ARAS-Z Methodology. In Proceedings of the 2019 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019; pp. 373–377. [Google Scholar]
- Pratibha, R.; Arunodaya, R.M.; Abbas, M.; Fausto, C.; Melfi, A.; Afaf, A. A novel approach to extended fuzzy TOPSIS based on new divergence measures for renewable energy sources selection. J. Clean. Prod. 2020, 257, 120352. [Google Scholar]
- Liu, J.; Lv, J.; Dinçer, H.; Yüksel, S.; Karakuş, H. Selection of Renewable Energy Alternatives for Green Blockchain Investments: A Hybrid IT2-based Fuzzy Modelling. Arch. Comput. Methods Eng. 2021, 1–15. [Google Scholar] [CrossRef]
- STEG. 2015. Available online: www.steg.com.tn/fr/institutionnel/publication/rapport_act2015/Rapport_Annuel_steg_2015_fr.pdf (accessed on 20 April 2021).
- Norman, D.; Olaf, H. An Experimental Application of the Delphi Method to the Use of Experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).