Multivariable State-Feedback Controller Design for PV Inverter Connected to a Weak Grid
Abstract
:1. Introduction
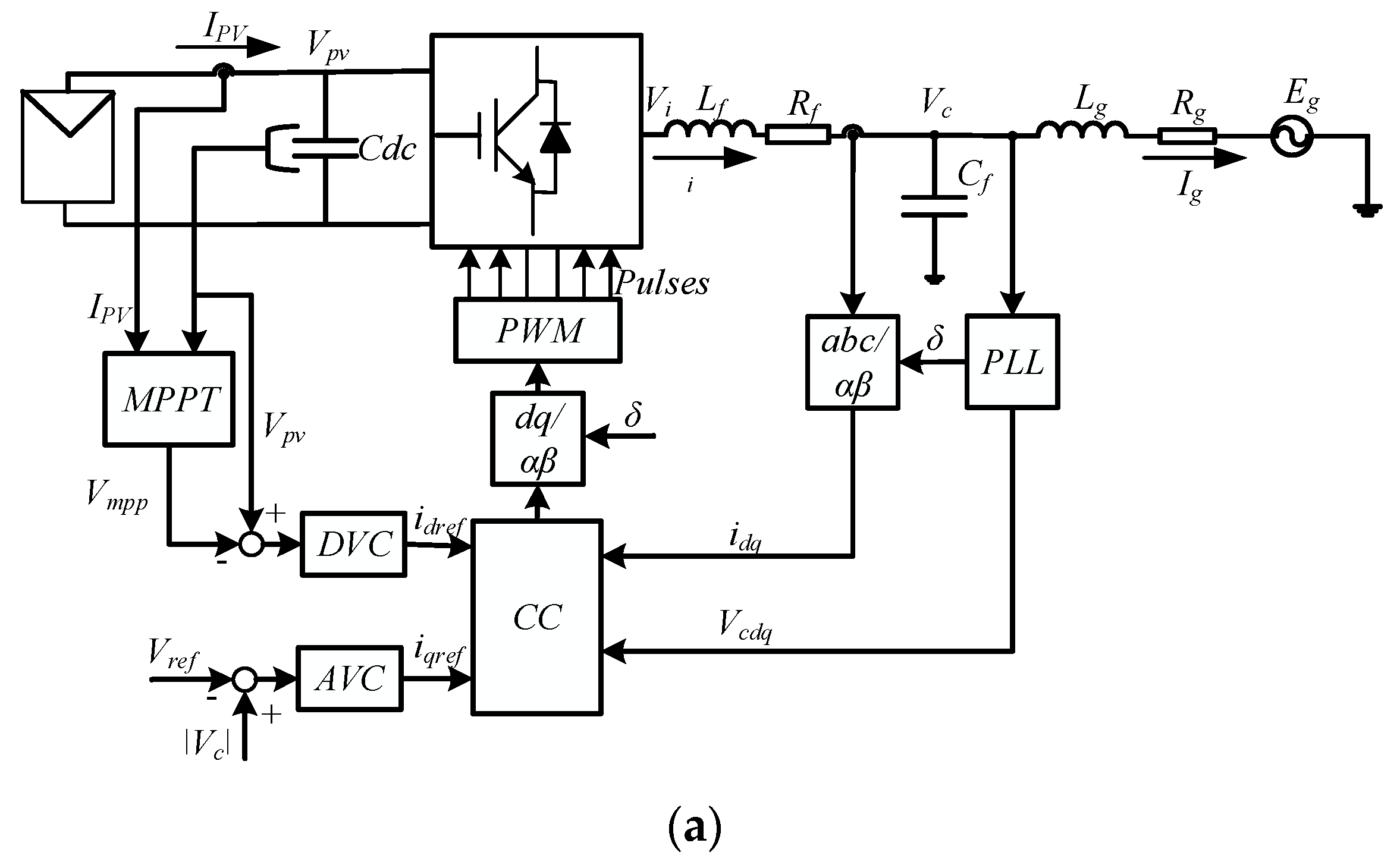
2. Structure of the Single-Stage Grid-Connected PV Inverter
3. Grid-Connected PV Inverter Modelling
3.1. Phase-Locked Loop (PLL)
3.2. DC-Link Dynamics
3.3. Filter Inductor and Grid Inductor Dynamics
3.4. PCC Voltage Dynamics
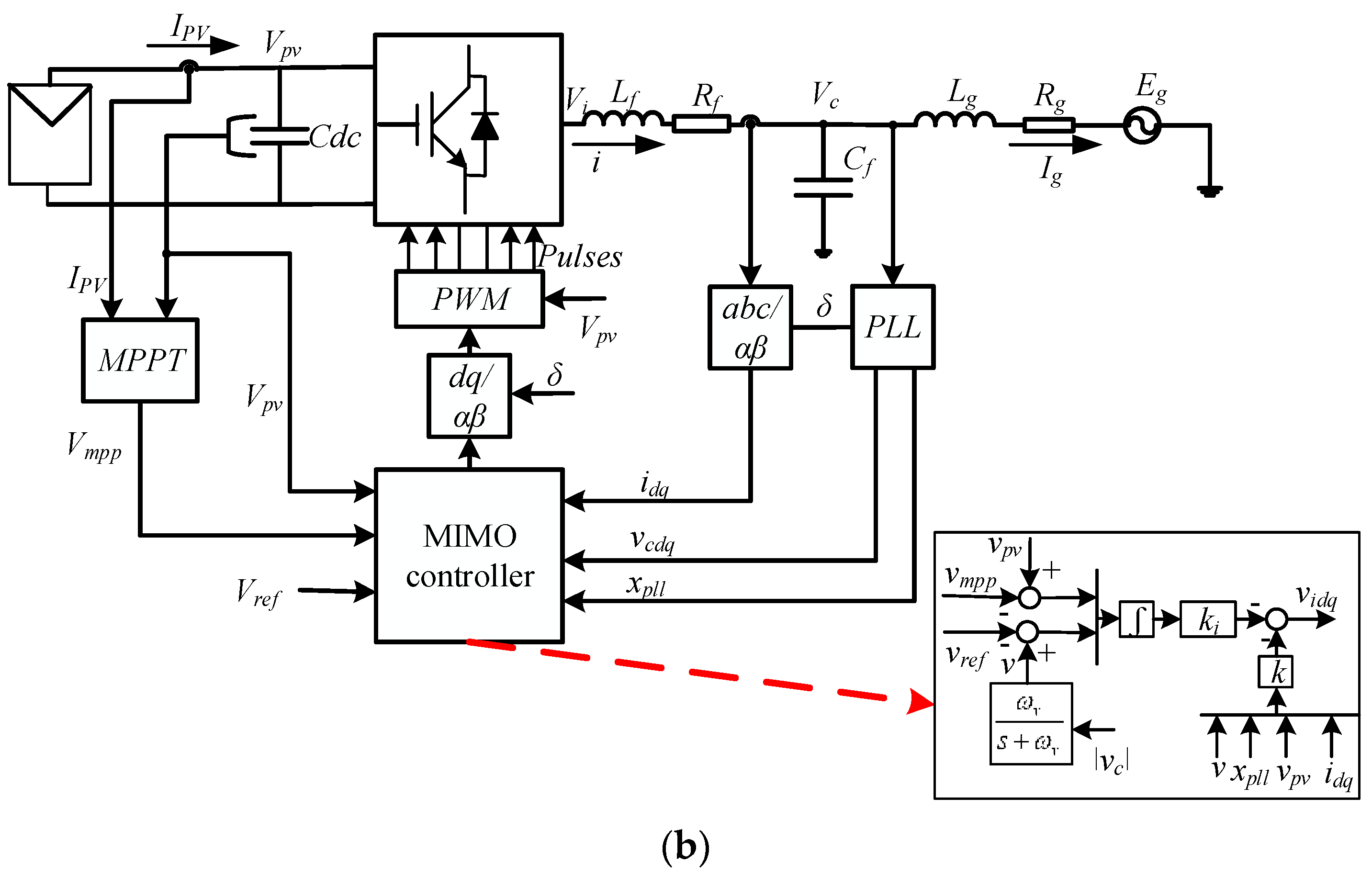
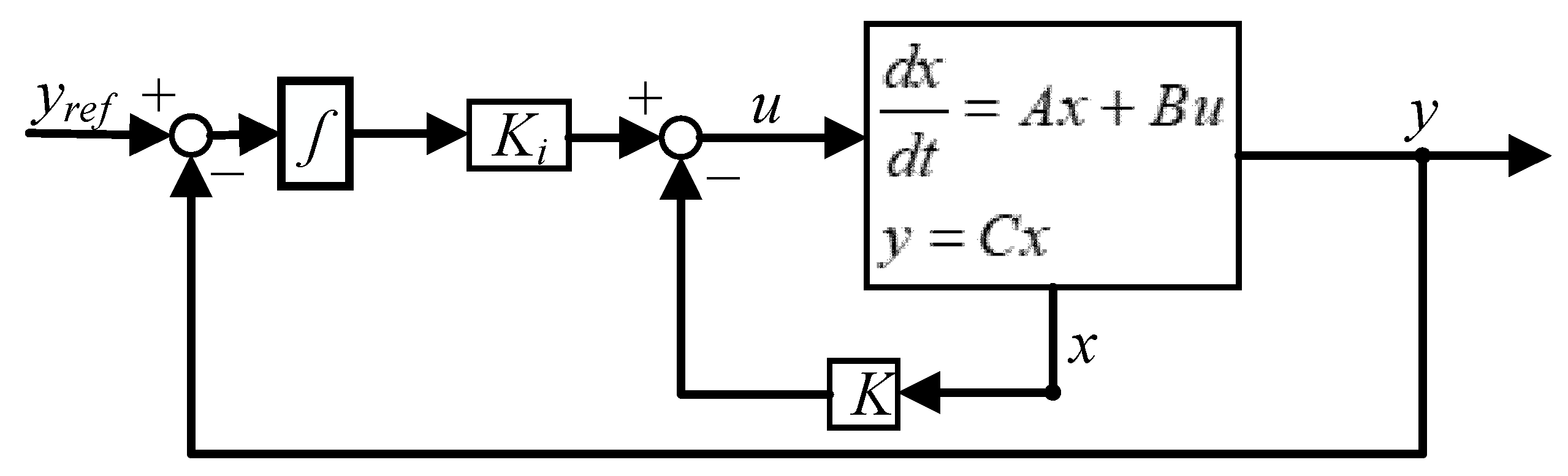
4. Proposed MIMO Controller Design
5. Comparative Stability Analysis and Simulation Results
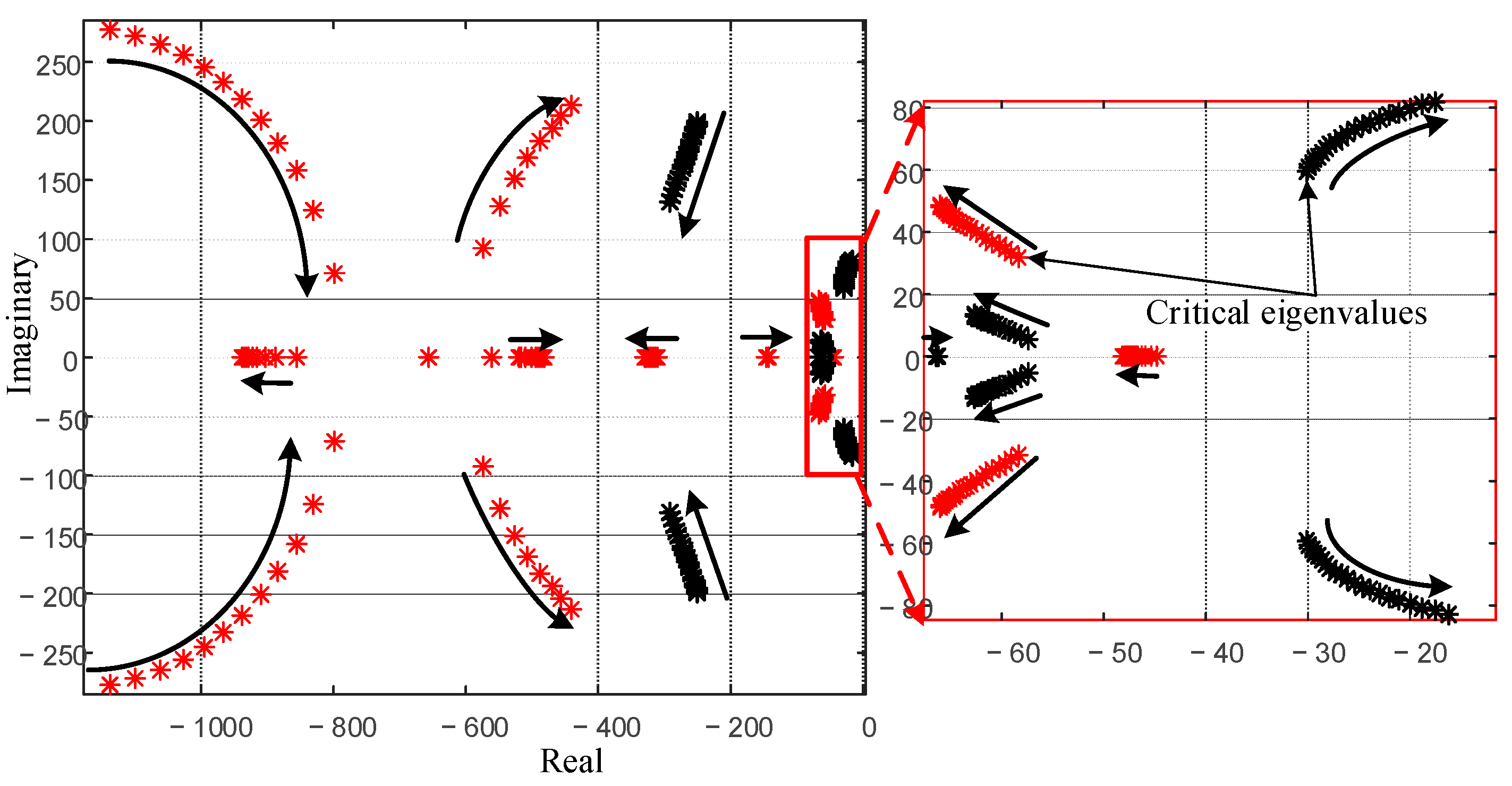
5.1. Stability Analysis
5.1.1. Impact of the Power Level
5.1.2. Impact of the Grid Inductance
5.1.3. Impact of PLL
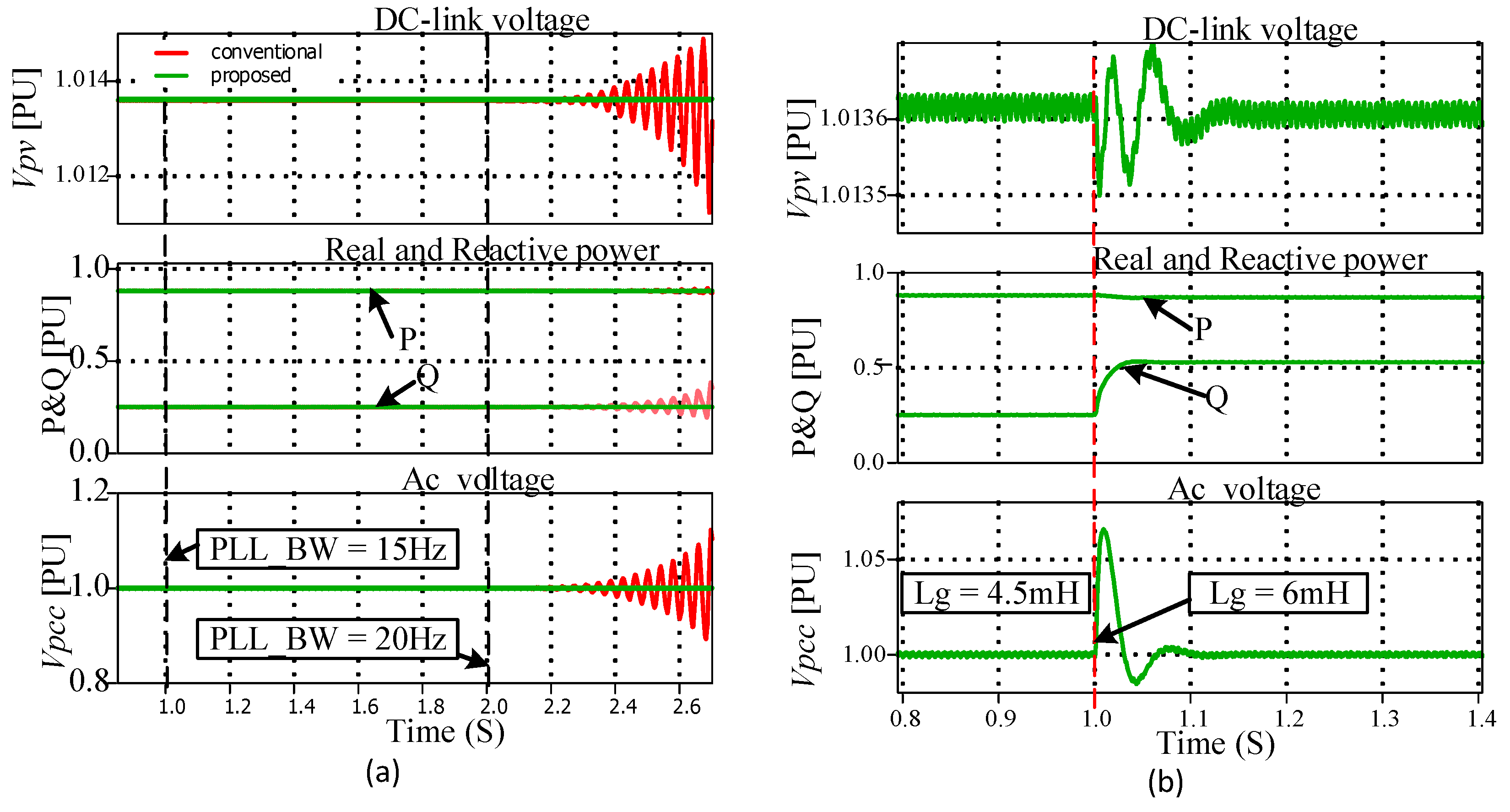
5.2. Simulations and Experimental Results of the Case Study
5.2.1. Simulations Results
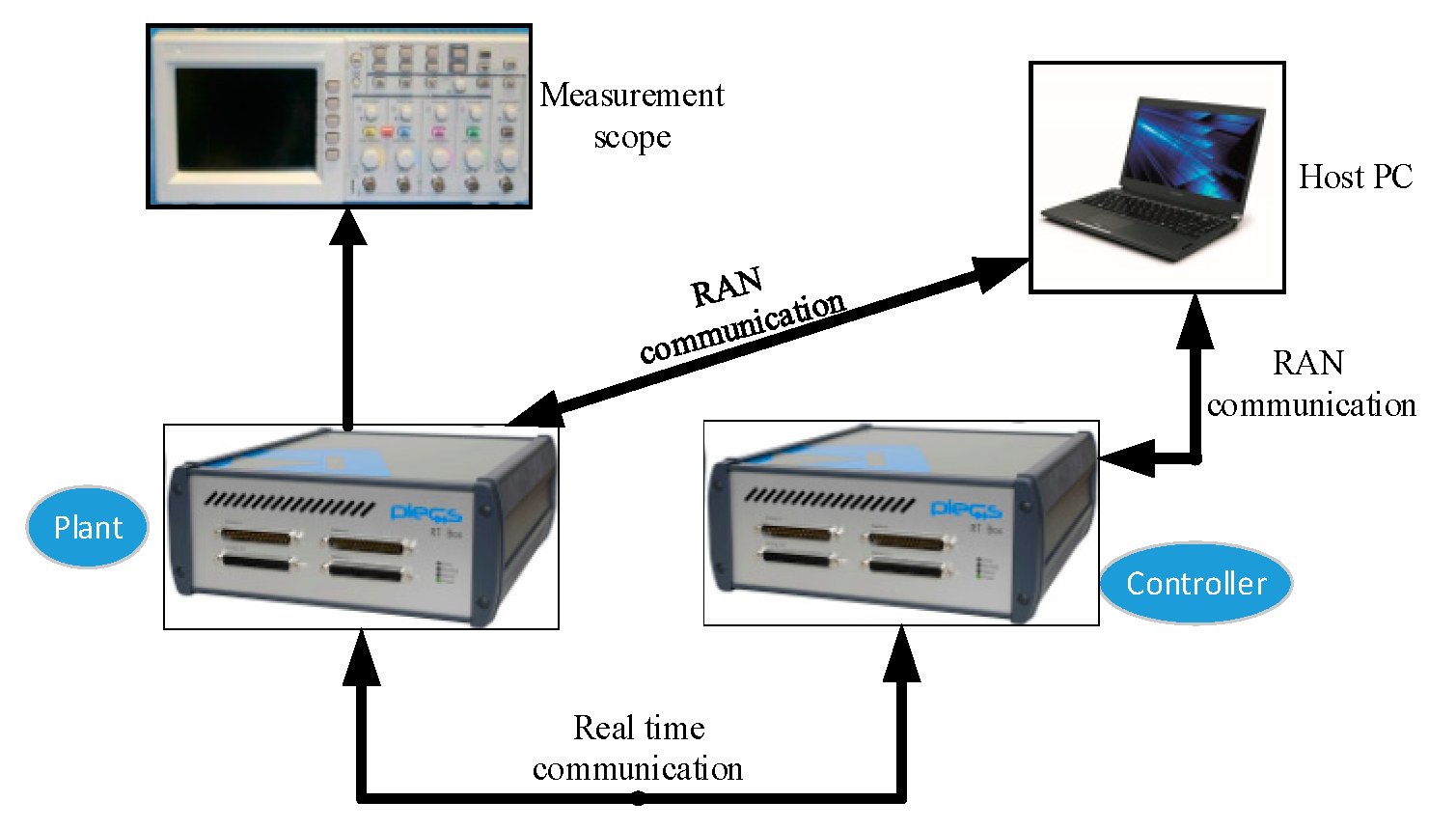
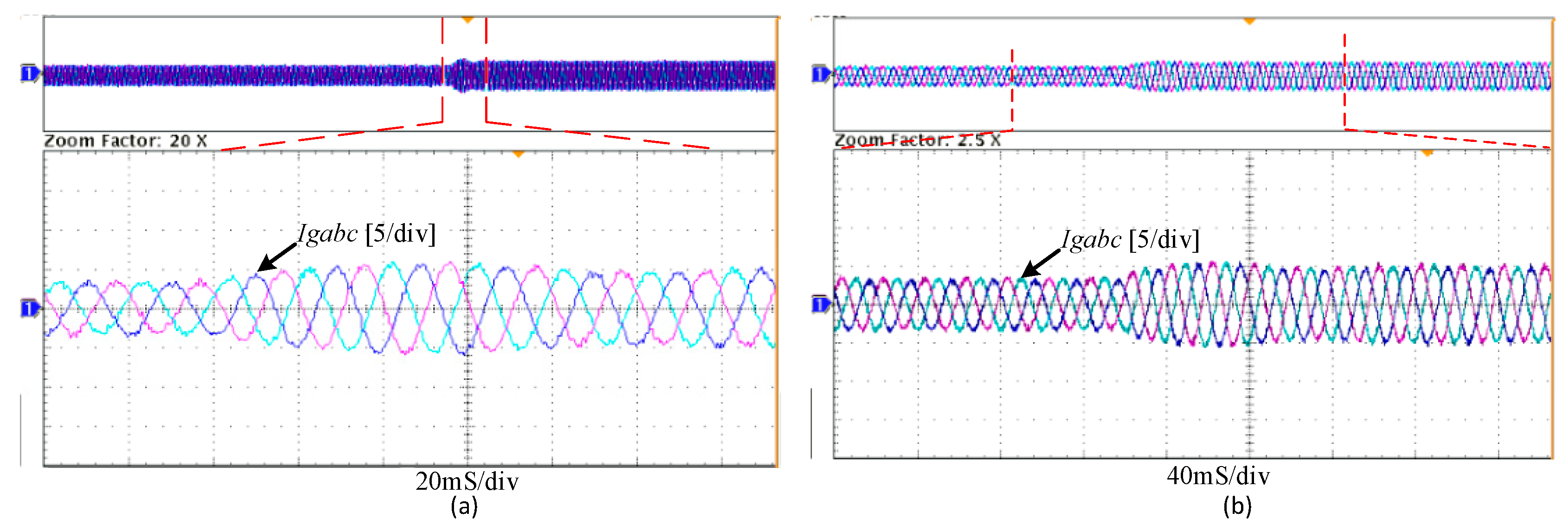
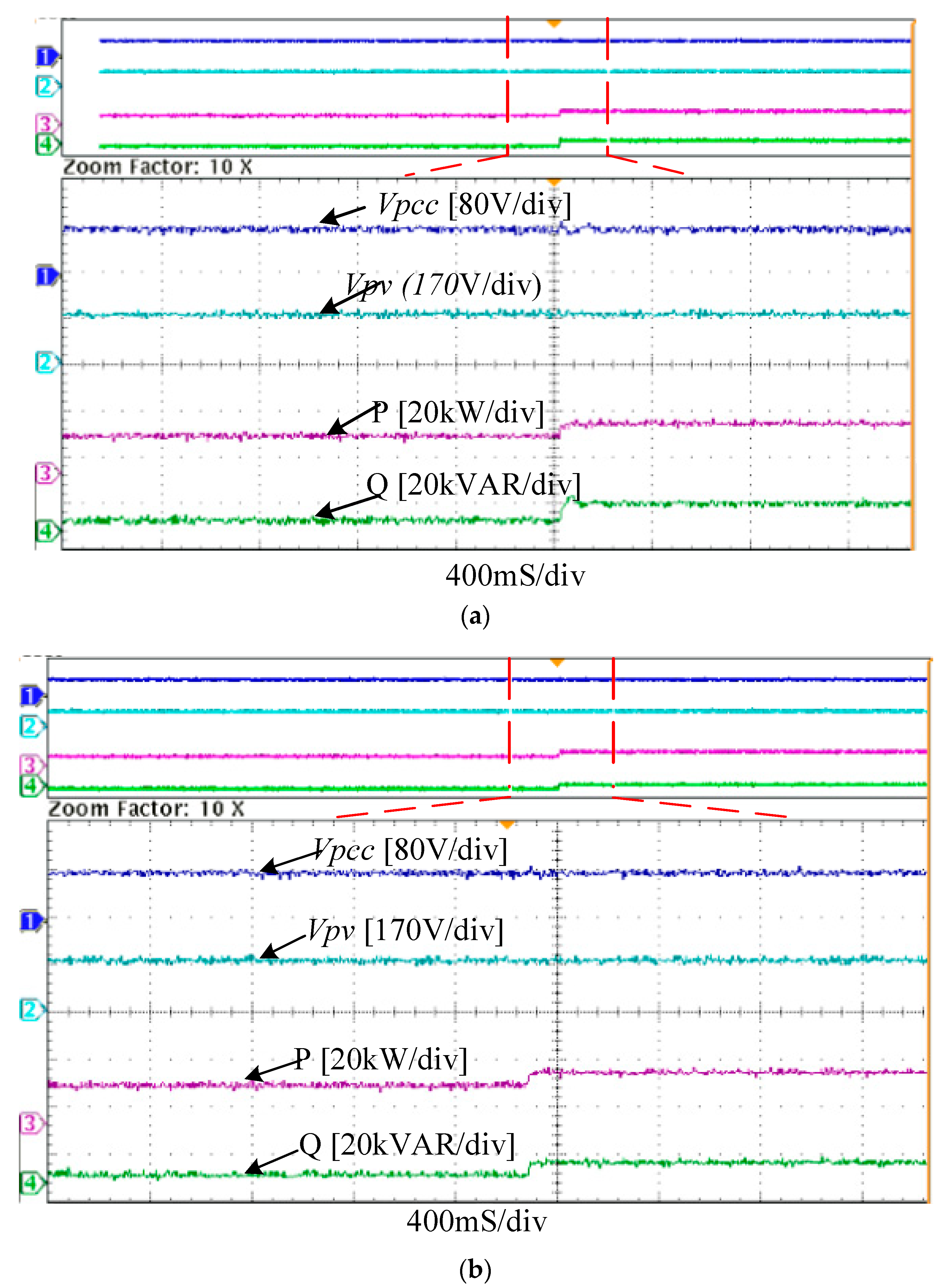
5.2.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Jia, Q.; Yan, G.; Cai, Y.; Li, Y.; Zhang, J. Small-signal stability analysis of photovoltaic generation connected to weak AC grid. J. Mod. Power Syst. Clean Energy 2019, 7, 254–267. [Google Scholar] [CrossRef] [Green Version]
- IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities. In IEEE Standards 1204-1997; IEEE: Piscataway, NJ, USA, 1997; pp. 1–216.
- Yazdani, A. Voltage-Sourced Converters in Power Systems. Modeling, Control, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P. Modeling of VSC Connected to Weak Grid for Stability Analysis of DC-Link Voltage Control. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1193–1204. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P.; Wang, D. DC-Bus Voltage Control Stability Affected by AC-Bus Voltage Control in VSCs Connected to Weak AC Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 445–458. [Google Scholar] [CrossRef]
- Wang, D.; Liang, L.; Shi, L.; Hu, J.; Hou, Y. Analysis of Modal Resonance Between PLL and DC-Link Voltage Control in Weak-Grid Tied VSCs. IEEE Trans. Power Syst. 2018, 34, 1127–1138. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Gole, A.M. VSC transmission limitations imposed by AC system strength and AC impedance characteristics. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; pp. 1–6. [Google Scholar]
- Rezaee, S.; Radwan, A.; Moallem, M.; Wang, J. Voltage Source Converters Connected to Very Weak Grids: Accurate Dynamic Modeling, Small-Signal Analysis, and Stability Improvement. IEEE Access 2020, 8, 201120–201133. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling of Grid-Connected VSCs for Power System Small-Signal Stability Analysis in DC-Link Voltage Control Timescale. IEEE Trans. Power Syst. 2017, 32, 3981–3991. [Google Scholar] [CrossRef]
- Kalcon, G.O.; Adam, G.P.; Anaya-Lara, O.; Lo, S.; Uhlen, K. Small-Signal Stability Analysis of Multi-Terminal VSC-Based DC Transmission Systems. IEEE Trans. Power Syst. 2012, 27, 1818–1830. [Google Scholar] [CrossRef]
- Hu, J.; Huang, Y.; Wang, D.; Yuan, H.; Yuan, X. Modeling of Grid-Connected DFIG-Based Wind Turbines for DC-Link Voltage Stability Analysis. IEEE Trans. Sustain. Energy 2015, 6, 1325–1336. [Google Scholar] [CrossRef]
- Samanes, J.; Gubia, E.; Lopez, J. MIMO Based Decoupling Strategy for Grid Connected Power Converters Controlled in the Synchronous Reference Frame. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018; pp. 1–8. [Google Scholar]
- Li, Y.; Fan, L.; Miao, Z. Stability Control for Wind in Weak Grids. IEEE Trans. Sustain. Energy 2019, 10, 2094–2103. [Google Scholar] [CrossRef]
- Ashtiani, N.A.; Azizi, S.M.; Khajehoddin, S.A. Robust Control Design for High-Power Density PV Converters in Weak Grids. IEEE Trans. Control. Syst. Technol. 2018, 27, 2361–2373. [Google Scholar] [CrossRef]
- Ashtiani, N.A.; Khajehoddin, S.A.; Karimi-Ghartemani, M. Optimal Design of Nested Current and Voltage Loops in Grid-Connected Inverters. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 2397–2402. [Google Scholar]
- Karimi, H.; Karimi-Ghartemani, M.; Sheshyekani, K. Robust Control of Three-Phase Voltage Source Converters Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2019, 34, 11278–11289. [Google Scholar] [CrossRef]
- Davari, M.; Mohamed, Y.A.I. Robust Vector Control of a Very Weak-Grid-Connected Voltage-Source Converter Considering the Phase-Locked Loop Dynamics. IEEE Trans. Power Electron. 2017, 32, 977–994. [Google Scholar] [CrossRef]
- Se-Kyo, C. A phase tracking system for three phase utility interface inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef] [Green Version]
- Ottersten, R. On Control of Back-to-Back Converters and Sensorless Induction Machine Drives. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2003. [Google Scholar]
- Lal, V.N.; Singh, S.N. Control and Performance Analysis of a Single-Stage Utility-Scale Grid-Connected PV System. IEEE Syst. J. 2015, 11, 1601–1611. [Google Scholar] [CrossRef]
- Yazdani, A.; Fazio, A.R.D.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J.A. Modeling Guidelines and a Benchmark for Power System Simulation Studies of Three-Phase Single-Stage Photovoltaic Systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Xiao, W.; Zeineldin, H.H. A Simple Approach to Modeling and Simulation of Photovoltaic Modules. IEEE Trans. Sustain. Energy 2011, 3, 185–186. [Google Scholar] [CrossRef]
- Bacha, S.; Munteanu, I.; Bratcu, A. Power Electronic Converters Modeling and Control: With Case Studies; Springer: London, UK, 2013. [Google Scholar]
- Åström, K.J.; Murray, R. Feedback Systems: An Introduction for Scientists and Engineers. In Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Levine, W. The Control Handbook: Control System Advanced Methods; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Brissette, A.; Karimi, H.; Karimi-Ghartemani, M.; Sheshyekani, K. A Robust and Structurally Simple Controller for Inverter Applications. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 445–450. [Google Scholar]
- Hasanzadeh, A.; Edrington, C.S.; Maghsoudlou, B.; Mokhtari, H. Optimal LQR-based multi-loop linear control strategy for UPS inverter applications using resonant controller. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 3080–3085. [Google Scholar]
- Pradhan, J.K.; Ghosh, A.; Bhende, C.N. Small-signal modeling and multivariable PI control design of VSC-HVDC transmission link. Electr. Power Syst. Res. 2017, 144, 115–126. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal Vpv (V) | 850 | Switching frequency (kHz) | 5 |
| Lf, Lg (mH) | 0.75, 4.5 | Grid Line voltage Eg (V) | 380 |
| Rf, Rg(Ω) | 0.05, 0.3 | Grid frequency fg (Hz) | 50 |
| Cf, Cdc,(μF) | 100, 8500 | PCC Line voltage vcref (V) | 400 |
| Rated power (kVA) | 100 | Solar insolation G (W/m2) | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoine, M.; Li, H.; Zheng, X.; Yu, Y. Multivariable State-Feedback Controller Design for PV Inverter Connected to a Weak Grid. Energies 2021, 14, 4441. https://doi.org/10.3390/en14154441
Antoine M, Li H, Zheng X, Yu Y. Multivariable State-Feedback Controller Design for PV Inverter Connected to a Weak Grid. Energies. 2021; 14(15):4441. https://doi.org/10.3390/en14154441
Chicago/Turabian StyleAntoine, MUSENGIMANA, Haoyu Li, Xuemei Zheng, and Yanxue Yu. 2021. "Multivariable State-Feedback Controller Design for PV Inverter Connected to a Weak Grid" Energies 14, no. 15: 4441. https://doi.org/10.3390/en14154441
APA StyleAntoine, M., Li, H., Zheng, X., & Yu, Y. (2021). Multivariable State-Feedback Controller Design for PV Inverter Connected to a Weak Grid. Energies, 14(15), 4441. https://doi.org/10.3390/en14154441






