Improvement of Mathematical Model for Sedimentation Process
Abstract
1. Introduction
2. Materials and Methods
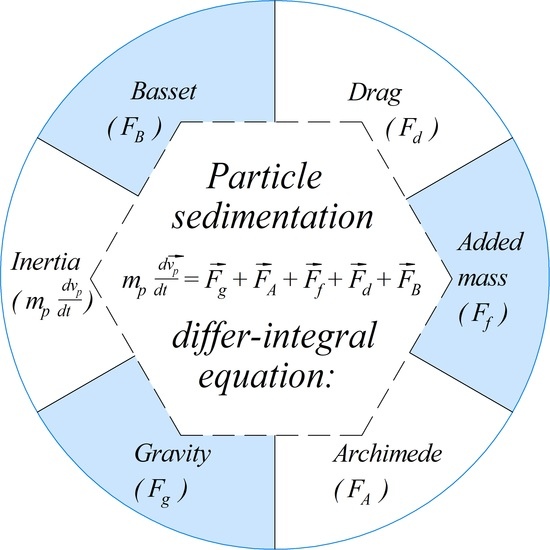
2.1. The Particle Motion Equation Considering the Basset Force
2.2. The Fractional-Order Differential Equation of Particles Sedimentation
3. Results
3.1. The General Solution of the Fractional-Order Differential Equation of Particles Sedimentation
3.2. The Particular Case Study
3.3. Analysis of Leading Orders of the General Solution
- Multiplier before , when the use of identity Equation (30) allows obtaining the leading component Equation (31). This component is responsible for the sedimentation velocity without considering the Basset force.
- Multiplier before . It allows us to obtain the velocity variation (34) proportional to the dimensionless parameter ε. This component allows us to reduce the general Equation (27) to the most simplified variation form (33) with respect to dimensionless parameters ε and τ.
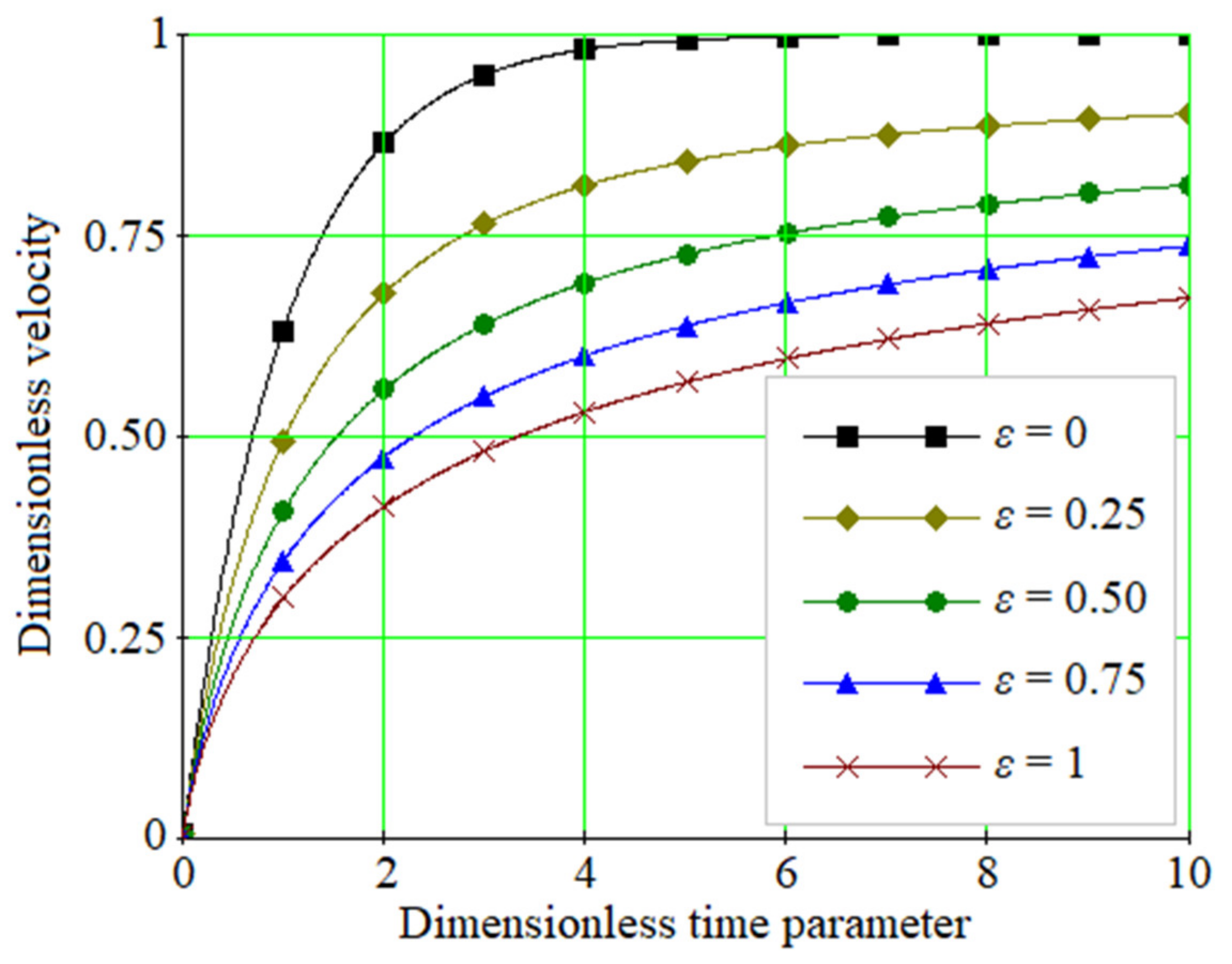
3.4. Comparison with the Numerical Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bombardelli, F.A.; González, A.E.; Niño, Y.I. Computation of the particle Basset force with a fractional-derivative approach. J. Hydraul. Eng. 2008, 134, 1513. [Google Scholar] [CrossRef]
- Parmar, M.; Annamalai, S.; Balachandar, S.; Prosperetti, A. Differential formulation of the viscous history force on a particle for efficient and accurate computation. J. Fluid Mech. 2018, 844, 970–993. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2009, 63, 010801. [Google Scholar] [CrossRef]
- Leal, L.G. Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 1980, 12, 435–476. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Loussaief, H.; Pasol, L.; Feuillebois, F. Motion of a spherical particle in a viscous fluid along a slip wall. Q. J. Mech. Appl. Math. 2015, 68, 115–144. [Google Scholar] [CrossRef]
- Coimbra, C.; Kobayashi, M. On the viscous motion of a small particle in a rotating cylinder. J. Fluid Mech. 2002, 469, 257–286. [Google Scholar] [CrossRef]
- Oppenheimer, N.; Navardi, S.; Stone, H.A. Motion of a hot particle in viscous fluids. Phys. Rev. Fluids 2016, 1, 014001. [Google Scholar] [CrossRef]
- Moreno-Casas, P.A.; Bombardelli, F.A. Computation of the Basset force: Recent advances and environmental flow applications. Environ. Fluid Mech. 2016, 16, 193–208. [Google Scholar] [CrossRef]
- Van Hinsberg, M.A.T.; Ten Thije Boonkkamp, J.H.M.; Clercx, H.J.H. An efficient, second order method for the approximation of the Basset history force. J. Comput. Phys. 2011, 230, 1465–1478. [Google Scholar] [CrossRef]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Agila, A.; Baleanu, D.; Eid, R.; Irfanoglu, B. A freely damped oscillating fractional dynamic system modeled by fractional Euler–Lagrange equations. J. Vib. Control 2018, 24, 1228–1238. [Google Scholar] [CrossRef]
- He, X.; Liu, Q.; Huang, X.; Chen, Y. Dynamic response analysis of the fractional-order system of MEMS viscometer. CMES-Comput. Model. Eng. Sci. 2015, 108, 159–169. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Sandev, T. Effects of a fractional friction with power-law memory kernel on string vibrations. Comput. Math. Appl. 2011, 62, 1554–1561. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. New approach for the analysis of damped vibrations of fractional oscillators. Shock Vib. 2009, 16, 387676. [Google Scholar] [CrossRef]
- Hu, S.; Nadim, A. Three models for rectilinear particle motion with the basset history force. Electron. J. Differ. Equ. 2015, 2015, 1–19. [Google Scholar]
- Pavlenko, I.; Liaposhchenko, O.; Pitel, J.; Sklabinskyi, V. Parameter identification of the Basset force acting on particles in fluid flow induced by the oscillating wall. J. Appl. Math. Comput. Mech. 2019, 18, 53–63. [Google Scholar] [CrossRef]
- Ahmad, B.; Alghanmi, M.; Alsaedi, A. Existence results for a nonlinear coupled system involving both Caputo and Riemann-Liouville generalized fractional derivatives and coupled integral boundary conditions. Rocky Mt. J. Math. 2021, 50, 1901–1922. [Google Scholar] [CrossRef]
- Brzeziński, D.W. Fractional order derivative and integral computation with a small number of discrete input values using Grünwald-Letnikov formula. Int. J. Comput. Methods 2020, 17, 1940006. [Google Scholar] [CrossRef]
- Qi, F.; Guo, B.-N. From inequalities involving exponential functions and sums to logarithmically complete monotonicity of ratios of gamma functions. J. Math. Anal. Appl. 2021, 493, 124478. [Google Scholar] [CrossRef]
- Azennar, R.; Mentagui, D. On some properties of the conformable fractional derivative. Moroc. J. Pure Appl. Anal. 2020, 6, 210–217. [Google Scholar] [CrossRef]
- Liu, L.; Xue, D.; Zhang, S. Closed-loop time response analysis of irrational fractional-order systems with numerical Laplace transform technique. Appl. Math. Comput. 2019, 350, 133–152. [Google Scholar] [CrossRef]
- Yüce, A.; Tan, N. Inverse Laplace transforms of the fractional order transfer functions. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 775–779. [Google Scholar] [CrossRef]
- Du, F.; Jia, B. Finite time stability of fractional delay difference systems: A discrete delayed Mittag-Leffler matrix function approach. Chaos Solitons Fractals 2020, 141, 110430. [Google Scholar] [CrossRef]
- Jumarie, G. Laplace’s transform of fractional order via the Mittag-Leffler function and modified Riemann-Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Abbas, S. Proving the extended binomial theorem using ordinary differential equations. Math. Mag. 2020, 93, 33–35. [Google Scholar] [CrossRef]
- Tokibetov, J.; Abduakhitova, G.; Assadi, A. Representations of the solutions of the first-order elliptic and hyperbolic systems via harmonic and wave functions respectively. Complex Var. Elliptic Equ. 2020, 65, 1565–1574. [Google Scholar] [CrossRef]
- Lytvynenko, A.; Yukhymenko, M.; Pavlenko, I.; Pitel, J.; Mizakova, J.; Lytvynenko, O.; Ostroha, R.; Bocko, J. Ensuring the reliability of pneumatic classification process for granular material in a rhomb-shaped apparatus. Appl. Sci. 2019, 9, 1604. [Google Scholar] [CrossRef]
- Vasylyev, V.V.; Simak, L.O.; Zelenkov, O.A.; Voronova, O.S.; Rybnikova, G.M. Analysis and Mathematical Modeling of Dynamical Systems Based on Non-Classical Operational Calculus; National Aviation Institute: Kyiv, Ukraine, 2006. [Google Scholar]
- Li, Y.; Sun, N. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput. Math. Appl. 2011, 62, 1046–1054. [Google Scholar] [CrossRef]
- Vasilyev, V.V.; Simak, L.A. Fractional Calculus and Approximating Approaches in Modeling Dynamic Systems; National Academy of Sciences of Ukraine: Kyiv, Ukraine, 2008. [Google Scholar]
- Khan, A.; Jahanzaib, L.S.; Trikha, P. Fractional inverse matrix projective combination synchronization with application in secure communication. In Proceedings of the International Conference on Artificial Intelligence and Applications, Maharaja Surajmal Institute of Technology, New Delhi, India, 6–7 February 2020; Bansal, P., Tushir, M., Balas, V., Srivastava, R., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2021; Volume 1164, pp. 93–101. [Google Scholar] [CrossRef]
- Wan, Y.; French, R.M. Fractional calculus of hydraulic drag in the free falling process. In Conference Proceedings of the Society for Experimental Mechanics Series; Proulx, T., Ed.; Experimental and Applied Mechanics; Springer: New York, NY, USA, 2011; Volume 6, pp. 529–539. [Google Scholar] [CrossRef]
- Visitskii, Y.V.; Petrov, A.G.; Shunderyuk, M.M. The motion of a particle in a viscous fluid under gravity, vibration and Basset’s force. J. Appl. Math. Mech. 2009, 73, 548–557. [Google Scholar] [CrossRef]
- Saadatmandia, A.; Dehghanb, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Sobral, Y.D.; Oliveira, T.F.; Cunha, F.R. On the unsteady forces during the motion of a sedimenting particle. Powder Technol. 2007, 178, 129–141. [Google Scholar] [CrossRef]
- Vakal, V.; Pavlenko, I.; Vakal, S.; Hurets, L.; Ochowiak, M. Mathematical modeling of nutrient release from capsulated fertilizers. Period. Polytech. Chem. Eng. 2020, 64, 562–568. [Google Scholar] [CrossRef]
- Chernysh, Y.Y.; Plyatsuk, L.D.; Yakhnenko, O.M.; Trunova, I.O. Modelling of the vertical migration process of phosphogypsum components in the soil profile. J. Eng. Sci. 2017, 4, G6–G11. [Google Scholar] [CrossRef][Green Version]
- Lytvynenko, A.; Pavlenko, I.; Yukhymenko, M.; Ostroha, R.; Pitel, J. Hydrodynamics of two-phase upflow in a pneumatic classifier with the variable cross-section. In Advances in Design, Simulation and Manufacturing III. DSMIE 2020; Ivanov, V., Pavlenko, I., Liaposhchenko, O., Machado, J., Edl, M., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 216–227. [Google Scholar] [CrossRef]
- Sklabinskyi, V.; Liaposhchenko, O.; Pavlenko, I.; Lytvynenko, O.; Demianenko, M. Modelling of liquid’s distribution and migration in the fibrous filter layer in the process of inertial-filtering separation. In Advances in Design, Simulation and Manufacturing. DSMIE 2018; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2019; pp. 489–497. [Google Scholar] [CrossRef]
- Moiseev, V.; Manoilo, E.; Hrubnik, A.; Vasyliev, M.; Davydov, D. Cleaning and disposal of gas emissions from the production of calcinated soda ash. J. Eng. Sci. 2017, 4, B1–B6. [Google Scholar] [CrossRef][Green Version]
- Plyatsuk, L.D.; Ablieieva, I.Y.; Vaskin, R.A.; Yeskendirov, M.; Hurets, L.L. Mathematical modeling of gas-cleaning equipment with a highly developed phase contact surface. J. Eng. Sci. 2018, 5, F19–F24. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, I.; Ochowiak, M.; Agarwal, P.; Olszewski, R.; Michałek, B.; Krupińska, A. Improvement of Mathematical Model for Sedimentation Process. Energies 2021, 14, 4561. https://doi.org/10.3390/en14154561
Pavlenko I, Ochowiak M, Agarwal P, Olszewski R, Michałek B, Krupińska A. Improvement of Mathematical Model for Sedimentation Process. Energies. 2021; 14(15):4561. https://doi.org/10.3390/en14154561
Chicago/Turabian StylePavlenko, Ivan, Marek Ochowiak, Praveen Agarwal, Radosław Olszewski, Bernard Michałek, and Andżelika Krupińska. 2021. "Improvement of Mathematical Model for Sedimentation Process" Energies 14, no. 15: 4561. https://doi.org/10.3390/en14154561
APA StylePavlenko, I., Ochowiak, M., Agarwal, P., Olszewski, R., Michałek, B., & Krupińska, A. (2021). Improvement of Mathematical Model for Sedimentation Process. Energies, 14(15), 4561. https://doi.org/10.3390/en14154561