Modeling and Simulation of Monolithic Single-Supply Power Operational Amplifiers

Abstract

In this paper a simple PSpice (Personal Simulation Program with Integrated Circuit Emphasis) macro-model was developed, and verified for monolithic power operational amplifiers operated with a single-supply voltage. The proposed macro-model is developed using simplification and build-up techniques for macro-modeling of operational amplifiers and simulates the basic static and dynamic characteristics, including input impedance, small-signal frequency responses at various voltage gains, output power versus supply voltage, slew-rate-limiting, voltage limiting, output offset voltage versus supply voltage ripples, and output resistance. Furthermore, the macro-model also takes into account the ground reference voltage in the amplifier at a single power supply voltage. The model is implemented as a hierarchical structure suitable for the PSpice circuit simulation platform. The sub-circuit is built using standard PSpice components and analog behavioral modeling blocks. The accuracy of the model is verified by extracting the model parameters for single-supply power operational amplifier TDA2005 from ST Microelectronics as example. The effectiveness of the model is validated by comparing the simulation results of the electrical parameters with the corresponding measured values obtained by experimental testing of sample circuits. The comparative analysis shows that the relative error of the modeled large-signal parameters is less than 15%. Moreover, an error of 15% is quite acceptable, considering the technological tolerances of the electrical parameters for this type of analog ICs.

1. Introduction

Despite the growing part of the digital devices in the modern electronic systems, there are still many applications that will always perform by analog circuits. One application of this type is when, for example, a small signal from a microphone or digital-to-analog converter needs to be amplified and to drive an outside load (e.g., actuator, loudspeaker, or wireline). In many cases, the amplifier has to transmit a significant electrical power (e.g., P_L ≥ 1 W) to a certain load with high energy efficiency and without significant distortion. According to the value of the higher cutoff frequency f_h, the power amplifiers are low-frequency (with f_h ≤ 100 kHz) and high-frequency (with f_h > 100 kHz) circuits.

The low-frequency monolithic power operational amplifiers are essential building blocks of the audio power amplifiers and the output drivers in many industrial controllers. To take full advantage of the monolithic powerful amplifiers and to provide the process of implementation of new electronic systems, a detailed analysis and evaluation is needed. In the process of circuit design, it is necessary to perform a preliminary evaluation of the various electronic circuit topologies in terms of static and dynamic modes of operation. For example, the achieving a certain operating frequency range at a certain value of the power gain is examined, as well as the ability to provide the output power on a load while maintaining the stability of the circuit. Moreover, the functionality of the designed electronic circuit must be simulated, the values of the passive components has to be adjusted and the obtained structure has to be experimentally tested to prove in advance the fulfillment of the requirements in the technical specification. Conducting accurate analog circuit simulations is conditioned by the simple and accurate models or macro-models of the passive and active components. The majority of the previously developed macro-models of operational amplifiers (op amps), suitable for the PSpice (Personal Simulation Program with Integrated Circuit Emphasis) circuit simulation program, have been intended for low power applications (ranging up to 100 mA) [1,2,3,4,5,6,7,8,9]. Moreover, the description of all models is adapted to the circuit simulators based on the SPICE (Simulation Program with Integrated Circuit Emphasis) program. In [2,6] a midpoint has been realized in the equivalent circuits, for relating all internal voltages to it, and to provide the proper operation of the macro-model at an asymmetrical power supply voltage. Also, in [7,9] through external resistor dividers, it has been possible to work with a single power supply voltage. However, these additional functional blocks do not provide a full possibility for the implementation of class-B and class-AB of the output stages in the power amplifiers, when only a single- supply voltage is used.

In this paper, based on the simulation models, represented in [1,2,7], a simple electrical macro-model was developed, and verified for monolithic power amplifiers operated with a single-supply voltage. The developed macro-model included the basic static and dynamic effect of the real device and it was implemented as a hierarchical structure, suitable for the PSpice circuit simulation program. The paper is an extension of work [10] originally reported in the 28th International Conference on Mixed Design of Integrated Circuits and Systems—MIXDES 2021.

The paper is organized as follows. Section 2 presents the macro-model description—structure of the commercially available monolithic power amplifiers, block diagram of the proposed macro-model and mathematical equations with the corresponding model parameters. Also, in Section 2 are represented the analytical expressions for determination of the modeling parameters of the proposed model. The verification of the developed macro-model is given in Section 3 and is performed by comparing the simulation results with experimental results at frequency and time domain for sample electronic circuits. For verification of the workability and efficiency of the macro-model, the model parameters are extracted for IC TDA2005 from STMicroelectronics as example. Finally, in Section 4 of the paper, the concluding remarks and guidelines for future work are given.

2. Macro-Model Description

2.1. Macromodel Development

The basic technical requirements to the monolithic power amplifiers are: (1) to provide a certain electrical power to an external load, which in the general case has active and reactive components; (2) introduce minimal non-linear distortions into the wave-form of the amplified input signal; (3) to provide high energy efficiency (in this way, the greater economy is ensured, which is essential at high output power); (4) to have large input and small output resistance (this makes it easier to match the load with the output stage of the amplifier and achieves a high value of the power gain); (5) to have protection stages against short circuit or thermal overload of the output transistors. The implementation by the semiconductor manufacturers of the above requirements determines the efficiency and workability of the power amplifiers in a wide range of variations of the input voltage or power supply voltage.

Several semiconductor manufacturers, such as Maxim^®, Analog Devices^®, Philips^®, Sanyo^®, Samsung^®, SGS Thomson^®, ST Microelectronics^®, and Texas Instruments^® offer commercially available various types of monolithic power amplifiers. Some integrated circuits of the power amplifiers contain only an output stage, but often a preamplifier is included in the chip. Their basic electrical circuit is similar to those with discrete components [11,12,13,14,15]. The passive components that cannot be integrated into the chip (such as, capacitors with high capacitance, coils, and potentiometers) are connected externally to the circuit. 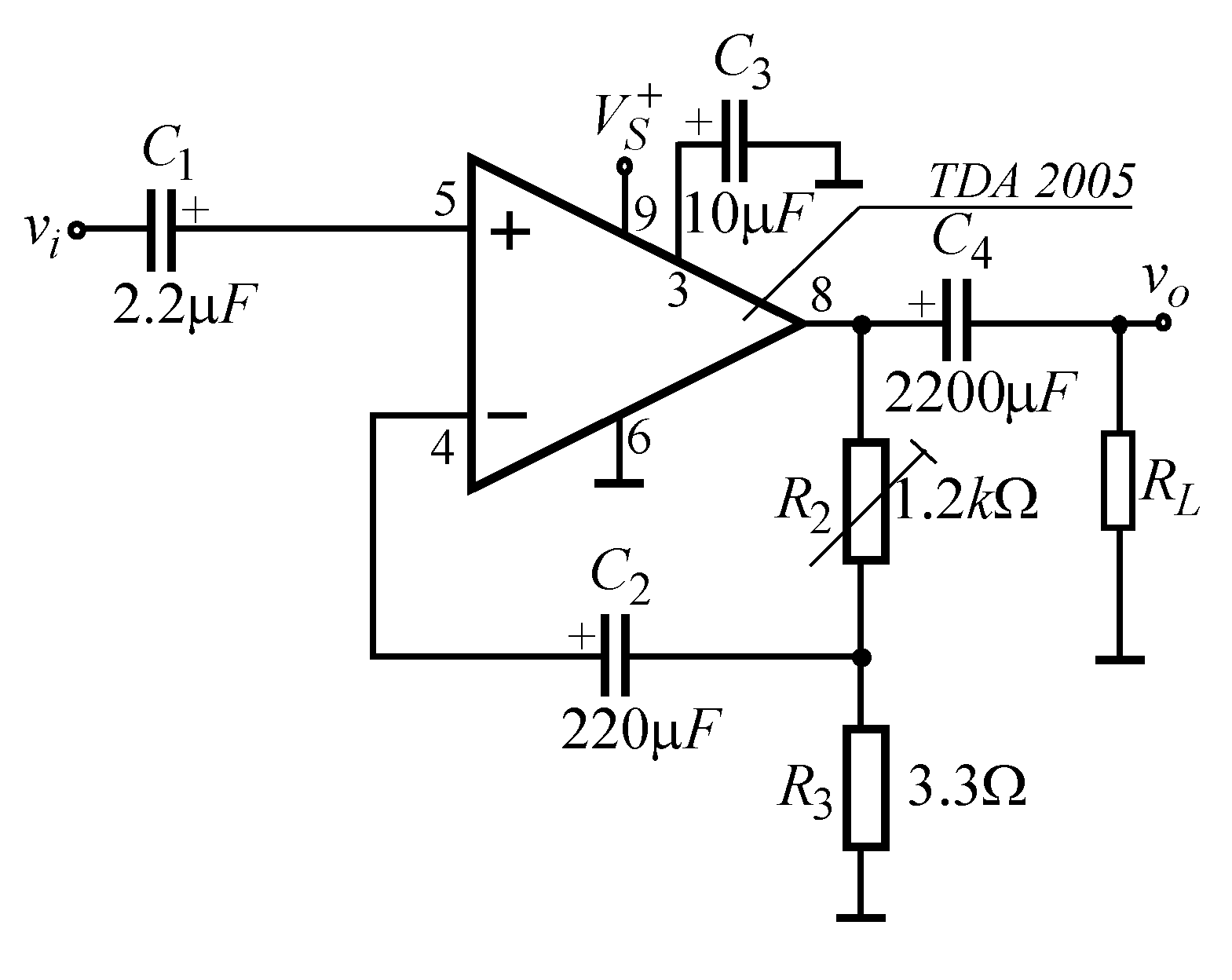One of the basic monolithic integrated power amplifiers is those of the ST Microelectronics from the TDA-series [14,15]. The basic DC and AC parameters and their typical values for the monolithic amplifiers from TDA-series are presented in

Table 1. Basic DC and AC electrical parameters for the monolithic amplifiers from TDA-series.

Name	Symbol	Range	Unit
Input offset voltage	$V_{os}$	from 2 to 10	mV
Input bias current	$I_{iB}$	from 100 to 300	nA
Power Supply Rejection Ratio	PSRR	<2	mV/V
Input differential-mode resistance	$r_{id}$	from 50 to 100	kΩ
Input differential-mode capacitance	$C_{id}$	from 2 to 10	pF
Input common-mode resistance	$r_{iCM}^{+},r_{iCM}^{-}$	from 100 to 200	kΩ
Open-loop voltage gain	$A_{d0}$	from 50 to 100	V/mV
Output voltage swing	$V_{OUT,pp}$	14 1	V
Peak output current	$I_{o\max }$	3.5 2	A
Output power	$P_L$	from 5 to 50 1	W
Energy efficiency	$\mathsf{\eta }$	from 50 to 70	%
Total harmonic distortion	$k_h$	≤1	%
Small-signal bandwidth	$f_1$	from 1 to 10 1	MHz
Slew Rate	$SR$	from 1 to 10 1	V/μs
Supply current	$I_{SS}$	from 50 to 100 3	mA
Open-loop output resistance	$R_o$	<2	Ω

¹ Typical value at $V_s=14.4\mathrm{V}$ and $R_L=4\Omega$. ² $V_{OUT}=0\mathrm{V}$. ³ $I_{OUT}=0\mathrm{A}$.

.

In Figure 1 is a simplified circuit diagram of a TDA2030 power amplifier is given. As can be seen, the electrical circuit is divided into three sections (or stages): input stage, intermediate (or driver) stage and output stage. The input stage is a differential amplifier with a symmetrical input and single-ended output port. It provides the input impedance of the circuit and part of the open-loop voltage gain. The intermediate stage is an active-loaded common emitter amplifier, preceded by a voltage limiting circuit. From the output terminal of the intermediate stage, the signal is applied to the output stage. Its structure is similar to the basic output stage and includes two complementary Darlington transistors. The output stage provides the output voltage swing and output resistance. The transistors $T_1$, and $T_2$ form the composite NPN-transistor according to the Darlington scheme, and the transistor $T_3$, together with the Darlington transistors $T_4$ and $T_5$, form a composite PNP-transistor. In addition to the main amplifier stages, the chip also includes thermal protection and current limiting circuits.

Based on the simplified circuit diagram in Figure 1, a block diagram of the proposed model (Figure 2) is developed. In Figure 2, the block diagram includes basically an input stage, an intermediate (amplifying) stage, and an output stage connected in a cascade structure. Additionally, three blocks are connected to the structure, providing the midpoint of the model, the floating ground, and the supply voltage rejection ratio. According to the complexity of the amplitude-frequency characteristic of a concrete amplifier, the number of frequency-shaping stages can be increased, as well as the structure of the stage modeling the suppression of the pulsations in the supply voltage can be changed.

2.2. PSpice Implementation

To develop PSpice macro-model for monolithic power amplifiers, simplification and build-up techniques for macro-modeling of operational amplifiers was used [1]. Based on the block diagram, shown in Figure 2, the macro-model was implemented as a two-level hierarchical structure. The higher-level block diagram with the modeling parameters, defined without concrete values, is presented in Figure 3. Depending on the choice of a certain type of amplifier in dialog mode, concrete numerical values can be set for the modeling parameters. The equivalent electrical circuit (the lower level of hierarchy) of the macro-model is given in Figure 4. As can be seen, there is a correspondence between the names of the external terminals (or pins), and also in the description of the block diagram (Figure 3) the name of the equivalent circuit in Figure 4 was set, so that it can be loaded and processed during of the simulation process.

In particular, the structure of the equivalent circuit (Figure 4) includes both standard PSpice components and analog behavioral modeling (ABM) blocks. The usage of ABM blocks, such as various controlled sources, provides the implementation of linear and non-linear mathematical functions in the PSpice program. As can be seen, the equivalent electrical circuit is represented as properly connected controlled sources, independently controlled sources, resistors, capacitors, and a small group of ideal diodes. The external interface terminals of the circuit are non-inverting input (input+), inverting input (input–), an output terminal (out), supply voltage ripple rejection terminal (SVRR), positive power supply (+Vs), and analog ground (GND). As can be seen, there is no ground reference in any of the signal-processing blocks. The only exception is the functional block, which simulates the attenuation of the power supply voltage ripples. All internally generated node voltages are referred to as the voltage at node nVgnd, which is the floating ground of the equivalent circuit. The node voltage nVgnd is produced by the VCVS E_H controlled by the midpoint and power supply voltage. The midpoint, called nVref in the model, was generated by two equal resistors (R_r1 and R_r2) connected between the supply rail and the external ground reference.

The input stage consists of $r_{id}$ and $C_{id}$, modeling the input resistance and capacitance between the two input terminals (1 and 7) at a small signal. $r_{iCM}^{+}$ and $r_{iCM}^{-}$ are the input resistances, reflecting the behavior at a common-mode input signal. The input resistance $r_{id}^{\prime }$ is defined as the resistance measured directly between the inverting and non-inverting input of the amplifier:

$$r_{id}^{\prime }=r_{id}\left|\right|(r_{iCM}^{+}+r_{iCM}^{-})\approx r_{id}$$

(1)

at $r_{id}<<(r_{iCM}^{+}+r_{iCM}^{-})$.

In the case of an amplifier circuit with asymmetric input, a circuit of a non-inverting amplifier with a grounded inverting input and an active non-inverting input are possible, and vice versa—a circuit of an inverting amplifier with a grounded non-inverting input.

The input resistance in these cases is represented by

$$\{\begin{array}{l}{r}_{id}^{+}=r_{id}\left|\right|r_{iCM}^{+}\\ r_{id}^{-}=r_{id}\left|\right|r_{iCM}^{-}\end{array}$$

(2)

The input common-mode resistance is represented, according to

$$r_{iCM}^{}=r_{iCM}^{+}\left|\right|r_{iCM}^{-}$$

(3)

For the majority of the amplifiers $r_{iCM}^{+}\approx r_{iCM}^{-}=2r_{iCM}$.

The input bias current was modeled by two ideal current sources ($I_{iB}^{+}$ and $I_{iB}^{-}$), connected between the two input terminals (1 and 7) and midpoint nVref. The input offset voltage and offset drift as a result of the power supply ripples is represented with a voltage-controlled voltage source (VCVS) $E_{os}$, connected between nodes 2 and 7. The offset voltage modelling power supply ripples (PSRR—power-supply rejection ratio), which are accurately referred to the VCVS $E_{os}$, come from two separate frequency shaping stages in the model. The first additionally defined stage consisted of a capacitor $C_{0SVR}$ and a grounded resistor $R_{0SVR}$. The $C_{0SVR}$ is connected between the power supply voltage (node Vsplus) and the input of the second shaping stage. The voltage drop over the $R_{0SVR}$ presents the voltage at a node 6 that depends on the ripples of the supply voltage ($V_S^{}\pm \Delta V_S^{}$). The transfer function of the stage is expressed by

$$T_{SVR1}(p)=\frac{V\left(6,0\right)}{V_S^{}\pm \Delta V_S^{}}=\frac{s{R}_{0SVR}{C}_{0SVR}}{1+s{R}_{0SVR}{C}_{0SVR}}$$

(4)

The second stage consisted of a voltage-controlled current source (VCCS) $G_{SVR}$ controlled by the power supply voltage, and the RLC-stage. The current source was chosen to be linear one-port generator, following the equation

$$I_{G_{SVR}}=k_{1,SVR}V(6,0)$$

(5)

The current $I_{G_{SVR}}$ will flow through the elements $R_{1SVR}$, $L_{1SVR}$, and $C_{SVR}=C_{1SVR}+C_3$ (where $C_3$ is an external grounded capacitor, connected to node SVR), towards the internal ground. In such a way, the voltage V(SVR,0) will depend on the amplitude and the frequency of the ripples of the supply line, and the transfer function of the stage can be expressed by

$$\begin{gathered} T_{G_{SVR2}}(s)=\frac{V\left(SVR,0\right)}{V(6,0)}=\frac{k_{1,GSVR}{R}_{1SVR}\left(s^2{L}_{1SVR}{C}_{SVR}+s\frac{L_{1SVR}}{R_{1SVR}}+1\right)}{s{R}_{1SVR}{C}_{SVR}+1}= \\ =k\frac{T_1^2{s}^2+2\mathsf{\xi }{T}_{1}s+1}{T_{2}s+1} \end{gathered}$$

(6)

where $k$ is DC proportionality constant, $T_1$ is the time-constant of the polynomic in the numerator, $\mathsf{\xi }$ is the damping factor, and $T_2$ is the time-constant of the polynomic in the denominator.

From the comparison of the left and right sides of the above equation, the following formulas were obtained for the main parameters: $k=k_{1,GSVR}{R}_{1SVR}$, $T_1=\sqrt{L_{1SVR}{C}_{SVR}}$—time constant determining the minimum in the frequency response, $\mathsf{\xi }={(2R_{1SVR})}^{-1}\sqrt{L_{1SVR}/C_{SVR}}$ and $T_2=R_{1SVR}{C}_{SVR}$, where $L_{1SVR}$ is equivalent series inductance, $C_{SVR}$ is equivalent series capacitance, and $R_{1SVR}$ is equivalent parallel resistance. The proposed stage from Figure 4 provides a serial resonance, determined by the inductance $L_{1SVR}$, and the capacitance $C_{SVR}$, with a minimum value of the resonance resistance. The voltage generated at node SVRR is used for the equation of VCVS $E_{os}$ as follows

$$V_{Eos}=k_{0,Eos}+k_{1,Eos}V\left(SVRR,0\right)$$

(7)

The component $k_{0,Eos}$ in Equation (6) determines the input offset voltage constant ($V_{os}$), the coefficient $k_{1,Eoos}$ presents the change in $V_{os}$ as a result of changing the supply voltage. Then, $PSRR$ will be determined by the following expression

$$\begin{gathered} PSRR=\frac{GAIN}{GAI{N}_{PSRR}}=\frac{V_{OUT}/V\left(1,7\right)}{V_{OUT}/(V_S^{}\pm \Delta V_S^{})}=\frac{V_S^{}\pm \Delta V_S^{}}{k_{1,Eos}V\left(SVRR,0\right)}= \\ =\frac{(s{R}_{0SVR}{C}_{0SVR}+1)(s{R}_{1SVR}{C}_{SVR}+1)}{s{R}_{0SVR}{C}_{0SVR}{k}_{1,GSVR}{R}_{1SVR}[s^2{L}_{1SVR}{C}_{SVR}+s\frac{L_{1SVR}}{R_{1SVR}}+1]} \end{gathered}$$

(8)

where $GAIN=V_{OUT}/V(1,7)$ is the differential voltage gain of the amplifier and $GAI{N}_{PSR}=V_{OUT}/(V_S^{}\pm \Delta V_S^{})$ is the voltage gain of the ripples in the power supply line.

The intermediate stage of the model consisted of controlled sources and ideal passive components. It simulated the open-loop voltage gain, the frequency resonance, and the output voltage limiting. The value of the open-loop voltage gain of the model is represented by the VCCS $G_1$, and the resistor $R_{p1}$. Therefore, the voltage at a node 3 can be determined by

$$V(3)=I_1{R}_{p1}\tanh (K_1\times V(1,7))$$

(9)

where $K_1$ $[V^{-1}]$ is the multiplication factor of the stage.

The transfer function (9) is represented in graphical form in Figure 5. Approximately linear region of this function is $-0.5K_1^{-1}<V(1,7)<0.5K_1^{-1}$.

The simplification of expression (9) can be performed if the function is decomposed in the Taylor order, i.e.,

$$\tanh x=x-\frac{1}{3}{x}^3+\frac{2}{15}{x}^5-\frac{17}{315}{x}^7\pm \dots$$

(10)

at $\left|x\right|<\mathsf{\pi }/2$.

If $|V(1,7)|<<K_1{}^{-1}$, elements can be taken only up to the third order term in the Taylor series, wherein the formula (9) yields

$$V(3)=I_1{R}_{p1}[K_1\times V(1,7)-{(K_1\times V(1,7))}^3]\approx I_1{R}_{p1}{K}_1\times V(1,7)$$

(11)

If $|V(1,7)|>K_1{}^{-1}$, the $V(3)\approx I_1{R}_{p1}$. The maximum output current $I_1$ charged the capacitor $C_{p1}$, which created a change of the output voltage per unit time of the amplifier. This rate of change of the voltage per unit time defined the maximum dV/dt (voltage change rate) or slew rate (or SR) of the amplifier:

$$SR=I_1/C_{p1}$$

(12)

For the model’s small-signal open-loop DC voltage gain, is obtained

$$A_{d0}=\frac{V(3)}{V(1,7)}=I_1{R}_{p1}{K}_1$$

(13)

To obtain minimal nonlinear distortions in the waveform of the output voltage ($k_h<(1\dots 2)\%$), it is necessary that the input voltage $V(1,7)$ is lower than $\left|0.5K_1^{-1}\right|$. Since the mathematical function $\tanh$ is symmetric with respect to the origin of the coordinate system, and with respect to the characteristics of the differential pair of transistors in the input stage (transistors have to be as close as possible to technological parameters, which is achieved by applying a single technological process of obtaining the electrical circuit), for the developed macro-model it is possible to obtain smaller values of the nonlinear distortions.

The voltage-limiting network consisted of two ideal diodes ($D_1$ and $D_2$) and two voltage sources ($V_1$ and $V_2$), connected in series. This network limited the voltage at node 3 and the other internal voltages of the macro-model up to values below the power supply voltage during an input-overdrive condition:

$$\{\begin{array}{c}{V}_{OUT,\max }==+V_s-V_1+{\phi }_T\ln (I_1/I_S)\\ V_{OUT,\min }=V_2+{\phi }_T\ln (I_1/I_S)\end{array}$$

(14)

where ${\phi }_T$ is the thermal voltage and $I_S$ is the saturation current for the two diodes.

The first (dominant) and the second pole frequency are represented in the model by two frequency shaping stages. The dominant pole was modeled by the VCCS $G_1$, the resistor $R_{p1}$ and the capacitor $C_{p1}$. The second (non-dominant) pole was modeled by the VCCS $G_2$, the resistor $R_{p2}$ and the capacitor $C_{p2}$. The DC voltage gain of the second frequency-shaping block was equal to unity, because the $g_{m2}$ of the VCCS $G_2$ is equal to the reciprocal of the resistance $R_{p2}$, connected from each node of the VCCS to the floating node of the circuit. In a wide frequency range, the open-loop amplitude-frequency response of the model can be represented by

$$|{\dot{A}}_d|=\frac{|\dot{V}(5)|}{|\dot{V}(1,7)|}=\frac{I_1{R}_{p1}{K}_1}{\sqrt{1+{\left(f/f_{p1}\right)}^2}}\times \frac{g_{m2}{R}_{p2}}{\sqrt{1+{\left(f/f_{p2}\right)}^2}}$$

(15)

where $f_{p1}=1/2\mathsf{\pi }{R}_{p1}{C}_{p1}$ is the first pole frequency and $f_{p2}=1/2\mathsf{\pi }{R}_{p2}{C}_{p2}$ is the secondary pole frequency.

The output stage of the model consisted of controlled sources and passive components provided the output signal. It simulated the output resistance and the DC and dynamic of the current consumed by the external power supply device. The VCCS $G_o$ in the output block drives the resistor $R_o$, connected between the node 5 and the floating ground. The $G_o$ acted as an active current generator and provided the desired voltage drop over its parallel resistor. The DC voltage gain of the output block was equal to unity, because the $g_{mo}$ of the VCCS $G_o$ was equal to the reciprocal of the resistance $R_o$.

The limitation of the output current was presented in the macro-model through the controlled voltage source $E_{\lim }$, the resistor $R_{sense}$, and the pair of diodes $D_{L1}$ and $D_{L2}$ [16]. When the voltage drop across the resistor $R_{sense}$ becomes approximately equal to 0.6 V, one of the two diodes ($D_{L1}$ or $D_{L2}$) turns on and the current is limited to $I_{o\max }=0.6V/R_{sense}$.

When there is no load at the output, the model draws only a quiescent current from the power-supply rail by the independent current source $I_{CC}$ in the model, thus behaves similarly to an ideal class-B output stage with a gain equal to unity. When an AC voltage is applied to the input port, as a result of the amplification, the output voltage will have greater amplitude, which is obtained by increasing the power consumption. In the proposed model, the dynamic behavior of the supply current is produced through a pair of current-controlled current sources (CCCSs) ($F_1$ and $F_2$) with unity gain and a pair of ideal diodes ($D_3$ and $D_4$), similar to the op amp models, presented in [2,3,6]. The $F_1$ is controlled by the magnitude of the output current through the load, which in turn generates a current, driving the two diodes. Depending on the magnitude and the direction of the current through the F₂, an AC current flows from the power supply to the ground, which average value $I_{CC,av}$ is proportional to the real consumed current. Another technique for modeling the supply current variations is by using relatively complex high-order (n > 2) nonlinear current source F₂ [4].

2.3. Parameter Extraction

Based on the theoretical analysis of the proposed equivalent circuit in this subsection are proposed analytical expressions for determining the modeling parameters of the proposed model (Figure 4) for simulations of monolithic power amplifiers. For better clarity, the expressions are systematized in a table (see

Table 2. Analytical expressions for the modeling parameters.

Input Stage

(1) The parameters $r_{id}$, $C_{id}$, $r_{iCM}^{+}\approx r_{iCM}^{-}=2r_{iCM}$, $I_{iB}$, $k_{0,Eos}=V_{io}$ and $I_{o\max }$ of the input stage is obtained from the datasheet and are substituted directly into the macro-model. (2) Power-supply rejection stage: $R_{0SVR}={1.10}^6\Omega$, $C_{0SVR}=1/(2\mathsf{\pi }{f}_{\min }{R}_{0SVR})$, where $f_{\min }$ is the lower frequency with a minimum value of the PSRR. The damping factor is $\mathsf{\xi }=1/2Q$ (where Q is the quality factor), $T_1=1/2\mathsf{\pi }{f}_{\max }$ ($f_{\max }$ is the frequency, at which the PSRR has maximum value), $C_{1SVR}=10\mathrm{pF}$—parasitic terminal capacitance, $R_{1SVR}=(2\mathsf{\xi }{T}_1)/C_3$ (where $C_3$ is the value from the datasheet), $L_{1SVR}=T_1^2/C_{1SVR}$—series inductor, $T_2=R_{1SVR}{C}_{1SVR}$ and $k_{1,SVR}=1/PSR{R}_{\max }{R}_{1SVR}$, where $PSR{R}_{\max }$ is the maximum value of the PSRR at $f_{\max }$.

Intermediate (Second) Stage

(3) The current $I_1$ according to the datasheet is set to be equal to 1 mA, 0.1 mA, or 0.01 mA. The value of the $I_1$ has to be less than the quiescent current. (4) Voltage gain stage and dominant pole frequency shaping stage $C_{p1}=\frac{I_1}{SR}$; $R_{p1}=1/2\mathsf{\pi }{f}_{p1}{C}_{p1}$, where $f_{p1}\approx f_1/A_{d0}$ is the dominant pole frequency, $f_1$ is a unity-gain bandwidth and $K_1=A_{d0}/(I_1{R}_{p1})$; (5) Non-dominant pole shaping stage $R_{p2}={1.10}^6\Omega$, $C_{p2}=1/2\mathsf{\pi }{f}_{p2}{R}_{p2}$ and $g_{m2}=1/R_{p2}$ is the transconductance of the VCCS $G_2$; (6) Voltage limiting stage The values of the voltage sources in a voltage-limiting network are: $V_1=+V_s-V_{OUT,\max }+{\phi }_T\ln (I_1/I_S)$ and $V_2=-V_{OUT,\min }+{\phi }_T\ln (I_1/I_S)$, where ${\phi }_T=0.02585 \mathrm{V}$ at $T=27 {}^{°}\mathrm{C}$ and $I_S={1.10}^{-12} \mathrm{A}$ for both diodes.

Output Stage

(7) Output resistance and voltage gain of the output stage The $R_o=r_{OUT}$ is the output resistance from the datasheet; $g_{mo}=1/R_o$ is the transconductance of the output VCCS $G_o$; (8) Current limiting stage and quiescent current For the maximum output current the sense resistor is $R_{sense}=0.6 \mathrm{V}/I_{o\max }$; The total quiescent current that flows from the power supply rail to the ground in the model is $I_{SS}=I_1+\frac{V_S^{+}}{R_{p1}}+\frac{V_S^{+}}{R_{p2}}+\frac{V_S^{+}}{R_{r1}+R_{r2}}+I_{CC}$.

) and they are given separately for each of the individual building blocks. When determining the values of the model parameters, some of them are obtained directly from the datasheet typical values, while others are typical estimated values from device design.

3. Results and Discussion

To verify the efficiency of the proposed macro-model the simulation results of the electrical parameters were compared with the corresponding results obtained by the experimental testing of sample analog circuit, using commercially available monolithic power amplifier TDA2005 [17]. The modeling parameters were extracted for TDA2005 by analyzing semiconductor data books and through some characterization measurements. All the modeling parameters for the proposed model that are in good agreement with the experimental results related to the TDA2005 model at $V_S^{+}=14.4 \mathrm{V}$, $R_L=4 \Omega$ and $T_A=25 {}^{°}\mathrm{C}$, are: $k_{0,Eos}=2.5 \mathsf{\mu }\mathrm{V}$, $r_{id}=70 \mathrm{k}\Omega$, $r_{iCM}^{+}=r_{iCM}^{-}=140 \mathrm{k}\Omega$, $C_{id}=5 \mathrm{p}\mathrm{F}$, $I_{iB}^{+}=I_{iB}^{-}=100 \mathrm{n}\mathrm{A}$, $PSR{R}_{\max }=562.34$ (or 55 dB at $f_{\max }=400 \mathrm{Hz}$), $C_{0SVR}=16 \mathrm{n}\mathrm{F}$ (at $f_{\min }=10 \mathrm{Hz}$), $C_{1SVR}=10 \mathrm{pF}$, $L_{1SVR}=15.84 \mathrm{m}\mathrm{H}$, $R_{1SVR}=79.6 \Omega$, $I_1=1 \mathrm{m}\mathrm{A}$, $C_{p1}=0.1 \mathrm{n}\mathrm{F}$, $R_{p1}=7.96 \mathrm{M}\Omega$ (at $f_{p1}=200 \mathrm{Hz}$), $K_1=3.92$ (at $A_{d0}=90 \mathrm{dB}$), $C_{p2}=16 \mathrm{fF}$ ($f_{p2}=10 \mathrm{MHz}$), $g_{m2}=1/R_{p2}$, $V1=V2=0.2 \mathrm{V}$, $R_o=0.01 \Omega$, $g_{mo}=1/R_o$, $I_{o\max }=3.5 \mathrm{A}$, and $I_{CC}=75 \mathrm{m}\mathrm{A}$.

To obtain the amplitude-frequency responses for the various voltage gains, the test circuit, shown in Figure 6 was used. The circuit for the simulation with OrCAD PSpice^® 9.0 (previously MSIM^® 8) was based on the test condition, given in the datasheet. For the experimental testing, the same circuit was implemented on an FR4 printed circuit board laminate with through-hole device passive components. The recommended area of aluminum plate heatsink was $S_{HS}\ge 400 \mathrm{c}{\mathrm{m}}^2$ [15], where the junction-to-case thermal resistance is $R_{th j-c}=3 {}^{°}\mathrm{C}/\mathrm{W}$ [17]. Figure 7 displays the frequency responses for the two values of the feedback resistor R₂, as well as the open-loop voltage gain versus frequency obtained by simulation testing. Thus, the simulated value for the 3-dB cutoff (corner) frequencies were $f_b=18.12 \mathrm{Hz}$ and $f_h=17.05 \mathrm{kHz}$ at $A_V=364.63$, respectively, and the corresponding measured values were $f_b=20 \mathrm{Hz}$—lower cutoff frequency and $f_h=18.6 \mathrm{kHz}$—upper cutoff frequency, respectively. Also, the simulated values for $A_V=181.22$ were $f_b=23.48 \mathrm{Hz}$, and $f_h=34.4 \mathrm{kHz}$, and the corresponding measured values were $f_b= 21.5 \mathrm{Hz}$, and $f_h=32.7 \mathrm{kHz}$. The maximum relative error between the simulation results of the cutoff frequencies and the measured values was not greater than 10%.

Figure 8 illustrates the frequency response for the simulated PSRR at V_S = 14.4 V and R_L = 4 Ω. The comparative analysis showed that the simulated response fitted quite closely the actual response [17] (the relative error was below 8%) with correct amount of maximal value of PSRR and the slope of characteristic in the transition area.

The workability of the proposed macro-model was validated by examining the transient characteristics at a large-signal using the electronic circuits with various external load resistance. For a large-signal, the simulation and experimental results of the energy parameters at R_L = 2 Ω ± 5%, and 4 Ω ± 5%, are plotted in Figure 9 and Figure 10. To obtain the electrical parameters, the test circuit with R₂ = 1.2 kΩ, given in Figure 6, was used. The sinusoidal input signal with a frequency of 1 kHz was obtained by SFG-2010. The amplitude of the input signal had an amplitude, at which the output signal had no visible non-linear distortions (below 5%). The supply voltage was swept from 8 V to 18 V by using HY3005D-3. The achieved relative error between the measured values for the output power $P_{L,\max }=V_{o,\max }^2/2R_L$ and the simulations for the proposed model, was up to 10%. The error for the energy efficiency $\mathsf{\eta }=P_{L,\max }/P_{CC,\max }$ ($P_{CC,\max }=I_{CC,av}\times V_S^{+}$, where $I_{CC,av}$ is the average value of the supply current) was below 10% (see Figure 10a,b) at V_s > 12 V and R_L = 2 Ω and 4 Ω. For V_s ≤ 12 V, and R_L = 4 Ω, Figure 10b the supply current had lower value in comparison with the $I_{CC,av}$ at R_L = 2 Ω (Figure 10a), and the error was up to 15% due to the relatively greater influence of the nonlinearities of the volt-ampere characteristics of the transistors.

Additionally, at a large signal in Figure 11a,b, the results of a simulation study of the nonlinear distortions at V_s ≤ 14.4 V and $A_V=364.63$ ($\approx 50 \mathrm{dB}$) are shown. For this purpose, a transient analysis in combination with a Fourier analysis was performed in the PSpice program environment. An input signal with a sinusoidal form was applied to the input terminals of the circuit to provide approximately the output power for which a value was given for the nonlinear distortions in the datasheet of the real device. For the frequency range from 50 Hz to 15 kHz, a final simulation time equal to 100 ms was selected. In this case, the print step and the step celling had the same values equal to 1 μs. In this way, a waveform of the output signal can be provided with a print step of no more than PERIOD OF THE INPUT SIGNAL/100. As can be seen, the relative error, for some values of the input frequency, was greater than 20% (as the maximum value of the total harmonic distortion (THD) was below 1%), therefore the results showed that the proposed macro-model can simulate the trend of change of nonlinear distortions in the process of preliminary studies of sample electronic circuits. The average value of the absolute deviation (taking into account the algebraic sign for each value of the coefficient) at a load equal to 2 Ω is 13.069%, and at a load equal to 4 Ω is 20.821%. In many practical cases, the modeled direction of change of nonlinear distortions is sufficient, taking into account the technological tolerances of the parameters of the integral and discrete components, as well as the instability of the supply voltage. For the maximum output power with a typical value of 20 W, when bridging two power operational amplifiers, according to the test conditions in the datasheet of the real amplifier, as a result of the simulation study for each of the output voltages a THD was equal to 3.9%. According to the datasheet, the THD was up to 10%.

To obtain large-signal transient responses for the various load resistances the test circuit, given in Figure 12 is used. For this purpose, a signal with a pulse form of the voltage and amplitude at which a maximum swing of the output voltage is obtained was applied to the input terminals of the circuit. For the purpose of the simulation study, a transient analysis with a final time of 100 ms (frequency of the input signal 1 kHz and duty cycle 0.5) was set, and the print step and the step celling had the same values equal to 0.1 μs. For the transient response, the simulation and the experimental results of the output signal at R_L = 4 Ω ± 5%, and 8 Ω ± 5%, are plotted in Figure 13 and Figure 14. The output signal, obtained from the simulation study, was reported from the beginning of the time moment equal to 50 ms, because due to the influence of the coupling capacitors in the circuit there was a transient process of obtaining the steady-state value of the output voltage’s amplitude. The measured values were $SR=10.2 \mathrm{V}/\mathsf{\mu }\mathrm{s}$—$R_L=4 \Omega$ (Figure 13a) and $SR=10.6 \mathrm{V}/\mathsf{\mu }s$—$R_L=8 \Omega$ (Figure 14a), respectively and the corresponding simulated value for the slew rates were $SR=9.98 \mathrm{V}/\mathsf{\mu }s$ at $R_L=4 \Omega$ (Figure 13b) and $SR=10.1 \mathrm{V}/\mathsf{\mu }s$ at $R_L=8 \Omega$ (Figure 14b), respectively. The simulated results for the positive slew rate at both external load resistances are given in Figure 13c and Figure 14c, respectively. The relative error between the simulation results of the slew rates and the measured values was below 5%. The voltage drop ($\mathsf{\delta }=\Delta U_0/U_{0\max }$) in the flat region of the output pulse was due to the influence of the coupling capacitors in the input and output network of the circuit, and the value of the load. As can be seen, for a load resistance of $R_L=8 \Omega$, the voltage drop had a smaller value. At $R_L=4 \Omega$ the simulated value of the voltage drop was equal to 5.41% (Figure 13d) and the measured value was 4.95%. For $R_L=8 \Omega$, the simulated value was 2.72% (Figure 14d) and the measured value was 2.25%. The maximum value of the relative error was up to 10%, that is acceptable comparing with the manufacturing tolerances, especially for the commercially available coupling capacitors.

Table 3. Comparison with other simulation models.

Parameter	This Model	Ref. [2]	Ref. [6]	Ref. [7]	Ref. [9]
Input offset voltage	Yes	Yes	Yes	Yes	Yes
Input bias current	Yes	Yes	Yes	Yes	Yes
Power Supply Rejection Ratio	Yes	No	Yes	No	No
Internal floating ground with midpoint	Yes	No	No	No	No
Frequency response for the PSRR	Yes	No	Yes	No	No
Input impedance	Yes	Yes	Yes	Yes	Yes
Open-loop voltage gain	Yes	Yes	Yes	Yes	Yes
Small-signal bandwidth	Yes	Yes	Yes	Yes	Yes
Slew Rate	Yes	Yes	Yes	Yes	Yes
Supply current	Yes	Yes	Yes	Yes	Yes
Dynamic behavior of the supply current	Yes	Yes	Yes	No	No
Output voltage swing	Yes	Yes	Yes	Yes	Yes
Energy efficiency	Yes	No	No	No	No
Total harmonic distortion	Yes	No	No	Yes	Yes
Short-circuit current	Yes	Yes	Yes	Yes	Yes
Open-loop output resistance	Yes	Yes	Yes	Yes	Yes
Year	2021	1990	2013	2014	2015

presents a comparison of the created model with known models of various types of operational amplifiers. As can be seen, all models and macro-models simulate the basic DC and AC parameters, for small signal operation and in most of them at dual power supply voltage from symmetrical external voltage source. When working with high output current and voltage, and single-supply voltage, for some of the macro-models [7,9] are added external stages and function blocks allowing modeling of nonlinear distortions and the floating ground at the single-supply voltage without simulating simultaneous effects at large-signal on the operational amplifiers.

4. Conclusions

An electrical macro-model for monolithic power amplifiers was developed, implemented, and verified. The proposed model is intended for the PSpice-based simulation platform. The proposed model showed a good agreement between the simulation and the experimental testing, and the relative error for the basic static and dynamic small-signal parameters was below 10%. The maximum value of the relative error for the energy efficiency at a large signal was up to 15% (for supply voltages between 8 and 12 V) and below 10% at V_s > 12 V, which guarantees a sufficient degree of accuracy, considering the technological tolerances of the electrical parameters of the components and some variations of the power supply voltage. Further, the also takes into account the internal floating ground with midpoint, offset drift as a result of the power supply ripples, dynamic behavior of the supply current, nonlinear distortion, and internal voltage- and current- limiting networks. This makes the developed model especially useful for analog single-supply processing circuit design at a block level, as thereby to use for predicting and optimize the values of the passive components for the performance of the functional blocks; for instance, to define and analyze the energy parameters, according to the power dissipation.

One possible direction for future work of the author is to develop a behavioral model by using VHDL-AMS or Verilog-A languages. As a result, the created models will allow describing the structure of the model with a smaller number of passive elements and con-trolled sources, as well as a smaller number of nodes. For example, one possible advantage of using VHDL-AMS is that the complete set of equations, that represent the behavior of the real device, can be implemented by combining behavioral elements and structural description as a net-list. By using this technique, the obtained behavioral models can have better convergence during the computation process, especially to simulate the transient responses at a large signal.