Optimization of Low Head Axial-Flow Turbines for an Overtopping BReakwater for Energy Conversion: A Case Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Approach
2.2. Study Area Overview
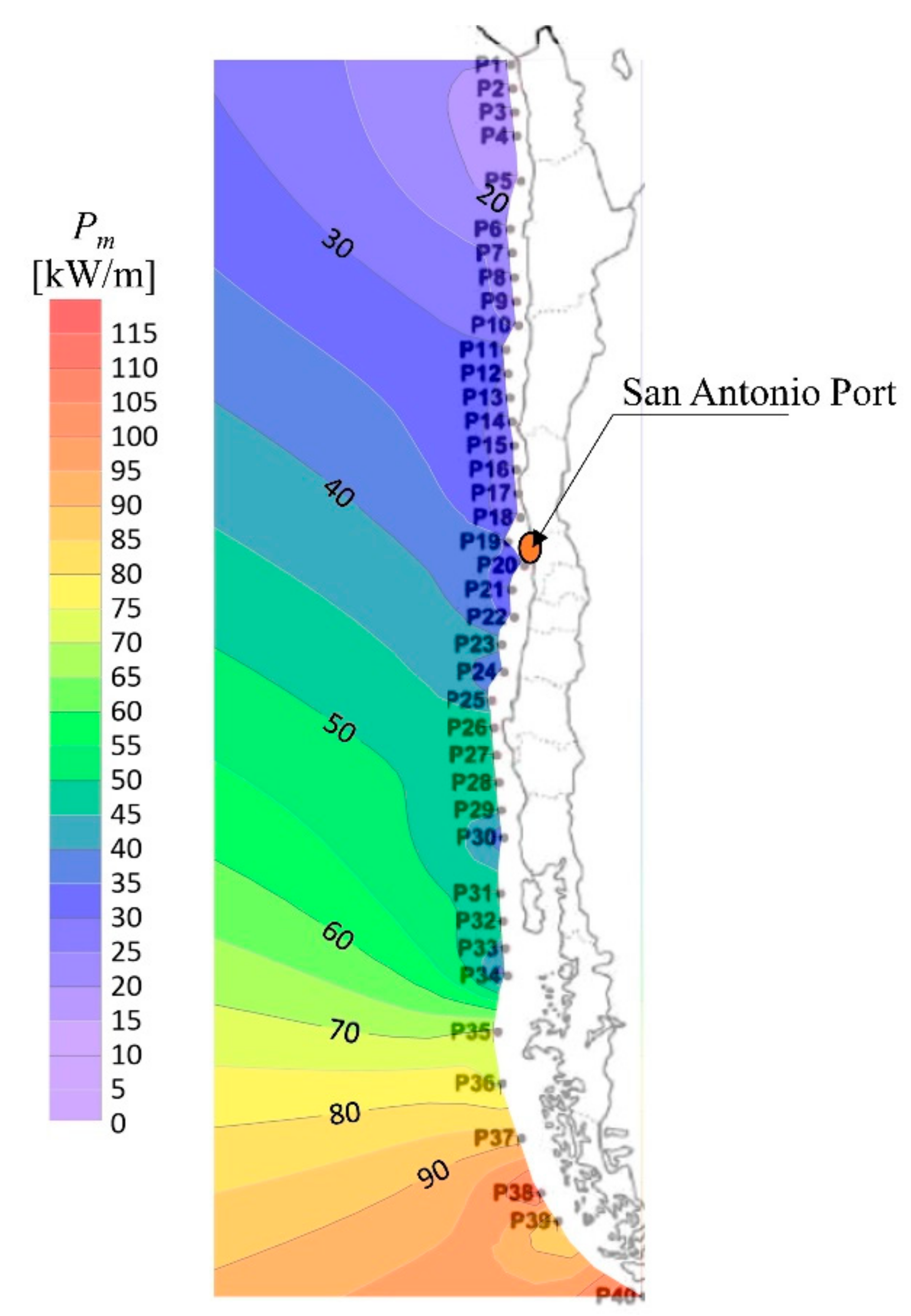
2.2.1. Site Selection and Wave Data
- •
- The 10-year dataset from ERA-Interim for the point P20, with coordinates 33.75° S and 72.00° W
- •
- A 4-year dataset (from January 2017 to December 2020) from ERA5 reanalysis, for the point P20 (ERA5), in Figure 1b, with coordinates 33.8° S and 72.00° W.
2.2.2. Offshore Wave Climate
2.2.3. Wave Propagation
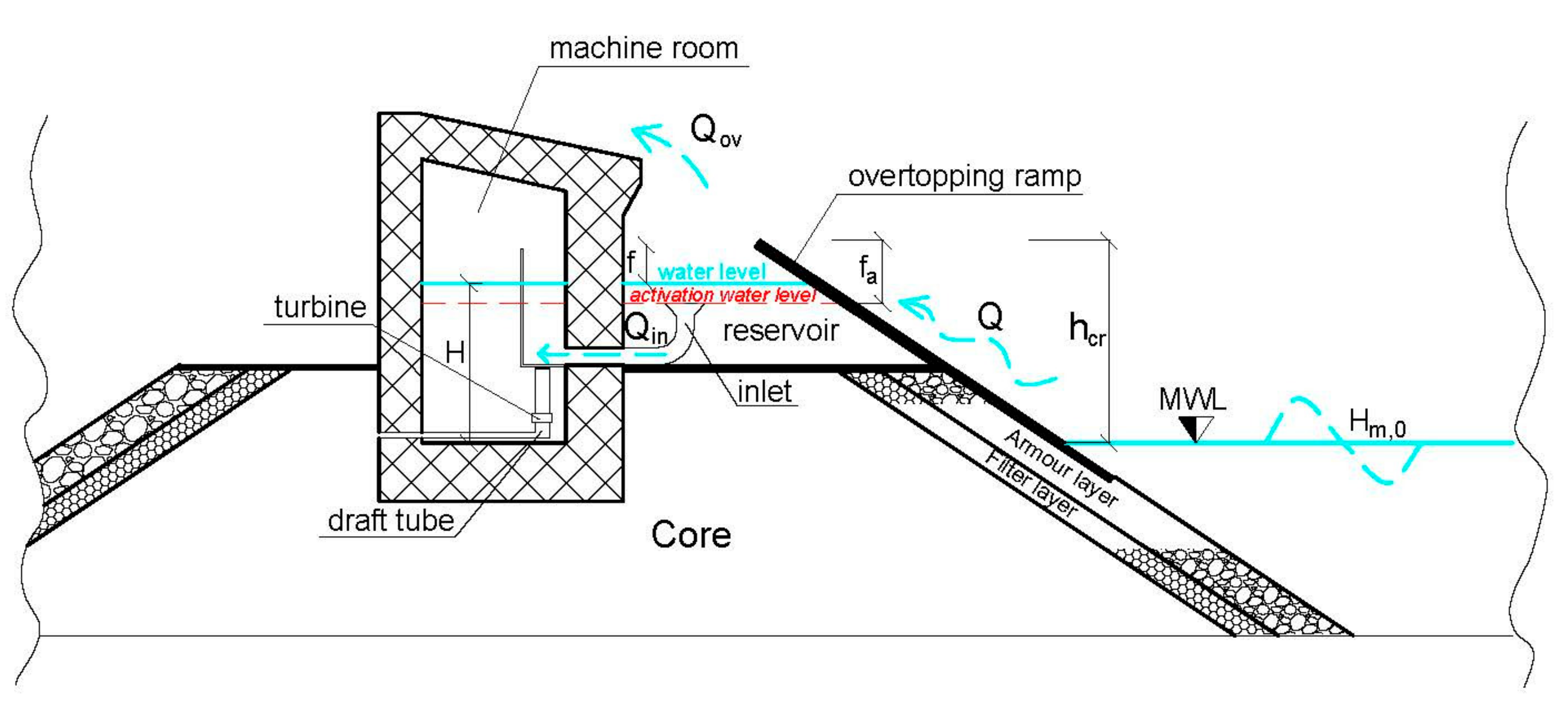
2.3. OBREC Structure
2.4. Turbine Control Strategy
2.5. Flow Model
- •
- Sea states
- •
- Ramp crest level
- •
- Turbine performance curve
- •
- Turbine control strategy
2.5.1. Sea States
2.5.2. Crest Level
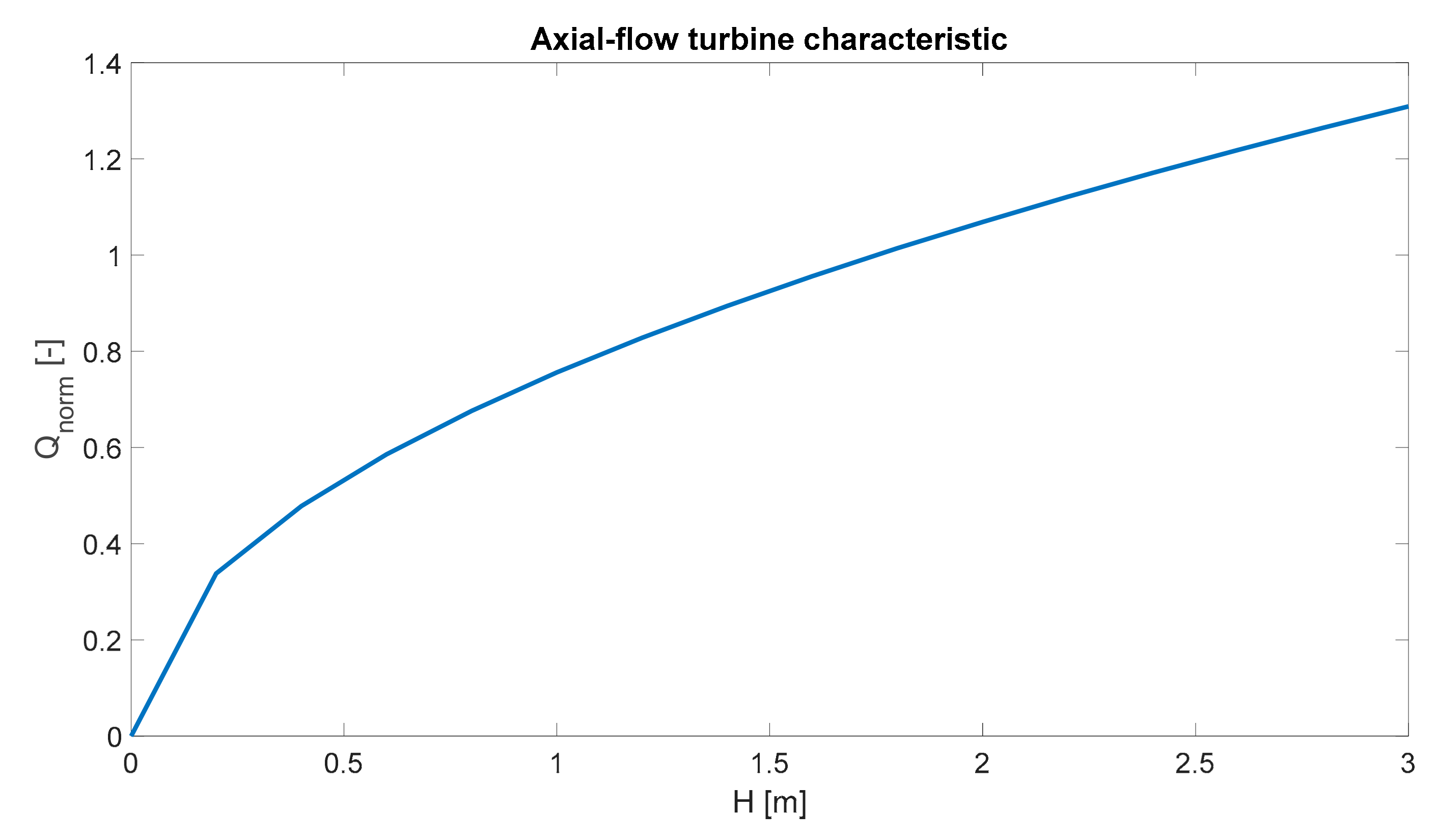
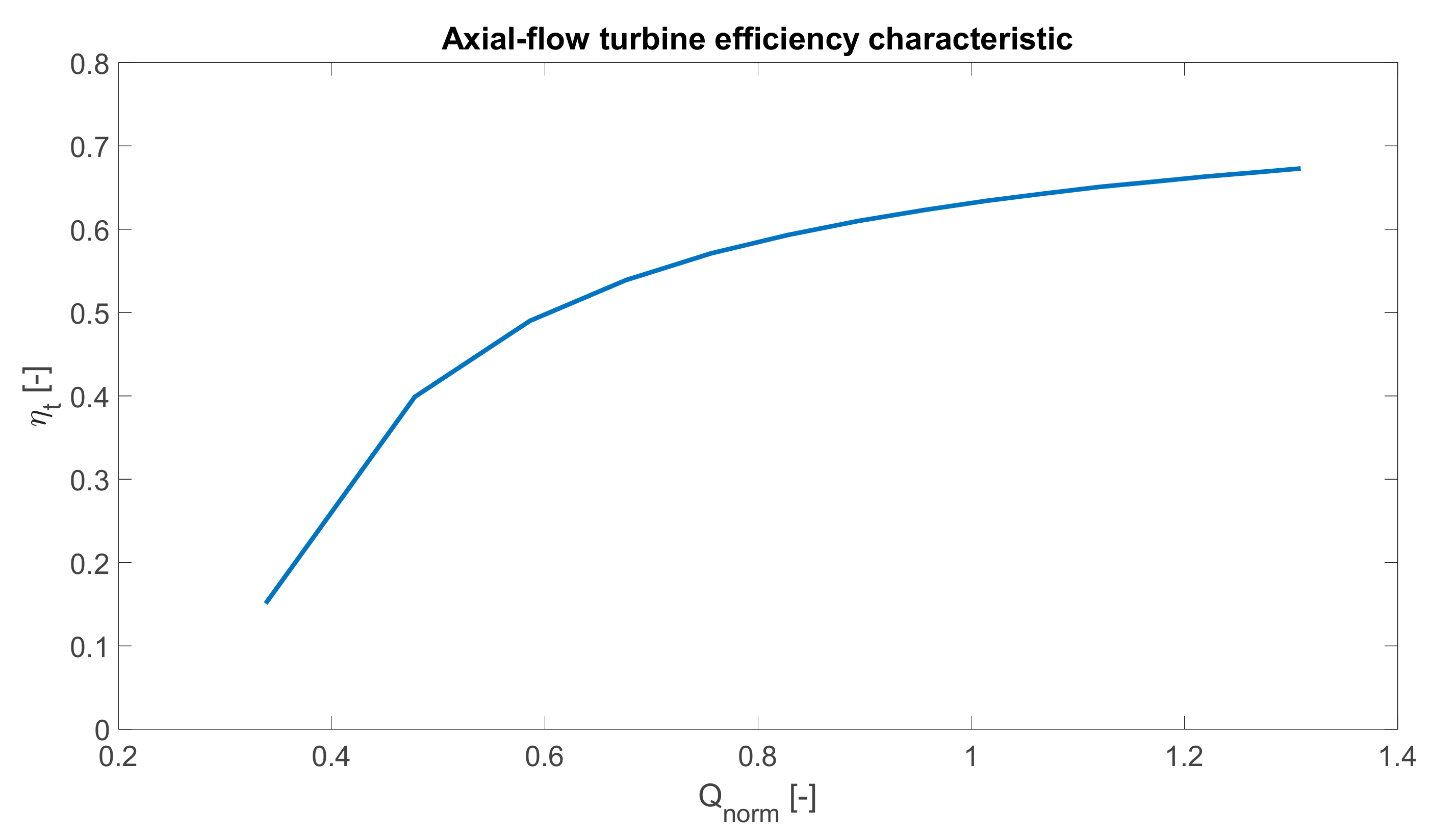
2.6. Turbine Characteristics
2.6.1. Turbine Performance Curves
2.6.2. Similitude
2.7. OBREC Efficiency
- •
- ηRAMP is the efficiency of the ramp, i.e., the rate of total incident power overtopping the crest.
- •
- ηRESERVOIR represents the efficiency of the reservoir, in terms of the potential energy stored or lost due to overflow.
- •
- ηt is the turbine efficiency calculated considering the electrical energy produced.
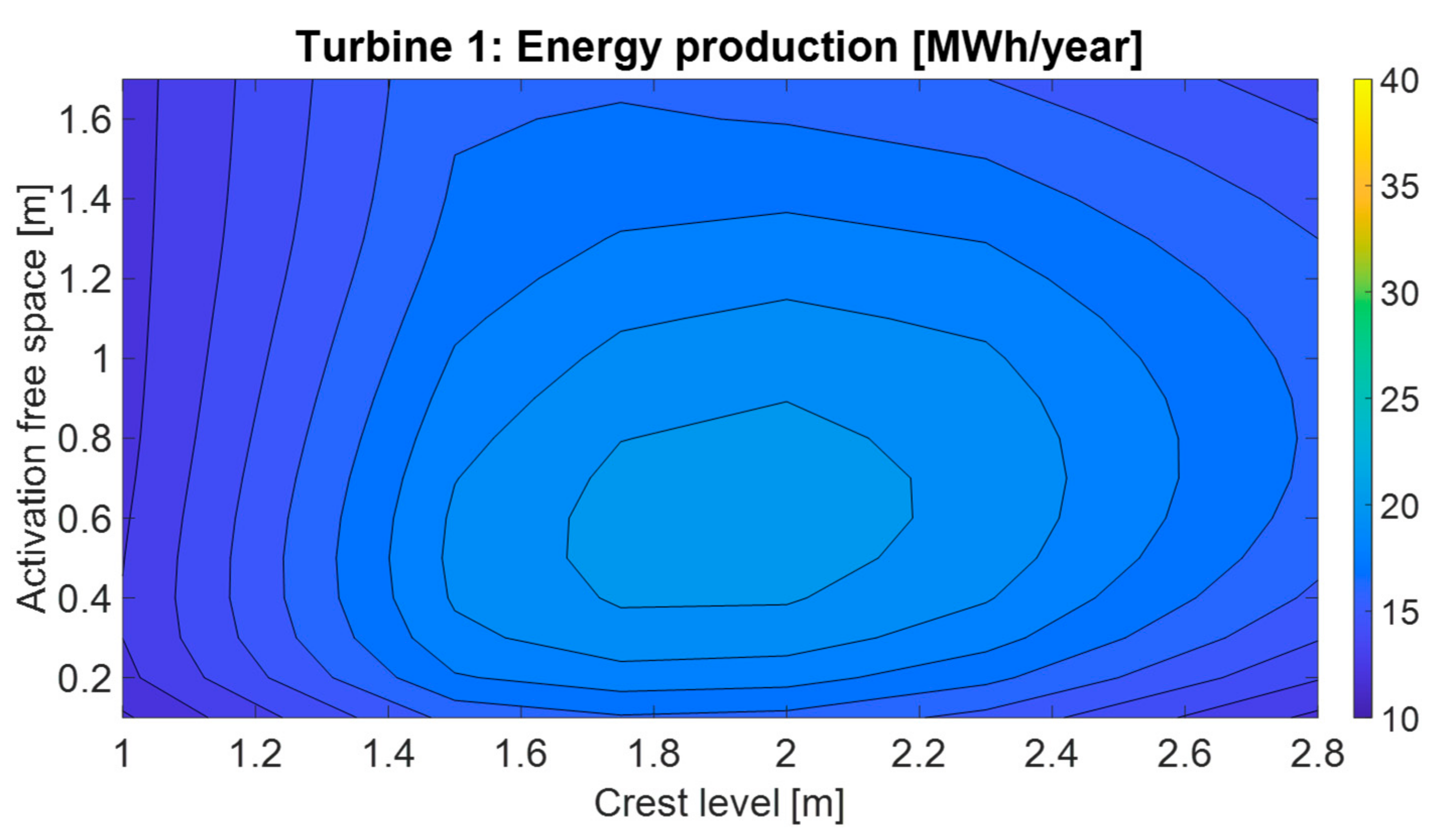
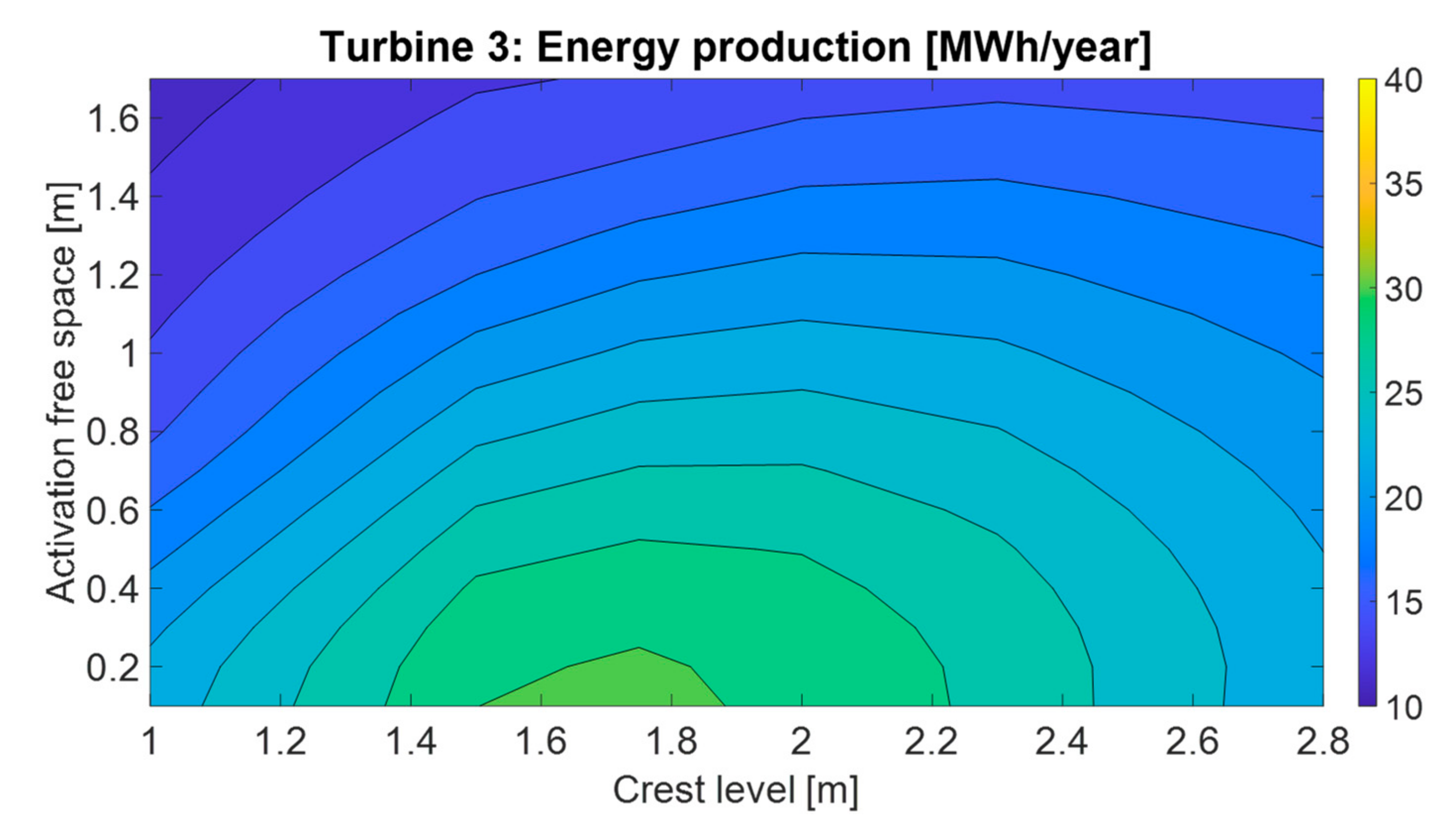
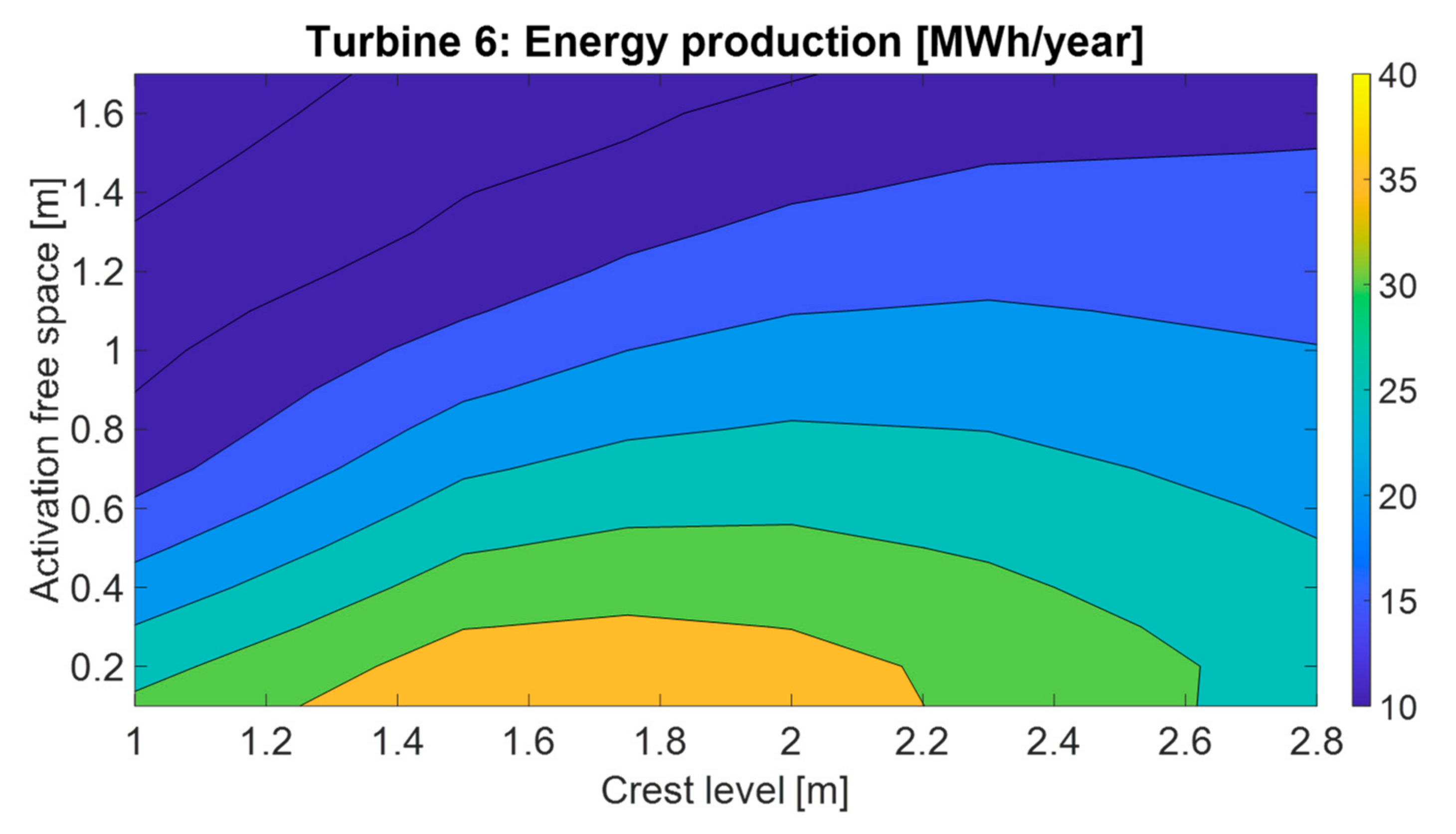
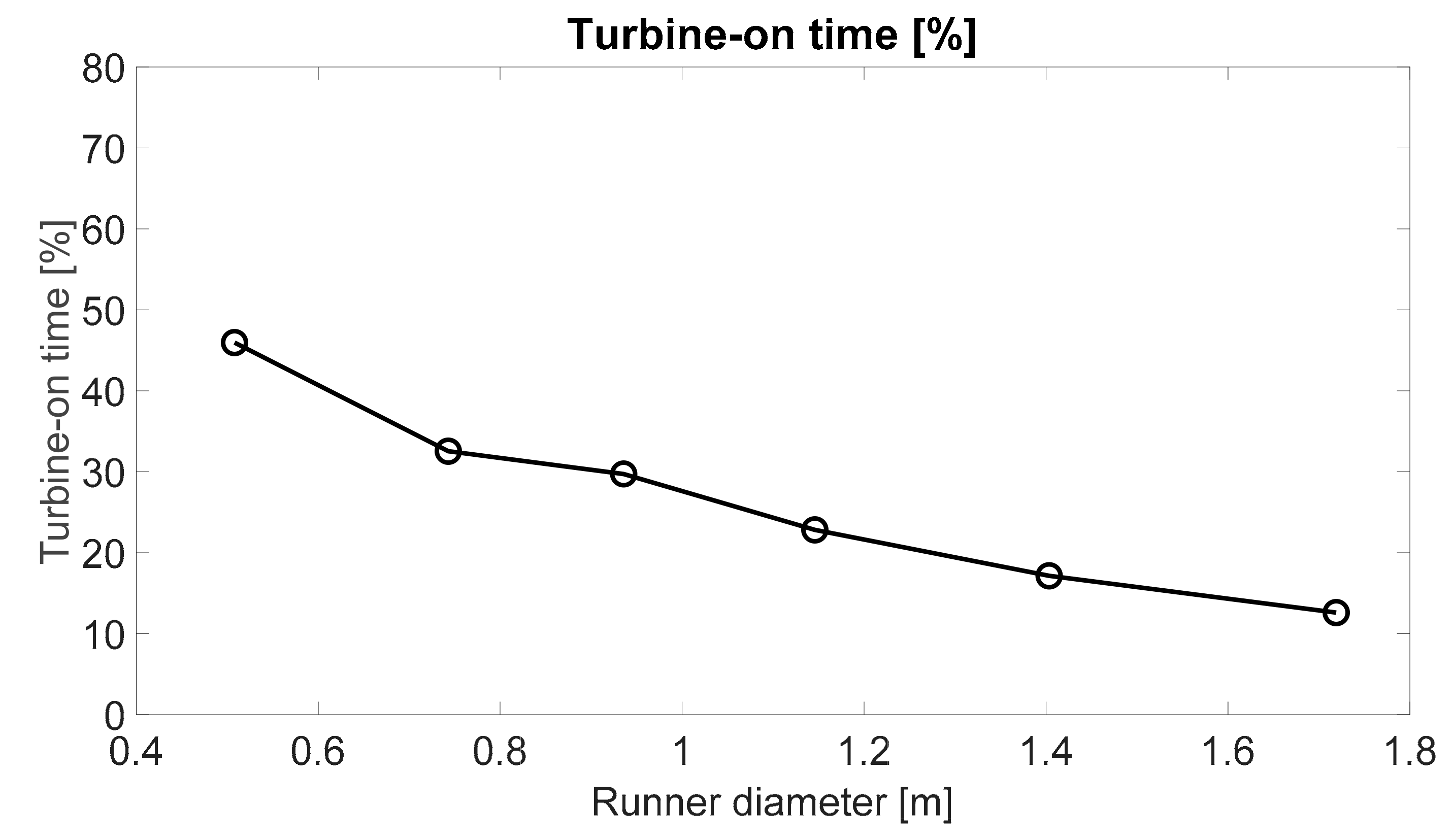
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Aderinto, T.; Li, H. Ocean Wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef] [Green Version]
- Falcao, A. Modelling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator. Ocean Eng. 2007, 34, 2021–2032. [Google Scholar] [CrossRef]
- Fernandez, H.; Iglesias, G.; Carballo, R.; Castro, A.; Fraguela, J.A.; Taveira-Pinto, F.; Sanchez, M. The new wave energy converter WaveCat: Concept and laboratory tests. Mar. Struct. 2012, 29, 58–70. [Google Scholar] [CrossRef]
- Vicinanza, D.; Contestabile, P.; Quvang Harck Nørgaard, J.; Lykke Andersen, T. Innovative rubble mound breakwaters for overtopping wave energy conversion. Coast. Eng. 2014, 88, 154–170. [Google Scholar] [CrossRef]
- Contestabile, P.; Crispino, G.; Di Lauro, E.; Ferrante, V.; Gisonni, C.; Vicinanza, D. Overtopping breakwater for wave Energy Conversion: Review of state of art, recent advancements and what lies ahead. Renew. Energy 2020, 147, 705–718. [Google Scholar] [CrossRef]
- Boren, B.C.; Lomonaco, P.; Batten, B.A.; Paasch, R.K. Design, Development, and Testing of a Scaled Vertical Axis Pendulum Wave Energy Converter. IEEE Trans. Sustain. Energy 2017, 8, 155–163. [Google Scholar] [CrossRef]
- Patrizi, N.; Pulselli, R.M.; Neri, E.; Niccolucci, V.; Vicinanza, D.; Contestabile, P.; Bastianoni, S. Lifecycle environmental impact assessment of an overtopping wave energy converter embedded in breakwater systems. Front. Energy Res. 2019, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of Innovative Harbor Breakwaters for Wave-Energy Conversion. J. Waterw. Port. Coast. Ocean Eng. 2019, 145, 1–18. [Google Scholar] [CrossRef]
- Contestabile, P.; Crispino, G.; Russo, S.; Gisonni, C.; Cascetta, F.; Vicinanza, D. Crown wall modifications as response towave overtopping under a future sea level scenario: An experimental parametric study for an innovative composite seawall. Appl. Sci. 2020, 10, 2227. [Google Scholar] [CrossRef] [Green Version]
- Iuppa, C.; Cavallaro, L.; Musumeci, R.E.; Vicinanza, D.; Foti, E. Empirical overtopping volume statistics at an OBREC. Coast. Eng. 2019, 152, 103524. [Google Scholar] [CrossRef]
- Palma, G.; Formentin, S.M.; Zanuttigh, B.; Contestabile, P.; Vicinanza, D. Numerical simulations of the hydraulic performance of a breakwater-integrated overtopping wave energy converter. J. Mar. Sci. Eng. 2019, 7, 38. [Google Scholar] [CrossRef] [Green Version]
- Rosa-Santos, P.; Taveira-Pinto, F.; Clemente, D.; Cabral, T.; Fiorentin, F.; Belga, F.; Morais, T. Experimental study of a hybrid wave energy converter integrated in a harbor breakwater. J. Mar. Sci. Eng. 2019, 7, 33. [Google Scholar] [CrossRef] [Green Version]
- Palma, G.; Formentin, S.M.; Zanuttigh, B.; Contestabile, P.; Vicinanza, D. Design optimization of a multifunctional wave energy device. In Progress in Renewable Energies Offshore, Proceedings of the 2nd International Conference on Renewable Energies Offshore (RENEW2016), Lisbon, Portugal, 24–26 October 2016; Taylor & Francis Group: London, UK, 2016; pp. 235–240. [Google Scholar] [CrossRef]
- Di Lauro, E.; Lara, J.L.; Maza, M.; Losada, I.J.; Contestabile, P.; Vicinanza, D. Stability analysis of a non-conventional breakwater for wave energy conversion. Coast. Eng. 2019, 145, 36–52. [Google Scholar] [CrossRef]
- Senior, J.; Saenger, N.; Müller, G. New hydropower converters for very low-head differences. J. Hydraul. Res. 2010, 48, 703–714. [Google Scholar] [CrossRef]
- Quaranta, E. Optimal Rotational Speed of Kaplan and Francis Turbines with Focus on Low-Head Hydropower Applications and Dataset Collection. J. Hydraul. Eng. 2019, 145, 1–5. [Google Scholar] [CrossRef]
- Knapp, W.; Holmén, E.; Schilling, R. Considerations for Water Turbines to be used in Wave Energy Converters. In Proceedings of the Fourth European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000. [Google Scholar]
- Aderinto, T.; Li, H. Review on power performance and efficiency of wave energy converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef] [Green Version]
- dos Santos, E.D.; Machado, B.N.; Zanella, M.M.; Das Neves Gomes, M.; Souza, J.A.; Isoldi, L.A.; Rocha, L.A.O. Numerical study of the effect of the relative depth on the overtopping wave energy converters according to constructal design. Defect Diffus. Forum 2014, 348, 232–244. [Google Scholar] [CrossRef]
- Musa, M.A.; Maliki, A.Y.; Ahmad, M.F.; Yaakob, O.; Samo, K.B.; Ibrahim, M.Z. Prediction of energy performance by adopting overtopping breakwater for energy conversion (OBREC) concept in Malaysia waters. J. Environ. Sci. Technol. 2016, 9, 417–426. [Google Scholar] [CrossRef] [Green Version]
- Kralli, V.E.; Theodossiou, N.; Karambas, T. Optimal Design of Overtopping Breakwater for Energy Conversion (OBREC) Systems Using the Harmony Search Algorithm. Front. Energy Res. 2019, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Calheiros-Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Ramos, V.; Morais, T.; Cestaro, H. Evaluation of the annual electricity production of a hybrid breakwater-integrated wave energy converter. Energy 2020, 213, 118845. [Google Scholar] [CrossRef]
- Victor, L.; Troch, P.; Kofoed, J.P. On the effects of geometry control on the performance of overtopping wave energy converters. Energies 2011, 4, 1574–1600. [Google Scholar] [CrossRef] [Green Version]
- Cavallaro, L.; Iuppa, C.; Castiglione, F.; Musumeci, R.E.; Foti, E. A simple model to assess the performance of an overtopping wave energy converter embedded in a port breakwater. J. Mar. Sci. Eng. 2020, 8, 858. [Google Scholar] [CrossRef]
- Cumbajín, M.; Sánchez, P.; Hidalgo, A.; Gordón, C. Multi-criteria analysis of turbines for pico-hydro power plant in water irrigation channel. Adv. Intell. Syst. Comput. 2020, 1137 AISC, 200–209. [Google Scholar] [CrossRef]
- Williamson, S.J.; Stark, B.H.; Booker, J.D. Low head pico hydro turbine selection using a multi-criteria analysis. Renew. Energy 2014, 61, 43–50. [Google Scholar] [CrossRef]
- Di Lauro, E.; Contestabile, P.; Vicinanza, D. Wave Energy in Chile: A Case Study of the Overtopping Breakwater for Energy Conversion (OBREC). In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; Volume 27. [Google Scholar]
- European Centre for Medium-Range Weather Forecasts (ECMWF). Available online: https://climate.copernicus.eu/climate-reanalysis (accessed on 30 March 2021).
- Mazzaretto, O.M.; Lucero, F.; Besio, G.; Cienfuegos, R. Perspectives for harnessing the energetic persistent high swells reaching the coast of Chile. Renew. Energy 2020, 159, 494–505. [Google Scholar] [CrossRef]
- Lucero, F.; Catalán, P.A.; Ossandón, Á.; Beyá, J.; Puelma, A.; Zamorano, L. Wave energy assessment in the central-south coast of Chile. Renew. Energy 2017, 114, 120–131. [Google Scholar] [CrossRef]
- Paredes, J.; Cruz, J.; Thomson, M.D.; Stavroulia, E.R.-S.R. Preliminary Site Selection—Key to Document Classification; Garrad Hassan and Partners Limited: Bristol, UK, 2009. [Google Scholar]
- Bay, B.; Sea, T.; Contestabile, P.; Conversano, F.; Centurioni, L.; Golia, U.M.; Musco, L.; Danovaro, R.; Vicinanza, D. Multi-Collocation-Based Estimation of Wave Climate in a Non-Tidal Bay: The Case Study. Water 2020, 12, 1936. [Google Scholar]
- Monárdez, P.; Acuña Hugo, S.D. Evaluation of the potential of wave energy in Chile. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Mediavilla, D.G.; Sepúlveda, H.H. Nearshore assessment of wave energy resources in central Chile (2009–2010). Renew. Energy 2016, 90, 136–144. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- HR Wallingford to Undertake Studies for San Antonio Port Expansion Project. Available online: https://www.hrwallingford.com/news/hr-wallingford-to-undertake-studies-for-san-antonio-port-expansion-project (accessed on 5 May 2021).
- Cornett, A. A global wave energy resource assessment. Sea Technol. 2008, 50, 59–64. [Google Scholar]
- Contestabile, P.; Ferrante, V.; Vicinanza, D. Wave energy resource along the coast of Santa Catarina (Brazil). Energies 2015, 8, 14219–14243. [Google Scholar] [CrossRef] [Green Version]
- Contestabile, P.; Di Lauro, E.; Galli, P.; Corselli, C.; Vicinanza, D. Offshore Wind and wave energy assessment around Malè and Magoodhoo Island (Maldives). Sustainability 2017, 9, 613. [Google Scholar] [CrossRef] [Green Version]
- DHI. Available online: https://www.dhigroup.com (accessed on 30 March 2021).
- GEBCO. Available online: https://download.gebco.net/ (accessed on 30 March 2021).
- Jensen, P.M.; Gilling, L.; Kofoed, J.P. User Manual for SSG Power Simulation 2; Technical Report; Department of Civil Engineering, Aalborg Universit: Aalborg, Denmark, 2006. [Google Scholar]
- Bogarino, B.; Kofoed, J.P.; Meinert, P. Development of a Generic Power Simulation Tool for Overtopping Based WEC; DCE Technical Report; Department of Civil Engineering, Aalborg Universit: Aalborg, Denmark, 2007. [Google Scholar]
- Contestabile, P.; Vicinanza, D. Coastal defence integrating wave-energy-based desalination: A case study in Madagascar. J. Mar. Sci. Eng. 2018, 6, 64. [Google Scholar] [CrossRef] [Green Version]
- Palma, G.; Contestabile, P.; Zanuttigh, B.; Formentin, S.M.; Vicinanza, D. Integrated assessment of the hydraulic and structural performance of the OBREC device in the Gulf of Naples, Italy. Appl. Ocean Res. 2020, 101, 1–14. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery; Elsevier Inc.: Burlington, MA, USA, 2010; ISBN 978-1-85617-793-1. [Google Scholar]
- Krivchenko, G. Hydraulic Machines: Turbines and Pumps; CRC Press Inc.: Boca Raton, FL, USA, 1993; ISBN 1-56670-001-9. [Google Scholar]








| Point | Lat | Lon | Hs [m] | Tm [s] | θm [°] | Pm | Ew | |
|---|---|---|---|---|---|---|---|---|
| [°] | [°] | Mean | Max | Mean | Mean | [kW/m] | [MWh/(m∙y)] | |
| 1 | 18.75 S | 70.50 W | 1.8 | 3.99 | 10.49 | 214.5 | 21.2 | 185.9 |
| 2 | 19.50 S | 70.50 W | 1.46 | 3.32 | 10.49 | 221.8 | 14.0 | 122.8 |
| 3 | 20.25 S | 70.50 W | 1.46 | 3.32 | 10.49 | 221.8 | 14.0 | 122.8 |
| 4 | 21.00 S | 70.50 W | 1.75 | 3.83 | 10.29 | 219.4 | 19.4 | 170.2 |
| 5 | 21.75 S | 70.50 W | 1.42 | 3.37 | 10.59 | 226.9 | 13.4 | 117.0 |
| 6 | 23.25 S | 71.25 W | 1.91 | 4.29 | 10.36 | 219.6 | 23.4 | 204.9 |
| 7 | 24.00 S | 71.25 W | 1.94 | 4.52 | 10.39 | 220.5 | 24.1 | 211.2 |
| 8 | 24.75 S | 71.25 W | 1.91 | 4.45 | 10.38 | 221.5 | 23.4 | 204.8 |
| 9 | 25.50 S | 71.25 W | 1.9 | 4.26 | 10.34 | 222.8 | 23.0 | 201.4 |
| 10 | 26.25 S | 71.25 W | 1.84 | 4.18 | 10.31 | 224.9 | 21.5 | 188.6 |
| 11 | 27.00 S | 72.00 W | 2.23 | 5.14 | 10.15 | 219.8 | 30.9 | 270.2 |
| 12 | 27.75 S | 72.00 W | 2.19 | 4.95 | 10.09 | 220.6 | 29.8 | 260.8 |
| 13 | 28.50 S | 72.00 W | 2.17 | 4.74 | 10.05 | 221.8 | 29.0 | 253.9 |
| 14 | 29.25 S | 72.00 W | 2.14 | 4.71 | 10.04 | 223.2 | 28.1 | 246.2 |
| 15 | 30.00 S | 72.00 W | 2.08 | 4.8 | 10.04 | 224.4 | 26.8 | 234.4 |
| 16 | 30.75 S | 72.00 W | 2.15 | 5.44 | 10.02 | 224.5 | 28.6 | 250.3 |
| 17 | 31.50 S | 72.00 W | 2.07 | 5.36 | 10.09 | 227.0 | 26.8 | 235.1 |
| 18 | 32.25 S | 72.00 W | 1.83 | 5.02 | 10.24 | 231.7 | 21.3 | 186.3 |
| 19 | 33.00 S | 72.75 W | 2.44 | 6.39 | 9.96 | 225.2 | 36.4 | 318.8 |
| 20 | 33.75 S | 72.00 W | 2.13 | 5.95 | 9.95 | 231.9 | 28.0 | 245.1 |
| 21 | 34.50 S | 72.75 W | 2.27 | 5.89 | 9.96 | 233.2 | 31.9 | 279.3 |
| 22 | 35.25 S | 72.75 W | 2.27 | 5.89 | 9.96 | 233.2 | 31.9 | 279.3 |
| 23 | 36.00 S | 73.50 W | 2.6 | 6.4 | 10.13 | 230.0 | 42.5 | 372.0 |
| 24 | 36.75 S | 73.50 W | 2.32 | 6.1 | 10.17 | 236.4 | 34.2 | 299.8 |
| 25 | 37.50 S | 74.25 W | 2.47 | 6.02 | 10.26 | 235.2 | 39.2 | 343.2 |
| 26 | 38.25 S | 74.25 W | 2.81 | 6.73 | 10.34 | 233.2 | 51.1 | 447.3 |
| 27 | 39.00 S | 74.25 W | 2.76 | 7.02 | 10.37 | 237.9 | 50.0 | 437.7 |
| 28 | 39.75 S | 74.25 W | 2.65 | 7.03 | 10.34 | 243.3 | 46.1 | 404.1 |
| 29 | 40.50 S | 74.25 W | 2.65 | 7.03 | 10.34 | 243.3 | 46.1 | 404.1 |
| 30 | 41.25 S | 74.25 W | 2.32 | 6.75 | 10.45 | 250.4 | 36.3 | 317.7 |
| 31 | 42.75 S | 75.00 W | 2.77 | 7.81 | 10.16 | 253.6 | 49.8 | 435.8 |
| 32 | 43.50 S | 75.00 W | 2.73 | 7.98 | 10.02 | 255.2 | 47.9 | 420.0 |
| 33 | 44.25 S | 75.00 W | 2.63 | 8.03 | 9.87 | 257.4 | 43.7 | 382.8 |
| 34 | 45.00 S | 75.00 W | 2.41 | 7.66 | 9.82 | 258.8 | 36.6 | 320.7 |
| 35 | 46.50 S | 76.50 W | 3.35 | 9.2 | 10.27 | 256.8 | 74.2 | 650.0 |
| 36 | 48.00 S | 76.50 W | 3.35 | 9.57 | 10.17 | 261.8 | 74.1 | 648.8 |
| 37 | 50.25 S | 76.50 W | 3.65 | 10.47 | 10.02 | 266.6 | 86.6 | 758.9 |
| 38 | 52.50 S | 75.75 W | 4.05 | 12.66 | 10.15 | 266.3 | 110.1 | 964.2 |
| 39 | 54.00 S | 74.25 W | 3.51 | 10.57 | 9.52 | 262.5 | 77.4 | 678.4 |
| 40 | 55.50 S | 70.50 W | 4.09 | 12.82 | 10.13 | 265.1 | 113.3 | 992.3 |
| Point | Hs [m] | Tm [s] | Tp [s] | θm [°] | Pm | Ew |
|---|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | [kW/m] | [MWh/(m∙y)] | |
| 20 (ERA-Interim + ERA5) | 2.09 | 9.42 | 12.66 | 233.1 | 27.5 | 240.8 |
| Point | Hs [m] | Tm [s] | Tp [s] | θm [°] | Pm | Pm,a | Ew |
|---|---|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | [kW/m] | [kW/m] | [MWh/(m∙y)] | |
| S | 1.69 | 4.98 | 12.64 | 244.9 | 17.7 | 15.3 | 134.1 |
| No. [-] | Hs [m] | Tp [s] | Prob [%] | Ew [MWh/y] |
|---|---|---|---|---|
| 1 | 0.10 | 2.5 | 0.1 | 1.00 · 10−3 |
| 2 | 0.50 | 5.7 | 0.1 | 3.20 · 10−2 |
| 3 | 0.75 | 7.0 | 0.4 | 3.53 · 10−1 |
| 4 | 1.00 | 8.0 | 4.6 | 8.33 · 100 |
| 5 | 1.25 | 9.0 | 16.7 | 5.28 · 101 |
| 6 | 1.50 | 9.9 | 25.0 | 1.25 · 102 |
| 7 | 1.75 | 10.6 | 22.9 | 1.68 · 102 |
| 8 | 2.00 | 11.4 | 14.6 | 1.50 · 102 |
| 9 | 2.25 | 12.1 | 7.5 | 1.03 · 102 |
| 10 | 2.50 | 12.7 | 3.9 | 6.98 · 101 |
| 11 | 2.75 | 13.4 | 1.8 | 4.09 · 101 |
| 12 | 3.00 | 13.9 | 1.2 | 3.39 · 101 |
| 13 | 3.50 | 15.1 | 0.8 | 3.32 · 101 |
| 14 | 4.00 | 16.1 | 0.4 | 2.32 · 101 |
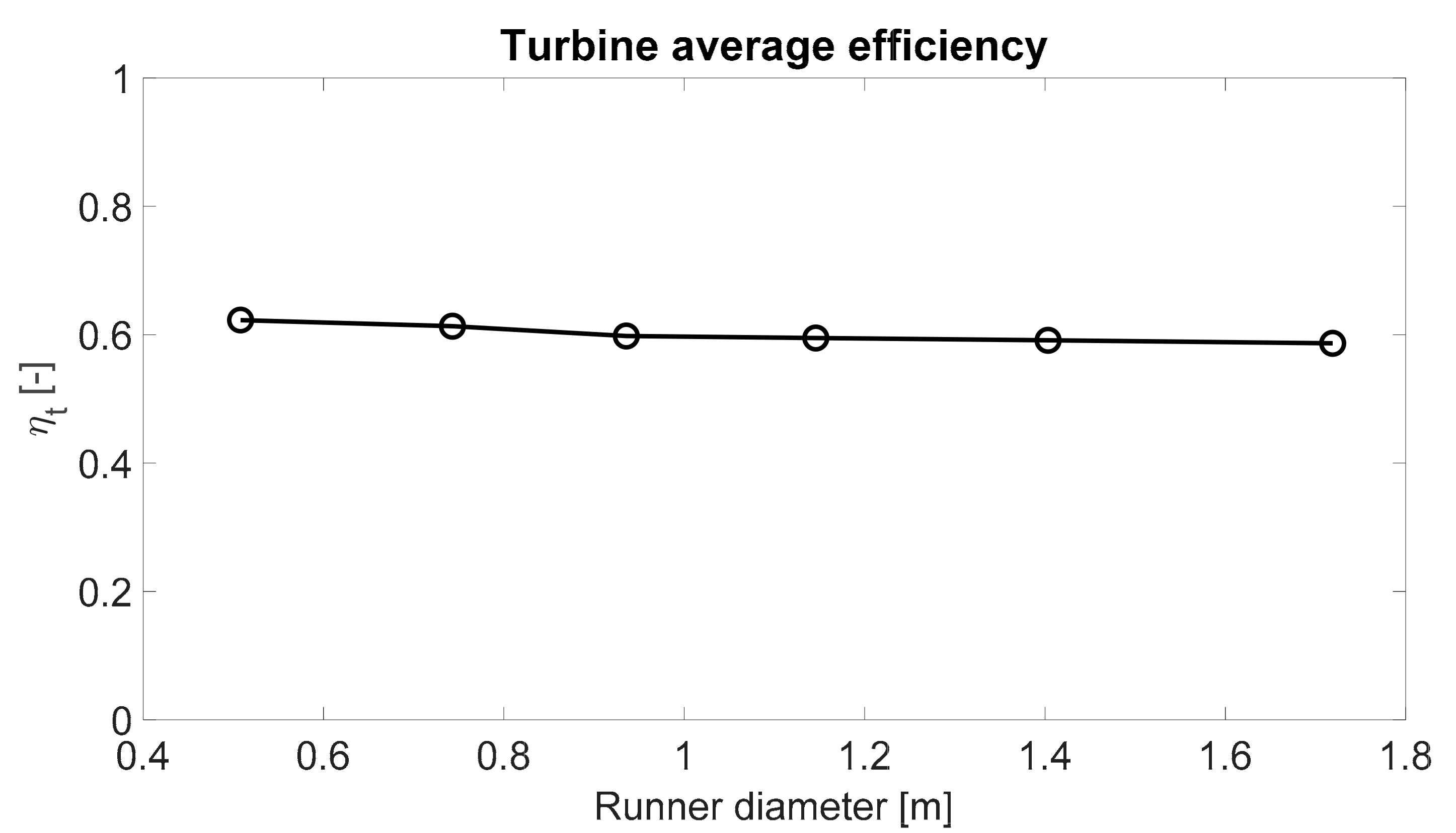
| Turbine | Rummer Diameter [m] | Qref [m3/s] |
|---|---|---|
| 1 | 0.51 | 0.49 |
| 2 | 0.74 | 1.04 |
| 3 | 0.94 | 1.65 |
| 4 | 1.15 | 2.48 |
| 5 | 1.40 | 3.71 |
| 6 | 1.72 | 5.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mariani, A.; Crispino, G.; Contestabile, P.; Cascetta, F.; Gisonni, C.; Vicinanza, D.; Unich, A. Optimization of Low Head Axial-Flow Turbines for an Overtopping BReakwater for Energy Conversion: A Case Study. Energies 2021, 14, 4618. https://doi.org/10.3390/en14154618
Mariani A, Crispino G, Contestabile P, Cascetta F, Gisonni C, Vicinanza D, Unich A. Optimization of Low Head Axial-Flow Turbines for an Overtopping BReakwater for Energy Conversion: A Case Study. Energies. 2021; 14(15):4618. https://doi.org/10.3390/en14154618
Chicago/Turabian StyleMariani, Antonio, Gaetano Crispino, Pasquale Contestabile, Furio Cascetta, Corrado Gisonni, Diego Vicinanza, and Andrea Unich. 2021. "Optimization of Low Head Axial-Flow Turbines for an Overtopping BReakwater for Energy Conversion: A Case Study" Energies 14, no. 15: 4618. https://doi.org/10.3390/en14154618
APA StyleMariani, A., Crispino, G., Contestabile, P., Cascetta, F., Gisonni, C., Vicinanza, D., & Unich, A. (2021). Optimization of Low Head Axial-Flow Turbines for an Overtopping BReakwater for Energy Conversion: A Case Study. Energies, 14(15), 4618. https://doi.org/10.3390/en14154618










