High-Gain High-Efficiency DC–DC Converter with Single-Core Parallel Operation Switched Inductors and Rectifier Voltage Multiplier Cell
Abstract
:1. Introduction
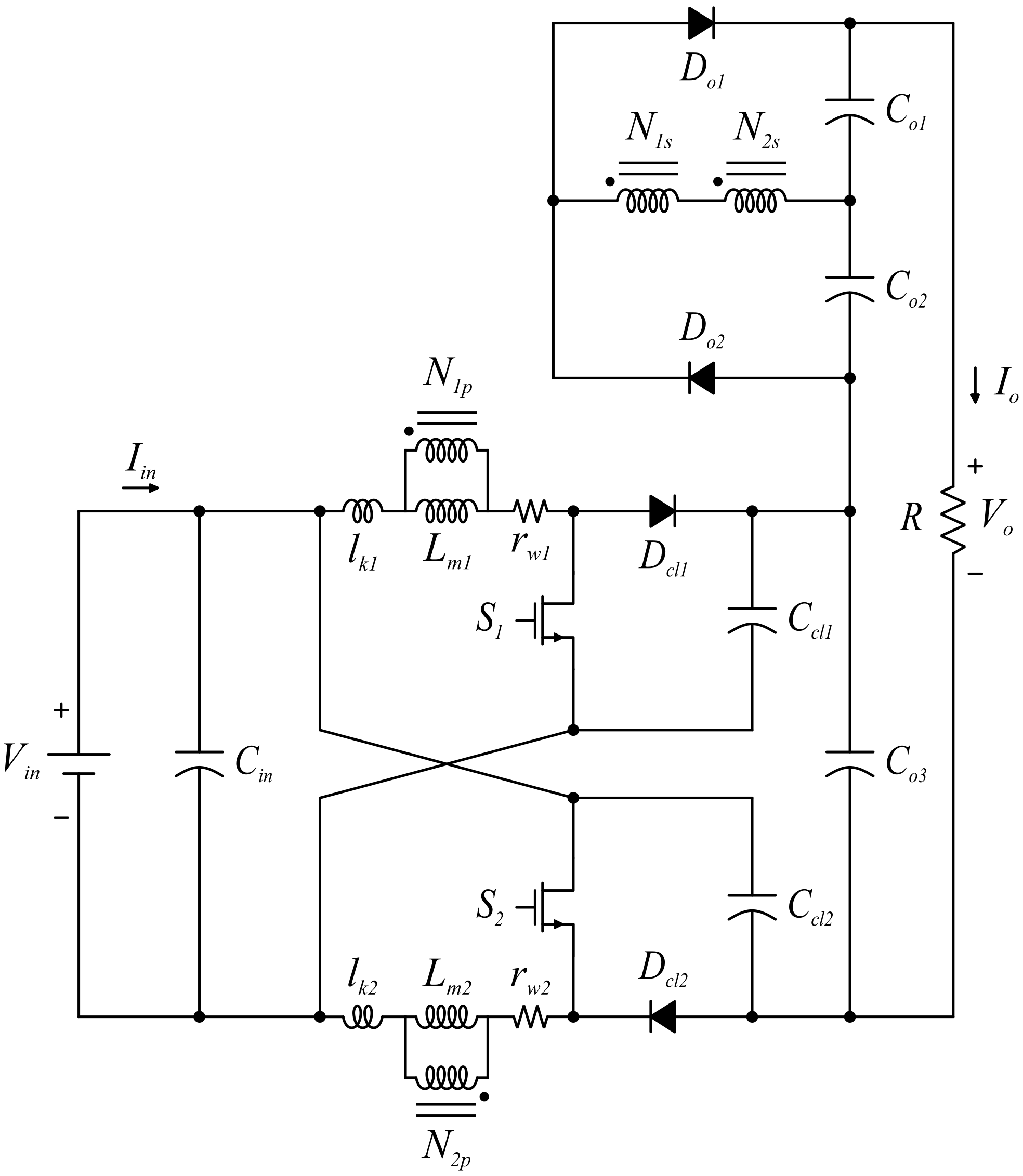
2. Proposed Converter Topology and Operation Analysis
- , , and are, respectively, the number of turns of the primary and the secondary windings of the first and the second coupled-inductor, where ;
- , are the resistances on the windings of the first and the second coupled-inductor, respectively;
- , are the leakage inductances of the first and the second coupled-inductor, respectively;
- and are the magnetizing inductances of the first and the second coupled-inductor, respectively;
- and are the switches;
- and are the output diodes;
- and are the clamper circuit diodes;
- , and are the output capacitors;
- and are the clamper circuit capacitors;
- is the input capacitor.
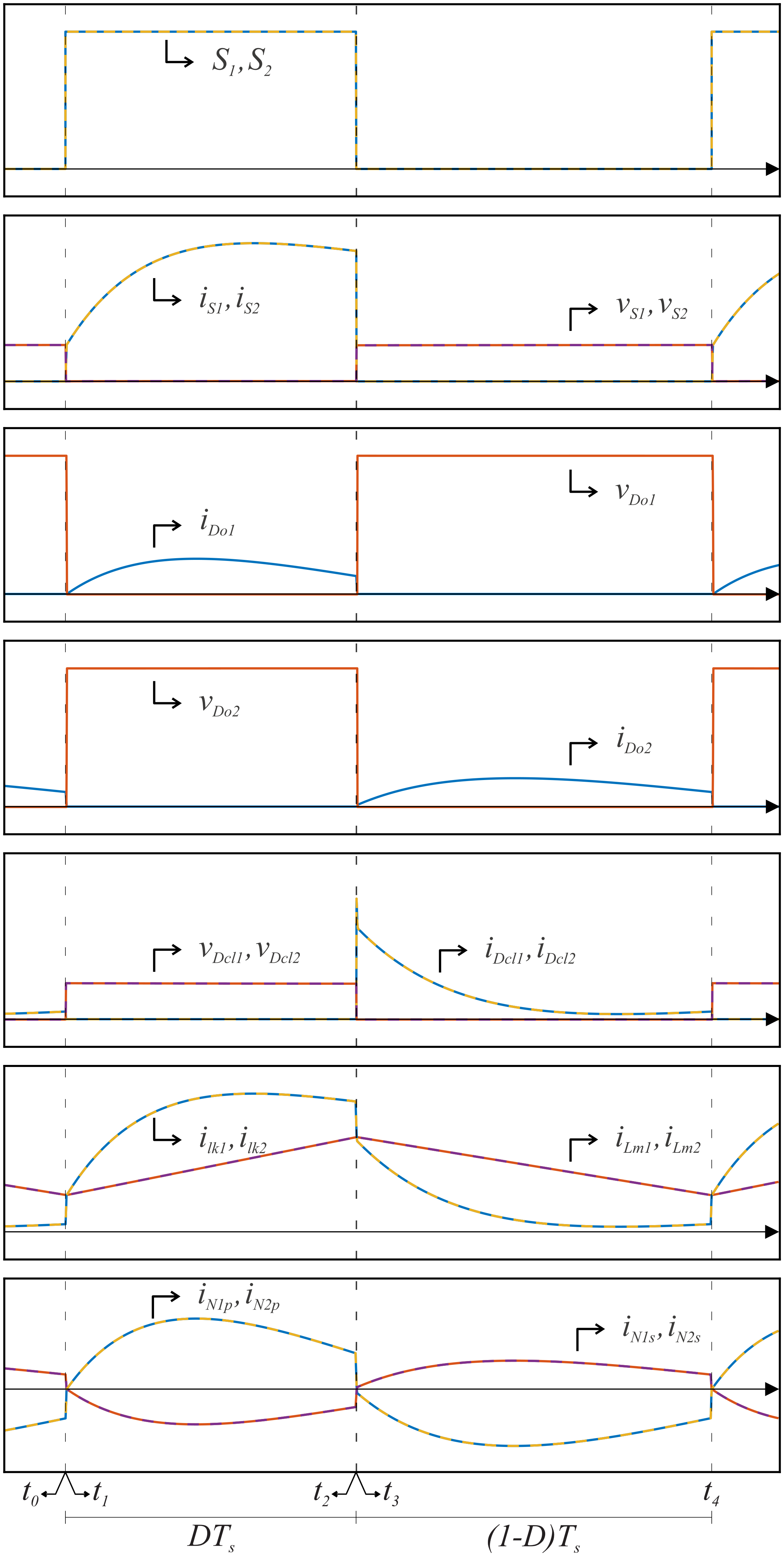
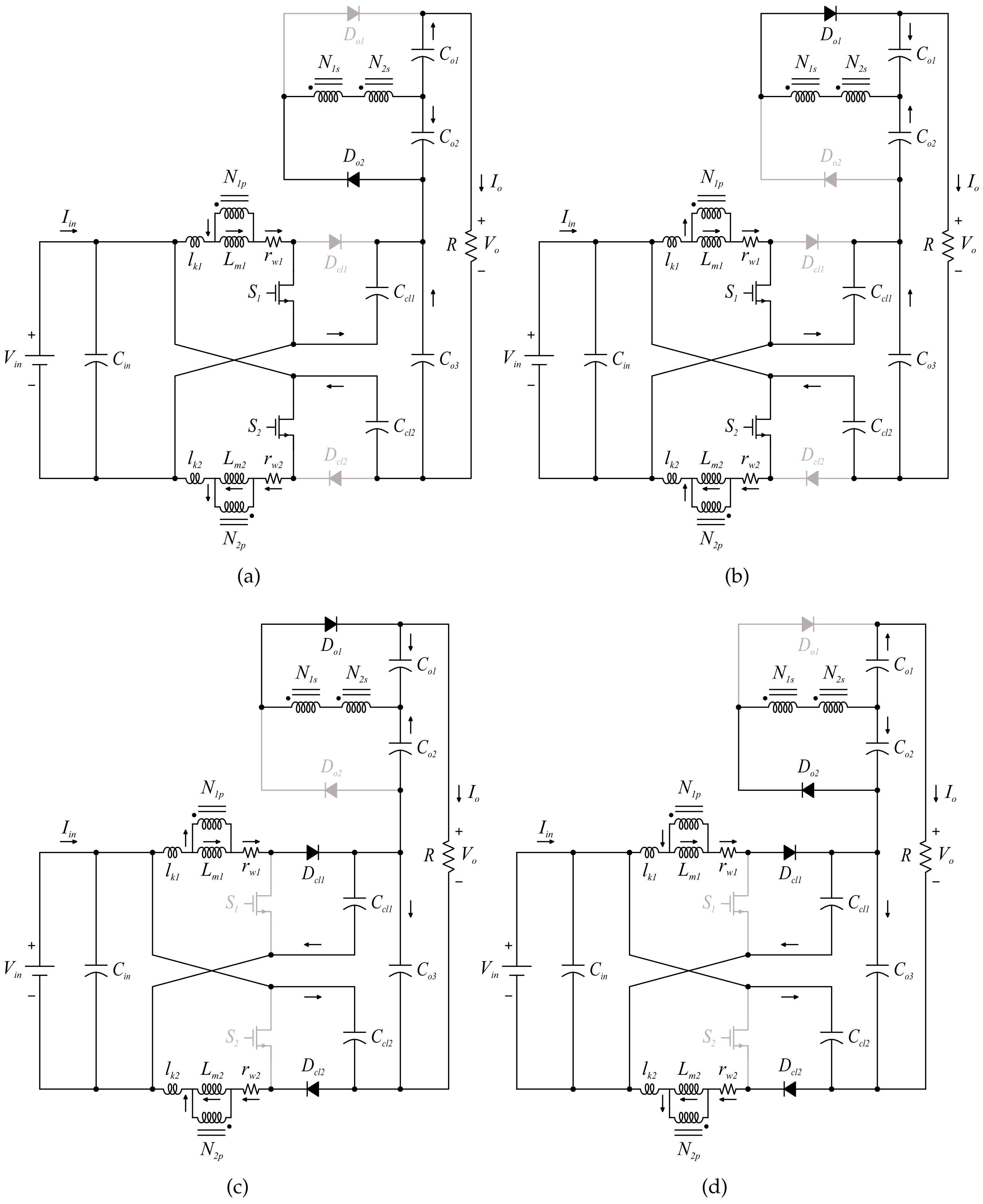
2.1. State I
2.2. State II
2.3. State III
2.4. State IV
3. Proposed Converter Steady-State Analysis
- All components are ideal;
- The magnetizing inductances have the same value;
- ;
- The voltages across the capacitors are constant.
3.1. Voltage Stresses on the Capacitors
3.2. Voltage Stresses on the Semiconductors
3.3. Voltage Gain
3.4. Average Current Stresses
3.5. Maximum Current Stresses
4. Performance Comparison
5. Design Considerations
5.1. Semiconductors Design
5.2. Coupled-Inductor Design
5.3. Capacitor Design
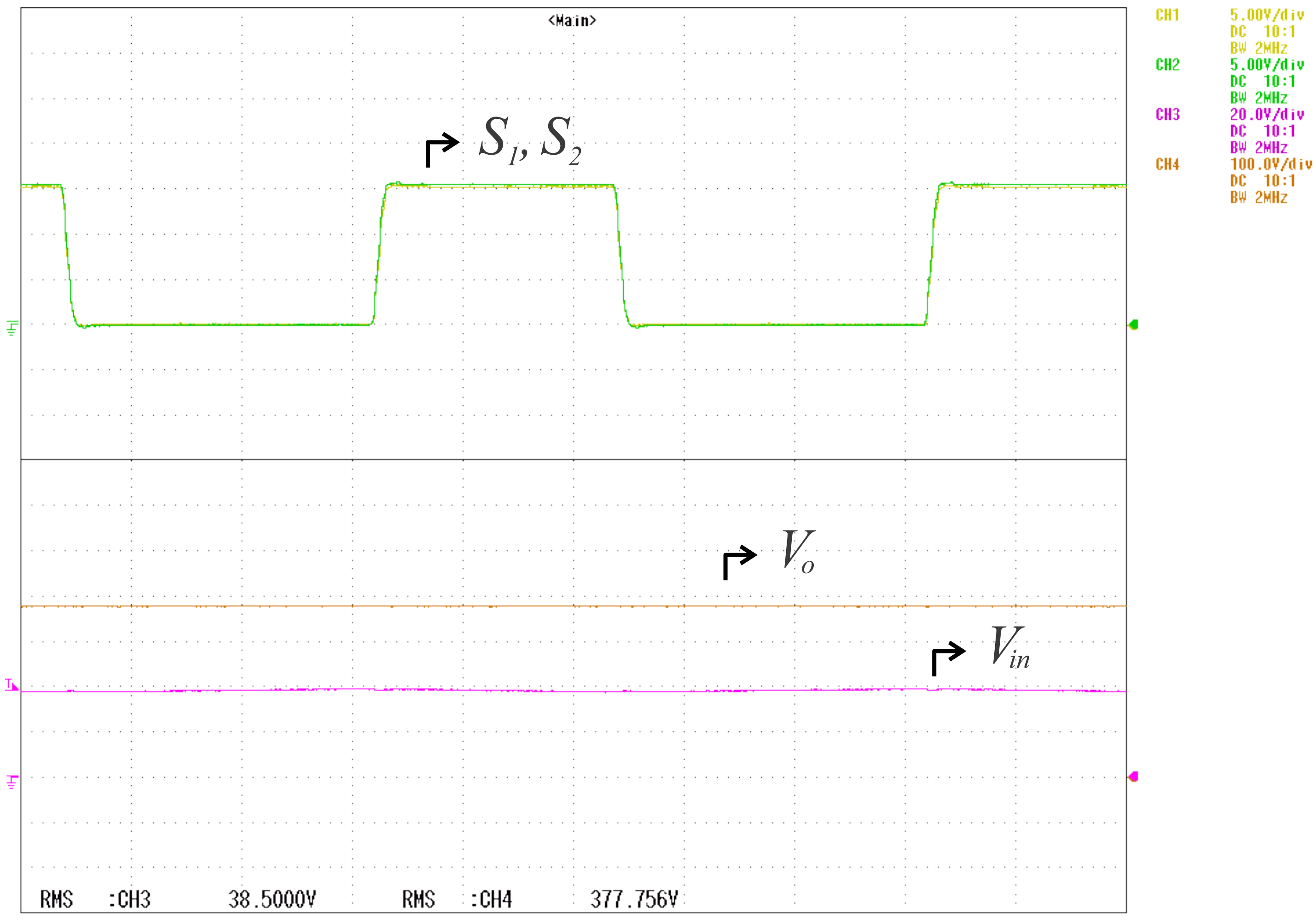
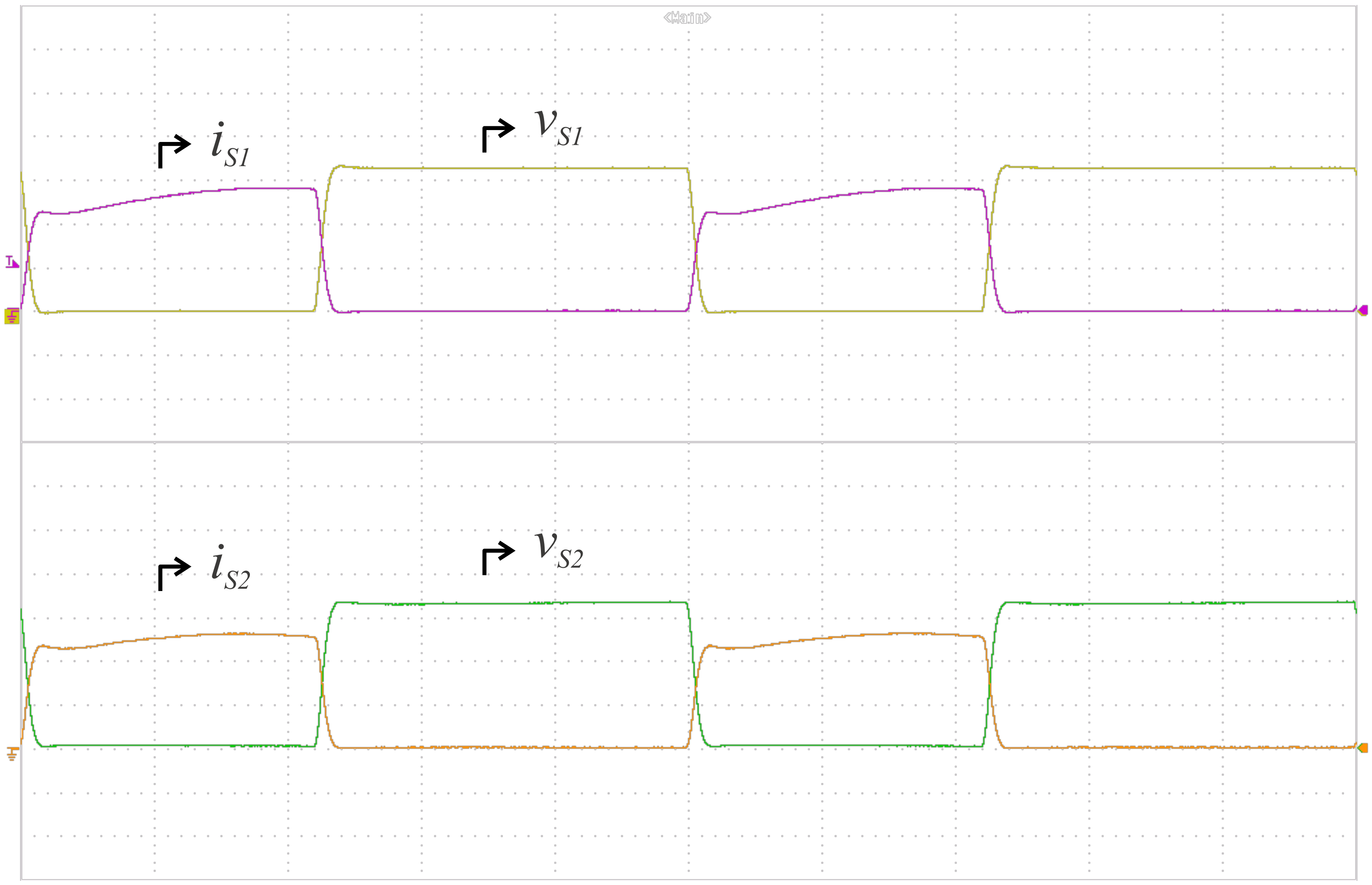
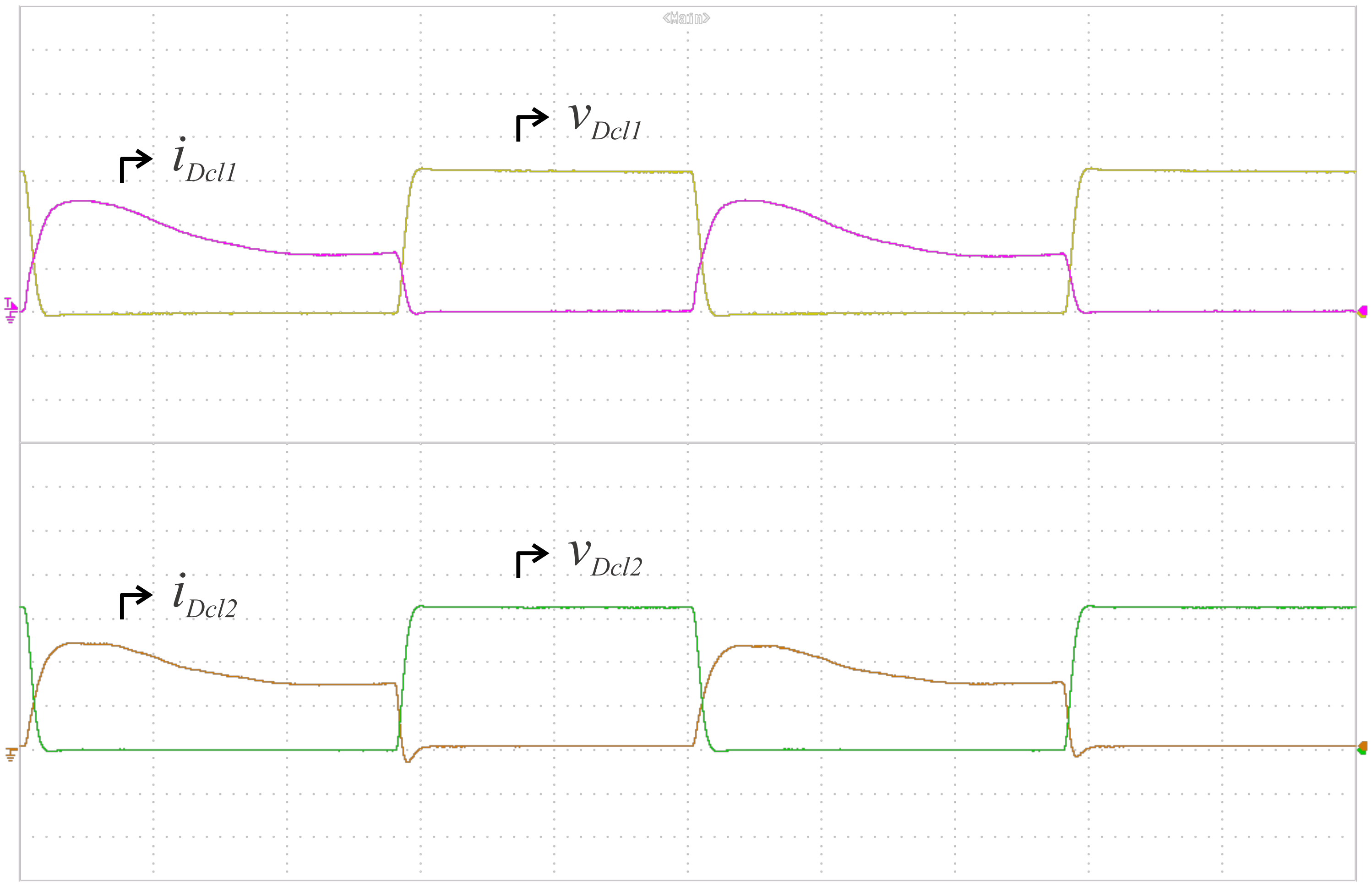
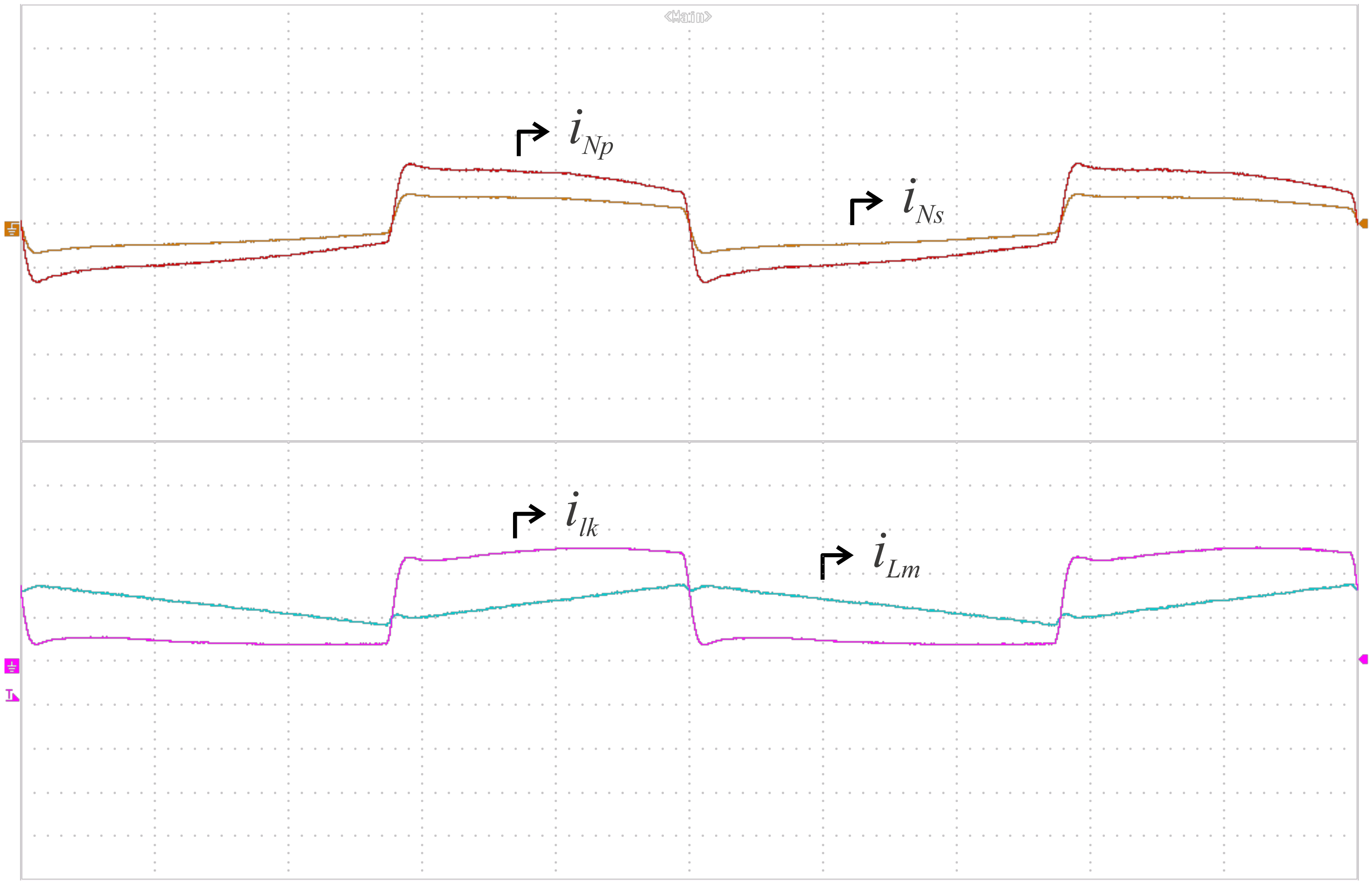
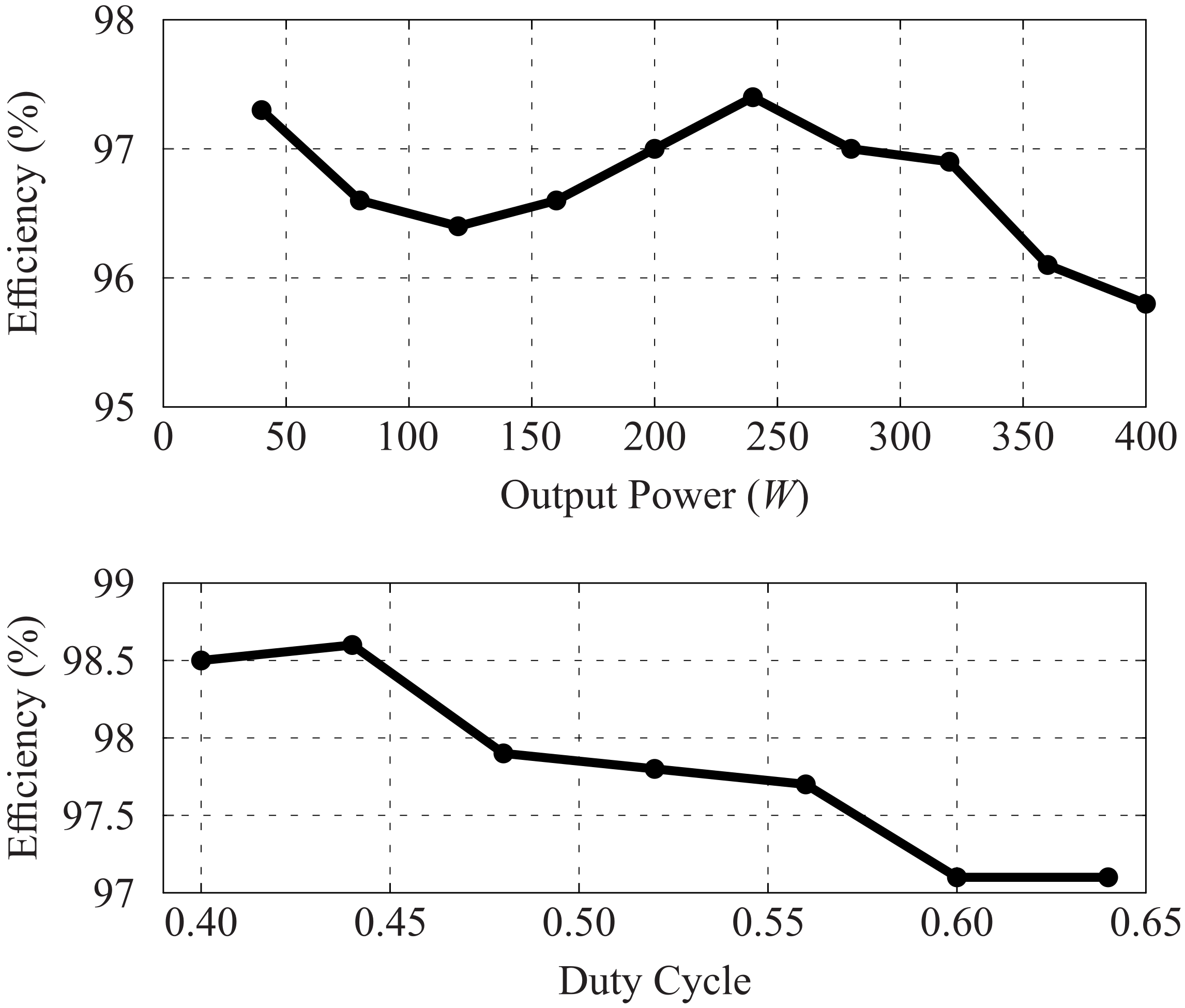
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, L.-Y.; Chang, J.-H.; Chao, K.-H.; Chung, Y.-N. A Low-Cost High-Performance Interleaved Inductor-Coupled Boost Converter for Fuel Cells. Energies 2016, 9, 792. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, J.; Zaid, M.; Sarwar, A.; Lin, C.-H.; Asim, M.; Yadav, R.K.; Tariq, M.; Satpathi, K.; Alamri, B. A New High-Gain DC-DC Converter with Continuous Input Current for DC Microgrid Applications. Energies 2021, 14, 2629. [Google Scholar] [CrossRef]
- Sayed, K.; Gronfula, M.G.; Ziedan, H.A. Novel Soft-Switching Integrated Boost DC-DC Converter for PV Power System. Energies 2020, 13, 749. [Google Scholar] [CrossRef] [Green Version]
- Gu, B.; Dominic, J.; Chen, B.; Zhang, L.; Lai, J. Hybrid Transformer ZVS/ZCS DC–DC Converter with Optimized Magnetics and Improved Power Devices Utilization for Photovoltaic Module Applications. IEEE Trans. Power Electron. 2015, 30, 2127–2136. [Google Scholar] [CrossRef]
- Yan, F.; Li, J.; Du, C.; Zhao, C.; Zhang, W. A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles. Energies 2019, 12, 1689. [Google Scholar] [CrossRef] [Green Version]
- Bi, H.; Wang, P.; Che, Y. A Capacitor Clamped H-Type Boost DC-DC Converter with Wide Voltage-Gain Range for Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 276–290. [Google Scholar] [CrossRef]
- Wu, X.; Yang, M.; Zhou, M.; Zhang, Y.; Fu, J. A Novel High-Gain DC-DC Converter Applied in Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 12763–12774. [Google Scholar] [CrossRef]
- Aamir, M.; Ullah Tareen, W.; Ahmed Kalwar, K.; Ahmed Memon, M.; Mekhilef, S. A High-Frequency Isolated Online Uninterruptible Power Supply (UPS) System with Small Battery Bank for Low Power Applications. Energies 2017, 10, 418. [Google Scholar] [CrossRef] [Green Version]
- Marroqui, D.; Garrigós, A.; Torres, C.; Orts, C.; Blanes, J.M.; Gutierrez, R. Interleaved, Switched Inductor and High-Gain Wide Bandgap Based Boost Converter Proposal. Energies 2021, 14, 800. [Google Scholar] [CrossRef]
- Forouzesh, M.; Yari, K.; Baghramian, A.; Hasanpour, S. Single-switch high step-up converter based on coupled inductor and switched capacitor techniques with quasi-resonant operation. IET Power Electron. 2017, 10, 240–250. [Google Scholar]
- Siwakoti, Y.P.; Blaabjerg, F. Single Switch Nonisolated Ultra-Step-Up DC–DC Converter with an Integrated Coupled Inductor for High Boost Applications. IEEE Trans. Power Electron. 2017, 32, 8544–8558. [Google Scholar] [CrossRef]
- Tofoli, F.L.; Pereira, D.D.C.; Josias de Paula, W.; Oliveira Junior, D.D.S. Survey on non-isolated high-voltage step-up dc-dc topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef] [Green Version]
- Wong, Y.-S.; Chen, J.-F.; Liu, K.-B.; Hsieh, Y.-P. A Novel High Step-Up DC-DC Converter with Coupled Inductor and Switched Clamp Capacitor Techniques for Photovoltaic Systems. Energies 2017, 10, 378. [Google Scholar] [CrossRef] [Green Version]
- Axelrod, B.; Berkovich, Y.; Ioinovici, A. Switched-Capacitor/Switched-Inductor Structures for Getting Transformerless Hybrid DC–DC PWM Converters. IEEE Trans. Circuits Syst. 2008, 55, 687–696. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, D.; Wang, T.; Xu, Z. Analysis of Active-Network Converter with Coupled Inductors. IEEE Trans. Power Electron. 2015, 30, 4874–4882. [Google Scholar] [CrossRef]
- Liu, H.; Li, F. Novel High Step-Up DC–DC Converter with an Active Coupled-Inductor Network for a Sustainable Energy System. IEEE Trans. Power Electron. 2015, 30, 6476–6482. [Google Scholar] [CrossRef]
- Liu, H.; Li, F. A Novel High Step-up Converter with a Quasi-active Switched-Inductor Structure for Renewable Energy Systems. IEEE Trans. Power Electron. 2016, 31, 5030–5039. [Google Scholar] [CrossRef]
- Cao, Y.; Samavatian, V.; Kaskani, K.; Eshraghi, H. A Novel Nonisolated Ultra-High-Voltage-Gain DC–DC Converter with Low Voltage Stress. IEEE Trans. Ind. Electron. 2017, 64, 2809–2819. [Google Scholar] [CrossRef]
- Ai, J.; Lin, M. Ultralarge Gain Step-Up Coupled-Inductor DC–DC Converter with an Asymmetric Voltage Multiplier Network for a Sustainable Energy System. IEEE Trans. Power Electron. 2017, 32, 6896–6903. [Google Scholar] [CrossRef]
- Forouzesh, M.; Shen, Y.; Yari, K.; Siwakoti, Y.P.; Blaabjerg, F. High-Efficiency High Step-Up DC–DC Converter with Dual Coupled Inductors for Grid-Connected Photovoltaic Systems. IEEE Trans. Power Electron. 2018, 33, 5967–5982. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Chen, S. A High Step-up PWM DC-DC Converter with Coupled-Inductor and Resonant Switched-Capacitor. IEEE Trans. Power Electron. 2017, 32, 7739–7749. [Google Scholar] [CrossRef]
- Meier, M.B.; da Silva, S.A.; Badin, A.A.; Romaneli, E.F.R.; Gules, R. Soft-Switching High Static Gain DC–DC Converter without Auxiliary Switches. IEEE Trans. Ind. Electron. 2018, 65, 2335–2345. [Google Scholar] [CrossRef]
- Hassan, W.; Lu, D.D.-C.; Xiao, W. Single-Switch High Step-Up DC–DC Converter with Low and Steady Switch Voltage Stress. IEEE Trans. Ind. Electron. 2019, 66, 9326–9338. [Google Scholar] [CrossRef]
- Sathyan, S.; Suryawanshi, H.M.; Singh, B.; Chakraborty, C.; Verma, V.; Ballal, M.S. ZVS–ZCS High Voltage Gain Integrated Boost Converter for DC Microgrid. IEEE Trans. Ind. Electron. 2016, 63, 6898–6908. [Google Scholar] [CrossRef]
- Nouri, T.; Vosoughi, N.; Hosseini, S.H.; Babaei, E.; Sabahi, M. An Interleaved High Step-Up Converter with Coupled Inductor and Built-In Transformer Voltage Multiplier Cell Techniques. IEEE Trans. Ind. Electron. 2019, 66, 1894–1905. [Google Scholar] [CrossRef]
- Chen, S.-J.; Yang, S.-P.; Huang, C.-M.; Chen, Y.-H. Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems. Energies 2020, 13, 2537. [Google Scholar] [CrossRef]
- De Carvalho, M.R.S.; Bradaschia, F.; Rodrigues Limongi, L.; de Souza Azevedo, G.M. Modeling and Control Design of the Symmetrical Interleaved Coupled-Inductor-Based Boost DC-DC Converter with Clamp Circuits. Energies 2019, 12, 3432. [Google Scholar] [CrossRef] [Green Version]
- Orosz, T.; Tamus, Z.Á. Non-linear Impact of the Short Circuit Impedance Selection on the Cost Optimized Power Transformer Design. Period. Polytech. Electr. Eng. Comput. Sci. 2020, 64, 221–228. [Google Scholar] [CrossRef] [Green Version]
- Alzahrani, A.; Shamsi, P.; Ferdowsi, M. Interleaved Multistage Step-Up Topologies with Voltage Multiplier Cells. Energies 2020, 13, 5990. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]



| No. of Comp. | Voltage Gain | Max. Voltage Stress | Efficiency | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S | D | C | Cor. | Switches | Diodes | Max. | Full Load | ||
| Proposed | 2 | 4 | 6 | 1 | 97.3% | 95.9% | |||
| [16] | 2 | 2 | 2 | 1 | 95.9% | 95.1% | |||
| [17] | 2 | 3 | 3 | 1 | 96.4% | 95.2% | |||
| [18] | 2 | 5 | 5 | 2 | 94.0% | 93.0% | |||
| [21] | 2 | 2 | 3 | 1 | 93.9% | 93.3% | |||
| [22] | 2 | 6 | 5 | 2 | 96.1% | 95.9% | |||
| [24] | 2 | 6 | 5 | 1 | 96.5% | 95.5% | |||
| [26] | 2 | 7 | 6 | 2 | 98.0% | 91.1% | |||
| Parameter/Component | Value/Specification |
|---|---|
| Rated Power | 400 W |
| Input Voltage | 25–45 V |
| Output Voltage | 400 V |
| Switching Frequency | 100 kHz |
| Coupled-Inductor | Thornton NEE-55/28/21-496-IP12R |
| H | |
| 1:1:2:2 | |
| 2 × 10 F | |
| , and | 10 F |
| and | 1 F |
| and | IPP110N20N3 G |
| , , and | STTH3R04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, E.A.O.; Carvalho, M.R.S.d.; Rodrigues Limongi, L.; Cavalcanti, M.C.; Barbosa, E.J.; Azevedo, G.M.d.S. High-Gain High-Efficiency DC–DC Converter with Single-Core Parallel Operation Switched Inductors and Rectifier Voltage Multiplier Cell. Energies 2021, 14, 4634. https://doi.org/10.3390/en14154634
Barbosa EAO, Carvalho MRSd, Rodrigues Limongi L, Cavalcanti MC, Barbosa EJ, Azevedo GMdS. High-Gain High-Efficiency DC–DC Converter with Single-Core Parallel Operation Switched Inductors and Rectifier Voltage Multiplier Cell. Energies. 2021; 14(15):4634. https://doi.org/10.3390/en14154634
Chicago/Turabian StyleBarbosa, Eduardo Augusto Oliveira, Márcio Rodrigo Santos de Carvalho, Leonardo Rodrigues Limongi, Marcelo Cabral Cavalcanti, Eduardo José Barbosa, and Gustavo Medeiros de Souza Azevedo. 2021. "High-Gain High-Efficiency DC–DC Converter with Single-Core Parallel Operation Switched Inductors and Rectifier Voltage Multiplier Cell" Energies 14, no. 15: 4634. https://doi.org/10.3390/en14154634
APA StyleBarbosa, E. A. O., Carvalho, M. R. S. d., Rodrigues Limongi, L., Cavalcanti, M. C., Barbosa, E. J., & Azevedo, G. M. d. S. (2021). High-Gain High-Efficiency DC–DC Converter with Single-Core Parallel Operation Switched Inductors and Rectifier Voltage Multiplier Cell. Energies, 14(15), 4634. https://doi.org/10.3390/en14154634









