A Multi-Model Probability Based Two-Layer Fusion Modeling Approach of Supercapacitor for Electric Vehicles

Abstract

The improvement of the supercapacitor model redundancy is a significant method to guarantee the reliability of the power system in electric vehicle application. In order to enhance the accuracy of the supercapacitor model, eight conventional supercapacitor models were selected for parameter identification by genetic algorithm, and the model accuracies based on standard diving cycle are further discussed. Then, three fusion modeling approaches including Bayesian fusion, residual normalization fusion, and state of charge (SOC) fragment fusion are presented and compared. In order to further improve the accuracy of these models, a two-layer fusion model based on SOC fragments is proposed in this paper. Compared with other fusion models, the root mean square error (RMSE), maximum error, and mean error of the two-layer fusion model can be reduced by at least 23.04%, 8.70%, and 30.13%, respectively. Moreover, the two-layer fusion model is further verified at 10, 25, and 40 °C, and the RMSE can be correspondingly reduced by 60.41%, 47.26%, 23.04%. The results indicate that the two-layer fusion model proposed in this paper achieves better robustness and accuracy.

1. Introduction

In recent decades, a new energy technology, which has been rapidly developed and applied in the field of electric vehicles (EV) has attracted the attention of many countries such as China, the United States, Germany, the United Kingdom and Japan [1]. Lithium-ion batteries are widely used in EV power systems due to their high energy and power density and low self-discharge rate [2,3]. The high rate of charge and discharge current will seriously affect the life of the battery, which can generally only be controlled within 2C rate. However, supercapacitors can not only achieve high-rate charge and discharge, but also have unparalleled advantages in terms of power density and long cycle life. Therefore, in the EVs application, supercapacitors are often combined with lithium-ion batteries to serve as a hybrid energy storage system for EV energy supply [4,5,6]. In view of the prominent characteristic of the high power density, supercapacitors can not only provide the peak current urgently needed by electric vehicles and absorb excessive braking current, but also extend the cycle life of the power system and alleviate the impact of surge current on bus voltage. Supercapacitor models are strongly related to the optimal control of EV power systems. Therefore, inaccurate model parameters easily degrade the monitoring function of the power system, and may also lead to potential problems such as low efficiency, fires, and explosion of electric vehicles [7,8]. Therefore, the increased redundancy of the supercapacitor model is the significant approach to enhance the accuracy and guarantee the reliability of power systems for EVs.

At present, the most commonly used models of supercapacitor include the black box model, electrochemical model, and equivalent circuit model (ECM) [9,10].

(1) The black box model can describe the relationship between specific parameters and external characteristics with good flexibility and model precision. Optimization algorithms, including neural networks, fuzzy control, and machine learning, are employed to train the model on a large number of experimental data [11]. Wu et al. established an equivalent circuit neural network nonlinear dynamics model with temperature and voltage as input variables. Although the results are reliable, a large amount of data is needed for simulation [12]. Zhang et al. constructed a residual capacity estimation model based on an artificial neural network to represent the dynamic performances of supercapacitors, considering various currents and uncertain temperatures [13]. The experimental results show that the proposed model is feasible and effective, which can provide accurate prediction of residual capacity. Nevertheless, the black box model requires a large amount of data for training to improve the prediction accuracy.

(2) In order to accurately describe the internal parameters and external characteristics of supercapacitors, the electrochemical model, including many partial differential equations, is widely used in supercapacitor modeling [14]. Drummond et al. studied two electrochemical models to simulate the nonlinear partial differentiation of supercapacitors and found that the spectral discrete model can improve computational efficiency while ensuring accuracy. [15] Wang et al. proposed a three-dimensional model, which not only makes it possible to simulate the dynamic performances of electric double layer capacitors (EDLCs), but also provides standard rules for achieving the maximum charging performance of EDLCs [16]. Drummond et al. presented an absolute voltage stability method, which combines the electrochemical parameters with electrical properties of the supercapacitor. The method can obtain a stable voltage with less experimental data [17]. Tian et al. conducted a comparative study on five fractional models and found that the composition and structure of the models would affect the voltage simulation and state of charge (SOC) estimation [18]. In fact, the model accuracy is not directly proportional to the parameter complexity. Although the electrochemical model has many advantages, it is not conducive to practical application due to its complex structure and huge computation [19].

(3) An equivalent circuit model is a circuit network composed of a capacitor, inductor, resistor, and other circuit elements to represent the voltage response characteristics of supercapacitors. At present, equivalent circuit models mainly include the internal resistance model, RC model, and PNGV model, etc. [20]. Since the equivalent circuit model has fewer parameters and can balance the accuracy and complexity of dynamic simulation, it has been extensively used in the model construction of automotive supercapacitors [21,22,23]. Spyker et al. proposed a classical equivalent circuit, which consists of an equivalent series resistance, equivalent parallel resistance, and main capacitor, but it only describes the dynamic performance of supercapacitors in a short time [24]. From ref [22], a variable resistance equivalent circuit model for supercapacitors is presented to accurately simulate the charging, redistribution, and self-discharge processes of supercapacitors. Compared with the energy recursive model, it can provide a more accurate terminal voltage estimation of the supercapacitor. Liu et al. described the relationship between model parameters and temperature variation based on different functions. In this way, an equivalent circuit model considering temperature uncertainty is introduced for enhancing model fitness at various temperatures [25,26,27].

There is a lot of research that has discussed the supercapacitor models, but most of this has focused on the methods to improve the accuracy under a single model. However, each model has the particular advantage under different SOC ranges. Therefore, the improvement of model accuracy and the offset of the single model drawback are the key problems in the supercapacitor modeling field. The fusion model modeling method is an effective and popular solution to the problem. The fusion method consists of a physical fusion method and a data fusion method. Additionally, the combination of physical fusion method and data fusion method can theoretically further improve the model accuracy. Liu et al. established a model on the basis of a composite model [28] and presented a model combination method, which can be used to construct data fusion by a multi-model combination. Moreover, many data fusion methods including SOC fusion estimation and weight allocation optimization fusion are introduced in the literature [29]. Li et al. proposed a fusion estimation method of SOC based on Gaussian process regression (GPR), which significantly improved the accuracy of the model [30]. However, a single Gaussian distribution is difficult to resist external interference, and the results are uncertain. Wei et al. used the normalized weights of multiple Gaussian distributions to calculate the weight of Gaussian components, and proposed a SOC estimation method based on Gaussian mixture model (GMM). The simulation results show that this method can effectively resist external interference and improve the accuracy of the model [31]. Meanwhile, Lyu et al. proposed a data fusion model method to estimate battery capacity by local charging curve using Gaussian regression, and smoothing incremental capacity curve by local weighted scatter smoothing can effectively improve the model accuracy [32]. Researchers can also use a data fusion method when constructing a terminal voltage fusion model. However, because the different fusion methods will affect the accuracy of the supercapacitor model, how to choose the fusion method effectively is a problem worth studying.

In this paper, a two-layer fusion model based on a multi-model supercapacitor is proposed. This fusion method adopts physical data fusion, including three fusion models: a fusion model based on SOC fragments, a fusion model based on a Bayesian algorithm [33], and fusion model based on residual normalization.

This paper is organized as follows. Section 2 introduces the feature experiments for supercapacitors. In addition, eight popular equivalent circuit models of supercapacitors are presented in Section 3. Section 4 discusses the parameter identification method for supercapacitor models. In Section 5, a two-layer fusion model is proposed, and the conclusion is in Section 6.

2. Characteristics of Supercapacitors

The characteristic experiments of the supercapacitors mainly include hybrid pulse power characterization (HPPC) and urban dynamometer driving schedule (UDDS). The HPPC experiment can reflect the relationship between voltage characteristics, depth of discharge (DoD), and charge–discharge rate under different SOCs, which aims to provide experimental data supporting the parameter identification of the supercapacitor model. The UDDS character experiments are mainly used to test the performance of the supercapacitor under actual driving conditions.

The capacitance of the experimental supercapacitor is 1500 F, and the upper cut-off voltage is 2.7 V (SOC = 100%) and the lower cut-off voltage is set as 0.5 V (SOC = 0%). The HPPC test procedure is shown follows:

Step 1: Charge the supercapacitor to 2.7 V with constant current 1 A;

Step 2: Hold the supercapacitor for 10 h to reach a stable state;

Step 3: Discharge the supercapacitor with low current to 0.5 V;

Step 4: Hold for 5 min;

Step 5: Then, charge with 1 A constant current constant voltage (CC-CV) up to the cut-off voltage of 2.7 V, until the current is less than 0.05 A (define: t = 0).

Step 6: Complete charging and discharging tests in different rates of current, t = t + 1. Firstly, discharge for 5 s and charge for 5 s at a current of 1A; then, discharge for 5 s and charge for 5 s at a current of 5A; finally, discharge at 10A for 5 s and charge for 5 s. It is worth noting the need to stand for a period of time after each charge and discharge.

Step 7: Keep 10% of the rated capacity of 1 A constant discharge. If t ≤ 10, return to Step 6.

The pulse step, rest step, and discharge step of the test are shown in Figure 1. Positive denotes current discharge and negative denotes current charge.

3. Introduction to the Supercapacitor Model

Since there are many models of supercapacitors, the accuracy of the model and its complexity should be taken into consideration when selecting the model.

The accuracy and complexity of supercapacitor models are the significant factors of concern in EV application. Moreover, there are many common supercapacitor models reported in previous literatures. Consequently, eight popular equivalent circuit models including the Rint model [6], Thevenin model [6], dual-polarization model [6], PNGV model [34], GNL model [35], dynamic model [24], first-order RC model with one-state hysteresis [36], and second-order RC model with one-state hysteresis [36], were comprehensively considered and selected in this paper.

The Rint model consists of a power module and an internal resistance module.

The Thevenin model considers the polarization characteristics of the supercapacitor. In the model, the ideal voltage source, U_oc, describes the open-circuit voltage, and R_D and C are the polarization internal resistance and polarization capacitance, respectively. U_D is the voltage drop of RC parallel link, which is used to simulate the polarization voltage of the supercapacitor.

In the dual-polarization model, two RC modules in series are added on the basis of the Rint model to describe the supercapacitor polarization characteristics.

In the PNGV model, U_oc is the ideal voltage source and represents the open-circuit voltage. R₀ is the ohmic resistance of the battery. R_p is the battery polarization resistance. C_p is the parallel capacitance beside R_p. C_p describes the change in open-circuit voltage as the load current accumulates over time.

GNL model considers the effects of ohmic polarization, electrochemical polarization, concentration polarization, and self-discharge. In the model, the open-circuit voltage is represented as U_oc. R₁ and C₁ are concentration polarization resistance capacitance parameters, respectively. R₂ and C₂ are the resistance-capacitance parameters of the electrochemical polarization of the power source. R_e is ohmic internal resistance and R_s is the internal resistance of self-discharge.

The dynamic model is composed of a series resistor, a series capacitor, and two RC networks. In the model, U_oc is the ideal pressure source. u0, u1, and u2 correspondingly represent the main capacity and the terminal voltages of the two RC networks.

The model with one-state hysteresis considers changes in y (dependent variable) behind changes in x (independent variable). In the supercapacitor energy storage system, the voltage changes behind the current changes. Therefore, the lag level h is added in the calculation of the first-order RC model with one-state hysteresis, and second-order RC model with one-state hysteresis.

4. Model Parameter Identification

4.1. Genetic Algorithm (GA)

GA is a kind of adaptive global optimization probabilistic search algorithm, which has good adaptability and optimization ability in parameter identification. It starts with a randomly generated population. After the initial population is generated, the principle of survival of the fittest needs to be implemented in order to finally approach the optimal solution. In each generation, individuals are selected according to the fitness in the problem field, and the filial generation representing the new solution set is generated by genetic operators. This process is the same as natural selection to make offspring better adapted to the environment. After decoding, the optimal individual in the last generation population may be used as the optimal solution of the problem. In this paper, the fitness function of genetic algorithm is the square sum of the error between the terminal voltage of the equivalent circuit model and the actual measured terminal voltage.

The genetic algorithm flow diagram is shown in Figure 2. The specific steps of genetic algorithm are listed as follows:

Step 1. Set the boundary conditions of the parameters.

Step 2. Generate the initial population.

Step 3. Calculate the fitness of individuals in the population and judge whether the requirements are met. If satisfied, identification is over; otherwise, proceed the next step.

Step 4. Carry out inheritance, crossover, and mutation of the population to obtain offspring.

Step 5. Return to Step 3.

4.2. Parameter Identification

This section takes the Thevenin model as an example to describe, and the rest of the models are similar. Circuit diagrams of the Thevenin model of the supercapacitor is shown in

Table 1. Circuit diagram and equation of each model.

Model	Circuit Diagram	Equation
Rint model		$U_{\mathrm{t}}=U_{\mathrm{oc}}-i_{\mathrm{L}}{R}_{\mathrm{i}}$
Thevenin model		$\{\begin{array}{l}{\dot{U}}_{\mathrm{D}}=\frac{i_{\mathrm{L}}}{C}-\frac{U_{\mathrm{D}}}{R_{\mathrm{D}}C}\\ U_{\mathrm{t}}=U_{\mathrm{oc}}-U_{\mathrm{D}}-i_{\mathrm{L}}{R}_{\mathrm{i}}\end{array}$
Dual-polarization model		$\{\begin{array}{l}{U}_{\mathrm{D}1}=\frac{i_{\mathrm{L}}}{C_{\mathrm{D}1}}-\frac{U_{\mathrm{D}1}}{R_{\mathrm{D}1}{C}_{\mathrm{D}1}}\\ U_{\mathrm{D}2}=\frac{i_{\mathrm{L}}}{C_{\mathrm{D}2}}-\frac{U_{\mathrm{D}2}}{R_{\mathrm{D}2}{C}_{\mathrm{D}2}}\\ U_{\mathrm{t}}=U_{\mathrm{oc}}-U_{\mathrm{D}1}-U_{\mathrm{D}2}-I_{\mathrm{L}}{R}_{\mathrm{i}}\end{array}$
PNGV model		$\{\begin{array}{l}\left[\begin{array}{c}\frac{d{U}_{\mathrm{p}}}{dt}\\ \frac{d{U}_{\mathrm{b}}}{dt}\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{C_{\mathrm{p}}{R}_{\mathrm{p}}}& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{U}_{\mathrm{p}}\\ U_{\mathrm{b}}\end{array}\right]+\left[\begin{array}{c}\frac{1}{C_{\mathrm{p}}}\\ \frac{1}{C_{\mathrm{b}}}\end{array}\right]\left[I\right]\\ \left[U_L\right]=[U_{oc}]+\left[\begin{array}{cc}-1& -1\end{array}\right]\left[\begin{array}{c}{U}_{\mathrm{p}}\\ U_{\mathrm{b}}\end{array}\right]-R_0\left[I\right]\end{array}$
GNL model		$\{\begin{array}{l}{I}_m=\frac{U_1}{R_1}+C_1\frac{d{U}_1}{dt}\\ I_m=\frac{U_2}{R_2}+C_2\frac{d{U}_2}{dt}\\ U_{\mathrm{L}}=U_{\mathrm{oc}}-I_m{R}_{\mathrm{e}}-U_1-U_2\\ U_{\mathrm{L}}=(I-I_m)R_{\mathrm{s}}\end{array}$
Dynamic model		$\{\begin{array}{l}\frac{u_1}{R_1}+C_1\frac{d{u}_1}{dt}=i_{\mathrm{c}}\\ \frac{u_2}{R_2}+C_2\frac{d{u}_2}{dt}=i_{\mathrm{c}}\\ u_1+u_2+R_{0}i=u_{\mathrm{c}}\end{array}$
First-order RC model with one-state hysteresis		$\{\begin{array}{l}h=-\left|\kappa i_{\mathrm{L}}\right|h+\left|\kappa i_{\mathrm{L}}\right|\mathrm{sgn}(i_{\mathrm{L}})\\ U=-\frac{1}{C{R}_{\mathrm{d}}}U+\frac{1}{C}{i}_{\mathrm{L}}\\ U_{\mathrm{L}}=U_{\mathrm{oc}}+hM-U-i_{\mathrm{L}}{R}_0\end{array}$
Second-order RC model with one-state hysteresis.		$\{\begin{array}{l}h=-\left|\kappa i_{\mathrm{L}}\right|h+\left|\kappa i_{\mathrm{L}}\right|\mathrm{sgn}(i_{\mathrm{L}})\\ U_1=-\frac{1}{C_1{R}_{\mathrm{d}1}}{U}_1+\frac{1}{C_1}{i}_{\mathrm{L}}\\ U_2=-\frac{1}{C_2{R}_{\mathrm{d}}{}_2}{U}_2+\frac{1}{C_2}{i}_{\mathrm{L}}\\ U_{\mathrm{L}}=U_{\mathrm{oc}}+hM-U_1-U_2-i_{\mathrm{L}}{R}_0\end{array}$

, where i_L is the load current; R_D and C are the polarization internal resistance and polarization capacitance, respectively; and U_D is the voltage drop of RC parallel link, which is used to simulate the polarization voltage of the supercapacitor [37]. The circuit equation of this circuit model is Equation (1).

$$\{\begin{array}{l}{\dot{U}}_{\mathrm{D}}=\frac{i_{\mathrm{L}}}{C}-\frac{U_{\mathrm{D}}}{R_{\mathrm{D}}C}\\ U_{\mathrm{t}}=U_{\mathrm{oc}}-U_{\mathrm{D}}-i_{\mathrm{L}}{R}_{\mathrm{i}}\end{array}$$

(1)

The model is discretized before parameter identification. The polarization voltage of the supercapacitor model is obtained as Equation (2).

$$U_{\mathrm{D}}[(k+1)\Delta t]=e^{-\Delta t/\tau }{U}_{\mathrm{D}}(k\Delta t)+R_{\mathrm{D}}{i}_{\mathrm{L}}[(k+1)\Delta t][1-e^{-\Delta t/\tau }]$$

(2)

Among them, $\tau =R_{\mathrm{D}}\times C$. Meanwhile, the discretization calculation equation of the supercapacitor SOC can be obtained as shown in Equation (3).

$$z_k=z_{k-1}-{\eta }_i{i}_{\mathrm{L}}\Delta t/C_{\max }$$

(3)

Z_k represents the SOC value at time k; $\Delta t$ represents the segment time of current acquisition; ${\eta }_i$ represents the coulomb efficiency; and C_max represents the rated capacity of the supercapacitor.

The parameters to be identified in the Thevenin model of the supercapacitor include R_i, R_D, and $\tau$. Since the parameters will change under different SOC state estimations, it is necessary to identify the three parameters in each SOC segment. In order to balance the identification accuracy and efficiency, the discharge segment of the supercapacitor was divided into ten segments ranging from 100% to 0%. The identification results and errors are shown in

Table 2. Parameter identification results of Thevenin model for supercapacitors.

SOC	${\mathit{R}}_{\mathbf{i}}\left(\mathbf{m}\mathbf{\Omega }\right)$	${\mathit{R}}_{\mathbf{D}}\left(\mathbf{m}\mathbf{\Omega }\right)$	$\mathbf{\tau }$
100%−90%	0.5760	4.079	318.778
90%−80%	0.5874	4.956	159.593
80%−70%	0.5790	4.289	124.776
70%−60%	0.5679	9.450	263.936
60%−50%	0.5557	3.965	134.347
50%−40%	0.5437	7.719	254.746
40%−30%	0.5488	9.117	309.871
30%−20%	0.5494	6.066	180.197
20%−10%	0.5530	6.383	225.290
10%−0%	0.4853	0.681	11.2813

:

Figure 3 shows the error diagram of the terminal voltage simulation results and experimental values under UDDS conditions. In general, the identification error can be divided into two ranges, namely the SOC range of [50%–100%] and [0%–50%]. As can be seen from the Figure 3, the Thevenin model has a relatively excellent simulation accuracy in the segment of [50%–100%], and the error in this segment can be controlled within 10 mV without large fluctuations. Similar results were obtained by verifying the other seven models. When the SOC drops to [0%–50%], the accuracy of all models decreases. When the SOC is above 50%, a better precision can be obtained. The results show that the genetic algorithm can effectively identify the relevant parameters in each model.

After parameter identification based on the data obtained from the HPPC, the maximum error, mean error, and root mean square error (RMSE) of the eight models were, respectively, calculated under the UDDS, as shown in

Table 3. Errors of the eight models.

Model	Maximum Error (mV)	Mean Error (mV)	Root Mean Square Error (mV)
Rint model	15.062	2.2248	3.0864
Thevenin model	15.953	2.2727	3.1445
Dual-polarization model	18.411	3.9966	4.5970
PNGV model	17.110	3.9035	5.3282
GNL model	15.317	2.2960	3.1851
First-order RC model with one-state hysteresis	20.038	5.5645	6.8858
Second-order RC model with one-state hysteresis.	26.105	12.2051	12.948
Dynamic model	18.775	3.6325	4.4737

.

By analyzing the terminal voltage error model of supercapacitors, it can be seen that more complex models can not necessarily achieve higher accuracy of training data sets. In fact, if the nature of the model is too complex, it will be more susceptible to uncertainty. Then, models with overly complex features are not suitable for model validation datasets.

From Table 3, the Rint model has better simulation accuracy compared with other models. Due to the difference in the simulation accuracy of the SOC segment, the variation of the SOC segment should be taken into consideration in the comparison. For example, in the SOC range of (90%–100%), the RMSE of the Rint model is 0.0285 mV, which is the model with the highest accuracy in this SOC range. However, in the SOC range of (50%–60%), the accuracy of the dynamic model is the highest, and the root mean square error is 1.7946 mV.

On account of model differences affecting the simulation accuracy of terminal voltage, none of the models can maintain the optimal simulation accuracy of terminal voltage at different times. It is difficult for a single model to maintain the optimal accuracy in a changing external environment. Therefore, the supercapacitor fusion model based on multi-model probabilistic is proposed in this paper.

5. Multi-Model Probabilistic Fusion Model

It has been verified that the model with the best accuracy is different in the varying SOC interval. Therefore, results based on a single model are not guaranteed to be optimal in the entire SOC segment. It is worth proposing an optimization algorithm based on multiple models to further optimize accuracy. Consequently, four kinds of multi-model voltage residuals are presented to scientifically determine the model switching objective function.

Fusion model based on SOC fragments: The objective function was established to find the minimum root mean square error model in different SOC intervals, and the fusion model was established by combining them. The operation is to divide the SOC into 10 segments, and then calculate the RMSE of the different models in each segment. The model with the smallest RMSE value is used as the fusion model of the current SoC segment.

Fusion model based on Bayesian algorithm: The advantages of different models are combined by giving weight to the eight models, respectively, for fusion. In order to determine the weight of each model, the probability is adopted in this paper to describe the degree of closeness between the predicted terminal voltage and the real voltage. When selecting weights, the statistical characteristics of the residual are added, and a Bayesian algorithm is used to obtain the conditional distribution probability of terminal voltage. A Bayesian algorithm is the estimation of the prior knowledge to the posterior knowledge in the inspection process. By using the discrete Bayesian algorithm, the probability of the previous moment is considered as a deterministic probability, and then the probability of the later moment can be estimated. In this way, the weight of each model at the next moment is obtained.

Fusion model based on residual normalization: The fusion result is the weighted sum of each model, which is taken as the initial value of the state estimation at the next moment, so as to obtain the prior estimate. When the weight is selected, the instantaneous terminal voltage residuals represent the estimation accuracy. The specific operation is to normalize the terminal voltage residuals of the eight models, and the obtained probability based on the normalization of the residual is the model weight.

5.1. Fusion Model Based on SOC Fragments

RMSEs of different models are calculated under the SOC segment, and the model corresponding to the minimum RMSE is determined. The model terminal voltage is taken as the terminal voltage of the segment under the fusion model. According to the minimum RMSE of each model in 10 SOC segments, the models selected for each SOC segment are shown in

Table 4. Selection of different SOC fragment models.

SOC	The Target Model
100%−90%	second-order RC model with one-state
90%−80%	GNL model
80%−70%	Rint model
70%−60%	Rint model
60%−50%	PNGV model
50%−40%	Rint model
40%−30%	Rint model
30%−20%	Rint model
20%−10%	Rint model
10%−0%	Thevenin model

.

It can be seen from the selection of models in different SOC segments that the Rint model has the highest probability of being defined as the target model. There is a 60% probability that the Rint model will be selected, which is in line with the overall optimal result of the Rint model in Table 3. The fusion model method based on the SOC segment incorporates 75% of the target model through optimization selection. This method eliminated some models with poor accuracy in each SOC segment and retained the models with better accuracy, which greatly reduced the operation time and improved the fusion efficiency.

5.2. Fusion Model Based on Bayesian Algorithm

The Bayesian estimation process is simple and fast, and considering the influence of the previous moment on the next moment, the predicted value of terminal voltage is set as:

$$\hat{U}(k)={\displaystyle \sum _{i=1}^8{w}_i{\tilde{U}}_i(k)}$$

(4)

Among them, ${\tilde{U}}_i(k)$ is the predicted value of terminal voltage of a single model, $w_i$ is the weight coefficient of each model, and $w_i$ satisfies ${\displaystyle \sum _{i=1}^8{w}_i=1}$.

According to Bayes’ theorem:

$$p(\tilde{U}(k)|p(U(k)))=\frac{p(U(k)|\tilde{U}(k))p(w(k))}{p(U(k))}$$

(5)

U(k) is the terminal voltage to be evaluated at k, and p is the probability. The fusion probability of each target model is calculated as follows:

$$p(s_i(k)|U(k))=\frac{p(s_i(k),U(k))}{p(U(k))}$$

(6)

where s_i(k) is the parameter set of the ith model under the SOC basis at time k.

The predicted value of terminal voltage can be rewritten as:

$$\hat{U}(k)={\displaystyle \sum _{i=1}^8{p}_i{\tilde{U}}_i(k)}$$

(7)

Residuals for: $e_i(k)=U_i(k)-{\tilde{U}}_i(k)$

Then:

$$\begin{array}{l}{\Psi }_i(k)=\frac{1}{{(2\pi )}^{1/2}{Q}_i{}^{1/2}(k)}\exp (-e_i{(k)}^2{Q}_i{(k)}^{-1}/2)\\ \end{array}$$

(8)

Among them, $Q_i(k)={\displaystyle \sum _{k=1}^n}{e}_i(k{)}^2/n$. This is the variance of the residuals of each model.

Therefore, the weight coefficient is:

$$w_i(k)=\frac{{\Psi }_i(k)w_i(k-1)}{{\displaystyle \sum _{i=1}^8{\Psi }_i(k)w_i(k-1)}}$$

(9)

5.3. Fusion Model Based on Residual Normalization

Without considering the influence of weights at the previous moment on the weights at the later moment, the probability is adopted to describe the approximation degree between the predicted terminal voltage and the real value. The predicted value of terminal voltage is:

$$\hat{U}(k)={\displaystyle \sum _{i=1}^8{w}_i{z}_k}$$

(10)

Z_k is the SOC value. $w_i$ is the weight coefficient of each model, and $w_i$ satisfies ${\displaystyle \sum _{i=1}^8{w}_i=1}$.

Residuals for: $e_i(k)=U_i(k)-{\tilde{U}}_i(k)$

Then,$w_i(k)=\frac{S(k)-e_i{}^2(k)}{(N-1)S(k)}$, S(k) is the sum of squares of the residuals of each model. In other words, $S(k)={\displaystyle \sum _{i=1}^8{e}_i{}^2(k)}$.

5.4. Two-Layer Fusion Model

In order to further improve the accuracy and adaptability of the model, the two-layer fusion model is proposed. The optimal root mean square error (RMSE) is taken as the decision variable, and the corresponding data to be fused is taken as the result of the two-layer fusion model. The algorithm process of the double-layer fusion model is shown in Figure 4.

The specific steps are as follows:

Step 1: Input the error matrices E₁, E₂ and E₃ under UDDS of each model.

Step 2: Calculate RMSE with SOC segment to obtain matrix RE_ij, i = 3, j = 10.

Step 3: Search the position information of the minimum RMSE of each segment, respectively, to obtain M_ij and N_ij.

Step 4: Assign the position information M_ij and N_ij to the corresponding objective function. That is, get the objective function of different SOC segments.

Under different SOC segments, the selected target models are shown in

Table 5. Selection of two-layer fusion model of different SOC fragments.

SOC	The Target Model
100%−90%	Fusion model based on residual normalization
90%−80%	Fusion model based on residual normalization
80%−70%	Fusion model based on Bayesian algorithm:
70%−60%	Fusion model based on residual normalization
60%−50%	Fusion model based on SOC fragments
50%−40%	Fusion model based on residual normalization
40%−30%	Fusion model based on residual normalization
30%−20%	Fusion model based on residual normalization
20%−10%	Fusion model based on residual normalization
10%−0%	Fusion model based on residual normalization

.

In the selection of two-layer fusion models of different SOC fragments, it can be seen that the fusion model based on residual normalization has the highest probability to be defined as the target model, up to 80%. However, the fusion model based on SOC fragments and the fusion model based on a Bayesian algorithm only have a 10% probability to be defined as the target model. The results show that the fusion model based on residual normalization is more advantageous in general. However, it is not reliable to explain the accuracy of the model only according to the probability of the model being selected. Therefore, it is more necessary to compare and analyze each model in depth.

5.5. Results and Analysis of Different Fusion Models

Based on the data obtained from the fusion model, it is divided into 10 segments according to per 10% SOC under the UDDS to verify its errors. On the basis of the errors, the maximum error, mean error, and RMSE of the four fusion models are calculated, respectively. The comparison between the simulated values of the four fusion models and the measured terminal voltages is shown in Figure 5.

It can be concluded that, due to the good convergence and small error, the two-layer fusion model does not show obvious advantages to improve the accuracy in high SOC segments. In the middle and low SOC segments, the initial data is more volatile than that of high SOC segment, while the two-layer fusion model obviously shows the advantage of fast convergence. Combined with

Table 6. Errors of the four fusion models.

Model	Maximum Error (mV)	Mean Error (mV)	Root Mean Square Error (mV)
Fusion model based on SOC fragments	15.062	2.1179	3.0023
Fusion model based on Bayesian algorithm	15.062	2.1973	3.0567
Fusion model based on residual normalization	12.565	1.5112	2.1043
two-layer fusion model	12.565	1.4798	2.0756

, the mean error and RMSE of the two-layer fusion model under the three fusion models are reduced by at least 2.08% and 1.36%, respectively. Moreover, compared with the other three fusion models, the two-layer fusion model can make different SOC segments retain the optimal simulation voltage. The two-layer fusion model can reduce the errors of the single fusion model in different SOC segments to further improve the model precision.

5.6. Validation of Fusion Models at Different Temperatures

The supercapacitor model should adapt to the complex and changeable operation environment. It is well known that different temperatures will make a difference in the performance of supercapacitor [38]. In order to take into account the temperature, this paper selected test data under the experimental environment of 10, 25, and 40 °C, respectively, and repeated the parameter identification processes of GA to obtain the eight parameter sets. Similarly, the obtained parameter set is substituted into the UDDS to verify and calculate the simulation value of the terminal voltage. Then, the maximum error, mean error, and RMSE of the four fusion models are obtained.

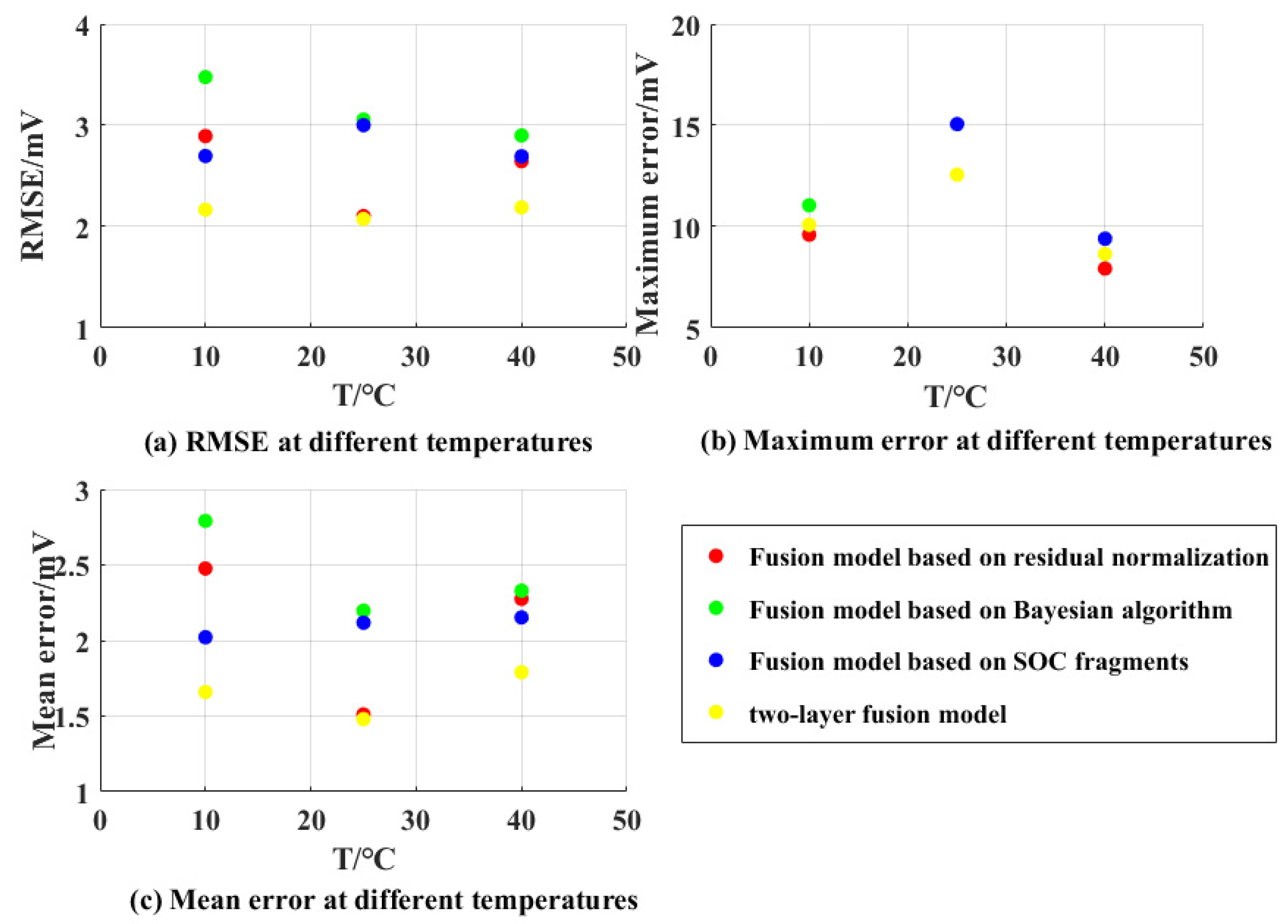
From Figure 6, it is found that the two-layer fusion model can ensure the minimum root mean square error and average error in the optimal section at different temperatures. Figure 6 shows that, under the experimental conditions of 10, 25, and 40 °C, the RMSE can be reduced by 60.41%, 47.26%, and 23.04%, the maximum error can be decreased by 9.51%, 19.87%, and 8.70%, and the mean error can be declined by 68.21%, 48.48%, and 30.13%, respectively. The improvement effect of the maximum error is not as obvious as that of the mean error and the RMSE. In fact, the two-layer fusion model takes the minimum RMSE as the decision variable and imports the fusion data again for settlement based on the SOC segment. Therefore, for the two-layer fusion model, the interference of other fusion models in the period of large estimation error can be greatly avoided in terms of RMSE and mean error, so as to improve the accuracy of the model again. It is demonstrated that the two-layer fusion model has strong adaptability against temperature and can combine the advantages of each fusion model at different temperatures to achieve the optimal results.

6. Conclusions

A two-layer fusion model is proposed in this paper based on three fusion models. In the two-layer fusion model, the terminal voltages at different times can quickly converge to the true values, and RMSE can reduce by 23.04%, which indicates that it significantly improves the accuracy of the model. The two-layer fusion model was validated at ambient temperatures of 10, 25, and 40 °C, respectively. Compared with the previous three fusion models, the RMSE, maximum error, and mean error of the two-layer fusion model are all reduced. For RMSE, the two-layer fusion model correspondingly reduced by 60.41%, 47.26%, and 23.04%, which indicates that it has reliability redundancy. Finally, the two-layer fusion model proposed in this paper can effectively play the advantages of physical fusion and data fusion with rapid convergence. It can significantly avoid the interference of the larger model errors in different SOC intervals, improves the accuracy of the estimation results, and has high applicability.