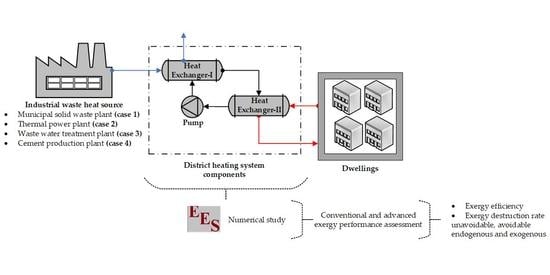
4.2. Exergetic Assessment
In this study, the exergetic performance of the WH source DH system, along with its components, was numerically assessed based on four different cases, through the EES-based written code. In this regard, as presented in
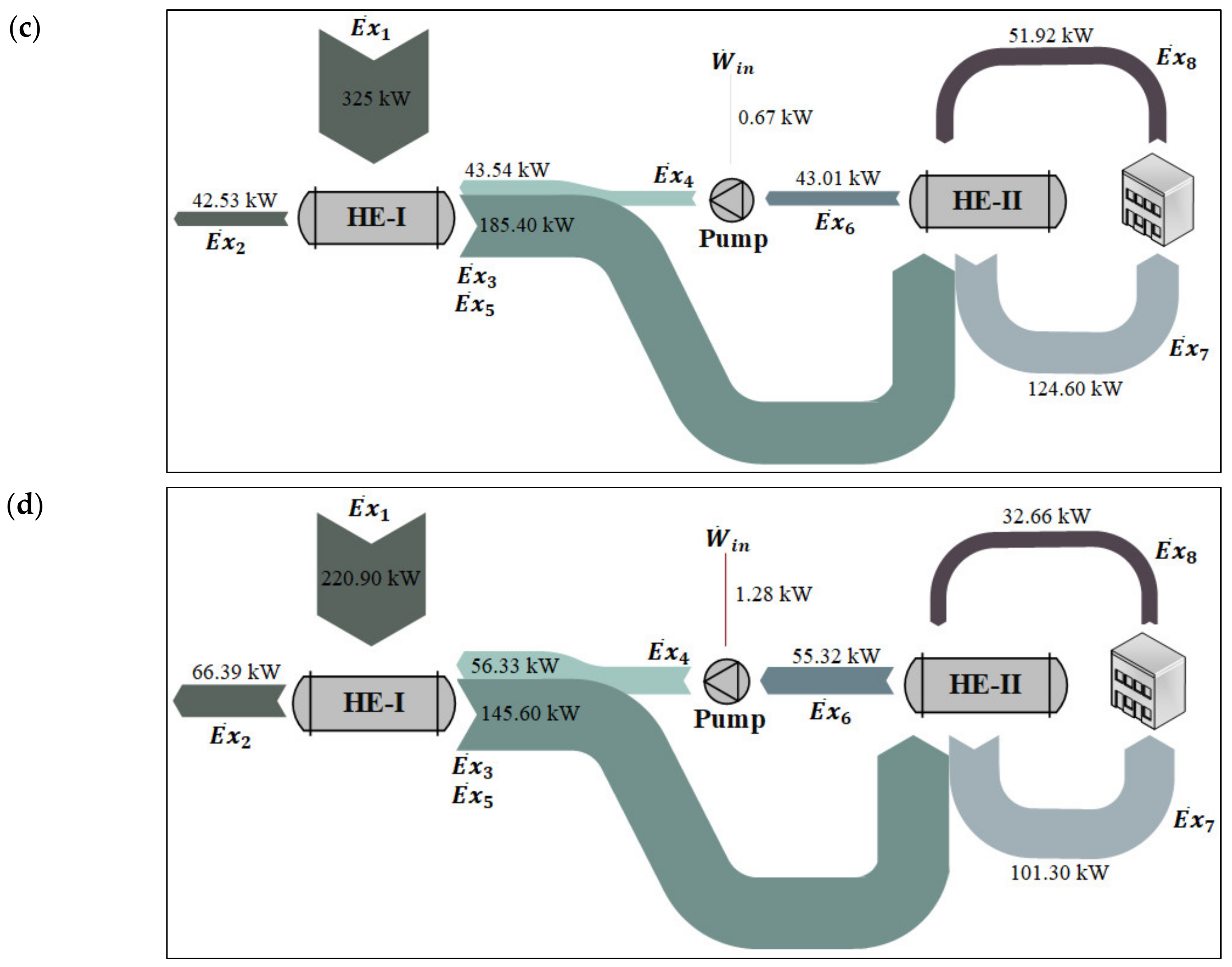
Figure 3a–d, the exergy flows between the main system components were determined by applying the conventional exergy method to the system, based on the created cases one, two, three, and four, respectively. As can be seen in
Figure 3, the highest exergy rates were simulated for the WH source (
), which was as high as 4903 kW (case one) and as low as 220.90 kW (case four). Hereafter, the highest exergy rates were found for the DH network supply (
), ranging from 145.60 kW (case four) to 2042 kW (case one). Following the DH network supply, the highest values for the exergy rate were obtained for the water supply to the dwellings (
), between 101.30 kW (case four) and 1300 kW (case one). On the other hand, the minimum exergy rates were simulated for the work consumption by the pump (
), which had its lowest value for case four, with 0.67 kW, and had its highest value for case one, with 7.41 kW. After that, the lowest exergy rates were computed for the DH network return at the pump’s inlet (
), except case three where the WH source that was discharged into the atmosphere (
) had the lowest exergy rate after the WH source inlet. Following the DH network return at the inlet of the pump, the lowest values for the exergy rate were obtained for the DH network return at the outlet of the pump (
), between 43.54 kW (case three) and 479.50 kW (case one).
The obtained results of exergy flow between the main components, based on the created cases given in
Figure 3, enable the conduction of conventional exergy assessment on a component level (see
Figure 2) and for the whole system (see Equations (8) and (9)) as well. The simulated results of the performance indicators are presented in
Figure 4a,b, respectively, for the exergy destruction rate and exergy efficiency, based on each created case.
As shown in
Figure 4a, the exergy destruction rates were computed quite high for the entire system
and each system component (
) in case one, compared to other cases. The main reason is the high exergy rate of the WH source of this case (see
in
Figure 3). Meanwhile, as shown in the figure, the exergy destruction rates of the whole system and the component HE-I, change proportionally with the exergy rate of the WH source, which is the maximum in case one, followed by cases two to four, respectively. However, the HE-II and pump did not have a similar change as in HE-I and the whole system. As illustrated in the figure, the exergy destruction rate of HE-II was found to be higher in case three, with a value of 69.76 kW, than in case two, with a value of 56.10 kW, although the exergy rate of the WH source was lower (see
Figure 3). This is because the fuel exergy rate of this component in case three was simulated to be 56.17% of in case two (142.40 kW to 253.50 kW), although the product exergy rate of this component in case three was simulated to be only 36.79% of in case two (72.64 kW to 197.40 kW). For the pump, the exergy destruction rate in case four (0.23 kW) was found to be higher than in case three (0.12 kW), although the exergy rate of the WH source was lower, because the fuel exergy rate of this component in case four (1.28 kW) was computed to be higher than in case three (0.67 kW).
As presented in
Figure 4b, the lowest exergy efficiency values were calculated in case one, followed by case three, case two, and case four, respectively, for the whole system (
,
) and for the HE-I (
). Therefore, it may be concluded that the heat potential of the WH source is used more effectively in case four, followed by case two, case three, and case one, respectively, to produce the useful energy for the DH network supply and the dwellings. However, the exergy efficiency of HE-II (
) was determined to be as high as 0.78 in case two, rather than 0.76 in case four. This is because the exergy fuel rate of this component is 2.80 times more in case two than case four, while the exergy production rate is 2.87 times more in case two than case four. Meanwhile, although the exergy rate of the WH source (see
Figure 3) changed from 220.90 kW (case four) to 4903 kW (case one), the exergy efficiency values belonging to the pump (
) were found to be almost similar in all the created cases, varying between 0.82 and 0.83.
As shown in
Figure 4a,b, the exergy destruction rates, due to the pump, were quite low (0.12 kW–1.27 kW) among other system components (21.65 kW–810 kW for HE-II and 65.26 kW–2413 kW for HE-I). In addition, the exergy efficiency values belonging to these components were higher (0.82–0.83) among other system components (0.48–0.78 for HE-II and 0.39–0.58 for HE-I). When two HEs were assessed together, higher exergy destruction rates (65.26 kW–2413 kW to 21.65 kW–810 kW) and lower exergy efficiencies (0.39–0.58 to 0.48–0.78) were observed for HE-I in all the cases. Therefore, it can be concluded that the priority for improvement should be given to HE-I, then HE-II, and finally the pump, based on the conventional exergy assessment. However, this analysis fails to identify the origin of the exergy destruction rates, namely, from the component itself (endogenous) or due to other components (exogenous), and can be (avoidable), or cannot be, (unavoidable) enhanced under the current technology status. In this regard, the advanced exergy performances of the employed components in each created case were assessed, and the obtained results are illustrated in
Figure 5 and
Figure 6, based on the endogenous/exogenous and avoidable/unavoidable splitting parts of exergy destruction rates, respectively.
As observed in
Figure 5, the exergy destruction rate, due to the pump, is mostly avoidable, ranging from 78.32% (case one) to 78.56% (case two). The simulated values for the avoidable exergy destruction rate of the remaining cases are 78.36% (case three) and 78.56% (case two). These obtained results show that the possible minimum exergy destruction rate can be realized between 0.02 kW in case three and 0.27 kW in case one under today’s technological status for the pump. On the other hand, as shown in the above figure, the exergy destruction rates that occurred in the HEs are mostly unavoidable, ranging between 70.79% (case four) and 87.89% (case three) for HE-I, and between 66.61% (case four) and 97.13% (case three) for HE-II. The simulated values for the unavoidable exergy destruction rate of the remaining cases are 84.69% (case one) and 87.27% (case two) for HE-I, and 90.12% (case one) and 79.32% (case two) for HE-II. These obtained results reveal that if the maximum possible operation condition is provided for the HEs considering the current technological status, most of the exergy destruction rate cannot be avoided (unavoidable), ranging between 46.20 kW in case four and 2043.66 kW in case one for HE-I, between 14.42 kW in case four and 730 kW in case one for HE-II. Therefore, it can be concluded that the priority for improvement should be given to the pump in all cases, based on the advanced exergy assessment considering the avoidable and unavoidable splitting parts of the exergy destruction rate. After this component, HE-I in cases one and three should be improved, similarly to HE-II in cases two and four.
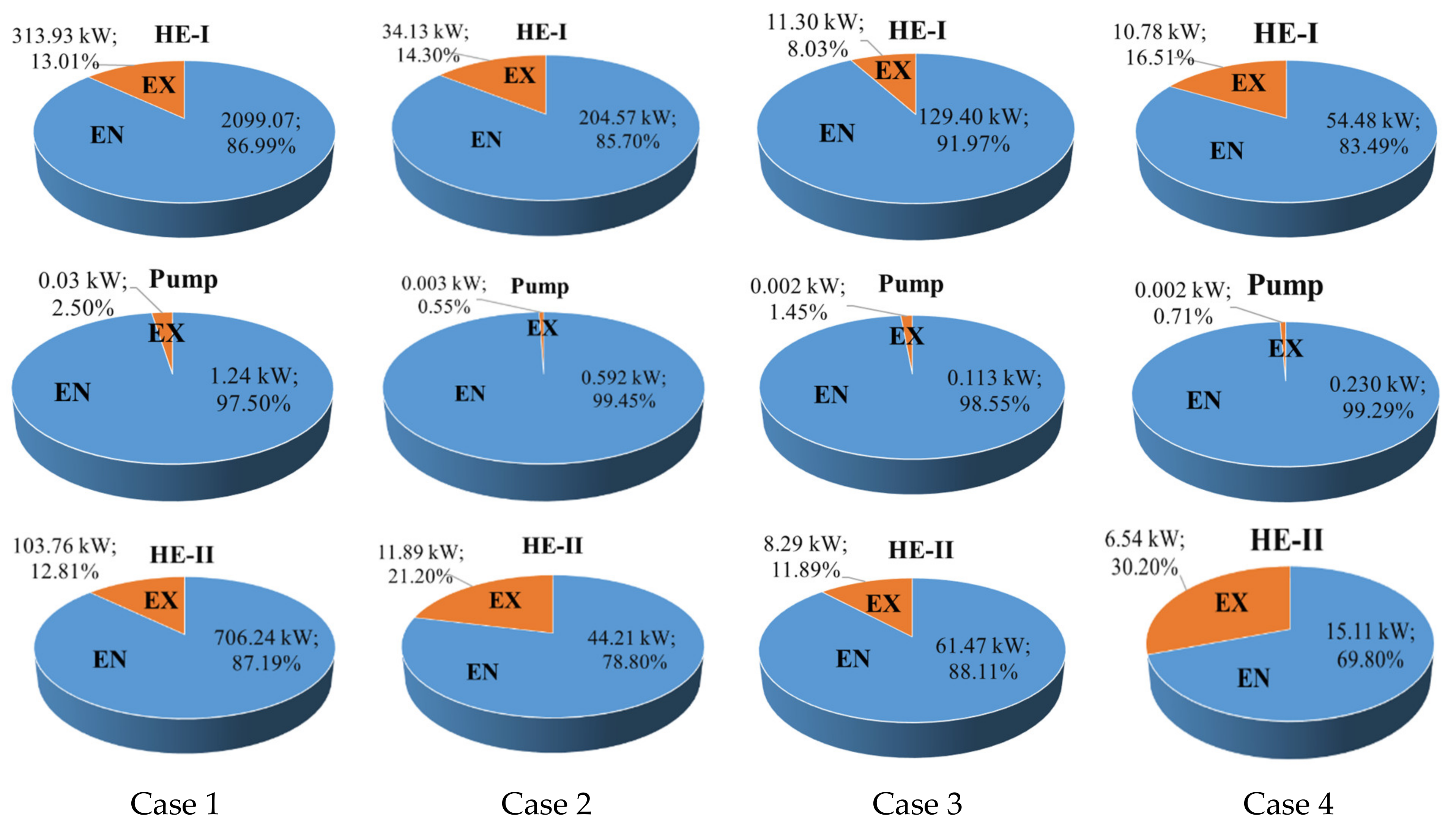
As shown in
Figure 6, the exergy destruction rates that arose in the system components are mostly endogenous, which are as low as 69.80% (case four) for HE-II, and as high as 99.45% (case two) for the pump. These obtained results show that the interactions among the system components are not strong; in other words, the exergy destruction rates are mostly due to the component itself. On the other hand, if the remaining components operate under the hypothetical ideal condition (see
Table 3), together with the studied component operating under the actual condition, the exergy destruction can be reduced to as low as 0.55% (case two) for the pump, and as high as 30.20% (case four) for HE-II. Therefore, it may be concluded that the origin of the exergy destruction rate is quite low, due to the remaining system components ranging between 0.002 kW and 313.93 kW, which shows the exogenous part of exergy destruction. As observed in the above figure, the endogenous part of the exergy destruction changes from 0.133 kW (case two for the pump) to 2099.07 kW (case one for HE-I).
The obtained results of conventional and advanced exergy analyses were also compared with the literature studies, based on the component level, considering the performance indicators, namely, the exergy efficiency and splitting parts of the exergy destruction rate (avoidable, unavoidable, endogenous, exogenous). Hepbasli and Keçebaş [
9] assessed the performance of a geothermal DHS in Turkey, through conventional and advanced exergetic analysis methods, based on real operational data. The exergy efficiency for the six HEs and seven circulation pumps in the real Afyon geothermal DHS, were calculated from 0.45 to 0.84 and from 0.49 to 0.91, respectively. Meanwhile, the exergy destruction rates that arose in the system components were found to be mostly endogenous, ranging between 51.80% and 65.70% for HEs, and between 21.69% and 46.66% for the pumps. On the other hand, the exergy destruction rates, due to the HEs, were determined to be mostly avoidable, between 72.60% and 92.41%, whereas they were mostly unavoidable for the pumps between 53.34% and 75.49%. Yamankaradeniz [
11] assessed the conventional and advanced exergy performances of a geothermal DHS located in Bursa, in Turkey, considering four HEs and four pumps located after the HEs. While the exergy efficiencies were determined from 79.68% to 97.05% for the HEs, they were calculated from 79.36% to 87.20% for the pumps. Meanwhile, the exergy destruction rates that occurred in the components were determined to be mostly avoidable, varying between 86.32% and 98.12%, and between 75.03% and 86.45%, respectively, for the HEs and pumps. Besides, the exergy destruction rates were determined to be mostly endogenous for the HEs two to four (between 65.25% and 79.89%), whereas they were mostly exogenous for HE 1 (63.65%) and for the employed pumps (between 95.61% and 97.50%). Liao et al. [
22] conducted advanced exergy analysis for ORC-based layout, to recover the WH of flue gas. The thermodynamic performance of a proposed ORC–ORC system revealed that the exergy efficiencies of low-temperature HE, high-temperature HE, pump one and pump two, were 51.47%, 62.49%, 80.65% and 80.64%, respectively. Meanwhile, the splitting parts of the exergy destruction rates were simulated mostly endogenous for the considered components, varying between 91.24% for high-temperature HE and 100% for low-temperature HE. Besides, the exergy destruction rates occurring in the considered components were found to be mostly unavoidable for the HEs (89.75% for high-temperature HE and 100% for low-temperature HE), whereas they were mostly avoidable for the pumps, with a rate of 78.62%. Wang et al. [
38] applied a conventional and advanced exergy assessment method to a cascade absorption heat transformer, for the recovery of low-grade waste heat. The simulated results of the proposed system showed that the exergy efficiencies of the HEs (lithium bromide and ammonia) and pumps (lithium bromide and ammonia) varied from 90.05% to 94.32%, and from 25.45% to 60.69%, respectively. Meanwhile, the exergy destruction rates occurring in the HEs were computed as mostly exogenous, which were 76.16% for lithium bromide HE and 78.65% for ammonia HE. On the other hand, the exergy destruction rates occurring in the pumps were calculated to be mostly endogenous, which ranged from 86.74% to 87.80% for lithium bromide pumps and from 89.01% to 89.57% for ammonia pumps. For the avoidable and unavoidable splitting parts, the dominant part was determined to be unavoidable for each system component, which was as low as 80.13% for ammonia–HE and as high as 82.46% for lithium bromide pump one. Oyekale et al. [
43] applied advanced exergy analysis to a hybrid solar-biomass ORC plant having an organic fluid pump and HEs (condenser and evaporator). Based on the conventional exergy assessment, the exergy efficiencies were computed as almost 80% for the pump, almost 28% for the condenser, and 85% for the evaporator. Based on the advanced exergy analysis, the exergy destruction rates were found to be mostly endogenous (80% for the pump, 80.60% for the condenser, and 90.30% for the evaporator) and avoidable (80% for the pump, 77.50% for the condenser, and 88.10% for the evaporator). The comparison of the results of these literature studies with the presented study is summarized in
Table 5.
As observed in
Table 5, the exergy performance indicators (exergy efficiency in the conventional exergy assessment and splitting parts of the exergy destruction rate, unavoidable and endogenous, in the advanced exergy assessment) vary in very different ranges. The main reason for this is the choice of the dead state values, determination of endogenous and unavoidable conditions, and the type of fluid used. As a result of the selection of these parameters, the closest exergy efficiency values for HEs and pumps appeared in Ref. [
9] and in Ref. [
22], respectively. On the other hand, the closest values for the endogenous and unavoidable parts of exergy destruction were observed in Ref. [
22], both for HEs and pumps.
4.3. Key Parameters and Their Effects on an Actual Implementation
In Turkey, the WH potential of the considered plants, based on the created cases, namely, municipal solid waste (case one), thermal power (case two), wastewater treatment (case three), and cement production (case four), is remarkably high. At the end of 2018, the total number of municipalities around the country was 1399, having an average amount of municipal solid waste per capita of 1.16 kg/day [
27]. For the same year, 37.2% of the electricity need of Turkey was generated by coal-based thermal power plants, with a total number of 68 [
44]. Meanwhile, the total number of wastewater treatment plants in Turkey reached 991 by the end of 2018, where approximately 4237 Mm
3/year of wastewater was treated [
30]. Finally, as of 2016, 71.4 million tons of production was realized by 70 cement production plants (52 integrated facilities and 18 grinding–packaging facilities) [
45].
In this study, the functional exergy efficiency of the whole system (see Equation (8)) was recalculated when the WH potential of the municipal solid waste plant (case one was selected because it is more in number) was met with the DH system in the real world. In this regard, the key parameters were determined to be the ambient (dead state) temperature and the heat loss in the DH network for the selected sites, where soil temperature, the depth where the pipes are placed, and the geometric and thermal properties of the pipes become important. Therefore, as shown in
Figure 7, four different provinces were selected, considering degree-day regions in Turkey and the situation with the highest population density [
46,
47]. Consequently, the İstanbul, İzmir, Ankara, and Kayseri provinces were determined to represent zones one, two, three, and four, respectively.
The long-term (1929–2020) average ambient temperature (T
a,ave) values measured in the seasonal normal of the selected provinces were considered for the winter months (October, December, January, February), using the weather forecast from the Turkish State Meteorological Service [
48], and the obtained values are given in
Table 6. In this table, the average soil temperature (T
s,ave) values below 100 cm from the surface are also given based on each month, which was determined by using the annual average T
s,ave values [
49] and by assuming that these values are identical with the monthly variation in the T
a,ave for the considered sites.
The heat losses in the DH network, during operation for the considered sites, were evaluated based on the supply and return sides, by using Equations (14) and (15) given below, respectively [
50].
where
and
illustrate the heat loss in the DH network at the supply and return sides, respectively, during operation in kW. The
is the total heat transfer coefficient of the pipeline in W/m
2K. The
Do and
L are the outer diameter and length of the pipeline in m, respectively. While the
values were found by Equation (16) given below, and
Do was considered as 157.8 mm for a typical DH system arrangement, defined as model A in Ref. [
51]. For the
L, four different distances between the WH source and the dwellings were considered, using 5, 10, 15 and 20 km values.
where the outer (
Do), inner (
Di), and intermittent (inner with pipe wall thickness) (
Dt) diameters were taken into account as 157.8 mm, 88.9 mm, and 95.3 mm, respectively, for a typical DH system arrangement, defined as model A in Ref. [
51]. Meanwhile, the thermal conductivities of steel (
) and insulation (
) were considered as 16.27 W/m·K and 0.0265 W/m·K, respectively [
51]. To calculate the convective heat transfer coefficient on the inner surface (
hi), the equation steps given below were used [
34].
In the above-given equations (from (17) to (20)), the density (
), viscosity (
), Prandtl number (
Pr), and thermal conductivity (
kw) properties of water were calculated using built-in thermophysical property functions by the written code. Following the calculation of
hi, the heat losses on the supply and return sides (see Equations (14) and (15)) were computed, which cause a temperature drop at states five and four (see
Figure 2), respectively, considering the mass flow rates, the specific heats, and the inlet temperatures of the water (states three and six), given in
Table 1. With these temperature drops, the simulated values for the functional exergy efficiency of the whole system are given in
Table 7, based on case one.
As observed from
Table 7, the highest functional exergy efficiencies were calculated for the shortest distances between the WH source and dwellings, based on each considered site. When all the zones are considered, the maximum functional exergy efficiencies were found between 0.1415 and 0.1782 for a 5 km distance. On the other hand, the minimum values were observed from 0.0519 to 0.0558 for a 20 km distance, considering all the zones. Note that, as given in
Table 7, the average ambient temperature and the functional exergy efficiency are inversely proportional. When the shortest distance is considered (5 km) for all the zones, the highest functional exergy efficiency values were obtained in January, followed by February, December, and November, respectively. As shown in
Table 6, these months are ordered from the coldest to the warmest. Therefore, it may be concluded that it is better to implement a WH source DH system with a possible shorter pipeline. Additionally, it is possible to operate with the highest functional exergy efficiency in colder ambient temperatures, although the heat loss would be higher. This is because this situation also affects the dead state temperature, which is highly significant on the functional exergy efficiency.