A Novel Island Detection Threshold Setting Using Phasor Measurement Unit Voltage Angle in a Distribution Network
Abstract
:1. Introduction
2. Methodology
2.1. Slip Angle and Acceleration Angle
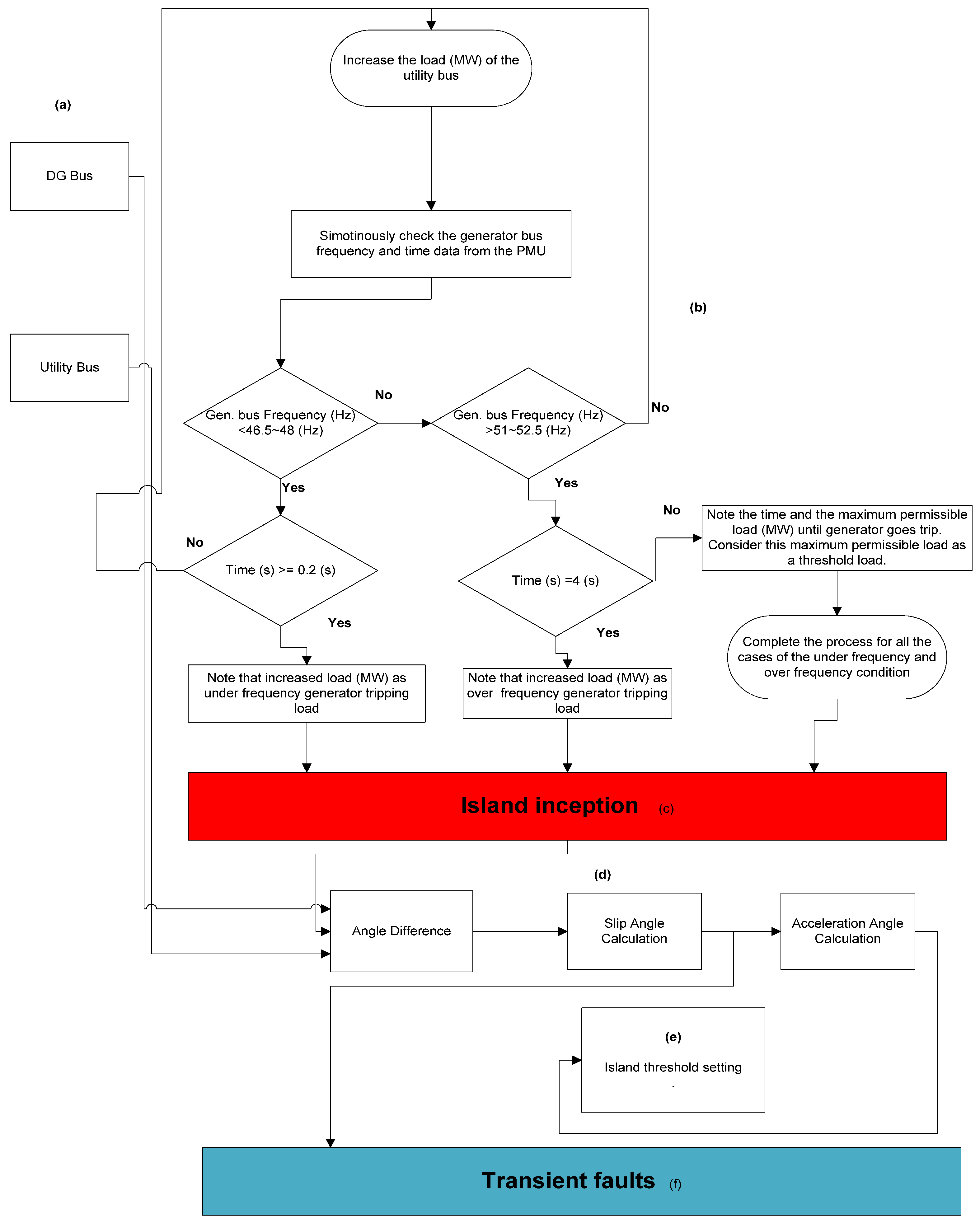
2.2. Proposed Island Detection Threshold Setting Method
- (a)
- Bus
- (b)
- Determining Load Threshold
- (c)
- Island Inception
- (d)
- Threshold Value Calculation
- (e)
- Island Threshold Setting
- (f)
- Transient Faults
3. Simulation
4. Results and Discussion
4.1. Case A1, A2, and A3
4.2. Cases B1, B2, and B3
4.3. Case F1 and F2
4.4. Threshold Setting
4.5. Results Comparison
5. Conclusions
- This research work proposed a novel islanding threshold setting method using the slip angle and acceleration angle.
- The proposed research work overcame the limitation of the local area-based islanding detection threshold setting.
- The proposed research method can distinguish the actual islanding event and the transient fault event.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khamis, A.; Shareef, H.; Bizkevelci, E.; Khatib, T. A review of islanding detection techniques for renewable distributed generation systems. Renew. Sustain. Energy Rev. 2013, 28, 483–493. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, V.; Tyagi, B. Islanding detection for reconfigurable microgrid with RES. IET Transm. Distrib. 2021, 15, 1187–1202. [Google Scholar] [CrossRef]
- Seong-Cheol, K.; Ray, P.; Salkuti, S.R. Islanding detection in a distribution network with distributed generators using signal processing techniques. Int. J. Power Electron. Drive Syst. 2020, 11, 2099–2106. [Google Scholar]
- Motter, D.; Vieira, J.C. Improving the islanding detection performance of passive protection by using the undervoltage block function. Electr. Power Syst. Res. 2020, 184, 106293. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Salem, A.A.; Oda, E.S.; Eldesouky, A.A. Islanding detection of microgrid incorporating inverter based DGs using long short-term memory network. IEEE Access 2020, 8, 106471–106486. [Google Scholar] [CrossRef]
- Khichar, S.; Lalwani, M. An analytical survey of the islanding detection techniques of distributed generation systems. Technol. Econ. Smart Grids Sustain. Energy 2018, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Azim, R.; Li, F.; Xue, Y.; Starke, M.; Wang, H. An islanding detection methodology combining decision trees and Sandia frequency shift for inverter-based distributed generations. IET Gener. Transm. Distrib. 2017, 11, 4104–4113. [Google Scholar] [CrossRef]
- Zamani, R.; Golshan, M.E.H.; Alhelou, H.H.; Hatziargyriou, N. A novel hybrid islanding detection method using dynamic characteristics of synchronous generator and signal processing technique. Electr. Power Syst. Res. 2019, 175, 10591. [Google Scholar] [CrossRef]
- Babakmehr, M.; Dehghanian, F.H.P.; Enslin, J. Artificial intelligence-based cyber-physical events classification for islanding detection in power inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2020. [Google Scholar] [CrossRef]
- Reddy, C.R.; Goud, B.S.; Reddy, B.N.; Pratyusha, M.; Kumar, C.V.; Rekha, R. Review of islanding detection parameters in smart grids. In Proceedings of the 2020 8th IEEE International Conference on Smart Grid (icSmartGrid), Paris, France, 17 June 2020; pp. 78–89. [Google Scholar]
- Wang, X.; Freitas, W.; Dinavahi, V.; Xu, W. Investigation of positive feedback anti-islanding control for multiple inverter-based distributed generators. IEEE Trans. Power Syst. 2009, 24, 785–795. [Google Scholar] [CrossRef]
- Lopes, L.A.; Zhang, Y. Islanding detection assessment of multi-inverter systems with active frequency drifting methods. IEEE Trans. Power Deliv. 2007, 23, 480–486. [Google Scholar] [CrossRef]
- Zhou, B.; Cao, C.; Li, C.; Cao, Y.; Chen, C.; Li, Y.; Zeng, L. Hybrid islanding detection method based on decision tree and positive feedback for distributed generations. IET Gener. Transm. Distrib. 2018, 9, 1819–1825. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Vahedi, H.; Khazaeli, F.; Oraee, H. A novel hybrid islanding detection method for inverter-based DGs using SFS and ROCOF. IEEE Trans. Power Deliv. 2015, 32, 2162–2170. [Google Scholar] [CrossRef]
- Chandak, S.; Mishra, M.; Rout, P.K. Hybrid islanding detection with optimum feature selection and minimum NDZ. Int. Trans. Electr. Energy Syst. 2018, 28, e2602. [Google Scholar] [CrossRef]
- Faqhruldin, O.N.; El-Saadany, E.F.; Zeineldin, H.H. A universal islanding detection technique for distributed generation using pattern recognition. IEEE Trans. Smart Grid 2014, 5, 1985–1992. [Google Scholar] [CrossRef]
- Mishra, M.; Chandak, S.; Rout, P.K. Taxonomy of islanding detection techniques for distributed generation in microgrid. Renew. Energy Focus 2018, 31, 9–30. [Google Scholar] [CrossRef]
- Buduma, P.; Pinto, S.J.; Panda, G. Loss of utility detection and seamless operation of distributed generation system. IEEE Trans. Ind. Appl. 2020, 56, 3149–3158. [Google Scholar] [CrossRef]
- Xu, W.; Mauch, K.; Martel, S. An assessment of dg islanding detection methods and issues for canada, report# cetc-varennes 2004-074 (tr), canmet energy technology centre–varennes. Nat. Resour. Can. July 2004, 53. [Google Scholar]
- Micky, R.; Sunitha, R.; Ashok, S. Techno-Economic analysis of wams based islanding detection algorithm for microgrids with minimal pmu in smart grid environment. In Wide Area Power Systems Stability, Protection, and Security; Springer: Berlin/Heidelberg, Germany, 2020; pp. 499–522. [Google Scholar]
- Guo, Y.; Li, K.; Laverty, D.M.; Xue, Y. Synchrophasor-based islanding detectin for distributed generation systems using systematic principal component analysis approaches. IEEE Trans. Power Deliv. 2015, 30, 2544–2552. [Google Scholar] [CrossRef] [Green Version]
- Najda, V.M.; Gopakumar, P.; Sunitha, R. PMU based voltage angular dynamic monitoring and supervision system for emerging deregulated power grids. In Proceedings of the International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 23–25 January 2019; pp. 1–4. [Google Scholar]
- Lidula, N.W.A.; Rajapakse, A.D. A pattern-recognition approach for detecting power islands using transient signals—Part II: Performance evaluation. IEEE Trans. Power Deliv. 2012, 27, 1071–1080. [Google Scholar] [CrossRef]
- Galvan, F.; Wells, C.H. Detecting and managing the electrical island created in the aftermath of Hurricane Gustav using Phasor Measurement Unit (PMUs). In Proceedings of the IEEE PES T&D, New Orleans, LA, USA, 19–22 April 2010; pp. 1–5. [Google Scholar]
- Lin, Z.; Xia, T.; Ye, Y.; Zhang, Y.; Chen, L.; Liu, Y.; Tomsovic, K.; Bilke, T.; Wen, F. Application of wide area measurement systems to islanding detection of bulk power systems. IEEE Trans. Power Syst. 2013, 28, 2006–2015. [Google Scholar] [CrossRef]
- Liu, X.; Laverty, D.M.; Best, R.J.; Li, K.; Morrow, D.J.; McLoone, S.S. Principal component analysis of wide-area phasor measurements for islanding detection-a geometric view. IEEE Trans. Power Del. 2015, 30, 976–985. [Google Scholar] [CrossRef]
- Azim, R.; Sun, K.; Li, F.; Zhu, Y.; Saleem, H.A.; Shi, D.; Sharma, R. A comparative analysis of intelligent classifiers for passive island detection in micro-grids. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June 2015; pp. 1–6. [Google Scholar]
- Azim, R.; Zhu, Y.; Saleem, H.A.; Sun, K.; Li, F.; Shi, D.; Sharma, R. A decision tree-based approach for microgrid island detection. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, WA, USA, 18–20 February 2015; pp. 1–5. [Google Scholar]
- Sun, R.; Centeno, V.A. Wide area system islanding contingency detecting and warning scheme. IEEE Trans. Power Syst. 2014, 29, 2581–2589. [Google Scholar] [CrossRef]
- Alam, M.R.; Muttaqi, K.M.; Bouzerdoum, A. A multifeature-based approach for islanding detection of DG in the subcritical region of vector surge relays. IEEE Trans. Power Del. 2014, 29, 2349–2358. [Google Scholar] [CrossRef]
- Hashiesh, F.; Mostafa, H.E.; Mansour, M.M.; Khatib, A.R.; Helal, I. Wide area transient stability prediction using on-line Artificial Neural Networks. In Proceedings of the Electric Power Conference, Vancouver, BC, Canada, 6–7 October 2008; pp. 1–7. [Google Scholar]
- Arefin, A.A.; Hasan, K.N.M.; Romlie, M.F.; Abdullah, M.F.; Ali, M.L.; Othman, M.L. Determining islanding operation using micro grid phasor measurement unit parameters. Int. J. Emerg. Trends Eng. Res. 2020, 8, 97–101. [Google Scholar] [CrossRef]
- Liu, X.A.; Laverty, D.; Best, R. Islanding detection based on probabilistic PCA with missing values in PMU data. In Proceedings of the IEEE PES General Meeting Conference & Exposition, Washington, WA, USA, 27–31 July 2014; pp. 1–6. [Google Scholar]
- Liu, X.; Kennedy, J.M.; Laverty, D.M.; Morrow, D.J.; McLoone, S. Wide-area phase-angle measurements for islanding detection—An adaptive nonlinear approach. IEEE Trans. Power 2017, 31, 1901–1911. [Google Scholar] [CrossRef] [Green Version]
- Ohno, T.; Yasuda, T.; Takahashi, O.; Kaminaga, M.; Imai, S. Islanding protection system based on synchronized phasor measurements and its operational experiences. In Proceedings of the IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–5. [Google Scholar]
- Kumar, D.; Bhowmik, P.S. Wide area islanding detection using phasor measurement unit. In Proceedings of the IEEE 11th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 5–6 January 2017; pp. 49–54. [Google Scholar]
- Chen, H.; Martin, K.; Bhargava, B.; Budhraja, V.; Balance, J. On-Line Islanding Detection Application in the RealTime Dynamics Monitoring System. In Proceedings of the IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 24 July 2014. [Google Scholar]
- Ebrahim, M.A.; Wadie, F.; Abd-Allah, M.A. An algorithm for detection of fault, islanding, and power swings in dg-equipped radial distribution networks. IEEE Syst. J. 2019, 14, 3893–3903. [Google Scholar] [CrossRef]
- Vatani, M.; Sanjari, M.J.; Gharehpetian, G.B. Islanding detection in multiple-DG microgrid by utility side current measurement. Int. Trans. Electr. Energy Syst. 2015, 25, 1905–1922. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Hizam, H.; Othman, M.L.; Radzi, M.A. Islanding detection method using ridgelet probabilistic neural network in distributed generation. Neurocomputing 2019, 329, 188–209. [Google Scholar] [CrossRef]
- Mulhausen, J.; Schaefer, J.; Mynam, M.; Guzmán, A.; Donolo, M. Anti-islanding today, successful islanding in the future. In Proceedings of the 2010 IEEE 63rd Annual Conference for Protective Relay Engineers, College Station, TX, USA, 29 March–1 April 2010; pp. 1–8. [Google Scholar]
- Ravikumar, K.G.; Upreti, A.; Nagarajan, A. State-of-the-Art islanding detection and decoupling systems for utility and industrial power systems. In Proceedings of the 69th Annual Georgia Tech Protective Relaying Conference, Atlanta, GA, USA, 29 April 2015. [Google Scholar]
- Schwartfeger, L.; Santos-Martin, D.; Wood, A.; Watson, N.; Miller, A. Review of Distributed Generation Interconnection Standards; EEA Conference & Exhibition: Auckland, The Newzealand, 2014. [Google Scholar]
- Ahmad, I. A Lyapunov-based direct adaptive controller for the suppression and synchronization of a perturbed nuclear spin generator chaotic system. Appl. Math. Comput. 2021, 395, 125858. [Google Scholar]
- Samui, A.; Samantaray, S.R. Wavelet singular entropy-based islanding detection in distributed generation. IEEE Trans. Power Del. 2013, 28, 411–418. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, S.R.; Kishor, N. Disturbance detection in grid connected distributed generation system using wavelet and S-transform. Elect. Power Syst. Res. 2011, 81, 805–819. [Google Scholar] [CrossRef]
- Niaki, A.H.M.; Afsharnia, S. A new passive islanding detection method and its performance evaluation for multi-DG systems. Elect. Power Syst. Res. 2014, 110, 180–187. [Google Scholar] [CrossRef]
- Dubey, R.; Popov, M.; Samantaray, S.R. Transient monitoring function-based islanding detection in power distribution network. IET Gener. Transm. Distrib. 2019, 13, 805–813. [Google Scholar] [CrossRef]
- Admasie, S.; Bukhari, S.B.A.; Haider, R.; Gush, T.; Kim, C.-H. A passive islanding detection scheme using variational mode decomposition basedmode singular entropy for integrated microgrids. Elect. Power Syst. Res. 2019, 177, 105983. [Google Scholar] [CrossRef]
- Kumar, D.; Bhowmik, P.S. Artificial neural network and phasor data-based islanding detection in smart grid. IET Gener. Transm. Distrib. 2018, 12, 5843–5850. [Google Scholar] [CrossRef]
- Matik-Cuka, B.; Kezunovic, M. Islanding detection for inverter based distributed generation using support vector machine method. IEEE Trans. Smart Grid 2014, 5, 2676–2686. [Google Scholar] [CrossRef]
- Manikonda, S.K.G.; Gaonkar, D.N. Islanding detection method based on image classification technique using histogram of oriented gradient features. IET Gener. Transm. Distrib. 2020, 14, 2790–2799. [Google Scholar] [CrossRef]
- Mishra, M.; Sahani, M.; Rout, P.K. An islanding detection algorithm for distributed generation based on hilbert–huang transform and extreme learning machine. Sustain. Energy Grids Netw. 2017, 9, 13–26. [Google Scholar] [CrossRef]
- Alshareef, S.; Talwar, S.; Morsi, W.G. A new approach based on wavelet design and machine learning for islanding detection of distributed generation. IEEE Trans. Smart Grid 2014, 5, 1575–1583. [Google Scholar] [CrossRef]
- Adari, B.; Bhalja, B.B. Islanding detection of distributed generation using random forest technique. In Proceedings of the IEEE 6th International Conference on Power Systems, New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Chaitanya, B.K.; Yadav, A.; Pazoki, M. Reliable islanding detection scheme for distributed generation based on pattern-recognition. IEEE Trans. Ind. Inform. 2020, 17, 5230–5238. [Google Scholar] [CrossRef]







| Cases | Interconnection Points | Scenarios | Threshold Loads of Bus 4 (132 KV) | Conditions | DG1 | DG2 | |||
|---|---|---|---|---|---|---|---|---|---|
| To Bus | From Bus | MW | MVAR | MW | MVAR | ||||
| A1 | 4 | 12 | 1 | 0.5 MW | Over frequency | 72 | 27 | 48 | 21 |
| A2 | 6 | 9 | 2 | 0.80 MW | 67 | 29 | |||
| A3 | 6 | 10 | 3 | 1.10 MW | 38 | 38 | |||
| B1 | 4 | 12 | 1 | 18.600 MW | Under frequency | 25 | 22 | ||
| B2 | 6 | 9 | 2 | 18.85 MW | 67 | 28 | |||
| B3 | 6 | 10 | 3 | 18.150 MW | 19 | 37 | |||
| F1 | 4 | 12 | 1 | 0.5 MW | Single line to ground (SLG) fault | 27 | 21 | ||
| F2 | 4 | 12 | 1 | 0.5 MW | Three-phase balance (3PB) fault | 27 | 21 | ||
| Name of the Parameters | Settings |
|---|---|
| System frequency | 50 Hz |
| DG bus | Bus 13 (Hancock) |
| Utility bus | Bus 3 (Kumis) |
| Island event | Open the line between Bus 3 and 4 |
| Island incepted | 2 s |
| Time step | 0.02 s |
| Figures | Legends | |
|---|---|---|
| x-axis | y-axis | |
| 3, 5 | Timestamp | Frequency |
| 4, 6, 7, 8 | Timestamp | Voltage angle |
| Cases | Slip Angle (Deg/s) | Acceleration Angle (Deg) | Time |
|---|---|---|---|
| A1 | 169.815 | 5490.75 | 20 ms |
| A2 | 90.85 | 4542.5 | |
| A3 | 91.81 | 4590.5 |
| Cases | Slip Angle (Deg/s) | Acceleration Angle (Deg) | Time |
|---|---|---|---|
| B1 | 0.525 | 26.25 | 20 ms |
| B2 | 1.5 | 75 | |
| B3 | 2.54 | 127 |
| Cases | Slip Angle (Deg/s) | Time |
|---|---|---|
| F1 | 14.57 | 20 ms |
| F2 | 503.945 |
| Slip Angle (Deg/s) | Acceleration Angle (Deg) | Thresholds |
|---|---|---|
| 0.525 | 26.25 | Islanding threshold |
| 14.57 | NA | SLG fault threshold |
| 503.945 | NA | 3PB fault threshold |
| Ref. | Methods | Transient Faults | Detection Time |
|---|---|---|---|
| [45] | WSE | Not considered | <10 ms |
| [46] | ST | Not considered | 26 ms |
| [47] | EMD | Not considered | <35 ms |
| [48] | TMF | Not considered | 55 ms |
| [49] | VMD | Not considered | 10 ms |
| [50] | ANN | Considered | 0.5 s |
| [51] | SVM | Considered | 50 ms |
| [52] | HoGF+ SVMs | Considered | 218 ms |
| [53] | ELM | Considered | NA |
| [54] | Ensemble tree | Considered | NA |
| [55] | RF | Considered | NA |
| [56] | MIMF | Considered | <70 ms |
| [41] | Slip frequency and acceleration | Considered | 500 ms |
| Proposed method | Considered | 20 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arefin, A.A.; Hasan, K.N.B.M.; Othman, M.L.; Romlie, M.F.; Saad, N.; Nor, N.B.M.; Abdullah, M.F. A Novel Island Detection Threshold Setting Using Phasor Measurement Unit Voltage Angle in a Distribution Network. Energies 2021, 14, 4877. https://doi.org/10.3390/en14164877
Arefin AA, Hasan KNBM, Othman ML, Romlie MF, Saad N, Nor NBM, Abdullah MF. A Novel Island Detection Threshold Setting Using Phasor Measurement Unit Voltage Angle in a Distribution Network. Energies. 2021; 14(16):4877. https://doi.org/10.3390/en14164877
Chicago/Turabian StyleArefin, Ahmed Amirul, Khairul Nisak Binti Md. Hasan, Mohammad Lutfi Othman, Mohd Fakhizan Romlie, Nordin Saad, Nursyarizal Bin Mohd Nor, and Mohd Faris Abdullah. 2021. "A Novel Island Detection Threshold Setting Using Phasor Measurement Unit Voltage Angle in a Distribution Network" Energies 14, no. 16: 4877. https://doi.org/10.3390/en14164877
APA StyleArefin, A. A., Hasan, K. N. B. M., Othman, M. L., Romlie, M. F., Saad, N., Nor, N. B. M., & Abdullah, M. F. (2021). A Novel Island Detection Threshold Setting Using Phasor Measurement Unit Voltage Angle in a Distribution Network. Energies, 14(16), 4877. https://doi.org/10.3390/en14164877







