Energy Savings by Optimization of Thrusters Allocation during Complex Ship Manoeuvres

Abstract

The International Maritime Organization adopted a strategy to reduce the total annual GHG emissions from international shipping by at least 50% by 2050, compared to 2008 levels. The European Union proposed an even farther reaching transformation: the European Commission adopted a set of proposals to make the EU’s transport policies fit for reducing net greenhouse gas emissions by at least 55% by 2030, compared to 1990 levels. Therefore, all industrial actions in line and consistent with these strategies are essential. One of such activities may be a gradual transition from the most common independent controls of transport ships’ thrusters, propellers, and rudders to an integrated, power optimized, 3 degrees of freedom joystick control. In this paper, the full mission bridge simulator (FMBS) research on potential energy savings and, consequently, a GHG emission reduction, while steering a RoPax twin-screw ferry equipped with bow thrusters by a joystick control, is presented. The task of navigators engaged in the research was to steer the vessel either via classic engine, rudder, and thruster levers or via a joystick while (1) following the predefined straight track, (2) rotating at the turning area, and (3), finally, crabbing (moving sideways) until stopping at the quay fenders. The conclusions are that energy savings of approximately 10% can be expected for berthing manoeuvres controlled by a joystick, compared to independent actuators’ controls. These conclusions have been drawn from a statistical analysis of the ship’s energy consumption during typical manoeuvring phases of 18 berthing operations performed in FMBS.

1. Introduction

Environmental pollution is one of the identified negative effects of contemporary shipping and there is a clear link between a manner of manoeuvring ships in fairways, harbour approaches, port waters, and amounts of pollutants emitted into the air. The concept of green manoeuvring is an approach to integrate the aspects of minimizing greenhouse gases (GHG) and particle emissions and maximizing energy efficiency into the process of ship’s manoeuvring [1,2,3]. This concept covers controlling the ship’s movement in a way that emissions of CO₂, and nitric and sulphur oxides (NO_x, SO_x) and other particles are as low as reasonably possible and, as a side effect, possibly fuel is saved. Fuel or energy saving is considered the major, but not the only, factor for emission reduction. The focus has been more and more shifted towards ecological aspects nowadays. Therefore, the pressure on fuel saving, either through the ship’s design or operation, is, thus, emphasized, but the rational ship owner will predict his return from investment in a long-term perspective [4].

In this paper, the authors present the simulation studies of potential direct energy (fuel) savings and, consequently, a major GHG reduction while steering a RoPax twin-screw ferry equipped with bow thrusters (BTUs) via a manual joystick control instead of an individual, independent control of ship propulsors’ and rudders’ levers.

A manual joystick control system, similar to the dynamic positioning (DP) system [5], can enable a complex control of ship’s propulsion and rudders by providing the required resultant force and moment to a thrust allocator. Replacing the need for the individual setting of multiple actuators onboard, it allows the navigator to steer the ship more instinctively in an ergonomic and comfortable way by setting only two parameters: (1) a force vector via the joystick lever and (2) a force moment via the joystick knob (at the top of the lever). Numerically, three parameters are being set therein: the value and direction of the force vector and the value of the force moment. This led to the assumption that using a joystick controller and obtaining the desired ship’s motion based on simpler commands should result in a significant difference of the required navigator’s manoeuvring skilfulness and, consequently, in less energy consumption during ship’s berthing, as the most critical and skill-demanding phase of navigation. The steering of a ship by a joystick, the optimal allocation of component forces to ship thrusters by a thrust allocator of such a joystick system and the quantitative analysis of energy savings during common berthing manoeuvres are the main problems dealt with within this paper.

Background and Related Work

A control system can be described as fully actuated if it is able to command an instantaneous acceleration in an arbitrary direction. If it is not able to command an instantaneous acceleration in an arbitrary direction then such a system is in an underactuated state. In case of ship’s control, the problem is considered to be 3-DOF (degrees of freedom) or solved in 2-dimensional space. Any movement in the z-direction (up/down) or around the x- and y-axis of the ship-body reference frame can be ignored because common actuators of vessels do not have the ability to produce thrust in these directions and most of the manoeuvring situations do not require compensations of heaving, rolling, or pitching. The optimal allocation of forces generated by thrusters is the main problem to be solved by the thrust allocator of such a control system [6,7,8]. In general, the control allocation problem for marine craft is a non-convex optimization problem that is hard to solve [6]. It can be locally approximated with and solved by convex optimization methods [9] depending on the criteria and constraints used.

The presented research is one of few in the area of evaluating the human-based ship manoeuvring and handling performance in terms of energy consumed in complex operations. To perform a complex manoeuvre such as berthing, usually a number of actuators must be operated almost simultaneously and separately. The decisions determined by the ship operators on how much and when to control the propellers, rudders, and thrusters require the high level of experience, mental concentration, and workload. This human control is also a complicated, often not optimal process, and as such is subject to some randomness. Progress has been made in the research methodology of this field over the decades [10,11]. With the computer revolution and progress in the knowledge of ship manoeuvring hydrodynamics, an FMBS has been widely introduced to studies aimed at the harbour and waterway design or improvement of operational performance of ship and crew. FMBS has provided a real-world environment for human decision-making, including realistic response dynamics to steering orders and weather/hydraulic conditions [12,13,14].

In the 1990s, Kobayashi et al. [15,16] started the development of a joystick type controller that could control the ship’s motion more easily by providing visual coincidence with the direction of the joystick lever and the ship’s motion. That study proposed a fuzzy allocation of actuators to achieve commanded velocities of a vessel and its surge and sway motion, but it did not concern the energy consumed during such an allocation. Much earlier, even since the 1970s, optimization methods had been introduced into DP control [6,17]. These methods were concerned with the control of fully actuated ships, with a greater number of thrusters than usually met in cargo vessels or ferries, in terms of stationary position keeping or predefined track following. More recent research was performed on the portable DP system as a practical alternative for ships lacking professional DP facilities [18]. Analyses of potential energy savings if manual control had to be performed either via joystick usually available in such systems or via levers commanding individual actuators have not been concluded, though some DP operators prefer using an independent joystick instead of the so called individual thruster sticks. The knowledge about force allocation principles either using individual thruster sticks or using a joystick is still essential, as a lack of this knowledge can even lead to DP accidents [19].

Lately, studies on energy-related DP control strategies [20] and energy consumption by conventional (thruster-based) and anchor-based dynamic positioning of a ship [21] have been conducted. In the latter, despite some methodical deficiencies of comparing two different cases, the focus was mostly on station keeping. Nevertheless, those studies have not taken into account the potential energy savings if the optimized joystick control was used instead of individual thrusters and, moreover, in dynamic harbour manoeuvres of non-DP ships.

In the research reported in this paper, the authors calculated and analysed the total energy (in J) absorbed during a specific yet representative phase of twin-screw ferry harbour manoeuvring. The energy and emission reduction are not exactly equivalent to each other (in terms of NO_x/SO_x emission) and related to main engine load. This is especially true in ship transient manoeuvres such as harbour manoeuvres, where there is a lot of acceleration/deceleration phases that are quite different from almost steady-state route sailing and, thus, more difficult to analyse [22]. The route free-sailing phase often dominates in the overall ship operation and is interesting to most of the researchers, but the harbour berthing/unberthing phase (with or without tug assistance) causes a concentration of toxic emission. Another problem is that it is hard to optimise the operation-related fuel saving (or CO₂ emission) during self or tug-dependent manoeuvres of merchant ships in narrow or limited water areas of harbours. Generally, for ocean shipping, this is performed in terms of the widely used energy efficiency operational indicator (EEOI). With regard to harbour manoeuvring, however, it is necessary to adopt a dedicated definition of the “useful (transport) work” in the EEOI denominator [23,24,25] which is a real challenge.

2. Problem Formulation and Methods

In this paper, the analysis of potential energy savings is presented while berthing a ship controlled via a joystick, compared to berthing a ship controlled traditionally via individual levers of propellers and rudders’ actuators. The analysis was conducted for a specific case study vessel described in Section 2.1. This section includes ship particulars and other data used in the simulation. The assumptions and principles of the thrust allocator model which was built in MATLAB/C++ is presented in Section 2.2. The Full Mission Bridge Simulator (FMBS), which was used in the study, is presented in Section 2.3.

2.1. Case Study Vessel

The vessel selected for the simulation study was of generic ferry type operating in the Baltic Sea between Poland and Sweden (Figure 1). The simulated ship’s parameters were:

• Length overall (LOA) 174 m;
• Length between perpendiculars (LBP) 158 m;
• Beam moulded (B) 24 m;
• Draught (T) 6.4 m;
• Displacement 16,000 t;
• Service speed 27 kn;
• Two main diesel engines, of total power 31,700 kW, connected via shafts to controllable pitch propellers (CPPs) of inwards revolutions, each generating maximum bollard pull force ahead 100 tF (981 kN, at forced pitch reduction by ca. 20% vs. design pitch due to engine overload) and astern 72 tF (706 kN, at traditionally, arbitrarily reduced pitch for astern order up to 60% of design pitch) for 100% bridge throttle in both directions, the propeller diameter (D), revolutions, and nominal pitch ratio (P/D (–)) of 4.9 m, 156 rpm, 1.1, respectively;
• Two semi-balanced rudders of maximum deflection angle 35° and maximum deflection rate 5°/s;
• Three bow tunnel thrusters (of CPP type) of total power 2800 kW, superseded in the study by 1 equivalent bow tunnel thruster generating maximum lateral bollard pull force of 42 tF (412 kN);
• The reference origin (RO) for component thruster forces and their moments calculation fixed midships (0, 0) in the ship-body reference frame (consistent with the origin for differential equations of motion);
• Capability to generate n = 3 component thruster forces of magnitude u_i (tf), acting at p_i = (p_xi, p_yi) (m, m) in directions θ_i (°), i = 1, 2, 3 (Figure 2), where:

  $$p_x={[p_{x1}\hspace{0.17em}\hspace{0.17em}{p}_{x2}\hspace{0.17em}\hspace{0.17em}{p}_{x3}\hspace{0.17em}]}^{\mathrm{T}}={[66.0\hspace{0.17em}\hspace{0.17em}-79.0\hspace{0.17em}\hspace{0.17em}-79.0]}^{\mathrm{T}}$$

  (1)

  $$p_y={[p_{y1}\hspace{0.17em}\hspace{0.17em}{p}_{y2}\hspace{0.17em}\hspace{0.17em}{p}_{y3}]}^{\mathrm{T}}={[0.0\hspace{0.17em}\hspace{0.17em}5.0\hspace{0.17em}\hspace{0.17em}-5.0]}^{\mathrm{T}}$$

  (2)
• The component thrust force limits u_{max i} (tf):

  $$\begin{gathered} 0\le u_i\le u_{\max i} \\ {u}_{\max }={[u_{\max 1}\hspace{0.17em}\hspace{0.17em}{u}_{\max 2}\hspace{0.17em}\hspace{0.17em}{u}_{\max 3}]}^{\mathrm{T}}={[42\hspace{0.17em}\hspace{0.17em}100\hspace{0.17em}\hspace{0.17em}100]}^{\mathrm{T}} \end{gathered}$$

  (3)
• The thrust angle (direction) limits θ_i (°):

  $$\begin{array}{l}{\theta }_1=90\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}{\theta }_1=270\\ 315\le {\theta }_2<360\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}0\le {\theta }_2\le 45\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}{\theta }_2=180\\ 315\le {\theta }_3<360\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}0\le {\theta }_3\le 45\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}{\theta }_3=180\end{array}$$

  (4a)

  $$\begin{array}{l}{\theta }_{start}={\left[\begin{array}{ccc}{\theta }_{start1}& {\theta }_{start2}& {\theta }_{start3}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{ccc}-90& -45& -45\end{array}\right]}^{\mathrm{T}}\\ {\theta }_{end}={\left[\begin{array}{ccc}{\theta }_{end1}& {\theta }_{end2}& {\theta }_{end3}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{ccc}90& 45& 45\end{array}\right]}^{\mathrm{T}}\end{array}$$

  (4b)

The choice of this particular ship was dictated by its ability to perform self-dependent manoeuvres (i.e., without tugs), in typical weather conditions accepted by the harbour rules. The advanced mathematical model of such a ship had been developed by the authors within the FMBS open modelling software, and later calibrated and validated in the course of various research and crew training projects (see Section 2.3 for details).

The implicit and explicit values of 45° thrust angle limits applied in (4a) and (4b) were set differently than the maximum passive stern rudder deflection of 35° for the ship. Since the allocation algorithm (presented in the next section) was basically designed for azimuth thrusters, where the difference between the actuator’s angle and thrust angle is practically negligible, the need arose to calculate the actual, hydrodynamically developed thrust angle for a propeller–rudder combination. This was performed both in terms of constraints and output value. Finally, the computed optimal value of propeller–rudder thrust angle in ahead direction, if non-zero, was converted to rudder deflection by a reduction factor (called rudder factor) of 0.78. Accordingly, 45° thrust was produced by the physical rudder deflection of 35°. This ratio seems to well represent the propeller–rudder hydrodynamics in close to bollard pull conditions (high propeller loading) within standard rudder angles up to 35°, where the resulting thrust is in some excess of the physical angle.

2.2. Thrust Allocator Model

The problem to solve was to find u_i and θ_i that yield the desired resultant force and moment (of force) applied to ship’s hull while minimizing the energy consumption. The problem can be described as follows:

• Solution is sought in 3-DOF or in 2-dimensional horizontal plane space;
• The desired resultant force F (tf) acting at p_F = (p_xF, p_yF) (m, m) in direction α (°) can be broken into longitudinal and transverse components:

  $$F=\sqrt{F_x^2+F_y^2}$$

  (5)
  If resultant force is 0 then p_F is assumed (0, 0) and α = 0°;
• The component longitudinal force acting at p_i:

  $$u_{xi}=u_i\cos {\theta }_i$$

  (6)
• The resultant longitudinal force (along x-axis in ship-body frame) (tf):

  $$F_x=F\cos \alpha ={\displaystyle \sum _{i=1}^n{u}_{xi}}=\mathbf{1}{u}_x$$

  (7)

  where: $\mathbf{1}=[\begin{array}{ccc}1& 1& 1\end{array}],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x={[\begin{array}{ccc}{u}_{x1}& u_{x2}& u_{x3}\end{array}]}^{\mathrm{T}}$
  The component transverse force acting at p_i:

  $$u_{yi}=u_i\sin {\theta }_i$$

  (8)
• The resultant transverse force (along y-axis in ship-body frame) (tf):

  $$F_y=F\sin \alpha ={\displaystyle \sum _{i=1}^n{u}_{yi}}=\mathbf{1}{u}_y$$

  (9)

  where: $u_y={[\begin{array}{ccc}{u}_{y1}& u_{y2}& u_{y3}\end{array}]}^{\mathrm{T}}$
• The resultant moment of force (tfm), positive clockwise:

  $$M_z={\displaystyle \sum _{i=1}^n(p_{xi}{u}_{yi}-p_{yi}{u}_{xi})}=\mathbf{1}\left(p_x•u_y-p_y•u_x\right)$$

  (10)

  where the operator $•$ means Hadamard product (elementwise multiplication of matrices),
• The energy, fuel consumption, and GHG emission, per time (or aggregate power used) are strictly dependent on u_i and are assumed to be correlated to:

  $${\displaystyle \sum _{i=1}^n{u}_i^2}=u_1^2+u_2^2+u_3^2=u_x^T{u}_x+u_y^T{u}_y$$

  (11)

  which is subsequently minimised in the allocator to obtain the component thrusts u_i. For a single propulsor, this formula means that delivered power (linearly dependent on torque) is proportional to the thrust squared and is especially true for CPP (controllable pitch propeller) based solutions for main propeller and auxiliary thrusters, such as tunnel thrusters, where constant rpm is maintained. This was also the case of the studied ship. Verification of this assumption can be found in [26,27] and is generally accepted within the practice of thrusters allocation in DP systems.

If variables u_i and θ_i are converted to u_xi and u_yi (longitudinal and transverse components of forces u_i), the mathematical optimization problem will have the form of quadratic program (QP) [9] where objective function is convex quadratic, and the constraints functions are affine. When linear inequality constraints are added, the problem becomes QP-constrained regression. If the objective as well as the inequality constraint functions are quadratic, the problem becomes a quadratically constrained quadratic program (QCQP). In QCQP, a convex quadratic function is minimized over a feasible region.

For solving such optimization problems of the following form (12) [9]:

$$\begin{array}{l}\mathrm{minimize}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}_0\left(x\right)\\ \mathrm{subject} \mathrm{to}\hspace{0.17em}\hspace{0.17em}{f}_i\left(x\right)\le 0,\hspace{0.17em}\hspace{0.17em}i=1,\hspace{0.17em}\hspace{0.17em}\dots \hspace{0.17em}\hspace{0.17em},m\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}Ax=b\end{array}$$

(12)

where functions f₀, . . ., f_m: Rⁿ → R are convex and twice continuously differentiable, and A ∈ R^p×n with rank A = p < n (Rⁿ are real n-vectors or n × 1 matrices), the interior-point methods or algorithms are commonly used.

To solve the ship’s thrust allocation problem, a specific QCQP algorithm was developed by the authors in MATLAB^TM and C++ according to the guidance given in [9]. The formulation of the objective function and constraints in case of the selected exemplary vessel was given in matrix notation as four separate problems depending on ahead or astern operation of ship’s main engines or propellers (15–18). This was due to constraints on thrusters’ work sectors (limits of θ_i) given by (4). These constraints are defined by hyperplanes, limiting the sector angle in analogy to the method elaborated in [8] and used in [28]. The limits imposed on ship propulsion system, as presented in Section 2.1, indicated non-convexity in case of main propellers working in reverse mode and lateral thrusters working either to port or starboard. When the propeller is working astern, a line-shaped thrust region appears, as the rudder cannot generate lift in this situation. This is defined by equality and inequality constraints added to the problem as a disjunctive thrust region of the propeller–rudder pair. In case of a lateral thruster, there are also two disjunctive thrust regions. The method to deal with disjunctive thrust regions of the lateral thruster is to replace the alternative geometrical equalities by one conjunctive dual equality:

$$u_{x1}=0$$

(13)

Additionally, analogically, in case of a propeller–rudder pair operating astern, the geometrical equality is replaced by dual inequality and equality:

$$\begin{array}{cc}\begin{array}{l}{u}_{x2}<0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{or}\\ u_{y2}\hspace{0.17em}=0\end{array}& \begin{array}{l}{u}_{x3}<0\\ u_{y3}\hspace{0.17em}=0\end{array}\end{array}$$

(14)

The method to solve the optimization problem of a propeller–rudder pair operating ahead when disjunctive thrust regions are defined is first to generate all the possible combinations of the thrust regions, picking one disjunctive convex region for each thruster. The total number of combinations can be derived from the number of disjunctive thrust regions for each thruster. So, for each of the defined thrust region combinations, the QP problem was formulated as follows:

(1)

If the ship’s both propeller–rudder pairs are operating ahead:

$$\begin{array}{l}\mathrm{minimize}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^T{u}_x+u_y^T{u}_y\\ \mathrm{subject} \mathrm{to}\hspace{0.17em}\hspace{0.17em}{u}_{x1}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x2}\ge 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x3}\ge 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_x=\hspace{0.17em}\mathbf{1}{u}_x\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_y=\hspace{0.17em}\mathbf{1}{u}_y\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_z=\mathbf{1}\left(p_x•u_y-p_y•u_x\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^2+u_y^2\le u_{\max }^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cc}\sin {\theta }_{start2}& -\cos {\theta }_{start2}\\ -\sin {\theta }_{end2}& \cos {\theta }_{end2}\end{array}\right]\left[\begin{array}{c}{u}_{x2}\\ u_{y2}\end{array}\right]\le \left[\begin{array}{c}0\\ 0\end{array}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cc}\sin {\theta }_{start3}& -\cos {\theta }_{start3}\\ -\sin {\theta }_{end3}& \cos {\theta }_{end3}\end{array}\right]\left[\begin{array}{c}{u}_{x3}\\ u_{y3}\end{array}\right]\le \left[\begin{array}{c}0\\ 0\end{array}\right]\end{array}$$

(15)

(2)

If the first propeller–rudder pair is operating ahead, while the second one is operating astern:

$$\begin{array}{l}\mathrm{minimize}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^T{u}_x+u_y^T{u}_y\\ \mathrm{subject} \mathrm{to}\hspace{0.17em}\hspace{0.17em}{u}_{x1}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x2}\ge 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x3}\le 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{y3}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_x=\hspace{0.17em}\mathbf{1}{u}_x\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_y=\hspace{0.17em}\mathbf{1}{u}_y\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_z=\mathbf{1}\left(p_x•u_y-p_y•u_x\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^2+u_y^2\le u_{\max }^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cc}\sin {\theta }_{start2}& -\cos {\theta }_{start2}\\ -\sin {\theta }_{end2}& \cos {\theta }_{end2}\end{array}\right]\left[\begin{array}{c}{u}_{x2}\\ u_{y2}\end{array}\right]\le \left[\begin{array}{c}0\\ 0\end{array}\right]\end{array}$$

(16)

(3)

If the second propeller–rudder pair is operating ahead, while the first one is operating astern:

$$\begin{array}{l}\mathrm{minimize}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^T{u}_x+u_y^T{u}_y\\ \mathrm{subject} \mathrm{to}\hspace{0.17em}\hspace{0.17em}{u}_{x1}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x2}\le 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x3}\ge 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{y2}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_x=\hspace{0.17em}\mathbf{1}{u}_x\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_y=\hspace{0.17em}\mathbf{1}{u}_y\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_z=\mathbf{1}\left(p_x•u_y-p_y•u_x\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^2+u_y^2\le u_{\max }^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cc}\sin {\theta }_{start3}& -\cos {\theta }_{start3}\\ -\sin {\theta }_{end3}& \cos {\theta }_{end3}\end{array}\right]\left[\begin{array}{c}{u}_{x3}\\ u_{y3}\end{array}\right]\le \left[\begin{array}{c}0\\ 0\end{array}\right]\end{array}$$

(17)

(4)

If both propeller–rudder pairs are operating astern:

$$\begin{array}{l}\mathrm{minimize}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^T{u}_x+u_y^T{u}_y\\ \mathrm{subject} \mathrm{to}\hspace{0.17em}\hspace{0.17em}{u}_{x1}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x2}\le 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{x3}\le 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{y2}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{y3}=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_x=\hspace{0.17em}\mathbf{1}{u}_x\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_y=\hspace{0.17em}\mathbf{1}{u}_y\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_z=\mathbf{1}\left(p_x•u_y-p_y•u_x\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_x^2+u_y^2\le u_{\max }^2\end{array}$$

(18)

The thrust allocator model works by solving each of the QP sub-problems (15–18) and storing the corresponding solutions. The best–minimum solution of the whole problem is found by comparing the four objective functions costs (values of the minimized goal functions) and, finally, all u_i are converted to individual propeller, rudder and thruster commands, i.e., main propellers and tunnel thruster pitch and rudder deflection angle.

Within the designed allocator model, the impacts on u_i of main propeller advance/inflow speed versus rpm and pitch, as well as ship forward speed effect upon tunnel thruster performance, were not modelled. They were not assumed significant as the speed effects were expected not to be considerable in terms of the adopted berthing scenario and tactics (presented in Section 3), where the maximum forward ship’s speed was up to 3 kn (1.54 m/s) with relatively high propeller rpm and pitch that meant nearly bollard pull conditions. However, such effects were fully accounted for in the simulator environment, where the complete ship hydrodynamics were applied to computation of ship’s motions. The computed thrusts of particular propulsors: main propellers or tunnel thruster, all of CPP type in the RoPax ship, were transformed linearly to pitch settings in terms of the background hydrodynamics [27].

Figure 3 (with the data table attached) shows the example of thrust allocation for the simulated vessel where F = 0 and M_z = −2751.5 tFm. With the aforementioned rudder factor 0.78, the computed thrust angle of 23.5° was converted finally to rudder angle of 19°.

2.3. Simulation Environment

The study was performed in the FMBS of Kongsberg Polaris type [29] in Maritime University of Szczecin, Poland (MUS). The main bridge of this simulator (Figure 4) consisted of 270° vision projectors and mix of real and screen simulated shipborne equipment, including thrusters and rudders’ controls, speed and heading measuring devices, receivers of electronic position fixing systems, electronic chart and display information system (ECDIS), bird’s eye view display, radar equipment, conning station, and DP control stations. There were manual physical controls for two engines with fixed-shaft propellers (of any type), two rudders (of any type, up to max. angle 70°), two azimuth thrusters, and multiple lateral thrusters.

In order to create own ship models, the simulator software has open architecture of hydrodynamic ship-modelling scripts. This enables building or customizing almost any ship type model of high fidelity hydrodynamics in 6 DOF (surge, sway, yaw, roll, pitch, and heave). As aforementioned, the hydrodynamic model of the studied ferry was in-house prepared, using ultimate, lookup table-based architecture for hydrodynamic relationships [27]. This model was extensively used in MUS for many years in research and training, and was well calibrated and validated by the authors, including onboard measurements and quantitative feedback from ferry captains collected in the course of various past research and training projects. All significant hydrodynamic effects of twin-screw ship were included. Among others, these comprised the so-called four quadrant hull and propeller hydrodynamics and various interaction effects within the hull–propeller–rudder complex, e.g., the side effect of propeller operating astern and oblique inflow to propeller. The architecture of the simulator model inspired a development of similar independent or supportive software and methods [30] that make the model preparation much easier.

The FMBS was additionally supplemented by the authors with a 3DOF joystick station (Figure 5b). The proprietary joysticks of DP control stations (Figure 5c) [31] were not considered in the research as their usage was software and hardware limited only to several specific offshore vessels. The ZF joystick (Figure 5a) [32] was considered but not selected as configured by producer only to cooperation with ZF JMS^TM system. The alternative, common in the automotive industry, Apem joystick (Figure 5b) [33] was chosen and connected via the USB to PC station with the thrust allocator application. This PC-generated output signals replacing CAN bus signals from physical boards of propellers/thrusters/rudders’ manual levers. Necessary command information was provided to the thrust allocator application as a numerical vector of 3 angular parameters: (1) the direction, (2) inclination of a joystick lever, and (3) angle of a joystick knob as being handled. When these characteristics were applied to ship handling, the direction of the joystick lever was the direction of the force, the inclination (tilt value) was the magnitude of the force, and the angle of knob was the magnitude of the force moment ordered. This way the control of the vessel was shifted from individual thruster manual levers to the joystick station consisting of one lever capable to tilt up to 36° in any direction of range (0°,360°) and to rotate from centre in range −30° to +30°.

The Apem joystick used in the simulation scenario is modern industrial Hall effect sensor of highly linear output voltage from 0 to 5 V between minimum and maximum lever’s and knob’s shift. Studies performed by Ermakova and others [34,35] proved that magnetic maps of such sensors can be rescaled to output very precisely. Performing designed scenario navigators became easily accustomed to the joystick with no evident preference for classic control.

During simulation runs values of F and α were set by the inclination and direction commands of the joystick, and value of M_z were set by the angle command via the rotatable knob at the top of the joystick lever. These values were scaled linearly between 0 and maximum derived geometrically from (3) and α. Maximum resultant force in a specific direction corresponded to the maximum tilt of the joystick lever.

3. Simulation Scenario

A scenario covering the typical manoeuvring phases of a ship’s berthing operation was designed. Navigators’ task was to steer the vessel either via the classic engine, rudder and thruster levers, or via a joystick while: (1) following the predefined straight track, (2) rotating at the turning area and (3), finally, crabbing (moving sideways) until stopping at the quay fenders. The port of Świnoujście, Poland, and its multi-berth ferry terminal was selected as a reference virtual test bed site according to the methodology proposed by Hahn [36]. The Electronic Chart Display and Information System (ECDIS) screens (Figure 6 and Figure 7) show the planned berthing approach and an exemplary recorded trajectory of ship’s RO.

The planned berthing approach trajectory and turning area were marked by the electronic bearing line (EBL) and the variable range marker (VRM) in the simulator’s ECDIS (Figure 6) in order to force the navigators to follow the established manoeuvring tactics.

The joystick-based scenario covered 10 runs by five experienced navigators of 2 runs each, with a time separation of at least 2 h between runs by the same navigator to avoid overtraining. The scenario based on the independent actuators’ control consisted of eight approaches (one navigator less). In this scenario, every expert performed four runs, two in each mode. Only local experts, familiar with the ship handling in Świnoujście harbour, twin-screw ferry operation, and the FMBS in MUS were engaged. Conditions and manoeuvring tactic guidelines (recommended velocities, permitted thrust values) were fixed equivalently in both scenarios. Calm weather conditions in all cases were assumed, where wind, wave, and current effects were negligible.

Figure 8 presents a view to the ferry terminal from the ship’s bridge, and the particular quay being approached in the FMBS experiment.

The tactic imposed upon the ship handler was to move a ship, initially at rest, straight linearly from the position marked in Figure 6 towards the centre of the turning area, represented by the displayed offset EBL marker, but not faster than approximately 3 kn. Then, the ship was rotated in place anticlockwise and subjected to the final sideways movement with the constant heading parallel to the quay, where the ship should touch the fenders starboard side alongside (Figure 7). The maximum allowable lateral velocity at the moment of the fender impact was restrained to 0.5 kn. Minimizing the time for the total manoeuvre was requested from the participating navigators. Because it could lead to the execution of the maximum allowable control (pitch) settings, they were operationally/arbitrarily limited to 50% for the bow thruster and 30% for the main propellers. These settings matched the control lever positions due to the adopted linear rule. It should be borne in mind that the maximum astern pitch of the main propeller for the maximum throttle lever (i.e., bridge telegraph, operated −100% to +100%) amounted to 60% of the maximum ahead value for the studied ship (usually 60–70% in design practice of CPP steering system). That is why the actual astern pitch for the same absolute throttle position (as being directly controlled) was reduced to the latter figure (taking in the experiment the maximum value of approximately −18% for −30% throttle). The above pitch limits were equally kept in both modes: the independent actuators’ controls and the joystick-based one.

Thus, the manoeuvres consisted accordingly of a forward acceleration and deceleration, turning, and crabbing (lateral acceleration and deceleration).

4. Results

The data from the conducted simulation experiment, regarding energy consumption, are gathered in

Table 1. Details of the simulation experiment output.

Run Name	Time (s)	Time (min)	Energy PORT (MJ)	Energy STBD (MJ)	Energy BTU (MJ)	Energy Total (MJ)	Energy Main (P&S) (MJ)	Energy Ratio BTU/Total (–)
ind #1	766	12.8	251.0	393.0	325.6	969.6	644.0	0.34
ind #2	798	13.3	231.1	392.6	243.4	867.0	623.7	0.28
ind #3	726	12.1	272.8	500.3	314.2	1087.3	773.1	0.29
ind #4	1072	17.9	163.8	336.5	189.1	689.4	500.3	0.27
ind #5	904	15.1	195.7	523.9	212.3	931.9	719.6	0.23
ind #6	990	16.5	249.0	503.3	193.8	946.1	752.3	0.20
ind #7	858	14.3	249.6	409.5	236.8	895.9	659.1	0.26
ind #8	786	13.1	209.2	391.1	254.5	854.7	600.2	0.30
j/s #1	1054	17.6	164.2	266.1	145.3	575.7	430.3	0.25
j/s #2	902	15.0	190.1	558.4	145.0	893.4	748.5	0.16
j/s #3	816	13.6	184.0	410.5	216.0	810.5	594.5	0.27
j/s #4	948	15.8	188.5	499.1	183.1	870.8	687.7	0.21
j/s #5	714	11.9	188.3	409.9	211.8	810.0	598.3	0.26
j/s #6	770	12.8	184.1	448.8	243.7	876.7	632.9	0.28
j/s #7	784	13.1	188.9	419.1	194.6	802.5	608.0	0.24
j/s #8	846	14.1	210.3	446.1	236.0	892.4	656.4	0.26
j/s #9	770	12.8	152.7	409.8	189.3	751.8	562.5	0.25
j/s #10	837	14.0	189.5	455.2	197.2	841.9	644.7	0.23

. The table is divided into runs where the ship was controlled either by the independent levers of actuators or by the joystick, correspondingly marked by ‘ind #’ and ‘j/s #’. The parameter “Time” means the duration of the manoeuvre completed (as instructed). In the next columns, the energy consumed by the port and starboard main propeller, bow thruster unit, and the total energy (as sum of the former) are depicted. Finally, the aggregate contribution of both propellers and relative BTU usage are presented. The energy was calculated by an integration in the time domain of the power used by the particular propulsor, which is square-dependent on the actual pitch setting (whilst thrust changes linearly with pitch). Although this energy, consumed by or delivered to the propulsor and referred as the hydrodynamic power, is less than the energy produced for the propulsion/steering purpose by the main engines or diesel generators onboard, it is sufficient and a representative indicator of the energetic processes to evaluate the conducted experiment and the joystick-based manoeuvring performance.

The power absorbed hydrodynamically, in analogy to the one calculated by the mathematical model of FMBS, was off-line calculated for the CPP-type propulsor of BTU according to:

$$N_{BTU}=N_{BTU}^{nom}·{\left(P_{BTU}^{\%}\right)}^2$$

(19)

where $N_{BTU}^{nom}$ stands for the nominal power of BTU and $P_{BTU}^{\%}$ stands for pitch percentage (max. 100%) of the thruster.

The power absorbed hydrodynamically for each of the main propellers was calculated according to:

$$N_{main}=2\pi \rho n^3{D}^5{\left(\frac{P}{D}\right)}^2{k}_{Q0}^{*}$$

(20)

assuming a low advance speed as practically equivalent to bollard pull conditions, where: ρ—water density: n—nominal propeller revolutions (1/s); D—propeller diameter; P/D—actual propeller pitch ratio (–); $k_{Q0}^{*}$ (–)—propeller torque coefficient (almost constant in the range of low propeller advance speed or more precisely of so-called propeller advance coefficient), practically equal to 0.05 for standard propellers independent of their design pitch value.

The selected statistical parameters of the data in Table 1 are presented in

Table 2. Statistical summary.

Parameter	Time (min)	Energy BTU (MJ)	Energy Main (P&S) (MJ)	Energy Total (MJ)	Energy Ratio BTU/Total (–)
ind—mean	14.4	246.2	659.0	905.2	0.27
ind—st. dev.	2.0	51.1	89.0	113.6	0.04
j/s—mean	14.1 (−2.1%)	196.2 (−20.3%)	616.4 (−6.5%)	812.6 (−10.2%)	0.24 (−10.8%)
j/s—st. dev.	1.7 (−16.0%)	33.2 (−35.0%)	84.1 (−5.6%)	95.0 (−16.4%)	0.03 (−16.6%)
test F	0.6123	0.2278	0.8515	0.6030	0.5998
test t (1-tail)	0.3634	0.0115	0.1564	0.0388	0.0571

. These are means, standard deviations, and p-values of statistical tests, 1-tailed t- and F-tests. The former statistical tests measured equality of means in the two groups to prove their significant difference.

The energy data in Table 1 are also presented as graphs in Figure 9, supplementary as a function of manoeuvre duration.

Figure 10 presents the basic kinematics of the manoeuvre in terms of linear/angular velocities and the ship’s positions, including its swept path. These kinematics data are presented in the paper only for the independent steering mode, case ‘ind #3’ (see Table 1), since they are similar and, thus, representative for other cases, also including joystick steering. With regard to the simulation scenario, due to data integration, the ship kinematics were not so much sensitive to instant steering orders.

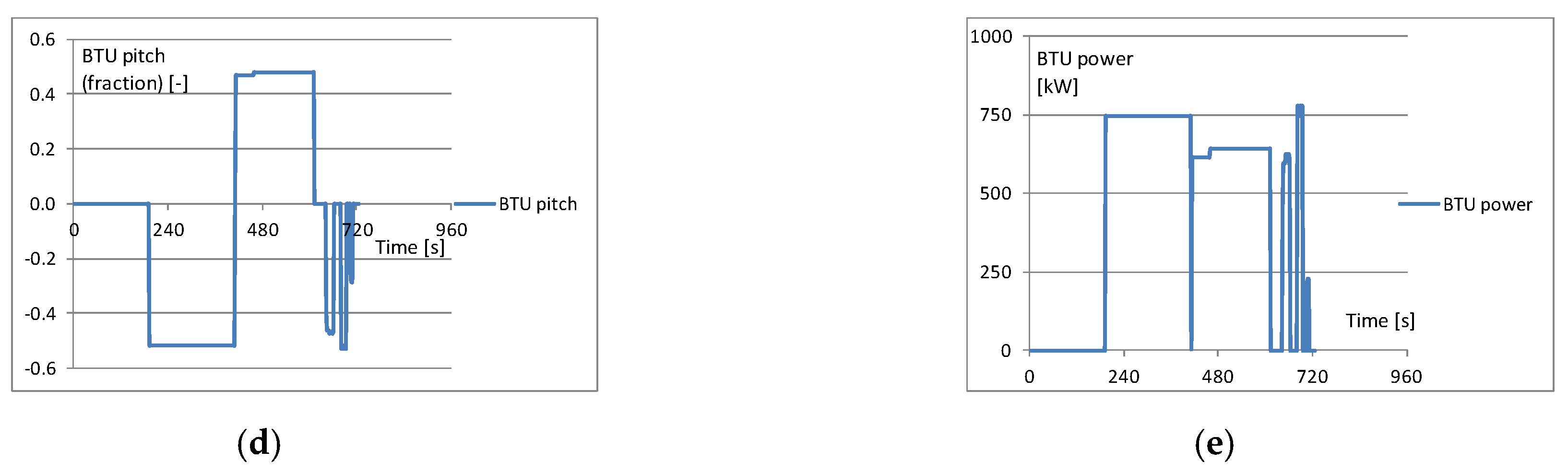
Figure 11 illustrates the instant settings of particular steering devices and their corresponding power for the same case ‘ind #3’. For the comparison, Figure 12, in identical format, reveals the device settings for a random joystick-based case, herein ‘j/s #7’.

5. Discussion

Analysing Table 1, and particularly Table 2, one can find that a general performance of joystick-supported ship handling (with a thrust allocation algorithm) for a large sea-going twin-screw ferry with BTUs, as opposed to the traditional (manual or independent) steering, was approximately 10% better in terms of energy saving. The energy saving came in almost equal shares from the main propellers (6–7% saving by Table 2, at 3/4 usage of main propulsion) and BTU (20% saving, but with 1/4 usage of BTU over the manoeuvre duration). Additionally, the contribution of BTU in the total energy absorbed was lower by approximately 10% for steering by a joystick. However, one must take into account that the power of the installed BTU (typical for the designs of sea-going ferries) was also about 10% of the main propulsion power.

These values reflect the ship performance during basic, common manoeuvres (in general, constituting a part of the more complicated harbour entering and berthing process), the ideal weather conditions, and some operational control restrictions, that were assumed in the experiment. In more frequently met conditions, in terms of the harbour/waterway layout, manoeuvring objectives and tactics (planned track and expected kinematic parameters), and environmental/weather conditions, one can expect even higher potential energy-savings.

The achieved, essentially preliminary results were very promising and should encourage further research, especially with regard to other types of steering and propulsion, more complex berth approach and berthing manoeuvres, and statistical validation, especially among factors contributing to total energy-saving. It is interesting that for the main propellers, energy-saving while steering the ship by joystick vs. independent controls mode was negatively confirmed by statistical tests (high p-value despite 6–7% difference in nominal means), while the total saving of 10% was statistically significant at the significance level of α = 0.05. This, additionally, proved a certain role of BTU in the total energy-saving. Furthermore, there was obviously no significant difference between manoeuvres’ durations for the joystick and independent steering under the imposed constraints and operational guidelines.

Taking into consideration the spread of the manoeuvres’ duration and its correlation to energy used (as presented in Figure 9), it should be noted that the interval 12 to 18 min, independently for both modes, seemed to be a matter of human operator control. Experts relied on their own experience and feeling in their self-assessment of safety and efficiency of the executed manoeuvre. The correlation of energy with time exists only for BTU (Figure 9c,d). BTU energy decreased with the increase in time, equally for both steering modes.

Having a look at Figure 11 and Figure 12, one can notice that in the FMBS experiment the order of maximum magnitude of BTU and main propeller power was surprisingly nearly the same. However, for the joystick operation as combined with the thrust allocator, the produced device settings and their frequency seemed to be very sensitive to the joystick lever and knob shifts. It did not affect the energy-saving performance but suggests that non-linear scaling of joystick commands could be more appropriate for navigators. This sensitivity can especially be seen for allocation of the main propellers and rudders.

Other facts were also noticed during the research and widely stressed by the study participants. All navigators admitted that the joystick operation was much more comfortable and effortless, and as equally safe as the manual operation of independent levers. The steering by a joystick relieved the operator’s attention from five individual settings (1 BTU, two main propellers, two rudders) to two settings (joystick’s lever and knob) and allowed him/her to concentrate on other operational aspects and, thus, to achieve much higher situational awareness.

6. Conclusions and Future Research

The presented simulator study was aimed to improve sea-going ferry harbour manoeuvres, i.e., occurring in maritime emission-sensitive areas and performed by large ships of frequent and regular port calls without tug assistance, in terms of energy consumption and, consequently, GHG emissions. This type of ships is particularly predestined to operational (manoeuvring) optimization in terms of ecological and economical aspects because of its complex twin-screw conventional propulsion augmented with powerful bow tunnel thrusters. Such an optimization can be achieved via joystick and thrust allocator application (analogous to the one used in DP vessels). The purpose of the presented research was to evaluate potential benefits of steering a ferry by a joystick in comparison to steering it by independent actuators’ controls. The achieved overall 10% energy-saving is promising and justifies further research, including whether and when even higher benefits are possible and what group of ship control devices is suited for future exchange or supplementation. This is in the interest of ship designers, maritime administration, ship operators, and the general community as well.

There were also some limitations to the research done, which should be overcome and supplemented in the future. They mainly related to specific conditions of the ship, its propulsion and steering devices, the assumed manoeuvring scenario, and the thrust allocation algorithm. Therefore, further variations of ship parameters and scenarios are suggested. The thrust allocator can be more integrated with ship hydrodynamics to account for various physical effects and to reach a better agreement between the ordered excitations and motion response. Moreover, this study can be validated by a means of field tests on a real ship, especially with dedicated onboard instrumentation and sensors monitoring environmental variables.

The used energy indicators seemed to meet the proper criteria for evaluating and optimizing ship operations when records of ship motions and ordered commands were available. Such indicators have not been significantly and sufficiently dealt with within the literature so far. In addition, such criteria should be implemented in ship-handling training of mariners, closing another gap in their awareness of the need to protect Earth’s natural resources for future generations.