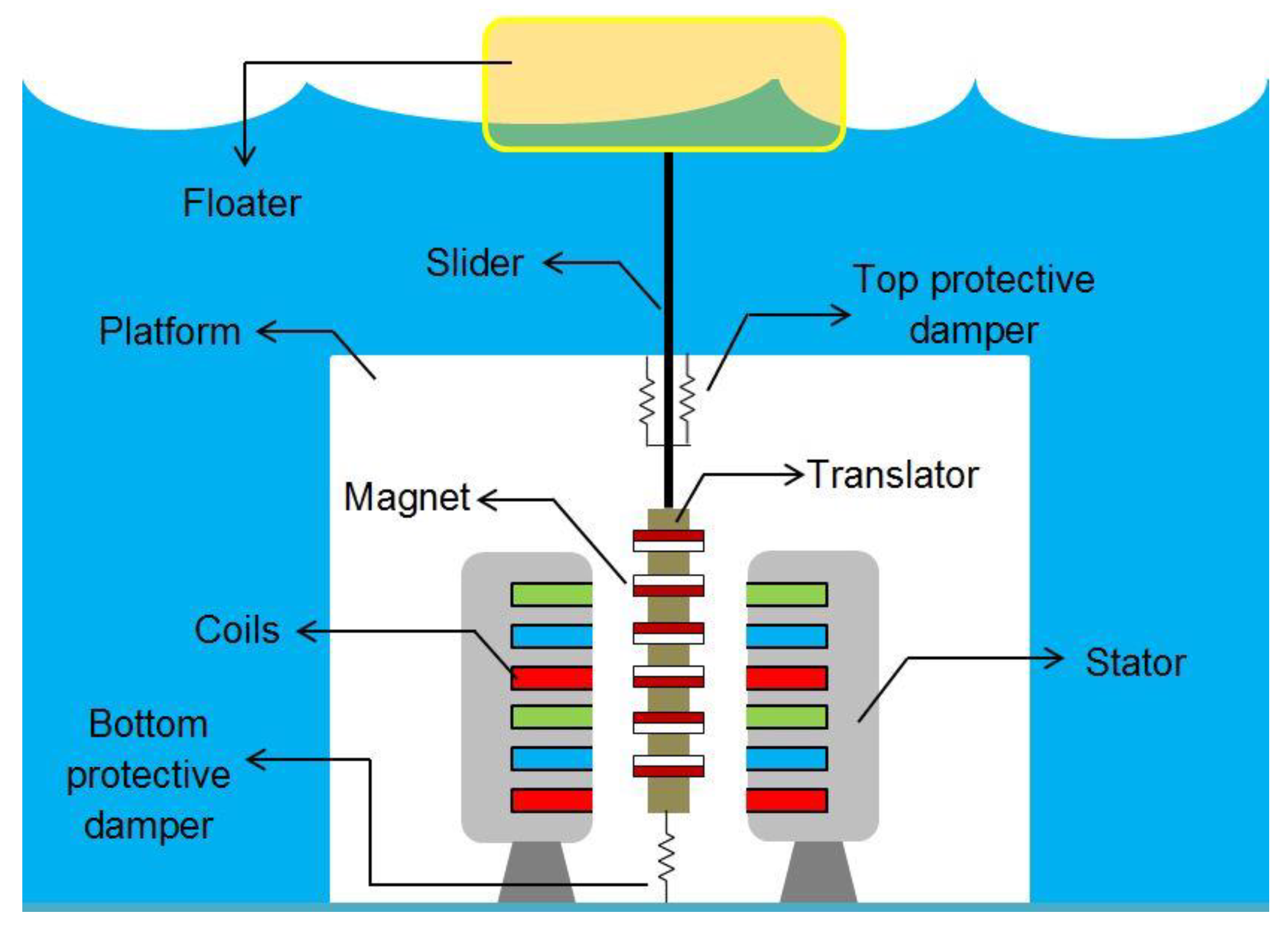
In this section, the unidirectional long-crested random waves, the floater dynamics based on the random waves, and the electrical output of the LPMGs will be explained.
3.2. Floater Dynamics under Random Waves
The wave motions will move the floater and translator in synchronized motions.
Figure 14 shows the resulted floater deviations under random wave configurations compared to those under the initial sinusoidal wave for several sampling times. The different wave characteristics result in different floater moving patterns in certain periods. Some points are explaining the resulted vertical deviations from different random wave parameters.
First, the floater deviation is proportional to the wave elevations, which are linear to the significant wave height.
Figure 14(left) shows that the random wave with higher significant wave height results in a higher floater’s vertical deviation. Meanwhile, in
Figure 14(right), different peak frequency random waves result in similar deviation, as the resulted wave’s particle elevations are also similar to each other (
Figure 13). Next, the deviation changes will determine the instantaneous vertical speed (
Figure 15). In this case, the relation between the deviation and speed results in the derivation of the wave parameters trends as shown in
Figure 14. Then, the significant wave height is linearly proportional to the average vertical speed. Inversely, as the peak frequency decreases, the average vertical speed slightly increases.
Table 6 tabulates the floater’s deviation and speed under different significant wave heights and peak frequencies.
For random waves with a significant wave height of higher than 2.5 m, the average floater deviations are higher than that from the initial regular wave. However, only a wave with a significant wave height of 4.5 m results in a higher average vertical speed than the regular wave. The wave mechanisms under regular scenarios are running stably and continuously, while in unidirectional long-crested random waves, the instantaneous values fluctuate irregularly. Then, that different trend results in a diverse average value. Meanwhile, the average floater’s deviations and vertical speed from all peak frequencies are smaller compared to that from the initial wave.
The vertical speed is proportional to the translation speed, which will govern the electromotive force. In an equal translator-stator position, higher instantaneous vertical speed will result in higher momentary induced voltage. From the data in
Table 6, it is reasonable to approximate that the electrical output of the WEC under the random waves will be smaller than that from the regular one, unless for a significant wave height of 4.5 m.
However, there is another effect that also plays a significant role. The average vertical deviation represents half of the average floater amplitude. The amplitude itself is linear to the displacement covered by the translator when moving between its two farthest ends. Compared to the effective translator stroke, random waves with a significant wave height of more than 2.5 m result in higher amplitudes. Nevertheless, all different wave parameters also have moments where the instantaneous floater amplitudes are higher than the effective stroke. This is because all wave variations have a larger significant wave height setting. Since the moments negatively affect the output voltage and power, there will be mixed influences along with the vertical speed factor.
3.3. Output of the LPMG
First,
Figure 16 (left) shows the induced voltage from both LPMGs under no wave influence. The translation speed is set constant at 1 m/s. Since the semi iron-cored LPMG has undergone modification in the number of turns (to compensate for the incomplete iron body), its resulted voltages are similar to the iron-cored. The constant unity speed put aside the
ds(t)/dt component, meaning this is the ‘basic’ induced voltage graph of both LPMG designs, regardless of the wave mechanisms that drive it. In this case, the translator moves uniformly from one end to another. The voltage first rises gradually until reaching the peak and then decreases. The maximum value is achieved at the optimum position: when the translator is directly facing the stator in a parallel position.
An experiment has been performed to measure the real output of the mini-models of LPMGs. The setup is shown in
Figure 16 (right). A belt is connecting a DC motor and a pulley. At the edge of the pulley, a metal bar is installed, which is connected to the translator. When energized, the DC motor will rotate the pulley through the belt. Next, the metal bar converts the rotating motion into linear motion, which will be delivered to the translator. In this experiment, the translation speed is 1 m/s. It can be set by regulating the DC motor speed, considering the ratio of the motor’s axis diameter and the pulley diameter.
Figure 17a,b show the output voltage of the small-scale models compared to the theoretical output from simulation and analytical calculation. Overall, the resulted sinusoidal graphs agree with the analytical calculation, with the resulted voltage from both real models being about one-seventh of the theoretical value. Then, it is assumed that the trends will also be relatively close in unidirectional random wave conditions.
Figure 17c presents the LPMGs’ operations under regular wave conditions. The shorter stator and translator lengths compared to the applied wave amplitude cause several disjoints in the voltage graph. The disjoints reduce the effective output voltage and power. However, the LPMG can still produce the expected power, because the LPMG establishment is arranged to gain the highest translation speeds in the optimum position. In a regular scenario, this arrangement is easier to conduct since the wave dynamics are mathematically simpler to model. The high speed that drives the translator when it directly faces the stator (optimum position) will result in high voltage and high output power. In
Figure 17c, the maximum voltage is resulted at the maximum speed. Then, the maximum voltage and power compensate for the disjointed outputs. From a design aspect, it allows the LPMGs’ sizes to be fitted and compacted.
On the other hand, the induced voltages under random wave variations are shown in
Figure 18 and
Figure 19. In random wave conditions, both the position and the translation speed (proportional to the floater’s vertical speed) mechanisms do not refer to any regular pattern (
Figure 14 and
Figure 15). Their values depend on the momentary excitation force of the wave. The maximum speed or high speeds do not always occur during the optimum position. The term of optimum position means the position where the translator vertical deviation (
y-axis) equals zero (
Figure 20(left)). Consequently, the higher speed that drives the translator in not optimum positions may result in lower voltage than the lower speed that occurs during the optimum position. Thus, even though the translation speed is proportional to the resulted voltage, under random waves, it still depends on the translator-stator’s instantaneous position. In
Figure 18 and
Figure 19, the maximum voltage does not always result in the maximum translation speed.
Parts of the not optimum position refer to the non-facing event (
Figure 20(right)). When the effective translator stroke is shorter than the floater amplitudes, there are moments when the floater movements position the translator not facing the stator completely. In this position, the leakage flux rises and the flux flows to the stator drops (
Figure 20(right)), thus reducing the induced voltage significantly. Then, the frequency of the event is inversely proportional to the overall induced voltage.
From a design aspect point of view, the LPMG needs to be installed with a longer translator to avoid the event. However, it will make a significant increase in manufacturing cost and total weight (additional magnet and translator yoke).
Figure 21 presents the percentage of time spent by the facing and non-facing events under the unidirectional long-crested random wave conditions. The higher the significant wave height, the higher the total duration of the non-facing event. Meanwhile, the peak frequency variation results in a similar percentage.
Then, from the induced voltage, the output power can be calculated.
Figure 22 shows the output power graphs from both LPMG designs under different random wave configurations. They make irregular forms with several disjoints (where the output values are close to zero) due to the non-facing events. Previously, the disjointed graphs were also resulted under regular wave tests [
44]. The design process under sinusoidal wave assumption allowed the translator length to be shorter than the wave amplitude, thus causing the events. In the next explanations, the output power will be analyzed in two aspects: maximum and effective (root mean square) values. The first is a measure of the system’s ability to produce as maximum output power as possible. Meanwhile, the latter value is used to analyze the overall delivered output power considering the limited and fixed dimension of the LPMG as well as the irregular wave forms.
Figure 23 and
Figure 24 show the effective and maximum output powers of both LPMGs under different wave variations for various load resistances. Then, the values for all configurations are tabulated in
Table 7. In previous induced voltage in random waves’ discussion, the resulted voltage is affected by two factors: the instantaneous translation speed that moves the translator and the translator position itself. Therefore, the output power under different wave parameters can be analyzed from two parameters: the floater’s average vertical speed and the non-facing frequency.
For both designs, the output powers under different significant wave heights have no specific trend. It is due to the mixed effect as mentioned in the previous subsection. While the average vertical speed that drives the translator is linear to the significant wave height, the frequency of the non-facing event also increases as the wave height rises. The first and second factors successively contribute in positive and negative ways to the output voltage and power. Then, the combination of the driving wave’s effects results in no specific trend in the output power.
On the other hand, the peak frequency is inversely proportional to the output power. This is in accordance with the JONSWAP energy spectrum as well as the average floater vertical speed trends. The higher vertical speed is linearly proportional to the induced voltage. Under an equal load, the output power is also proportional to the voltage. Meanwhile, the non-facing event frequency is relatively the same among different peak frequency random waves; thus, it has a similar influence on the output power trend.
Meanwhile, the output powers of the iron-cored LPMG are higher than the semi iron-cored ones. The comparison applies to equal random wave configurations. This is because the semi iron-cored has more winding than the iron-cored; hence, more impedance is formed. For similar induced voltage between the two LPMGs, the higher impedance will decrease the load current and the terminal voltage, which are two components composing the output power. The relation also applies to all load resistances.
Figure 23 and
Figure 24 also show the output powers trend for several load values. The output power of both designs initially rises as the load is increased. After reaching the peak, the output power slightly decreases to a convergent state.
Regarding the output powers resulting from different significant wave heights compared to those from peak frequency variation, there are two influencing factors. From
Table 6, the significant wave height variation produces a higher average vertical speed than the different peak frequencies. The vertical speed that next produces translation speed is linearly proportional to the induced voltage (Equation (13)) and linear to the output power (Equations (17) and (18)). On the other hand, the different significant wave heights also result in more frequent non-facing events than the peak frequency variation. Consequently, some of the high translation speeds occur during the moment. In case it happens, the higher translation speed will not positively affect the output voltage and the output power. Comparing the output powers resulting from both wave parameters’ variation, the higher translation speed’s effect outweighs the effect of the non-facing event.
There are also differences between the output powers from both designs compared to the rating of the LPMGs. This shows that under the unidirectional long-crested random wave, the designs (with their dimensions) have not been able to fulfill the expected output. Here, two notable factors can be considered in improving the LPMG designs. First, the wave height data in the placement location show the presence of high wave amplitudes in some periods. To model the wave as realistically as possible, those data are included in the random waves’ formation. Then, it causes a significant difference between the wave amplitude and the effective translator stroke. As a result of the event, the output power drops in some moments. Second, the LPMG design should also be considered. Under the unidirectional long-crested random wave scenario, the wave elevation and speed fluctuate irregularly throughout time. To optimize the output power, the shorter and limited dimension of the stator and translator should be able to gain high translation speeds during optimum position.
To understand the significance of the non-facing events to the output power, the outputs from the events need to be eliminated. In
Table 7, the output powers without the non-facing event are also presented. For both designs, the effective output powers are increasing. The changes show the negative impact resulted from non-facing events. The nearly zero output power during the events decreases the overall output. Meanwhile, the maximum powers are the same because they resulted during the facing event; thus, eliminating the non-facing event produces no effect. For different peak frequencies, the increase of the effective power is similar, because the non-facing event duration is similar between different frequencies. The increase is also not significant, as the non-facing event spends a minority time portion compared to the facing event. Meanwhile, the non-facing event frequency is linear with the significant wave height. Thus, the increase of the output power is rising with the increase of the height.
However, the increase in the effective output power is not significant enough to reach the expected output. The maximum output powers are also below the expected value. In this case, the more influencing factor is the LPMGs’ inability to harness high translation speeds within its effective translator stroke range. Unlike the regular wave, the dynamics of the unidirectional long-crested random wave do not follow any regular pattern. Thus, for LPMGs whose dimensions are shorter than the wave amplitude, not only are they vulnerable to the non-facing event, it is also difficult to position them or to arrange the translator-stator relative position so that it can optimally harness the wave’s high vertical speeds. Under regular waves, the LPMGs still experience non-facing events but are still able to produce the expected output.
Thus, in designing the LPMG-driven WEC, the shorter translator (than the wave amplitude) model cannot be employed. The easier way to improve is by extending the dimension, approaching or even equalizing the wave amplitude at the placement site. However, it still needs to be investigated whether other components also require upgrading. Furthermore, design optimization is also required to manage the manufacturing cost. In this case, the wave amplitude variation becomes an important parameter.
Under the operation of the irregular wave, the LPMGs also suffer losses in load conditions. Whether the component, such as the copper loss, is irregular depends on the load current. Meanwhile, the overall values of the hysteresis and the eddy current losses can be stated based on the maximum flux density.
Figure 25 shows the total loss resulted from the two designs under random wave variations. The total loss decreases as the significant wave height and peak frequency increase. Meanwhile, the loss also tends to decrease when the load resistance is increased. The trends of the power losses under several load resistances and random wave configurations are the same for both LPMG designs.
Then, the power loss affects the electrical efficiency of the LPMG. Overall, the electrical efficiency among the same LPMG design is similar under different random wave parameter variations. The trend of the two designs is also identical under the same wave parameter variations. The iron-cored results in electrical efficiencies in the range of 74–75%, while the semi iron-cored results in higher values, around 84% under all random waves. The higher electrical efficiency in the semi iron-cored model, even with higher copper loss, is supported by lower hysteresis and eddy current losses due to the smaller core volume. In
Figure 25, the total power loss of the semi iron-cored is lower than the iron-cored. Then,
Figure 26 presents the electrical efficiency of the two LPMG models under the same random wave parameter.
The resulted efficiencies are also affected by the output power. Under significant wave height variation, the WEC produces output power with the non-specific trend due to the mixed influence from the waves’ dynamics. Hence, the efficiency also has no specific trend. Meanwhile, under different peak frequencies, both the output power and total power loss increase as the wave parameter values decrease; thus, the resulted efficiency is also similar under all the parameter values.
Based on the electrical output results, the performance of the semi iron-cored LPMG is better in terms of power loss and electrical efficiency. For direct-drive WEC with a similar LPMG design (but with optimized dimensions), the obtained results can also be a consideration for selecting the placement location. Under unidirectional long-crested random wave scenarios with similar significant wave height, it is preferred to install the WEC in sites with lower peak frequency. It is favored, since the output power and efficiency will be higher, whereas the power loss will be smaller.
The advancement of this research in future work besides optimizing the LPMG dimensions is regarding the experiment for testing. The aim is to more approach real wave situations. The focus will still be on the same placement location, since the basic design and the wave height data are available. However, to move the translator according to the complete random wave dynamics is quite a challenge. It will be easier to take a portion of the random wave motion, which is composed of several regular waves. Then, each regular wave with certain parameters’ values (amplitude and frequency) can be taken as an input to experimentally move the translator at a time. The outputs are next combined to form the complete output of a random wave motion part.