Analysis on Influences of Intra-Couplings in a MISO Magnetic Beamforming Wireless Power Transfer System
Abstract
:1. Introduction
2. Theoretical Backgrounds
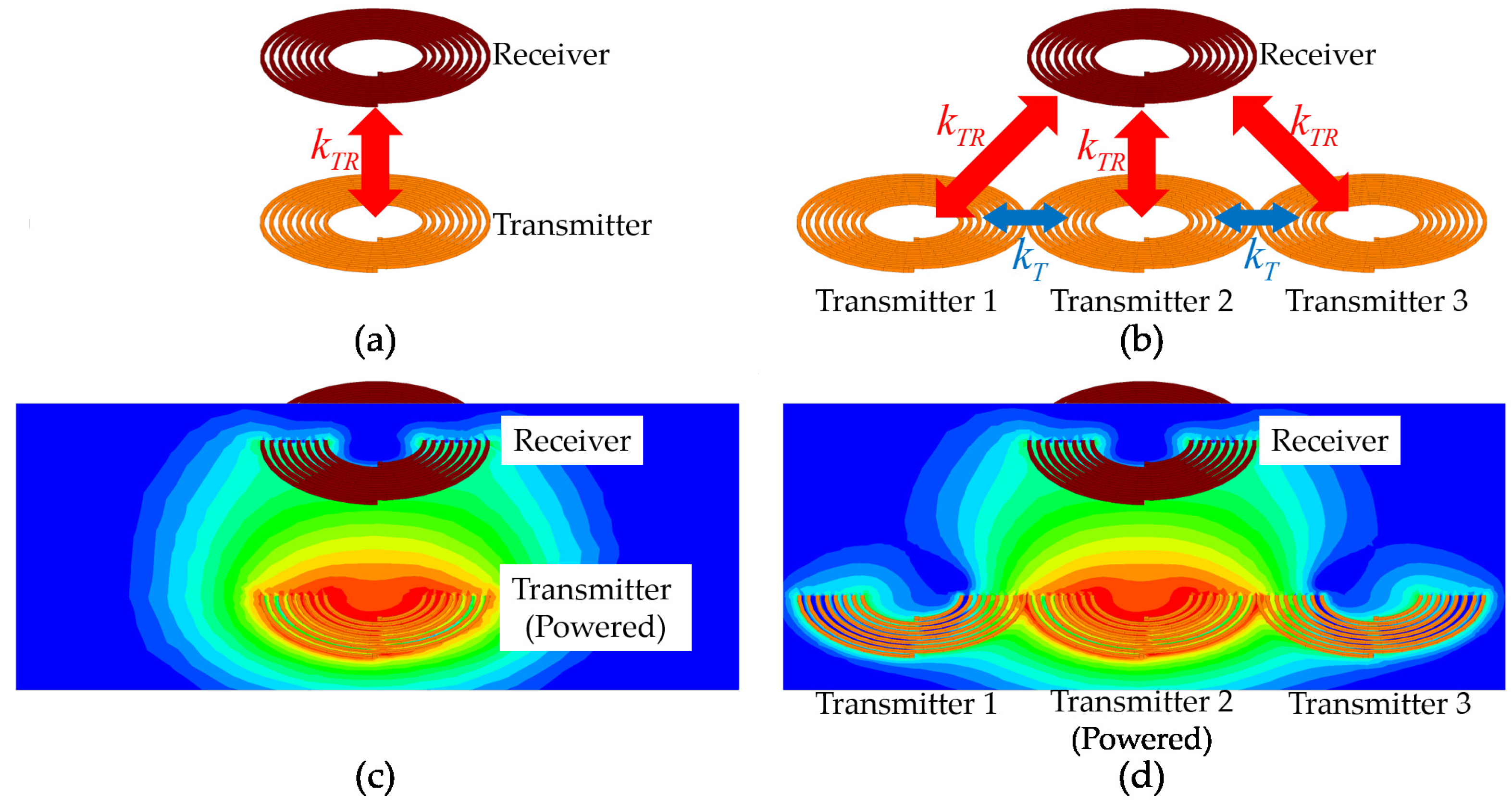
2.1. Magnetic Field-Based WPT
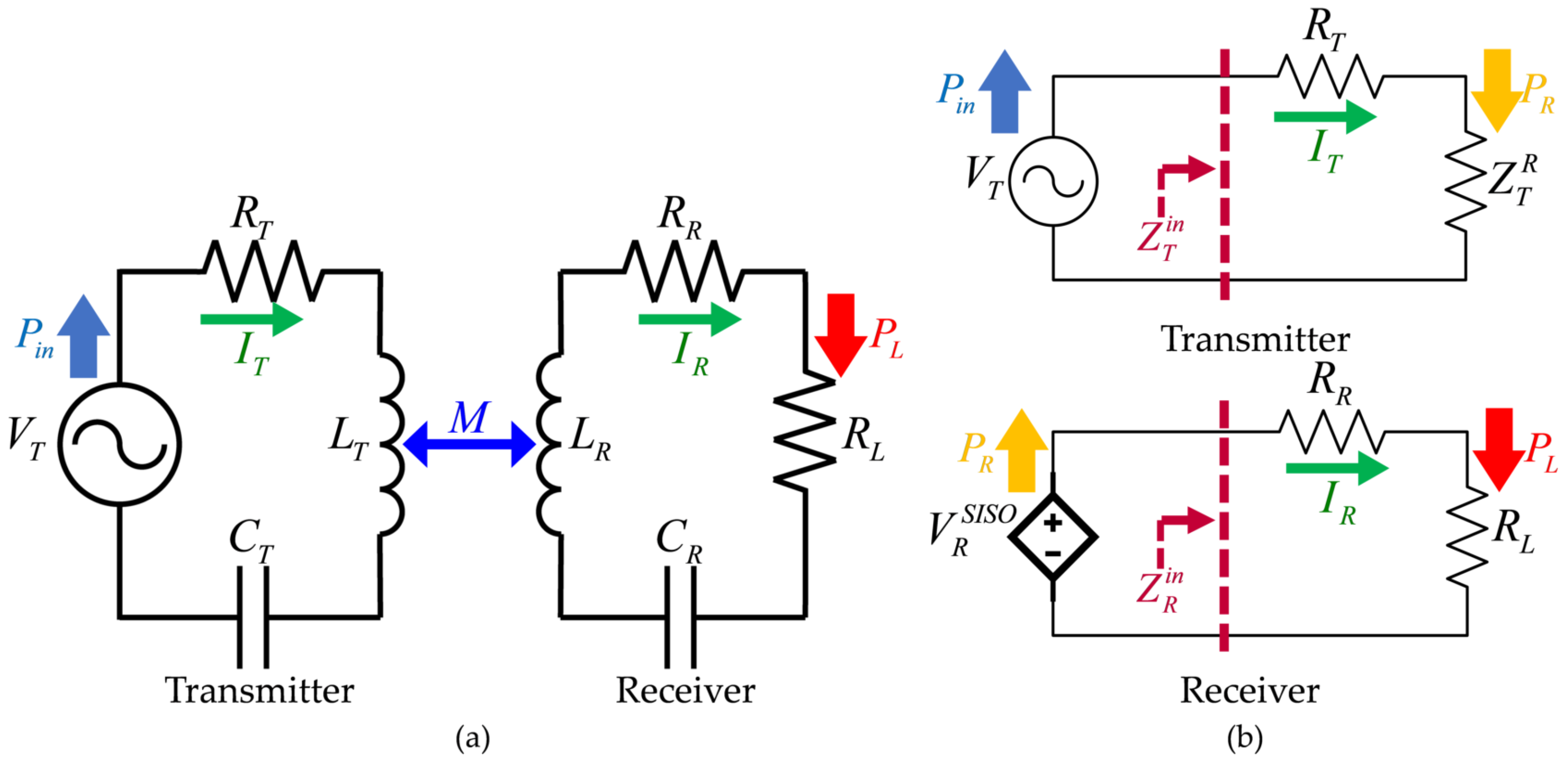
2.2. Circuit Modeling for Single-Input and Single-Output (SISO)-WPT
2.3. Circuit Modeling of Multiple-Inputs and Single-Output (MISO)-WPT
2.4. Introduction of Magnetic Beamforming
3. Theoretical Analysis on Influences of Intra-Couplings
3.1. Influences on Beamforming Voltage
3.2. Influences on Power Factor
3.3. Influences on Power Transfer Efficiency
4. Verification via Simulation and Experiment
4.1. Simulation and Experiment Setting
4.2. Simulation and Experiment Results
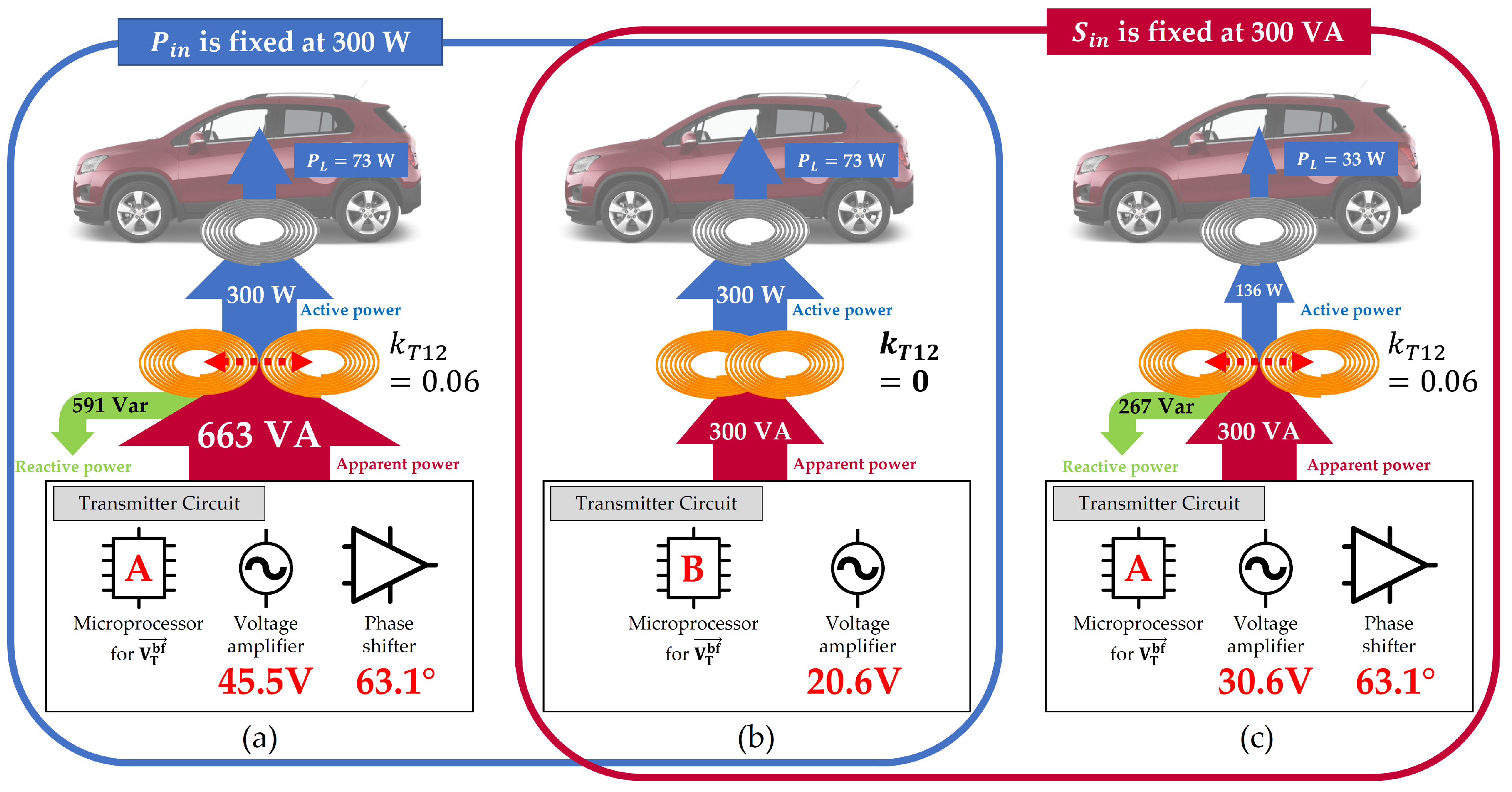
4.2.1. Fixed at 5 W
4.2.2. Fixed at 5 VA
4.3. Discussion
4.3.1. Comparison to the State-of-the-Art in Terms of Power Factor Correction
4.3.2. Advantages of Magnetically Independent Transmitters for Real-Life Scenarios
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WPT | Wireless Power Transfer |
| PTE | Power Transfer Efficiency |
| MIMO | Multiple-Inputs and Multiple-Outputs |
| MISO | Multiple-Inputs and Single-Output |
| Power factor |
Appendix A
References
- Mou, X.; Groling, O.; Sun, H. Energy-efficient and adaptive design for wireless power transfer in electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 7250–7260. [Google Scholar] [CrossRef] [Green Version]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C.C. A dynamic charging system with reduced output power pulsation for electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6580–6590. [Google Scholar] [CrossRef]
- Sampath, J.; Vilathgamuwa, D.M.; Alphones, A. Efficiency enhancement for dynamic wireless power transfer system with segmented transmitter array. IEEE Trans. Transp. Electrif. 2015, 2, 76–85. [Google Scholar] [CrossRef]
- Sun, L.; Ma, D.; Tang, H. A review of recent trends in wireless power transfer technology and its applications in electric vehicle wireless charging. Renew. Sustain. Energy Rev. 2018, 91, 490–503. [Google Scholar] [CrossRef]
- Hajiaghajani, A.; Ahn, S. Single-sided near-field wireless power transfer by a three-dimensional coil array. Micromachines 2019, 10, 200. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Wang, H.; Gao, Z.; Mao, Z.H.; He, J.; Sun, M. A novel mat-based system for position-varying wireless power transfer to biomedical implants. IEEE Trans. Magn. 2013, 49, 4774–4779. [Google Scholar] [CrossRef] [Green Version]
- Vamvakas, P.; Tsiropoulou, E.E.; Vomvas, M.; Papavassiliou, S. Adaptive power management in wireless powered communication networks: A user-centric approach. In Proceedings of the 2017 IEEE 38th Sarnoff Symposium, Newark, NJ, USA, 18–20 September 2017; pp. 1–6. [Google Scholar]
- Campi, T.; Cruciani, S.; Feliziani, M. Wireless power transfer technology applied to an autonomous electric UAV with a small secondary coil. Energies 2018, 11, 352. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless charging technologies: Fundamentals, standards, and network applications. IEEE Commun. Surv. Tutor. 2015, 18, 1413–1452. [Google Scholar] [CrossRef] [Green Version]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [Green Version]
- Masihpour, M.; Agbinya, J.I. Cooperative relay in Near Field Magnetic Induction: A new technology for embedded medical communication systems. In Proceedings of the 2010 Fifth International Conference on Broadband and Biomedical Communications, Malaga, Spain, 15–17 December 2010; pp. 1–6. [Google Scholar]
- Park, C.; Lee, S.; Cho, G.H.; Rim, C.T. Innovative 5-m-off-distance inductive power transfer systems with optimally shaped dipole coils. IEEE Trans. Power Electron. 2014, 30, 817–827. [Google Scholar] [CrossRef]
- Miwa, K.; Mori, H.; Kikuma, N.; Hirayama, H.; Sakakibara, K. A consideration of efficiency improvement of transmitting coil array in wireless power transfer with magnetically coupled resonance. In Proceedings of the 2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013; pp. 13–16. [Google Scholar]
- Jadidian, J.; Katabi, D. Magnetic MIMO: How to charge your phone in your pocket. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking, Maui, HI, USA, 7–11 September 2014; pp. 495–506. [Google Scholar]
- Shi, L.; Kabelac, Z.; Katabi, D.; Perreault, D. Wireless power hotspot that charges all of your devices. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, New Orleans, LA, USA, 25–29 October 2015; pp. 2–13. [Google Scholar]
- Waters, B.H.; Mahoney, B.J.; Ranganathan, V.; Smith, J.R. Power delivery and leakage field control using an adaptive phased array wireless power system. IEEE Trans. Power Electron. 2015, 30, 6298–6309. [Google Scholar] [CrossRef]
- Oodachi, N.; Ogawa, K.; Kudo, H.; Shoki, H.; Obayashi, S.; Morooka, T. Efficiency improvement of wireless power transfer via magnetic resonance using transmission coil array. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Atlanta, GA, USA, 7–12 July 2011; pp. 1707–1710. [Google Scholar]
- Kisseleff, S.; Akyildiz, I.F.; Gerstacker, W. Beamforming for magnetic induction based wireless power transfer systems with multiple receivers. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Kim, H.J.; Park, J.; Oh, K.S.; Choi, J.P.; Jang, J.E.; Choi, J.W. Near-field magnetic induction MIMO communication using heterogeneous multipole loop antenna array for higher data rate transmission. IEEE Trans. Antennas Propag. 2016, 64, 1952–1962. [Google Scholar] [CrossRef]
- Yoo, S.S.; Lee, K.Y.; Yoo, H.J. Coupling-Shielded Inductor for High Isolation Between PA and LC-Based DCO. IEEE Electron Device Lett. 2016, 38, 24–27. [Google Scholar] [CrossRef]
- Tang, S.; Hui, S.; Chung, H.H. Evaluation of the shielding effects on printed-circuit-board transformers using ferrite plates and copper sheets. IEEE Trans. Power Electron. 2002, 17, 1080–1088. [Google Scholar] [CrossRef]
- Tal, N.; Morag, Y.; Levron, Y. Magnetic induction antenna arrays for MIMO and multiple-frequency communication systems. Prog. Electromagn. Res. 2017, 75, 155–167. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Zhang, T.; Zhu, X.; Luk, P.C.K.; Ma, C. Compensation of cross coupling in multiple-receiver wireless power transfer systems. IEEE Trans. Ind. Inform. 2016, 12, 474–482. [Google Scholar] [CrossRef]
- Pantic, Z.; Bai, S.; Lukic, S.M. ZCS LCC-compensated resonant inverter for inductive-power-transfer application. IEEE Trans. Ind. Electron. 2010, 58, 3500–3510. [Google Scholar] [CrossRef]
- Sohn, Y.H.; Choi, B.H.; Lee, E.S.; Lim, G.C.; Cho, G.H.; Rim, C.T. General unified analyses of two-capacitor inductive power transfer systems: Equivalence of current-source SS and SP compensations. IEEE Trans. Power Electron. 2015, 30, 6030–6045. [Google Scholar] [CrossRef]
- Wang, C.S.; Stielau, O.H.; Covic, G.A. Design considerations for a contactless electric vehicle battery charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar] [CrossRef]
- Alexander, C.K.; Sadiku, M.N.O. Fundamentals of Electric Circuits; McGraw-Hill: New York, NY, USA, 2017; Volume 6. [Google Scholar]
- Glover, J.D.; Sarma, M.S.; Overbye, T. Power System Analysis & Design, SI Version; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Florian, C.; Mastri, F.; Paganelli, R.P.; Masotti, D.; Costanzo, A. Theoretical and numerical design of a wireless power transmission link with GaN-based transmitter and adaptive receiver. IEEE Trans. Microw. Theory Tech. 2014, 62, 931–946. [Google Scholar] [CrossRef]
- Tang, L.; Chinthavali, M.; Onar, O.C.; Campbell, S.; Miller, J.M. SiC MOSFET based single phase active boost rectifier with power factor correction for wireless power transfer applications. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 1669–1675. [Google Scholar]
- Chinthavali, M.S.; Onar, O.C.; Miller, J.M.; Tang, L. Single-phase active boost rectifier with power factor correction for wireless power transfer applications. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 3258–3265. [Google Scholar]
- Kiratipongvoot, S.; Yang, Z.; Lee, C.K.; Ho, S.S. Design a high-frequency-fed unity power-factor AC-DC power converter for wireless power transfer application. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 599–606. [Google Scholar]
- Pickelsimer, M.; Tolbert, L.; Ozpineci, B.; Miller, J.M. Simulation of a wireless power transfer system for electric vehicles with power factor correction. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–6. [Google Scholar]
- Liu, J.; Xu, W.; Chan, K.W.; Liu, M.; Zhang, X.; Chan, N.H.L. A three-phase single-stage AC–DC wireless-power-transfer converter with power factor correction and bus voltage control. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1782–1800. [Google Scholar] [CrossRef]
- Liu, J.; Chan, K.W.; Chung, C.Y.; Chan, N.H.L.; Liu, M.; Xu, W. Single-stage wireless-power-transfer resonant converter with boost bridgeless power-factor-correction rectifier. IEEE Trans. Ind. Electron. 2017, 65, 2145–2155. [Google Scholar] [CrossRef]
- González-Santini, N.S.; Zeng, H.; Yu, Y.; Peng, F.Z. Z-source resonant converter with power factor correction for wireless power transfer applications. IEEE Trans. Power Electron. 2016, 31, 7691–7700. [Google Scholar] [CrossRef]
- Hsieh, Y.C.; Lin, Z.R.; Chen, M.C.; Hsieh, H.C.; Liu, Y.C.; Chiu, H.J. High-efficiency wireless power transfer system for electric vehicle applications. IEEE Trans. Circuits Syst. II Express Briefs 2016, 64, 942–946. [Google Scholar] [CrossRef]
- Park, M.; Yu, S.D.; Yim, S.W.; Park, K.; Min, B.D.; Kim, S.D.; Cho, J.G. A study of wireless power transfer topologies for 3.3 kW and 6.6 kW electric vehicle charging infrastructure. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, Korea, 1–4 June 2016; pp. 689–692. [Google Scholar]
- Chivers, I.; Sleightholme, J. An introduction to Algorithms and the Big O Notation. In Introduction to Programming with Fortran; Springer: Berlin/Heidelberg, Germany, 2015; pp. 359–364. [Google Scholar]
- Strang, G. Introduction to Linear Algebra; Cambridge Press: Wellesley, MA, USA, 1993; Volume 3. [Google Scholar]
















| Symbol | Definition | Description |
|---|---|---|
| N | Number of transmitters | |
| Set of transmitter current | ||
| Set of transmitter voltage | ||
| Resistance and mutual inductance in transmitter array | ||
| Mutual inductance between transmitter array and receiver | ||
| Magnetic channel connecting transmitter and receiver current |
| Symbol | Value | Description |
|---|---|---|
| Winding resistance of inductance | ||
| Load impedance indicating the device to be charged | ||
| 3.4 nF | Capacitance for resonance at 1 MHz | |
| H | Inductance of transmitter and receiver | |
| F | Smoothing capacitance in receiver | |
| 1 MHz | Resonant frequency | |
| Coupling coefficient between each transmitter and receiver | ||
| H | Mutual inductance between each transmitter and receiver | |
| 0∼0.06 | Coupling coefficient in transmitter array | |
| 0∼0.44 H | Mutual inductance in transmitter array |
| Ref. | WPT Configuration | PFC Technique |
|---|---|---|
| [30,31,32,33] | SISO | Active—Front end rectifier |
| [34] | SISO | Active—Three phase rectifier |
| [35,36] | SISO | Active—Boost bridgeless rectifier |
| [37] | SISO | Active—Z-source converter |
| [38] | SISO | Passive—LCL toplology |
| [23] | SIMO | Active—Tuning resonance capacitance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Kim, H.-J.; Seo, D.-W.; Choi, J.-W. Analysis on Influences of Intra-Couplings in a MISO Magnetic Beamforming Wireless Power Transfer System. Energies 2021, 14, 5184. https://doi.org/10.3390/en14165184
Kim K, Kim H-J, Seo D-W, Choi J-W. Analysis on Influences of Intra-Couplings in a MISO Magnetic Beamforming Wireless Power Transfer System. Energies. 2021; 14(16):5184. https://doi.org/10.3390/en14165184
Chicago/Turabian StyleKim, Kyungtae, Han-Joon Kim, Dong-Wook Seo, and Ji-Woong Choi. 2021. "Analysis on Influences of Intra-Couplings in a MISO Magnetic Beamforming Wireless Power Transfer System" Energies 14, no. 16: 5184. https://doi.org/10.3390/en14165184
APA StyleKim, K., Kim, H. -J., Seo, D. -W., & Choi, J. -W. (2021). Analysis on Influences of Intra-Couplings in a MISO Magnetic Beamforming Wireless Power Transfer System. Energies, 14(16), 5184. https://doi.org/10.3390/en14165184







