Hydrodynamic Modeling of Oil–Water Stratified Smooth Two-Phase Turbulent Flow in Horizontal Circular Pipes
Abstract
:1. Introduction
2. Materials and Methods
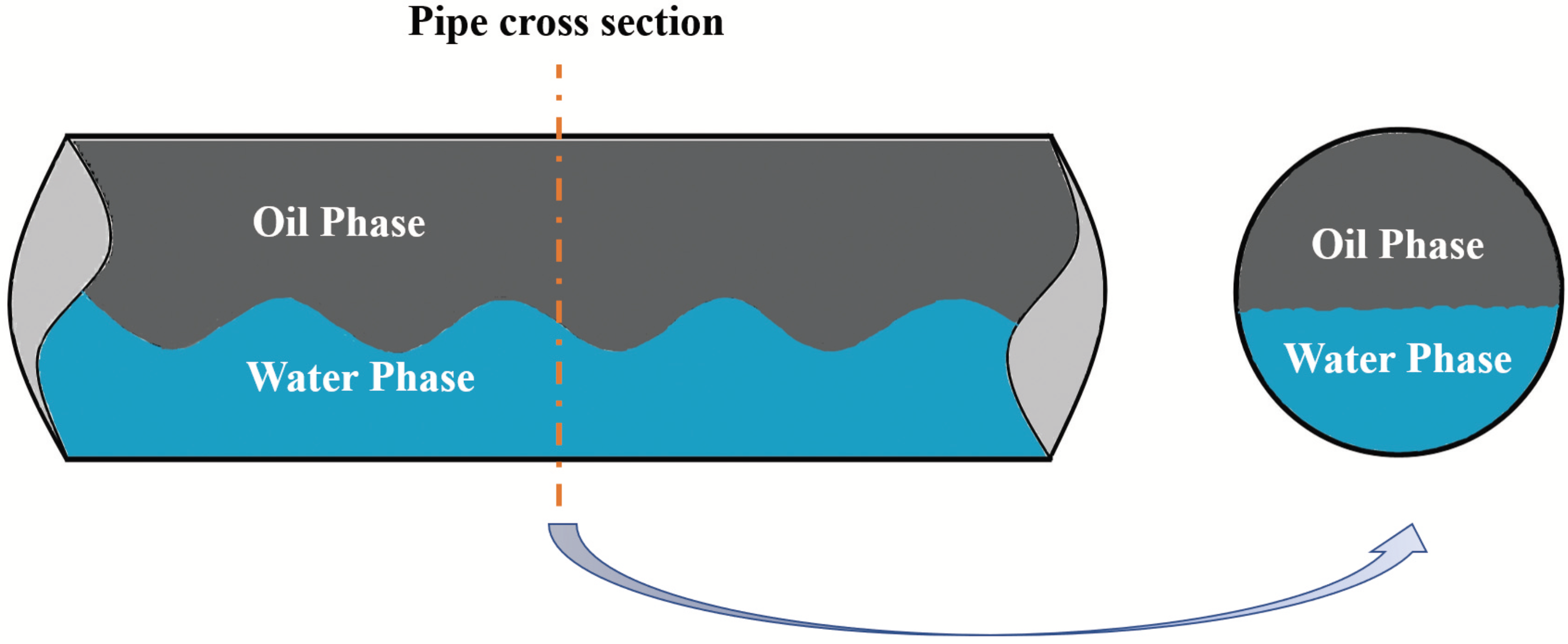
2.1. Problem Description and Model Assumption
2.2. Governing Equation
2.2.1. Mass Conservation Equation
2.2.2. Momentum Conservation Equation
2.2.3. Turbulence Model
2.3. Boundary Conditions
3. Numerical Method
3.1. Governing Equations Discretization
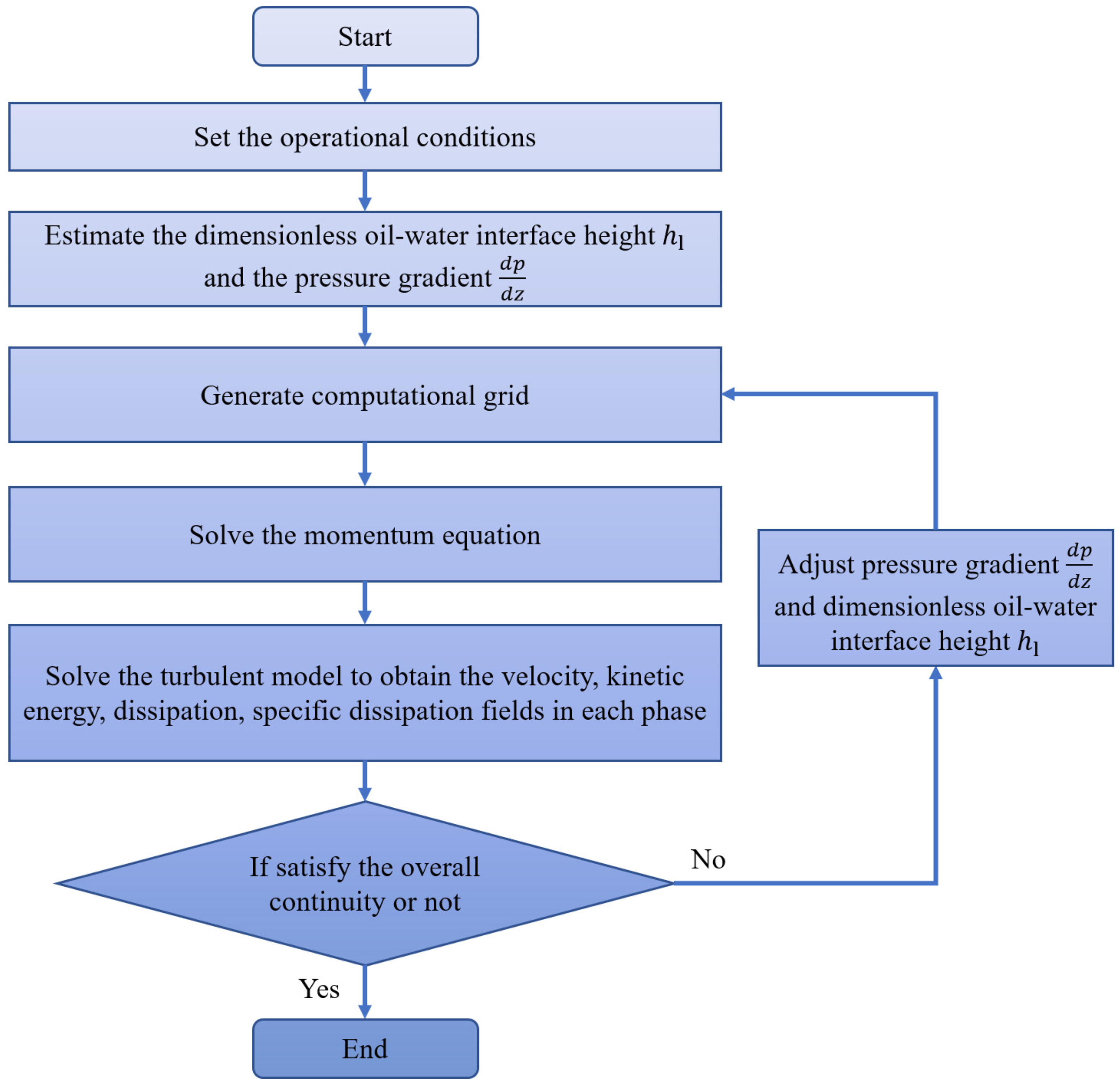
3.2. Solution Methodology
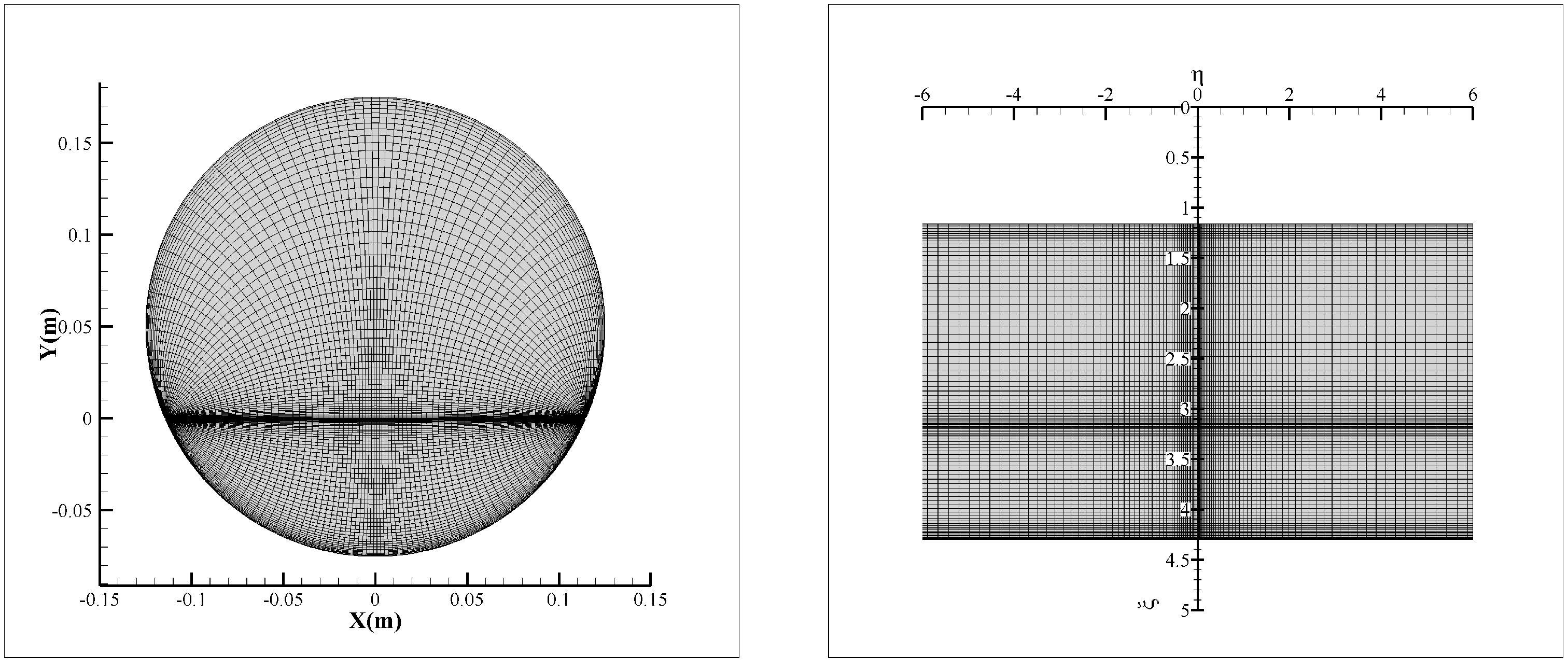
3.3. Grid-Independence Solution
4. Results and Discussion
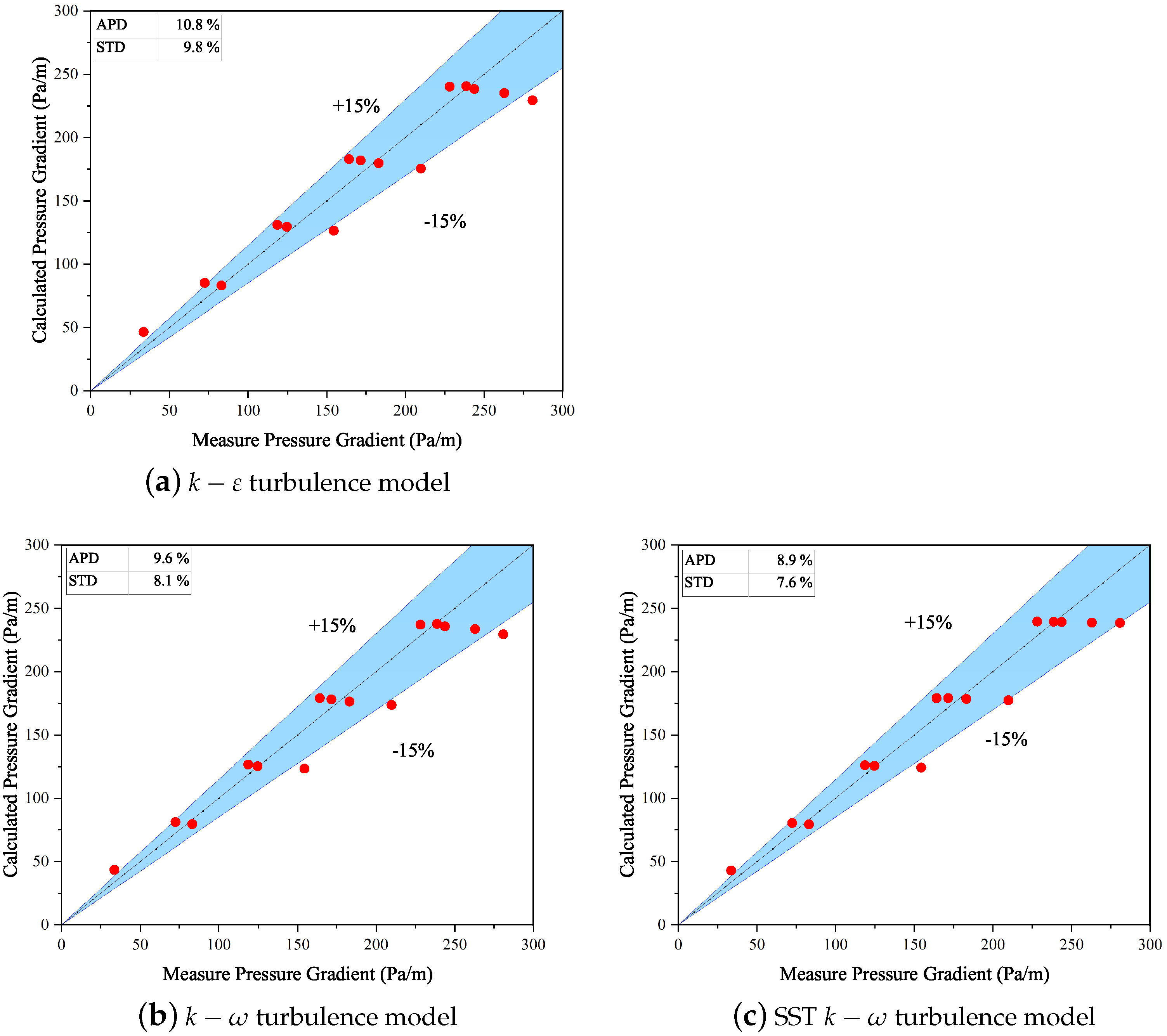
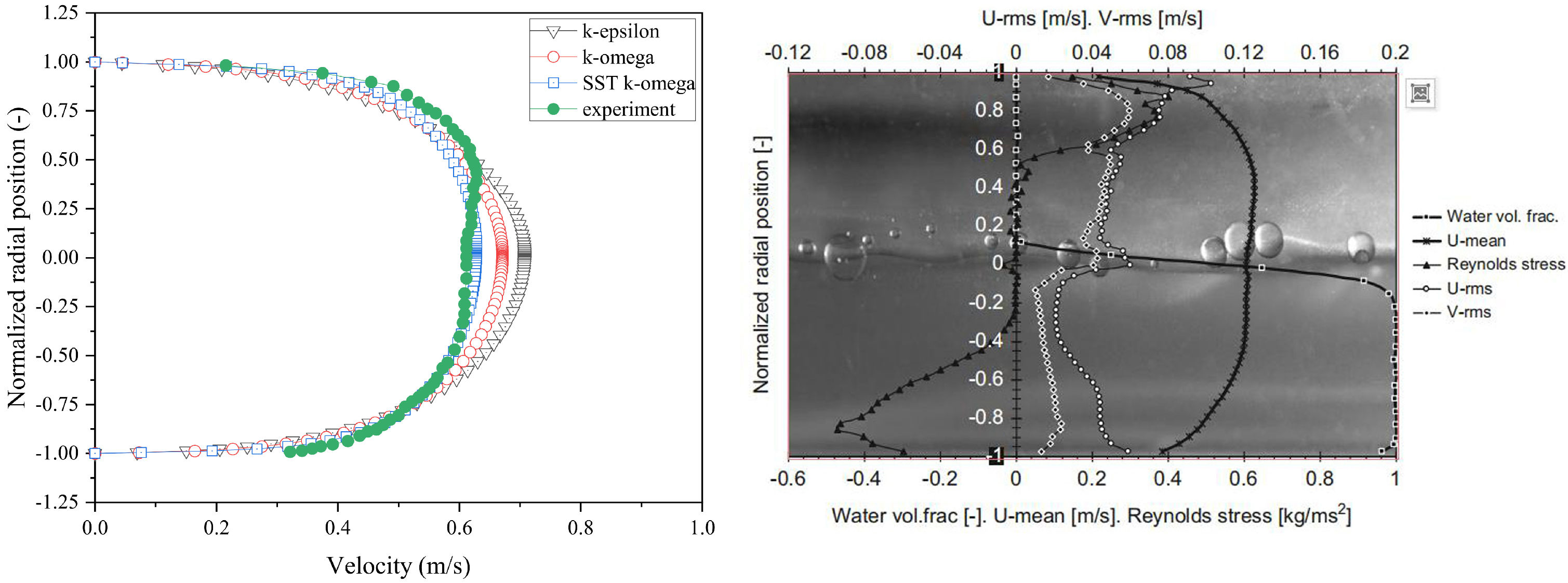
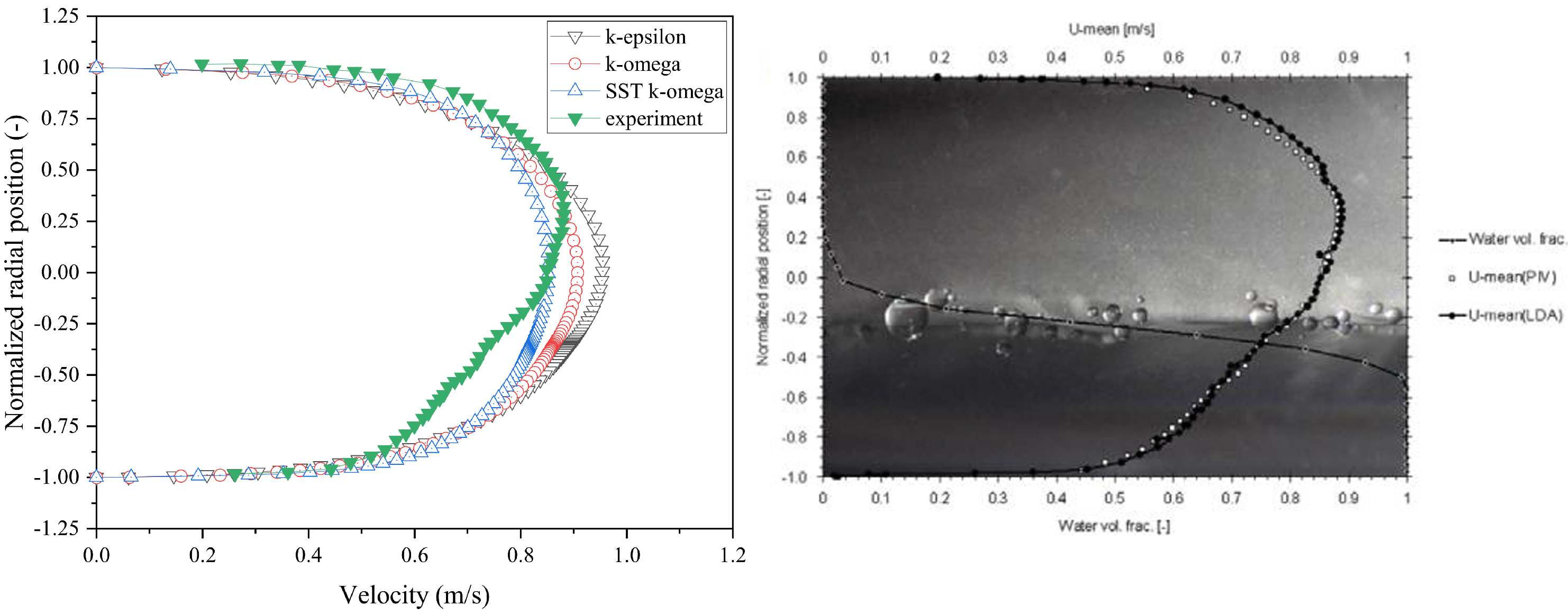
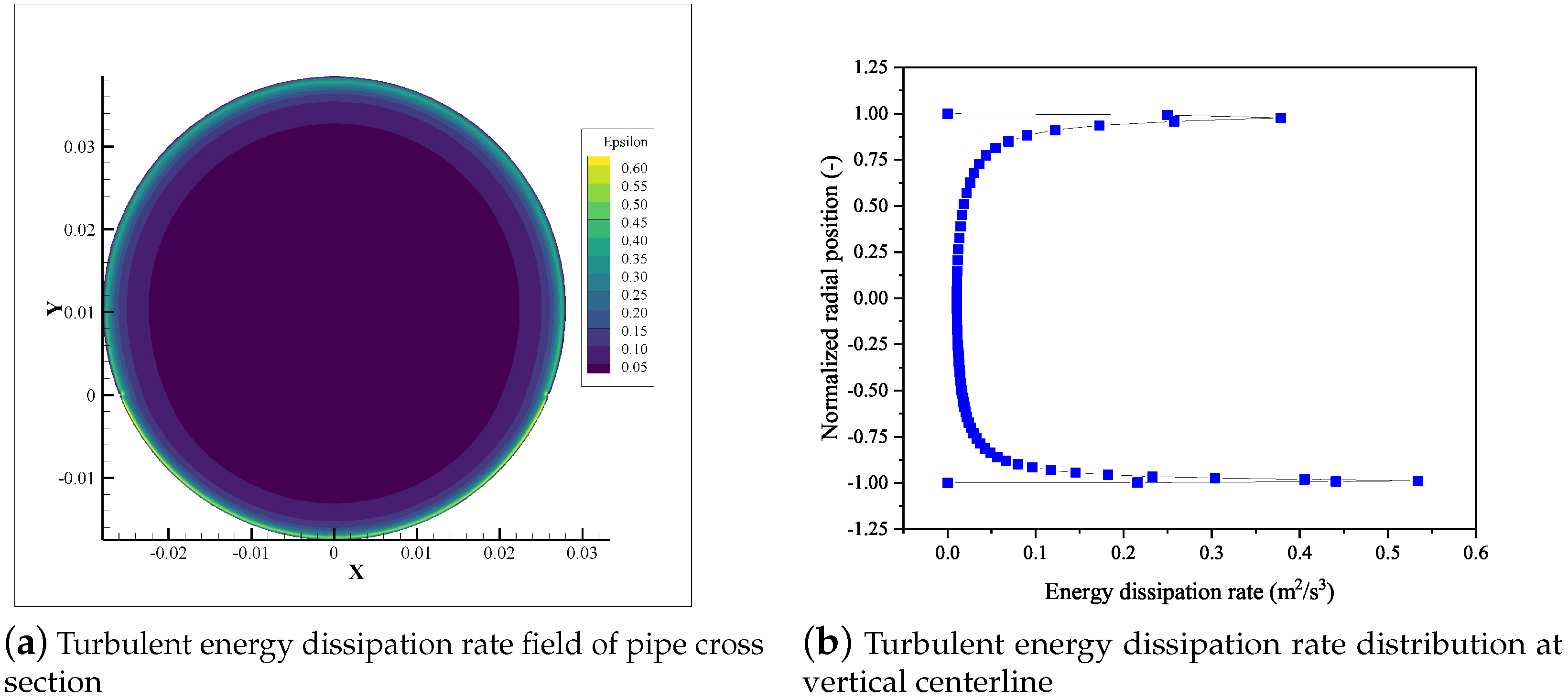
4.1. Turbulence Model Validation
4.2. Calculation of Two-Phase Flow Pressure Gradient
4.3. Calculation of Interface Height and Flow Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameter | |
| Density, kg/m | |
| a | Bipolar coordinate parameter |
| General variable | |
| Solve equation coefficients | |
| Effective diffusion coefficient | |
| b | Solve equation source term |
| Effective dynamic viscosity, N·s/m | |
| The flow area of water and oil phase, m | |
| Eddy viscosity, N·s/m | |
| d | Inner diameter of pipe, m |
| Specific dissipation rate, s | |
| Dimensionless oil–water interface height | |
| Energy dissipation rate, m/s | |
| k | The flow area of water and oil phase, m/s |
| Turbulence model parameter | |
| Karman constant number | |
| The coordinate in bipolar | |
| Lame coefficient | |
| The coordinate in bipolar | |
| Parameter of Newton–Raphson method | |
| Bipolar coordinate parameter | |
| p | Pressure, Pa |
| Turbulence production term | |
| Subscripts | |
| Volume flow rate of oil and water phase, m/s | |
| i | Either oil or water phase |
| Source term | |
| C | Near boundary cell |
| Deformation tensor, s | |
| o | Oil phase |
| Superficial oil velocity and water velocity, m/s | |
| w | Water phase |
| w | Fluid velocity, m/s |
| vis | Viscous sublayer of pipe flow |
| Cartesian coordinate system, m | |
| log | Logarithmic layer of pipe flow |
| Greek symbols | |
| Turbulence model parameter | |
| Turbulence model parameter | |
| Turbulence model parameter | |
References
- Liu, Y.; Lu, H.; Li, Y.; Xu, H.; Pan, Z.; Dai, P.; Wang, H.; Yang, Q. A review of treatment technologies for produced water in offshore oil and gas fields. Sci. Total Environ. 2021, 775, 145485. [Google Scholar] [CrossRef]
- Song, X.; Li, D.; Sun, X.; Mou, X.; Cheng, Y.F.; Yang, Y. Numerical modeling of the critical pipeline inclination for the elimination of the water accumulation on the pipe floor in oil-water fluid flow. Petroleum 2021, 7, 209–221. [Google Scholar] [CrossRef]
- Odiete, W.E.; Agunwamba, J.C. Novel design methods for conventional oil-water separators. Heliyon 2019, 5, e01620. [Google Scholar] [CrossRef] [Green Version]
- Garmroodi, M.R.D.; Ahmadpour, A. Numerical simulation of stratified waxy crude oil and water flows across horizontal pipes in the presence of wall heating. J. Pet. Sci. Eng. 2020, 193, 107458. [Google Scholar] [CrossRef]
- Song, G.; Li, Y.; Wang, W.; Jiang, K.; Shi, Z.; Yao, S. Hydrate formation in oil—water systems: Investigations of the influences of water cut and anti-agglomerant. Chin. J. Chem. Eng. 2020, 28, 369–377. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Z.M.; Song, G. Batch transportation of oil and water for reducing pipeline corrosion. J. Pet. Sci. Eng. 2020, 195, 107583. [Google Scholar] [CrossRef]
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Brauner, N.; Moalem Maron, D.; Rovinsky, J. A two-fluid model for stratified flows with curved interfaces. Int. J. Multiphase Flow 1998, 24, 975–1004. [Google Scholar] [CrossRef]
- Ahmed, S.A.; John, B. Liquid-Liquid horizontal pipe flow—A review. J. Pet. Sci. Eng. 2018, 168, 426–447. [Google Scholar] [CrossRef]
- Ullmann, A.; Goldstein, A.; Zamir, M.; Brauner, N. Closure relations for the shear stresses in two-fluid models for laminar stratified flow. Int. J. Multiphase Flow 2004, 30, 877–900. [Google Scholar] [CrossRef]
- Ullmann, A.; Brauner, N. Closure relations for two-fluid models for two-phase stratified smooth and stratified wavy flows. Int. J. Multiphase Flow 2006, 32, 82–105. [Google Scholar] [CrossRef]
- Awad, M.M.; Butt, S.D. A Robust Asymptotically Based Modeling Approach for Two-Phase Liquid-Liquid Flow in Pipes. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; pp. 409–418. [Google Scholar]
- Rodriguez, O.M.H.; Baldani, L.S. Prediction of pressure gradient and holdup in wavy stratified liquid-liquid inclined pipe flow. J. Pet. Sci. Eng. 2012, 96–97, 140–151. [Google Scholar] [CrossRef]
- Edomwonyi-Otu, L.C.; Angeli, P. Pressure drop and holdup predictions in horizontal oil–water flows for curved and wavy interfaces. Chem. Eng. Res. Des. 2015, 93, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Jeong, D.; Kim, J. A fast and practical adaptive finite difference method for the conservative Allen–Cahn model in two-phase flow system. Int. J. Multiphase Flow 2021, 137, 103561. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J. A novel Cahn–Hilliard–Navier–Stokes model with a nonstandard variable mobility for two-phase incompressible fluid flow. Comput. Fluids 2020, 213, 104755. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J. An improved scalar auxiliary variable (SAV) approach for the phase-field surfactant model. Appl. Math. Model. 2021, 90, 11–29. [Google Scholar] [CrossRef]
- Xie, B.; Jin, P.; Du, Y.; Liao, S. A consistent and balanced-force model for incompressible multiphase flows on polyhedral unstructured grids. Int. J. Multiphase Flow 2020, 122, 103125. [Google Scholar] [CrossRef]
- Sverdrup, K.; Nikiforakis, N.; Almgren, A. Highly parallelisable simulations of time-dependent viscoplastic fluid flow with structured adaptive mesh refinement. Phys. Fluids 2020, 30, 093102. [Google Scholar] [CrossRef] [Green Version]
- Schmidmayer, K.; Petitpas, F.; Daniel, E. Adaptive Mesh Refinement algorithm based on dual trees for cells and faces for multiphase compressible flows. J. Comput. Phys. 2019, 388, 252–278. [Google Scholar] [CrossRef] [Green Version]
- López-Herrera, J.M.; Popinet, S.; Castrejón-Pita, A.A. An adaptive solver for viscoelastic incompressible two-phase problems applied to the study of the splashing of weakly viscoelastic droplets. J. Non-Newtonian Fluid Mech. 2019, 264, 144–158. [Google Scholar] [CrossRef]
- Liu, A.; Sun, D.; Yu, B.; Wei, J.; Cao, Z. An adaptive coupled volume-of-fluid and level set method based on unstructured grids. Phys. Fluids 2021, 33, 012102. [Google Scholar] [CrossRef]
- Issa, R.I. Prediction of turbulent, stratified, two-phase flow in inclined pipes and channels. Int. J. Multiphase Flow 1988, 14, 141–154. [Google Scholar] [CrossRef]
- Newton, C.H.; Behnia, M. A numerical model of stratified wavy gas-liquid pipe flow. Chem. Eng. Sci. 2001, 56, 6851–6861. [Google Scholar] [CrossRef]
- De Sampaio, P.A.B.; Faccini, J.L.H.; Su, J. Modelling of stratified gas-liquid two-phase flow in horizontal circular pipes. Int. J. Heat Mass Transfer 2008, 51, 2752–2761. [Google Scholar] [CrossRef]
- Duan, J.; Gong, J.; Yao, H.; Deng, T.; Zhou, J. Numerical modeling for stratified gas-liquid flow and heat transfer in pipeline. Appl. Energy 2014, 115, 83–94. [Google Scholar] [CrossRef]
- Duan, J.; Liu, H.; Wang, N.; Gong, J.; Jiao, G. Hydro dynamic modeling of stratified smooth two-phase turbulent flow with curved interface through circular pipe. Int. J. Heat Mass Transfer 2015, 89, 1034–1043. [Google Scholar] [CrossRef]
- Duan, J.; Liu, H.; Jiang, J.; Xue, S.; Wu, J.; Gong, J. Numerical prediction of wax deposition in oil–gas stratified pipe flow. Int. J. Heat Mass Transfer 2017, 105, 279–289. [Google Scholar] [CrossRef]
- Duan, J.; Deng, S.; Xu, S.; Liu, H.; Chen, M.; Gong, J. The effect of gas flow rate on the wax deposition in oil-gas stratified pipe flow. J. Pet. Sci. Eng. 2018, 162, 539–547. [Google Scholar] [CrossRef]
- He, G.; Li, Y.; Yin, B.; Sun, L.; Liang, Y. Numerical simulation of vapor condensation in gas-water stratified wavy pipe flow with varying interface location. Int. J. Heat Mass Transfer 2017, 115, 635–651. [Google Scholar] [CrossRef]
- Maklakov, D.V.; Kayumov, I.R.; Kamaletdinov, R.R. Stratified laminar flows in a circular pipe: New analytical solutions in terms of elementary functions. Appl. Math. Model. 2018, 59, 147–163. [Google Scholar] [CrossRef]
- Li, Y.; He, G.; Sun, L.; Ding, D.; Liang, Y. Numerical simulation of oil-water non-Newtonian two-phase stratified wavy pipe flow coupled with heat transfer. Appl. Therm. Eng. 2018, 140, 266–286. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Method Appl. M 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transfer 2003, 4, 625–632. [Google Scholar]
- Ferziger, J.H.; PeriC, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 298–299. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab; Springer: Berlin/Heidelberg, Germany, 2016; pp. 711–724. [Google Scholar]
- Yusuf, N.; Al-Wahaibi, Y.; Al-Wahaibi, T.; Al-Ajmi, A.; Olawale, A.S.; Mohammed, I.A. Effect of oil viscosity on the flow structure and pressure gradient in horizontal oil-water flow. Chem. Eng. Res. Des. 2012, 90, 1019–1030. [Google Scholar] [CrossRef]
- Angeli, P.; Hewitt, G.F. Pressure gradient in horizontal liquid-liquid flows. Int. J. Multiphase Flow 1999, 24, 1183–1203. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, H.; Jin, N. Prediction of pressure drop for segregated oil-water flows in small diameter pipe using modified two-fluid model. Exp. Therm. Fluid Sci. 2020, 114, 110078. [Google Scholar] [CrossRef]
- Kumara, W.A.S.; Elseth, G.; Halvorsen, B.M.; Melaaen, M.C. Comparison of Particle Image Velocimetry and Laser Doppler Anemometry measurement methods applied to the oil–water flow in horizontal pipe. Flow Meas. Instrum. 2010, 21, 105–117. [Google Scholar] [CrossRef]
- Kumara, W.A.S.; Halvorsen, B.M.; Melaaen, M.C. Particle image velocimetry for characterizing the flow structure of oil-water flow in horizontal and slightly inclined pipes. Chem. Eng. Sci. 2010, 65, 4332–4349. [Google Scholar] [CrossRef]





| Turbulence Model | Grid Set | (Pa/m) | Relevate Change % | Relevate Change % | |
|---|---|---|---|---|---|
| 20 × 20 | 218.74 | - | 0.5533 | - | |
| 50 × 50 | 235.15 | 7.50 | 0.5597 | 1.15 | |
| 80 × 80 | 239.49 | 1.85 | 0.5608 | 0.20 | |
| 100 × 100 | 241.15 | 0.69 | 0.5612 | 0.07 | |
| 20 × 20 | 211.55 | - | 0.5608 | - | |
| 50 × 50 | 218.99 | 3.52 | 0.5683 | 1.34 | |
| 80 × 80 | 218.70 | 0.13 | 0.5693 | 0.18 | |
| 100 × 100 | 218.29 | 0.19 | 0.5696 | 0.05 | |
| SST | 20 × 20 | 199.00 | - | 0.5683 | - |
| 50 × 50 | 214.24 | 7.66 | 0.5723 | 0.71 | |
| 80 × 80 | 217.00 | 1.29 | 0.5723 | 0.01 | |
| 100 × 100 | 218.57 | 0.72 | 0.5726 | 0.06 |
| No | (m/s) | (m/s) | Exp Data (Pa/m) | SST | |||||
|---|---|---|---|---|---|---|---|---|---|
| Values (Pa/m) | Relative Error (%) | Values (Pa/m) | Relative Error (%) | Values (Pa/m) | Relative Error (%) | ||||
| 1 | 0.11 | 0.11 | 33.52 | 46.51 | 38.75 | 43.38 | 29.43 | 42.95 | 28.14 |
| 2 | 0.22 | 0.11 | 72.30 | 85.24 | 17.89 | 81.07 | 12.13 | 80.50 | 11.35 |
| 3 | 0.11 | 0.22 | 83.06 | 83.25 | 0.23 | 79.70 | −4.05 | 79.40 | −4.40 |
| 4 | 0.22 | 0.22 | 124.67 | 129.54 | 3.90 | 125.33 | 0.53 | 125.65 | 0.79 |
| 5 | 0.33 | 0.11 | 118.54 | 131.04 | 10.54 | 126.61 | 6.80 | 126.06 | 6.35 |
| 6 | 0.33 | 0.22 | 171.57 | 182.07 | 6.12 | 178.06 | 3.78 | 179.17 | 4.43 |
| 7 | 0.11 | 0.33 | 154.47 | 126.55 | −18.08 | 123.48 | −20.06 | 124.23 | −19.58 |
| 8 | 0.22 | 0.33 | 183.02 | 179.73 | −1.80 | 176.42 | −3.60 | 178.40 | −2.53 |
| 9 | 0.33 | 0.33 | 243.80 | 238.44 | −2.20 | 235.85 | −3.26 | 239.30 | −1.85 |
| 10 | 0.44 | 0.11 | 164.16 | 183.02 | 11.49 | 179.04 | 9.06 | 179.12 | 9.11 |
| 11 | 0.44 | 0.22 | 228.24 | 240.30 | 5.29 | 237.24 | 3.94 | 239.61 | 4.98 |
| 12 | 0.11 | 0.44 | 209.90 | 175.47 | −16.40 | 173.71 | −17.24 | 177.46 | −15.46 |
| 13 | 0.22 | 0.44 | 262.87 | 235.21 | −10.52 | 233.65 | −11.12 | 238.71 | −9.19 |
| 14 | 0.55 | 0.11 | 238.70 | 240.52 | 0.76 | 237.68 | −0.43 | 239.37 | 0.28 |
| 15 | 0.11 | 0.55 | 280.84 | 229.32 | −18.34 | 229.56 | −18.26 | 238.49 | −15.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Q.; Gu, J.; Qi, X.; Wu, T.; Wang, S.; Chen, S.; Wang, W.; Gong, J. Hydrodynamic Modeling of Oil–Water Stratified Smooth Two-Phase Turbulent Flow in Horizontal Circular Pipes. Energies 2021, 14, 5201. https://doi.org/10.3390/en14165201
Kang Q, Gu J, Qi X, Wu T, Wang S, Chen S, Wang W, Gong J. Hydrodynamic Modeling of Oil–Water Stratified Smooth Two-Phase Turbulent Flow in Horizontal Circular Pipes. Energies. 2021; 14(16):5201. https://doi.org/10.3390/en14165201
Chicago/Turabian StyleKang, Qi, Jiapeng Gu, Xueyu Qi, Ting Wu, Shengjie Wang, Sihang Chen, Wei Wang, and Jing Gong. 2021. "Hydrodynamic Modeling of Oil–Water Stratified Smooth Two-Phase Turbulent Flow in Horizontal Circular Pipes" Energies 14, no. 16: 5201. https://doi.org/10.3390/en14165201





