Review of Wind Turbine Icing Modelling Approaches
Abstract
:1. Introduction
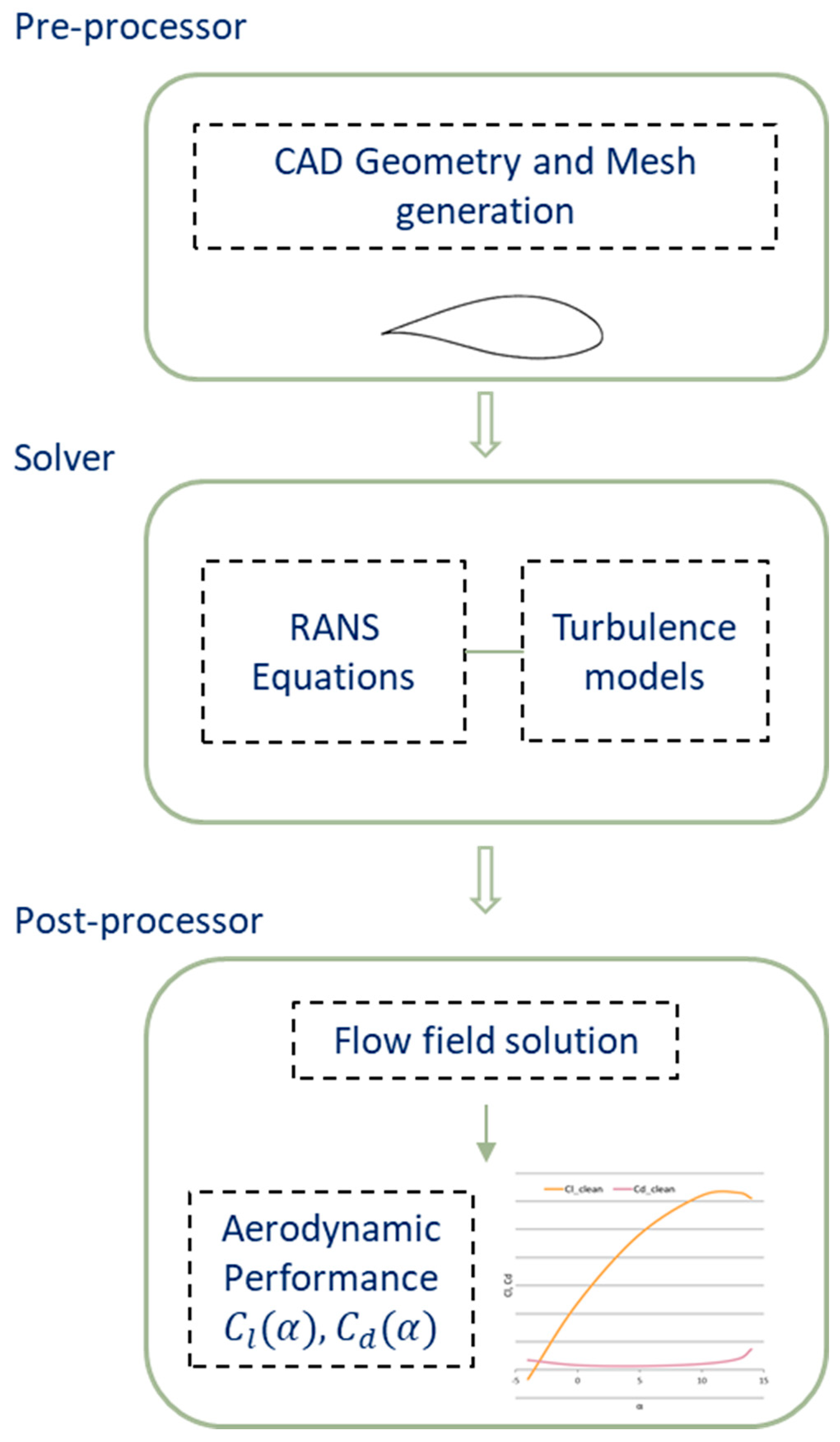
2. Computational Models for Ice Accretion
2.1. Aerodynamic Modelling
2.1.1. Turbulence Modelling
SPALART-ALLMARAS Turbulence Model
k-ε Turbulence Model
k-ω SST (Shear Stress Transport) Turbulence Model
2.1.2. Modelling of Surface Roughness
2.2. Multiphase Modelling of Droplet Trajectories
2.2.1. Lagrangian Approach
2.2.2. Eulerian Approach
2.3. Thermodynamic Modelling of Ice Accretion
3. Research Survey on Modelling and Simulation of Ice Accretion on Wind Turbines
3.1. Research on Surface Roughness Modelling
3.2. Research on Droplets Trajectory Modelling
3.3. Research on Modelling the Electro-Thermal Icing Protection Systems
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Local Collection Efficiency | |
| Airfoil Chord Length (m) | |
| Drag coefficient | |
| Lift coefficient | |
| Rotor diameter (m) | |
| Rotor radius/Blade span (m) | |
| Radius length of local blade element (m) | |
| Free stream velocity (m/s) | |
| Angle of attack (°) | |
| Rotational speed (rad/s) | |
| NREL | National Renewable Energy Laboratory |
| VTT | Technical Research Centre of Finland |
| LWC | Liquid Water Content (g/m3) |
| MVD | Median Volume Diameter (µm) |
| Static Ambient Temperature (°C) | |
| Surface Temperature (°C) | |
| Dynamic Viscosity (N·s/m2) | |
| Air density (kg/m3) | |
| Accretion time | |
| Gravitational acceleration constant (m/s2) | |
| roughness height (mm) | |
| Droplet Velocity (m/s) | |
| Air Velocity (m/s) | |
| Solidification factor |
References
- Natural Resources Canada. Energy and Greenhouse Gas Emissions (GHGs). Available online: https://www.nrcan.gc.ca/science-data/data-analysis/energy-data-analysis/energy-facts/energy-and-greenhouse-gas-emissions-ghgs/20063#shr-pg0 (accessed on 19 August 2021).
- Castellani, F.; Astolfi, D. Wind Turbine Power Optimization Technology; MDPI: Basel, Switzerland, 2020. [Google Scholar]
- bp Statistical Review of World Energy. 2020. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 19 August 2021).
- Kumar, Y.; Ringenberg, J.; Depuru, S.S.; Devabhaktuni, V.K.; Lee, J.W.; Nikolaidis, E.; Andersen, B.; Afjeh, A. Wind energy: Trends and enabling technologies. Renew. Sustain. Energy Rev. 2016, 53, 209–224. [Google Scholar] [CrossRef]
- IRENA. Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation Paper); International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Vindteknikk, K. Wind Energy Projects in Cold Climates. IEA Wind TCP Recommended Practice 13, Wind Energy in Cold Climates, 2nd ed. Available online: www.ieawind.org (accessed on 20 March 2021).
- Battisti, L. Wind Turbines in Cold Climates: Icing Impacts and Mitigation Systems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mayer, C.; Ilinca, A.; Fortin, G.; Perron, J. Wind tunnel study of the electro-thermal de-icing of wind turbine blades. Int. J. Offshore Polar Eng. 2007, 17. ISOPE–07–17–3–182. [Google Scholar]
- Battisti, L. Wind Turbines in Cold Climates, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015; p. 341. [Google Scholar]
- Lehtomäki, V. Wind Energy in Cold Climates Available Technologies-Report, in Task 19, Tech. Rep., IEA 2018. 2018. Available online: https://community.ieawind.org/HigherLogic/System/DownloadDocumentFile.ashx?DocumentFileKey=6697b7bd-b175-12b0-ecbf-2558c35d309bforceDialog=0 (accessed on 20 March 2021).
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2010, 65, 88–96. [Google Scholar] [CrossRef]
- Fortin, G. Simulation de L’accrétion de Glace sur un Obstacle Bidimensionnel par la Méthode des Bissectrices et par la Modélisation des Ruisselets et des Gouttes de Surface; Université du Québec à Chicoutimi: Chicoutimi, QC, Canada, 2003. [Google Scholar]
- Fortin, G. Thermodynamique de la Glace Atmosphérique; University Course; Université du Québec à Chicoutimi: Chicoutimi, QC, Canada, 2009. [Google Scholar]
- Fernando, V. Simulation Numérique de L’accrétion de Glace sur une Pale D’éolienne. Ph.D. Thesis, École Polytechnique de Montréal, Montréal, QC, Canada, 2013. [Google Scholar]
- Fakorede, O.; Feger, Z.; Ibrahim, H.; Ilinca, A.; Perron, J.; Masson, C. Ice protection systems for wind turbines in cold climate: Characteristics, comparisons and analysis. Renew. Sustain. Energy Rev. 2016, 65, 662–675. [Google Scholar] [CrossRef]
- Sagol, E. Three Dimensional Numerical Predicton of Icing Related Power and Energy Losses on a Wind Turbine. Ph.D. Thesis, École Polytechnique de Montréal, Montréal, QC, Canada, 2014. [Google Scholar]
- Dong, W.; Zhu, J.; Wang, R.; Chen, Y. Numerical Simulation of Icing on the Rotating Blade. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56628, p. V001T01A013. [Google Scholar]
- Fortin, G.; Perron, J. Wind turbine icing and de-Icing. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 274. [Google Scholar]
- Hochart, C. Simulation Numérique et Expérimentale de L’écoulement D’air et de L’accrétion de Glace Autour D’une Pale D’éolienne. Ph.D. Thesis, Université du Québec à Rimouski, Rimouski, QC, Canada, 2007. [Google Scholar]
- Thomas, S.K.; Cassoni, R.P.; MacArthur, C.D. Aircraft anti-icing and de-icing techniques and modeling. J. Aircr. 1996, 33, 841–854. [Google Scholar] [CrossRef]
- Fortin, G.; Peron, J. Temperature drop of a wet wing at takeoff. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NA, USA, 10–13 January 2005; p. 654. [Google Scholar]
- Son, C.; Kelly, M.; Kim, T. Boundary-layer transition model for icing simulations of rotating wind turbine blades. Renew. Energy 2020, 167, 172–183. [Google Scholar] [CrossRef]
- Turkia, V.; Huttunen, S.; Wallenius, T. Method for Estimating Wind Turbine Production Losses Due to Icing; VTT Technology No. 114; VTT Technical Research Centre of Finland: Espoo, Finland, 2013. [Google Scholar]
- Hudecz, A. Icing Problems of Wind Turbine Blades in Cold Climates; Department of Wind Energy, Technical University of Denmark: Copenhagen, Denmark, 2014; 166p. [Google Scholar]
- Makkonen, L.; Laakso, T.; Marjaniemi, M.; Finstad, K.J. Modelling and Prevention of Ice Accretion on Wind Turbines. Wind Eng. 2001, 25, 3–21. [Google Scholar] [CrossRef]
- Homola, M.C.; Virk, M.S.; Wallenius, T.; Nicklasson, P.J.; Sundsbø, P.A. Effect of atmospheric temperature and droplet size variation on ice accretion of wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2010, 98, 724–729. [Google Scholar] [CrossRef]
- Schaffarczyk, A.P. Introduction to Wind Turbine Aerodynamics; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Fregeau, M. Étude et Simulation de la Formation de Glace sur Aéronefs et Modélisation de Systèmes Antigivrants. Ph.D. Thesis, École Polytechnique, Palaiseau, France, 2004. [Google Scholar]
- Villalpando, F.; Reggio, M.; Ilinca, A. Assessment of Turbulence Models for Flow Simulation around a Wind Turbine Airfoil. Model. Simul. Eng. 2011, 2011, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sagol, E.; Reggio, M.; Ilinca, A. Assessment of Two-Equation Turbulence Models and Validation of the Performance Characteristics of an Experimental Wind Turbine by CFD. ISRN Mech. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Homola, M.C.; Virk, M.S.; Nicklasson, P.J.; Sundsbø, P.A. Performance losses due to ice accretion for a 5 MW wind turbine. Wind Energy 2011, 15, 379–389. [Google Scholar] [CrossRef]
- Hudecz, A.; Koss, H.; Hansen, M.O. Ice accretion on wind turbine blades. In Proceedings of the 15th International Workshop on Atmospheric Icing of Structures (IWAIS XV), St. John’s, NL, Canada, 8–11 September 2013; pp. 8–13. [Google Scholar]
- Makkonen, L.; Zhang, J.; Karlsson, T.; Tiihonen, M. Modelling the growth of large rime ice accretions. Cold Reg. Sci. Technol. 2018, 151, 133–137. [Google Scholar] [CrossRef]
- Mortensen, K. CFD Simulations of an Airfoil with Leading Edge Ice Accretion; Technical University of Denmark: Lyngby, Denmark, 2008; p. 117. [Google Scholar]
- Chocron, D. Étude Numérique de la Formation de Glace sur les Éoliennes à Axe Horizontal; École polytechnique de Montréal: Montréal, QC, Canada, 1997. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Tardif d’Hamonville, T. Modélisation et Analyse des Phénomènes Aéroélastiques Pour une Pale D’éolienne; Université du Québec à Chicoutimi: Chicoutimi, QC, Canada, 2009. [Google Scholar]
- Villalpando, F. Simulation Numérique Pour la Prédiction des Coefficients de Traînée et de Portance D’un Profil Givré; École Polytechnique: Montreal, QC, Canada, 2008. [Google Scholar]
- Han, W.; Kim, J.; Kim, B. Study on correlation between wind turbine performance and ice accretion along a blade tip airfoil using CFD. J. Renew. Sustain. Energy 2018, 10, 023306. [Google Scholar] [CrossRef]
- Harrison, M.; Batten, W.; Myers, L.; Bahaj, A. Comparison between CFD simulations and experiments for predicting the far wake of horizontal axis tidal turbines. IET Renew. Power Gener. 2010, 4, 613. [Google Scholar] [CrossRef] [Green Version]
- Suatean, B.; Colidiuc, A.; Galetuse, S. CFD methods for wind turbines. AIP Conf. Proc. 2012, 1493, 998–1002. [Google Scholar]
- Menter, F. Zonal Two Equation k-w Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar] [CrossRef]
- O’Brien, J.; Young, T.; O’Mahoney, D.; Griffin, P. Horizontal axis wind turbine research: A review of commercial CFD, FE codes and experimental practices. Prog. Aerosp. Sci. 2017, 92, 1–24. [Google Scholar] [CrossRef]
- Pedersen, M.C.; Yin, C. Preliminary Modelling Study of Ice Accretion on Wind Turbines. Energy Procedia 2014, 61, 258–261. [Google Scholar] [CrossRef] [Green Version]
- Hildebrandt, S. Modeling and Evaluation of Wind Turbine Operational Strategies during Icing Events. Master’s Thesis, Schulich School of Engineering, University of Calgary, Calgary, AB, Canada, 2019. [Google Scholar]
- Farzaneh, M. (Ed.) Atmospheric Icing of Power Networks; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Fortin, G.; Luliano, E.; Mingione, G.; Perron, J. CIRAAMIL Ice Accretion Code Improvements. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009; p. 3968. [Google Scholar]
- Makkonen, L. Heat transfer and icing of a rough cylinder. Cold Reg. Sci. Technol. 1985, 10, 105–116. [Google Scholar] [CrossRef]
- Szilder, K.; Lozowski, E.P. Simulation of Airfoil Icing with a Novel Morphogenetic Model. J. Aerosp. Eng. 2005, 18, 102–110. [Google Scholar] [CrossRef]
- Shin, J.; Berkowitz, B.; Chen, H.H.; Cebeci, T. Prediction of ice shapes and their effect on airfoil drag. J. Aircr. 1994, 31, 263–270. [Google Scholar] [CrossRef]
- ANSYS FENSAP-ICE User Manual, R1. 2020. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v202/en/fensap_manual/fensap_manual.html (accessed on 19 August 2021).
- Martini, F.; Ramdenee, D.; Ibrahim, H.; Ilinca, A. A multiphase CFX based approach into ice accretion modeling on a cylinder. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011; pp. 450–455. [Google Scholar] [CrossRef]
- Martini, F.; Ramdenee, D.; Ibrahim, H.; Ilinca, A. A lagrangean interactive interface to evaluate ice accretion modeling on a cylinder—A test case for icing modeling on wind turbine airfoils. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011; pp. 456–461. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, X.; Hu, C.; Chen, J.; Du, Z. Calculation of the Water Droplets Local Collection Efficiency on the Wind Turbines Blade. J. Energy Resour. Technol. 2017, 139, 051211. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, C. Numerical simulation for in-cloud icing of three-dimensional wind turbine blades. Simulation 2017, 94, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Borghi, R.; Anselmet, F. Turbulent Multiphase Flows with Heat and Mass Transfer; John Wiley Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Habashi, W.G. Recent advances in CFD for in-flight icing simulations. Jpn. Soc. Fluid Mech. 2009, 28, 99–118. [Google Scholar]
- Bourgault, Y.; Boutanios, Z.; Habashi, W.G. Three-dimensional Eulerian approach to droplet impingement simulation using FENSAP-ICE, Part 1: Model, algorithm, and validation. J. Aircr. 2000, 37, 95–103. [Google Scholar] [CrossRef]
- Boutanios, Z. An Eulerian 3D Analysis of Water Droplets Impingement on a Convair-580 Nose and Cockpit Geometry. Ph.D. Thesis, Concordia University, Montréal, QC, Canada, 1999. [Google Scholar]
- Yoon, T.; Yee, K. Correction of Local Collection Efficiency Based on Roughness Element Concept for Glaze Ice Simulation. J. Mech. 2020, 36, 607–622. [Google Scholar] [CrossRef]
- Messinger, B.L. Equilibrium Temperature of an Unheated Icing Surface as a Function of Air Speed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Fortin, G.; Ilinca, A.; Laforte, J.L. Modèle d’accrétion de glace sur un objet bidimensionnel fixe appliquable aux pales d’éoliennes. VertigO-La Rev. Électron. En Sci. Environ. 2004, 5, 1. [Google Scholar] [CrossRef]
- Lozowski, E.P.; Stallabrass, J.R.; Hearty, P.F. The icing of an unheated, nonrotating cylinder. Part II. Icing wind tunnel experiments. J. Appl. Meteorol. Climatol. 1983, 22, 2063–2074. [Google Scholar] [CrossRef]
- Lozowski, E.P.; Stallabrass, J.R.; Hearty, P.F. The icing of an unheated, nonrotating cylinder. Part I: A simulation model. J. Appl. Meteorol. Climatol. 1983, 22, 2053–2062. [Google Scholar] [CrossRef]
- Foder, M.H. ISO 12494 Atmospheric Icing of Structures and How to Use It. In Proceedings of the the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001. [Google Scholar]
- Dierer, S.; Oechslin, R.; Cattin, R. Wind turbines in icing conditions: Performance and prediction. Adv. Sci. Res. 2011, 6, 245–250. [Google Scholar] [CrossRef]
- Makkonen, L. Models for the growth of rime, glaze, icicles and wet snow on structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2000, 358, 2913–2939. [Google Scholar] [CrossRef]
- Jolin, N.; Bolduc, D.; Swytink-Binnema, N.; Rosso, G.; Godreau, C. Wind turbine blade ice accretion: A correlation with nacelle ice accretion. Cold Reg. Sci. Technol. 2018, 157, 235–241. [Google Scholar] [CrossRef]
- Virk, M.S.; Homola, M.C.; Nicklasson, P.J. Relation between Angle of Attack and Atmospheric Ice Accretion on Large Wind Turbine’s Blade. Wind Eng. 2010, 34, 607–613. [Google Scholar] [CrossRef]
- Barber, S.; Wang, Y.; Jafari, S.; Chokani, N.; Abhari, R.S. The Effect of Icing on Wind Turbine Performance and Aerodynamics. J. Sol. Energy Eng. 2010, 133, 011007. [Google Scholar] [CrossRef]
- Fu, P.; Farzaneh, M. A CFD approach for modeling the rimeice accretion process on a horizontal-axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2009, 98, 181–188. [Google Scholar] [CrossRef]
- Homola, M.C.; Wallenius, T.; Makkonen, L.; Nicklasson, P.J.; Sundsbø, P.A. The relationship between chord length and rime icing on wind turbines. Wind Energy 2009, 13, 627–632. [Google Scholar] [CrossRef]
- Homola, M.C.; Wallenius, T.; Makkonen, L.; Nicklasson, P.J.; Sundsbø, P.A. Turbine Size and Temperature Dependence of Icing on Wind Turbine Blades. Wind Eng. 2010, 34, 615–627. [Google Scholar] [CrossRef]
- Virk, M.S.; Homola, M.C.; Nicklasson, P.J. Effect of Rime Ice Accretion on Aerodynamic Characteristics of Wind Turbine Blade Profiles. Wind Eng. 2010, 34, 207–218. [Google Scholar] [CrossRef]
- Dimitrova, M.; Ibrahim, H.; Fortin, G.; Ilinca, A.; Perron, J. Software tool to predict the Wind Energy production losses due to icing. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011; pp. 462–467. [Google Scholar] [CrossRef]
- Virk, M.S.; Homola, M.C.; Nicklasson, P.J. Atmospheric icing on large wind turbine blades. Int. J. Energy Environ. 2012, 3, 1–8. [Google Scholar]
- Villalpando, F.; Reggio, M.; Ilinca, A. Numerical Study of Flow Around Iced Wind Turbine Airfoil. Eng. Appl. Comput. Fluid Mech. 2012, 6, 39–45. [Google Scholar] [CrossRef] [Green Version]
- Son, C.; Oh, S.; Yee, K. Quantitative analysis of a two-dimensional ice accretion on airfoils. J. Mech. Sci. Technol. 2012, 26, 1059–1071. [Google Scholar] [CrossRef]
- Reid, T.; Baruzzi, G.; Ozcer, I.; Switchenko, D.; Habashi, W. FENSAP-ICE Simulation of Icing on Wind Turbine Blades, Part 1: Performance Degradation. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Reid, T.; Baruzzi, G.; Ozcer, I.; Switchenko, D.; Habashi, W. FENSAP-ICE Simulation of Icing on Wind Turbine Blades, Part 2: Ice Protection System Design. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Etemaddar, M.; Hansen, M.O.; Moan, T. Wind turbine aerodynamic response under atmospheric icing conditions. Wind Energy 2012, 17, 241–265. [Google Scholar] [CrossRef]
- Switchenko, D.; Habashi, W.; Reid, T.; Ozcer, I.; Baruzzi, G. FENSAP-ICE Simulation of Complex Wind Turbine Icing Events, and Comparison to Observed Performance Data. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Pallarol, J.; Wu, Z. On Ice Accretion for Wind Turbines and Influence of Some Parameters. Engineering 2014, 1, 129–159. [Google Scholar] [CrossRef] [Green Version]
- Virk, M.; Mughal, U.; Hu, Q.; Jiang, X. Multiphysics Based Numerical Study of Atmospheric Ice Accretion on a Full Scale Horizontal Axis Wind Turbine Blade. Int. J. Multiphys. 2016, 10, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Villalpando, F.; Reggio, M.; Ilinca, A. Prediction of ice accretion and anti-icing heating power on wind turbine blades using standard commercial software. Energy 2016, 114, 1041–1052. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H.; Ozgen, S. Ice Accretion Prediction on Wind Turbines and Consequent Power Losses. J. Phys. Conf. Ser. 2016, 753, 22022. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, M.C.; Sørensen, H. Towards a CFD Model for Prediction of Wind Turbine Power Losses due to Icing in Cold Climate. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Shu, L.; Liang, J.; Hu, Q.; Jiang, X.; Ren, X.; Qiu, G. Study on small wind turbine icing and its performance. Cold Reg. Sci. Technol. 2017, 134, 11–19. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, X.; Hu, C.; Chen, J.; Du, Z. Wind turbines ice distribution and load response under icing conditions. Renew. Energy 2017, 113, 608–619. [Google Scholar] [CrossRef]
- Zanon, A.; De Gennaro, M.; Kühnelt, H. Wind energy harnessing of the NREL 5 MW reference wind turbine in icing conditions under different operational strategies. Renew. Energy 2018, 115, 760–772. [Google Scholar] [CrossRef]
- Shu, L.; Li, H.; Gaohui, H.; Jiang, X.; Qiu, G.; He, G.; Liu, Y. 3D numerical simulation of aerodynamic performance of iced contaminated wind turbine rotors. Cold Reg. Sci. Technol. 2018, 148, 50–62. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, X.; Chen, J.; Shen, X.; Du, Z. Numerical simulation of rime ice on NREL Phase VI blade. J. Wind Eng. Ind. Aerodyn. 2018, 178, 57–68. [Google Scholar] [CrossRef]
- Jin, J.Y.; Virk, M.S. Study of ice accretion along symmetric and asymmetric airfoils. J. Wind Eng. Ind. Aerodyn. 2018, 179, 240–249. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Sun, C.; Yi, X.; Guo, W.; Zhou, Z.; Feng, F. Icing distribution of rotating blade of horizontal axis wind turbine based on Quasi-3D numerical simulation. Therm. Sci. 2018, 22, 681–691. [Google Scholar] [CrossRef]
- Ibrahim, G.; Pope, K.; Muzychka, Y. Effects of blade design on ice accretion for horizontal axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2018, 173, 39–52. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C.; Jiang, Y.; Yi, X.; Xu, Z.; Guo, W. Temperature effect on icing distribution near blade tip of large-scale horizontal-axis wind turbine by numerical simulation. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Shu, L.; Qiu, G.; Hu, Q.; Jiang, X.; McClure, G.; Yang, H. Numerical and field experimental investigation of wind turbine dynamic de-icing process. J. Wind Eng. Ind. Aerodyn. 2018, 175, 90–99. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C.; Jiang, Y.; Yi, X.; Zhang, Y. Effect of liquid water content on blade icing shape of horizontal axis wind turbine by numerical simulation. Therm. Sci. 2019, 23, 1637–1645. [Google Scholar] [CrossRef] [Green Version]
- Kollár, L.E.; Santos, F.O.S. Consideration of Icing in the Design of Wind Turbine Blade Sections. In Proceedings of the International Workshop on Atmospheric Icing of Structures (IWAIS), Reykjavik, Iceland, 23–28 June 2019. [Google Scholar]
- Kollar, L.E.; Mishra, R. Inverse design of wind turbine blade sections for operation under icing conditions. Energy Convers. Manag. 2018, 180, 844–858. [Google Scholar] [CrossRef] [Green Version]
- Yirtici, O.; Cengiz, K.; Ozgen, S.; Tuncer, I.H. Aerodynamic validation studies on the performance analysis of iced wind turbine blades. Comput. Fluids 2019, 192, 104271. [Google Scholar] [CrossRef]
- Jin, J.Y.; Virk, M.S.; Hu, Q.; Jiang, X. Study of Ice Accretion on Horizontal Axis Wind Turbine Blade Using 2D and 3D Numerical Approach. IEEE Access 2020, 8, 166236–166245. [Google Scholar] [CrossRef]
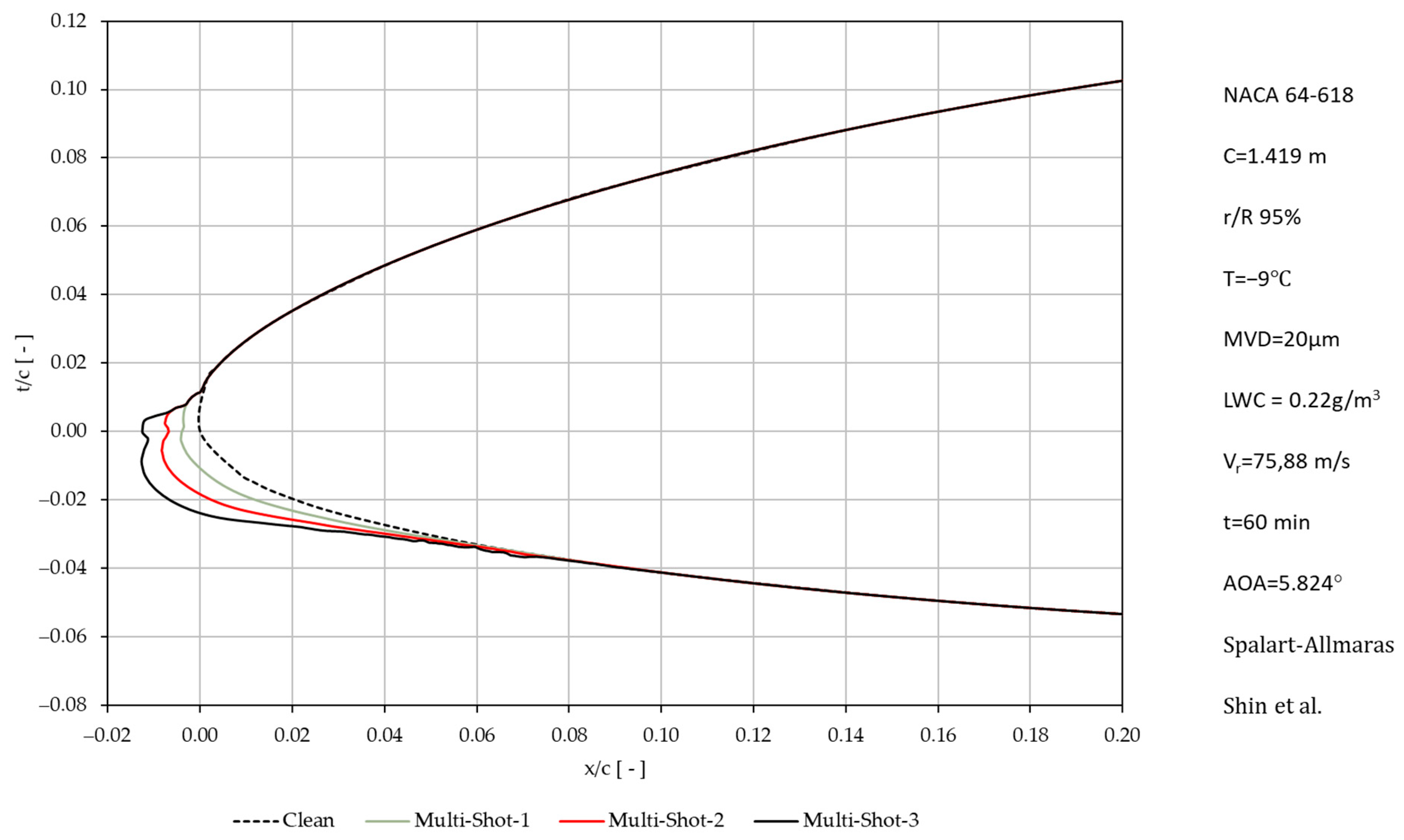
- Wang, Q.; Yi, X.; Liu, Y.; Ren, J.; Li, W.; Wang, Q.; Lai, Q. Simulation and analysis of wind turbine ice accretion under yaw condition via an Improved Multi-Shot Icing Computational Model. Renew. Energy 2020, 162, 1854–1873. [Google Scholar] [CrossRef]
- Son, C.; Kim, T. Development of an icing simulation code for rotating wind turbines. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104239. [Google Scholar] [CrossRef]
- Hansman, R.J.; Turnock, S.R. Investigation of microphysical factors which influence surface roughness during glaze ice accretion. In Proceedings of the Fourth International Conference on Atmospheric Icing of Structures, Paris, France, 5–7 September 1988. [Google Scholar]
- Hansman, R.J.; Turnock, S.R. Investigation of surface water behavior during glaze ice accretion. J. Aircr. 1989, 26, 140–147. [Google Scholar] [CrossRef]
- Broeren, A.; Bragg, M. Effect of Airfoil Geometry on Performance with Simulated Intercycle Ice Accretions. J. Aircr. 2005, 42, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Achenbach, E. The effect of surface roughness on the heat transfer from a circular cylinder to the cross flow of air. Int. J. Heat Mass Transf. 1977, 20, 359–369. [Google Scholar] [CrossRef]
- Timmer, W. An Overview of NACA 6-Digit Airfoil Series Characteristics with Reference to Airfoils for Large Wind Turbine Blades. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Fortin, G.; Laforte, J.-L.; Ilinca, A. Heat and mass transfer during ice accretion on aircraft wings with an improved roughness model. Int. J. Therm. Sci. 2006, 45, 595–606. [Google Scholar] [CrossRef]
- Davis, N. Icing Impacts on Wind Energy Production; DTU Wind Energy: Copenhagen, Denmark, 2014; 156p. [Google Scholar]
- Lehtomäki, V.; Karlsson, T.; Rissanen, S. Wind Turbine Ice Protection System Benchmark Analysis; VTT Technology No. 341; VTT Technical Research Centre of Finland: Espoo, Finland, 2018. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Fakorede, C.O. Modélisation du Transfert Thermique et du Transfert de Masse Lors du Processus D’accrétion de Glace et de Dégivrage des Ples D’éoliennes. Ph.D. Thesis, Université du Québec à Chicoutimi, Chicoutimi, QC, Canada, 2018. [Google Scholar]
- Wei, K.; Yang, Y.; Zuo, H.; Zhong, D. A review on ice detection technology and ice elimination technology for wind turbine. Wind Energy 2019, 23, 433–457. [Google Scholar] [CrossRef]
- Madi, E.; Pope, K.; Huang, W.; Iqbal, T. A review of integrating ice detection and mitigation for wind turbine blades. Renew. Sustain. Energy Rev. 2019, 103, 269–281. [Google Scholar] [CrossRef]
- Sunden, B.; Wu, Z. On Icing and Icing Mitigation of Wind Turbine Blades in Cold Climate. J. Energy Resour. Technol. 2015, 137, 051203. [Google Scholar] [CrossRef]
- Habibi, H.; Cheng, L.; Zheng, H.; Kappatos, V.; Selcuk, C.; Gan, T.-H. A dual de-icing system for wind turbine blades combining high-power ultrasonic guided waves and low-frequency forced vibrations. Renew. Energy 2015, 83, 859–870. [Google Scholar] [CrossRef] [Green Version]
- Patreau, V. Modélisation Numérique D’un Système Électrothermique de Dégivrage des Pales D’éolienne à Axe Horizontal; École Polytechnique de Montréal: Montréal, QC, Canada, 1998. [Google Scholar]
- Ibrahim, H.; Ould Rouis, L.; Masson, C.; Rousse, D. Optimisation par contrôle d’un système de dégivrage électrothermique d’une pale d’éolienne. In Proceedings of the Comptes rendus du XIIème Colloque Interuniversitaire Franco-Québécois sur la Thermique des Systèmes, Sherbrooke, QC, Canada, 8–10 June 2015. [Google Scholar]
- Croce, G.; Habashi, W.; Guevremont, G.; Tezok, F. 3D thermal analysis of an anti-icing device using FENSAP-ICE. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 193. [Google Scholar]
- Fakorede, O.; Ibrahim, H.; Ilinca, A.; Perron, J. Experimental Investigation of Power Requirements for Wind Turbines Electrothermal Anti-icing Systems. In Wind Turbines—Design, Control and Applications; BoD–Books on Demand: Norderstedt, Germany, 2016; Chapter 14. [Google Scholar]
- Danyluk, R. Numerical Investigation of Anti-Icing Systems for Wind Turbine Blades. Master’s Thesis, Technical University of Denmark, Lyngby, Denmark, 2009. [Google Scholar]
- Bu, X.; Lin, G.; Yu, J.; Yang, S.; Song, X. Numerical simulation of an airfoil electrothermal anti-icing system. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 227, 1608–1622. [Google Scholar] [CrossRef]
- Shu, L.; Qiu, G.; Hu, Q.; Jiang, X.; McClure, G.; Liu, Y. Numerical and experimental investigation of threshold de-icing heat flux of wind turbine. J. Wind Eng. Ind. Aerodyn. 2018, 174, 296–302. [Google Scholar] [CrossRef]
- Mohseni, M.; Amirfazli, A. A novel electro-thermal anti-icing system for fiber-reinforced polymer composite airfoils. Cold Reg. Sci. Technol. 2013, 87, 47–58. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Liu, Q.; Feng, F.; Tagawa, K. Characteristics of ice accretions on blade of the straight-bladed vertical axis wind turbine rotating at low tip speed ratio. Cold Reg. Sci. Technol. 2018, 145, 1–13. [Google Scholar] [CrossRef]





| Authors | Software 1 | Roughness Model | Turbulence Model | Output Parameters | Validation |
|---|---|---|---|---|---|
| Homola, et al. [26] | TURBICE FLUENT | Shin et al., Model | k-ε | Ice shape. Streamlines around clean and iced profiles. Aerodynamic Coefficients. Torque Coefficient. | No |
| Muhammad S. Virk, et al. [69] | FENSAP-ICE | Shin et al., Model | Spalart-Allmaras | Ice shape. Accreted ice mass. Ice thickness. | No |
| Barber, et al. [70] | LEWICE CFX | N/A | N/A | Ice shape. Power Coefficient vs. TSR | Exp. |
| Fu and Farzaneh [71] | FLUENT | N/A | k-ε | Local collision coefficient. Ice shape. Ice load. Ice thickness | No |
| Homola, et al. [72] | TURBICE | Sand Grain roughness | N/A | Ice shape. Ice mass. Ice thickness. | No |
| Matthew C. Homola, et al. [73] | TURBICE | Time-dependent roughness calculation | N/A | Ice mass. Ice thickness. Ice shape. Stagnation line temperatures. Heat balance at the stagnation line. | No |
| Muhammad S. Virk, et al. [74] | TURBICE FLUENT | Constant Value: 1.5 mm | k-ε (realizable) | Ice thickness. Aerodynamic Coefficients. Torque Coefficient. | No |
| M. Dimitrova, et al. [75] | PROICET (CIRALIMA, XFOIL and PROPID) | N/A | N/A | Ice shape. Ice mass. Aerodynamic Coefficients. Power Curve. Production Losses. | No |
| Homola, et al. [31] | FENSAP-ICE In-house code for BEM simulation | Shin et al., Model | Spalart-Allmaras | Ice shape. Aerodynamic Coefficients. Power Coefficient vs. TSR Power Curve. Power Losses. | No |
| Virk, et al. [76] | FENSAP-ICE | Shin et al., Model | Spalart-Allmaras | Droplet collision efficiency. Ice shape. Ice thickness. Ice mass. | No |
| Fernando Villalpando, et al. [77] | FLUENT | N/A | k-ω SST | Aerodynamic Coefficients. Pressure Coefficient. | Exp. |
| Son, et al. [78] | In-House Panel Method | N/A | N/A | Ice shape. Ice thickness. Ice accretion area. | Exp. Num. |
| Turkia, et al. [23] | TURBICE FLUENT FAST | Shin et al., Model | Spalart-Allmaras | Ice Shape. Aerodynamic Coefficients. Power Curve. Ice mass. Power loss. | Exp. |
| Hudecz, et al. [32] | TURBICE FLUENT | Sand Grain roughness | Spalart-Allmaras and k-ω SST | Ice shape. Aerodynamic Coefficients vs. Time. | Exp. |
| Reid, et al. [79] | FENSAP-ICE | N/A | Spalart-Allmaras | Pressure, Thrust and Torque Coefficients. Ice shape. Power loss. | Exp. Num. |
| Design Reid, et al. [80] | FENSAP-ICE | N/A | Spalart-Allmaras | Droplet collection efficiency. Heat Flux Heating power as a function of spanwise radial distance. Effective IPS power and coverage. | Exp. |
| Etemaddar, et al. [81] | LEWICE FLUENT BEM WT-Perf | Constant Value: 0.5 mm | k-ε | Ice Shape. Ice mass. Ice thickness Ice load. Aerodynamic Coefficients. Power Coefficient vs. TSR. Thrust Coefficient vs. TSR. Bending moment. Fatigue damage. | Exp. |
| Switchenko, et al. [82] | FENSAP-ICE | Constant values: 1, 3, and 10 mm | Spalart-Allmaras | Ice shape. Power curve. Pressure and velocity distributions. | Exp. |
| Hudecz [24] | TURBICE FLUENT | N/A | Spalart-Allmaras and k-ω SST | Ice shape. Aerodynamic coefficients. Velocity streamlines. Pressure coefficient. | Exp. |
| Sagol [16] | FLUENT In-house BEM method | N/A | k-ω SST | Ice shape. Torque vs. Radius Aerodynamic coefficients. Power loss. | Exp. |
| Pedersen and Yin [44] | FLUENT | N/A | Spalart-Allmaras, Realizable k-ε and k-ω SST | Collection efficiency. Aerodynamic coefficients | Exp. Num. |
| Pallarol, et al. [83] | LEWINT (Based on LEWICE) | N/A | N/A | Ice thickness | No |
| Virk, et al. [84] | FENSAP-ICE | N/A | N/A | Collision efficiency. 3D Ice shape. | No |
| Villalpando, et al. [85] | FLUENT MATLAB | N/A | RNGk-ε | Ice shape. Ice thickness. Ice accretion area. | Exp. |
| Ozcan Yirtici, et al. [86] | In-house model (ice accretion) XFOIL (BEM Method) | N/A | N/A | Ice shape. Power curve. | Exp. Num. |
| Pedersen and Sørensen [87] | FLUENT | Shin et al., Model | k-ω SST | Ice shape. Ice Thickness. | Num. |
| Shu, et al. [88] | FLUENT MATLAB | Estimated from experimental data | k-ε | Ice shape. Ice Load. Ice thickness Pressure coefficient. Power coefficient vs. Time | Exp. |
| Hu, et al. [89] | LEWICE FLUENT | Constant values: 0.05 mm (clean) and 0.5 mm (iced) | k-ω SST | Ice Shape. Ice mass. Ice thickness. Aerodynamic coefficients. | Exp. Num. |
| Wang and Zhu [55] | FLUENT | N/A | k-ω SST | Droplet trajectory. Droplet collection efficiency. Ice shape. Ice thickness. | Exp. |
| Han, et al. [39] | STAR-CCM+ BLADED | Shin et al., Model | k-ω SST | Ice shape. Ice mass. Ice Thickness. Aerodynamic coefficients. Power curve. | Exp. |
| Zanon, et al. [90] | CFX ICEAC2D BEM WT_Perf | Shin et al., Model | k-ω SST | Ice shape. Aerodynamic coefficients. Power curve. Power coefficient vs. time. AoA vs. radius. | Exp. |
| Shu, et al. [91] | FLUENT | N/A | k-ω SST | Ice shape. Output power. Power coefficient vs. TSR Pressure distribution. Torque. Power curve. | Exp. |
| Hu, et al. [92] | FLUENT | N/A | k-ω SST | Ice shape. Ice mass. Pressure coefficient. Droplet collection efficiency. Power curve. | Exp. Num. |
| Jin and Virk [93] | FENSAP-ICE FLUENT | NASA Roughness model | Spalart-Allmaras | Droplet collection efficiency. Ice shape. Ice thickness. Ice mass. Aerodynamic coefficients. Impingement Location. | Exp. |
| Li, et al. [94]. | Lagrangian Method based on Runge-Kutta method | N/A | N/A | Ice shape Maximum stationary thickness. Ice area. Ice volume. | No |
| Ibrahim, et al. [95] | FENSAP-ICE | Constant value: 0.0005 m | Spalart-Allmaras | Droplet collection efficiency. Ice mass. Ice shape. Aerodynamic coefficients. Torque coefficients. | Exp. Num. |
| Li, et al. [96] | Lagrangian Method based on Runge-Kutta methods | N/A | k-ε | Icing shape. Maximum stationary thickness. Ice area. Ice volume. | Exp. Num. |
| Shu, et al. [97] | COMSOL MATLAB | N/A | k-ω SST | Ice shape | Exp. |
| Hildebrandt [45] | FENSAP-ICE BEM code Turb-PSU | Shin et al., Model. Beading Surface Roughness Model. | Spalart-Allmaras | Ice shape. Aerodynamic coefficient. Power curve. | Exp. |
| Li, et al. [98] | Lagrangian Method based on Runge-Kutta method | N/A | k-ε | Ice shape Maximum stationary thickness. Ice area. Ice volume. | No |
| László E. Kollár and Santos [99] | FENSAP-ICE FLUENT MATLAB | N/A | k-ε | Ice shape. Lift-to-Drag ratio (%) | No |
| Kollar and Mishra [100] | FLUENT (iced profile) MATLAB (Panel Method) | N/A | k-ε | Ice shape. Aerodynamic coefficients. Lift-to-Drag ratio (%) Velocity distribution. | No |
| Yirtici, et al. [101] | XFOIL SU2 METUDES In-House DDES solver | N/A | Spalart-Allmaras | Ice shape. Pressure coefficient. Aerodynamic coefficients. Power curve. | Exp. Num. |
| Jin, et al. [102] | FENSAP-ICE | Shin et al., Model | k-ω SST | Pressure coefficient. Droplet collection efficiency. Ice shape. Max Ice density. Ice thickness. | No |
| Wang, et al. [103] | Improved Multi-Shot Icing Computational Model (IMSICM) | N/A | k-ω | Ice Shape. Aerodynamic coefficients. Upper and Lower horn peak thickness. Upper and Lower horn angle. Ice area. Ice thickness. Angle of attack. | Exp. |
| Son and Kim [104] | WISE | Shin et al., Model | Spalart-Allmaras | Pressure coefficient. Ice shape. | Num. |
| Son, et al. [22] | WISE | Surface roughness amplifier | Transitional Model | Skin friction coefficient. Ice Shape | Exp. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martini, F.; Contreras Montoya, L.T.; Ilinca, A. Review of Wind Turbine Icing Modelling Approaches. Energies 2021, 14, 5207. https://doi.org/10.3390/en14165207
Martini F, Contreras Montoya LT, Ilinca A. Review of Wind Turbine Icing Modelling Approaches. Energies. 2021; 14(16):5207. https://doi.org/10.3390/en14165207
Chicago/Turabian StyleMartini, Fahed, Leidy Tatiana Contreras Montoya, and Adrian Ilinca. 2021. "Review of Wind Turbine Icing Modelling Approaches" Energies 14, no. 16: 5207. https://doi.org/10.3390/en14165207
APA StyleMartini, F., Contreras Montoya, L. T., & Ilinca, A. (2021). Review of Wind Turbine Icing Modelling Approaches. Energies, 14(16), 5207. https://doi.org/10.3390/en14165207








