Frac-n-Flow Testing to Screen Brittle Fracture Stages in Wolfcamp Formation, Permian Basin, USA
Abstract
:1. Introduction
2. Background
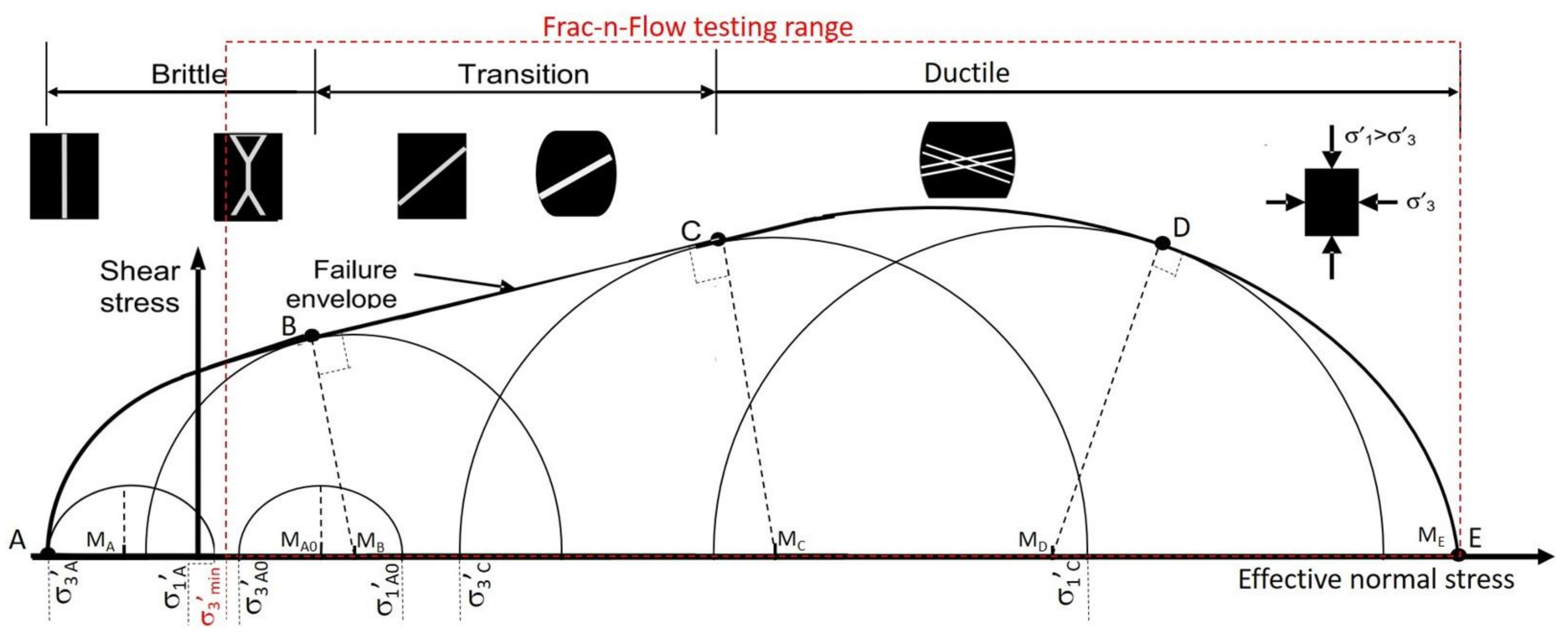
2.1. Rock Fracturability and Fracture Mode
2.2. Fracture Mode and Permeability Change
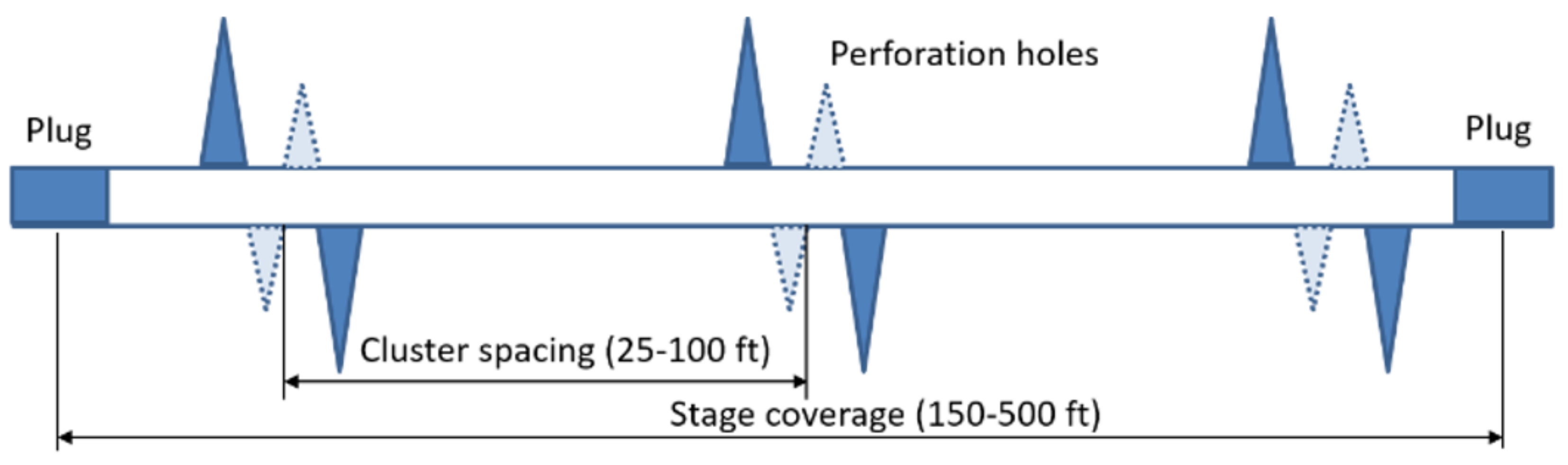
2.3. Stress Shadow Effect in Multistage HF Completion
2.4. Matrix Permeability and Pad-Fracture Conductivity
3. Frac-n-Flow Testing
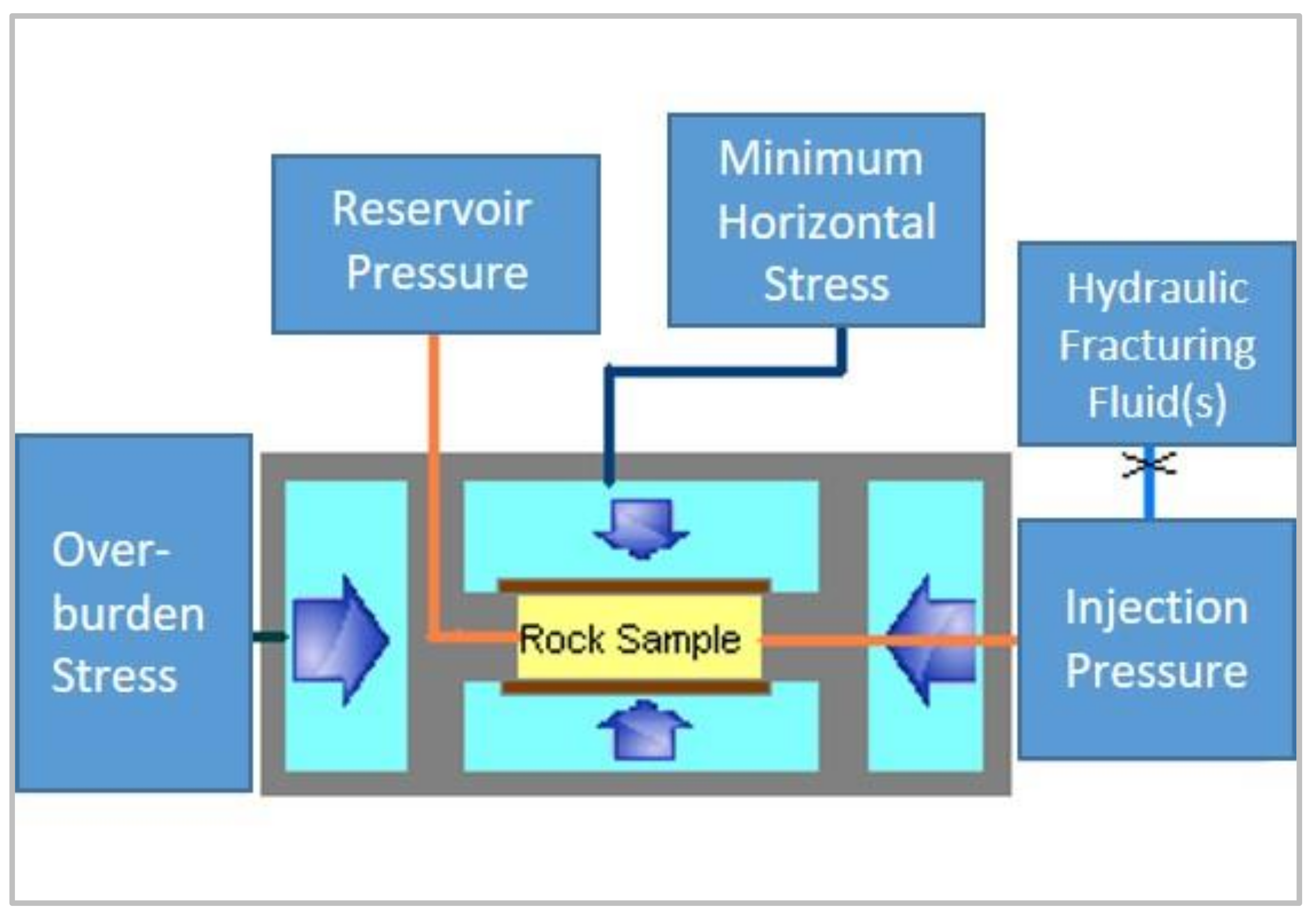
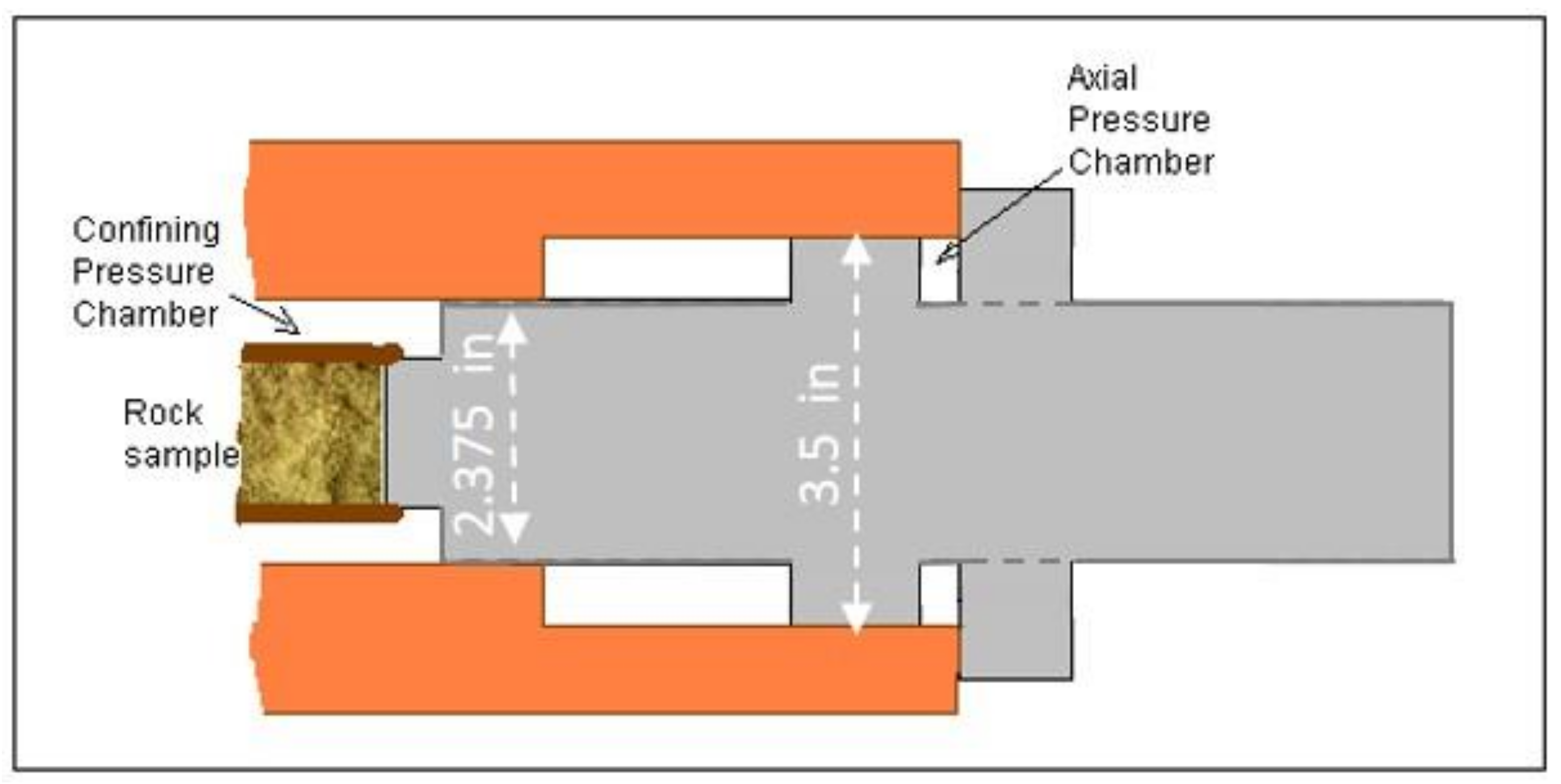
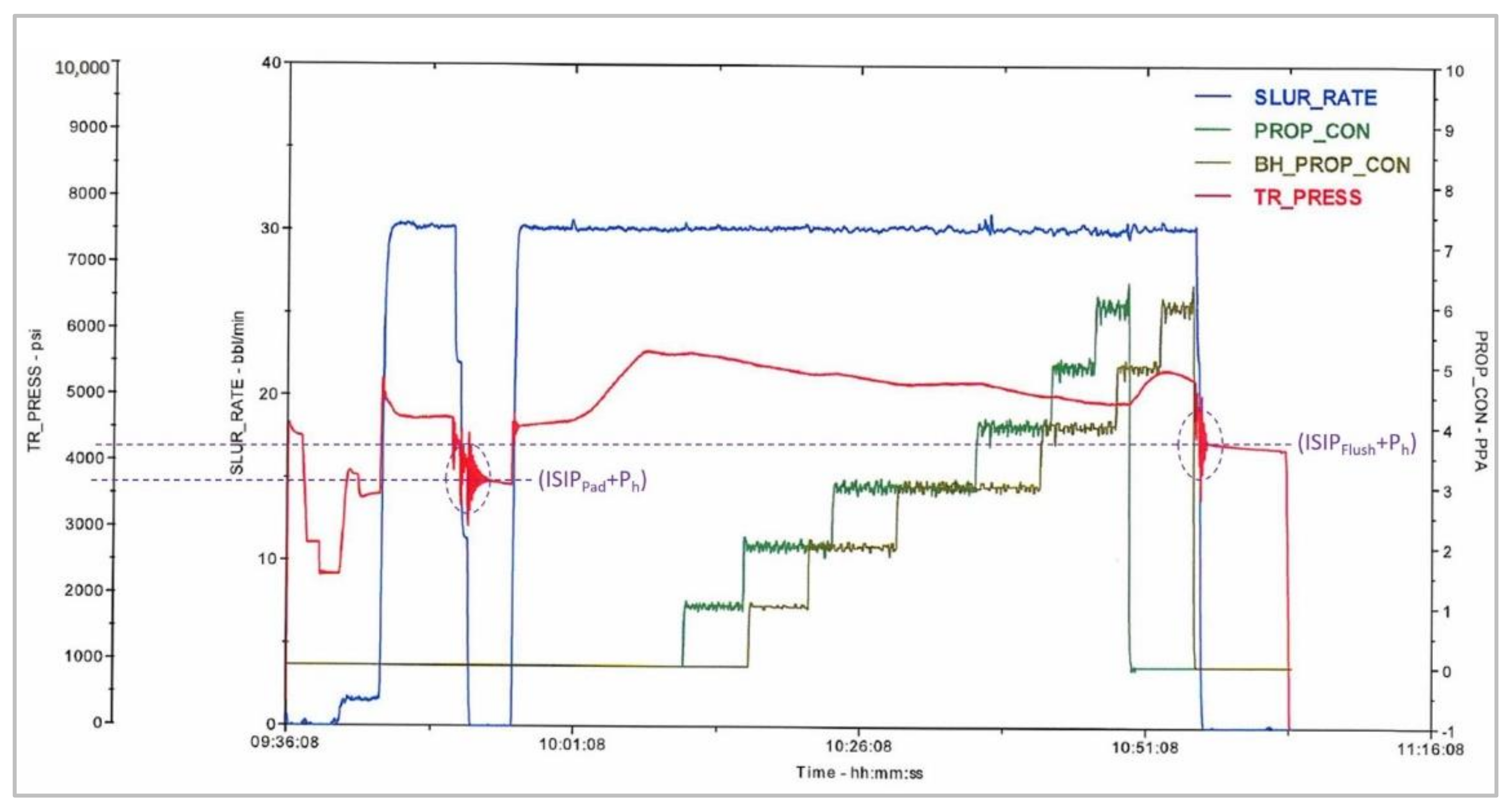
3.1. Testing Facility
3.2. Testing Methodology
3.2.1. Preparing the Sample
3.2.2. Initiating Frac-n-Flow Testing under Hydrostatic Pressure
3.2.3. Performing Frac-n-Flow Test under Non-Hydrostatic Pressure
3.2.4. Testing Control and Data Processing
- k—permeability, milli-Darcy;
- Q—injection rate, cm3/s, (1 cm3/s = 1 mL/s);
- ΔP—differential pressure across the rock sample, atm, (1 atm = 14.7 psi);
- μ—viscosity, cp, (μDI water ≈ 1 cp at the testing conditions in this paper);
- A—Cross-section area of rock sample, cm2, (2.54 cm = 1 in); and
- L—Length of rock sample, cm, (2.54 cm = 1 in).
4. Testing Results
4.1. Indiana Limestone Geology and Basic Petrophysical Properties
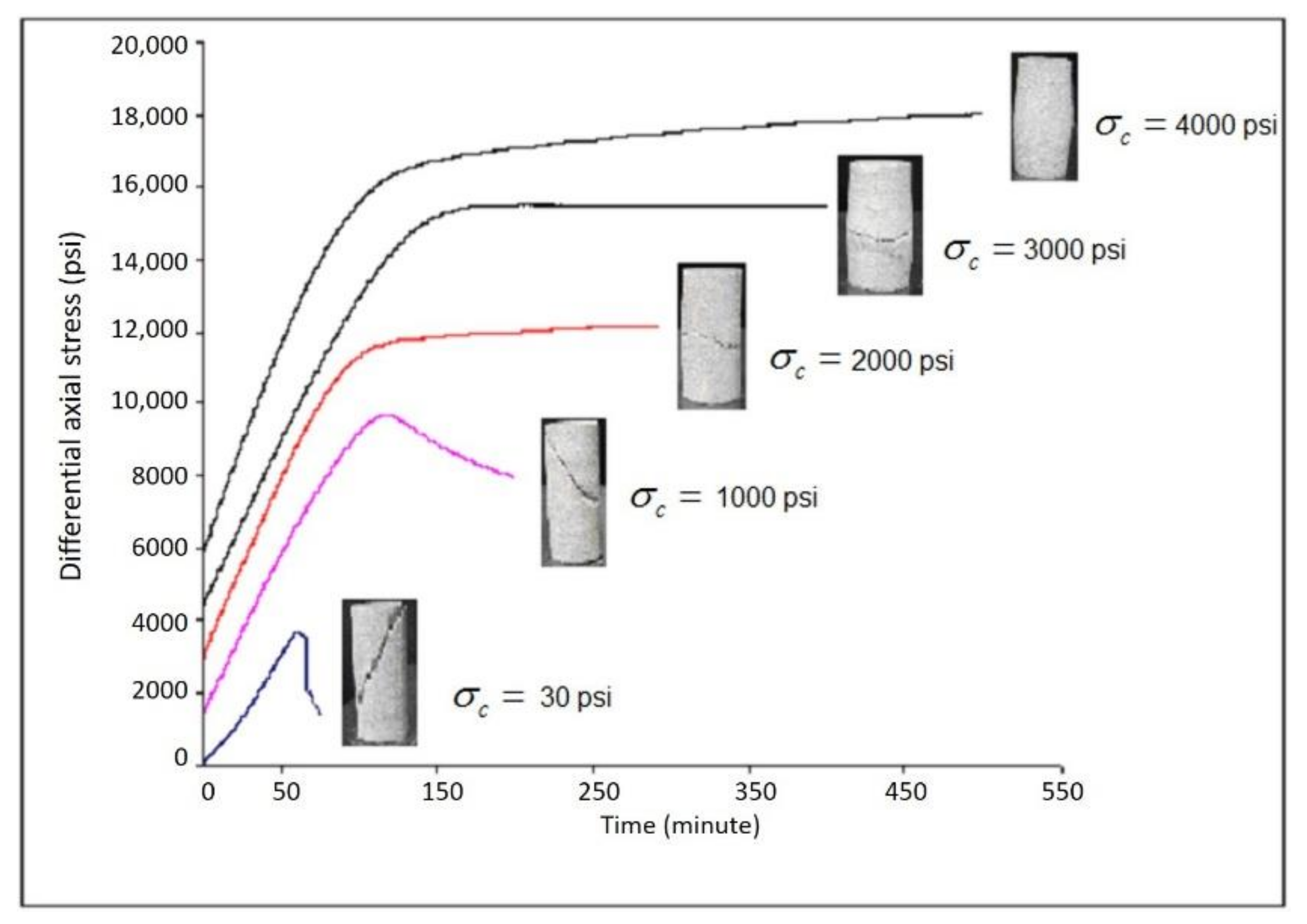
4.2. Failure Mode Impact on Post-Failure Axial Stress and Induced Fractures
- (1)
- When the confining pressure was low (σc ≤ 100 psi), the post-failure axial stress fell sharply. The sample experienced a sudden loss of strength. The rock fractured in a brittle mode. A single, straight, near vertical fracture was induced;
- (2)
- When the confining pressure was low to intermediate (σc = 1000 psi), the post-failure axial stress fell gradually. The rock experienced a gradual loss of strength. The rock fractured in a semi-brittle mode. A single, straight, near vertical fracture was induced, with a flattened toe;
- (3)
- When the confining pressure was intermediate to high (σc = 2000–3000 psi), there was no obvious peak or sign of failure in axial stress. The “post-failure” axial stress stayed almost constant or only slightly changed. The rock fails in a semi-ductile mode. A single, near horizontal fracture, i.e., almost perpendicular to the overburden– the maximum stress, was formed; and
- (4)
- When the confining pressure was extremely high (σc = 4000 psi), there was no peak or sign of failure in axial stress. Instead, the “post-failure” axial stress continued increasing, slightly but steadily. The rock experienced a ductile mode of failure. No obvious single fracture was formed. Instead, two sets of conjugating “fracture” networks were formed, with an obtuse angle (i.e., larger than 90°) facing to overburden stress.
4.3. Failure Mode Impact on Permeability Change
- (1)
- When the fracture was created in brittle mode, the permeability continuously improved during the fracturing process (Figure 6a). Accompanying the sudden loss of rock strength, the matrix permeability/fracture conductivity jumped up rapidly. As the fracturing process continued in the post-failure phase, fracture conductivity continued to be enhanced;
- (2)
- When the fracturing was semi-brittle, the matrix permeability significantly increased at the failure. However the total improvement was not as significant as when the sample failed in brittle mode because the matrix permeability experienced a bigger decrease at the initial phase of compression (Figure 6b);
- (3)
- When the fracturing process was semi-ductile, the matrix permeability decreased monotonically, except for small ripples at the failing moments (Figure 6c–e). In these three cases, obvious decreases in axial stress are observed in a short period of time during the failure phase. With the exception of Case C (Figure 6c), which had a small up-ripple in fracture conductivity at the failing phase, the overall impact was that fracture conductivity continued the reduction tendency of matrix permeability and experienced monotonic decline; and
- (4)
- When the rock failed in ductile mode, the matrix permeability decreased exponentially (Figure 6f). In this case, the matrix permeability was completely damaged to zero.
4.4. Frac-n-Flow Test-Based Folds of Increase in Matrix Permeability
- FOIt—test-based FOI in permeability induced by fracturing of the rock sample;
- Initial Permeability—rock matrix permeability at the beginning; and
- Post Frac Permeability—permeability after the rock is fractured or failed.
- (1)
- When the rock sample was fractured in brittle mode, its matrix permeability significantly improved. For instance, in Test 10IL08 (Figure 6a) the matrix permeability increased 13 times post fracturing, or 1300%;
- (2)
- When the rock sample was fractured in semi-brittle mode, its matrix permeability only slightly improved. For instance, in Test 09IL06 (Figure 6b) the matrix permeability increased by 0.08 time or 8% from intact matrix to post-fracture;
- (3)
- When the rock sample was fractured in semi-ductile mode, its matrix permeability was damaged to different degrees, instead of being improved. For instance, matrix permeability of Tests 08IL92, 08IL95 and 08IL12 (Figure 6c–e) decreased by 0.39, 0.59 and 0.71 time, i.e., 39%, 59% and 71%, respectively; and
- (4)
- When the rock sample failed in ductile mode, its matrix permeability was damaged completely. For instance, matrix permeability of Tests 08IL11 (Figure 6f) decreased 1.0 time, i.e., 100% lost.
5. Discussion
5.1. Brittle-Ductile Behavior under 3D Compression vs. 3D Extension
5.2. Estimation of the Stress Shadow Effect
5.2.1. Analytical Solution for the Stress Shadow Effect
5.2.2. Field Observation of Altered Minimum Horizontal Stress
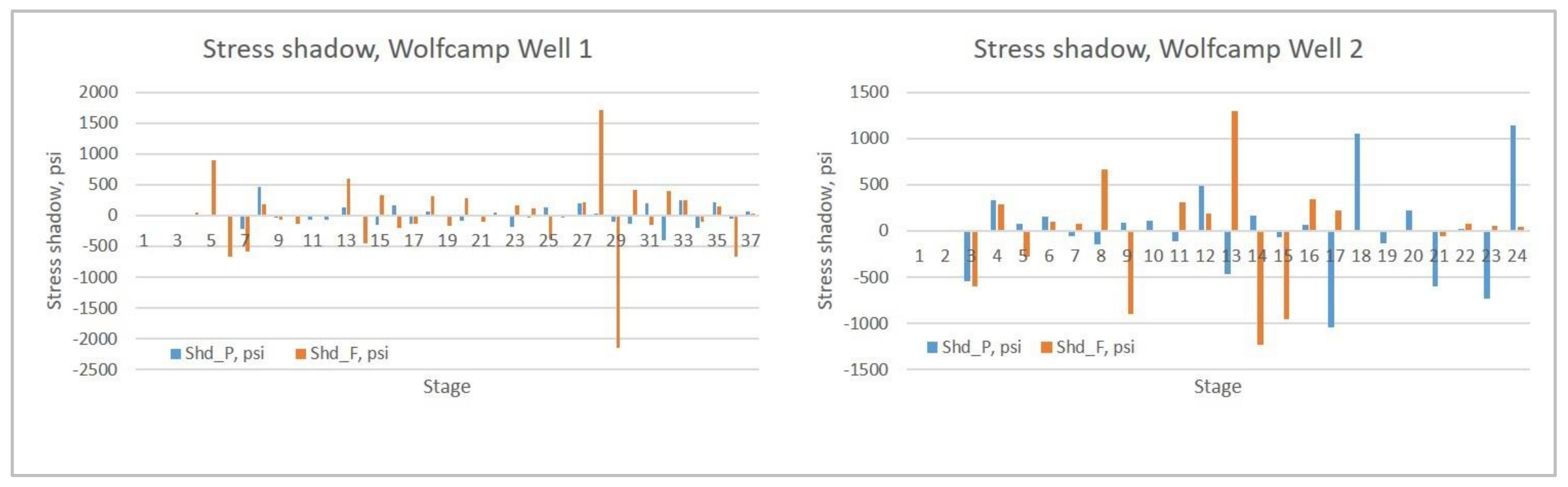
5.2.3. Case Study: Stress Shadows from Two Wolfcamp Wells
- (1)
- Pad phase stress shadows varied from a minimum of −398 psi (stress release) to a maximum of +460 psi (stress increase);
- (2)
- Flush phase stress shadows varied from −2149 psi (stress release) to 1716 psi (stress increase);
- (3)
- The average stress shadows of all stages was 0.89 psi in the pad phase, and 1.36 psi in the flush phase, meaning the overall stress shadow is well constrained within the horizontal section;
- (4)
- The median stress shadow of all stages was −9 psi in the pad phase, and −19 psi in the flush phase. These relatively small values, compared to the maximum and minimum shadows, were consistent with the near-zero average; and
- (5)
- Statistics of stress shadows in Well 2 show similar characteristics as seen in Well 1, except a wider range in the pad phase (−1045 psi to +1141 psi) and a narrower range in the flush phase (−1233 psi to +1297 psi).
5.3. Frac-n-Flow Test-Based FOIt vs. Field-Based FOI
- s—skin factor of the well pre-fracture;
- re—well drainage or reservoir radius,
- rw—normal wellbore radius,
- —equivalent wellbore radius post-fracture, defined in Equation (5) as below,where
- xf—half length of the fracture, as shown in Figure 10.
- (1)
- They were defined for different purposes. Field-based FOI was mainly used to guide the selection of fracture length based on pre-fracture well characterization results [62]. Test-based FOI is defined to quantify how much is the matrix permeability improvement at post-fracture, serving as an indicator for improvement of pad-injection fracture;
- (2)
- They were obtained in different ways. Field-based FOI was pre-determined based on the economic model for the success of HF treatment [9]. Test-based FOI is experimentally measured; and
- (3)
- They have different ranges of value. Field-based FOI was in general positive, and has a bigger magnitude in tight formation (e.g., 10+) than in medium permeable rocks (e.g., ~2) [80]. In contrast, test-based FOI is positive for brittle and semi-brittle fracturing, and negative for ductile failure.
5.4. Impact of Pore Pressure and Reservoir Temperature
5.5. Samples, Tests and Future Work
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclatures
| 2-D | two dimension(al) |
| 3-D | three dimension(al) |
| BPR | back pressure regulator |
| DFIT | diagnostic fracture injection test |
| DOE | Department of Energy (US) |
| FOI | folds of increase |
| FOIt | test-based folds of increase |
| frac-n-flow | fracturing-and-flowing |
| HD | horizontal drilling (drilled) |
| HDMHF | horizontal drilling and multistage hydraulic fracturing |
| HF | hydraulic fracturing |
| ID | inner diameter |
| ISIP ISIPF, ISIPFlush ISIPP, ISIPPad | instantaneous shut-in pressure instantaneous shut-in pressure at flush injection phase, psi instantaneous shut-in pressure at pad injection phase, psi |
| ISRM N, n | International Society for Rock Mechanics number of stage |
| OD Ph | outside diameter hydrostatic pressure, psi |
| plug-n-perf Pp | plug and perforation pore pressure, psi |
| R&D re rw rw′ s shd | research and development reservoir radius (well drainage), ft normal wellbore radius, ft equivalent post-fracture wellbore radius, ft skin factor stress shadow, psi |
| SPE | Society of Petroleum Engineers |
| Spf | shots per foot (holes per foot) |
| Std Dev. | Standard Deviation |
| TVD | true vertical depth |
| USSR σ′1 σ′3 σ′3min | the Union of Soviet Socialist Republics axial effective stress, psi radial effective stress, psi minimum confining pressure to seal the sleeve, psi |
Appendix A. Calculation of Injection Rate for Axial Loading Pump
| Item | Formula | Value | Unit |
|---|---|---|---|
| Axial strain rate 1, εa1 | Given | 1.0 × 10−4 | 1/s |
| Axial strain rate 2, εa2 | Given | 1.0 × 10−6 | 1/s |
| Sample length, L | Given | 2.000 | in |
| Sample diameter, D | Given | 1.000 | in |
| Axial pressure chamber OD, OD | Given | 3.500 | in |
| Axial pressure chamber ID, ID | Given | 2.375 | in |
| Axal chamber loading area, A | 1/4 × 3.14 × (OD2−ID2) | 5.188 | in2 |
| Sample axial deform rate 1, La1 | L × εa1 | 2.000 × 10−4 | in/s |
| Sample axial deform rate 2, La2 | L × εa2 | 2.000 × 10−6 | in/s |
| Axial injection rate 1, Q1 | A × La1 | 1.038 × 10−3 | in3/s |
| Axial injection rate 2, Q2 | A × La2 | 1.038 × 10−5 | in3/s |
| Axial inj. rate 1 in mL/min, Q1_mL/min | 2.543 × Q1 × 60 | 1.020 | mL/min |
| Axial inj. rate 2 in mL/min, Q2_mL/min | 2.543 × Q2 × 60 | 0.010 | mL/min |
References
- EIA. Review of Emerging Resources—US Shale Gas and Shale Oil Plays; Energy Information Administration (EIA): Washington, DC, USA, 2011; pp. 1–105.
- NETL. Shale Gas: Applying Technology to Solve America’s Energy Challenges; National Energy Tech. Lab. (NETL): Morgantown, WV, USA, 2011; pp. 1–8.
- Ma, Y.Z. Unconventional resources from exploration to production. In Unconventional Oil and Gas Resources Handbook; Ma, Y.Z., Holditch, S.A., Eds.; Gulf Professional Publishing: Waltham, MA, USA, 2016; pp. 3–52. [Google Scholar]
- Price, L.C.; LeFever, J. Dysfunctionalism in the Williston Basin: The Bakken/mid-Madison petroleum system. Bull. Can. Pet. Geol. 1994, 42, 187–218. [Google Scholar]
- Schrider, L.A.; Wise, R.L. Potential new sources of natural gas. J. Pet. Technol. 1980, 32, 703–716. [Google Scholar]
- Smith, M.B.; Montgomery, C.T. Hydraulic Fracturing; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–31. [Google Scholar]
- King, G.E. Thirty years of gas fracturing: What have we learned? In Proceedings of the SPE Annual Technical Conference and Exhibition, Paper SPE33456. Florence, Italy, 19–22 September 2010. [Google Scholar]
- Howard, G.C.; Fast, C.R. Hydraulic Fracturing; SPE: Richardson, TX, USA, 1970; pp. 1–10. [Google Scholar]
- Economides, M.J.; Nolte, K.G. Reservoir Stimulation, 3rd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2000; pp. 29–473. [Google Scholar]
- Veatch, R.W.; King, G.E.; Holditch, S.A. Essentials of Hydraulic Fracturing: Vertical and Horizontal Wellbores; PennWell Corporation: Tulsa, OK, USA, 2017; pp. 7–714. [Google Scholar]
- Veatch, R.W., Jr.; Moschovidis, Z.A.; Fast, C.R. An overview of hydraulic fracturing. In Recent Advances in Hydraulic Fracturing; Gidley, J.L., Holditch, S.A., Nierode, D.E., Veatch, R.W., Jr., Eds.; Society of Petroleum Engineers: Richardson, TX, USA, 1990; pp. 1–38. [Google Scholar]
- Pendleton, L.E. Horizontal drilling review. In Proceedings of the Archie Conference on Reservoir Definition and Description, Paper SPE23535. Houston, TX, USA, 3–6 November 1991. [Google Scholar]
- Reiss, L.H. Production from horizontal wells after 5 years. J. Pet. Technol. 1987, 39, 1411–1416. [Google Scholar]
- Joshi, S.D. A review of horizontal well and drain-hole technology. In Proceedings of the 62nd SPE Annual Technical Conference and Exhibition, Paper SPE16868. Dallas, TX, USA, 27–30 September 1987. [Google Scholar]
- Chen, D. Directional Drilling. In Petroleum Engineering Handbook; Mitchell, R.F., Ed.; Society of Petroleum Engineers: Richardson, TX, USA, 2006; Volume II, pp. 264–286. [Google Scholar]
- Strubhar, M.K.; Fitch, J.L.; Glenn, E.E., Jr. Multiple, vertical fractures from an inclined wellbore—A field experiment. J. Pet. Technol. 1975, 27, 641–647. [Google Scholar]
- Roegiers, J.C.; Detoumay, E. Considerations on failure initiation in inclined boreholes. In Proceedings of the The 29th U.S. Symposium on Rock Mechanics (USRMS), Paper ARMA 88-0461. Minneapolis, MN, USA, 13–15 June 1988. [Google Scholar]
- Zeng, Z. Imaging Hydraulic Fracturing: Analytical Solution, Numerical Modeling and Lab Testing; VDM-Publishing: Saarbrücken, Germany, 2009; pp. 33–53. [Google Scholar]
- McLennan, J.D.; Roegiers, J.-C.; Economides, M.J. Extended reach and horizontal wells. In Reservoir Stimulation, Chapter 19, 2nd ed.; Economides, M.J., Nolte, K.G., Eds.; Schlumberger Educational Services: Houston, TX, USA, 1990. [Google Scholar]
- Gaswirth, S.B.; Marra, K.R.; Lillis, P.G.; Mercier, T.J.; Leathers-Miller, H.M.; Schenk, C.J.; Klett, T.R.; Le, P.A.; Tennyson, M.E.; Hawkins, S.J.; et al. Assessment of Undiscovered Continuous Oil Resources in the Wolfcamp shale of the Midland Basin, Permian Basin Province, Texas, 2016; Fact Sheet 2016–3092; U.S. Geological Survey: Reston, VA, USA, 2016; p. 4. [CrossRef] [Green Version]
- Gaswirth, S.B.; French, K.L.; Pitman, J.K.; Marra, K.R.; Mercier, T.J.; Leathers-Miller, H.M.; Schenk, C.J.; Tennyson, M.E.; Woodall, C.A.; Brownfield, M.E.; et al. Assessment of Undiscovered Continuous Oil and Gas Resources in the Wolfcamp Shale and Bone Spring Formation of the Delaware Basin, Permian Basin Province, New Mexico and Texas; Fact Sheet 2018–3073; U.S. Geological Survey: Reston, VA, USA, 2018; p. 4. [CrossRef]
- Zeng, Z.; Harouaka, A. A new method for assessing stage-based hydraulic fracturing quality in Wolfcamp formation of Permian Basin. J. Pet. Sci. Eng. 2020, 195, 107740. [Google Scholar] [CrossRef]
- Nicolas, A.; Fortin, J.; Regnet, J.B.; Dimanov, A.; Guéguen, Y. Brittle and semi-brittle behaviors of a carbonate rock: Influence of water and temperature. Geophys. J. Int. 2016, 206, 438–456. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Shah, S.N.; Roegiers, J.-C.; Zhang, B. An integrated petrophysics and geomechanics approach for fracability evaluation in shale reservoirs. SPE J. 2015, 20, 518–526. [Google Scholar] [CrossRef]
- EIA. Trends in U.S. Oil and Natural Gas Upstream Costs; Energy Information Administration (EIA): Washington, DC, USA, 2016; pp. 1–141.
- Holguin, J.; Zeng, Z. Water Consumption Statistics in Fracking Wolfcamp Oil Fields in Permian Basin, Texas. In Proceedings of the 1st Permian Basin Water in Energy Conference, Midland, TX, USA, 20–23 February 2018. [Google Scholar]
- Harris, T. Long Game: Reliable, Interventionless Completions for Toe Stages. World Oil 2019, 204, 4. [Google Scholar]
- Olson, J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands. In Proceedings of the 42nd U.S. Rock Mechanics Symposium (USRMS), Paper ARMA 08-327. San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Olson, J.E.; Dahi-Taleghani, A. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, Paper SPE 119739. The Woodlands, TX, USA, 19–21 January 2009. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Investigation of the Impact of Fracture Spacing and Fluid Properties for Interfering Simultaneously or Sequentially Generated Hydraulic Fractures. SPE Prod. Oper. 2013, 28, 427–436. [Google Scholar] [CrossRef]
- Soliman, M.Y.; East, L.E.; Adams, D.L. Geomechanics aspects of multiple fracturing of horizontal and vertical wells. SPE Drill Compl. 2008, 23, 217–228. [Google Scholar]
- Min, K.S.; Zhang, Z.; Ghassemi, A. Numerical Analysis of Multiple Fracture Propagation In Heterogeneous Rock. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Paper ARMA 10-363. Salt Lake City, UT, USA, 27–30 June 2010; pp. 5–27. [Google Scholar]
- Weng, X.; Kresse, O.; Cohen, C.; Wu, R.; Gu, H. Modeling of Hydraulic-Fracture-Network Propagation in a Naturally Fractured Formation. SPE Prod. Oper. 2011, 26, 368–380. [Google Scholar] [CrossRef]
- Roussel, N.P.; Sharma, M.M. Optimizing Fracture Spacing and Sequencing in Horizontal-Well Fracturing. SPE Prod. Oper. 2011, 26, 173–184. [Google Scholar] [CrossRef]
- Roussel, N.P.; Sharma, M.M. Strategies to Minimize Frac Spacing and Stimulate Natural Fractures in Horizontal Completions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Paper SPE 146104. Denver, CO, USA, 30 October–2 November 2011. [Google Scholar] [CrossRef]
- Roussel, N.P. Analyzing ISIP Stage-by-Stage Escalation to Determine Fracture Height and Horizontal-Stress Anisotropy. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Paper SPE 184865. The Woodlands, TX, USA, 24–26 January 2017. [Google Scholar] [CrossRef]
- Cheng, Y. Impacts of the Number of Perforation Clusters and Cluster Spacing on Production Performance of Horizontal Shale-Gas Wells. SPE Reserv. Eval. Eng. 2012, 15, 31–40. [Google Scholar] [CrossRef]
- Wong, S.-W.; Geilikman, M.; Xu, G. The Geomechanical Interaction of Multiple Hydraulic Fractures in Horizontal Wells. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013; pp. 661–677. [Google Scholar]
- Nagel, N.B.; Zhang, F.; Sanchez-Nagel, M.; Lee, B.; Agharazi, A. Stress Shadow Evaluations for Completion Design in Unconventional Plays. In Proceedings of the SPE Unconventional Resources Conference Canada, Paper SPE 167128. Calgary, AB, Canada, 5–7 November 2013. [Google Scholar] [CrossRef]
- Nagel, N.B.; Gokaraju, D.; Mitra, A.; Sanchez-Nagel, M.A. Consideration of Stress Shadows in Stacked Plays. In Proceedings of the 51st U.S. Rock Mechanics/Geomechanics Symposium, Paper ARMA 17-884. San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Dohmen, T.; Zhang, J.; Blangy, J. Measurement and Analysis of 3D Stress Shadowing Related to the Spacing of Hydraulic Fracturing in Unconventional Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Paper SPE 170924. Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar] [CrossRef]
- Daneshy, A. Fracture shadowing: Theory, applications and implications. In Proceedings of the SPE Annual Technical Conference and Exhibition, Paper SPE 170611. Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R.W. Fundamentals of Rock Mechanics, 4th ed.; Blackwell Publishing: Malden, MA, USA, 2007; pp. 81–89. [Google Scholar]
- Terzaghi, K. Stress conditions for the failure of saturate concrete and rock. ASTM Proc. 1945, 45, 777–792. [Google Scholar]
- Griggs, D.; Handin, J. Observations on fracture and a hypothesis of earthquakes. In Rock Deformation; Memoir, G.S.A., Griggs, D., Handin, J., Eds.; Geological Society of America: Boulder, CO, USA, 1960; Volume 79, pp. 347–373. [Google Scholar] [CrossRef] [Green Version]
- Hudson, J.A.; Harrison, J.A. Engineering Rock Mechanics; Elsevier-Pergamon: Oxford, UK, 1997; pp. 95–112. [Google Scholar]
- Vutukuri, V.S.; Lama, R.D.; Saluja, S.S. Handbook on Mechanical Properties of Rocks; Trans Technology Publications: Clausthal, Germany, 1974; Volume I, pp. 216–219. [Google Scholar]
- Roegiers, J.-C. Elements of rock mechanics. In Reservoir Stimulation, Chapter 2, 2nd ed.; Economides, M.J., Nolte, K.G., Eds.; Schlumberger Educational Services: Houston, TX, USA, 1990. [Google Scholar]
- Harouaka, A.S.; Mtawea, B.; Al-Majed, A.; Abdulraheem, A.; Klimentos, T. Multistage triaxial testing of actual reservoir cores under simulated reservoir conditions. In Proceedings of the International Symposium of the Society of Core Analysts, Paper SCA9528. San Francisco, CA, USA, 12–14 September 1995. [Google Scholar]
- Klimentos, T.; Harouaka, A.S.; Mtawaa, B.; Saner, S. Experimental determination of the Biot elastic constant: Applications in formation evaluation (Sonic porosity, rock strength, earth stresses, and sanding predictions). SPE Reserv. Eval. Eng. 1998, 1, 57–63. [Google Scholar] [CrossRef]
- Fjar, E.; Holt, R.M.; Raaen, A.M.; Horsrud, P.; Risnes, R. Petroleum Related Rock Mechanics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 55–433. [Google Scholar]
- Wong, T.-F.; Baud, P. The brittle-ductile transition in porous rock: A review. J Struct. Geol. 2012, 44, 25–53. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Mechanisms of simultaneous hydraulic-fracture propagation from multiple perforation clusters in horizontal wells. SPE J. 2016, 21, 1000–1008. [Google Scholar] [CrossRef]
- Taghichian, A.; Zaman, M.; Devegowda, D. Stress shadow size and aperture of hydraulic fractures in unconventional shales. J. Petrol. Sci. Eng. 2014, 124, 209–221. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Branagan, P.T. Altered-stress fracturing. J. Pet. Technol. 1989, 41, 990–997. [Google Scholar] [CrossRef]
- Tiab, D.; Donaldson, E.C. Petrophysics, 4th ed.; Elsevier-Gulf Professional Publishing: Waltham, MA, USA, 2014; pp. 775–846. [Google Scholar]
- Zhang, J.; Kamenov, A.; Zhu, D.; Hill, A.D. Laboratory measurement of hydraulic-fracture conductivities in the Barnett shale. SPE Prod. Oper. 2014, 29, 216–227. [Google Scholar] [CrossRef]
- Smith, M.B.; Shlyapobersky, J.W. Basics of hydraulic fracturing. In Reservoir Stimulation, Chapter 5, 3rd ed.; Economides, M.J., Nolte, K.G., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2000. [Google Scholar]
- Zeng, Z.; Harouaka, A. A single core test for fracability, breakdown pressure and fracture conductivity. In Proceedings of the Unconventional Resources Technology Conference (URTeC), Paper URTeC2697595. Austin, TX, USA, 24–26 July 2017. [Google Scholar] [CrossRef]
- Zeng, Z.; Jakupi, A.; Bigelow, T.; Kringstad, J.; Belobraydic, M.; Zhou, X.; Grigg, R.B. Laboratory observation of CO2 phase transition induced seismic velocity change. In Proceedings of the 42nd US Rock Mechanics Symposium (USRMS), Paper ARMA 08-329. San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Dudley, J.W.; Brignoli, M.; Crawford, B.R.; Ewy, R.T.; Love, D.K.; McLennan, J.D.; Ramos, G.G.; Shafer, J.L.; Sharf-Aldin, M.H.; Siebrits, E.; et al. Suggested method for uniaxial-strain compressibility testing for reservoir geomechanics. Rock Mech. Rock Eng. 2016, 49, 4153–4178. [Google Scholar] [CrossRef]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Kovari, K.; Tisa, A.; Einstein, H.H.; Franklin, J.A. Suggested Methods for Determining the Strength of Rock Materials in Triaxial Compression: Revised Version (ISRM: Suggested Methods for Triaxial Compression Testing). Int. J. Rock Mech. Min. Sci. Geomech. Abs 1983, 20, 285–290. [Google Scholar]
- Grigg, R.B. Improving CO2 Efficiency for Recovering Oil in Heterogeneous Reservoirs; Technical Report; US Department of Energy: Washington, DC, USA, 2003; pp. 101–178. [CrossRef] [Green Version]
- Ling, K.; Zeng, Z. Geomechanical Study of Bakken Formation for Improved Oil Recovery; Technical Report; US Department of Energy: Washington, DC, USA, 2013; pp. 104–211. [CrossRef]
- Zhou, X.; Zeng, Z.; Liu, H. Laboratory testing on Pierre shale for CO2 sequestration under clayey caprock. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Paper ARMA10-107. Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Lockner, D.; Byerlee, J.; Kuksenko, V.; Ponomarev, A.; Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature 1991, 350, 39–42. [Google Scholar] [CrossRef]
- Bass, D.M., Jr. Properties of Reservoir Rocks. In Petroleum Engineering Handbook; Chapter 26; Bradley, H.B., Ed.; Society of Petroleum Engineers: Richardson, TX, USA, 1987; Volume 26, pp. 14–18. [Google Scholar]
- ILIA. Indiana Limestone Handbook, 22nd ed.; Institute of America (ILIA): Bedford, Indiana, USA, 2007; pp. 3–12. [Google Scholar]
- Lockner, D. The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Min. Sci. Geomech. Abst. 1993, 30, 883–899. [Google Scholar] [CrossRef]
- Warpinski, N.R. Hydraulic fracturing in tight, fissured media. J. Pet. Technol. 1991, 43, 146–209. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solid. Philos. Trans. R. Soc. Lond. Ser. A 1921, 221, 582–593. [Google Scholar]
- Sneddon, I.N. The distribution of stress in the neighborhood of a crack in an elastic solid. Proc. R. Soc. Lond. Ser. A 1946, 187, 229–260. [Google Scholar]
- Amadei, B.; Stephansson, O. Rock Stress and Its Measurement; Chapman & Hall: London, UK, 1997; pp. 95–325. [Google Scholar]
- Maleki, S.; Moradzadeh, A.; Riabi, R.G.; Sadaghzadeh, F. Comparison of several different methods of in-situ stress determination. Int. J. Rock Mech. Min. Sci. 2014, 71, 395–404. [Google Scholar] [CrossRef]
- Kim, H.; Xie, L.; Min, K.-B.; Bae, S.; Stephansson, O. Integrated in-situ stress estimation by hydraulic fracturing, borehole observations and numerical analysis at the EXP-1 Borehole in Pohang, Korea. Rock Mech. Rock Eng. 2017, 50, 3141–3155. [Google Scholar] [CrossRef]
- Soliman, M.Y.; Kabir, C.S. Testing unconventional formations. J. Pet. Sci. Eng. 2012, 92/93, 102–109. [Google Scholar] [CrossRef]
- Haimson, B.C.; Cornet, F.H. ISRM suggested methods for rock stress estimation- Part 3: Hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF). Int. J. Rock Mech. Min. Sci. 2003, 40, 1011–1020. [Google Scholar] [CrossRef]
- Belyadi, H.; Fathi, E.; Belyadi, F. Hydraulic Fracturing in Unconventional Reservoirs; Gulf Professional Publishing Books-Elsevier: Cambridge, MA, USA, 2017; pp. 121–141. [Google Scholar]
- Smith, M.B.; Hannah, R.R. High-permeability fracturing: The evolution of a technology. J. Pet. Technol. 1996, 48, 628–633. [Google Scholar] [CrossRef]
- Noël, C.; Passelègue, F.X.; Violay, M. Brittle faulting of ductile rock induced by pore fluid pressure build-up. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021331. [Google Scholar] [CrossRef]
- Paterson, M.S.; Wong, T.-F. Experimental Rock Deformation—The Brittle Field, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 5–237. [Google Scholar]
- Castagna, A.; Ougier-Simonin, A.; Benson, P.M.; Browning, J.; Walker, R.J.; Fazio, M.; Vinciguerra, S. Thermal damage and pore pressure effects of the brittle-ductile transition in Comiso limestone. J Geophy. Res. Solid Earth 2018, 123, 7644–7660. [Google Scholar] [CrossRef]
- PETEX. Fundamentals of Petroleum; The University of Texas at Austin Petroleum Extension (PETEX): Austin, TX, USA, 2011; pp. 25–29. [Google Scholar]
- Zoback, M.; Kohli, A. Unconventional Reservoir Geomechanics: Shale Gas, Tight Oil, and Induced Seismicity; Cambridge University Press: Cambridge, UK, 2019; pp. 181–262. [Google Scholar] [CrossRef]



| Sample | Bulk Density | Saturated Density | Dry Density | Porosity |
|---|---|---|---|---|
| g/cm3 | g/cm3 | g/cm3 | % | |
| ILA0407 | 2.620 | 2.370 | 2.210 | 16.000 |
| ILA1107 | 2.610 | 2.370 | 2.220 | 15.000 |
| ILA1007 | 2.610 | 2.390 | 2.250 | 14.000 |
| ILA0207 | 2.620 | 2.400 | 2.260 | 14.000 |
| ILA0607 | 2.610 | 2.370 | 2.220 | 15.000 |
| ILA0107 | 2.590 | 2.360 | 2.220 | 14.000 |
| ILA0307 | 2.610 | 2.370 | 2.220 | 15.000 |
| ILA0707 | 2.580 | 2.350 | 2.200 | 15.000 |
| ILA1207 | 2.640 | 2.410 | 2.270 | 14.000 |
| Average | 2.610 | 2.377 | 2.230 | 14.667 |
| Std. Dev. | 0.016 | 0.018 | 0.023 | 0.667 |
| Test | Figure 6 | Confin. Press. | Pore Press. | Fail Mode | Perm., mD | Test-Based Folds of Increase (FOIt) | Comments | |
|---|---|---|---|---|---|---|---|---|
| σc, psi | Pp, psi | Initial | Post Frac. | |||||
| 10IL08 | a | 100 | 14.5 | Brittle | 0.50 | 7.00 | 13.00 | Greatly improved |
| 09IL06 | b | 300 | 14.5 | Semi-brittle | 0.62 | 0.67 | 0.08 | Slightly improved |
| 08IL92 | c | 1500 | 14.5 | Semi-ductile | 3.96 | 2.41 | −0.39 | Slightly damaged |
| 08IL95 | d | 2200 | 14.5 | Semi-ductile | 6.43 | 2.61 | −0.59 | Damaged |
| 08IL12 | e | 3000 | 14.5 | Semi-ductile | 5.00 | 1.44 | −0.71 | Severely damaged |
| 08IL11 | f | 4000 | 14.5 | Ductile | 0.55 | 0.00 | −1.00 | Completely damaged |
| Stage | Well 1 | Well 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TVD | ISIPP | ISIPF | ShdP | ShdF | TVD | ISIPP | ISIPF | ShdP | ShdF | |
| ft | psi | psi | psi | psi | ft | psi | psi | psi | Psi | |
| 1 | 8269.89 | 3092 | 8280.44 | 2886 | ||||||
| 2 | 8269.77 | 3402 | 2624 | 8284.07 | 3502 | 2632 | ||||
| 3 | 8269.99 | 3393 | 2605 | −9 | −19 | 8285.53 | 2955 | 2027 | −547 | −605 |
| 4 | 8270.43 | 3410 | 2650 | 17 | 45 | 8288.46 | 3288 | 2319 | 333 | 292 |
| 5 | 8275.68 | 3406 | 3553 | −4 | 903 | 8286.72 | 3359 | 2040 | 71 | −279 |
| 6 | 8279.32 | 3397 | 2883 | −9 | −670 | 8286.81 | 3508 | 2140 | 149 | 100 |
| 7 | 8275.93 | 3179 | 2299 | −218 | −584 | 8276.11 | 3454 | 2214 | −54 | 74 |
| 8 | 8271.63 | 3639 | 2485 | 460 | 186 | 8272.31 | 3306 | 2881 | −148 | 667 |
| 9 | 8267.58 | 3609 | 2417 | −30 | −68 | 8274.33 | 3390 | 1986 | 84 | −895 |
| 10 | 8272.86 | 3589 | 2274 | −20 | −143 | 8280.19 | 3502 | 1995 | 112 | 9 |
| 11 | 8277.36 | 3521 | −68 | 8285.08 | 3392 | 2301 | −110 | 306 | ||
| 12 | 8275.36 | 3459 | 1888 | −62 | 8279.05 | 3884 | 2492 | 492 | 191 | |
| 13 | 8169.08 | 3589 | 2477 | 130 | 589 | 8278.59 | 3412 | 3789 | −472 | 1297 |
| 14 | 8265.03 | 3565 | 2024 | −24 | −453 | 8276.13 | 3578 | 2556 | 166 | −1233 |
| 15 | 8264.14 | 3419 | 2354 | −146 | 330 | 8275.53 | 3513 | 1598 | −65 | −958 |
| 16 | 8266.4 | 3576 | 2153 | 157 | −201 | 8278.97 | 3573 | 1941 | 60 | 343 |
| 17 | 8270.7 | 3446 | 2026 | −130 | −127 | 8277.49 | 2528 | 2159 | −1045 | 218 |
| 18 | 8269.38 | 3505 | 2338 | 59 | 312 | 8277.12 | 3578 | 1050 | ||
| 19 | 8277.41 | 3498 | 2165 | −7 | −173 | 8277.76 | 3444 | 2187 | −134 | |
| 20 | 8271.77 | 3416 | 2449 | −82 | 284 | 8279.25 | 3667 | 2201 | 223 | 14 |
| 21 | 8268.74 | 3437 | 2344 | 21 | −105 | 8276.41 | 3065 | 2150 | −602 | −51 |
| 22 | 8270.57 | 3481 | 2324 | 44 | −20 | 8267.22 | 3086 | 2230 | 21 | 80 |
| 23 | 8272.12 | 3298 | 2489 | −183 | 165 | 8264.39 | 2358 | 2286 | −728 | 56 |
| 24 | 8274.39 | 3270 | 2599 | −28 | 110 | 8260.57 | 3499 | 2329 | 1141 | 43 |
| 25 | 8275.21 | 3405 | 2217 | 135 | −382 | |||||
| 26 | 8277.1 | 3363 | 2195 | −42 | −22 | |||||
| 27 | 8278.24 | 3555 | 2415 | 192 | 220 | |||||
| 28 | 8275.77 | 3593 | 4131 | 38 | 1716 | |||||
| 29 | 8266.94 | 3498 | 1982 | −95 | −2149 | |||||
| 30 | 8266.32 | 3358 | 2389 | −140 | 407 | |||||
| 31 | 8269.28 | 3555 | 2238 | 197 | −151 | |||||
| 32 | 8275.38 | 3157 | 2634 | −398 | 396 | |||||
| 33 | 8270.46 | 3403 | 2880 | 246 | 246 | |||||
| 34 | 8268.23 | 3194 | 2784 | −209 | −96 | |||||
| 35 | 8270.86 | 3416 | 2924 | 222 | 140 | |||||
| 36 | 8282.04 | 3365 | 2255 | −51 | −669 | |||||
| 37 | 8289.01 | 3433 | 2283 | 68 | 28 | |||||
| Max | 460 | 1716 | 1141 | 1297 | ||||||
| Min | −398 | −2149 | −1045 | −1233 | ||||||
| Average | 0.89 | 1.36 | −0.14 | −16.55 | ||||||
| Median | −9 | −19 | 40.5 | 65 | ||||||
| Std Dev. | 155 | 585 | 498 | 557 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z. Frac-n-Flow Testing to Screen Brittle Fracture Stages in Wolfcamp Formation, Permian Basin, USA. Energies 2021, 14, 5450. https://doi.org/10.3390/en14175450
Zeng Z. Frac-n-Flow Testing to Screen Brittle Fracture Stages in Wolfcamp Formation, Permian Basin, USA. Energies. 2021; 14(17):5450. https://doi.org/10.3390/en14175450
Chicago/Turabian StyleZeng, Zhengwen. 2021. "Frac-n-Flow Testing to Screen Brittle Fracture Stages in Wolfcamp Formation, Permian Basin, USA" Energies 14, no. 17: 5450. https://doi.org/10.3390/en14175450
APA StyleZeng, Z. (2021). Frac-n-Flow Testing to Screen Brittle Fracture Stages in Wolfcamp Formation, Permian Basin, USA. Energies, 14(17), 5450. https://doi.org/10.3390/en14175450





