Simulation of Hydrogen-Air-Diluents Mixture Combustion in an Acceleration Tube with FlameFoam Solver
Abstract
:1. Introduction
2. Methodology
2.1. FlameFoam Solver
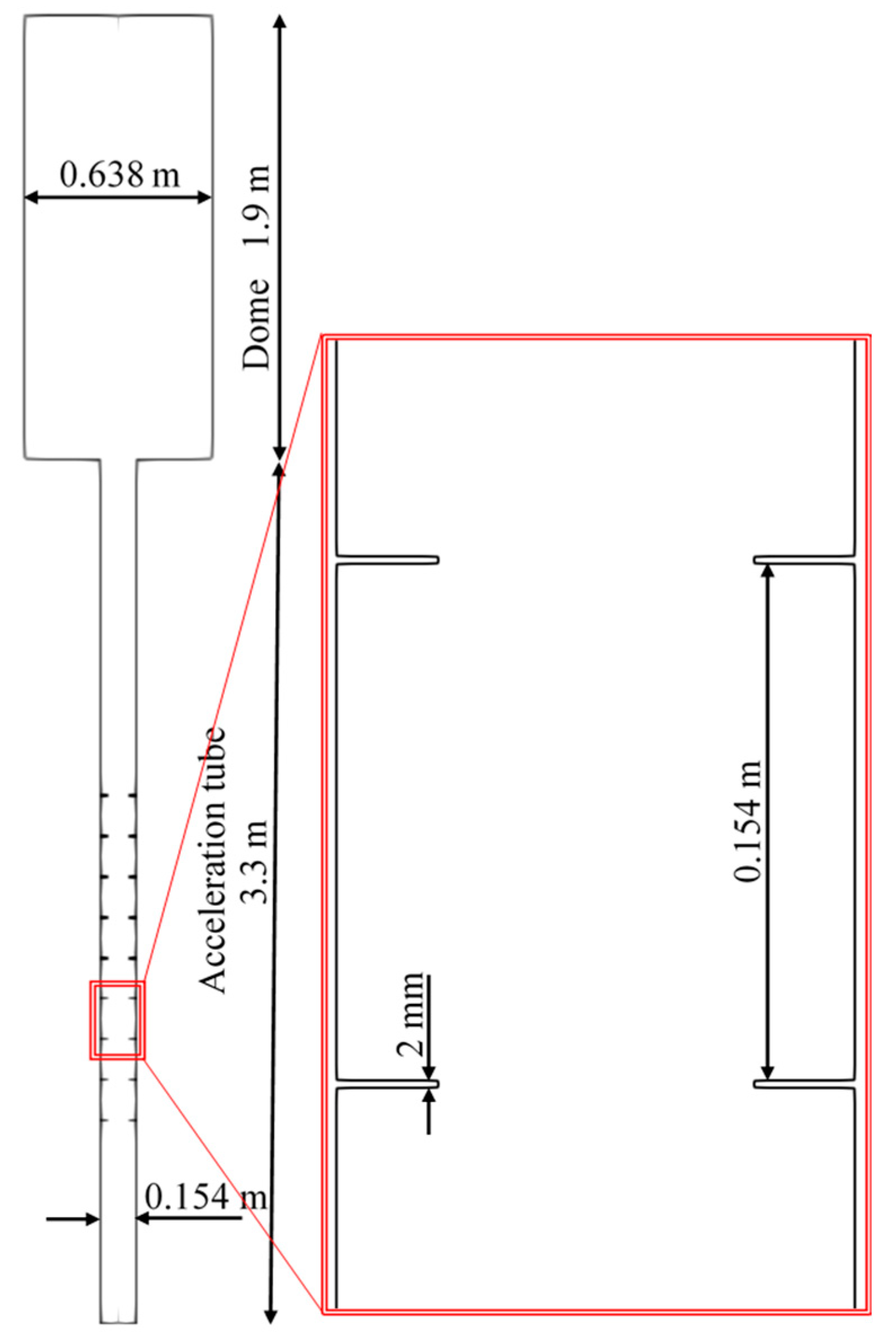
2.2. The ENACCEF Facility
2.3. Initial and Boundary Conditions
3. Results and Discussion
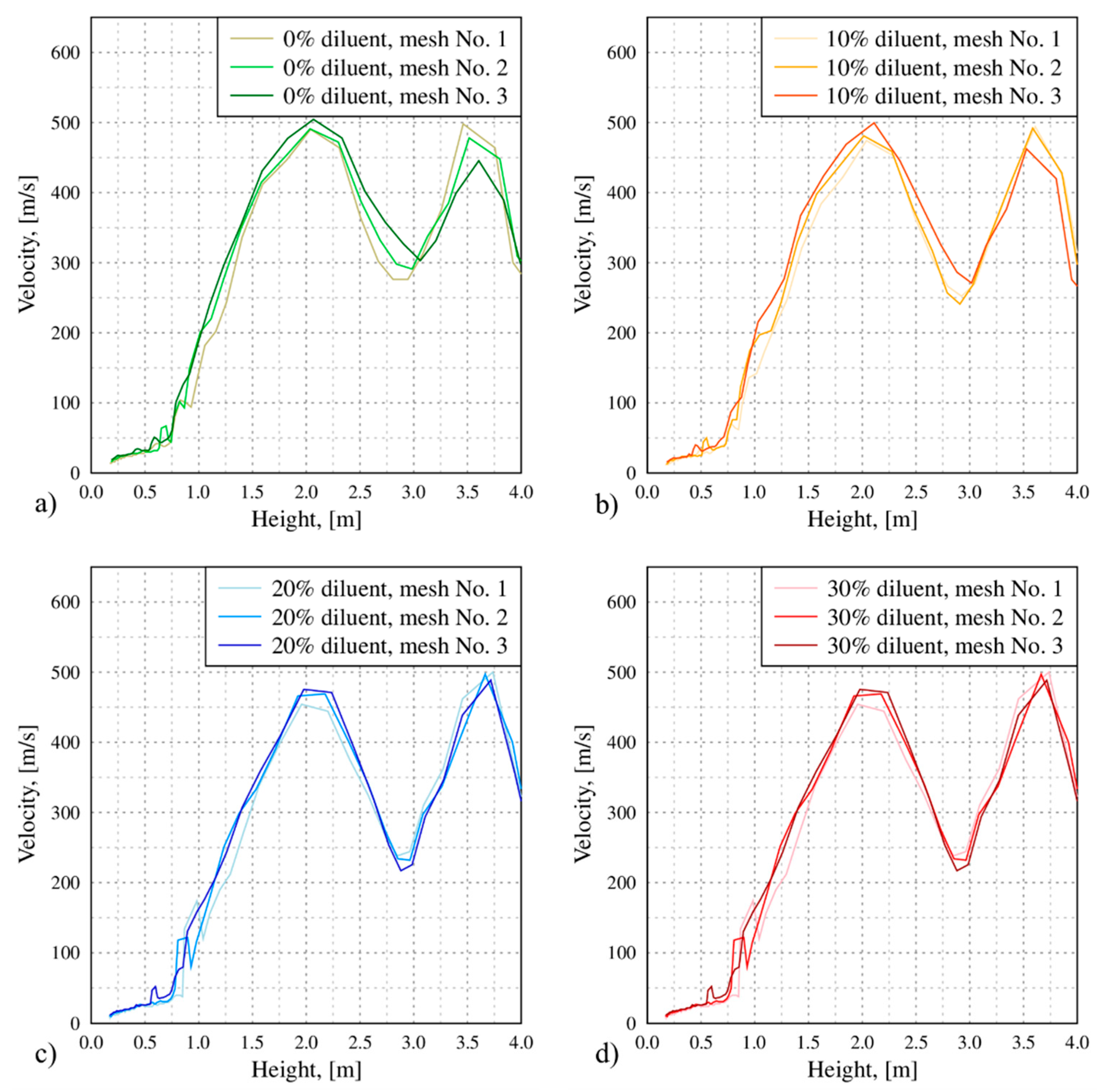
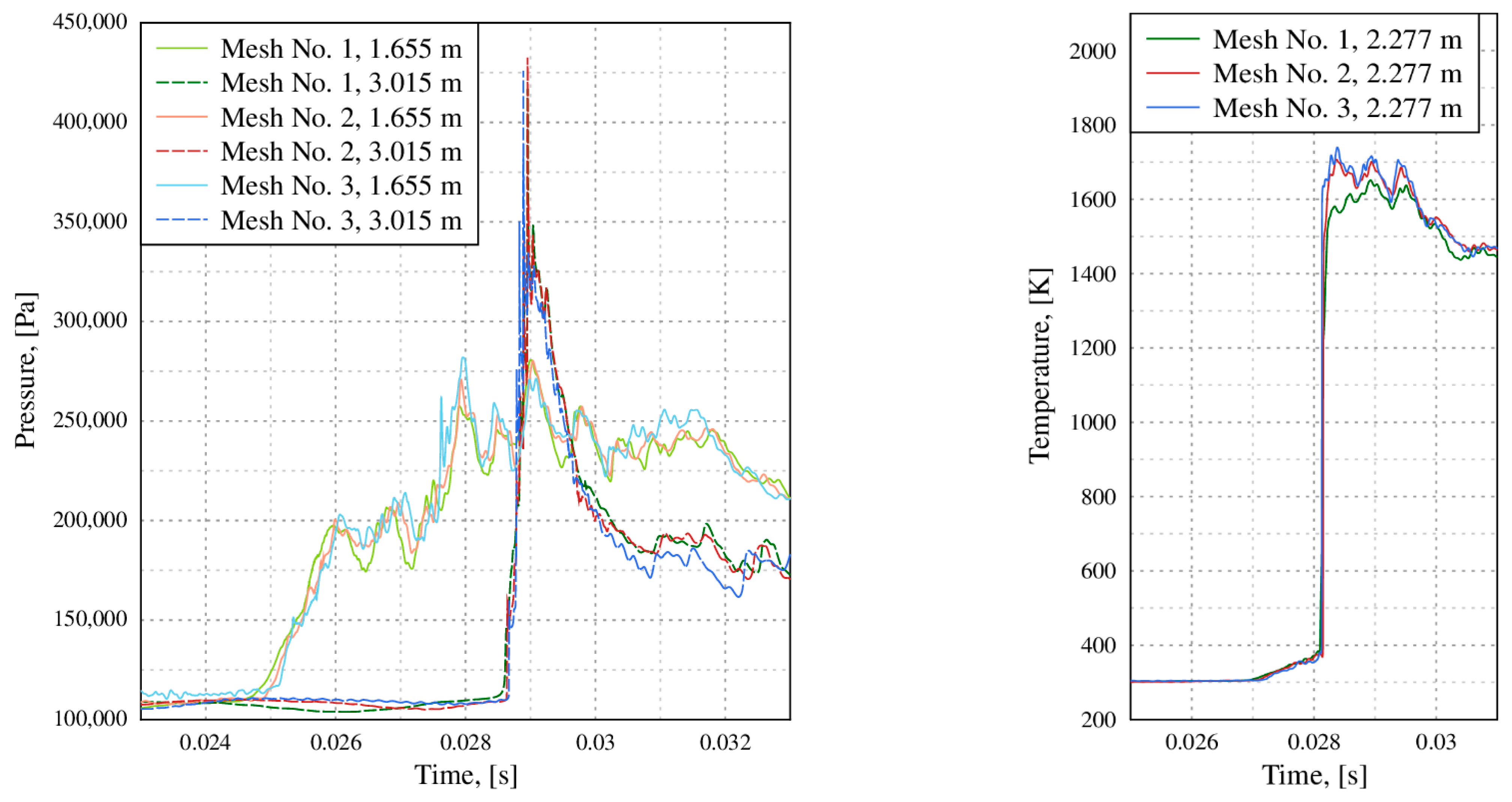
3.1. Turbulence Models
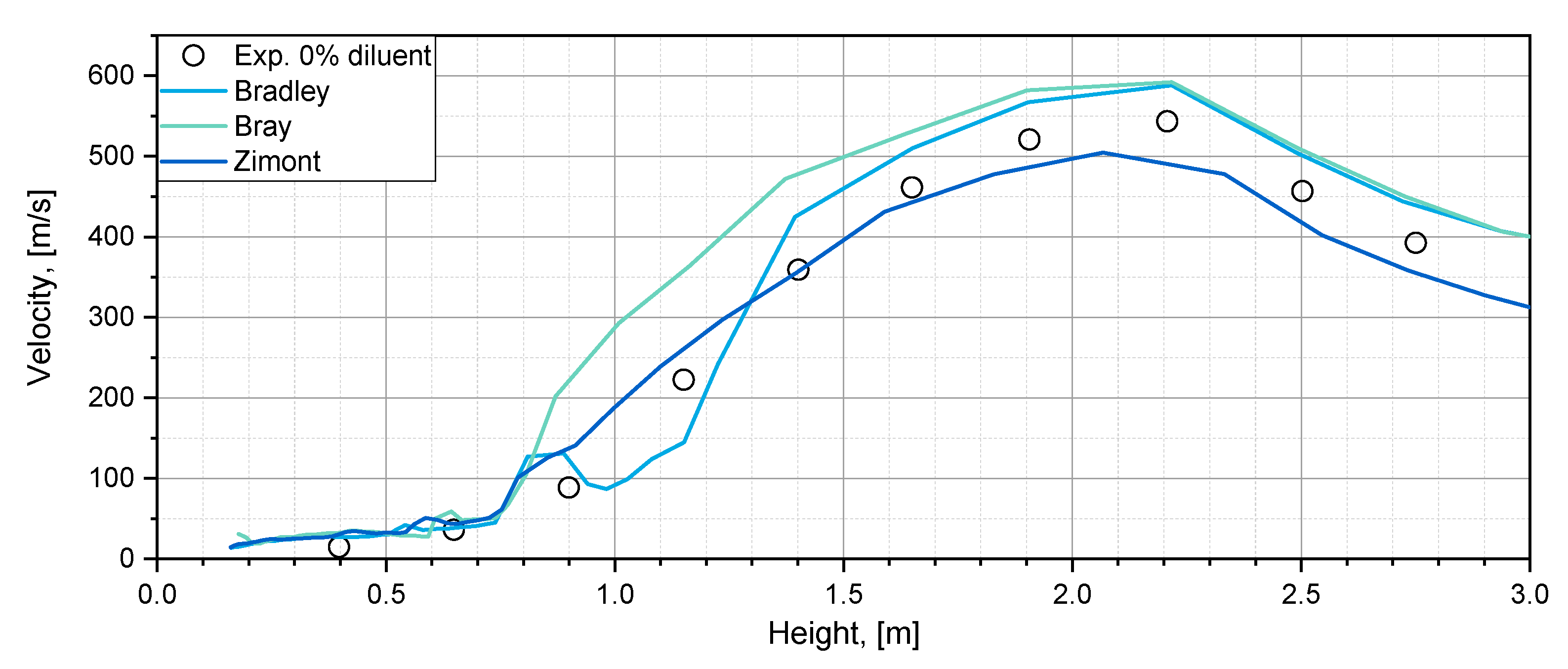
3.2. Turbulent Flame Speed Correlations
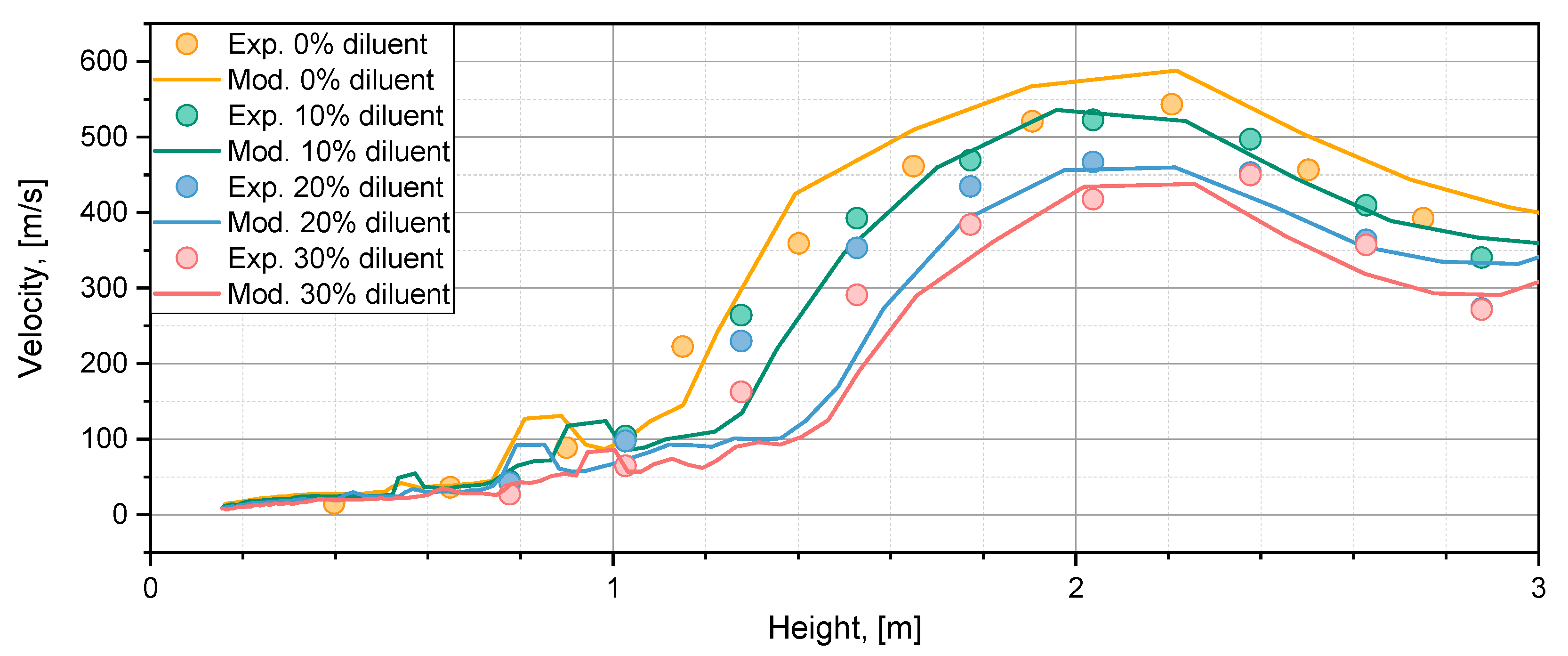
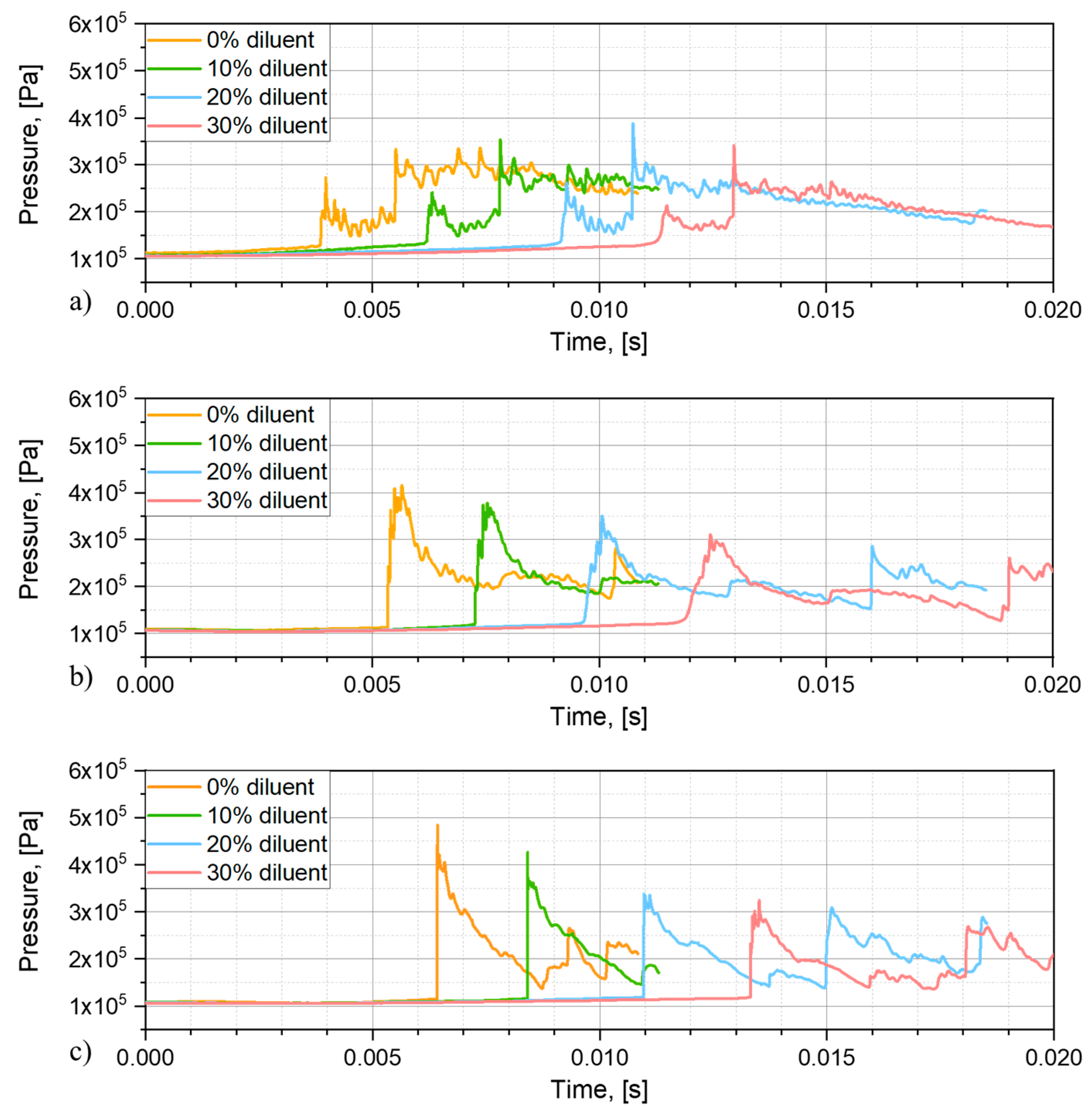
3.3. Concentration of Diluents
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Zimont correlation constant | |
| blockage ratio | |
| turbulent length scale constant | |
| combustion progress variable | |
| acceleration tube inner diameter | |
| obstacle diameter | |
| gravitational acceleration | |
| enthalpy | |
| kinetic energy | |
| turbulent kinetic energy | |
| turbulent length scale used in Bradley and Bray correlations | |
| turbulent length scale used in Zimont correlation | |
| pressure | |
| reference pressure | |
| combustion source | |
| enthalpy source | |
| laminar burning velocity | |
| reference laminar burning velocity | |
| turbulent burning velocity | |
| turbulent Schmidt number | |
| temperature | |
| reference temperature | |
| time | |
| velocity | |
| RMS of turbulent velocity fluctuation | |
| initial hydrogen mass fraction | |
| hydrogen mass fraction | |
| final hydrogen mass fraction | |
| initial steam volume fraction | |
| Karlovitz stretch factor | |
| Lewis number | |
| turbulent Reynolds number | |
| effective thermal diffusivity | |
| molecular thermal diffusivity of fresh mixture | |
| turbulent dissipation rate | |
| effective dynamic viscosity | |
| molecular kinematic viscosity | |
| turbulent kinematic viscosity | |
| specific turbulent dissipation rate | |
| mixture density | |
| fresh mixture density | |
| shear stress |
References
- Punetha, M.; Yadav, M.K.; Khandekar, S.; Sharma, P.K.; Ganju, S. Intrinsic transport and combustion issues of steam-air-hydrogen mixtures in nuclear containments. Int. J. Hydrog. Energy 2020, 45, 3340–3371. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Design of Reactor Containment Systems for Nuclear Power Plants; Safety Standards Series No. NS-G-1.10; IAEA: Vienna, Austria, 2004. [Google Scholar]
- Bentaib, A.; Bleyer, A.; Meynet, N.; Chaumeix, N.; Schramm, B.; Höhne, M.; Kostka, P.; Movahed, M.; Worapittayaporn, S.; Brähler, T.; et al. SARNET hydrogen deflagration benchmarks: Main outcomes and conclusions. Ann. Nucl. Energy 2014, 74, 143–152. [Google Scholar] [CrossRef]
- Giusti, A.; Mastorakos, E. Turbulent combustion modelling and experiments: Recent trends and developments. Flow Turbul. Combust. 2019, 103, 847–869. [Google Scholar] [CrossRef] [Green Version]
- Kotchurko, A. International Standard Problem ISP-49 on Hydrogen Deflagration; Final Report NEA/CSNI/R(2011)9; OECD: Paris, France, 2012. [Google Scholar]
- Bentaib, A.; Chaumeix, N.; Grosseuvres, R.; Bleyer, A.; Gastaldo, L.; Maas, L.; Jallais, S.; Vyazmina, E.; Kudriakov, S.; Studer, E.; et al. ETSON-MITHYGENE benchmark on simulations of upward flame propagation experiment in the ENACCEF2 experimental facility. In Proceedings of the International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Operation and Safety, Qingdao, China, 14–18 October 2018. [Google Scholar]
- Xiao, J.; Travis, J.R.; Kuznetsov, M. Numerical investigations of heat losses to confinement structures from hydrogen-air turbulent flames in ENACCEF facility. Int. J. Hydrog. Energy 2015, 40, 13106–13120. [Google Scholar] [CrossRef]
- Xiao, J.; Breitung, W.; Kuznetsov, M.; Zhang, H.; Travis, J.R.; Redlinger, R.; Jordan, T. GASFLOW-MPI: A new 3-D parallel all-speed CFD code for turbulent dispersion and combustion simulations: Part I: Models, verification and validation. Int. J. Hydrog. Energy 2017, 42, 8346–8368. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Xiao, J.; Jordan, T. Detached Eddy Simulation of hydrogen turbulent dispersion in nuclear containment compartment using GASFLOW-MPI. Int. J. Hydrog. Energy 2018, 29, 13659–13675. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Zhang, H.; Breitung, W.; Travis, J.; Kuznetsov, M.; Jordan, T. Numerical analysis of hydrogen release, dispersion and combustion in a tunnel with fuel cell vehicles using all-speed CFD code GASFLOW-MPI. Int. J. Hydrog. Energy 2021, 23, 12474–12486. [Google Scholar] [CrossRef]
- Zhao, H.; Luo, X.; Zhang, R.; Lyu, X.; Yin, H.; Kang, Z. Analysis on hydrogen risk under LOCA in marine nuclear reactor. Exp. Comput. Multiph. Flow 2021, 1–6. [Google Scholar] [CrossRef]
- Lucas, M.; Skjold, T.; Hisken, H. Computational fluid dynamics simulations of hydrogen releases and vented deflagrations in large enclosures. J. Loss Prev. Process Ind. 2020, 63, 103999. [Google Scholar] [CrossRef]
- Lucas, M.; Atanga, G.; Hisken, H.; Mauri, L.; Skjold, T. Simulating vented hydrogen deflagrations: Improved modelling in the CFD tool FLACS-hydrogen. Int. J. Hydrog. Energy 2021, 23, 12464–12473. [Google Scholar] [CrossRef]
- Gastaldo, L.; Babik, F.; Duval, F.; Lapuerta, C.; Latché, J.C. Simulation of accelerated deflagration using the P2REMICS software. In Proceedings of the International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Xi’an, China, 3–8 September 2017. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Zimont, V.; Polifke, W.; Bettelini, M.; Weisenstein, W. An efficient computational model for premixed turbulent combustion at high Reynolds numbers based on a turbulent flame speed closure. J. Eng. Gas Turbine Power 1998, 120, 526–532. [Google Scholar] [CrossRef]
- Bradley, D.; Lau, A.K.C.; Lawes, M.; Smith, F.T. Flame stretch rate as a determinant of turbulent burning velocity. Philos. Trans. A Math. Phys. Eng. Sci. 1992, 338, 359–387. [Google Scholar]
- Bray, K.N.C. Studies of the turbulent burning velocity. Proc. R. Soc. A 1990, 431, 315–335. [Google Scholar]
- Malet, F. Etude Expérimentale et Numérique de la Propagation de Flammes Prémélangées Turbulentes Dans une Atmosphère Pauvre en Hydrogène et Humide. Ph.D. Thesis, L’Universite D’Orleans, Orléans, France, 2005. [Google Scholar]
- Mahaffy, J.; Chung, B.; Song, C.; Dubois, F.; Graffard, E.; Ducros, F.; Heitsch, M.; Scheuerer, M.; Henriksson, M.; Komen, E.; et al. Best Practice Guidelines for the Use of CFD in Nuclear Reactor Safety Applications; Organization for Economic Co-Operation and Development: Paris, France, 2007. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Chou, S.K.; Yang, W.M.; Li, Z.W. Experimental and numerical study of the wall temperature of cylindrical micro combustors. J. Micromech. Microeng. 2008, 19, 015019. [Google Scholar] [CrossRef]
- Eriksson, P. The Zimont TFC model applied to premixed bluff body stabilized combustion using four different RANS turbulence models. Turbo Expo Power Land Sea Air 2007, 47918, 353–361. [Google Scholar]
- Akhtar, S.; Kurnia, J.C.; Shamim, T. A three-dimensional computational model of H2–air premixed combustion in non-circular micro-channels for a thermo-photovoltaic (TPV) application. Appl. Energy 2015, 152, 47–57. [Google Scholar] [CrossRef]
- Cebedi, T. Analysis of Turbulent Flows with Computer Programs; Butterworth-Heinemman: Oxford, UK, 2013. [Google Scholar]



| Initial Conditions | ||
|---|---|---|
| Pressure | p | 105 Pa |
| Temperature | T | 263.15 K |
| Initial hydrogen volume fraction | XH2 | 0.13 |
| Initial H2O volume fraction | XH2O | 0/0.1/0.2/0.3 |
| Model Constants | ||
| Zimont constant | A | 0.52 |
| Turbulent Scmidt number | ScT | 0.9 |
| Lewis number | Le | 0.4 |
| Parameter | OpenFOAM Wall Function | Details |
|---|---|---|
| k | kqRWallFunction | Zero gradient wrapper |
| ε | epsilonWallFunction | Viscous and inertial sublayer expressions depending on y+ |
| ω | omegaWallFunction | Viscous and inertial sublayer expressions depending on y+ |
| νt | nutkWallFunction | Viscous and inertial sublayer expressions depending on y+, based on k |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povilaitis, M.; Jaseliūnaitė, J. Simulation of Hydrogen-Air-Diluents Mixture Combustion in an Acceleration Tube with FlameFoam Solver. Energies 2021, 14, 5504. https://doi.org/10.3390/en14175504
Povilaitis M, Jaseliūnaitė J. Simulation of Hydrogen-Air-Diluents Mixture Combustion in an Acceleration Tube with FlameFoam Solver. Energies. 2021; 14(17):5504. https://doi.org/10.3390/en14175504
Chicago/Turabian StylePovilaitis, Mantas, and Justina Jaseliūnaitė. 2021. "Simulation of Hydrogen-Air-Diluents Mixture Combustion in an Acceleration Tube with FlameFoam Solver" Energies 14, no. 17: 5504. https://doi.org/10.3390/en14175504
APA StylePovilaitis, M., & Jaseliūnaitė, J. (2021). Simulation of Hydrogen-Air-Diluents Mixture Combustion in an Acceleration Tube with FlameFoam Solver. Energies, 14(17), 5504. https://doi.org/10.3390/en14175504






