Exploratory Data Analysis Based Short-Term Electrical Load Forecasting: A Comprehensive Analysis

Abstract

Power system planning in numerous electric utilities merely relies on the conventional statistical methodologies, such as ARIMA for short-term electrical load forecasting, which is incapable of determining the non-linearities induced by the non-linear seasonal data, which affect the electrical load. This research work presents a comprehensive overview of modern linear and non-linear parametric modeling techniques for short-term electrical load forecasting to ensure stable and reliable power system operations by mitigating non-linearities in electrical load data. Based on the findings of exploratory data analysis, the temporal and climatic factors are identified as the potential input features in these modeling techniques. The real-time electrical load and meteorological data of the city of Lahore in Pakistan are considered to analyze the reliability of different state-of-the-art linear and non-linear parametric methodologies. Based on performance indices, such as Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE) and Mean Absolute Error (MAE), the qualitative and quantitative comparisons have been conferred among these scientific rationales. The experimental results reveal that the ANN–LM with a single hidden layer performs relatively better in terms of performance indices compared to OE, ARX, ARMAX, SVM, ANN–PSO, KNN, ANN–LM with two hidden layers and bootstrap aggregation models.

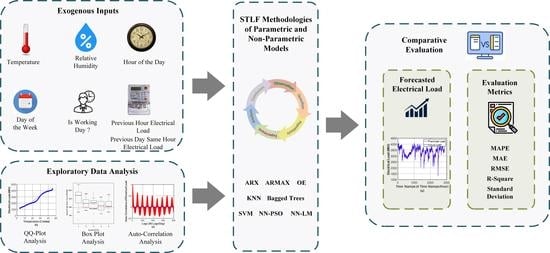
1. Introduction

Short-Term Electrical Load Forecasting (STLF) is used by planning authorities to forecast energy demand, ranging from one hour to one week ahead [1,2]. Energy management has become one of the most strategic and essential cutting-edge research areas in power system engineering [3,4,5]. Security and protection of electrical power systems can be malfunctioned by irregular power flows and system congestion due to an inaccurate electrical load forecast, which may lead towards imbalanced generation planning. Therefore, electricity generation, transmission and distribution networks governed by electric utilities over the world need an accurate STLF for reliable and economical short-term operations of power systems [6]. STLF also assists in economical fuel scheduling, automatic generation control, economic dispatch, voltage stability of HVAC and HVDC lines, and avoiding highly disruptive blackouts [7]. Therefore, the inspiration behind this research work is to empower the planning authorities of electric utilities with state-of-the-art linear and non-linear parametric methodologies since linear and non-linear parametric methodologies are more suitable to handle the system dynamics and non-linearities [8].

The latest annual report of the International Energy Agency (IEA) suggests that developing counties possess the fastest electricity demand growth rate than developed countries, which have limited annual electricity demand growth rates [9]. The exponential growth is driven by the rising industrial revolution and urbanization [10,11]. Therefore, it is necessary to forecast such a diversified annual electricity demand using robust and high-performance forecasting methods for appropriate power generation planning. It may be observed that the electric utilities of developing countries still rely on conventional statistical methodologies, such as a regression analysis, Auto-Regressive Integrated Moving Average (ARIMA) and bootstrap aggregation. However, these forecasting techniques are incapable of handling system dynamics effectively. Therefore, the motivation behind this paper is to empower electric utilities, specifically those of developing countries, with the potentials and strengths of the advanced AI-based computational intelligence methodologies.

Many research studies have been presented to manifest the role of high-performance Short-Term Electrical Load Forecasting (STLF) methods for reliable power system operations. However, most of the work focuses on the electrical load datasets of developed countries, which does not give any motivation to the power companies of the developing countries. Therefore, to overcome the above-stated research gap, this paper aims to exploit the potentials and strengths of the advanced machine learning and deep learning methodologies, especially the non-linear parametric methodologies over the traditional statistical linear parametric methodologies. For this purpose, this paper also delineates a clear qualitative and quantitative analysis among eight different linear and non-linear parametric STLF methodologies, such as Output Error (OE), Auto-Regressive with Exogenous Inputs (ARX), Auto-Regressive Moving Average with Exogenous Inputs (ARMAX), Support Vector Machine (SVM), Artificial Neural Network–Levenberg–Marquardt algorithm (ANN–LM) with one and two hidden layers, Artificial Neural Network–Particle Swarm Optimization (ANN–PSO), K-Nearest Neighbor (KNN) and bootstrap aggregation. Finally, the paper recommends the ANN–LM method with one hidden layer for the real-time applications of power system operations as an approved STLF model.

The electrical load dataset of LESCO, Pakistan is used in this study that comprises the real-time historical electrical load and meteorological data of Pakistan. The dataset of LESCO is different and highly non-linear compared to any leading country of Europe and America because of frequent power outages, load shedding, failures, blackouts and power shortfall. Therefore, the STLF is a challenging task and to the best of the authors’ knowledge, any state-of-the-art statistical and machine learning algorithms have never been tested on the mentioned dataset. The selection of the input parameters must be appropriate for the accurate forecasting of different statistical and machine learning models. Therefore, the input data selection for forecasting models is obtained through exploratory data analysis, auto-correlation analysis and quantile–quantile analysis in this study. The input and output datasets are then pre-processed to convert into useable multi-variate time-series electrical load data and a novel predictor matrix for the development of the above-discussed pre-trained electrical load forecasting models. After modeling, the evaluation will be performed to estimate the accuracy of the forecasting model using key performance indicators, such as Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), R-square value and standard deviation. Finally, the results show that the ANN–LM method with one hidden layer performs comparatively better than the other above-discussed methodologies. Considering the above-stated actualities, the main contributions of this research paper are as follows:

• For the first time, the historical electrical load data of Pakistan have been considered for the motivation of electric utilities of developing countries to implement machine learning-based STLF methodologies for reliable power system operations.
• To select the input features for the first time from the new unprecedented dataset, the exploratory data analysis, graphical observations and statistical techniques, such as auto-correlation analysis, quantile–quantile analysis and box-plot analysis, are implemented.
• A comprehensive predictor matrix is developed using selected input features for linear and non-linear parametric STLF models. The predictor matrix is not mathematically complex and does not necessarily require data outside the historical patterns.
• This study conducts a comprehensive qualitative and quantitative comparison between the traditional time-series statistical models, linear and non-linear parametric methodologies using several evaluation metrics, such as MAPE, RMSE, MSE, R-square and standard deviation. Moreover, we conducted a thorough seasonal analysis to evaluate and compare the performance of the recommended algorithms.

The rest of the paper is organized as follows: Section 2 presents a detailed literature review, Section 3 presents a comprehensive exploratory data analysis, Section 4 discusses various linear and non-linear parametric models implemented in our paper, Section 5 provides a detailed analysis and discussion on experimental results, and Section 6 is the concluding section, which concludes the paper with future directions.

2. Literature Review

The electrical load curve depends upon the massive multivariate and non-linear temporal and meteorological data, such as festivals and holidays, humidity and temperature, which make the STLF challenging and demanding [12]. Over the past two decades, extensive research work has been presented on the STLF problem to develop several forecasting methodologies. Several regression models, such as Auto-Regressive Integrated Moving Average (ARIMA) and seasonal-ARIMA (SARIMA) have been proposed in [13,14]. ARIMA and SARIMA utilize the lagged average values of STLF time-series data to convert non-stationary data into stationary ones. This seasonality can be observed by using auto-correlation (ACF) and partial auto-correlation (PACF) analysis [15]. Moreover, a review of several other statistical regression models and their variables and methods have been discussed in [16], such as single linear regression and multiple linear regression. However, the statistical regression algorithms are inadequate in capturing the temporal variations and non-linear electrical load patterns [17,18].

To overcome the above-mentioned shortcomings for STLF, Principal Component Analysis (PCA), sensitivity analysis and step-wise regression can be used to enhance the performance of statistical regression models [16]. PCA uses a dimension reduction algorithm based on the matrix decomposition technique by finding eigenvalues of the multi-variate electrical load data through correlation analysis [19]. However, the selection of the coefficients of the co-variance matrix is tedious in PCA, which may lose the key seasonal impact of temperature influences on the electrical load data [20]. In contrast, Singular Value Decomposition (SVD) is proficient in extracting both seasonal and random components and is more robust than PCA [21]. However, SVD manipulates a complex unitary matrix which is computationally expensive [22].

Machine Learning (ML) models have been introduced later on to reduce the time complexity of SVD in the STLF problem. ML algorithms have enhanced the performance of STLF by showing profound accuracy in dealing with non-linearities of the electrical load data and accurate forecasting of the peaks of electrical load as compared to the statistical regression and dimension reduction models [23,24,25]. ML methods mainly comprise Artificial Neural Networks (ANNs) which can handle the stochastic nature of the weather-sensitive loads during the prediction of electrical load forecasting [26,27,28]. The conventional ANN algorithms experience overfitting problems. For overcoming the overfitting issue, the authors in [29] proposed an improved ANN with a learning method that applies a novel search technique that abstains from overfitting. However, some major drawbacks, such as a vanishing gradient and complex hyper-parameters tuning problems due to high-dimensional input data, restrict the applications of the above-mentioned ANN models [30,31,32,33]. K-Nearest Neighbor (KNN) is also proposed as a ML algorithm, which can deal with non-linear temporal variations in electrical load data using k-most similar instances. In the KNN algorithm, when the k most similar samples are detected, the target is attained by local interpolation of the targets associated with the k detected instances [16,33]. The KNN method has proved to be imperfect while forecasting the consumption of electrical load due to insufficient hyperparameters which also results in overfitting [34]. Moreover, the curse of dimensionality occurs when KNN is subjected to high-dimensional electrical load data. The Support Vector Regression (SVR) model is another prominent ML model for STLF and was implemented as a better alternative in [35]. In [32], a new nu support vector machine (nu–SVR) based on the tuning of a newly introduced hyperparameter called nu was recommended for STLF, which generates less error than the ANN but the selection of reasonable parameters in SVR is still a challenging task [33].

The above-mentioned STLF issues can be resolved with achieving higher prediction accuracy than the old ML models, such as SVR, ANN and KNN, by using hybrid ML models. In hybrid ML models, every constituent algorithm delivers robustness and higher accuracy in STLF [36]. In [33], the weights of weighted K-Nearest Neighbor (W-KNN) are optimized using a Genetic Algorithm (GA). Moreover, the fusion of learning algorithms and clustering in KNN–ANN and KNN–SVR architectures extract prominent features, such as temperature, humidity and weekdays before the self-learning process [37]. However, the complex architectures and an unspecified number of optimal clusters limit the validity of KNN-based hybrid ML models [36]. Although, the forecasting performance of feedforward neural networks (FF–NN) can be increased through an improved learning accuracy using the Elaboration Likelihood Model (ELM) merged with the Levenberg–Marquardt (LM) and the Conditional Mutual Information-based Feature Selection (CMIFS) [38]. In [39], a hybrid BA–ELM was proposed to improve the performance of STLF model. The input weights of an extreme learning machine (ELM) and bias threshold are optimized by a Bat Algorithm (BA) to predict the electric load. However, the critical gradient and Hessian calculations for the STLF model raise the time complexity of the ELM method to a larger extent [40]. Furthermore, the Empirical Mode Decomposition (EMD)-based deep learning method has been contemplated to improve the generalization ability of the STLF model in which multivariate electrical load data are segmented into Intrinsic Mode Functions (IMFs) and then Deep Belief Networks (DBNs) are deployed in the architecture to train the extracted IMFs. Eventually, the electrical load forecasting results are acquired by summing up the weighted outputs from each DBNs by using an ensemble learning algorithm. However, the EMD-based DBN algorithm is complex and loses the original information about the electrical load and electrical load features when selecting IMFs, which eventually squashes the large forecasting errors during the training of deep learning models. Moreover, the segmentation of electrical load data into IMFs using EMD and the neural network training of the captured IMFs separately using DBNs require a high computational time [41]. Additionally, an Adaptive Network-based Fuzzy Inference System (ANFIS) enlarges the learning capacity of NNs by fusing neural architecture with high-level reasoning methodologies of fuzzy logic [42]. However, the intricate rules, a large number of antecedents and mode delays increase the complexity of the learning phase in ANFIS architectures [43].

The second group of hybrid ML algorithms incorporates stochastic global methods or metaheuristic methods, such as Particle Swarm Optimization (PSO) and GA merged with neural networks [44]. PSO and GA can be utilized to find the best input weights of an ANN in step-ahead and multi-step ahead STLF models. A GA-based Non-Linear Auto-Regressive Exogenous input Neural Network (NARX–NN) manages the feedback loop in the backpropagation path of the NN to capture unreliable weather dependencies in the input dataset [12,45]. The metaheuristic model, such as ANN, can easily converge to a local optimum but remains unsuccessfully converged to the global optimum in the diversified feature space [46].

3. Exploratory Data Analysis

Exploratory Data Analysis (EDA) is a statistical approach that examines the presence of multiple hidden features and patterns present in a dataset. Several statistical visual methodologies can be used for this purpose, such as auto-correlations plots, QQ plots, box plots, histograms and many others. EDA is quite important in developing time-series forecasting models since it exhibits and explores the relationship between input and output variables. Therefore, EDA must be performed before formal hypothesis investigation and modeling [47].

3.1. Dataset Description

Real-time accumulated datasets of electrical load consumption and climate data of Lahore, Pakistan, are used in our research work. The electrical load real-time dataset of Lahore Electric Supply Corporation (LESCO) is acquired from the Power Information Technology Company (PITC), which is a faction of the Ministry of Energy, Pakistan, and is responsible for monitoring generation, transmission and distribution through Pakistan [48]. The electrical load data is recorded in real-time at 15 min intervals and consists of 96 samples per day from 2017 to 2019 at an aggregated level (of the whole Lahore region). Moreover, the climatic dataset consists of temperature and humidity data recorded at the 15 min interval from 2017–2019 and is acquired from an online database for Lahore, Pakistan of a Russian company “Raspisaniye Pogodi Ltd.” (St. Petersburg, Russia) having operating stations over the globe [49].

3.2. Input Parameter Description

Several climatic factors, such as temperature and humidity, and temporal factors influence the electrical load demand profile of a certain area [50]. The share of domestic load is quite significant in the entire electrical load been consumed. Therefore, weekends and festival holidays show a more distinguished electrical load-consuming profile than normal working days [51]. Generally, the STLF model not only integrates historical electrical load patterns, but also the meteorological and temporal parameters as well [12]. Figure 1 shows that the EDA performed on the above-mentioned datasets identifies multiple exogenous inputs parameters, which are essential for STLF models.

3.2.1. Auto-Correlation Analysis

Auto-correlation is a statistical representation of the degree of resemblance between a given time-series and a lagged version of itself over consecutive time intervals. Figure 1a represents the auto-correlation of the electrical load consumption for the month of January-2019 over the lagged consecutive time intervals up to 1 week (96 lags/day). Here, one lag represents a lagged version of 15 min; therefore, 96 lags represent the lagged version of one complete day. The electrical load data is normalized between (0, 1). The strong correlation in these plots suggests that the present electrical load consumption value has a strong correlation with previous lagged electrical load consumption values, such as the previous hour electrical load value and the previous day same hour electrical load value.

3.2.2. Quantile–Quantile Plots

QQ plots in Figure 1b,c illustrates that there exists a relationship between the consumed electrical load and climatic data since the values of temperature and humidity seem to be directly proportional to the electrical load consumption profile. Moreover, Figure 1d–e shows the quantile–quantile (QQ) plots of the present electrical load that are plotted against its lagged values for the month of January-2019. The QQ plots show a straight line at 45 degrees, which demonstrates that there exists a strong correlation between present electrical load consumption and its highlighted lagged values and are best suited for developing our STLF model.

3.2.3. Box Plots

Weekend days, festivals and public holidays exhibit a more reduced electrical load consumption profile than normal working days due to the closure of commercial markets, offices and industries. To validate this hypothesis, a box plot analysis of the electrical load consumption profile for January-2019 is performed in Figure 1g. The box plot analysis graphically depicts groups of numerical datasets using their quartiles and validates the presence of the aforementioned temporal factors in the electrical load dataset.

The electrical load curve for the month of January-2019 is plotted in Figure 1f. Apart from the EDA performed, the plotted electrical load curve highlights the presence of seasonal patterns with the electrical load consumption profile throughout the day and the entire week. Therefore, the hour number of the day and the day number of the week are also considered in our developed STLF predictor matrix.

As per the suggestions of EDA, some potential input parameters for STLF models are highlighted and are presented in

Table 1. Selection of potential input parameters for STLF models using EDA.

Meteorological Factors	Temporal Factors	Historical Data
Temperature	Hour of the Day	Previous Hour Electrical Load
Humidity	Day of the Week	Previous Day Same Hour Electrical Load
	Is it a Working Day?

.

4. Methodology

The identification of various dynamic models can be explained using a number of models with each one relating various stochastic processes and selection measures. The forecasting methodologies used in this research project are explained below.

4.1. Auto-Regressive with Exogenous Inputs (ARX)

The dynamic processes driven by input in an uncertain environment can simply be described using the ARX models. ARX is a modified form of the Auto-Regressive (AR) model with exogenous inputs since AR models do not include inputs. ARX incorporates the stimulus signal and captures the stochastic nature of the environment as the system dynamics. The output of a process can be estimated using the sum of the previous input and output regression values as follows [52]:

$$y\left(t\right)+a_{1}y\left(t-1\right)+\dots +a_{na}y\left(t-na\right) = b_{1}u\left(t-nk\right) +\dots + b_{nb}u\left(t-nb+nk+1\right) + e\left(t\right).$$

(1)

The parameters $na$ and $nb$ are the orders of the ARX model, and $nk$ is the delay. A description of Equation (1) is given below:

▪

$t$: the output of process at time $t$;

▪

$na$: number of poles;

▪

$nb$: number of zeros;

▪

$nk$: number of input samples that occur before the input affects the output;

▪

$y\left(t-1\right)\dots y\left(t-na\right)$: previous outputs on which the current output depends;

▪

$u\left(t-nk\right)\dots u\left(t-nk-nb+1\right):$ previous and delayed inputs on which the current output depends;

▪

$e\left(t\right)$: white-noise disturbance value.

The difference equation can be written in a more compact way as the following [52]:

$$A\left(q\right)y\left(t)=B\left(q\right)u(t-nk\right) + e\left(t\right)$$

(2)

where $q$ is the delay operator. The developed load forecasting model is a MISO system having multiple input parameters and the single output of electrical load, so the differential equation of the ARX model used in this paper would become [52]:

$$A\left(q\right)y\left(t)=B_1\left(q\right)u_1(t-n{k}_1\right) + B_2\left(q\right)u_2\left(t-n{k}_2\right) +\dots + B_{nu}\left(q\right)u_{nu}\left(t-n{k}_{nu}\right) + e\left(t\right).$$

(3)

The estimation error can be minimized by selecting the high order model than the actual order of the model. However, increasing the model order impacts the stability of the system. The identification method usually used in ARX is the least square method since it is the most competent polynomial estimation technique [52]. The interpretation of the ARX models can be represented in Figure 2a [52]. Here $u$ is the input and $y$ is the output.

4.2. Auto-Regressive Moving Average with Exogenous Inputs (ARMAX)

The equation error of complex stochastic environment having dynamic process may be defined using the ARMAX model, which is a time-series model and is developed by means of both processes, i.e., Auto-Regressive (AR) and Moving-Average (MA), having exogenous inputs incorporated. ARMAX consists of both lagged variables, i.e., dependent and independent variables, and incorporates stochastic dynamics present in its system’s structure, such as noise existence in linear dynamic systems. The model parameters are usually estimated using the Recursive Extended Least Square (RELS) method since RELS minimizes the sum of the squares of the prediction errors of a linear ARMAX model. The following Equation (4) gives a mathematical representation of the ARMAX model [53]:

$$y\left(t\right) + a_{1}y\left(t-1\right) +\dots + a_{na}y\left(t-na\right) =b_{1}u\left(t-nk\right) +\dots + b_{nb}u\left(t-nk-nb+1\right) + c_{1}e\left(t-1\right) +\dots +c_{nc}e\left(t-nc\right) + e\left(t\right).$$

(4)

The parameters $na$ and $nb$ are the orders of the ARX model, and $nk$ is the delay. A description of Equation (4) is given below:

■

$y\left(t\right)$: output at time $t$;

■

$na$: number of poles;

■

$nb$: number of zeroes plus 1;

■

$nc$: number of C coefficients;

■

$nk$: number of input samples that occur before the input affects the output;

■

$y\left(t-1\right)\dots y\left(t-na\right)$: previous outputs on which the current output depends;

■

$u\left(t-nk\right)\dots u\left(t-nk-nb+1\right):$ previous and delayed inputs on which the current output depends;

■

$e\left(t-1\right)\dots e\left(t-nc\right)$: white-noise disturbance value.

The difference equation can be written in a more compact way as [53]:

$$A\left(q\right)y\left(t)=B\left(q\right)u(t-nk\right) + C\left(q\right)e\left(t\right),$$

(5)

where $q$ is the delay operator. In our research work, we are employing the MISO forecasting model, so the differential equation of the ARMAX model becomes [53]:

$$A\left(q\right)y\left(t)=B_1\left(q\right)u_1(t-n{k}_1\right) + B_2\left(q\right)u_2\left(t-n{k}_2\right) +\dots +B_{nu}\left(q\right)u_{nu}\left(t-n{k}_{nu}\right) + C\left(q\right)e\left(t\right).$$

(6)

The ARMAX model can be represented by using Figure 2b. Here, $u$ is the inputs of the system, $e$ is the system’s disturbance and $y$ is the output [53].

4.3. Output Error Model (OE)

OE is a special configuration of polynomial models and represents a conventional transfer function that relates outputs to the observed inputs with the addition of white-noise as an additive output disturbance. Therefore, disturbances need no modeling while using OE models, which gives it an advantage over other models. OE’s methodology has usually a quadratic parameters-based cost function, which solves the problem of asymptotic convergence. These parameters can be obtained by the minimization of the loss function which can be performed using various non-linear optimization techniques. The Gauss–Newton method is usually preferred. OE’s configuration can be presented as [53]:

$${\epsilon }_{\mathrm{OE}}=y-\widehat{y}=y-\frac{\widehat{B}}{\widehat{A}}u,$$

(7)

or with delay, the above Equation (7) becomes [53]:

$$y\left(t\right) =\frac{B\left(q\right)}{F\left(q\right)}u\left(t-nk\right) + e\left(t\right)$$

(8)

where $y\left(t\right)$ is the measured output, $\widehat{y}$ is the transfer function models output, u is the excitation or input to the system. $\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$A$}\right.$ is known as the true system and $\widehat{B}/\widehat{A}$ is the estimated or predicted model of the system. The output disturbance or error is $e\left(t\right)$. The OE model is created using the specified model delays, orders, and estimation options, where the order $\left[nbnfnk\right]$ defines the number of parameters in each component of the estimated polynomial. Figure 2c represents the structure of OE based on the Equations (7) and (8) [53].

4.4. Support Vector Machine (SVM)

One of the finest models of supervised machine learning is the Support Vector Machine (SVM), which develops a set of hyperplanes in a high dimensional space for classification, outlier detection, regression and pattern detection [54]. An SVM hyperplane, based on the knowledge of the data patterns known as features, classifies the observations of one class from another. The linear SVM classifier is a type of SVM classifier that predicts a given input into two possible outputs/classes, thus making it a non-probabilistic binary linear classifier. The hypothesis of a linear SVM classifier can be described in Equation (9) [54]. The most expected label for the new input data can be predicted using that hyperplane. These features are a type of interpolations extracted from the data patterns during feature selection. The prediction is made using either linear or non-linear hyperplane as per the application.

$$h\left(x_i\right)=\left[\begin{array}{l}+1 if \left(w.x+b\right)\ge 0\\ -1 if \left(w.x+b\right) <0 \end{array}\right].$$

(9)

Support vectors are the values that are close to the classification margin. The goal of SVM is to maximize the margin between the support vectors and hyperplane. If we are having s hyperplanes, with each having $B_i$ value, then we will choose the hyperplane having the largest $B_i$ value [54].

$$\mathrm{H}=\underset{i=1\dots s}{\max } \{\left.h_i\right|B_i\},$$

(10)

In SVM, the margin size is inversely proportional to the generalization error; therefore, an accurate separation is accomplished by lowering the classifier’s generalization error using the hyperplane that has the largest widened distance to the closest training data point. A hyperplane that maximizes the margin is called an optimal hyperplane. The margins of SVM’s could be made either hard or soft, depending upon the data and the application has been used to predict its future output. The model overfitting can be avoided with the appropriate selection of hyperplane margins, so a trade-off between training error and hyperplane complexity occurs during margin selection [54].

4.5. K-Nearest Neighbour (KNN)

K-nearest neighbor algorithm is a non-parametric model that has no presumptions about the decision boundary in parametric form and can perform regression and classification on both binary and multiclass datasets. KNN searches for exemplars in the training observation dataset which most suitably corresponds to the new data point. Based on the weighted means of the nearest neighbors, the predicted outcome is allocated to the newly entered input datapoint of the most alike exemplar [55]. The value of K should be chosen wisely since it significantly affects the performance of the KNN algorithm. The optimal value of K can be chosen using several heuristic techniques, such as the hyperparameter optimization method. The Euclidean distance is used to define the closeness among the datasets and can be computed using the following Equation (11). Here $A$ and $B$ are the two points in the Euclidean n-space between which the distance is to be measured [55].

$$similarity\left(A.B\right)=\frac{A.B}{\left|A\left|B\right|\right|},$$

(11)

Minkowski distance is another distance metric used by cubic KNN and can be computed by the following Equation (12). Here, $r$ parameter of the Minkowski distance metric represents the order of the norm, and $A$ and $B$ are the two points in space between which the distance is to be measured [55].

$$Minkowski\left(A,B\right)={\displaystyle \sum }_{i=1}^m{\left({\left|A_i-B_i\right|}^r\right)}^{1/r}$$

(12)

4.6. Bootstrap Aggregation (Bagged Trees)

Bootstrap aggregation is an ensemble machine learning algorithm, which bags ensemble trees for either regression or classification problems and is capable of reducing the variance of the forecasting model without increasing the bias. The trees found in the ensemble are grown on the bootstrap replica of the input data point. Several subsets of data are created from the provided training samples, which are selected randomly with substitution. Each subset group of a dataset is then used for the training of decision trees. Resultantly, an ensemble of several models is created. Since the decision tree is solely a weak learner and is quite responsive and sensitive to the training patterns, therefore a single decision tree results overfit the specific patterns in the dataset which results in model overfitting. Bagged decision trees upgrade the performance of decision trees by using many trees that are assembled in parallel structures for learning, and the prediction against new observation is obtained from the average prediction outcomes of all the decision trees [56].

4.7. Artificial Neural Network (ANN)

The ANN methodology in a data processing network is invented based on the human nervous system as depicted in Figure 3 [57]. The human brain is capable of learning instructions through experiences. These experiences and instructions are the training data provided to ANN to learn things in different scenarios. The ANN network can be tuned by learning rules and instructions, network structures, interconnection techniques and the output transfer functions. The neuron weights are optimized during the learning process to obtain the desired accuracy. ANN’s methodology has self-learning abilities with modified standards competitive to that of statistical methodologies and solves those problems which seem to be difficult for statistical analysis or humans. Neural networks are modern-day state-of-the-art methodologies that not only learn non-linear patterns in the data provided but also handle dynamic systems and extract out hidden relationships between inputs and outputs. ANNs are believed to be powerful tools for time-series modeling and prediction.

The neurons in ANNs are actually the replica of cells of the human nervous system’s neurons interconnected by nodes to form a web-like network, where each neuron contributes its part by processing information. Based on the internal weighting system, this information is continuously updated upon receiving new information from observed values of the process and is used to predict the future output. Learning rules are established in an ANN using backpropagation methodologies. The optimization methods used in our research paper are the Particle Swarm Optimization (PSO) algorithm and the Levenberg–Marquardt (LM) algorithm.

4.7.1. Particle Swarm Optimization Algorithm (PSO)

Particle Swarm Optimization Algorithm (PSO) is inspired by the activities and social behavior of fishes and birds, such as schooling, regrouping, flocking and a sudden direction-changing action by varying their velocity. A population (called a swarm) of candidate solutions, which consists of dubbed particles, is formed where these particles are moved around in a free search area having very large spaces. The velocity and position of particle movements are calculated using Equation (13) [57]. Each solution in the PSO is known as a single particle and has four features: (1) the current position $x_i^{\mathrm{t}}$, (2) the best historical position $\widetilde{p_i{}^{\mathrm{t}}}$, which is analyzed using the objective function, (3) the best historical position $\widehat{p_i{}^{\mathrm{t}}}$, which is located in all particles, and (4) the current velocity $v_i^{\mathrm{t}}$. The following Equation (13) describes the changes in position and velocity.

$$\left[\begin{array}{c}{v}_i^{\mathrm{t}+1}=w{v}_i^{\mathrm{t}}+ c_1{r}_1()\left(\widetilde{p_i{}^{\mathrm{t}}}-x_i^{\mathrm{t}}\right)+c_2{r}_2()\left(\widehat{p_i{}^{\mathrm{t}}}{x}_i{}^{\mathrm{t}}\right)\\ x_i^{\mathrm{t}+1}=x_i^{\mathrm{t}}+v_i^{\mathrm{t}+1}\end{array}\right]$$

(13)

Here, $c_1$ and $c_2$ are known as acceleration factors, $r_1()$ and $r_2()$ as uniformly generated random values ranging from $\left(0,1\right)$, and $w$ as the weight of inertia. The algorithms move towards the best-known positions in this search space and try to search the local best position of each particle and are directed by their own best-known positions found in an individual iteration as the algorithms seek towards an optimized solution. Therefore, the best positions of these particles keep on updating at each iteration. The process is recursed until a reasonable solution is found. The PSO algorithm updates the internal weights of ANN using this iterative procedure [57].

4.7.2. Levenberg–Marquardt (LM) Algorithm

Levenberg–Marquardt algorithm is a hybrid method that incorporates both the steepest descent and Gauss–Newton approaches and is quite efficient for parameter extraction. An application of a system having a large number of parameters and non-linear least square problems in the application of a least squares curve fitting can be effectively solved using the LM method. LM uses this approximation to the Hessian matrix to compute the performance of the overall ANN network as represented in Equation (14) [58].

$$x_{k+1}=x_k-{\left[J^{T}J+\mu I\right]}^{-1}{J}^{T}e$$

(14)

Here, $J$ is a Jacobian matrix that is computed through the standard backpropagation method, and it compromises the first derivatives of the ANN network errors with respect to biases and weights of outputs and inputs, and the factor $\mu$ is a scalar quantity. During this commutative iterative process, the objective is to move towards the Gauss–Newton method swiftly since the Gauss–Newton method is pretty fast and precise near the minima of error. Thus, after each successful iteration, the µ is decreased so the process may become faster near error minima. The LM algorithm updates the internal weights of the ANN network using this iterative procedure [58].

5. Experimental Results and Discussions

To evaluate the effectiveness of the non-linear parametric models, specifically NN–LM with a single hidden layer, over the traditional statistical linear parametric models, such as ARX, ARMAX and OE, this section presents a comprehensive overview of quantitative and qualitative analysis based on the evaluation metrics as discussed below.

5.1. Selection of Evaluation Metrics

The evaluation of forecasting accuracy is quite important to obtain the measure of the model’s performance. The performance of the forecasting/prediction algorithms can be determined by using various error functions. The following key performance metrics are used to evaluate the model’s performance: Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), Root Mean Square Error (RMSE), R-square value and standard deviation, and the relevant formulas are given in Equations (15)–(19) [57]. Here $x_i$ represents the actual output value, $y_i$ represents the predicted/forecasted output value and $n$ represents the number of data points.

$$MAPE=\frac{1}{2}{\displaystyle \sum }_{i=1}^n\left|\frac{x_i-y_i}{x_i}\right|$$

(15)

$$MAE=\frac{{\Sigma }_{\mathrm{i}=1}^n\left|y_i-x_i\right|}{n}$$

(16)

$$\mathrm{RMSE}=\sqrt{\frac{{\Sigma }_{\mathrm{i}=1}^N{\left(x_i-y_i\right)}^2}{n}}$$

(17)

$$R^2=\frac{1-Sum Square Regression Error}{Sum Squared Total Error}$$

(18)

$$Standard Deviation \left(Std. Dev.\right)=\sigma =\sqrt{\frac{\Sigma {\left(x_i-\mu \right)}^2}{n}}$$

(19)

5.2. Experimental Background

First, the potential input parameters have been identified using a rigorous exploratory data analysis in Section 2. The temporal and seasonal potential input determined for our STLF model is shown in Table 1. The present electrical load is considered as the output for the training and testing of all the linear and non-linear algorithms.

The real-time electrical load data were recorded at 15 min intervals from 2017 to 2019 at an aggregated level (of the whole LESCO region). First, the data is segregated month-wise because the statistical and correlation analysis of every month was different from other months due to seasonality patterns in the yearly load curve. After the segregation, the entire data has been divided into two data sets. The training dataset consists of 2 years’ quarter-hourly electrical load data from 2017 to 2018. Whereas the remaining dataset, which consists of 1-year quarter-hourly data of 2019, is used for testing purposes. The training and testing of every month have been performed on an individual basis.

5.3. Experimental Analysis

First, the linear parametric models named ARX, ARMAX and OE have been deployed in MATLAB for the STLF problem. The predicted electrical load for every month of the year 2019 of the linear models is evaluated and compared using performance evaluation metrics. For instance, the MAPE of January for OE, ARX and ARMAX are 8.42, 6.82 and 5.12, respectively. Moreover, the other performance metrics, such as RMSE, MAE, R-square and standard deviation are also recapitulated in

Table 2. Quantitative comparison of alternative models for short-term electrical load forecasting of winter season.

Period (2019)	OE	ARX	ARMAX	KNN	Bagged Trees	SVM	NN–PSO	ANN–LM (Two Hidden Layer)	ANN–LM (Single Hidden Layer)	Errors
January	8.42	6.82	5.12	7.56	4.46	3.71	3.95	3.85	2.47	MAPE
	142.87	120.08	92.05	136.15	80.51	65.32	71.14	70.12	44.41	MAE
	173.14	155.08	120.25	172.14	105.12	87.08	95.42	90.94	57.96	RMSE
	0.65	0.72	0.83	0.65	0.87	0.91	0.89	0.90	0.96	$R^2$
	4.61	4.18	4.31	4.89	4.40	4.87	4.81	4.91	4.87	Std. Dev.
February	5.47	3.12	2.75	6.33	3.50	3.42	3.46	4.97	2.76	MAPE
	92.09	53.66	47.92	109.63	58.94	58.13	60.29	84.23	47.63	MAE
	110.57	72.15	66.10	143.71	83.81	77.19	81.73	123.62	66.33	RMSE
	0.83	0.93	0.94	0.71	0.90	0.92	0.91	0.78	0.94	$R^2$
	4.84	4.78	4.92	4.87	4.54	4.66	4.60	4.94	4.66	Std. Dev.
March	4.23	3.29	3.35	5.32	2.99	2.96	2.87	3.40	2.28	MAPE
	77.86	60.56	61.91	100.39	55.14	54.85	52.87	62.43	42.49	MAE
	127.84	94.33	95.23	129.94	77.47	76.48	77.88	87.49	60.54	RMSE
	0.75	0.86	0.86	0.74	0.91	0.91	0.91	0.88	0.94	$R^2$
	5.16	4.51	4.70	4.23	4.39	4.53	4.57	4.35	4.53	Std. Dev.
October	5.61	2.45	3.27	5.56	2.61	2.69	3.37	4.67	1.92	MAPE
	125.00	55.42	72.83	126.28	58.47	59.91	75.67	106.07	43.30	MAE
	145.49	86.89	103.54	161.38	85.10	85.89	101.08	147.06	64.47	RMSE
	0.74	0.91	0.87	0.69	0.91	0.91	0.88	0.74	0.95	$R^2$
	5.16	5.11	4.92	4.97	4.98	5.11	5.30	5.38	5.11	Std. Dev.
November	2.33	2.07	2.30	4.79	2.33	2.39	2.37	2.31	1.69	MAPE
	42.52	38.53	42.91	88.12	43.54	44.54	44.25	43.07	31.40	MAE
	121.26	54.34	58.60	113.30	59.01	59.66	59.66	60.27	43.90	RMSE
	0.74	0.95	0.94	0.77	0.94	0.94	0.94	0.93	0.97	$R^2$
	4.64	4.30	4.29	4.36	4.21	4.25	4.35	4.26	4.25	Std. Dev.
December	3.75	2.71	3.29	5.21	2.53	2.53	2.98	3.67	1.65	MAPE
	63.46	47.75	57.82	92.22	44.59	44.52	51.99	64.15	29.09	MAE
	85.93	62.62	74.29	122.25	60.64	58.16	67.83	84.84	38.26	RMSE
	0.90	0.95	0.93	0.80	0.95	0.96	0.94	0.91	0.98	$R^2$
	5.59	4.72	4.56	4.92	4.74	4.84	4.73	4.89	4.84	Std. Dev.

and

Table 3. Quantitative comparison of alternative models for short-term electrical load forecasting of summer season.

Period (2019)	OE	ARX	ARMAX	KNN	Bagged Trees	SVM	NN–PSO	ANN–LM (Two Hidden Layer)	ANN–LM (Single Hidden Layer)	Errors
April	4.46	2.26	3.05	6.49	3.58	2.98	2.64	3.26	2.24	MAPE
	105.40	53.03	72.20	153.69	79.79	68.90	59.49	76.41	52.98	MAE
	258.59	108.92	119.80	206.89	132.18	111.25	94.67	103.62	76.53	RMSE
	0.50	0.91	0.89	0.68	0.87	0.91	0.93	0.92	0.96	$R^2$
	7.82	6.48	6.54	5.36	6.06	6.33	6.33	6.55	6.33	Std. Dev.
May	2.37	4.30	3.50	5.83	3.41	2.60	3.18	2.66	1.99	MAPE
	72.45	123.04	104.10	180.37	104.95	76.89	97.64	82.61	61.28	MAE
	104.58	180.15	160.74	234.70	152.99	118.70	143.03	113.82	84.12	RMSE
	0.93	0.78	0.83	0.64	0.85	0.91	0.87	0.92	0.95	$R^2$
	6.60	6.82	6.58	6.17	5.95	6.74	6.17	6.47	6.74	Std. Dev.
June	3.71	2.86	3.82	6.36	3.05	2.43	2.44	3.00	1.81	MAPE
	120.38	90.67	122.98	209.54	99.10	75.53	79.60	98.41	58.77	MAE
	186.74	143.48	171.35	269.87	152.86	130.70	113.97	126.41	82.45	RMSE
	0.75	0.85	0.79	0.48	0.83	0.88	0.91	0.89	0.95	$R^2$
	6.67	6.26	5.96	5.63	5.67	6.33	6.34	5.99	6.33	Std. Dev.
July	5.19	2.44	2.59	5.24	3.40	2.48	4.43	4.43	1.82	MAPE
	178.29	77.40	82.01	170.63	112.84	77.61	151.55	148.24	59.70	MAE
	217.83	141.37	148.72	242.24	177.35	144.56	205.33	197.60	95.08	RMSE
	0.73	0.89	0.87	0.67	0.82	0.88	0.76	0.78	0.95	$R^2$
	9.19	7.45	7.30	6.25	6.47	7.39	6.38	7.23	7.39	Std. Dev.
August	2.72	1.75	1.72	3.62	2.13	1.70	2.68	5.91	1.72	MAPE
	90.93	57.95	56.84	123.59	72.35	56.22	88.81	204.76	57.19	MAE
	126.50	95.93	99.05	165.82	110.31	92.61	133.20	253.36	90.37	RMSE
	0.84	0.91	0.90	0.73	0.88	0.92	0.82	0.37	0.92	$R^2$
	5.39	5.30	5.48	4.79	5.06	5.45	4.95	3.20	5.45	Std. Dev.

. The values reveal that ARMAX performs comparatively better than OE and ARX models for January. ARMAX mainly consists of two hyperparameters. The first parameter relates to the order of the Auto-Regressive (AR) process, which acquires the pattern of lag values of electrical load data. The second prominent parameter is the Moving Average (MA), which is used for obtaining the trends between potential input features in electrical load data. ARMAX model is suitable when there is a strong auto-correlation between the present electrical load and the lagged values of an electrical load. January has a strong auto-correlation between the present electrical load and the lagged values of an electrical load. Therefore, ARMAX would be able to capture the lagged values of electrical load and the local trends between the nominated input features comparatively better than OE and ARX. ARMAX also detected the peak load and sudden change of electrical load accurately in Figure 4b than the rest of the linear parametric models. Conversely, the ARMAX does not map the predicted and actual load accurately for the month of June as shown in Figure 5b. Similarly, the bar chart represented in Figure 6a between aforesaid statistical models suggests that for some months of the year, such as April, ARX performs better than the ARMAX. The MAPE for ARX and ARMAX for April is 2.26 and 3.05, respectively. ARX is effective when there is a weak auto-correlation between the present electrical load and the lagged values of an electrical load. The month of April has weak auto-correlation between the present electrical load and the lagged values of an electrical load as illustrated in Figure 7. Thus, ARX shows less MAPE as compared to ARMAX. Further qualitative analysis between the statistical parametric models concludes that other forecasting errors, such as RMSE, MAE, R-square and standard deviation of the statistical models as indicated in Table 2 and Table 3, are still at a higher level. The said forecasting errors suggest that there should be a further advancement in the STLF models so that the error functions can be reduced for a more superior prediction of electrical load. Moreover, Figure 4a–c and Figure 5a–c also shows that the above-mentioned linear models are incapable of forecasting electrical load peaks and abrupt changes in the load consumption, which is quite important for managing hot and cold reserves in power systems.

Next, the five non-linear parametric STLF models, such as KNN, Bagged Trees, SVM, NN–PSO and ANN–LM with one and two hidden layers have been employed for the same STLF problem. The ANN–LM models were trained on different learning rates and the number of neurons to obtain the best possible forecasting results. The quantitative analysis of the above-mentioned non-linear models is also performed for every month of the year to validate the performance of non-linear models in the presence of highly diversified non-linear factors, such as temperature and humidity. The forecasting errors are also mentioned in Table 2 and Table 3. Considering the month of January of the year 2019, the KNN achieve the MAPE values of 7.56. While the Bagged Trees, SVM, NN–PSO, ANN–LM with one dense layer and ANN–LM with two dense layers achieve the MAPE values of 4.46, 3.71, 3.95, 3.85 and 2.47, respectively. Bagged Tree significantly improves the error compared to the KNN for STLF. The KNN has only one hyperparameter denoted by “K”, which determines the number of neighbors from which similar instances have been deduced. Due to an insufficient number of parameters and lack of capability of adding regularization effect in KNN, the KNN experiences the overfitting problem which limits the forecasting performance. Therefore, the KNN may not be able to match the peaks of the predicted electrical load with the peaks of the actual electrical load as shown in Figure 4d. Therefore, KNN degrades the accuracy of the STLF model while Bagged Tree ensures better forecasting results by matching the peaks of the predicted and actual electrical load as illustrated in Figure 4e and Figure 5e. The SVM also yields fewer errors in the prediction of one-step-ahead electrical load as compared to the KNN and the Bagged Trees algorithms if the tunning hypermeters are wisely selected. Therefore, the SVM delivers the closest match between the peaks of the forecasts and the actual electrical load as depicted in Figure 4f and Figure 5f. Due to the limitations of the hyperparameters running in SVM, SVM cannot be improved further. NN–PSO, which is a metaheuristic-based NN model, also fails to remove the shortcomings of the above-discussed non-linear parametric models because they are unable to converge globally. Eventually, NN–PSO renders slightly higher MAPE than SVM for January, and the peak detection of NN–PSO is also more inadequate than SVM. At last, a sufficient improvement in the minimization of the forecasting errors has been observed when the ANN–LM model with one and two dense layers have been considered for the STLF problem. The MAPE of ANN–LM, which implements one dense layer, is 2.74, which is relatively less than the remaining above-mentioned non-linear ML models. The higher MAPE values of two hidden layers ANN–LM, as compared to MAPE values of one hidden layer ANN–LM, suggests that the former model of ANN–LM delivers higher forecasting errors due to increase in the complexity of the model. Moreover, ANN–LM with two dense layers may lose generalization capability due to how the impact of the overfitting issue increases with the increase in hidden layers [59]. However, the single hidden layer ANN–LM model is simple and does not experience overfitting. The difference in the MAPE values of the above-mentioned linear and non-linear parametric methodologies also shows the validity of a single hidden layer ANN–LM over other discussed STLF methodologies as represented in the bar chart, Figure 6b. The bar chart also suggests that a single hidden layer ANN–LM also produces fewer MAPE values for the rest of the year, which reveals the stability of ANN–LM when implemented with one hidden layer over the remaining aforesaid non-linear ML models. Therefore, ANN–LM with one hidden layer can extract both linear and non-linear relationships between the electrical load and the seasonal trends. A one hidden layer ANN–LM also generates the strongest match between the forecasted and the actual electric load, especially during the peak load and the valley load as shown in Figure 4h and Figure 5h.

We extend our analysis by comparing the forecasting performance of different linear and non-linear models in order to authenticate which algorithm can effectively perceive the real electrical load pattern in both winter and summer seasons. For this purpose, two months have been selected. The month of January generally represents the winter season. Whereas June relates to summer. In winter, the consumption of electrical load decreases in Pakistan due to the low temperature. Therefore, the efficient STLF model should find the closest match between the actual and forecasted electrical load for the months of January and June, which will ensure that the algorithm remains reliable and stable even the season undergoes different variations. As far as the best results of ANN–LM architecture are concerned, ANN–LM with a single hidden layer achieves MAPE of 2.47 and 1.81 for January and June as mentioned in Table 2 and Table 3, which is the lowest MAPE value compared to the other under-considered linear and non-linear parametric models. The illustrations in Figure 4 and Figure 5 explain that the ANN–LM with a single hidden layer forecasts the electrical load pattern accurately in both seasons as compared to the above-mentioned linear and non-linear parametric models. Similarly, the detection of peak load and the valley load is relatively finer in a single hidden layer ANN–LM than other parametric models. A single hidden layer ANN–LM enhances the efficiency of the STLF model due to the following reasons:

• A single layer ANN–LM is different from conventional ANN which uses ANN with regularization parameters. The regularization parameter enables ANN to overcome the overfitting problem.
• A single layer NN–LM improves the training accuracy by using a more advanced optimization algorithm termed as Levenberg–Marquardt (LM).

Considering the above-discussion and quantitative and qualitative analysis based on different forecasting errors, one hidden layer ANN–LM delivers fewer forecasting errors among all the linear and non-linear parametric methodologies. Similarly, ANN–LM with a one hidden layer forecasts the consumed electrical load accurately by detecting the non-linear temporal and seasonal variations accurately. This paper proposes the use of the ANN–LM algorithm with one hidden layer for the STLF problem, especially for those electric utilities, rather than conventional statistical methodologies.

6. Conclusions

This research paper discusses the effectiveness of eight different state-of-the-art linear and non-linear parametric methodologies, i.e., OE, ARX, ARMAX, KNN, Bagged Trees, SVM, NN–PSO, a single hidden layer ANN–LM and a two hidden layer ANN–LM, on real-time electrical load data for STLF problems. The temporal and climatic factors are also embedded as input parameters in STLF models after careful statistical correlation analysis. A quantitative and qualitative comparison based on different evaluation metrics, such as MAPE, RMSE, MAE, R-square and standard deviation, has been accomplished among the aforesaid linear and non-linear parametric modeling techniques. By assessing the MAPE values of the above-stated linear and non-linear methodologies, ANN–LM with one hidden layer generates less error for all the months of the year as compared to the errors of other foregoing linear and non-linear methodologies.

The efficacy of ANN–LM, when deployed with one hidden layer in the STLF problem, is also observed in the case of seasonal variations. Experimental results explain that the ANN–LM with one hidden layer detects the peaks of the electrical load in both the winter and summer seasons relatively better than the rest of the other linear and non-linear parametric methodologies used in this research. Therefore, a single hidden layer ANN–LM forecasts the electrical load accurately.

Finally, the explanation due to which a single hidden layer ANN–LM shows an improvement for predicting the electrical load is discussed in brief to motivate those electrical utilities which merely depend on conventional statistical methodologies. At last, the ANN–LM with one dense layer is recommended as a reliable STLF model for accurate electrical load forecasting.

In the expansion of the presented research work, we will look over the following future directions: (a) multi-step ahead STLF using neural networks to predict multiple hours or even days ahead forecast and (b) deep-learning-based STLF to achieve a much accurate prediction of load peaks.