Independent Upper- and Lower-Arm Switching Scheme Based on Reference Current Polarity for Three-Level NPC Inverters
Abstract
:1. Introduction
2. 3 Phase Three-Level NPC Inverter
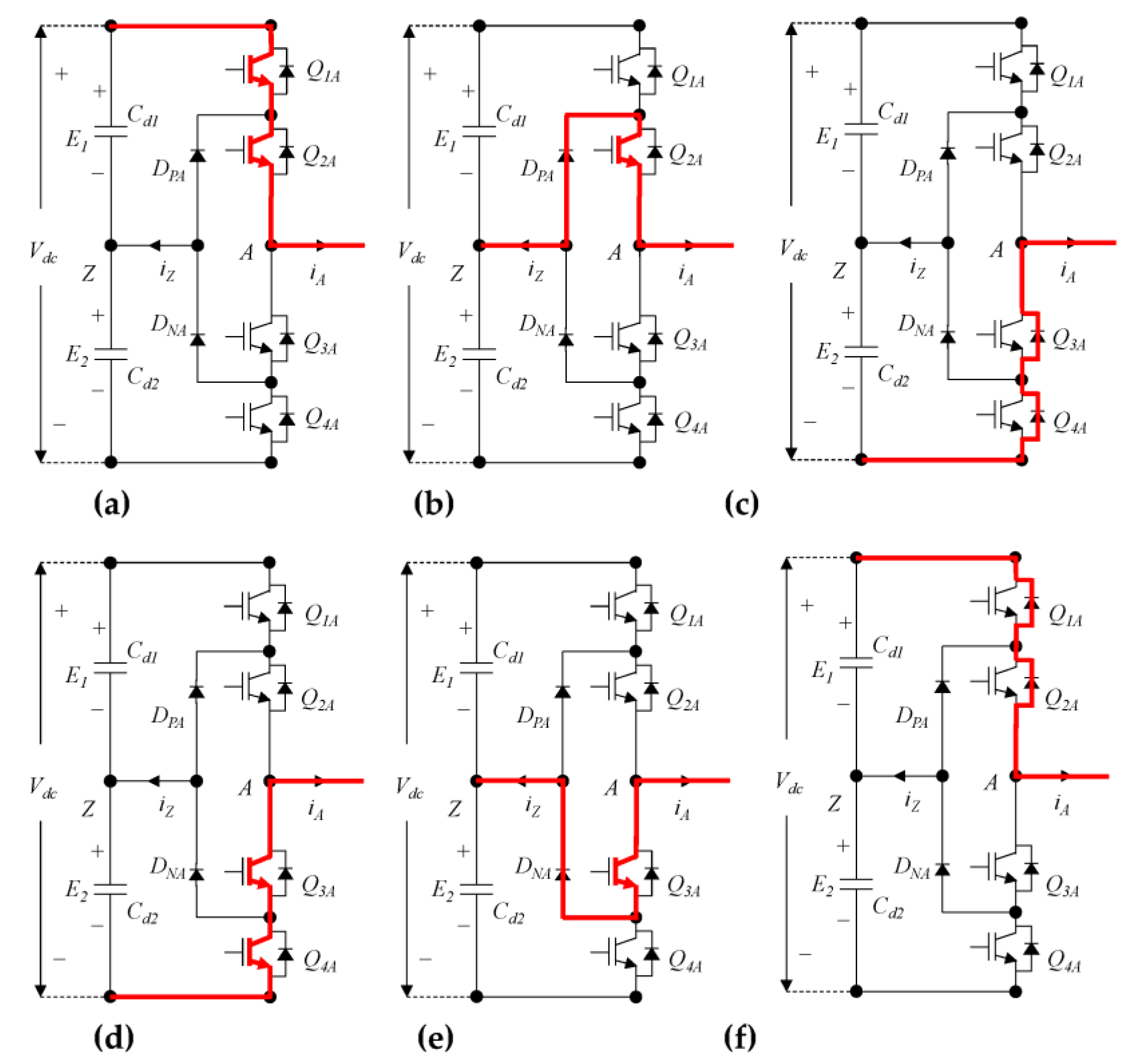
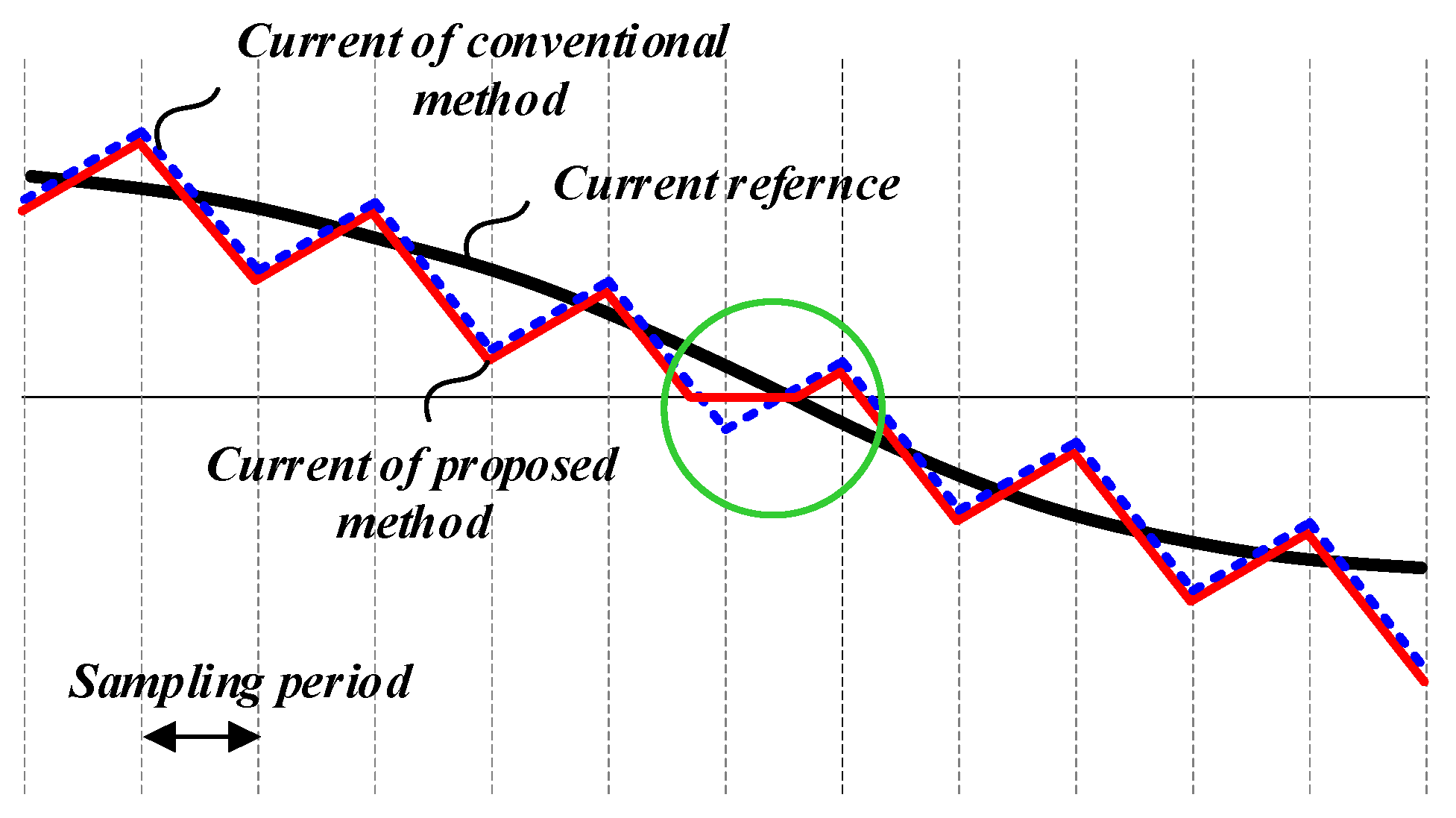
3. Proposed Switching Scheme
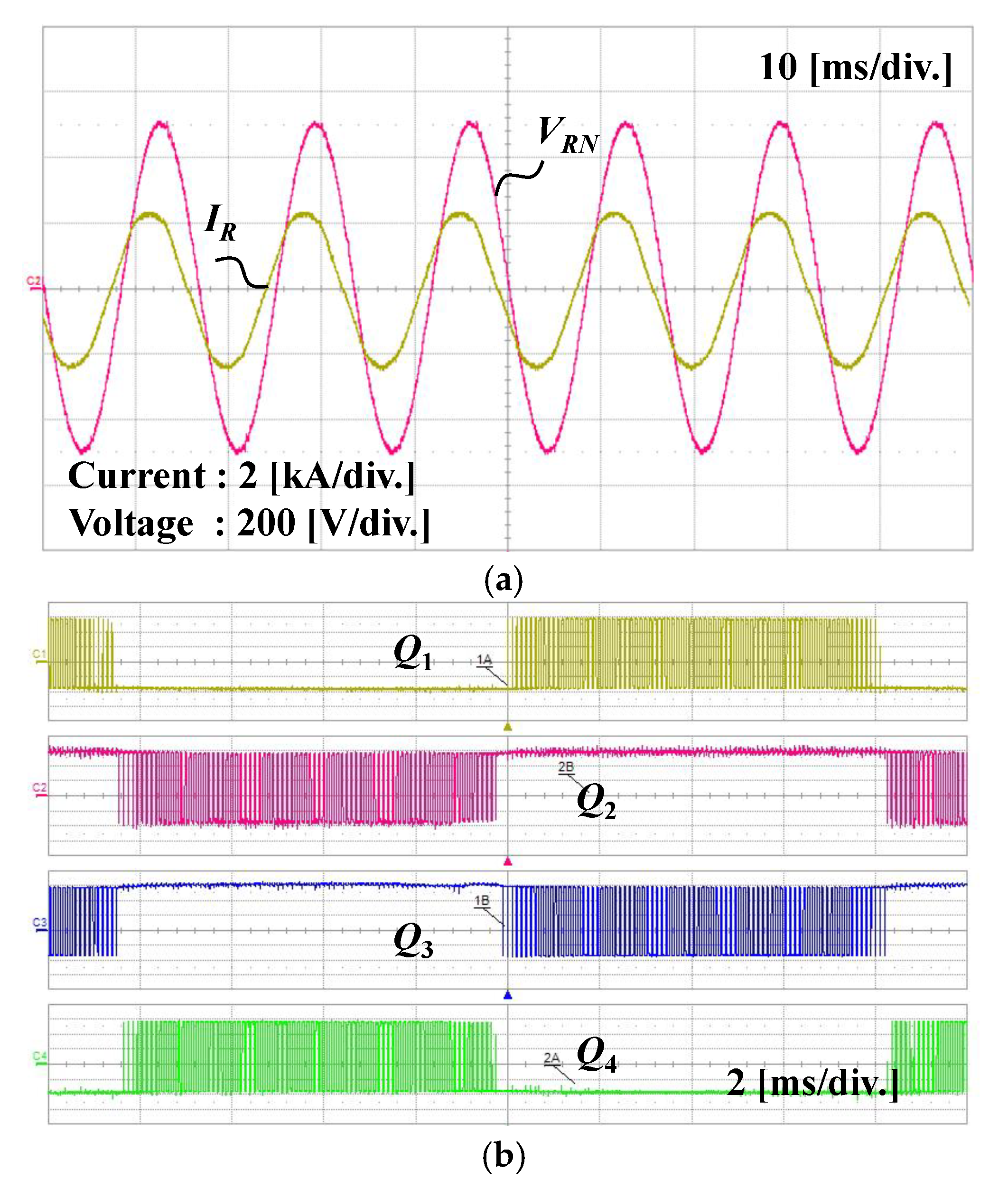
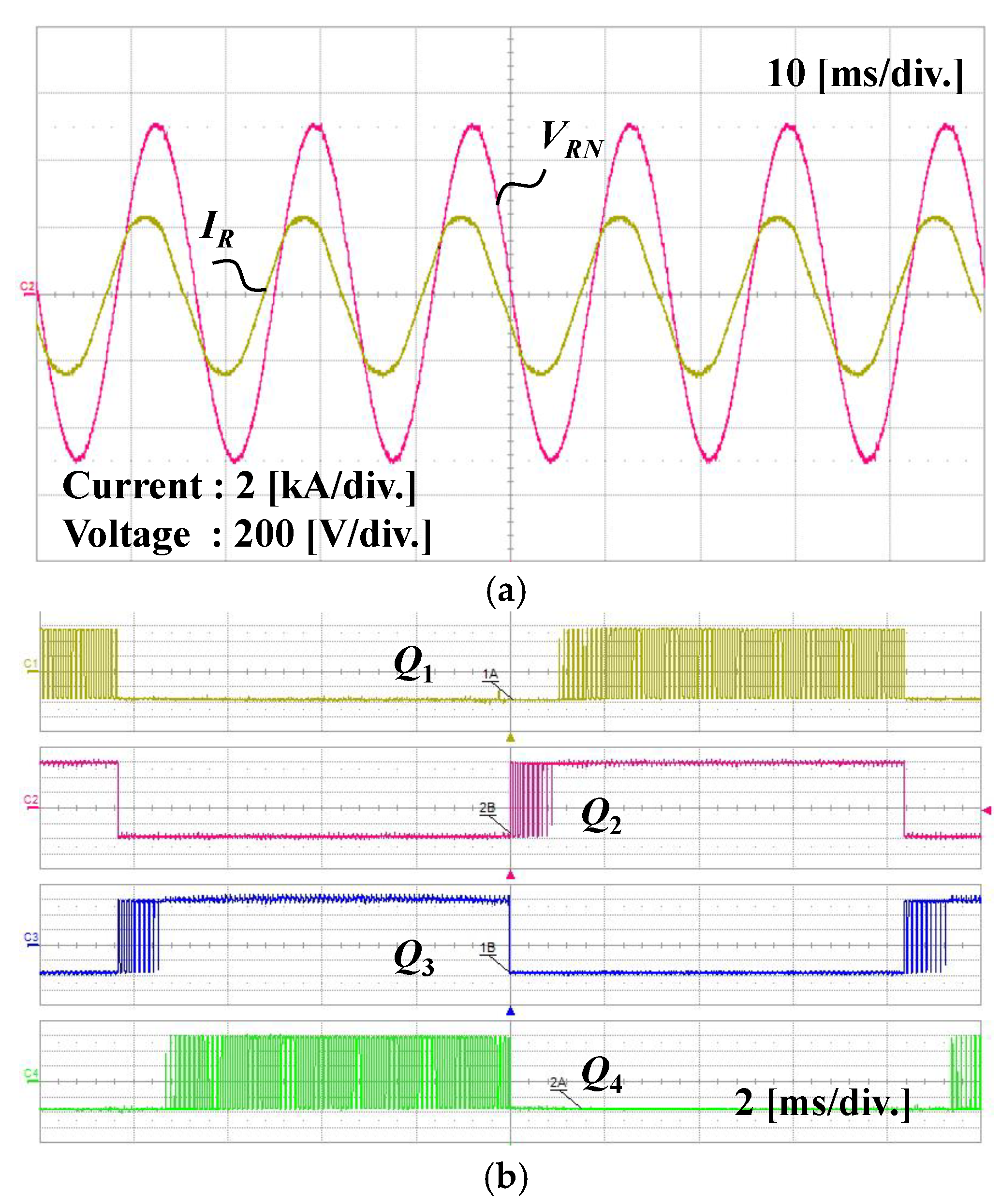
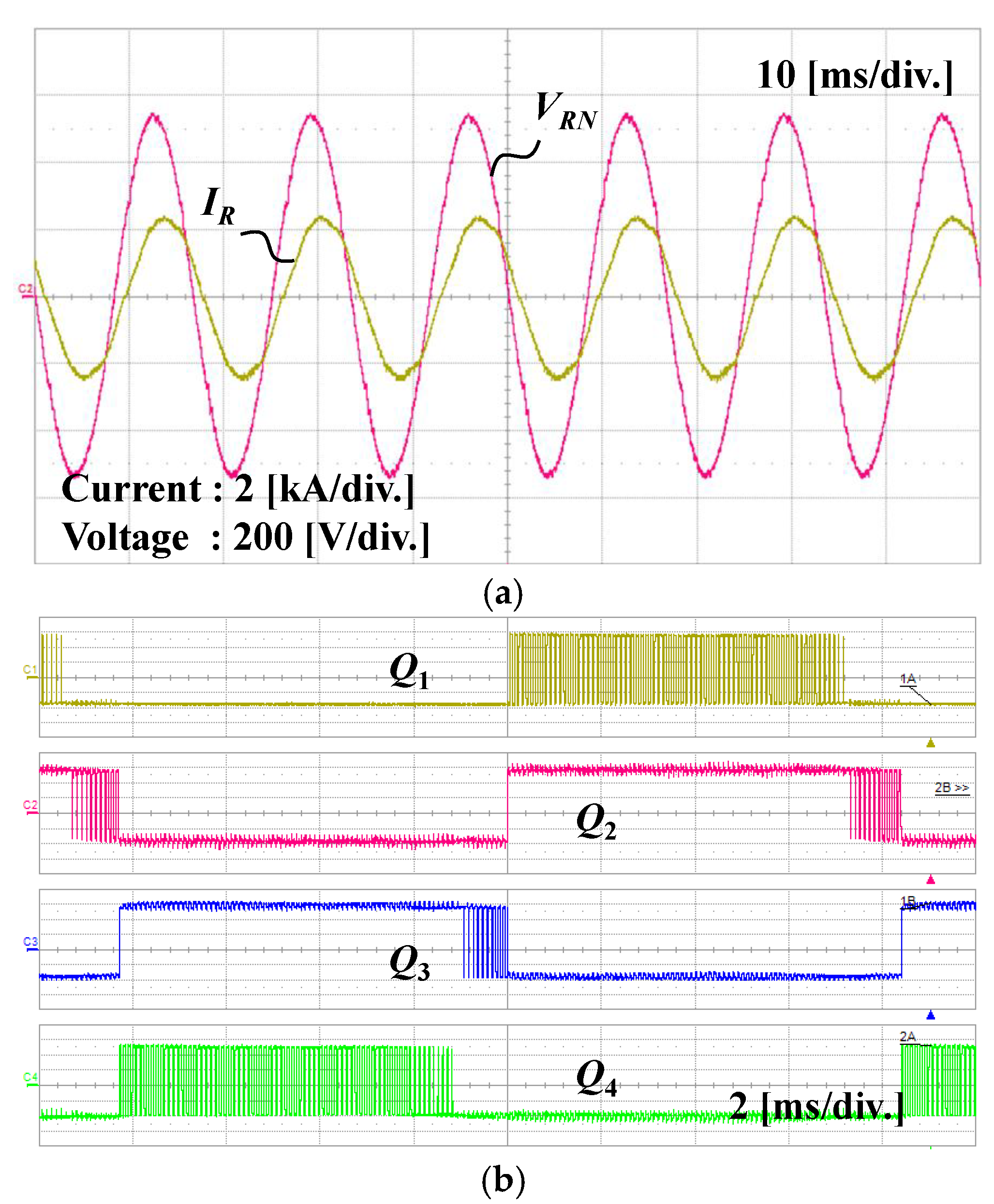
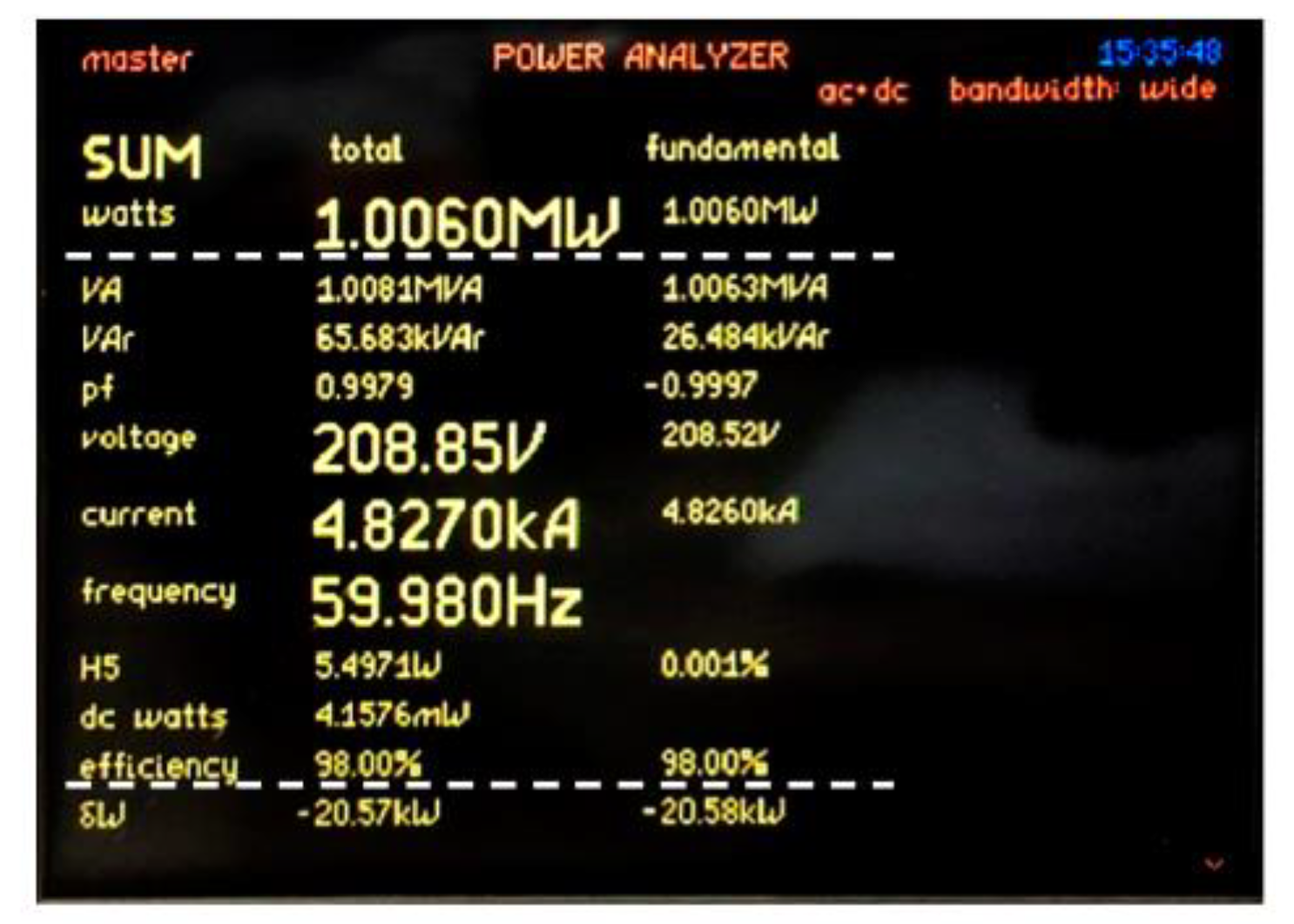
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shibata, N.; Tanaka, T.; Kinoshita, M. Development of a 3.2MW Photovoltaic Inverter for Large Scale PV Power Plants. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 ECCE Asia), Niigata, Japan, 20–24 May 2018; p. 39293933. [Google Scholar]
- Yan, C.; Xu, D. Design Study of MW Photovoltaic Inverter. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; p. 16. [Google Scholar]
- Li, H.; Li, Y.; Ge, Q. Dead Time Compensation of 3Level NPC Inverter for Medium Voltage IGCT Drive System. In Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; p. 35243528. [Google Scholar]
- Dolguntseva, I.; Krishna, R.; Soman, D.; Leijon, M. Contour Based Dead-Time Harmonic Analysis in a Three-Level Neutral Point Clamped Inverter. IEEE Trans. Ind. Electron. 2015, 62, 203210. [Google Scholar] [CrossRef]
- Jing, G.; Xuegeng, G.; Feng, Z.; Xuhui, W. A Strategy Novel Dead-time Compensation of Three-level Inverter. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Beijing, China, 31 August–3 September 2014; p. 15. [Google Scholar]
- Piao, C.; Hung, J. Analysis and Compensation of Dead-Time Effect in Multi-Level Diode Clamped VSI Based on Simplified SVPWM. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications, Auckland, New Zealand, 15–17 June 2015; p. 375380. [Google Scholar]
- Li, X.; Akin, B.; Rajashekara, K. Vector Based Dead-Time Compensation for Three-Level T-Type Converters. IEEE Trans. Ind. Appl. 2016, 52, 15971607. [Google Scholar]
- Wang, S.; Song, W.; Ma, J.; Zhao, J.; Feng, X. Study on Comprehensive Analysis and Compensation for the Line Current Distortion in Single-Phase Three-Level NPC Converters. IEEE Trans. Ind. Electron. 2018, 65, 21992211. [Google Scholar] [CrossRef]
- Niu, J.; Chen, R.; Zhang, Z.; Gui, H.; Wang, F.; Tolbert, L.; Blal, B.; Costinett, D.; Choi, B. Analysis of Circulating Harmonic Currents in Paralleled Three Level ANPC Inverters using SVM. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 17–21 March 2019; p. 24812487. [Google Scholar]
- Sprenger, M.; Alvarez, R.; Bernet, S. Direct Dead-Time Control—A Novel DC-Link Neutral-Point Balancing Method for the Three-Level Neutral-Point-Clamped Voltage Source Inverter. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 5–20 September 2012; p. 11571163. [Google Scholar]
- Kulkarni, A.; Mazumder, S. Deadtime Elimination in a GaN-Based Grid-Connected Differential-Mode Ćuk Inverter. IEEE Trans. Ind. Electron. 2019, 66, 32963302. [Google Scholar] [CrossRef]
- Yuan, J.; Zhao, Z.; Chen, B.; Li, C.; Wang, J.; Tian, C.; Chen, Y. An Immune-Algorithm-Based Dead-Time Elimination PWM Control Strategy in a Single-Phase Inverter. IEEE Trans. Power Electron. 2015, 30, 39643975. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, R.; Yuan, X.; Ma, W.; He, J. A DSOGI-FLL-Based Dead-Time Elimination PWM for Three-Phase Power Converters. IEEE Trans. Power Electron. 2019, 34, 28052818. [Google Scholar] [CrossRef]
- Cho, K.; Oh, W.; Kim, Y.; Kim, H. A New Switching Strategy for Pulse Width Modulation (PWM) Power Converters. IEEE Trans. Ind. Electron. 2007, 54, 330337. [Google Scholar] [CrossRef]
- Kan, Y.; Hyun, S.; Hong, S.; Won, C. Zero Deadtime PWM Implementation Method for Reducing Total Harmonic Distortion in 3Level NPC Inverter. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; p. 10691073. [Google Scholar]
- Hyun, S.; Hong, S.; Won, C. A Compensation Method to Reduce Sampling Delay of Zero Dead-Time PWM Using 3Level NPC PWM Inverter. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, Korea, 1–4 June 2016; p. 465469. [Google Scholar]
- Alawieh, H.; Riachy, L.; Tehrani, K.; Azzouz, Y.; Dakyo, B. A New Dead-Time Effect Elimination Method for H-bridge Inverters. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; p. 31533159. [Google Scholar]
- Ahn, K.; Oh, Y.; Cho, K. A Study on the Development of a 1 MW Grid-Connected Photovoltaic Inverter System. In Proceedings of the IEEE 60th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 7–9 October 2019; p. 19. [Google Scholar]
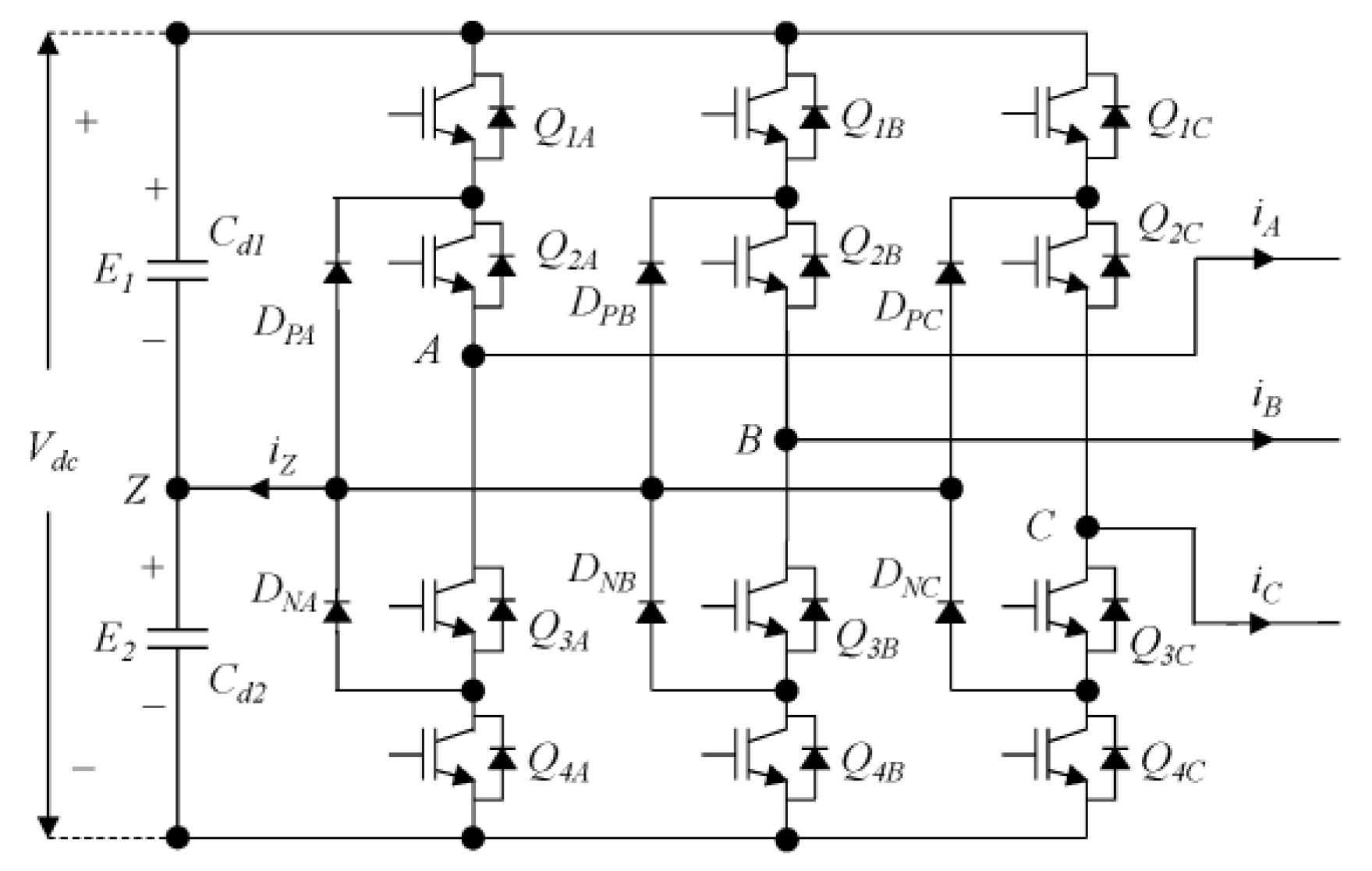
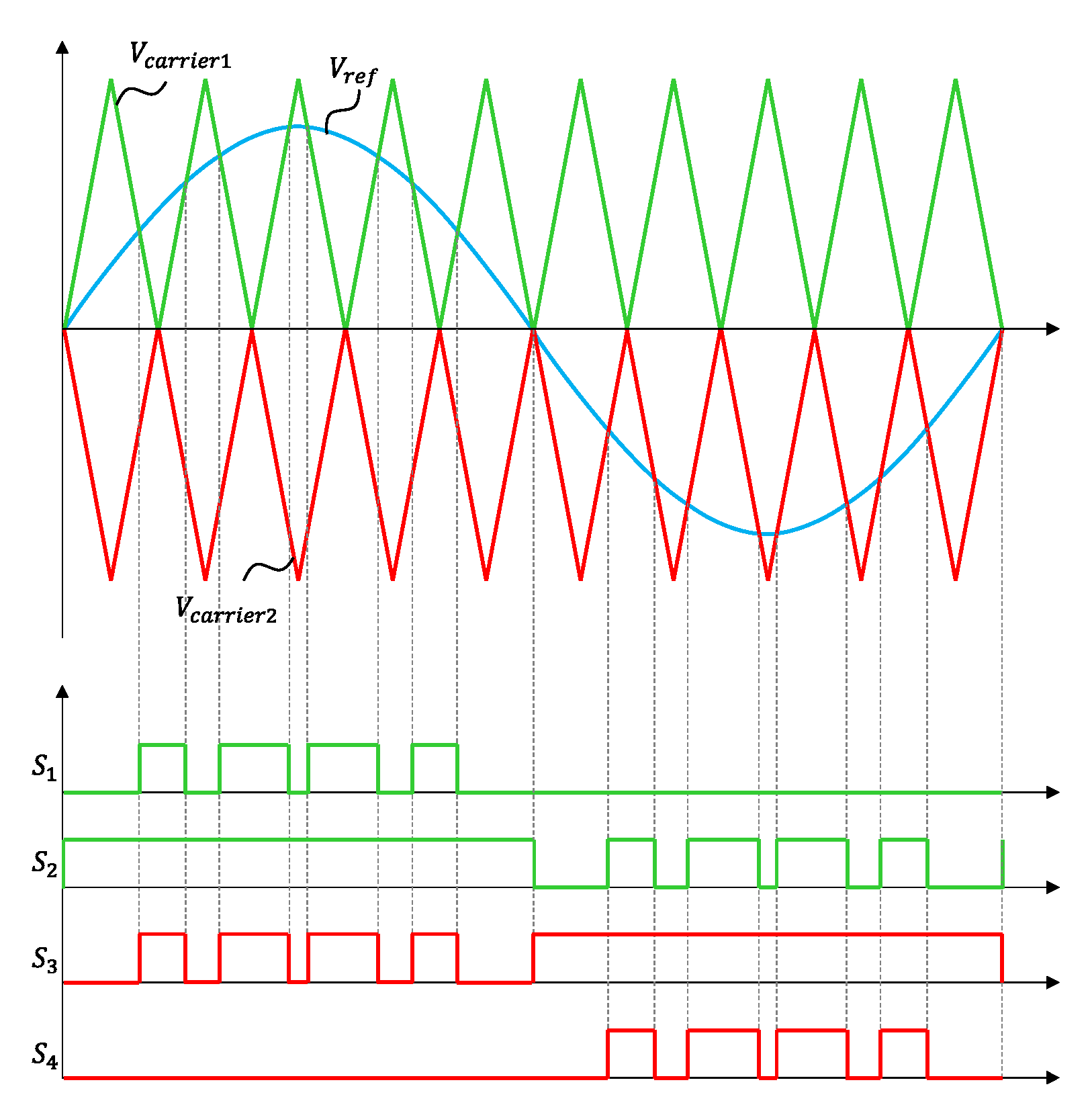
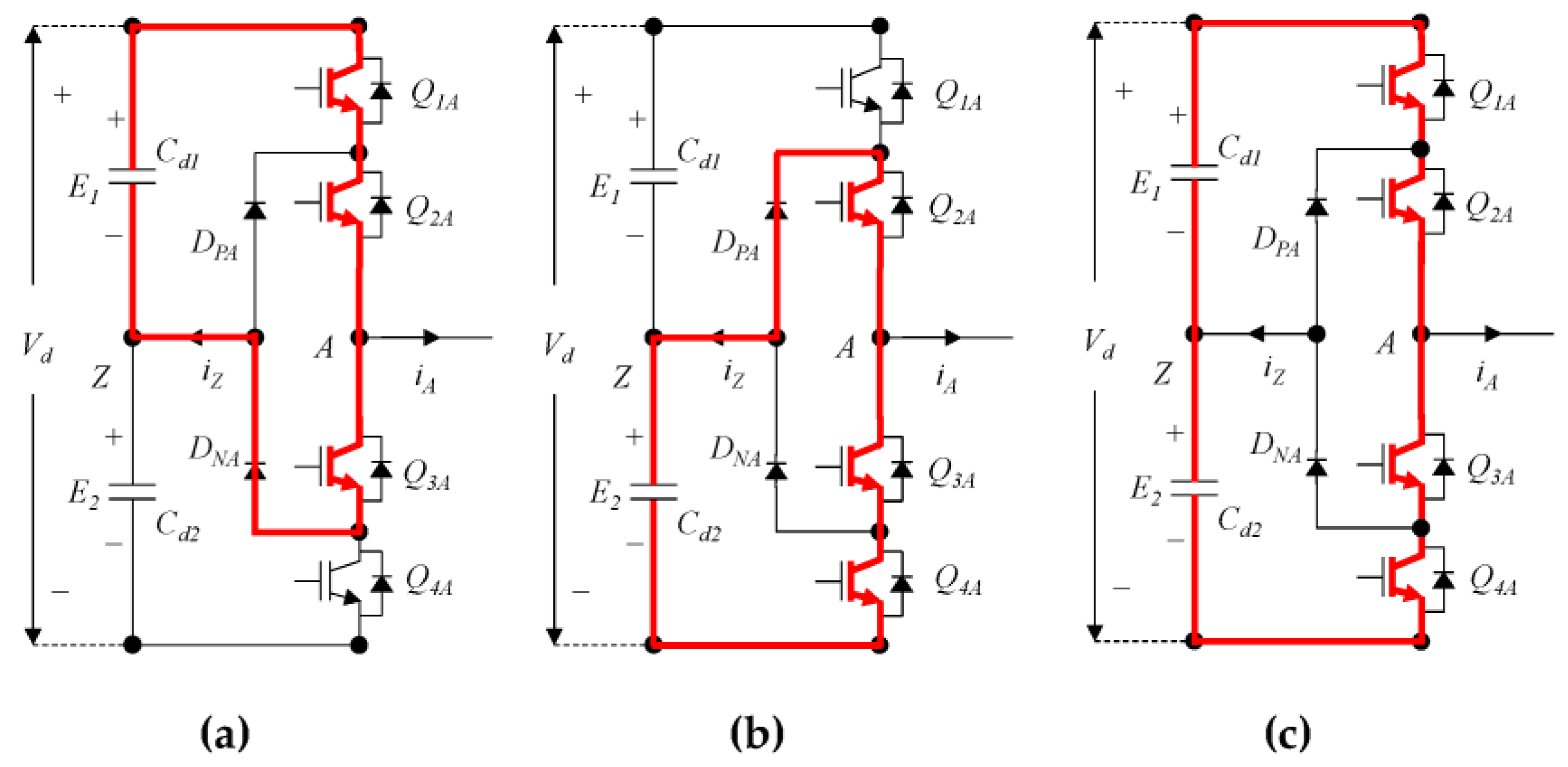
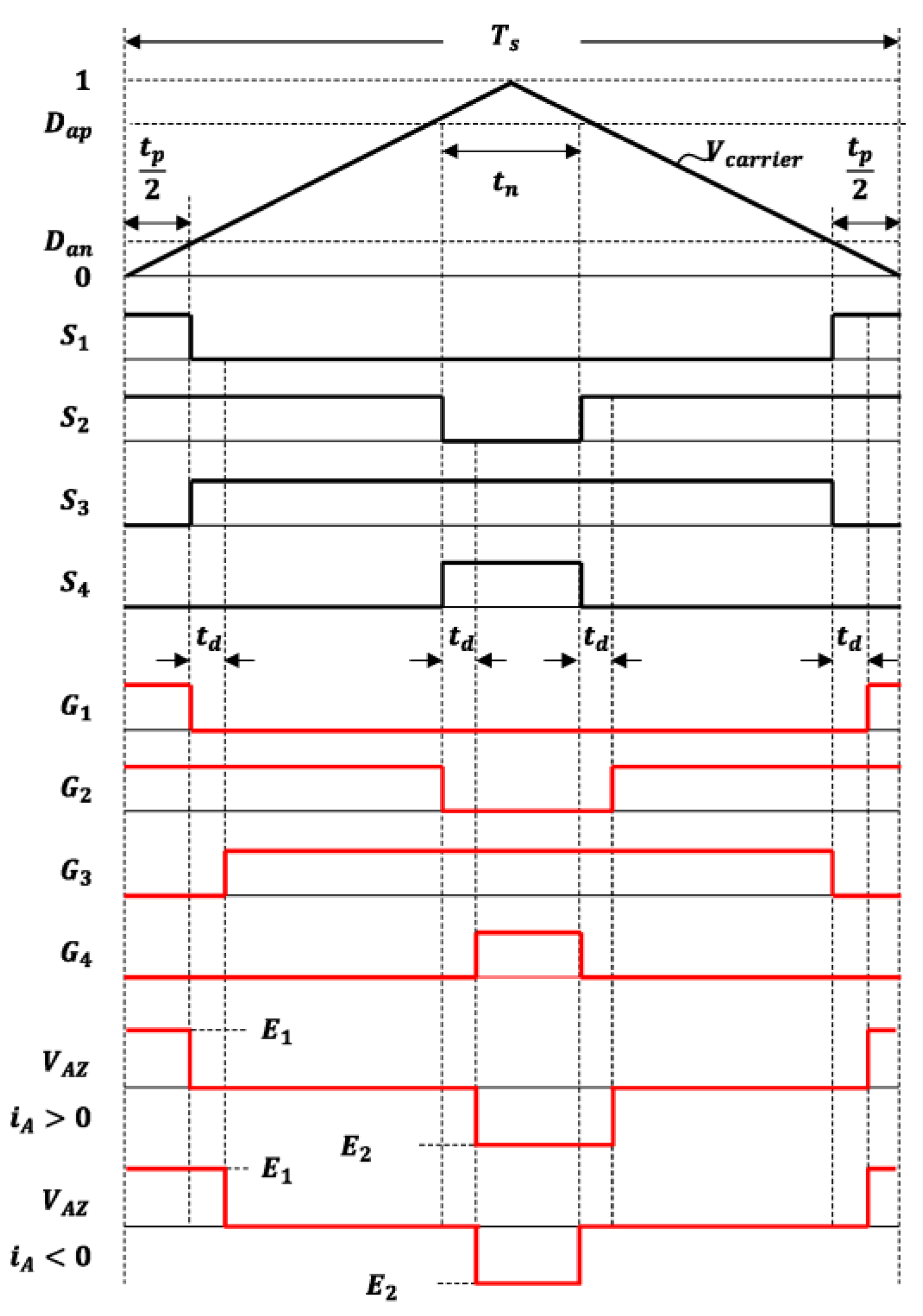










| Switching Mode | Switching Signal | Expected Inverter Terminal Voltage VAZ | |||
|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | ||
| P | On | On | Off | Off | E1 |
| O | Off | On | On | Off | 0 |
| N | Off | Off | On | On | −E2 |
| Conduction Mode | Switch Status | Terminal Voltage VAZ/VBZ/VCZ | |||
|---|---|---|---|---|---|
| Q2 | Q2 | Q3 | Q4 | ||
| PP | On | On | Off | Off | E1 |
| PO | Off | On | Off | Off | 0 |
| OO | Off | Off | Off | Off | E1 (I < 0)/−E2 (I > 0) |
| NO | Off | Off | On | Off | 0 |
| NN | Off | Off | On | On | −E2 |
| Operation Mode | Current Reference Polarity | Voltage Polarity | Conduction Mode |
|---|---|---|---|
| Mode-I | Positive | Positive | PP/PO |
| Mode-II | Positive | Negative | PO/OO |
| Mode-III | Negative | Negative | NN/NO |
| Mode-IV | Negative | Positive | NO/OO |
| A-C Conduction Mode | Conduction Mode of Phase A | Conduction Mode of Phase C | A-C Line to Line Voltage |
|---|---|---|---|
| Mode-1 | PP | NN | E1 + E2 |
| Mode-2 | PP | NO | E1 |
| Mode-3 | PP | OO | 0 |
| Mode-4 | PO | NN | E2 |
| Mode-5 | PO | NO | 0 |
| Mode-6 | PO | OO | −E1 |
| Mode-7 | OO | NN | 0 |
| Mode-8 | OO | NO | −E2 |
| Mode-9 | OO | OO | −E1 − E2 |
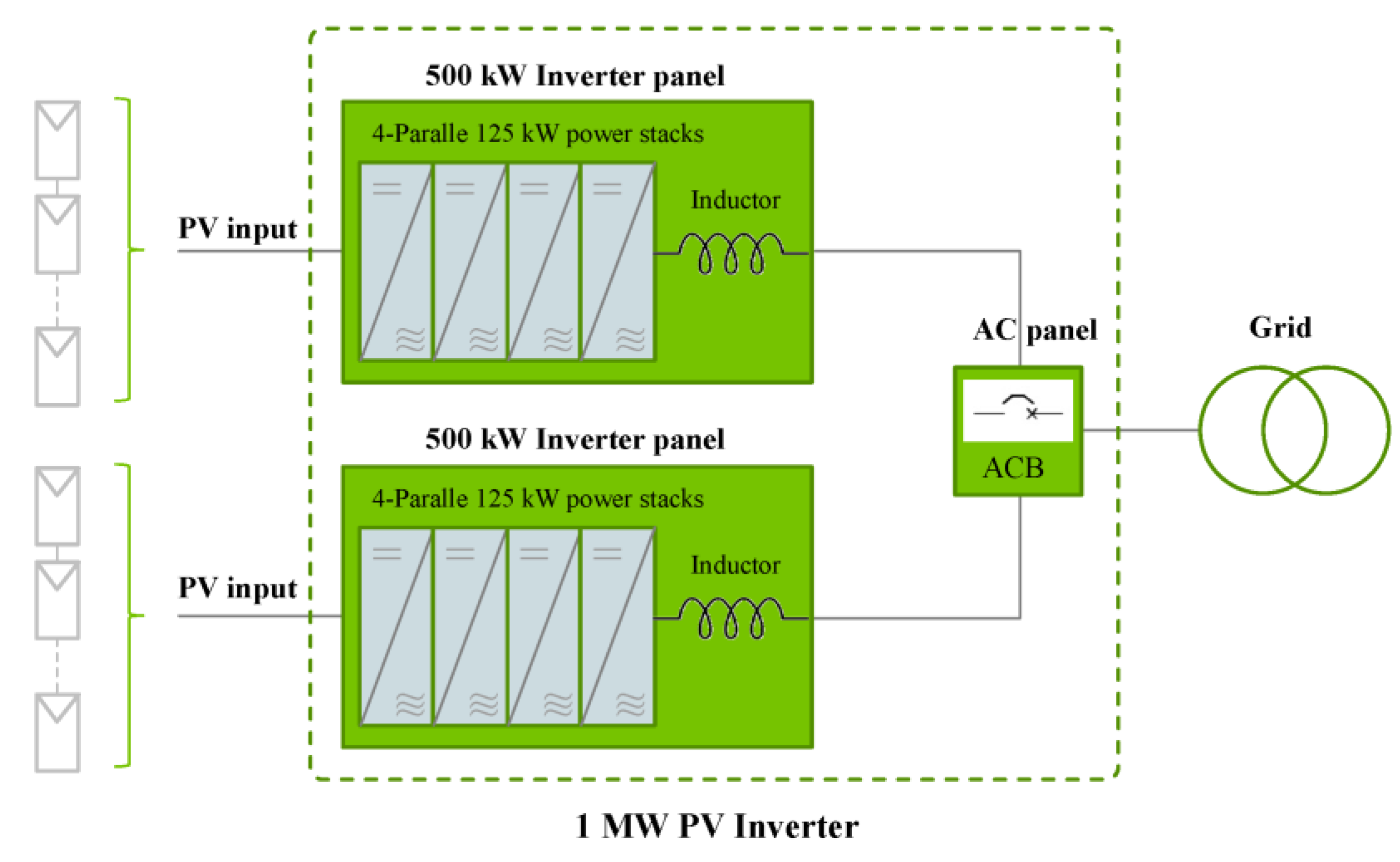
| Item | Value | |
|---|---|---|
| Input | PV voltage (max) | 1000 V |
| Operation voltage range | 550–1000 V | |
| MPPT voltage range | 550–1000 V | |
| PV current (max) | 1652.8 A | |
| Output | Power | 1000 kW |
| Frequency | 60 Hz (59.3–60.5) | |
| Voltage | 340 V (3Φ3W) | |
| Current (max) | 1698 A | |
| ETC | Operating temperature | −20–50 °C |
| IP degree | IP44 | |
| Cooling | Forced air | |
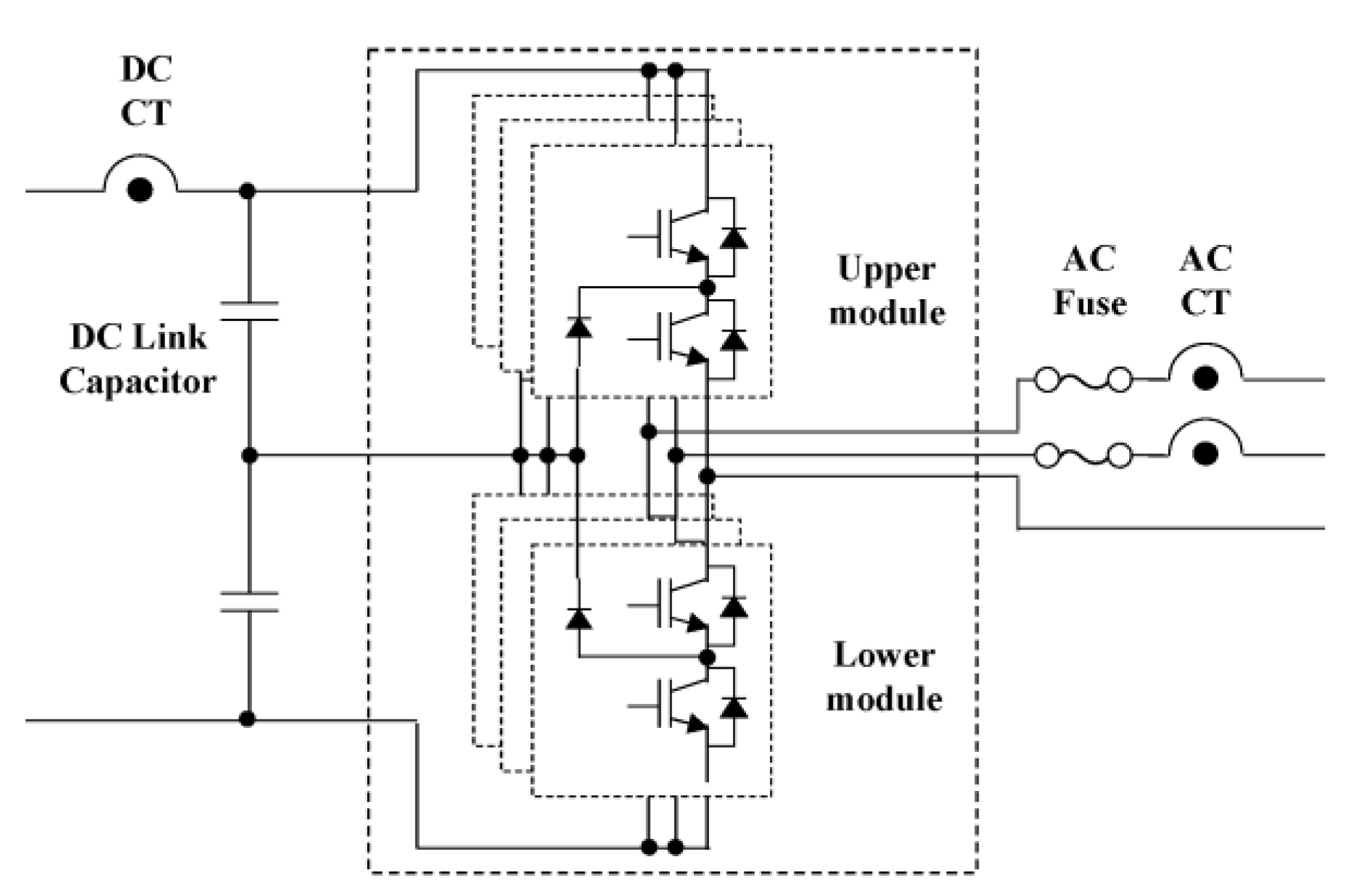
| Item | Value |
|---|---|
| DC CT | 300 A |
| DC link capacitor | 1000 μF/700 V 3P2S |
| IGBT Module (upper) | 650 V/400 A 3 EA |
| IGBT Module (lower) | 650 V/400 A 3 EA |
| AC Fuse | 700 V/300 A |
| AC CT | 300 A |
| Item | Value |
|---|---|
| Power stack | 125 kW 4P |
| DC Fuse | 630 A, 1000 V 2P |
| DC SPD | 1000 V/40 kA |
| DC EMI Core | Nano crystal/200 mm |
| DC Switch | 1000 A/1000 V |
| Filter inductor | 0.1 mH/1000 A |
| Filter capacitor | 40 μF/450 V 4P |
| MC | 1260 A/1000 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, K.; Oh, Y.; Oh, W.; Cho, K. Independent Upper- and Lower-Arm Switching Scheme Based on Reference Current Polarity for Three-Level NPC Inverters. Energies 2021, 14, 5535. https://doi.org/10.3390/en14175535
Ahn K, Oh Y, Oh W, Cho K. Independent Upper- and Lower-Arm Switching Scheme Based on Reference Current Polarity for Three-Level NPC Inverters. Energies. 2021; 14(17):5535. https://doi.org/10.3390/en14175535
Chicago/Turabian StyleAhn, Kangsoon, Yongseung Oh, Wonseok Oh, and Kyumin Cho. 2021. "Independent Upper- and Lower-Arm Switching Scheme Based on Reference Current Polarity for Three-Level NPC Inverters" Energies 14, no. 17: 5535. https://doi.org/10.3390/en14175535
APA StyleAhn, K., Oh, Y., Oh, W., & Cho, K. (2021). Independent Upper- and Lower-Arm Switching Scheme Based on Reference Current Polarity for Three-Level NPC Inverters. Energies, 14(17), 5535. https://doi.org/10.3390/en14175535






