Sensitivity Analysis of Influencing Factors of Supercritical Methane Flow and Heat Transfer in a U-Tube

Abstract

Due to the existence of a Dean vortex in a U-tube, the flow and heat transfer process of supercritical methane is complex, and its thermophysical property are greatly influenced by different factors. Based on computational fluid dynamics theory, the numerical simulation of the turbulent flow and heat transfer characteristics of supercritical methane in a U-tube with an inner diameter of 10 mm and a radius of curvature of 27 mm carried out by using the finite volume method. On the basis of verifying the reliability of the model, the influences of inlet mass flux (G), heat flux on the tube wall boundary (q), pressure on the outlet (P), and gravity acceleration factors (g) on heat transfer characteristics were analyzed. The calculation results show that the sensitivity of the effects of G, q, P, and g on the heat transfer coefficient is, from large to small, in the order of P, G, g, and q. Compared with a horizontal straight tube, a U-tube can significantly improve heat transfer in the elbow part, but the presence of the elbow reduces heat transfer in the subsequent straight pipe section. The research in this paper has significance as a reference for the construction of the LNG gasification process.

1. Introduction

In recent years, with the development of supercritical fluid technology, it is being widely used in power engineering, the chemical industry, aerospace, and other fields. The physical properties of a fluid under supercritical pressure near the pseudocritical point vary greatly, and its heat transfer characteristics are extremely complex. As one of the world’s recognized clean energy sources, liquefied natural gas (LNG) adopted by many countries for its low air pollution and high heat emission after combustion. The main component of LNG is methane (CH₄), with a content of more than 90%. Li et al. [1] used methane to replace LNG for numerical simulation and found that the accuracy of the calculation results could guaranteed. U-tubes are widely used in LNG intermediate medium vaporizers [2], LNG submerged combustion vaporizers [3], and LNG temperature vaporizers [4] because they can change the flow direction of the fluid, save space, and improve the heat transfer efficiency. The critical pressure and temperature of methane, the main component of natural gas, are 4.59 MPa and −82.57 °C, respectively [5]. In many processes of natural gas liquefaction, storage, transportation, and gasification, the working conditions reach the supercritical flow and heat transfer state. A supercritical fluid (SF) is a kind of vapor-like and liquid-like fluid under supercritical pressure; an interesting definition of an SF is any substance that presents the properties of both gases and liquids above its critical temperature and pressure. Besides, solubility is a key concept in supercritical fluid technology (SFT), and it is widely used in various fields, such as medicine, environment, and chemistry [6]. Temperature and pressure are two important influencing parameters. On the one hand, under certain pressure, the density of a supercritical fluid decreases with an increase in temperature, resulting in a decrease in solubility. On the other hand, the effect of pressure on solubility becomes more significant at high temperatures [7]. Owing to the drastic change in its physical properties near the quasi-critical temperature, the heat transfer law of supercritical methane is complicated and affected by many factors. Therefore, it is necessary deeply study the flow and heat transfer characteristics of supercritical methane in a U-tube near the pseudocritical temperature point and analyze the sensitivity of its influencing factors.

Among the commonly used pipeline forms for fluid transportation, the straight pipe (including horizontal, vertical, and inclined) is the simplest and most common one. The analysis of the heat transfer characteristics of a supercritical fluid in straight pipes is the basis for studying its flow and heat transfer in complex pipes. For instance, Gu et al. [8] conducted an experimental study on convective heat transfer of supercritical methane in horizontal microtubes. They found that the heat transfer in the quasi-critical zone enhanced under the conditions of high mass flux and low heat flux, whereas deterioration is noted at high heat flux and low mass flux in the pseudocritical region. Han et al. [9] used a turbulence model to investigate the characteristics of supercritical methane flow in a horizontal straight pipe, and the influence of mass flux and pressure on the flow and heat transfer were discussing. The results showed that the increase in mass flow leads to a significant enhancement in the heat transfer coefficient and the increase in pressure reduces the peak value of the heat transfer coefficient. By studying the heat transfer characteristics of supercritical CO₂ cooled in a vertical tube, Bruch et al. [10] found that when the fluid flows upward, the heat transfer coefficient increases with the mass flux, completely different from the result in downward flow. Koshizuka et al. [11] numerically simulated the mixed convection between supercritical-pressure water and CO₂ in a vertical tube. They illustrated that most of the low-Re-number turbulence models examined reproduced heat transfer deterioration under the influence of buoyancy. In addition to the above-mentioned studies, the numerical analysis of supercritical CO₂ in vertical tubes with 4.4 mm and 9.0 mm inner diameters was conducting by Song et al. [12]. The results showed that a similarity of heat transfer behavior maintains both normal heat transfer mode and deteriorated heat transfer mode with the same length-to-diameter ratio and the wall-heat-flux-to-mass-flux ratio. After various turbulence models for upward flow in a circular tube at supercritical pressure were studied by Kim et al. [13], they presented that optimal predicted results can obtained by the RNG k-ε model with enhanced near-wall treatment. The above model showed abrupt temperature changes, which were different from the experimental results under a relatively high heat flux. Walisch et al. [14] measured the heating of turbulent supercritical CO₂ in a vertical, horizontal, and inclined tube with a diameter of 10 mm and observed that the buoyancy effect related to the flow Reynolds number.

Compared with the straight pipe, a bent pipe not only improves the space usage rate but also remarkably contributes to the heat transfer efficiency, which is widely used in engineering practice as an enhanced heat transfer pipeline. Dong [15] used a turbulence model to simulate the flow and heat transfer characteristics of LNG in a single snake-shaped heat exchanger tube under constant heat flux by using methane instead of LNG. The results showed that the local heat transfer coefficient increases first and then decreases along the pipeline and the peak value appears near the quasi-critical temperature. The larger the heat flux is, the earlier the peak appears, the faster the decline is, and the heat transfer deteriorates. Nu showed an upward trend along the flow direction, it tended to be flat after the quasi-critical point, and a mutation occurred at the elbow. A three-dimensional calculation model was established by Zhang et al. [16] to study the flow and heat transfer characteristics of supercritical LNG in SCV coil pipes. Their results demonstrated that due to the secondary flow, the local heat transfer coefficient suddenly increases and its maximum increases with the inlet velocity. In the range of operating pressure, the maximum local heat transfer coefficient decreases with an increase in tube side pressure. Fu et al. [17] experimentally studied the characteristics of the flow heat transfer of supercritical aviation kerosene RP-3 in U-shaped tubes with a bending radius of 10, 15, and 20 mm. They concluded that due to centrifugal force, the convective heat transfer capacity of the curved tube significantly improves and the convective heat transfer coefficient increases with a decrease in the radius of curvature. Wei et al. [18] studied the influence of the curvature radius on the characteristics of the flow heat transfer of supercritical CO₂ in a U-pipe by using the SST k-ω turbulence model. They found that fluid separation and reattachment occur in the U-tube, which gradually decreases after turning as the radius of curvature increases from 0.5 to 3.0.

As mentioned above, most scholars’ researches on supercritical fluids focused particularly on carbon dioxide or supercritical methane in a straight tube. However, there are few studies on the flow heat transfer of methane in a U-tube, and discussions of the sensitivity of various factors to the influence of the heat transfer process are limited. Consequently, a U-tube model with an inner diameter of 10 mm and a radius of curvature of 27 mm was establishing to simulate the convective heat transfer of methane under supercritical pressure in the current work. The research objective of this study was to analyze the sensitivity of the effects of mass flux G, heat flux q, pressure P, and gravity g on heat transfer characteristics.

2. Mathematical and Physical Models

2.1. Physical Model

Figure 1 displays the schematic diagram of the 2D computational domain in the present study; the inner diameter of the tube was 10 mm, with a thickness of 2 mm, and the radius of curvature was 27 mm. The length of the tube was fixing at 1585 mm. To reduce the inlet effect and outlet reflux phenomenon, L_in of the adiabatic inlet section and L_out of the adiabatic outlet section were set to 600 mm each.

2.2. Meshing

The computational domain was establishing and meshing by the O-block function of ICEM 14.0 software. Owing to the physical properties of the near-wall fluid change significantly near the pseudocritical temperature point, the near-wall grid was encrypting. The cross-sectional grid of the horizontal straight pipe as shown in Figure 2. On the premise of ensuring the first layer near the wall grid y⁺ < 1, the independence of the U-tube grid was verified. Three groups of satisfactory calculation results were selecting, and the specific grid settings shown in

Table 1. The grid settings.

Case	Radial	Circumferential	Axial	Number
1	50	40	1740	1,400,000
2	60	40	1740	1,700,000
3	70	40	1740	2,000,000

. By comparing the curves of the convective heat transfer coefficient h, we found that the calculation results of case 2 and case 3 remained basically the same as the number of grids increased.

Figure 3 shows the distribution of h along the L/D in different grids. The Grid Convergence Index (GCI) was using to quantify the grid independence [19]. The GCI₁₂ for fine and medium grids was 1.76%. The GCI₂₃ for medium and coarse grids was 4.50%. The value of GCI₂₃/(r^pGCI₁₂) was 0.96, which was approximately 1 and indicated that the solutions were well within the asymptotic range of convergence. Considering the needs of calculation time and solution accuracy, hence, the grid setting of case 2 was finally selecting for analysis of the following calculation results.

2.3. Governing Equations

In this study, the Re was much larger than the critical value under all operating conditions and the flow was in turbulent state without an internal heat source. The fluid was compressible, and the heat exchange with the environment was negligible, taking into account gravity. This paper only studied the steady state, so the time term can ignored in all equations. The governing equations included a continuity equation, a momentum equation, and an energy equation, which also solved in the Lagrangian manner [20], as illustrated below.

The continuity equation [21]:

$$\frac{\partial \left(\rho u\right)}{\partial x}+\frac{\partial \left(\rho v\right)}{\partial y}+\frac{\partial \left(\rho w\right)}{\partial z}=0$$

(1)

The momentum equation:

$$\{\begin{array}{l}\frac{\partial \left(\rho uu\right)}{\partial x}+\frac{\partial \left(\rho uv\right)}{\partial y}+\frac{\partial \left(\rho uw\right)}{\partial z}=\frac{\partial }{\partial x}\left(\mu \frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial u}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial u}{\partial z}\right)-\frac{\partial p}{\partial x}\\ \frac{\partial \left(\rho vu\right)}{\partial x}+\frac{\partial \left(\rho vv\right)}{\partial y}+\frac{\partial \left(\rho vw\right)}{\partial z}=\frac{\partial }{\partial x}\left(\mu \frac{\partial v}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial v}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial v}{\partial z}\right)-\frac{\partial p}{\partial y}\\ \frac{\partial \left(\rho wu\right)}{\partial x}+\frac{\partial \left(\rho wv\right)}{\partial y}+\frac{\partial \left(\rho ww\right)}{\partial z}=\frac{\partial }{\partial x}\left(\mu \frac{\partial w}{\partial x}\right)+\frac{\partial }{\partial y}\left(\mu \frac{\partial w}{\partial y}\right)+\frac{\partial }{\partial z}\left(\mu \frac{\partial w}{\partial z}\right)-\frac{\partial p}{\partial z}\end{array}$$

(2)

The energy equation [22]:

$$\frac{\partial \left(\rho uT\right)}{\partial x}+\frac{\partial \left(\rho vT\right)}{\partial y}+\frac{\partial \left(\rho wT\right)}{\partial z}=\frac{\partial }{\partial x}\left(\frac{\lambda }{c_p}\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\lambda }{c_p}\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{\lambda }{c_p}\frac{\partial T}{\partial z}\right)$$

(3)

where ρ, p, λ, c_p, and T denote the density, bulk fluid pressure, thermal conductivity, specific heat at constant pressure, and bulk fluid temperature, respectively.

In this paper, the Re number under all working conditions was much higher than the critical value and the flow was in a turbulent state, so the additional turbulent transport equation was observed. The realizable k-ε model used for predicting the turbulence flow, because this model could not only calculate flows in pipelines and boundary layer flows but also calculate the flows with separation [23]. The transport equations are as follows:

$$\frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_{\mathrm{t}}}{{\sigma }_{\mathrm{k}}}\right)\frac{\partial k}{\partial x_j}\right]+G_{\mathrm{k}}-\rho \epsilon$$

(4)

$$\frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_{\mathrm{t}}}{{\sigma }_{\mathsf{\epsilon }}}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}E\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}$$

(5)

where,

$$C_1=\max \left(0.43,\frac{\eta }{\eta +5}\right)$$

(6)

$$\eta ={\left(2E_{ij}\cdot E_{ij}\right)}^{1/2}\frac{k}{\epsilon }$$

(7)

$$E_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_i}+\frac{\partial u_j}{\partial x_j}\right)$$

(8)

$${\mu }_{\mathrm{t}}=\rho C_{\mu }\frac{k^2}{\epsilon }$$

(9)

where u, μ, μ_t, G_k, k, ε, E, and ν are the bulk fluid velocity, dynamic viscosity, turbulent viscosity, the generation of turbulence kinetic energy, turbulent kinetic energy, dissipation rate of turbulent kinetic energy, total energy, and kinematic viscosity, respectively. The model constants C₂, σ_k, and σ_ε were established to ensure that the model performed well for canonical flows, and C_μ is a function of the turbulence fields. The above model constants were σ_k = 1, σ_ε = 1.2, C₂ = 1.9, and C_μ = 0.09 [24].

2.4. Data Reduction Method

The local heat transfer coefficient calculated using the following equations:

$$h=\frac{q_w}{T_w-T_b}$$

(10)

$$T_b=f\left(H_b,P\right)$$

(11)

$$H_b=\frac{{\displaystyle {\int }_A\rho wHdA}}{{\displaystyle {\int }_A\rho wdA}}$$

(12)

where $q_w$, $T_w$, $T_b$, w, A, and H represent the local heat flux of the outer tube wall, averaging temperature of the inner wall, bulk fluid temperature, bulk fluid axial velocity, cross-sectional area of the tube, and bulk fluid enthalpy, respectively.

The dimensionless independent parameter Re obtained by Equation (13):

$$Re=\frac{\rho ud}{\mu }$$

(13)

The local Nusselt number Nu and Dean number Dn were defined as

$$Nu=\frac{hd}{\lambda }$$

(14)

$$D_n=Re{\left(r/R\right)}^{0.5}$$

(15)

where d is the tube inner diameter, r is the bend radius, and R is the curvature radius of the bend. The Dean number Dn is the ratio of the centrifugal force and viscous force of fluid flow in the elbow, which used to measure the strength of the Dean vortex (secondary flow).

2.5. Boundary Conditions

The software ANSYS Fluent 14.0 was using for the calculations in this paper. The boundary conditions for each structure of the computational model, including the fluid domain and the solid domain, were set before the simulation began.

• It was assumed that the flow at the inlet was fully developed, its boundary condition was determined by the mass flux inlet, with the specific value changing from 50 to ~100 kg/m² s, and temperature was set to 180 K. The pressure ranged from 5.43 to 9.55 MPa and the gravity acceleration from −6.8 to −12.8 m/s². The outlet pressure was set to 6.93 MPa. Meanwhile, a constant heat flow boundary and no-slip-velocity conditions adopted for the outer wall of the heating section tube, and the wall heat flux varied from 60 to 100 kW/m². In the case of other boundary conditions remaining unchanged, by changing the single-variable, the comparative analysis of its specific impact on heat transfer characteristics is carrying out.
• In the process of solving by Fluent 14.0 software, the physical properties of methane were regarding as a single-value function of temperature. According to the methane physical property data provided by the National Institute of Standards and Technology Database (NIST) [25], the physical property parameters were obtaining by the piecewise-liner linear interpolation method. Figure 4 shows the curves of specific heat at constant pressure c_p, density ρ, dynamic viscosity μ, and thermal conductivity λ changing with methane temperature under different pressure conditions.

The pressure–velocity coupling equation was solved by the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm, and the pressure terms were discretized by the standard format. Turbulent kinetic energy and turbulent kinetic energy dissipation were discretizing by the first-order upwind scheme, and the momentum and energy were discretizing by the second-order upwind scheme. When the residual of the momentum equation, turbulent kinetic energy, and turbulent kinetic energy dissipation rate was less than 1 × 10⁻⁶, the residual of energy equation was less than 1 × 10⁻⁸, in addition, the monitored average temperature and velocity of the outlet were stable, and the numerical simulation was considered to be converged. Figure 5 exhibits the basic algorithmic process of CFD. Every step from establishing control equations to obtaining convergent solutions is crucial.

2.6. Verification of the Method

The realizable k-ε model was validating with the experimental data of Lei et al. [26]; in the meantime, the model size, boundary conditions, pipeline materials, and fluid types were all set according to the experimental parameters. The numerical simulation results compared with the experimental data shown in Figure 6, where the x-coordinate is the enthalpy of the fluid and the y-coordinate is the coefficient of convection heat transfer. It found that the two curves have roughly the same trend, rising first and then falling with the increase in enthalpy. The average error between the two sets of data was 9.1%, within the permissible engineering limits (the error range is usually 20%). Therefore, the correctness of the model selected in this paper was verified.

3. Results and Discussion

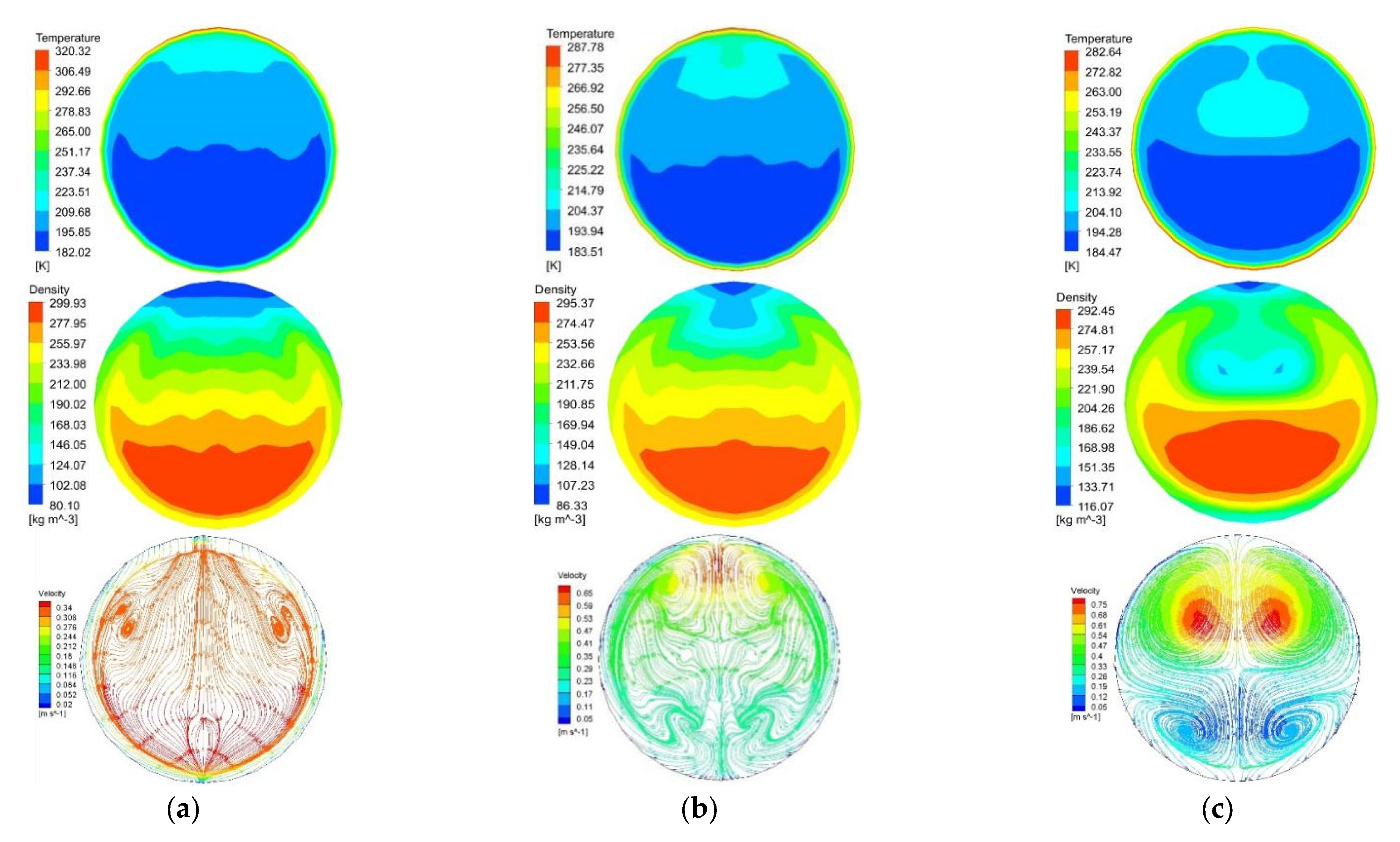
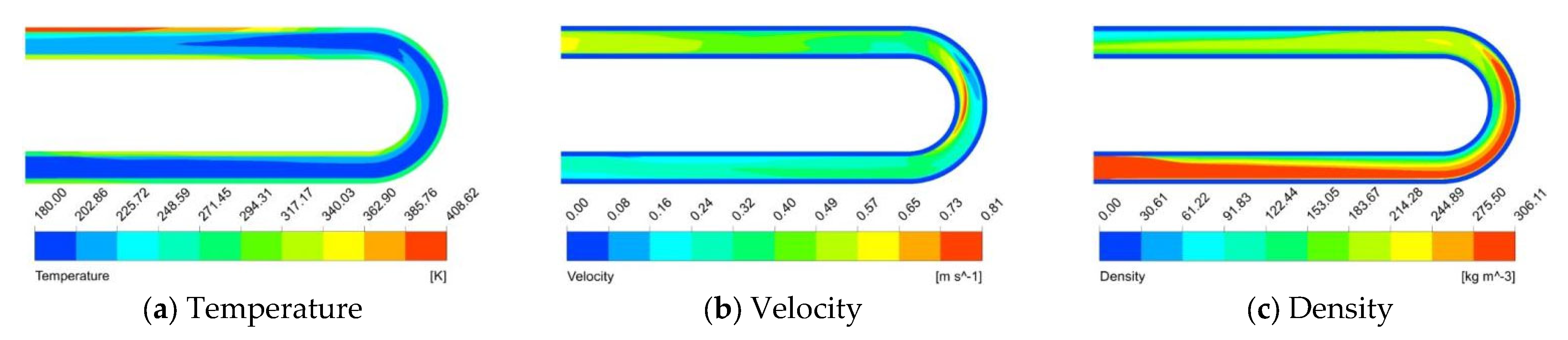
3.1. Analysis of the Flow Heat Transfer Process in a U-Tube Section

Figure 7 illustrates the distribution of temperature, density, and secondary flow trace on the different cross sections of a bent tube. According to the temperature and density contours, in addition to secondary flow vortices generated by the buoyancy force on the section of α = 0°, there is a pair of reverse symmetric vortices produced by the centrifugal force of the fluid, which are Dean vortices, whose vortices increase with heating. The two vortices near the wall generated by the buoyancy force move up gradually, while the Dean vortices generated by the centrifugal force move down gradually, and all of them can be clearly seen on the α = 120° section. In addition, the figure reveals that the temperature of supercritical methane in the vicinity of the inner wall is higher than in other regions. Because under the influence of the enhanced secondary flow, a thin layer of fluid nearby may absorb more heat, and the bulk temperature of supercritical methane in this layer may increase rapidly due to the significant decrease in density. To summarize, the secondary flow phenomenon can conduce to thinning of the boundary layer of supercritical methane, thus enhancing heat transfer.

Figure 8 shows the contours of temperature, density, and velocity of the xoy plane in the heating section. It found that before the fluid enters the bend channel, the fluid with high temperature and low density at the top and the fluid with low temperature and high density is at the bottom. The fluid separates after enters the elbow, forming a low-temperature and low-speed zone on the outer wall of the elbow and a high-temperature and high-speed zone on the inner wall. Along the flow direction, the high-temperature and high-speed zone is in the front and middle of the inner wall of the bend, while the low-temperature and low-speed zone is in the back and closer to the outlet of the bend. Finally, the fluid in the two regions remixed again on the outlet section of the U-tube. This is because after the fluid enters the elbow pipe, it flows from the inner to the outer wall under the action of a centrifugal force, and then the fluid squeezed, which leads to a decrease in velocity, thus forming a low-temperature and low-speed zone. The inner wall of the elbow therefore has a large space. As the heating process goes on, the inner wall fluid temperature and velocity increase, forming a high-temperature and high-speed zone. Meanwhile, the density of the fluid rises gradually along the wall and reaches the maximum value in the outlet section ultimately.

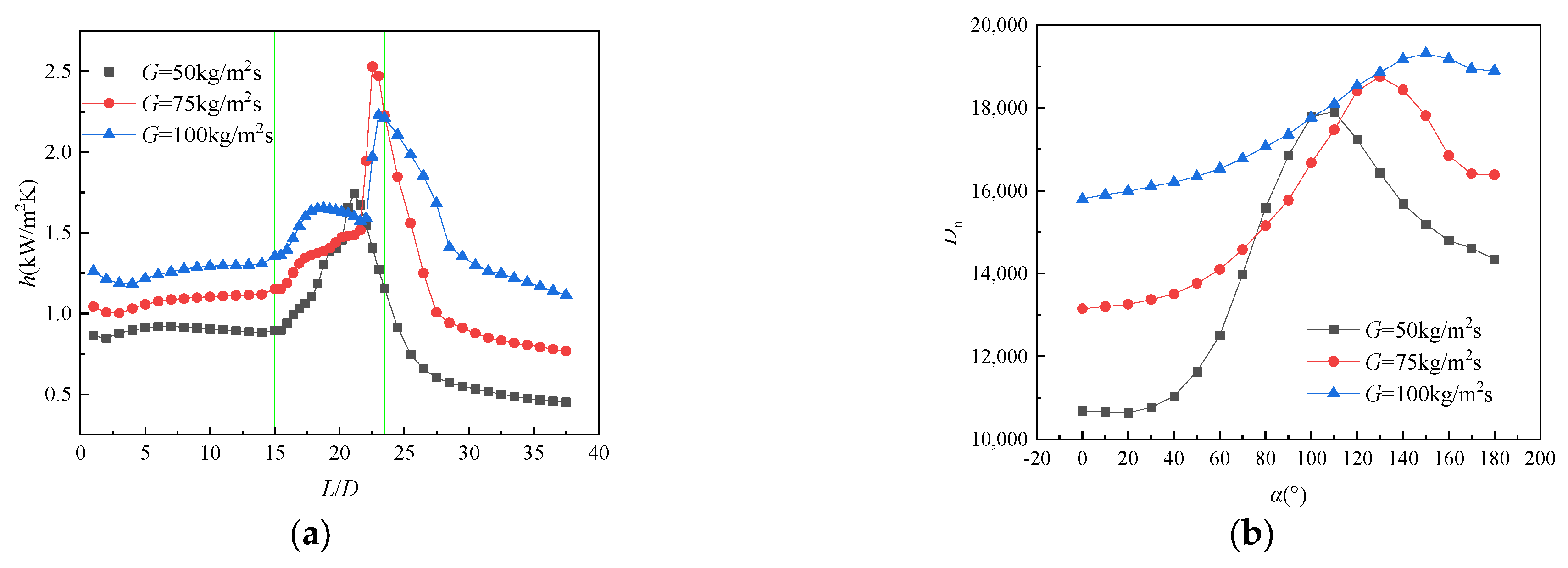
3.2. Effect of Mass Flux

In the momentum formula of flow, the corresponding term of mass flux factor is the inertial force. To understanding the influence of the flow factor on the heat transfer of supercritical methane in pipelines particularly, simulations under different flow rates were carrying out and calculated results were comparing. Figure 9 shows the change in the convective heat transfer coefficient h with L/D and the variation tendency of the Dean number Dn with bending angle α under different mass flux conditions. According to Figure 9a, before the fluid enters the elbow, h increases with the rise in mass flux. After the fluid enters the elbow, when G = 50 kg/m²·s, h peaks at the position of L/D = 21. When G = 75 kg/m²·s, h peaks at the position of L/D = 22.5. The mass flux increases from 50 kg/m²·s to 75 kg/m²·s, and the peak point of h moves to the right and increases by 45.2%. This is due to the raised mass flux, which increases the fluid velocity. It also improves the disturbance and intensifies the boundary heat transfer, which slows down the heating rate of the fluid and shifts the quasi-critical temperature point of the fluid to the right. Meanwhile, a higher mass flux causes an enhancement in the fluid’s Reynolds number, enhancing the strength of the Dean vortex, which results in heat transfer augmentation, as described by Figure 9b.

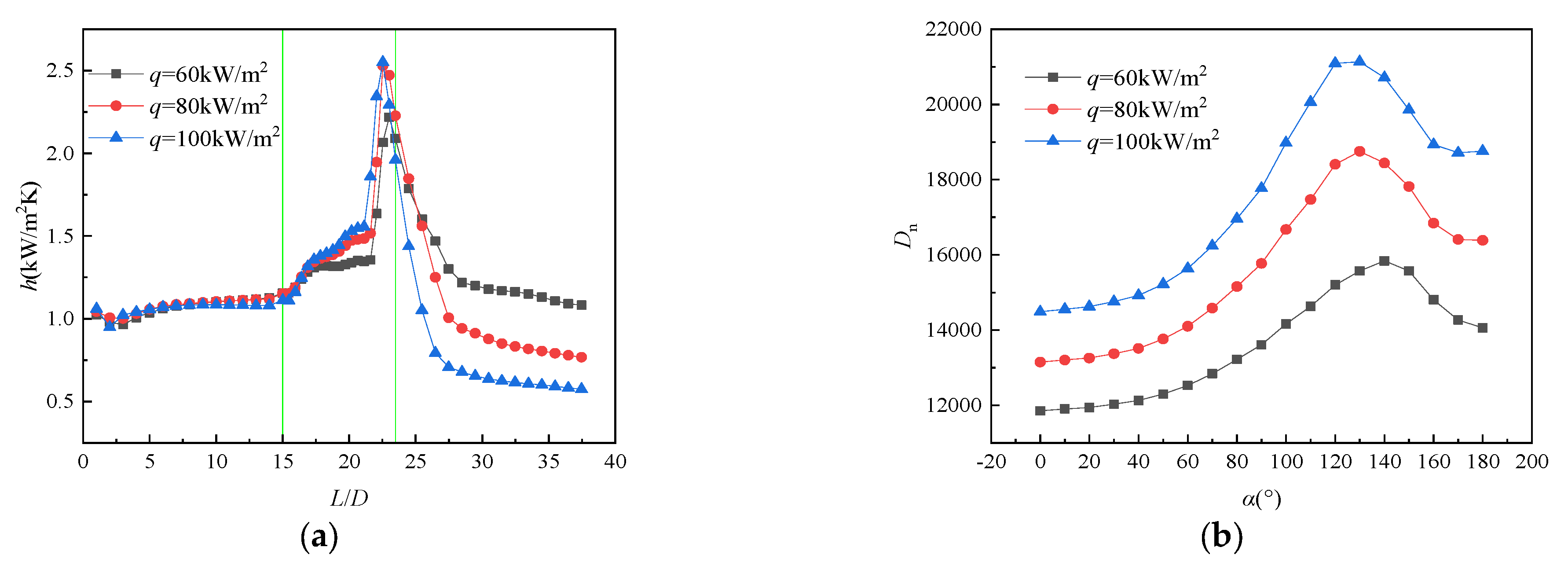
3.3. Effect of Heat Flux

In engineering applications, heating wall conditions are quite different, and the properties of supercritical methane are particularly sensitive to temperature. Therefore, it is necessary to study the heat transfer of changing heat flux. The variations in the heat transfer coefficient h along the tube length and in Dn with bending angle α both presented in Figure 10.

It can be seen from Figure 10a that before the fluid enters the bend, h under the condition of q = 100 kW/m² decreases significantly. The reason is that a fluid heats up faster under the condition of high heat flux, and the near-wall fluid passes the quasi-critical temperature before entering the bend. Thus the physical property of methane changes tends to be flat, the buoyancy effect also weakens, and the heat transfer capacity decreases. After the fluid enters the elbow, h increases at first and then decreases, and heat flux increases from 60 kW/m² to 100 kW/m², whose peak point moves to the left and increases by 15%. This is due to the fluid flow into the elbow caused by the centrifugal force after the Dean vortex, whose intensity related to fluid velocity. The fluid with a high heat flux has a high temperature, and the viscosity of the fluid is inversely proportional to the temperature. Therefore, this kind of fluid has a faster velocity, and the Dean vortex has greater strength, which significantly improves the convective heat transfer capacity of the fluid. As shown in Figure 10b, Dn under different heat flux conditions presents a change by first increasing and then decreasing. With the enhancement in heat flux, Dn increases and its peak point shifts to the left, indicating that the intensity of the Dean vortex increases gradually. That is, the phenomenon of secondary flow is more obvious and the disturbance in the tube is more intense. While the fluid temperature increases with the heat flux, the fluid density and viscosity decrease with a rise in temperature, resulting in an increase in fluid velocity, finally increasing the strength of the Dean vortex.

3.4. Effect of Pressure

Figure 11 presents the influence of the inlet pressure on the heat transfer coefficient of the surface along the tube length variation and the changes in Dn with bending angle α at different pressures. It reveals that the maximum heat transfer coefficient of the surface strongly depends on the inlet pressure. Figure 11a illustrates that h changes under the working conditions of P = 6.93 MPa and P = 9.55 MPa in the same way, showing a distribution of first decreasing, then increasing, and finally decreasing. Under the condition of P = 5.43 MPa, h slightly drops before the fluid enters the elbow, and the heat transfer capacity drops, resulting in a high wall temperature rise. The physical property of the fluid changes dramatically near the critical pressure, and the secondary flow strength generated by the buoyancy effect is greater, which makes heat transfer stronger. Therefore, the near-wall fluid temperature under the condition of P = 5.43 MPa first reaches the quasi-critical temperature. When the heating process proceeds, the near-wall fluid temperature begins to move away from the pseudocritical temperature and h decreases. After the fluid enters the elbow, the valley value of h appears under 5.43 MPa pressure, indicating that the heat transfer deteriorates. The reason is that the strength of the Dean vortex increases due to the centrifugal force of the bend after the fluid enters the elbow, while the Dean vortex could also deteriorate the heat transfer. However, as the fluid approaches the outlet of the bend, the centrifugal force weakens and the Dean vortex strength gradually decreases, thus making the heat transfer resume. When L/D > 22.5, h decreases with reducing pressure. For instance, the pressure drops from 9.55 MPa to 5.43 MPa, and the peak value of h decreases by 58.8%.

Figure 11b shows a change in Dn of first increasing and then decreasing under different pressure conditions. As the pressure increases, Dn decreases and the peak point shifts to the right, indicating that the strength of the Dean vortex decreases with an increase in pressure. Especially, the higher the strength of the Dean vortex is, the more the heat transfer deterioration should considered occur.

3.5. Effect of Gravity

Figure 12 demonstrates the variation in the convective heat transfer coefficient h with L/D and in Dean number Dn with bending angle α when g = −6.8 m/s², g = −9.8 m/s², and g = −12.8 m/s².

According to Figure 12a, since gravity increases from −12.8 m/s² to −6.8 m/s², the peak value of the surface heat transfer coefficient decreases from 2.5 W/m²·K to 2.2 W/m²·K, which is about 12%. This is because the buoyancy effect enhanced with the increase in gravity, that is, the buoyancy and flow acceleration caused by the change in bulk fluid density are considering. The secondary flow strength increases, which leads to the enhancement of heat transfer. The Dean number Dn under different gravity conditions has a similar magnitude in the horizontal direction, whereas its value differs greatly in other angle directions; this distribution pattern observed in Figure 12b. In summary, the influence of various parameters on the heat transfer performance is in the order of pressure p, mass flux G, gravity g, and heat flux q, from large to small.

3.6. Flow Heat Transfer Comparison between Different Tubes

It can be seen from Figure 13 that before the fluid enters the bend, the Nu curve in the two tube types is basically coincident, indicating that there is no difference in heat transfer of the fluid at this time. In the L/D = 15~32.5 section, h and Nu of the horizontal U-tube are greater than those of the horizontal circular tube. It is noteworthy that the bent tube sections have an important influence on the flow and heat transfer behaviors. Once supercritical methane flows into the bent tube sections, the heat transfer coefficient of the surface increases abruptly due to the secondary flow phenomenon, which believed to play an important role in the heat transfer of the bent tube sections [27]. When L/D > 32.5, h and Nu of the horizontal U-tube are less than those of the horizontal straight tube. The reason is that as the fluid temperature is far away from the quasi-critical temperature, the change in the physical property is relatively gentle, and the buoyancy effect caused by the density difference weakens, leading to the weakening of heat transfer. Such comparisons and trends in the heat transfer coefficient h are rare in similar literature. Overall, the equal-length horizontal U-tube is more advantageous than the horizontal straight tube in heat transfer.

4. Conclusions

In this study, the turbulent flow and heat transfer characteristics of methane at supercritical pressures in a heated U-tube were investigating used the realizable k-ε model. The main conclusions could draw as below:

• When the temperature of the main fluid is close to the quasi-critical temperature, the constant pressure specific heat capacity of the fluid increases rapidly and reaches its peak value. Thus methane can absorb more heat from the outer wall of the tube to increase temperature, reduce the temperature difference between the main fluid and the tube wall, increase the convective heat transfer coefficient of the local fluid, and enhance heat transfer.
• The Dean vortex can significantly increase or decrease the convective heat transfer capacity of the elbow, and the strength of h and Dean vortices shows a trend of increasing and then decreasing in the curved tube. The peak values of h and Dean vortices increase with the mass flux, whereas heat transfer deteriorates when G = 100 kg/m²·s.
• Increasing the heat flux could lead to a rise in the heat transfer coefficient, while the peak value gradually decreases with the augmentation of operating pressures. The pressure drop obviously increases along the flow direction due to the decrease in bulk fluid density, and heat transfer deteriorates in the elbow at P = 5.43 MPa.
• Compared with the horizontal straight tube, the U-tube can significantly improve heat transfer in the elbow part, but the presence of an elbow reduces heat transfer in the subsequent straight pipe section. The sensitivity to the effect of various parameters on the heat transfer performance of supercritical methane in a U-tube is in the order of pressure P, mass flux G, gravity g, and heat flux q, from large to small.

Therefore, further research needed to avoid the influence of the elbow on heat transfer in subsequent straight pipe sections.