Synthesis and Analysis of Three-Port DC/DC Converters with Two Bidirectional Ports Based on Power Flow Graph Technique
Abstract
:1. Introduction
2. A Review of Three-Port Configurations
3. Power Flow of Three-Port Converters
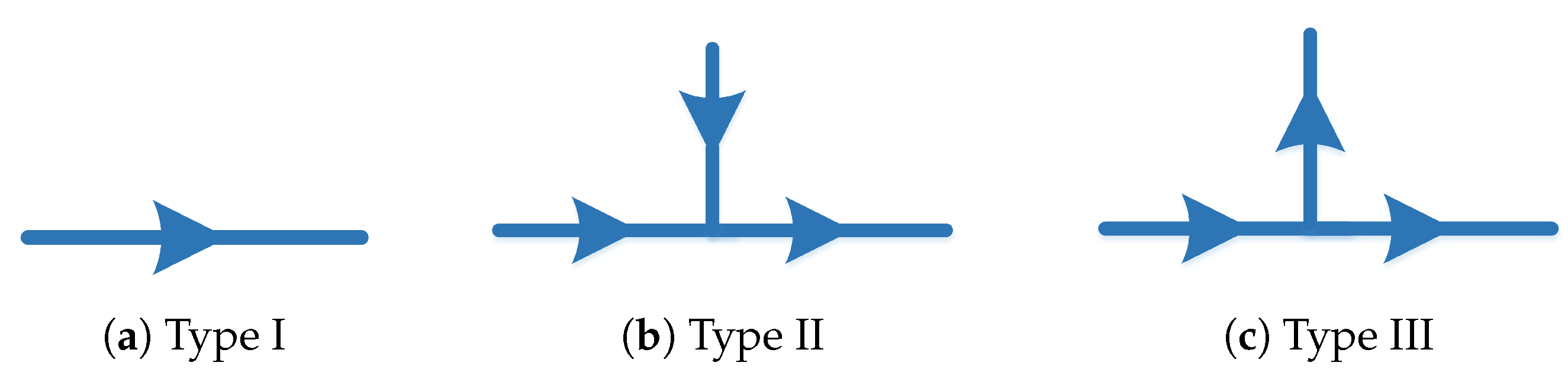
3.1. Power Flow Subgraphs
3.2. Power Flow Graphs for One Bidirectional Port
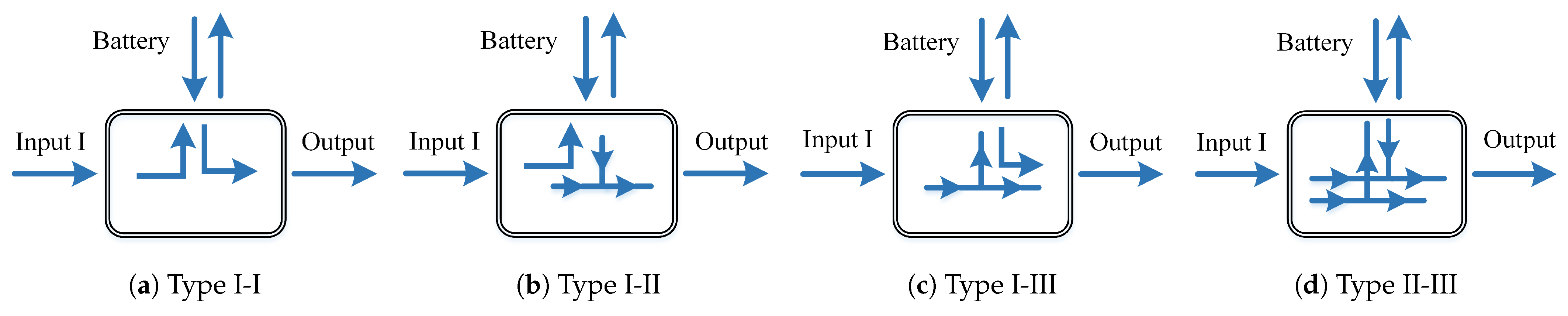
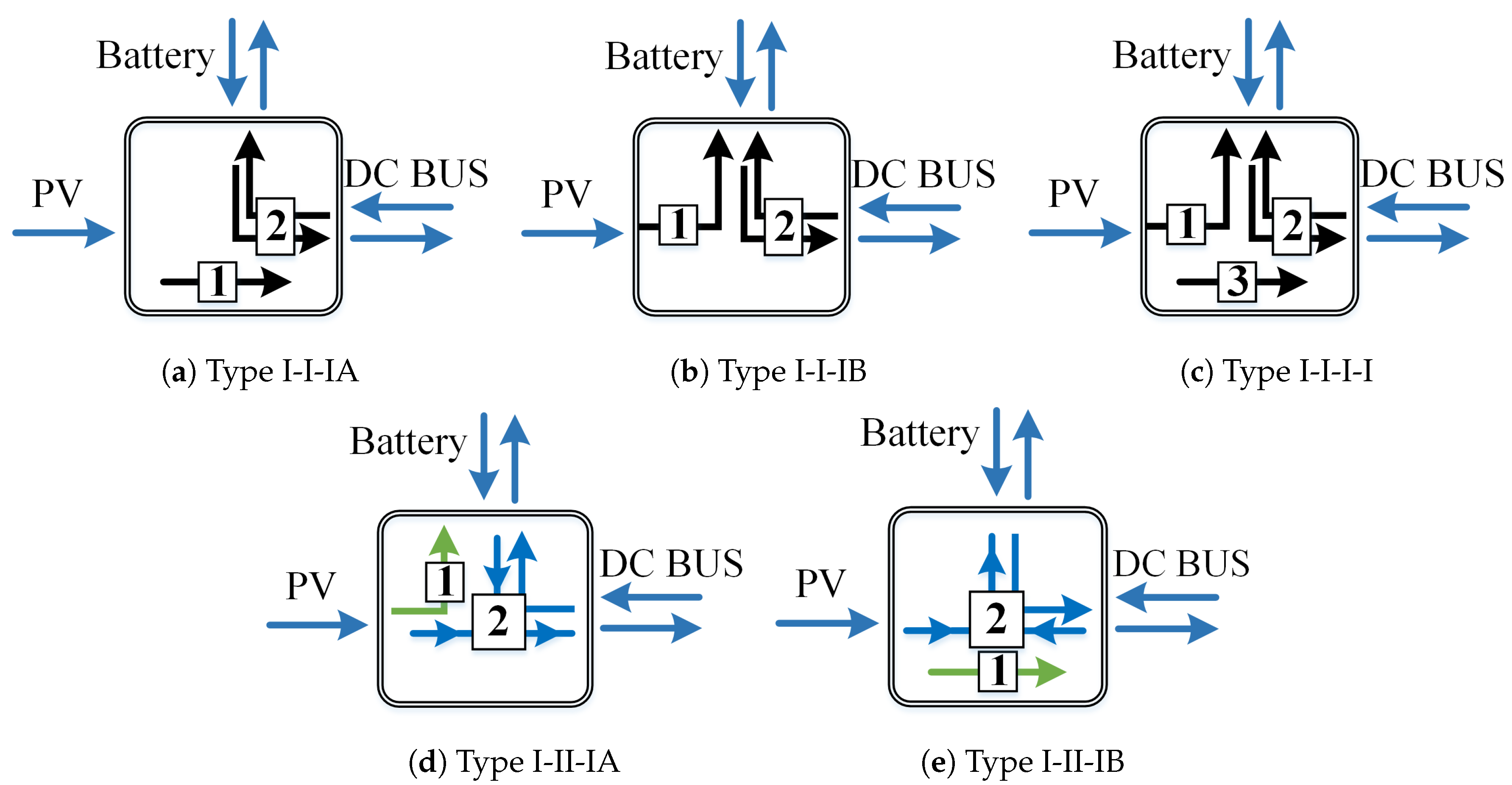
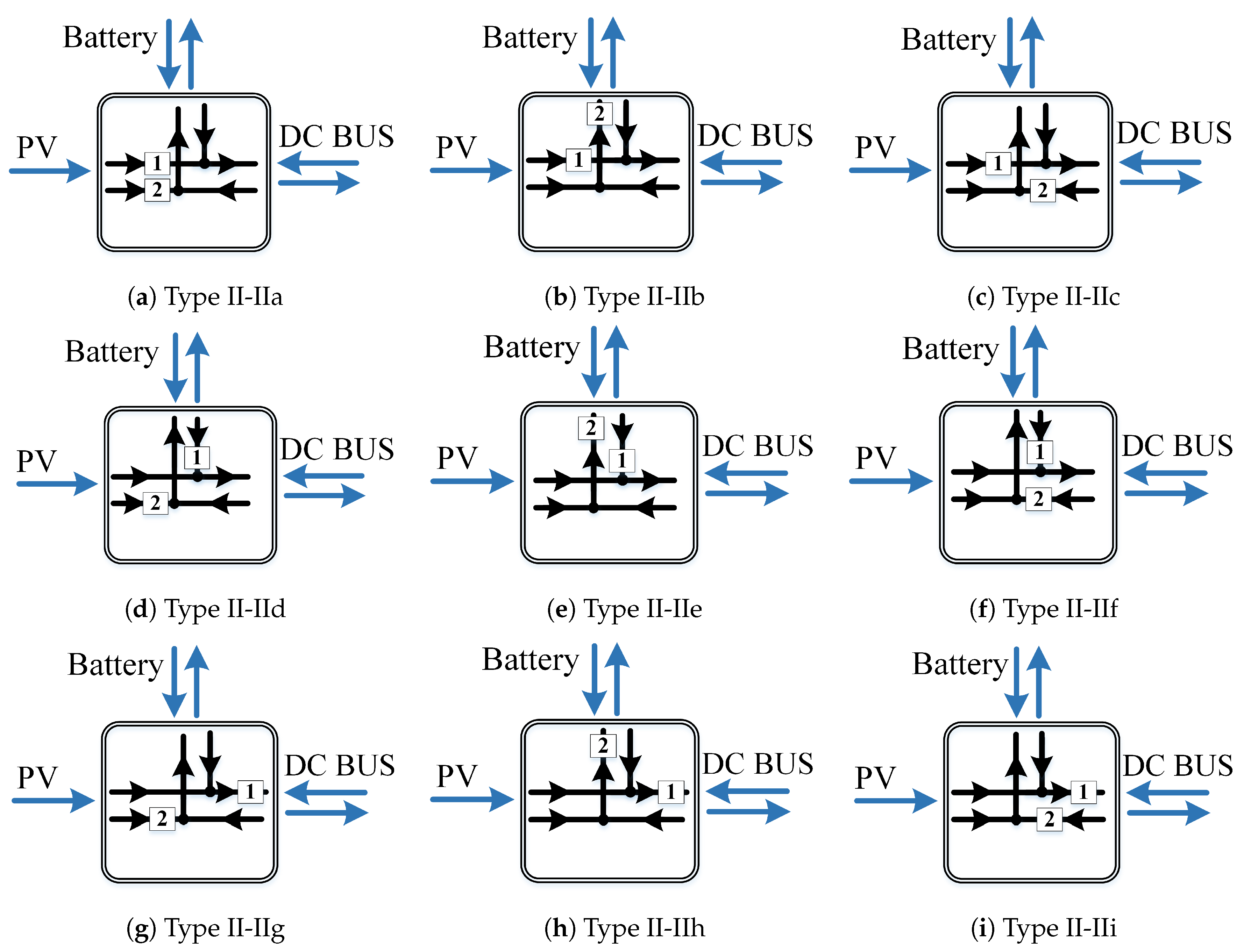
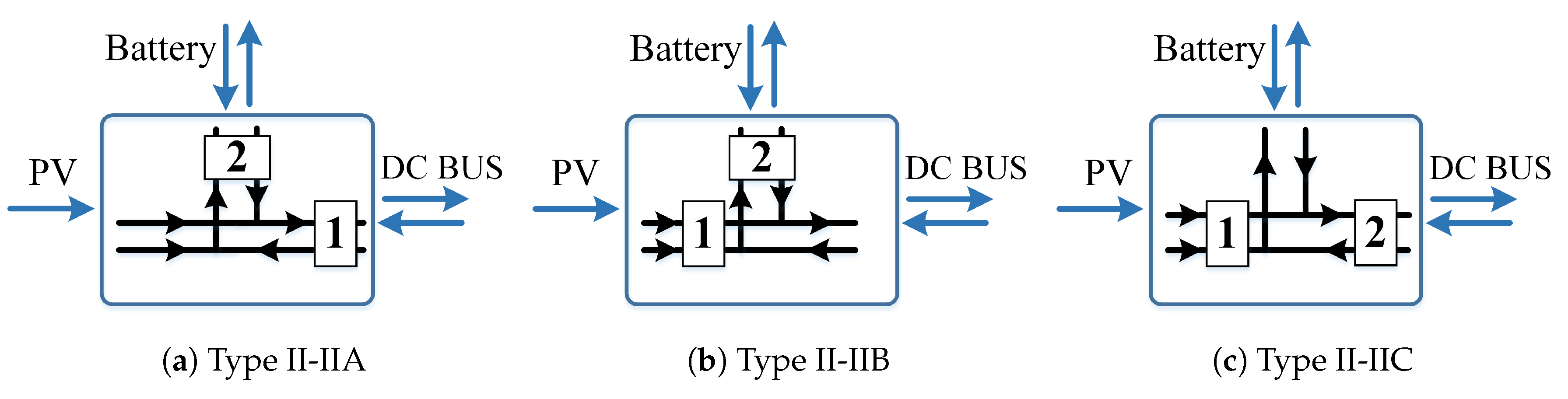
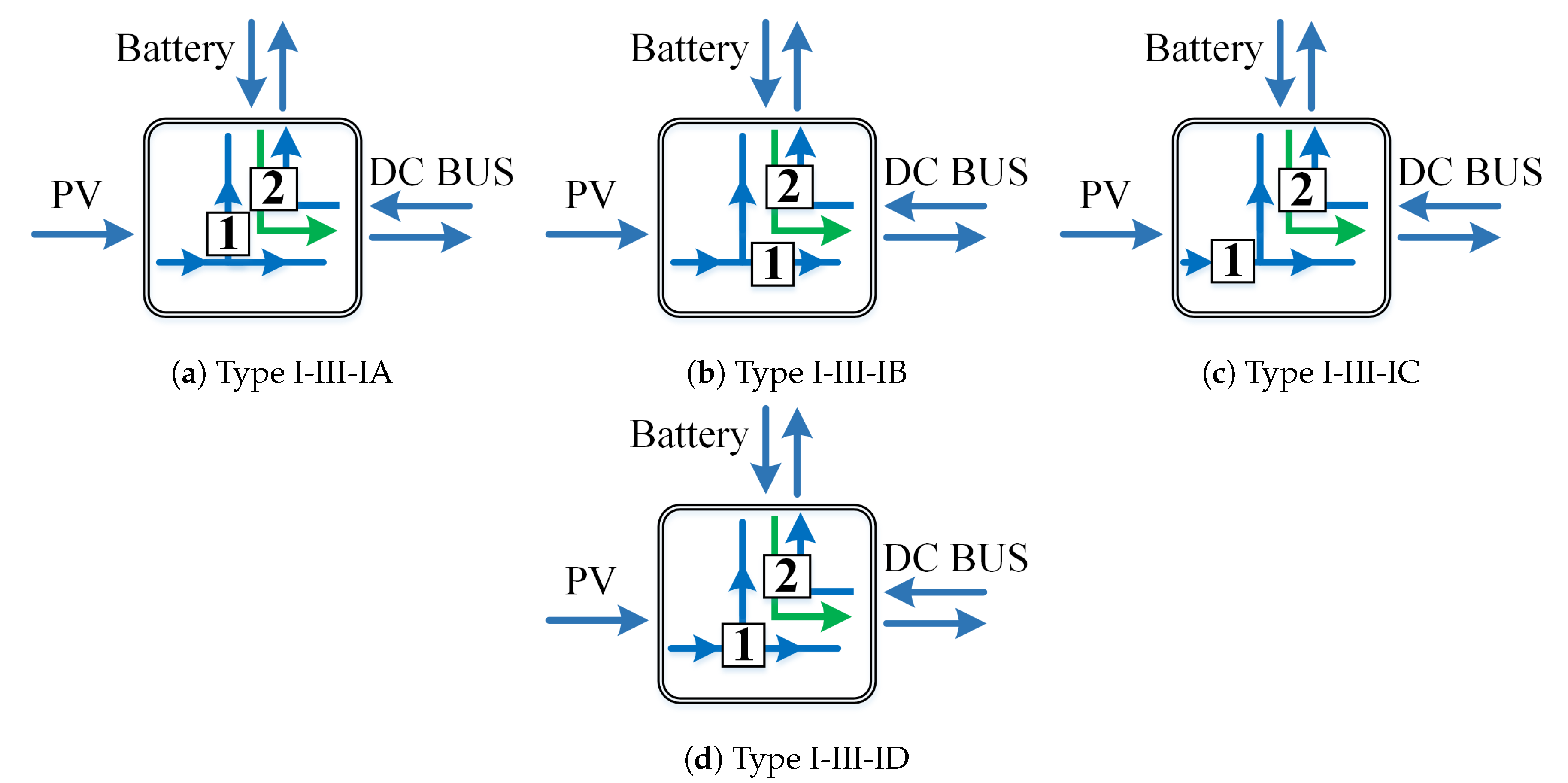
3.3. Proposed Power Flow Graphs Derivation for Two Bidirectional Port
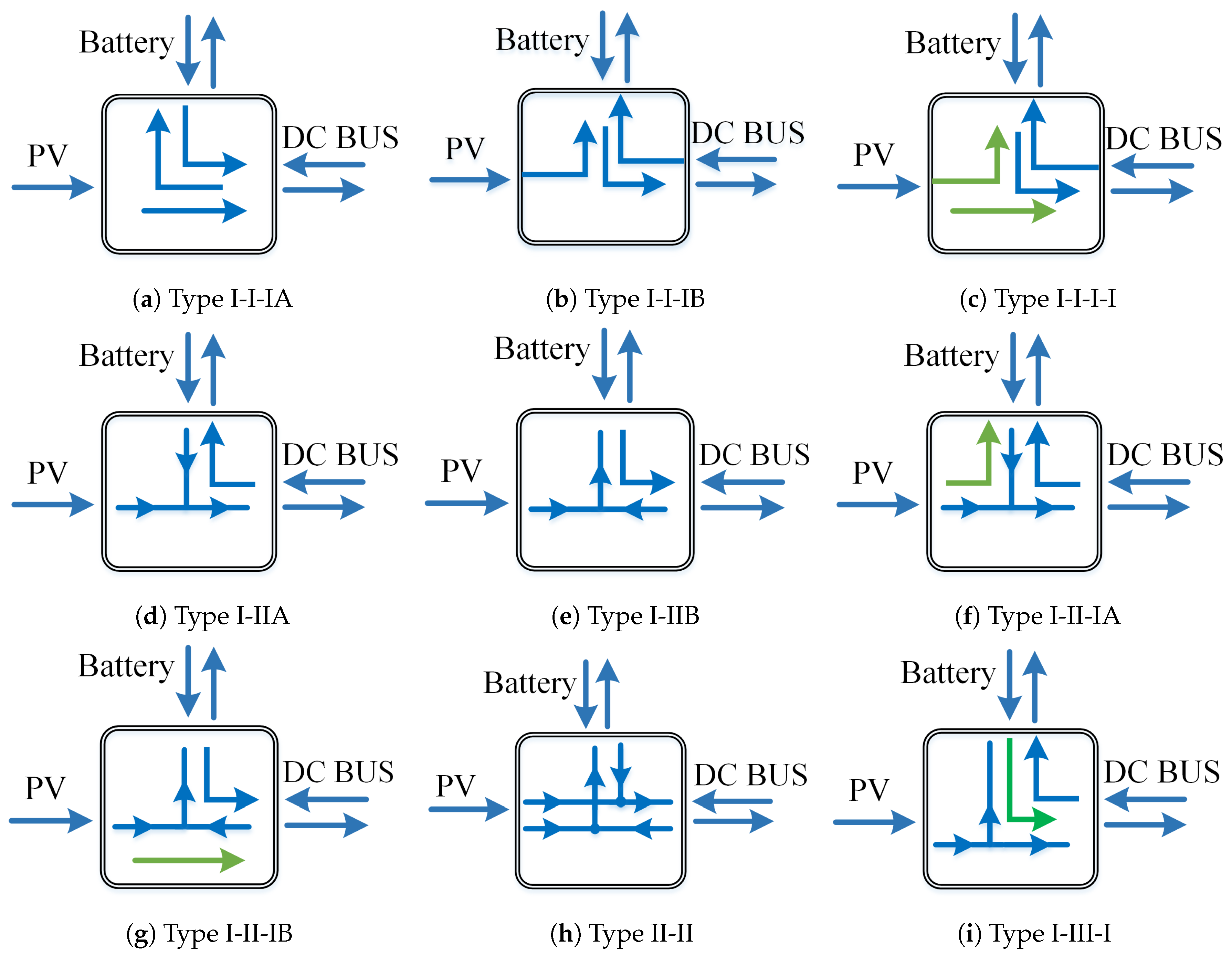
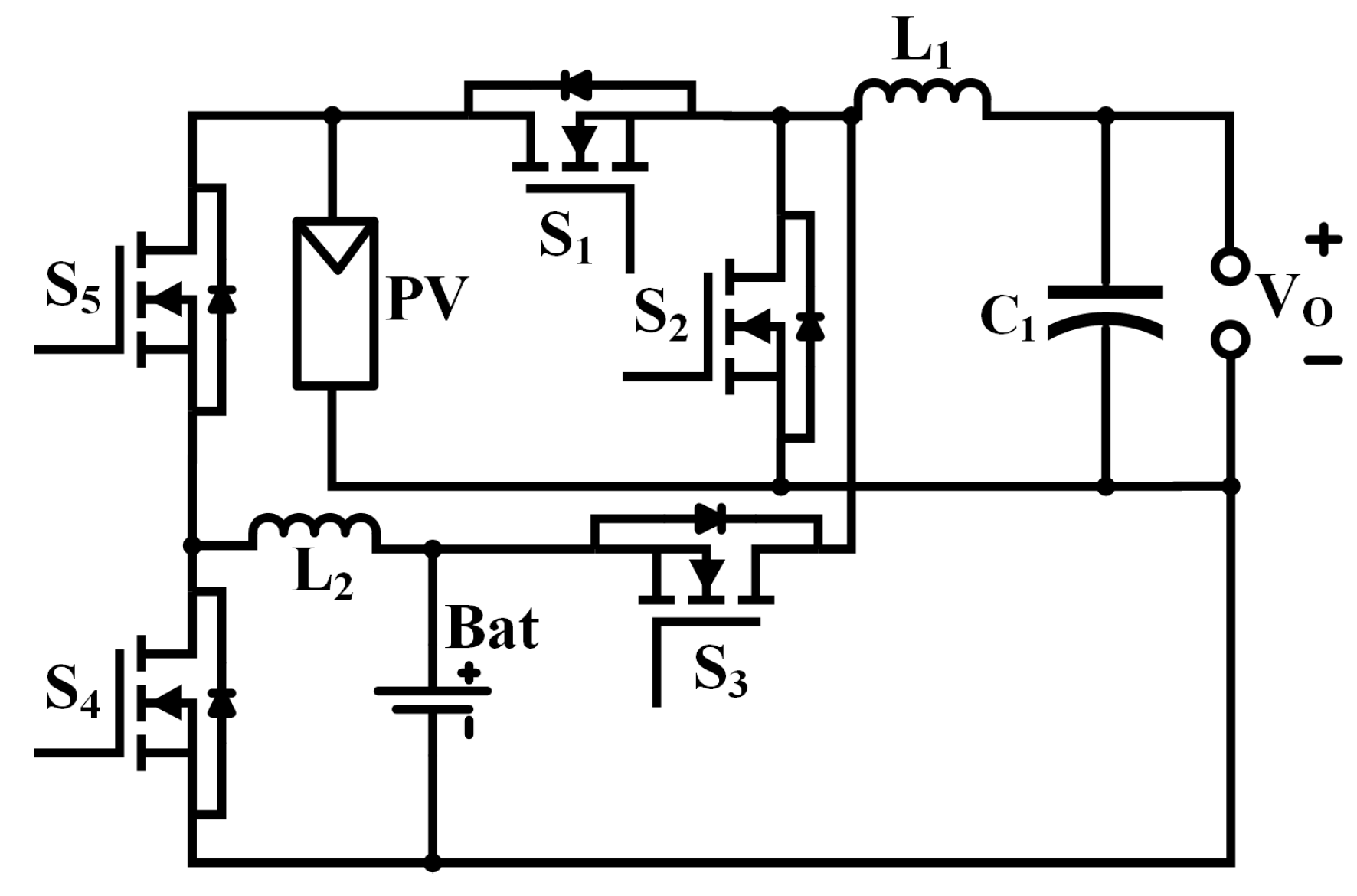
4. Circuit Realisation Based on Proposed Power Flow Graphs
5. Principles of Type I-III-IC Operation
- 1.
- PV to DC bus: In this mode, the PV source supplies the power only to the DC bus as the battery is at maximum SoC;
- 2.
- PV to battery: In this mode, the PV source supplies the power to the battery at no load condition;
- 3.
- Battery to DC bus: In this mode, the battery supplies the power to the DC bus as the PV source cannot supply power during nighttime;
- 4.
- DC bus to Battery: In this mode, the DC bus supplies the power to the battery as the PV source cannot supply power during nighttime;
- 5.
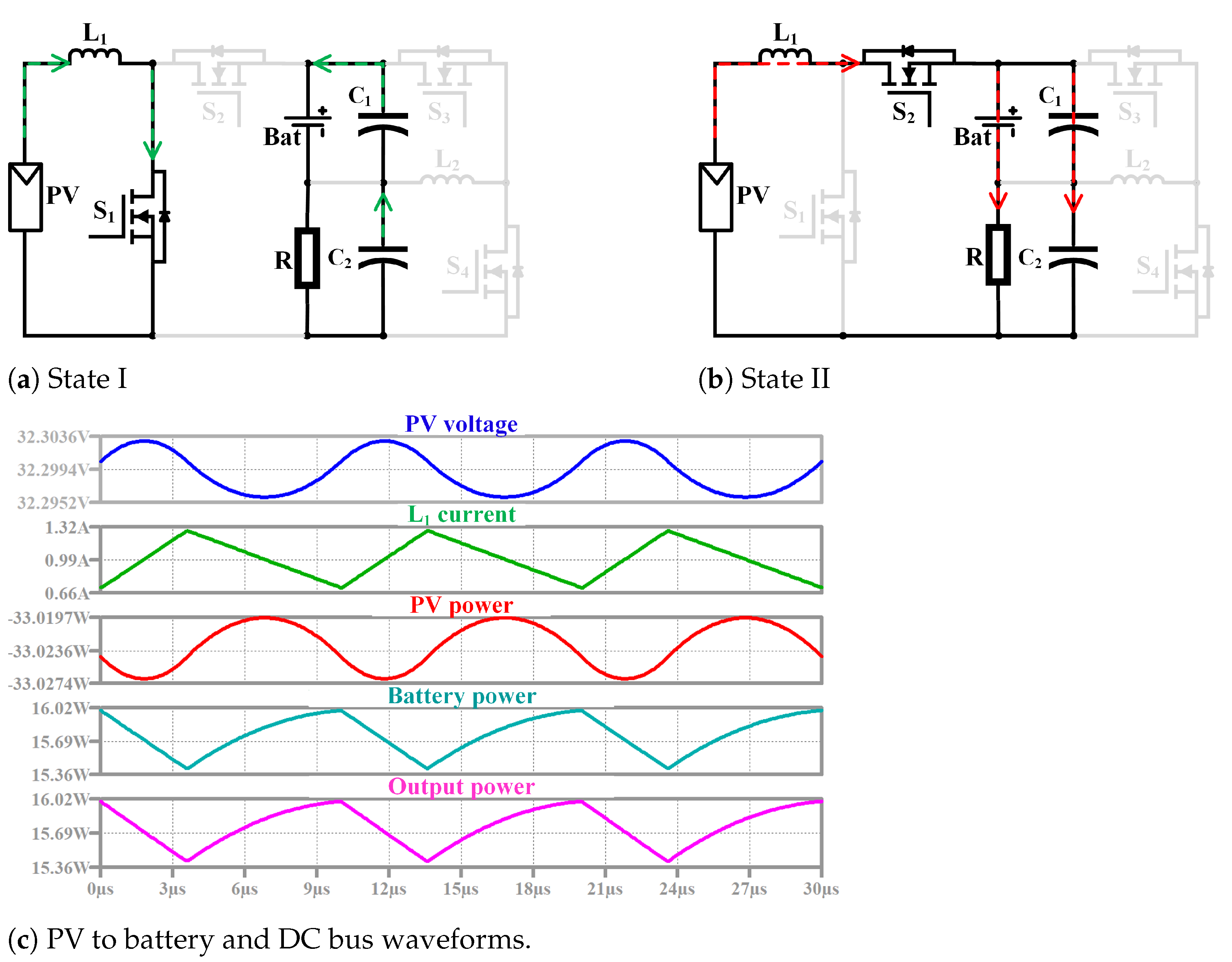
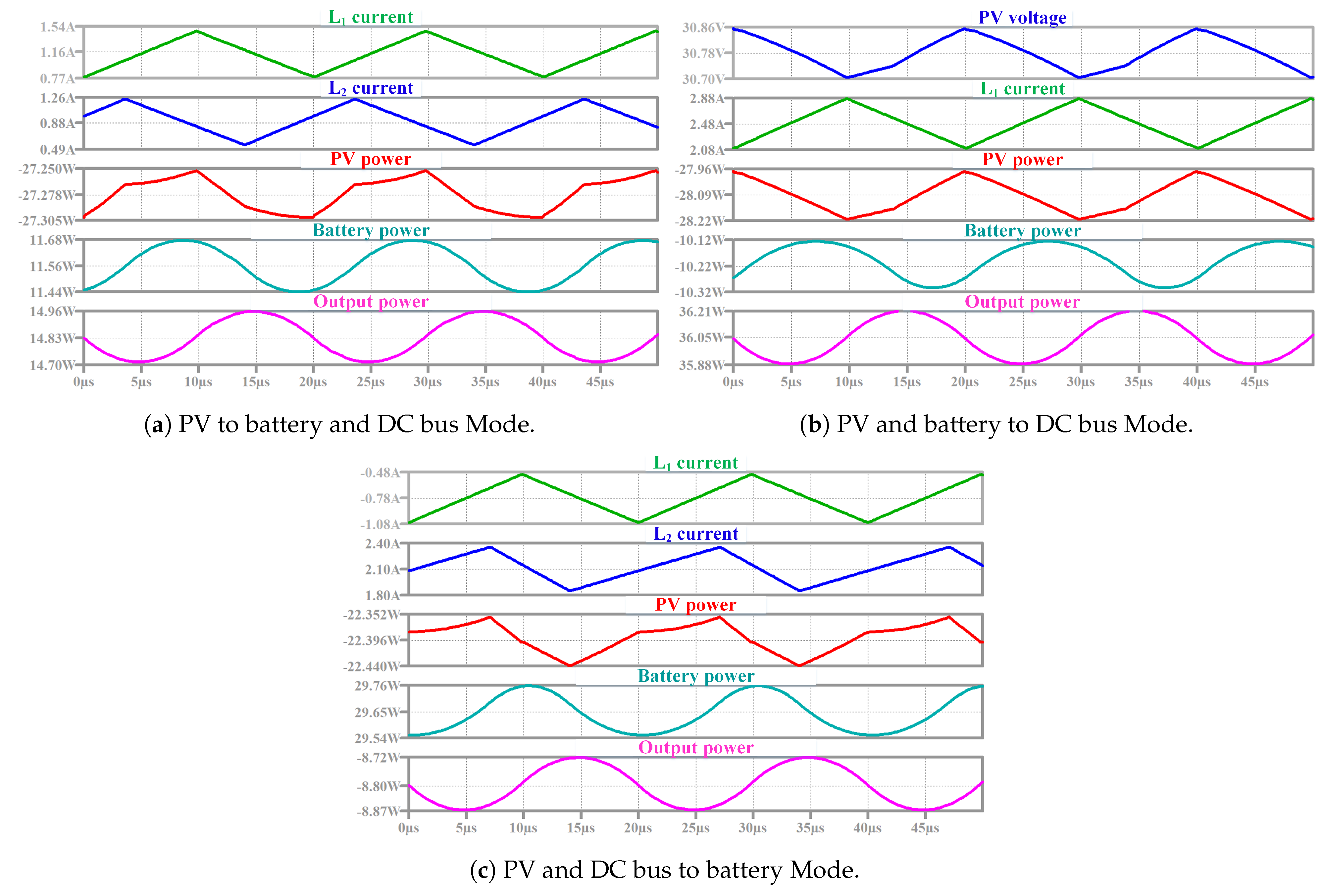
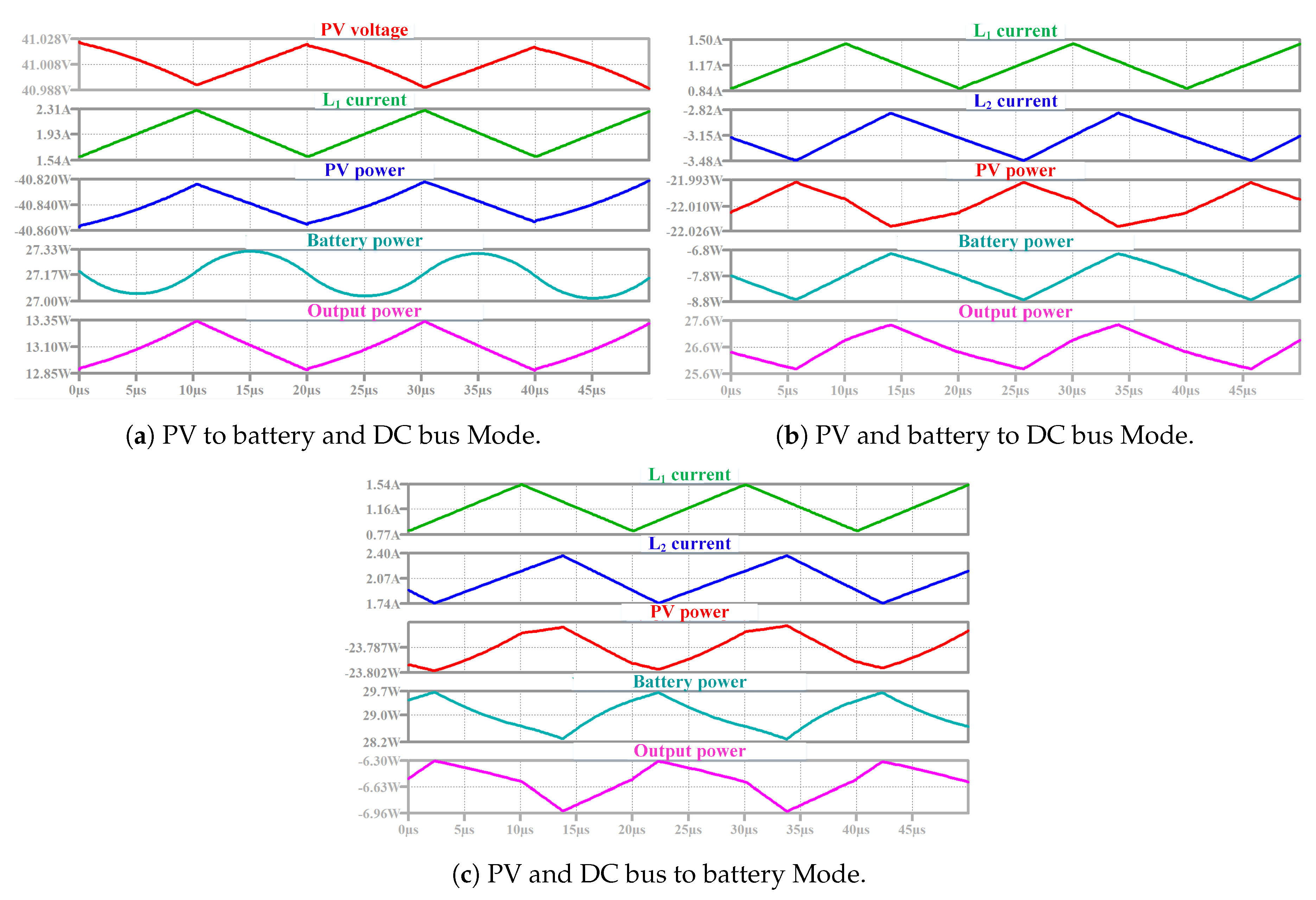
- PV to battery and DC bus: In this mode, the PV source has sufficient power to supply the battery and the DC bus. Figure 11 shows two switching states and explained as follows:
- State I [ < t < ]: is turned ON. The PV source starts to charge the inductor where = , as shown in Figure 11a. When turns OFF at t = , this state ends;
- 6.
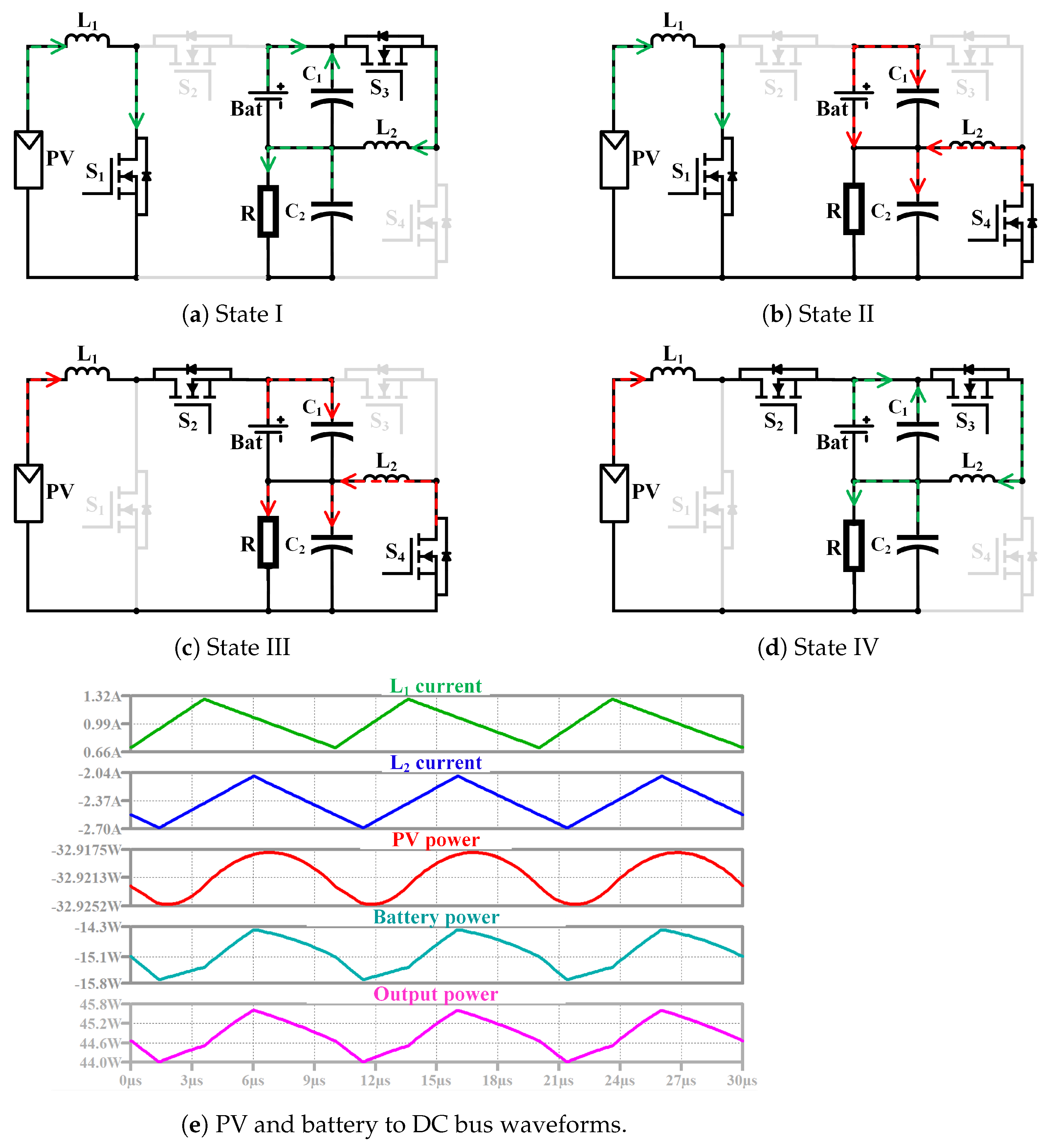
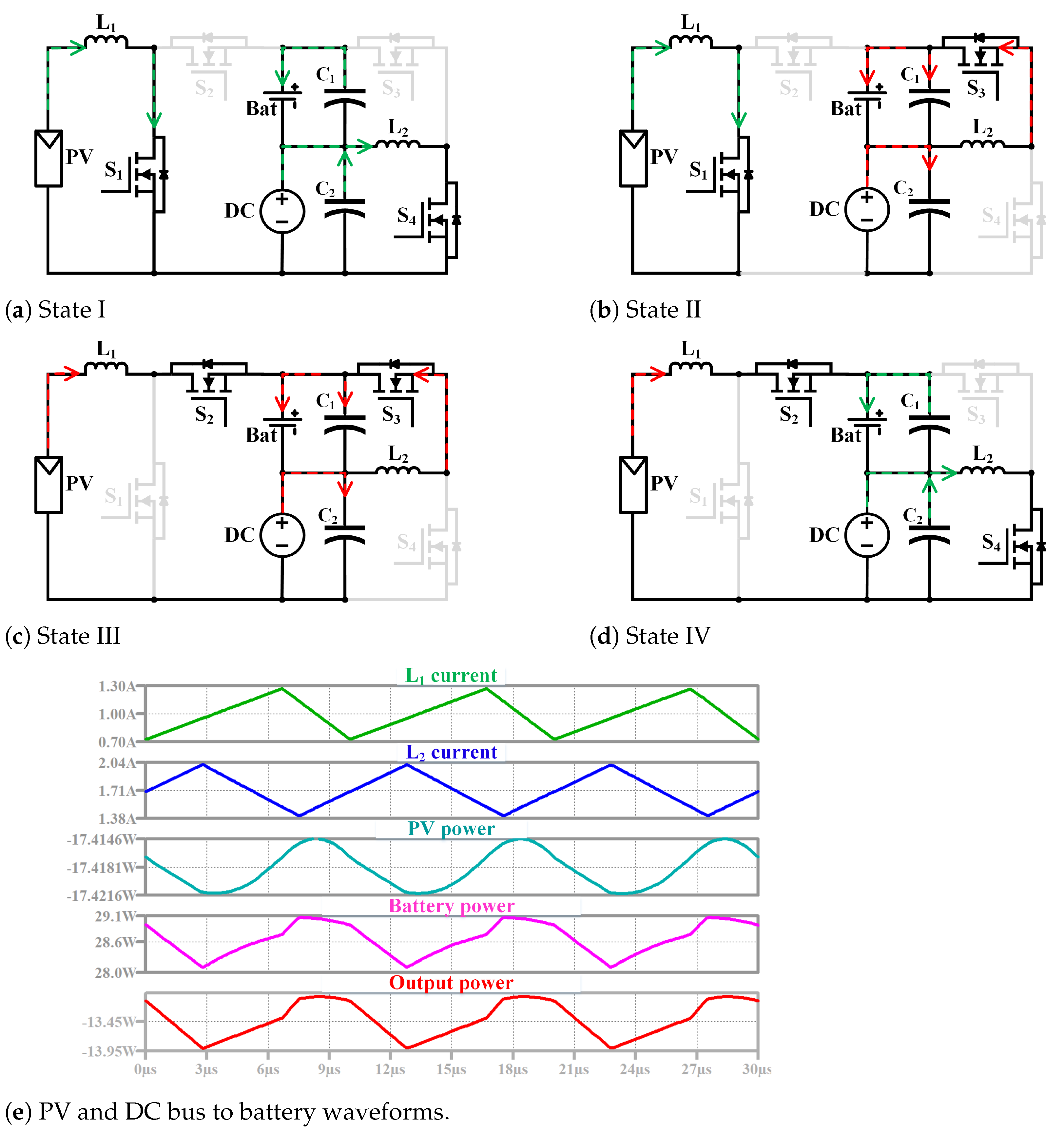
- PV and battery to DC bus: In this mode, the battery and the PV source provide the power to the DC bus. The system now operates as a DISO converter. Figure 12 shows four switching states and explained as follows:
- State I [ < t < ]: and are turned ON while , are OFF. PV starts to charge . In addition, starts to charge from the battery via , as shown in Figure 12a. The voltage across is given by = and that across the inductor is given by = . This mode ends when turns OFF at t = ;
- State II [ < t < ]: and are turned ON while , are OFF, PV source continues to charge . In addition, starts to discharge into the DC bus and , as shown in Figure 12b. The voltage across is given by = and across is given by = . This mode ends when turns OFF at t = .
- State III [ < t < ]: and are turned ON while , are OFF, starts to discharge to the battery via . In addition, continues to discharge into the DC bus and the capacitor , as shown in Figure 12c. The voltage across the inductor is given by = and across is given by = . This mode ends when turns ON at t = ;
- State IV [ < t < ]: and are turned ON while , are OFF. continues to discharge into the battery. In addition, start to charge from the battery and , as shown in Figure 12d. The voltage across is given by = and across is given by = . This mode ends when turns ON at t = . The simulation waveforms are shown in Figure 12e;
- 7.
- PV and DC bus to battery: As the battery is low in SoC, as well as PV source is generating less power, therefore DC bus and PV source together charge the battery at the rated current. The TPC operates as a DISO converter. This mode consists of four switching states, as shown in Figure 13 and as follows:
- State I [ < t < ]: and are turned ON while and are OFF. The PV source starts to charge where = . In addition, starts to be charged from the DC bus via where = + , as shown in Figure 13a. When turns OFF at t = , this state ends;
- State II [ < t < ]: and are turned ON while and are OFF. continues to be charged from the PV source and starts to discharge into the battery, as shown in Figure 13b. When turns OFF at t = , this state ends;
- State III [ < t < ]: and are turned ON while and are OFF. starts to discharge into the battery via and continues to discharge into the battery, as shown in Figure 13c. When turns ON at t = , this state ends.
6. Proposed Circuits Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPCs | Three-port converters; |
| RESs | Renewable energy sources; |
| SISO | Single-input single-output; |
| DISO | Double-input single-output. |
References
- Sinha, S.; Chandel, S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Rajesh, R.; Mabel, M.C. A comprehensive review of photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 51, 231–248. [Google Scholar] [CrossRef]
- Mei, Q.; Zhen-Lin, X.; Wu, W.Y. A novel multi-port DC/DC converter for hybrid renewable energy distributed generation systems connected to power grid. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008; pp. 1–5. [Google Scholar]
- Chiu, H.J.; Yao, C.J.; Lo, Y.K. A DC/DC converter topology for renewable energy systems. Int. J. Circuit Theory Appl. 2009, 37, 485–495. [Google Scholar] [CrossRef]
- An, L.; Lu, D.D.C. Design of a single-switch DC/DC converter for a PV-battery-powered pump system with PFM + PWM control. IEEE Trans. Ind. Electron. 2015, 62, 910–921. [Google Scholar] [CrossRef]
- Bhattacharjee, A.K.; Kutkut, N.; Batarseh, I. Review of multiport converters for solar and energy storage integration. IEEE Trans. Power Electron. 2019, 34, 1431–1445. [Google Scholar] [CrossRef]
- Kim, S.K.; Jeon, J.H.; Cho, C.H.; Ahn, J.B.; Kwon, S.H. Dynamic modeling and control of a grid-connected hybrid generation system with versatile power transfer. IEEE Trans. Ind. Electron. 2008, 55, 1677–1688. [Google Scholar] [CrossRef]
- Jin, K.; Ruan, X.; Yang, M.; Xu, M. A hybrid fuel cell power system. IEEE Trans. Ind. Electron. 2009, 56, 1212–1222. [Google Scholar] [CrossRef]
- Zhang, N.; Sutanto, D.; Muttaqi, K.M. A review of topologies of three-port DC–DC converters for the integration of renewable energy and energy storage system. Renew. Sustain. Energy Rev. 2016, 56, 388–401. [Google Scholar] [CrossRef] [Green Version]
- Cheng, T.; Lu, D.D.; Gong, A.; Verstraete, D. Analysis of a three-port DC/DC converter for PV-battery system using DISO boost and SISO buck converters. In Proceedings of the Power Engineering Conference (AUPEC), 2015 Australasian Universities, Wollongong, Australia, 27–30 September 2015; pp. 1–6. [Google Scholar]
- Qian, Z.; Abdel-Rahman, O.; Al-Atrash, H.; Batarseh, I. Modeling and control of three-port DC/DC converter interface for satellite applications. IEEE Trans. Power Electron. 2010, 25, 637–649. [Google Scholar] [CrossRef]
- Kardan, F.; Alizadeh, R.; Banaei, M.R. A New Three Input DC/DC Converter for Hybrid PV/FC/Battery Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1771–1778. [Google Scholar] [CrossRef]
- Ganjavi, A.; Ghoreishy, H.; Ahmad, A.A.; Zhagn, Z. A Three-Level Three-port Bidirectional DC/DC Converter. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–4. [Google Scholar]
- Gao, S.; Shi, J.; Dong, X.; Jia, Y.; Wu, H.; Hu, H. Performance Evaluation of A Non-Isolated Three-Port Converter for PV-Battery Hybrid Energy System. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1394–1399. [Google Scholar]
- Yang, P.; Tse, C.K.; Xu, J.; Zhou, G. Synthesis and Analysis of Double-Input Single-Output DC/DC Converters. IEEE Trans. Ind. Electron. 2015, 62, 6284–6295. [Google Scholar] [CrossRef]
- Zogogianni, C.G.; Tatakis, E.C.; Vekic, M.S. Non-Isolated Reduced Redundant Power Processing DC/DC Converters: A Systematic Study of Topologies with Wide Voltage Ratio for High-Power Applications. IEEE Trans. Power Electron. 2019, 34, 8491–8502. [Google Scholar] [CrossRef]
- Chen, X.; Yang, P.; Peng, Y. Synthesis and Analysis of Power Management Units for IoT Applications. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 1383–1388. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Q.; Wei, Y.; Mou, D.; Lu, X.; Sun, P. Topology Analysis and Review of Three-Port DC–DC Converters. IEEE Trans. Power Electron. 2020, 35, 11783–11800. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.D.C.; Qin, L. Non-Isolated Single-Inductor DC/DC Converter with Fully Reconfigurable Structure for Renewable Energy Applications. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 351–355. [Google Scholar] [CrossRef]
- Al-Soeidat, M.R.; Aljarajreh, H.; Khawaldeh, H.A.; Lu, D.D.C.; Zhu, J. A Reconfigurable Three-Port DC–DC Converter for Integrated PV-Battery System. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3423–3433. [Google Scholar] [CrossRef]
- Waseem, M.; Saeed, L.; Khan, M.Y.A.; Saleem, J.; Majid, A. A multi input multi output bidirectional DC/DC boost converter with backup battery port. In Proceedings of the 2018 1st International Conference on Power, Energy and Smart Grid (ICPESG), Mirpur Azad Kashmir, Pakistan, 9–10 April 2018; pp. 1–6. [Google Scholar]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. A Family of Three-Port Three-Level Converter Based on Asymmetrical Bidirectional Half-Bridge Topology for Fuel Cell Electric Vehicle Applications. IEEE Trans. Power Electron. 2019, 34, 11706–11724. [Google Scholar] [CrossRef]
- Aljarajreh, H.; Lu, D.D.; Tse, C.K. Synthesis of Dual-Input Single-Output DC/DC Converters. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Marchesoni, M.; Passalacqua, M.; Vaccaro, L. A refined loss evaluation of a three-switch double input DC-DC converter for hybrid vehicle applications. Energies 2020, 13, 204. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Jin, Z.; Liu, Y.; Hu, Y.; Zhang, J.; Qing, X. Programmable Topology Derivation and Analysis of Integrated Three-Port DC–DC Converters with Reduced Switches for Low-Cost Applications. IEEE Trans. Ind. Electron. 2019, 66, 6649–6660. [Google Scholar] [CrossRef] [Green Version]
- Tse, C.K.; Chow, M.H.; Cheung, M.K. A family of PFC voltage regulator configurations with reduced redundant power processing. IEEE Trans. Power Electron. 2001, 16, 794–802. [Google Scholar] [CrossRef] [Green Version]
- Tse, C.K. Circuit theory of power factor correction in switching converters. Int. J. Circuit Theory Appl. 2003, 31, 157–198. [Google Scholar] [CrossRef] [Green Version]
- Aljarajreh, H.; Lu, D.D.C.; Siwakoti, Y.P.; Aguilera, R.P.; Tse, C.K. A Method of Seamless Transitions between Different Operating Modes for Three-Port DC/DC Converters. IEEE Access 2021, 9, 59184–59195. [Google Scholar] [CrossRef]
- Wang, B.; Xian, L.; Kanamarlapudi, V.R.K.; Tseng, K.J.; Ukil, A.; Gooi, H.B. A Digital Method of Power-Sharing and Cross-Regulation Suppression for Single-Inductor Multiple-Input Multiple-Output DC–DC Converter. IEEE Trans. Ind. Electron. 2017, 64, 2836–2847. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Ye, J.; Gooi, H.B. Deadbeat Control for a Single-Inductor Multiple-Input Multiple-Output DC–DC Converter. IEEE Trans. Power Electron. 2019, 34, 1914–1924. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.D.C. Three-port converters with a flexible power flow for integrating PV and energy storage into a DC bus. J. Power Electron. 2017, 17, 1433–1444. [Google Scholar]
- Passalacqua, M.; Marchesoni, M.; Vaccaro, L. A New Modulation Strategy for Exploiting Discontinuous Conduction Mode in a Double-Input Three-Switch Bidirectional DC–DC Converter. IEEE Trans. Ind. Electron. 2020, 68, 10815–10825. [Google Scholar] [CrossRef]
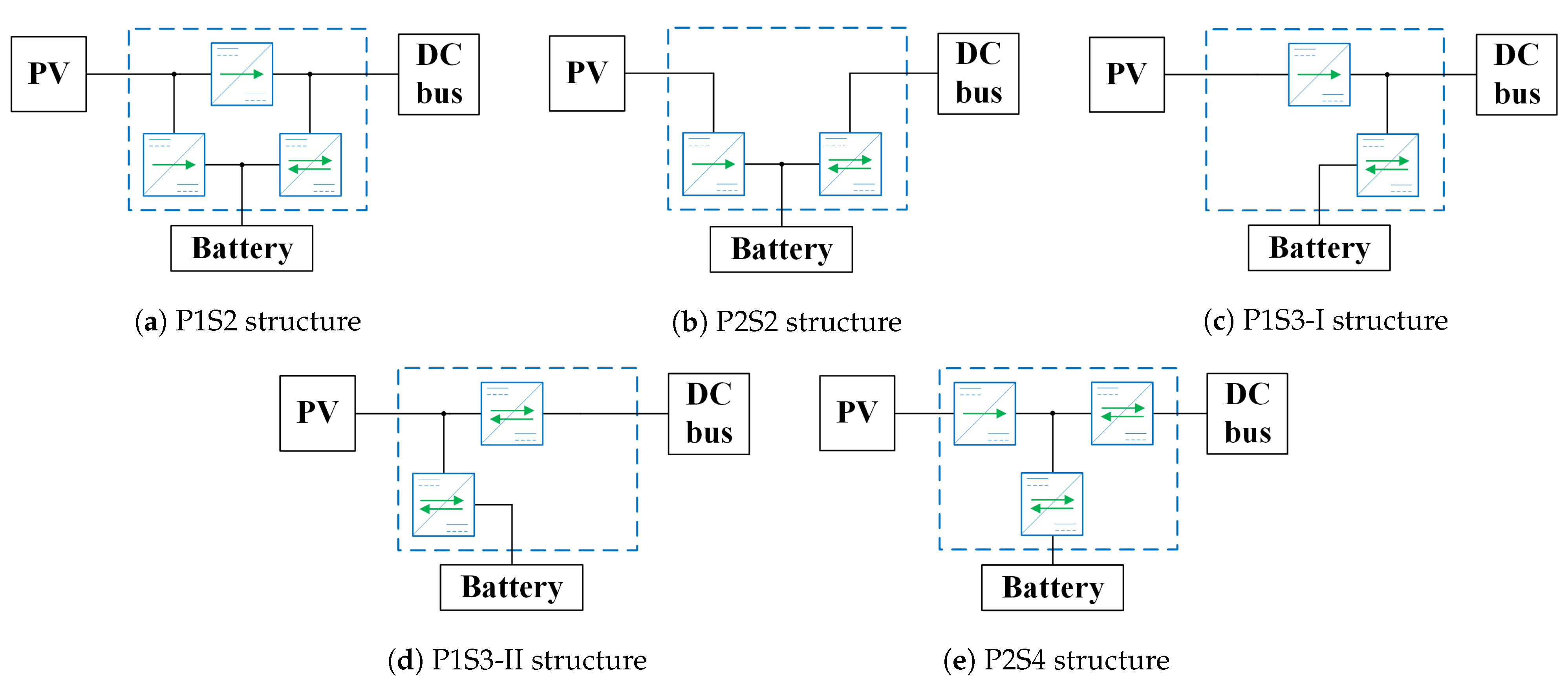
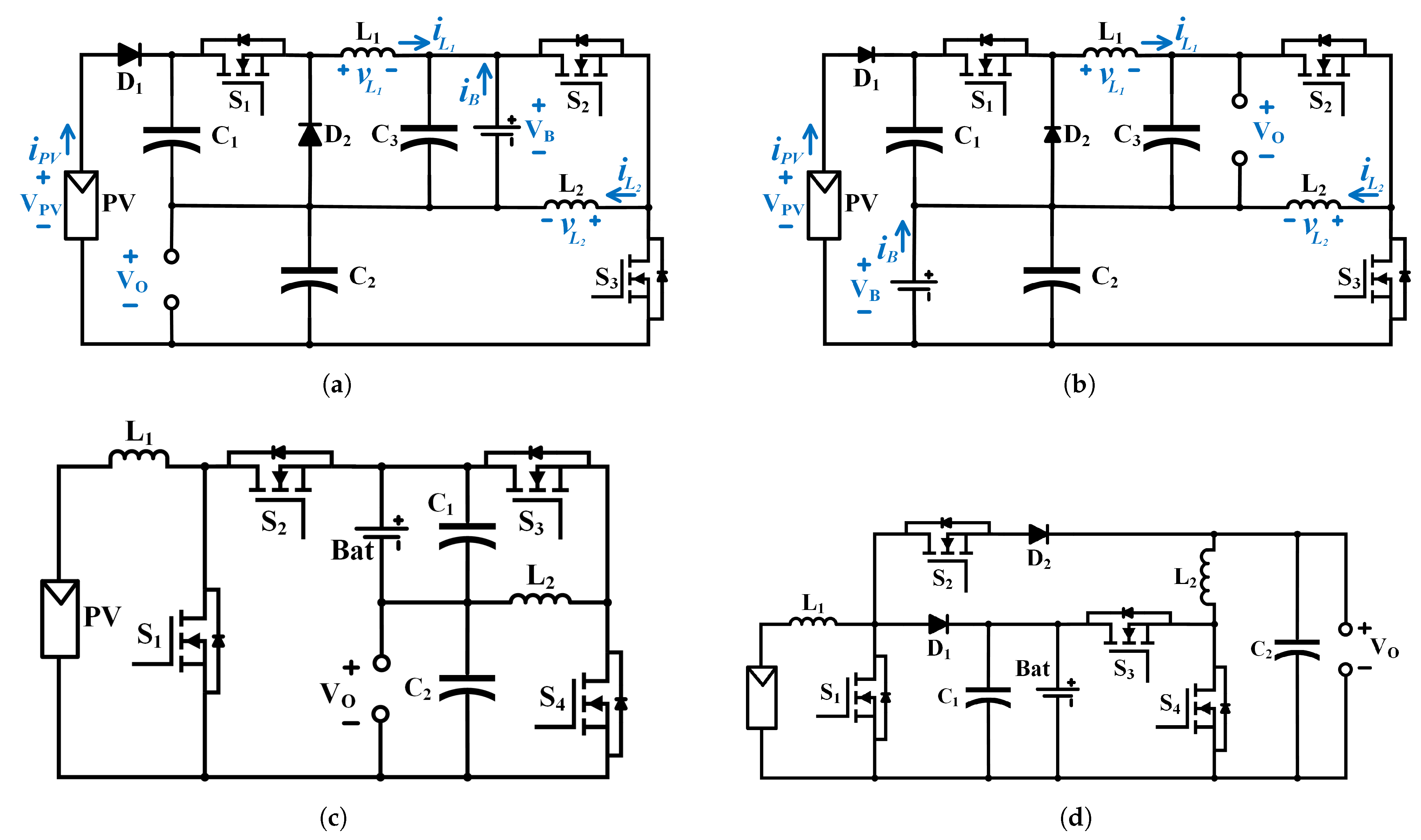

| Efficiency | The Complexity of the Topology | Control Simplicity | |
|---|---|---|---|
| P1S2 structure | Highest | High | Lowest |
| P2S2 structure | Low | Lowest | Highest |
| P1S3-I structure | High | Lowest | High |
| P1S3-II structure | High | Low | Highest |
| P2S4 structure | Lowest | Highest | Lowest |
| Configuration | Converter 1 | Converter 2 | Condition |
|---|---|---|---|
| Type I-I-IA | Any | Any | − |
| Type I-I-IB | Any | Any | − |
| Type II-IIA | Boost | Boost | << |
| Buck | < & < | ||
| Buck | Boost | < & < | |
| Buck | << | ||
| Buck-boost | Boost | < | |
| Buck | < | ||
| Type II-IIB | Boost | Boost | < & < |
| Buck | << | ||
| Buck | Boost | << | |
| Buck | < & < | ||
| Buck-boost | Buck-boost | ||
| Type II-IIC | Boost | Boost | << |
| Buck | < & < | ||
| Buck | Boost | < & < | |
| Buck | << | ||
| Type I-III-IA | Boost | Buck-boost | < |
| Buck | Buck-boost | < & < | |
| Type I-III-IC | Boost | Buck-boost | − |
| Buck | Buck-boost | < & < | |
| Type I-III-ID | Boost | Buck-boost | < & < |
| Buck | Buck-boost | < & < |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljarajreh, H.; Lu, D.D.-C.; Siwakoti, Y.P.; Tse, C.K.; See, K.W. Synthesis and Analysis of Three-Port DC/DC Converters with Two Bidirectional Ports Based on Power Flow Graph Technique. Energies 2021, 14, 5751. https://doi.org/10.3390/en14185751
Aljarajreh H, Lu DD-C, Siwakoti YP, Tse CK, See KW. Synthesis and Analysis of Three-Port DC/DC Converters with Two Bidirectional Ports Based on Power Flow Graph Technique. Energies. 2021; 14(18):5751. https://doi.org/10.3390/en14185751
Chicago/Turabian StyleAljarajreh, Hamzeh, Dylan Dah-Chuan Lu, Yam P. Siwakoti, Chi K. Tse, and K. W. See. 2021. "Synthesis and Analysis of Three-Port DC/DC Converters with Two Bidirectional Ports Based on Power Flow Graph Technique" Energies 14, no. 18: 5751. https://doi.org/10.3390/en14185751
APA StyleAljarajreh, H., Lu, D. D.-C., Siwakoti, Y. P., Tse, C. K., & See, K. W. (2021). Synthesis and Analysis of Three-Port DC/DC Converters with Two Bidirectional Ports Based on Power Flow Graph Technique. Energies, 14(18), 5751. https://doi.org/10.3390/en14185751








