An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing
Abstract
:1. Introduction
2. The Principle of the Proposed Algorithm
2.1. LSSVM Algorithm and Hyperparameters
2.2. Hyperparameters Optimization for the First Time
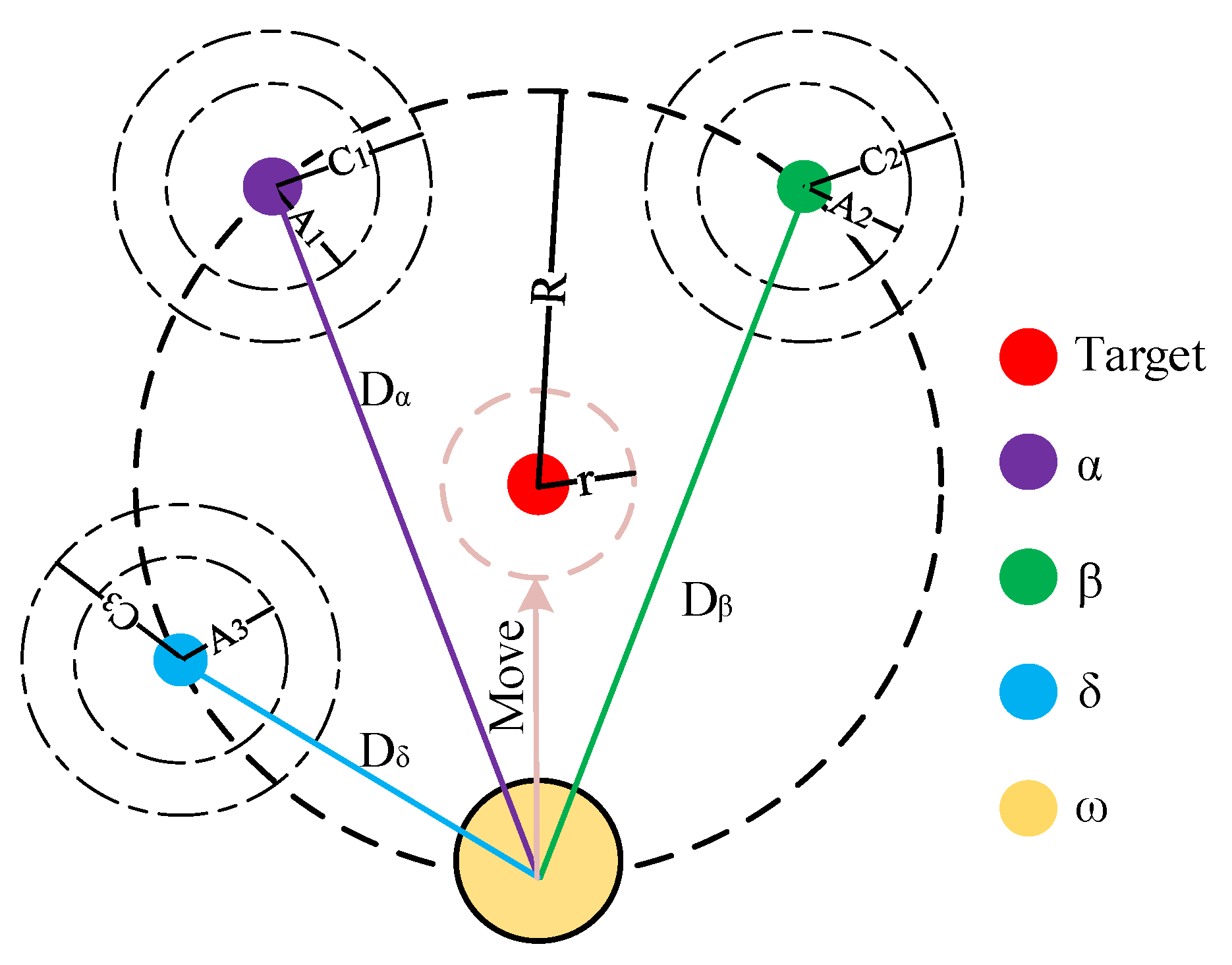
2.3. Chaos Initialization
2.4. Hyperparameters Accuracy Optimized by Hybrid Local Search
3. Comparison between the Proposed Algorithm and the Existing Algorithm
3.1. Data Collection
3.2. Data Classification and Normalization
3.3. Predictive Evaluation Index
3.4. Simulation Verification
3.5. Comprehensive Analysis of Predictive Power
4. Power Smoothing Application of the Proposed Algorithm
4.1. PV Power Generation System Equipped with HESS
4.2. Related Parameter Settings
4.3. The Design of PV-Storage Advanced Smoothing Control Strategy
4.4. The Verification of Power Smoothing Simulation
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, Y.; Alva, G.; Fang, G. Development and applications of photovoltaic–thermal systems: A review. Renew. Sustain. Energy Rev. 2019, 102, 249–265. [Google Scholar] [CrossRef]
- Omeran, W.; Kazerani, M.; Salama, M. Investigation of methods for reduction of power fluctuations generated from large grid-connected photovoltaic systems. IEEE Trans. Energy Convers. 2011, 26, 318–327. [Google Scholar] [CrossRef]
- Lappalainen, K.; Valkealahtis, S. Output power variation of different PV array configurations during irradiance transitions caused by moving clouds. Appl. Energy 2017, 190, 902–910. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.C.; Ramachandaramurthy, V.K. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Li, X. Fuzzy adaptive Kalman filter for wind power output smoothing with battery energy storage system. Renew. Power Gener. 2012, 6, 340–347. [Google Scholar] [CrossRef]
- Wu, T.; Shi, X.; Liao, L.; Zhou, C.; Zhou, H.; Su, Y. A capacity configuration control strategy to alleviate power fluctuation of hybrid energy storage system based on improved particle swarm optimization. Energies 2019, 12, 642. [Google Scholar] [CrossRef] [Green Version]
- Lamsal, D.; Sreeram, V.; Mishra, Y.; Kumar, D. Smoothing control strategy of wind and photovoltaic output power fluctuation by considering the state of health of battery energy storage system. IET Renew. Power Gener. 2019, 13, 578–586. [Google Scholar] [CrossRef]
- Anagnostos, D.; Schmidt, T.; Cavadias, S.; Soudris, D.; Poortmans, J.; Catthoor, F. A method for detailed, short-term energy yield forecasting of photovoltaic installations. Renew. Energy 2019, 130, 122–129. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Y.; Zhao, J.; Zhu, Y.; Liu, J. A dynamic wavelet-based robust wind power smoothing approach using hybrid energy storage system. Int. J. Electr. Power Energy Syst. 2020, 116, 105579. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, X.; Sun, X.; Jia, D.; Cao, Z.; Pan, J.; Xu, B. Model predictive control and improved low-pass filtering strategies based on wind power fluctuation mitigation. J. Mod. Power Syst. Clean Energy 2019, 7, 512–524. [Google Scholar] [CrossRef] [Green Version]
- Roy, P.K.S.; Karayaka, H.B.; Yan, Y.; Alqudah, Y. Investigations into best cost battery-supercapacitor hybrid energy storage system for a utility scale PV array. J. Energy Storage 2019, 22, 50–59. [Google Scholar] [CrossRef]
- Faria, J.; Pombo, J.; Calado, M.R.; Mariano, S. Power management control strategy based on artificial neural networks for standalone PV applications with a hybrid energy storage system. Energies 2019, 12, 902. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Wang, P.; Xu, W.; Zhang, S.; Wang, J.; Dai, Y. The survey of the combined heat and compressed air energy storage (CH-CAES) system with dual power levels turbomachinery configuration for wind power peak shaving based spectral analysis. Energy 2021, 215, 119167. [Google Scholar] [CrossRef]
- Xinsong, Z.; Juping, G.; Yue, Y.; Wang, M.; Cao, Y.; Hua, L.; Li, Z. Wind power fluctuation suppression strategy based on battery energy storage system. Proc. Chin. Soc. Electr. Eng. 2014, 34, 4752–4760. [Google Scholar]
- Qian, W.; Zhao, C.; Wan, C.; Song, Y.; Yang, G. Probabilistic Forecasting Based Sizing and Control of Hybrid Energy Storage for Wind Power Smoothing. IEEE Trans. Sustain. Energy 2021. [Google Scholar] [CrossRef]
- Wang, Y.; Tai, N.; Huang, W.; Liang, S. Rolling coordination control of the wind-storage hybrid system based on the ultra-short- term wind forecast. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1219–1223. [Google Scholar]
- Islam, F.; Al-Durra, A.; Muyeen, S.M. Smoothing of wind farm output by prediction and supervisory-control-unit- based FESS. IEEE Trans. Sustain. Energy 2013, 4, 925–933. [Google Scholar] [CrossRef]
- Yifu, P.; Junhua, Y. Power Smoothing strategy of wave power generation system based on power prediction method. Comput. Simul. 2018, 35, 68–72. [Google Scholar]
- Liu, Z.F.; Li, L.L.; Tseng, M.L.; Lim, M.K. Prediction short-term photovoltaic power using improved chicken swarm optimizer-Extreme learning machine model. J. Clean. Prod. 2020, 248, 119272. [Google Scholar] [CrossRef]
- Han, H.; Cui, X.; Fan, Y.; Qing, H. Least squares support vector machine (LS-SVM)-based chiller fault diagnosis using fault indicative features. Appl. Therm. Eng. 2019, 154, 540–547. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Xu, W.; Shi, Y. A weighted Lq adaptive least squares support vector machine classifiers–Robust and sparse approximation. Expert Syst. Appl. 2011, 38, 2253–2259. [Google Scholar] [CrossRef]
- Li, X.; Wu, S.; Li, X.; Yuan, H.; Zhao, D. Particle swarm optimization- support vector machine model for machinery fault diagnoses in high-voltage circuit breakers. Chin. J. Mech. Eng. 2020, 33, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Han, S.W.; Suh, D.Y. A 360-degree panoramic image inpainting network using a cube map. Comput. Mater. Contin. 2021, 66, 213–228. [Google Scholar] [CrossRef]
- Archetti, C.; Feillet, D.; Mor, A.; Speranza, M.G. An iterated local search for the Traveling Salesman Problem with release dates and completion time minimization. Comput. Oper. Res. 2018, 98, 24–37. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Wang, P. Unusual phenomenon of optimizing the Griewank function with the increase of dimension. Front. Inf. Technol. Electron. Eng. 2019, 20, 1344–1360. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. Bezier Search Differential Evolution Algorithm for numerical function optimization: A comparative study with CRMLSP, MVO, WA, SHADE and LSHADE. Expert Syst. Appl. 2021, 165, 113875. [Google Scholar] [CrossRef]
- Yufei, W.; Hua, X.; Lu, S. An Ultra-Short-Term Chaotic Prediction Method of Photovoltaic Output Power. Shanghai Patent CN106503828B, 27 December 2019. [Google Scholar]
- Suhua, L.; Yaowu, W.; Cui, Y.; Yi, L. Operation strategy of battery energy storage to smooth short-term wind power fluctuations. Autom. Electr. Power Syst. 2014, 38, 17–22+58. [Google Scholar]
- Zhang, H.; Li, S.; Wang, Y.; Wang, Y.; Yang, L. Real-time optimization strategy for single-track high-speed train rescheduling with disturbance uncertainties: A scenario-based chance-constrained model predictive control approach. Comput. Oper. Res. 2021, 127, 105135. [Google Scholar] [CrossRef]







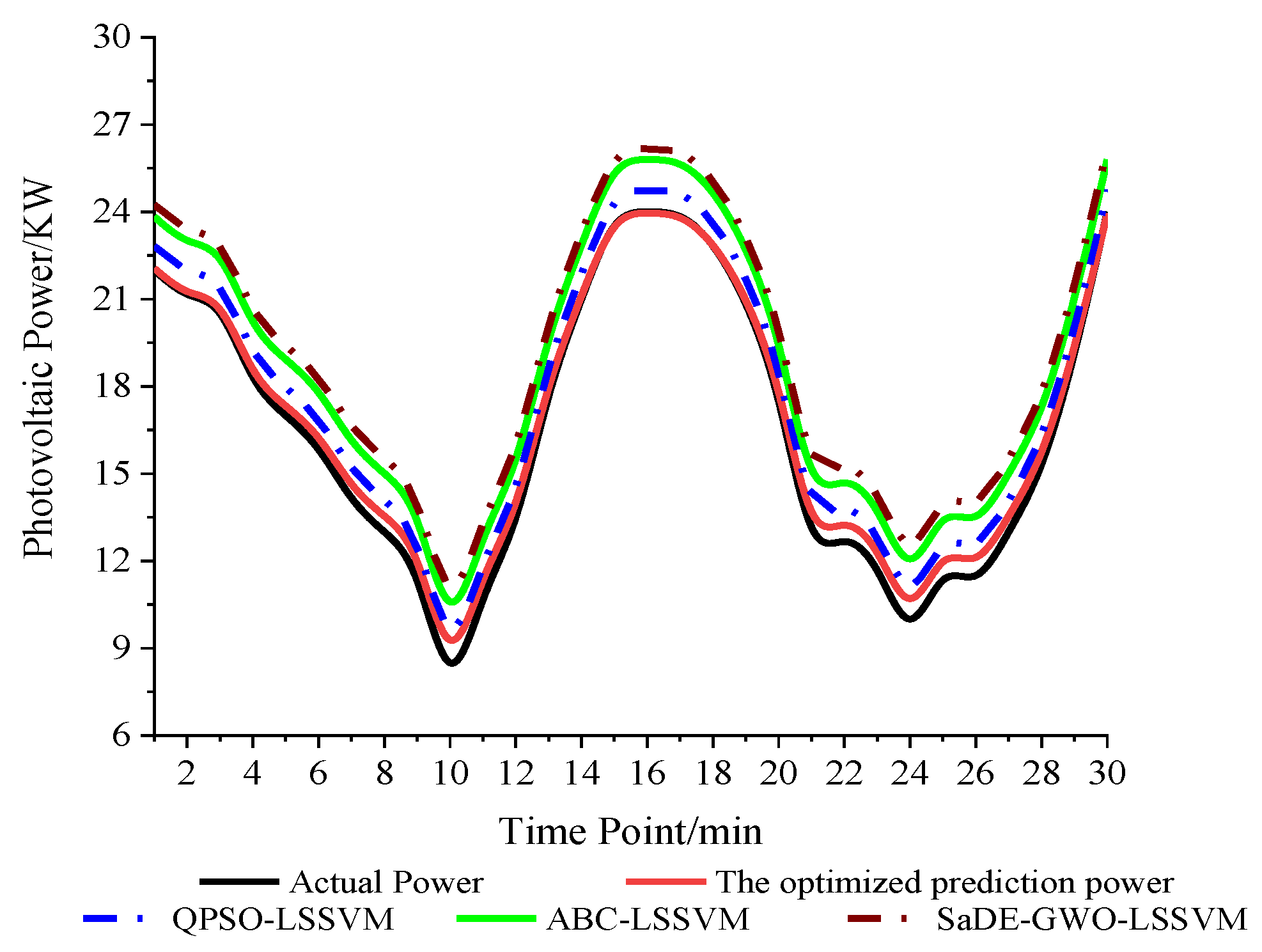




| Algorithm Type | MAPE | RMSE | Time |
|---|---|---|---|
| HLSGWO-LSSVM | 0.03% | 0.44% | 1.87 s |
| QPSO-LSSVM | 0.05% | 0.79% | 29.55 s |
| ABC-LSSVM | 0.13% | 1.94% | 46.72 s |
| SaDE-GWO-LSSVM | 0.16% | 2.42% | 54.31 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Chen, K.; Chen, Y.; Dai, Y.; Liu, Z.; Zhao, K.; Wang, H.; Peng, Z. An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing. Energies 2021, 14, 5752. https://doi.org/10.3390/en14185752
Zhao Z, Chen K, Chen Y, Dai Y, Liu Z, Zhao K, Wang H, Peng Z. An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing. Energies. 2021; 14(18):5752. https://doi.org/10.3390/en14185752
Chicago/Turabian StyleZhao, Zhenxing, Kaijie Chen, Ying Chen, Yuxing Dai, Zeng Liu, Kuiyin Zhao, Huan Wang, and Zishun Peng. 2021. "An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing" Energies 14, no. 18: 5752. https://doi.org/10.3390/en14185752
APA StyleZhao, Z., Chen, K., Chen, Y., Dai, Y., Liu, Z., Zhao, K., Wang, H., & Peng, Z. (2021). An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing. Energies, 14(18), 5752. https://doi.org/10.3390/en14185752






