Feasibility Evaluation on Elimination of DC Filters for Line-Commutated Converter-Based High-Voltage Direct Current Projects in New Situations
Abstract
:1. Introduction
- To scientifically demonstrate the feasibility on the elimination of DC filters, a ±800 kV/8000 MW in-service LCC-UHVDC project is taken as a representative example, including the DC loop parameters and surge arresters’ arrangement.
- In order to comprehensively research the impacts on the harmonic steady-state stresses and the transient stress on DC-side apparatus after removing the DCFs, the mature technologies (i.e., the standard steady-state frequency-domain analysis, and the PSCAD/EMTDC simulation) are adopted.
- Suggestions are put forward for the DCFs’ configuration or refurbishment of LCC-HVDC project in China, which could be a reference for similar LCC-HVDC projects in the world.
2. Development of Communication Technology
3. HVDC System Modeling
3.1. Subsection
3.2. Harmonic Voltage Source Model
3.3. DC Transmission Line Model
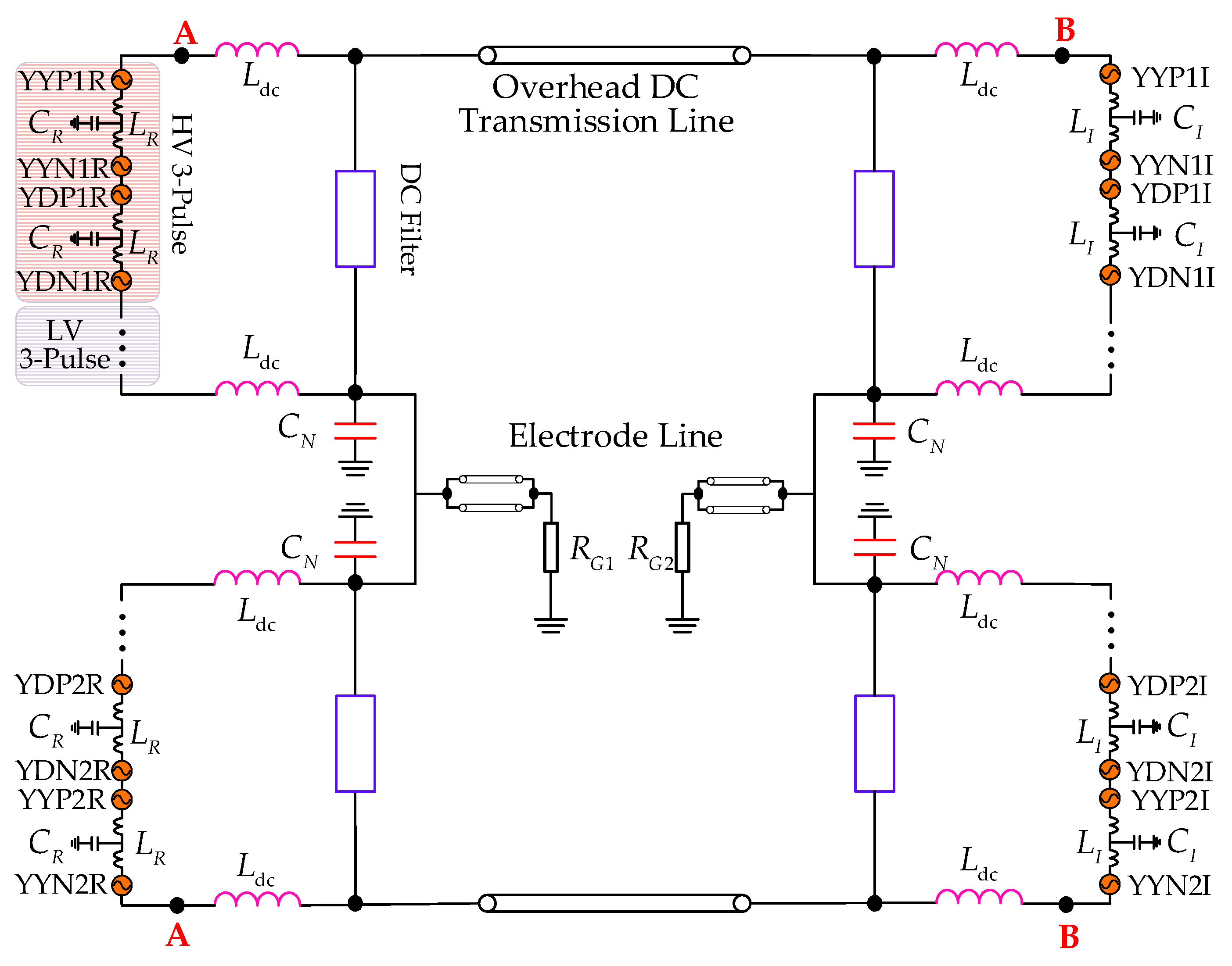
3.4. Solution for the DC-Side Circuit
- Step (1).
- Calculate the worst non-consistent sets of three-pulse harmonic voltage sources with the piecewise linear analysis approach derived in [15].
- Step (2).
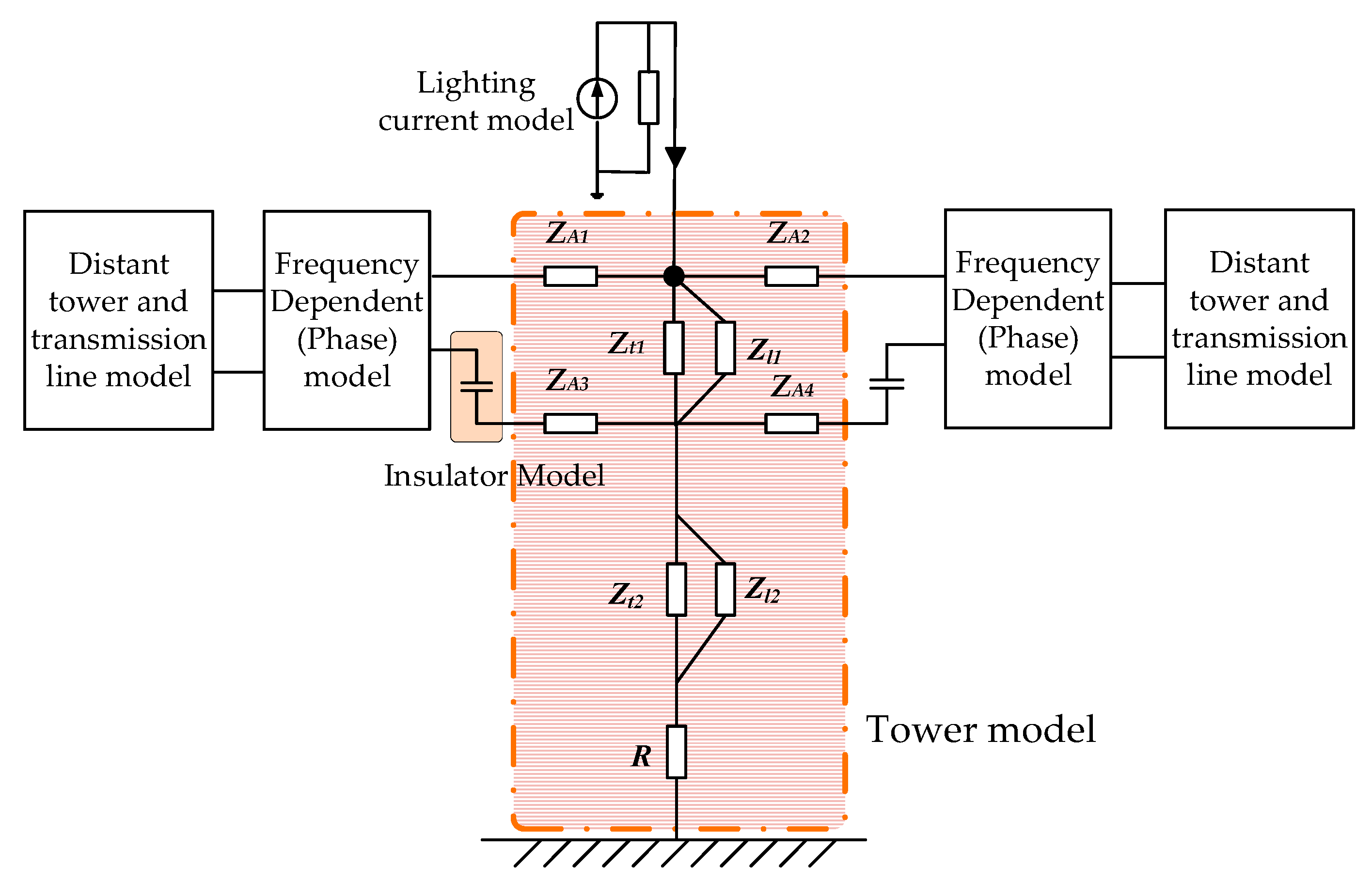
- Form the nodal admittance matrix Ydc(n) at nth-order harmonic. First, calculate the nodal admittance matrix of lines Yl(n) in (1), including the DC transmission line and the electrode lines. Then, insert the Yl(n) into Ydc(n) as multi-node elements. Finally, Ydc(n) is constructed by adding other elements in Figure 5 one by one.
- Step (3).
- Solve the entire DC circuit. First, suppose that the three-pulse sources at the rectifier act alone and the sources at the inverter are set to zero, the injection current vector I(n, 1) is calculated with the Norton equivalent. Second, the nodal voltage vector U(n, 1) is obtained with the nodal voltage analysis method. Then, repeat the similar process, the voltage vector U(n, 2) excited solely by the three-pulse sources at the inverter is acquired. Finally, the harmonic voltages Ue(n, i) that the elements bear and the harmonic currents Ie(n, i) flowing in elements are calculated. Here, i is 1 or 2, which denotes the rectifier or the inverter.
- Step (4).
- Calculate the steady-state stresses of elements. Synthesized with all individual harmonics, the steady state stresses of the capacitors are expressed as in:where N is the maximum harmonic order. The voltage stress expression of the reactors UL are the same as that of the capacitor, while the current stress of the reactors are calculated by the root sum of squares (RSS) method as:
- Step (5).
- Calculate the DC-loop impedance. Firstly, insert two identical test voltage sources at point A in Figure 5, whose schematics are shown in Figure 6. Here, is the voltage phasor of the inserted voltage source at the specified frequency f, Rin is the internal resistance; is the current phasor flowing through point A; and are the voltage phasors at point a and point b, respectively.
4. Parameters of the Test System
4.1. Subsection
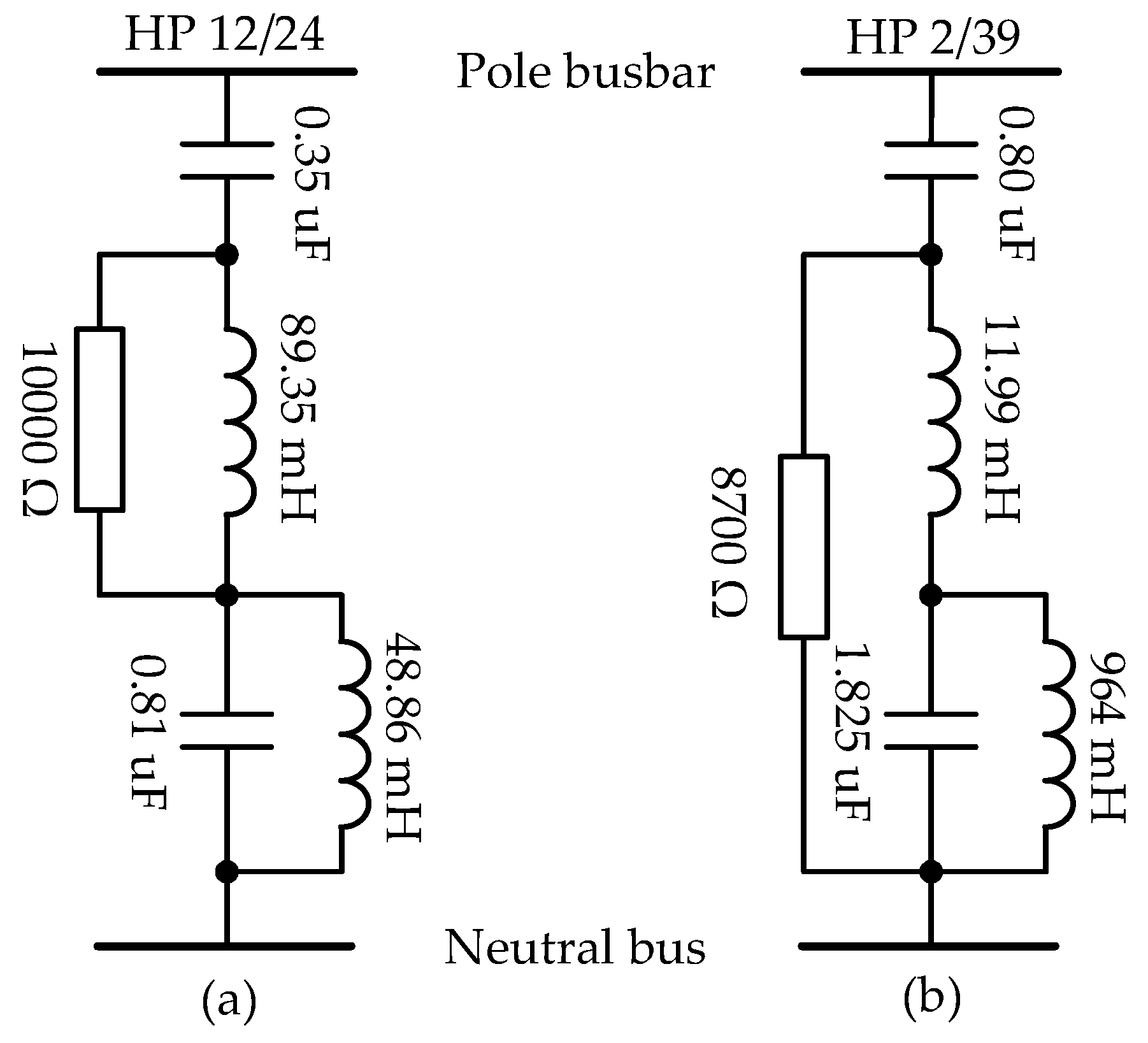
4.2. DC-Side Harmonic Filtering System
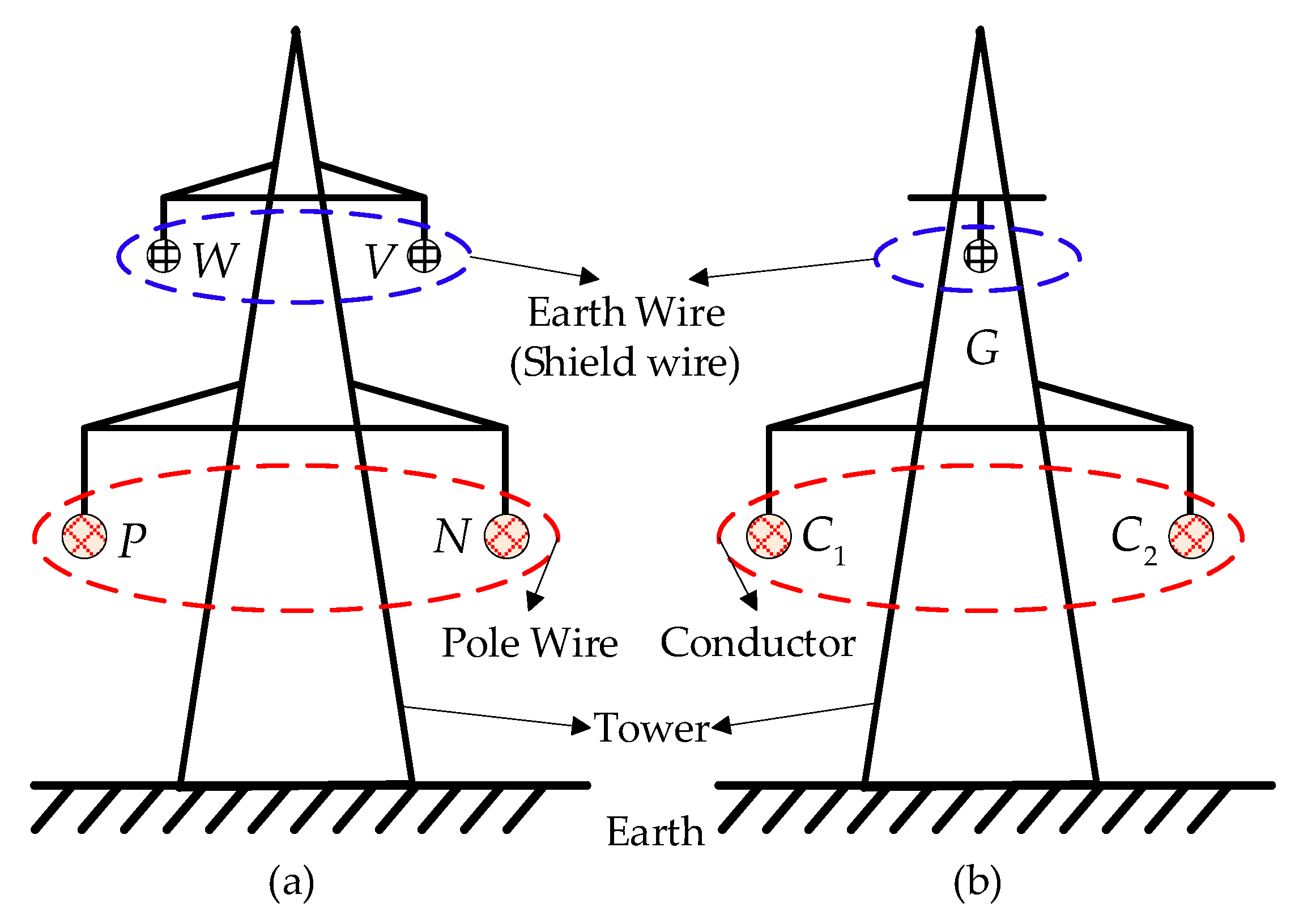
4.3. DC Transmission Lines
4.4. Surge Arrester Scheme
5. Study on Steady Stress
5.1. NBC
5.2. SR
5.3. Voltage at the DC Line Inlet
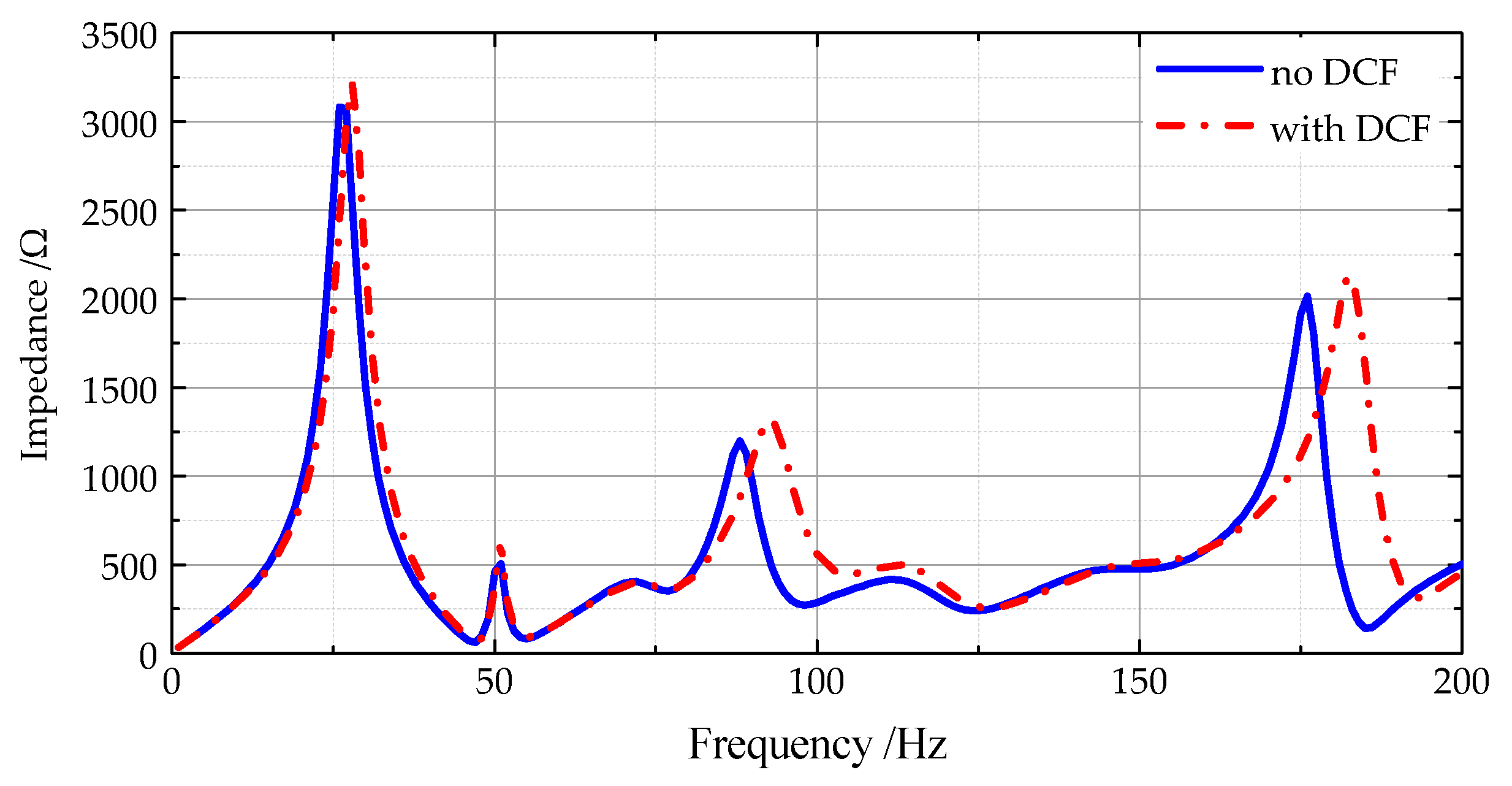
5.4. DC Loop Impedance
5.5. Summary
6. Study on Transient Stress
6.1. Switching Overvoltage
6.2. Lightning Overvoltage
6.3. Summary
7. Conclusions
- The DCF elimination mainly affects the harmonic steady-state stresses of the DC equipment, but has little influence on the transient stresses.
- In the case of refurbishment of older projects, if the equipment modification cost is lower, the DCF removal is technically feasible, and vice versa.
- For new LCC-HVDC projects, the enhancement on voltage rating and insulation of DC equipment may be a more economical and attractive alternative than installing the extensive DCFs, thereby reducing the footprint and cost. At least, the DCF branch could be simplified to a 2/12 double-tuned DCF.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meah, K.; Ula, S. Comparative evaluation of HVDC and HVAC transmission systems. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Kalair, A.; Abas, N.; Khan, N. Comparative study of HVAC and HVDC transmission systems. Renew. Sust. Energ. Rev. 2016, 59, 1653–1675. [Google Scholar] [CrossRef]
- Xu, Z.; Dong, H.; Huang, H. Debates on ultra-high-voltage synchronous power grid: The future super grid in China? IET Gener. Transm. Dis. 2015, 9, 740–747. [Google Scholar] [CrossRef]
- Kimbark, E.W. Direct Current Transmission; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Adamson, C.; Hingorani, N.G. High Voltage Direct Current Transmission; Garraway: London, UK, 1960. [Google Scholar]
- Cigre Working Group B4.72. DC Grid Benchmark Models for System Studies; Cigre Working Group B4.72: Paris, France, 2020. [Google Scholar]
- Rao, H.; Zhou, Y.; Zou, C.; Xu, S.; Li, Y.; Yang, L.; Huang, W. Design aspects of the hybrid HVDC system. CSEE J. Power Energy Syst. 2021, 7, 644–653. [Google Scholar]
- Ahrabi, R.R.; Li, Y.W.; Nejabatkhah, F. Hybrid AC/DC network with parallel LCC-VSC interlinking converters. IEEE Trans. Power Syst. 2021, 36, 722–731. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, J.; Guo, X.; Sun, T.; Zhang, J. Survey of technologies of line commutated converter based high voltage direct current transmission in China. CSEE J. Power Energy Syst. 2015, 1, 1–8. [Google Scholar] [CrossRef]
- Yue, B.; Li, W.; Wang, J.; Wang, S.; Liu, T.; Peng, Z. Electric field calculation and optimization of shielding device for filter capacitor tower in ± 1100 kV indoor DC yard. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018; pp. 1–4. [Google Scholar]
- Liu, Z.; Zhang, F.; Yu, J.; Gao, K.; Ma, W. Research on key technologies in ±1100 kV ultra-high voltage DC transmission. High Volt. 2018, 3, 279–288. [Google Scholar] [CrossRef]
- Alassi, A.; Bañales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC transmission: Technology review, market trends and future outlook. Renew. Sust. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Xue, Y.; Tang, G. DC-side harmonic currents calculation and DC-loop resonance analysis for an LCC–MMC hybrid HVDC transmission system. IEEE Trans. Power Del. 2015, 30, 642–651. [Google Scholar] [CrossRef]
- Shore, N.L.; Andersson, G.; Canelhas, A.P.; Asplund, G. A three-pulse model of DC side harmonic flow in HVDC systems. IEEE Trans. Power Del. 1989, 4, 1945–1954. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Z.; Huang, Y.; Li, X. DC harmonic current calculation for HVDC systems based on the classical transmission line model. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; pp. 1–5. [Google Scholar]
- CCITT. Directives Concerning the Protection of Telecommunication Lines against Harmful Effects from Electricity Lines; International Telegraph and Telephone Consultative Committee (C.C.I.T.T.): Geneva, Switzerland, 1989. [Google Scholar]
- Arrillaga, J. High Voltage Direct Current Transmission, 2nd ed.; The Institution of Engineering and Technology: London, UK, 2008. [Google Scholar]
- Kanngieβer, K.W. HVDC Systems and Their Planning; Siemens: Munich, Germany, 1996. [Google Scholar]
- IEEE Standard 1124. IEEE Guide for Analysis and Definition of DC Side Harmonic Performance of HVDC Transmission Systems; IEEE Std 1124-2003; The institute of Electrical and Electronics Engineers: New York, NY, USA, 2003.
- IEC TS 63014-1. High Voltage Direct Current (HVDC) Power Transmission—System Requirements for DC-Side Equipment; IEC Tech. Specification, Part. 1; The International Electrotechnical Commission (IEC): Geneva, Switzerland, 2018. [Google Scholar]
- Cigre Working Group B4.68. DC Side Harmonics and Filtering in HVDC Transmission Systems; Cigre Working Group B4.68: Paris, France, 2020. [Google Scholar]
- Wilhelm, D. High Voltage Direct Current Handbook, 1st ed.; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 1994. [Google Scholar]
- Ji, Y.; Zhang, J.; Zhang, P.; Yue, B.; Yang, Y.; Wu, F. Survey of electromagnetic interference of ±1100 kV HVDC project on communication network for DC filter necessity research. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018; pp. 1–10. [Google Scholar]
- Zhang, X.; Li, N.; Wu, X. Equivalent disturbing current limit for HVDC project in new period. In Proceedings of the 2010 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Beijing, China, 12–16 April 2010; pp. 814–817. [Google Scholar]
- Li, P.; Hao, Q. The algorithm for the parameters of AC filters in HVDC transmission system. In Proceedings of the Transmission and Distribution Exposition Conference: 2008 IEEE PES Powering Toward the Future (PIMS), Chicago, IL, USA, 21–24 April 2008; pp. 1–6. [Google Scholar]
- Carson, J.R. Wave propagation in overhead wires with ground return. Bell Syst. Tech. J. 1926, 5, 539–554. [Google Scholar] [CrossRef]
- Li, X.; Xu, Z.; Lai, Q.; Zhang, Z. Research on transmission line model based on phase-mode transformation in HVDC system. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 51–60. [Google Scholar] [CrossRef] [Green Version]
- IEC TS 60071-5. Insulation Co-Ordination—Procedures for High Voltage Direct Current (HVDC) Converter Stations; IEC Tech. Specification, Part. 5; The International Electrotechnical Commission (IEC): Geneva, Switzerland, 2014. [Google Scholar]
- Central Southern China Electric Power Design Institute Co. Ltd. of China Power Engineering Consulting Group. HVDC Transmission Design Manual; China Electric Power Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Guo, X.; Fu, Y.; Yu, J.; Xu, Z. A non-uniform transmission line model of the ±1100 kV UHV tower. Energies 2019, 12, 445. [Google Scholar] [CrossRef] [Green Version]



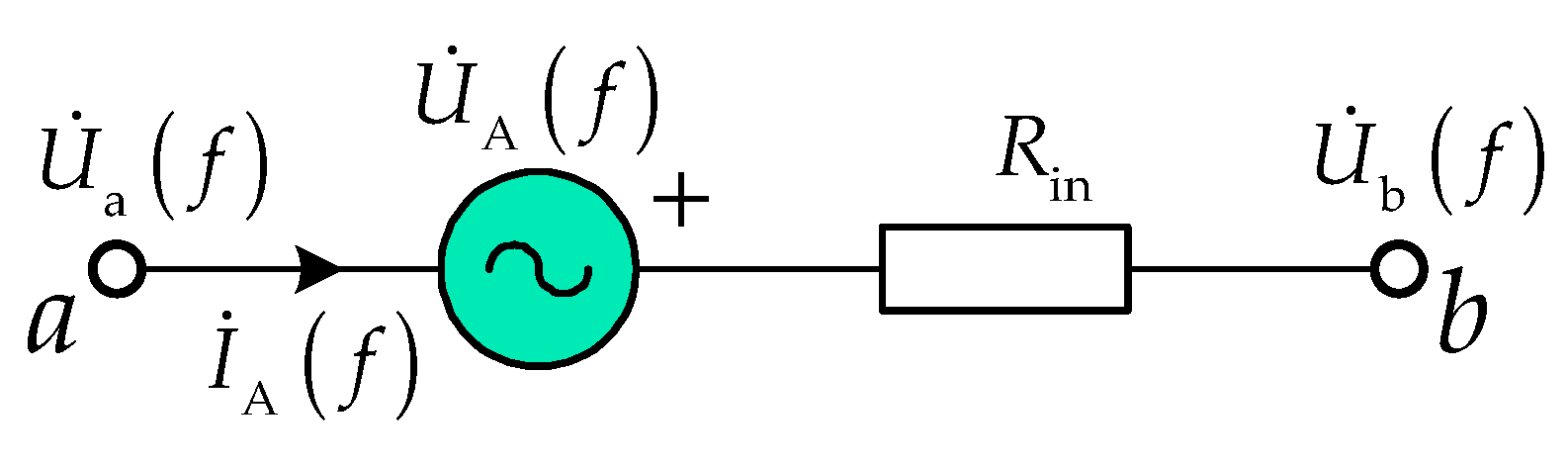

| Items | Values | ||
|---|---|---|---|
| Rectifier | Inverter | ||
| Nominal DC power (bipolar), PdcN, MW | 8000 | ||
| Nominal DC voltage, UdcN, kV | 800 | ||
| Nominal DC current, IdcN, kA | 5 | ||
| Nominal AC system frequency, f, Hz | 50 | ||
| Nominal AC system voltage, Uac, kV | 530 | 510 | |
| Nominal ideal no-load DC voltage, Udi0N, kV | 231.45 | 218.54 | |
| Firing angle, α, ° | 15 ± 2.5 | / | |
| Extinction angle, γ, ° | / | 17 ± 1 | |
| Converter transformer | Winding voltages (L-L), kV/kV | 530/171.4 | 510/161.83 |
| 3-phase capacity, MVA | 1212 | 1146 | |
| Commutation reactance, % | 19.5 | 19 | |
| Tap changer, % | 1.25 (+23/−5) | ||
| Three-pulse model | Internal inductance, L, mH | 14.16 | 13.34 |
| Stray capacitance, C, nF | 18.15 (HV) 24.36 (LV) | 15.82 (HV) 24.36 (LV) | |
| Earth electrode resistance, RG1/RG2, Ω | 0.25 | 0.25 | |
| 3-pulse voltages at positive pole, kV | ||||
| Order | Station | YYP1 | YYN1+YDP1 | YDN1 |
| 2nd | Rectifier | 1.76∠0° | 3.52∠0° | 1.76∠0° |
| Inverter | 1.52∠0° | 3.03∠0° | 1.52∠0° | |
| 12th | Rectifier | 3.98∠−24.06° | 7.95∠−24.06° | 3.98∠−24.06° |
| Inverter | 3.65∠−38.80° | 7.31∠−38.80° | 3.65∠−38.8° | |
| 24th | Rectifier | 2.64∠142.63° | 5.28∠142.63° | 2.64∠142.63° |
| Inverter | 2.48∠125.68° | 4.95∠125.68° | 2.48∠125.68° | |
| 3-pulse voltages at negative pole, kV | ||||
| Order | Station | YYN2 | YYP2+YDN2 | YDP2 |
| 2nd | Rectifier | 1.76∠10° | 3.52∠10° | 1.76∠10° |
| Inverter | 1.52∠10° | 3.03∠10° | 1.52∠10° | |
| 12th | Rectifier | 3.09∠−69.12° | 6.19∠−69.12° | 3.09∠−69.12° |
| Inverter | 4.02∠−17.51° | 8.04∠−17.51° | 4.02∠−17.51° | |
| 24th | Rectifier | 2.31∠70.89° | 4.63∠70.89° | 2.31∠70.89° |
| Inverter | 2.62∠161.67° | 5.25∠161.67° | 2.62∠161.67° | |
| Items | Overhead DC Line | Electrode Line | |||
|---|---|---|---|---|---|
| Section I | Section II | Rectifier | Inverter | ||
| Length, km | 1140 | 539.9 | 103 | 23.6 | |
| Earth resistivity, Ω*m | 180 | 300 | 180 | 300 | |
| Conductor data | Height, m | 42.2 | 42.2 | 22 | 24 |
| Horizontal spacing, m | 20 | 20 | 6.6 | 6 | |
| Sag, m | 21.2 | 21.2 | 11.5 | 15.52 | |
| Sub-conductor number | 6 | 6 | 2 | 2 | |
| Sub-conductors spacing, m | 0.45 | 0.45 | 0.5 | 0.4 | |
| Outer radius, m | 0.0203 | 0.01995 | 0.015 | 0.015 | |
| Total strands number | 84 | 72 | 48 | 48 | |
| Strand radius, m | 0.001845 | 0.001995 | 0.0018 | 0.0018 | |
| Resistivity, Ω*m | 2.84 × 10−8 | 2.84 × 10−8 | 2.84 × 10−8 | 2.84 × 10−8 | |
| Shield wire data | Height, m | 57 | 57 | 29 | 28 |
| Horizontal spacing, m | 16 | 16 | / | / | |
| Sag, m | 13 | 13 | 6.8 | 2.29 | |
| Outer radius, m | 0.007875 | 0.007875 | 0.0065 | 0.0065 | |
| Total strands number | 19 | 19 | 19 | 19 | |
| Strand radius, m | 0.00175 | 0.00175 | 0.0013 | 0.0013 | |
| Resistivity, Ω*m | 2.0 × 10−7 | 2.0 × 10−7 | 2.0 × 10−7 | 2.0 × 10−7 | |
| Arrester | CCOV, kV | Uref, kV | LIPL, kV/kA | SIPL, kV/kA | Columns | Energy Capability, MJ |
|---|---|---|---|---|---|---|
| DB1 | 824 | 969 | 1625/20 | 1391/1 | 3 | 14 |
| DB2 | 824 | 969 | 1625/20 | 1391/1 | 3 | 14 |
| DR | 44 | 483 rms | 900/05 | / | 1 | 3.4 |
| E | 95 | 304 | 478/5 | / | 2 | 3 |
| Neutral bus at positive pole in rectifier | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Voltage SUM, kV | 2.26 | 2.68 | 11.47 | 12.23 | 10.00 | 11.17 |
| Major harmonic (order/voltage), kV | 3/0.67 | 2/1.07 | 2/7.84 | 2/7.94 | 2/8.43 | 2/8.60 |
| 2/0.61 | 3/0.76 | 3/2.07 | 3/2.03 | 1/0.25 | 12/0.91 | |
| 6/0.40 | 6/0.32 | 6/0.83 | 6/1.01 | 3/0.22 | 4/0.29 | |
| 12/0.12 | 4/0.13 | 4/0.10 | 12/0.47 | 4/0.19 | 1/0.27 | |
| Neutral bus at positive pole in inverter | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Voltage SUM, kV | 2.99 | 3.23 | 4.34 | 5.52 | 2.63 | 3.70 |
| Major harmonic (order/voltage), kV | 3/1.39 | 3/1.55 | 6/2.13 | 6/2.80 | 2/0.83 | 12/1.12 |
| 6/0.63 | 6/0.51 | 2/0.78 | 2/0.79 | 6/0.34 | 2/0.84 | |
| 2/0.31 | 2/0.41 | 3/0.42 | 12/0.62 | 4/0.30 | 4/0.42 | |
| 4/0.20 | 4/0.35 | 39/0.28 | 3/0.44 | 39/0.26 | 6/0.39 | |
| Pole bus at positive pole in rectifier | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Current RSS, A | 36.23 | 25.78 | 37.72 | 25.77 | 65.55 | 46.61 |
| Major harmonic (order/current), A | 12/29.41 | 12/19.40 | 12/30.31 | 12/21.73 | 12/59.05 | 12/42.87 |
| 6/11.79 | 6/9.17 | 2/18.27 | 24/6.14 | 2/19.52 | 24/12.98 | |
| 39/7.12 | 24/5.97 | 39/7.43 | 2/6.00 | 24/15.16 | 2/6.73 | |
| 24/6.33 | 39/4.13 | 24/7.14 | 3/5.23 | 39/9.83 | 39/5.46 | |
| Pole bus at positive pole in inverter | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Current RSS, A | 41.12 | 26.86 | 46.10 | 28.37 | 65.38 | 43.55 |
| Major harmonic (order/current), A | 12/28.01 | 12/17.82 | 12/29.17 | 12/20.60 | 12/53.17 | 12/36.94 |
| 6/18.93 | 6/11.50 | 39/24.31 | 2/15.60 | 2/25.03 | 2/16.22 | |
| 39/14.22 | 2/6.23 | 2/23.69 | 24/5.65 | 39/22.35 | 24/12.63 | |
| 2/8.95 | 24/5.56 | 24/6.64 | 39/5.01 | 24/14.80 | 39/5.46 | |
| Pole line inlet at positive pole in rectifier | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Voltage RSS, kV | 18.01 | 25.93 | 17.29 | 20.67 | 16.39 | 25.40 |
| Major harmonic (order/voltage), kV | 2/12.73 | 6/18.9 | 2/15.12 | 2/14.88 | 2/16.00 | 12/18.24 |
| 6/9.79 | 2/11.83 | 6/6.73 | 12/9.56 | 14/2.31 | 2/15.71 | |
| 14/5.47 | 12/10.49 | 3/4.19 | 6/7.87 | 12/1.70 | 48/4.64 | |
| 3/5.37 | 3/4.63 | 14/2.32 | 3/3.83 | 1/1.08 | 24/3.90 | |
| Pole line inlet at positive pole in inverter | ||||||
| Operation mode | BIF | MGF | MGR | |||
| DCF | no DCF | DCF | no DCF | DCF | no DCF | |
| Voltage RSS, kV | 17.17 | 24.39 | 16.49 | 20.49 | 15.93 | 25.03 |
| Major harmonic (order/voltage), kV | 2/12.47 | 6/19.26 | 2/14.48 | 2/14.78 | 2/15.60 | 12/17.63 |
| 6/9.61 | 2/11.61 | 6/6.78 | 12/9.44 | 14/2.19 | 2/15.93 | |
| 14/5.54 | 12/5.96 | 3/3.08 | 6/8.24 | 12/1.53 | 48/4.74 | |
| 3/2.99 | 48/3.91 | 14/2.23 | 30/2.97 | 4/1.06 | 24/2.86 | |
| Event | Arrester | ||||
|---|---|---|---|---|---|
| DB1 | DB2 | DR | E | ||
| 1 | DC pole line to earth fault | √ | √ | √ | √ |
| 2 | AC phase to earth fault at valve side | √ | √ | ||
| 3 | AC earth fault at grid side | √ | √ | ||
| Residual Voltage, kV | ||||||
|---|---|---|---|---|---|---|
| Arrester | Event 1 | Event 2 | Event 3 | |||
| DCF | No DCF | DCF | No DCF | DCF | No DCF | |
| DB1 | 1121.58 | 1083.07 | 1060.87 | 1085.44 | 941.23 | 922.67 |
| DB2 | 1121.58 | 1083.07 | 1060.87 | 1085.44 | 941.23 | 922.67 |
| DR | 160.36 | 163.95 | 220.70 | 250.74 | 177.75 | 179.15 |
| E | 240.59 | 264.95 | 255.67 | 252.67 | 237.20 | 262.77 |
| Residual Voltage, kV | ||||
|---|---|---|---|---|
| Arrester | Counterstrike | Shielding Failure | ||
| DCF | No DCF | DCF | No DCF | |
| DB1 | 1253.44 | 1352.45 | 1566.09 | 1606.22 |
| DB2 | 1247.69 | 1346.15 | 1514.99 | 1564.84 |
| DR | 215.75 | 304.35 | 287.13 | 307.27 |
| E | 350.83 | 9.26 | 398.56 | 7.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, Z. Feasibility Evaluation on Elimination of DC Filters for Line-Commutated Converter-Based High-Voltage Direct Current Projects in New Situations. Energies 2021, 14, 5770. https://doi.org/10.3390/en14185770
Li X, Xu Z. Feasibility Evaluation on Elimination of DC Filters for Line-Commutated Converter-Based High-Voltage Direct Current Projects in New Situations. Energies. 2021; 14(18):5770. https://doi.org/10.3390/en14185770
Chicago/Turabian StyleLi, Xiaodong, and Zheng Xu. 2021. "Feasibility Evaluation on Elimination of DC Filters for Line-Commutated Converter-Based High-Voltage Direct Current Projects in New Situations" Energies 14, no. 18: 5770. https://doi.org/10.3390/en14185770
APA StyleLi, X., & Xu, Z. (2021). Feasibility Evaluation on Elimination of DC Filters for Line-Commutated Converter-Based High-Voltage Direct Current Projects in New Situations. Energies, 14(18), 5770. https://doi.org/10.3390/en14185770







