Recognizing VSC DC Cable Fault Types Using Bayesian Functional Data Depth
Abstract
:1. Introduction
- Construction of Bayesian spline model capturing measurement and parameter uncertainty,
- An algorithm for using Bayesian models to obtain data depth distributions allowing analysis of signal similarity,
- An extended case study using simulated voltage source converter (VSC) direct current DC cable fault data focusing on pole-to-pole and pole-to-ground short circuits.
2. Review of Cable Fault Modeling Research
3. Materials and Methods
3.1. Data Depth
- holds for any random vector X in , any nonsingular matrix A and any d-vector b;
- holds for any having center ;
- for any having deepest point holds for ;
- as , for each .
Mahalanobis Depth
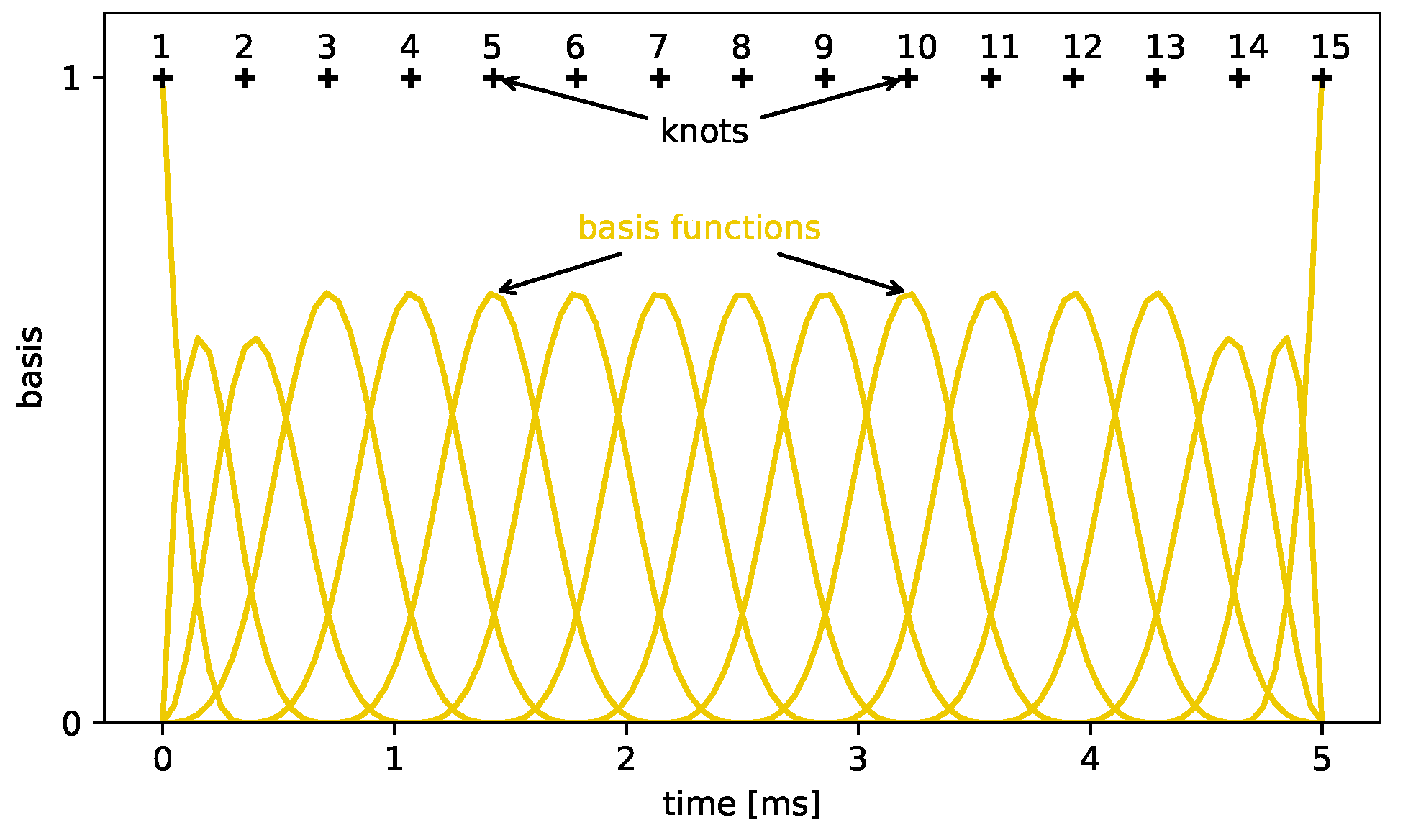
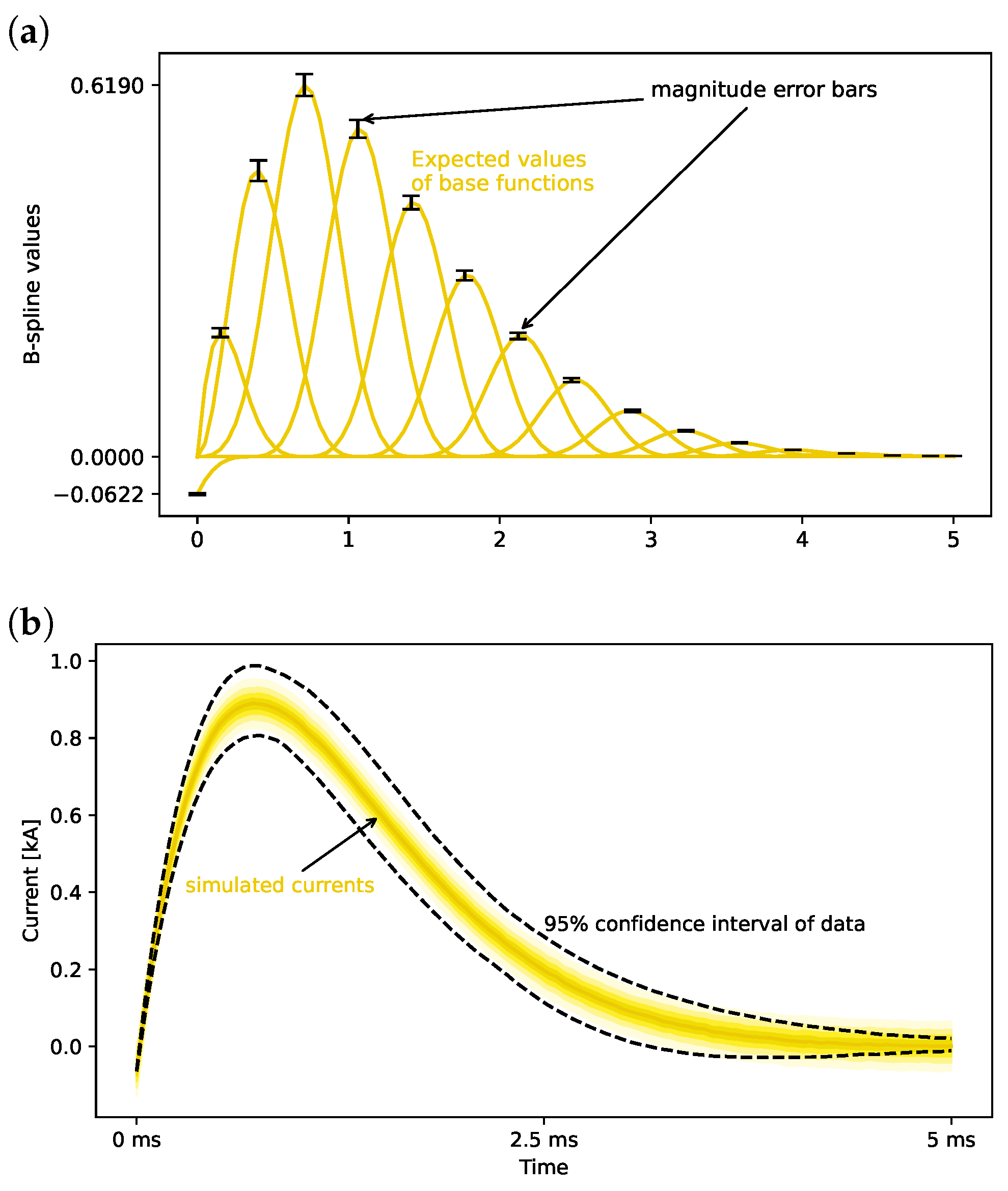
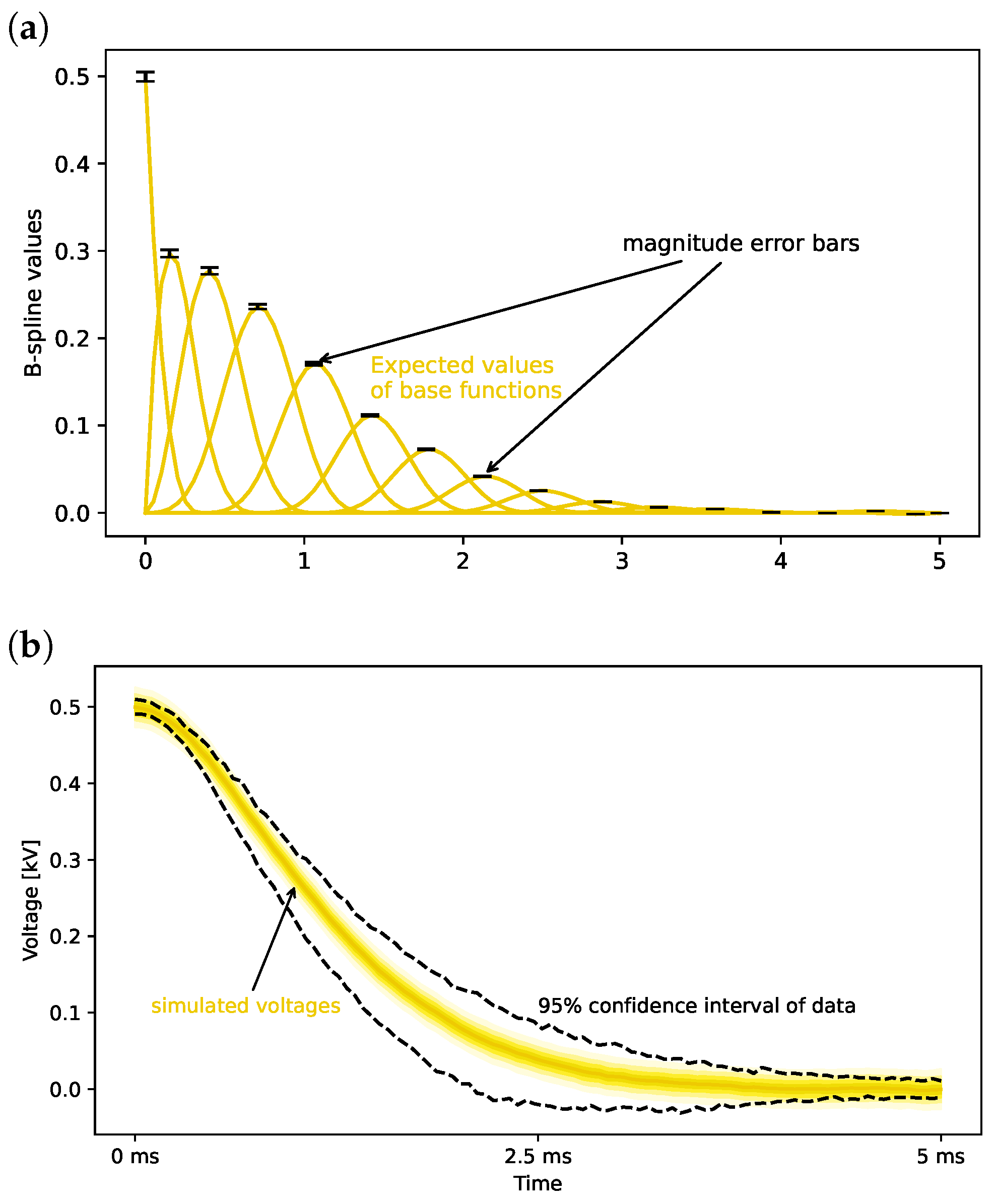
3.2. Bayesian Functional Spline Models
3.3. Algorithm for Fault Determination and Detection
- Create reference. Having a set of reference signals (for example, healthy behavior). Fit the model with them and obtain the set of samples of sequences.
- Compute Mahalanobis depth distribution. Using the obtained samples, compute mean and covariance matrices and determine depth of each of the samples. This will be our reference depth distribution. It can be summarized by a histogram if needed.
- Create model of the candidate. Using the same model, fit it with the candidate signal and obtain the set of samples of sequences.
- Compute the depth distribution of candidate with respect to reference. Using mean and covariance of the reference set compute the Mahalanobis depth of all the samples of the candidate. This gives a marginal probability distribution of depth of candidate with respect to reference.
- Analyze the overlap/distance. The marginal distribution of the depth allows us to verify if signal is ‘shallow’ with respect to the reference set or close to it. If there is an overlap we can state that the similarity is strong. If there is a large gap, we can say that the signal is an ‘outlier’ with respect to reference.
4. Results
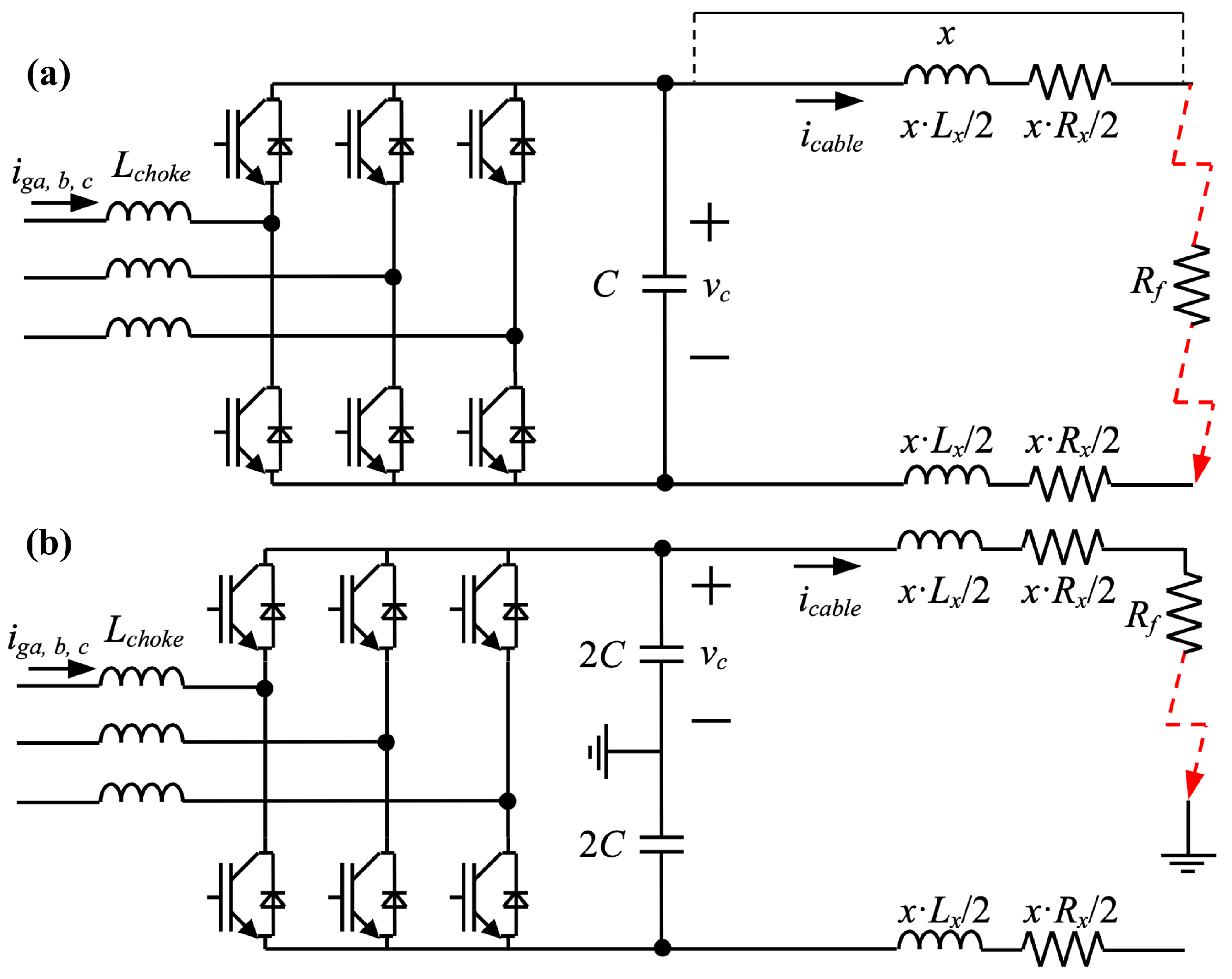
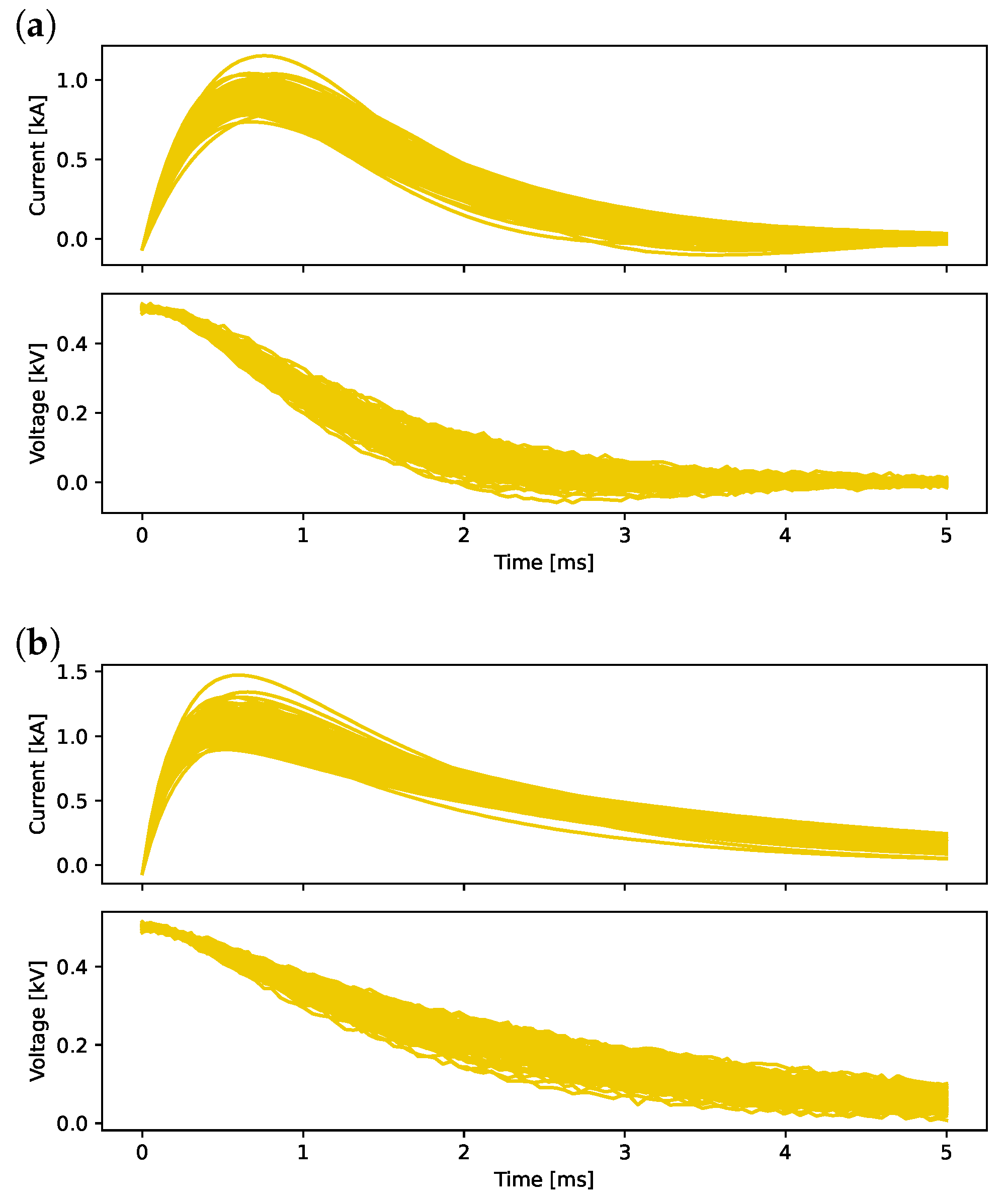
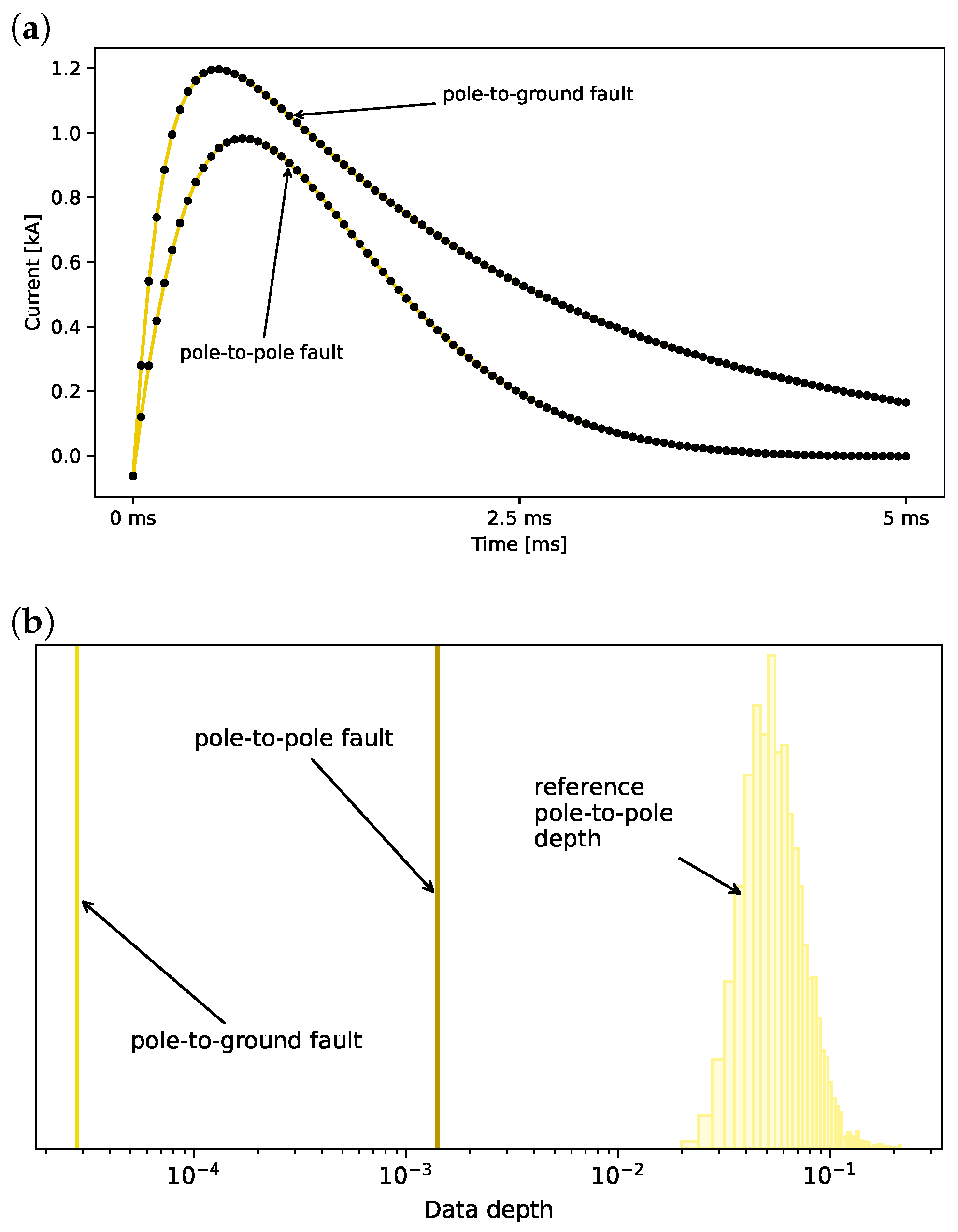
4.1. Considered Data
4.2. Computational Setup
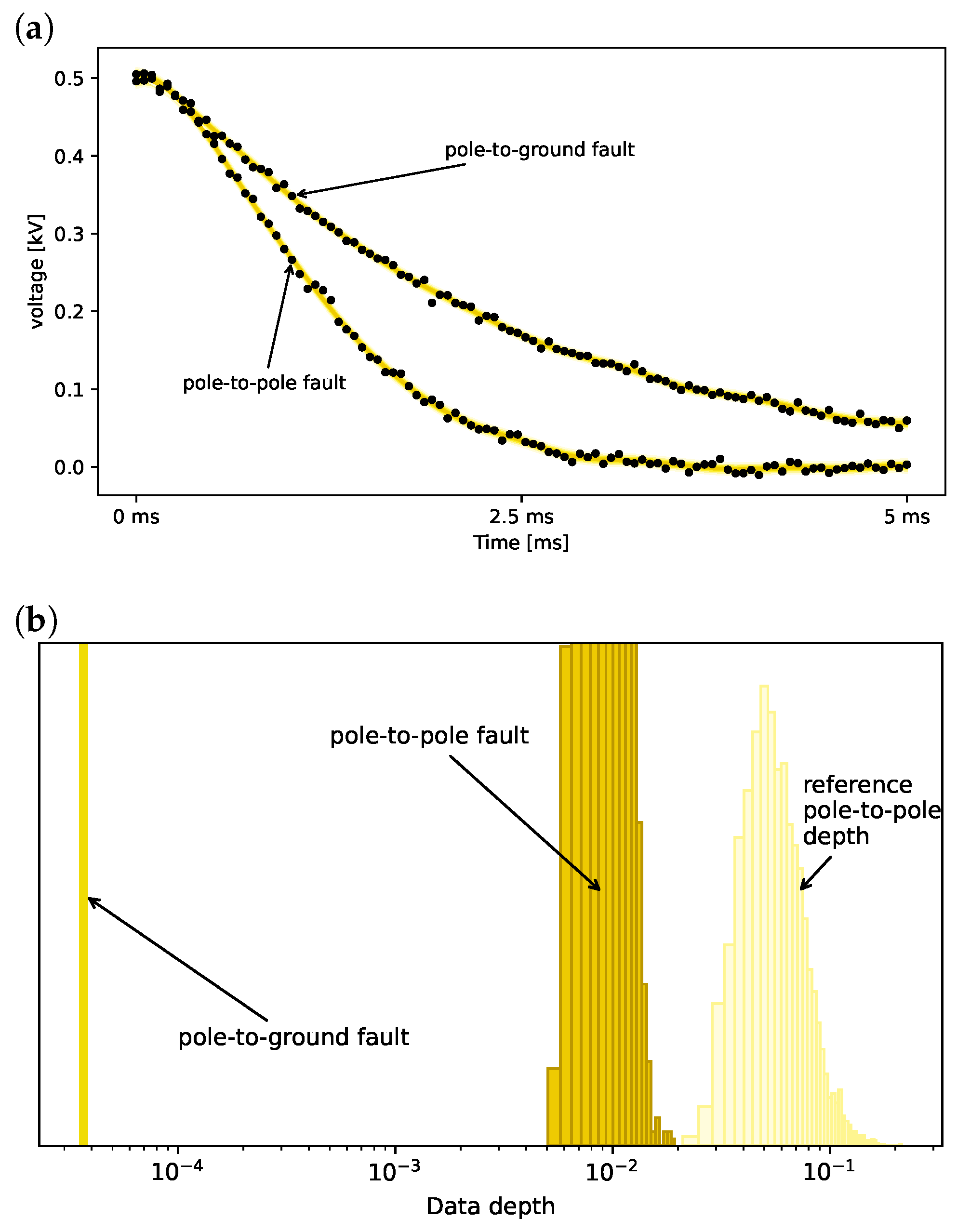
4.3. Analysis of Current Measurements
5. Analysis of Voltage Measurements
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FDA | Functional data analysis |
| VSC | Voltage Source Converter |
| DC | Direct Current |
| LCD | Liquid Crystal Display |
| TDR | Time Domain Reflectometry |
| HVDC | High Voltage Direct Current |
| RL | Resistor–Inductor |
| RLC | Resistor-Inductor-Capacitor |
| MMC-HVDC | Multi-Modular Converter High Voltage DC |
| PV | Photovoltaics |
| AC | Alternating Current |
| ATP | Alternative Transient Program |
| TACS | Transient analysis of control systems |
| BP | Backpropagation |
| HMC | Hamiltonian Monte Carlo |
| MCMC | Markov Chain Monte Carlo |
| HDI | Highest Density Interval |
| ESS | Effective Sample Size |
| MCSE | Monte Carlo Standard Error |
References
- Cai, B.; Sun, X.; Wang, J.; Yang, C.; Wang, Z.; Kong, X.; Liu, Z.; Liu, Y. Fault detection and diagnostic method of diesel engine by combining rule-based algorithm and BNs/BPNNs. J. Manuf. Syst. 2020, 57, 148–157. [Google Scholar] [CrossRef]
- Cai, B.; Fan, H.; Shao, X.; Liu, Y.; Liu, G.; Liu, Z.; Ji, R. Remaining useful life re-prediction methodology based on Wiener process: Subsea Christmas tree system as a case study. Comput. Ind. Eng. 2021, 151, 106983. [Google Scholar] [CrossRef]
- Cai, B.; Hao, K.; Wang, Z.; Yang, C.; Kong, X.; Liu, Z.; Ji, R.; Liu, Y. Data-driven early fault diagnostic methodology of permanent magnet synchronous motor. Expert Syst. Appl. 2021, 177, 115000. [Google Scholar] [CrossRef]
- Stief, A.; Tan, R.; Cao, Y.; Ottewill, J.; Thornhill, N.; Baranowski, J. A heterogeneous benchmark dataset for data analytics: Multiphase flow facility case study. J. Process Control 2019, 79, 41–55. [Google Scholar] [CrossRef]
- Stief, A.; Ottewill, J.R.; Baranowski, J.; Orkisz, M. A PCA and Two-Stage Bayesian Sensor Fusion Approach for Diagnosing Electrical and Mechanical Faults in Induction Motors. IEEE Trans. Ind. Electron. 2019, 66, 9510–9520. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Kruger, U.; Gu, F.; Ball, A.; Chen, Q. Monitoring nonstationary and dynamic trends for practical process fault diagnosis. Control Eng. Pract. 2019, 84, 139–158. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.L.; Chiou, J.M.; Müller, H.G. Functional Data Analysis. Annu. Rev. Stat. Its Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef] [Green Version]
- Aneiros, G.; Cao, R.; Fraiman, R.; Genest, C.; Vieu, P. Recent advances in functional data analysis and high-dimensional statistics. J. Multivar. Anal. 2019, 170, 3–9. [Google Scholar] [CrossRef]
- Mesas, J.; Monjo, L.; Sainz, L.; Pedra, J. Cable fault characterization in VSC DC systems. In Proceedings of the 2016 International Symposium on Fundamentals of Electrical Engineering (ISFEE), IEEE, Bucharest, Romania, 30 June–2 July 2016. [Google Scholar]
- Yang, J.; O’Reilly, J.; Fletcher, J.E. An overview of DC cable modelling for fault analysis of VSC-HVDC transmission systems. In Proceedings of the 2010 20th Australasian Universities Power Engineering Conference; IEEE, Christchurch, New Zealand, 5–8 December 2010. [Google Scholar]
- Loume, D.; Tuan, M.N.; Bertinato, A.; Raison, B. DC cable modelling and High Voltage Direct Current grid grounding system. In Proceedings of the 9th International Conference on Insulated Power Cables, Versailles, France, 21–25 June 2015. [Google Scholar]
- Li, J.; Li, Y.; Xiong, L.; Jia, K.; Song, G. DC fault analysis and transient average current based fault detection for radial MTDC system. IEEE Trans. Power Deliv. 2019, 35, 1310–1320. [Google Scholar] [CrossRef]
- Zhang, H.; Jovcic, D. Interconnecting subsea DC collection systems into a high reliability DC grid. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, IEEE, Istanbul, Turkey, 12–15 October 2014. [Google Scholar]
- Jovcic, D.; Taherbaneh, M.; Taisne, J.P.; Nguefeu, S. Developing regional, radial DC grids and their interconnection into large DC grids. In Proceedings of the 2014 IEEE PES General Meeting| Conference & Exposition, IEEE, Nashville, TN, USA, 27–31 July 2014. [Google Scholar]
- Bapiraju, J.V.; Manohar, P. Fault estimation with analytical cable model for MMC-HVDC in offshore applications. In Proceedings of the 2017 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), IEEE, Bangalore, India, 8–10 November 2017. [Google Scholar]
- Fonseca_Badillo, M.; Negrete_Navarrete, L.; González_Parada, A.; Castañeda_Miranda, A. Simulation and analysis of underground power cables faults. Procedia Eng. 2012, 35, 50–57. [Google Scholar] [CrossRef] [Green Version]
- PSCAD™. Available online: https://www.pscad.com/software/pscad/overview (accessed on 8 September 2021).
- Naidu, O.; George, N.; Pradhan, D. A new fault location method for underground cables in distribution systems. In Proceedings of the 2016 First International Conference on Sustainable Green Buildings and Communities (SGBC), IEEE, Chennai, India, 18–20 December 2016. [Google Scholar]
- Asif, R.M.; Hassan, S.R.; Rehman, A.U.; Rehman, A.U.; Masood, B.; Sher, Z.A. Smart underground wireless cable fault detection and monitoring system. In Proceedings of the 2020 International Conference on Engineering and Emerging Technologies (ICEET), IEEE, Lahore, Pakistan, 22–23 February 2020. [Google Scholar]
- Gajbhiye, S.; Karmore, S. Cable fault monitoring and indication: A review. arXiv 2013, arXiv:1309.5457. [Google Scholar]
- Govindarajan, S. An Online Monitoring and Fault Location Methodology for Underground Power Cables; Arizona State University: Tempe, AZ, USA, 2016. [Google Scholar]
- Zhang, Z.; Chen, Q.; Xie, R.; Sun, K. The fault analysis of PV cable fault in DC microgrids. IEEE Trans. Energy Convers. 2018, 34, 486–496. [Google Scholar] [CrossRef]
- He, B.; Zhou, Y.; Li, H.; Ye, T.; Fan, S.; Wang, X. Fault Identification of High-voltage Cable Sheath Grounding System Based on Ground Current Analysis. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), IEEE, Wuhan, China, 30 October–1 November 2020. [Google Scholar]
- He, W.; Li, H.; Tu, J.; Yang, T.; Meng, J.; Li, H.; Lin, F. Diagnosis and Location of High-voltage Cable Fault Based on Sheath Current. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), IEEE, Guangzhou, China, 6–9 November 2018. [Google Scholar]
- Wang, X.; Song, Y.; Ferguson, C. Sheath fault characteristics and modelling on underground power transmission cables. Eur. Trans. Electr. Power 2001, 11, 137–140. [Google Scholar]
- Shirkoohi, G. Modelling and simulation of fault detection in shielded twisted pair cables. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), IEEE, Taipei, Taiwan, 14–17 March 2016. [Google Scholar]
- Peng, Z.; Bai, R.; Li, B. A Fault Location Method for Shielded Cables based on Coupling Characteristics. In Proceedings of the 2020 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), IEEE, Hangzhou, China, 7–9 December 2020. [Google Scholar]
- Shi, Q.; Tröltzsch, U.; Kanoun, O. Analysis of the parameters of a lossy coaxial cable for cable fault location. In Proceedings of the Eighth International Multi-Conference on Systems, Signals & Devices. IEEE, Sousse, Tunisia, 22–25 March 2011. [Google Scholar]
- Wang, M.; Hou, Y.B. Modeling of cable fault system. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics (IEEE Cat. No. 04EX826), IEEE, Shanghai, China, 26–29 August 2004. [Google Scholar]
- Yuan, K.; Yu, Y.; Liu, X. Aircraft cable fault location system based on principle of regression analysis. In Proceedings of the 2010 5th International Conference on Computer Science & Education, IEEE, Hefei, China, 24–27 August 2010. [Google Scholar]
- Wang, M.; Hou, Y.B.; Wang, J.P. Intelligent system of cable fault location and its data fusion. In Proceedings of the International Conference on Machine Learning and Cybernetics, IEEE, Beijing, China, 4–5 November 2002. [Google Scholar]
- Tukey, J. Mathematics and the picturing of data. Proc. Int. Congr. Math. 1975, 2, 523–531. [Google Scholar]
- Idris, S.; Wachidah, L.; Sofiyayanti, T.; Harahap, E. The Control Chart of Data Depth Based on Influence Function of Variance Vector. J. Phys. Conf. Ser. 2019, 1366, 012125. [Google Scholar] [CrossRef]
- Chenouri, S.; Small, C.G.; Farrar, T.J. Data depth-based nonparametric scale tests. Can. J. Stat./La Rev. Can. De Stat. 2011, 39, 356–369. [Google Scholar] [CrossRef]
- Nagy, S.; Ferraty, F. Data depth for measurable noisy random functions. J. Multivar. Anal. 2019, 170, 95–114. [Google Scholar] [CrossRef]
- Nieto-Reyes, A.; Battey, H. A Topologically Valid Definition of Depth for Functional Data. Stat. Sci. 2016, 31, 61–79. [Google Scholar] [CrossRef]
- Gijbels, I.; Nagy, S. On a General Definition of Depth for Functional Data. Stat. Sci. 2017, 32, 630–639. [Google Scholar] [CrossRef]
- Zuo, Y.; Serfling, R. General notions of statistical depth function. Ann. Stat. 2000, 28, 461–482. [Google Scholar] [CrossRef]
- Zuo, Y. Multivariate Trimmed Means Based on Data Depth. In Statistical Data Analysis Based on the L1-Norm and Related Methods; Dodge, Y., Ed.; Birkhäuser Basel: Basel, Switzerland, 2002; pp. 313–322. [Google Scholar]
- Mosler, K. Depth statistics. In Robustness and Complex Data Structures, Festschrift in Honour of Ursula Gather; Springer: Berlin, Germany, 2013; pp. 17–34. [Google Scholar]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.; Vehtari, A.; Rubin, D. Bayesian Data Analysis, 3rd ed.; Chapman & Hall/CRC Texts in Statistical Science; Taylor & Francis: Abingdon, UK, 2013. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A Probabilistic Programming Language. J. Stat. Softw. Artic. 2017, 76, 1–32. [Google Scholar] [CrossRef] [Green Version]

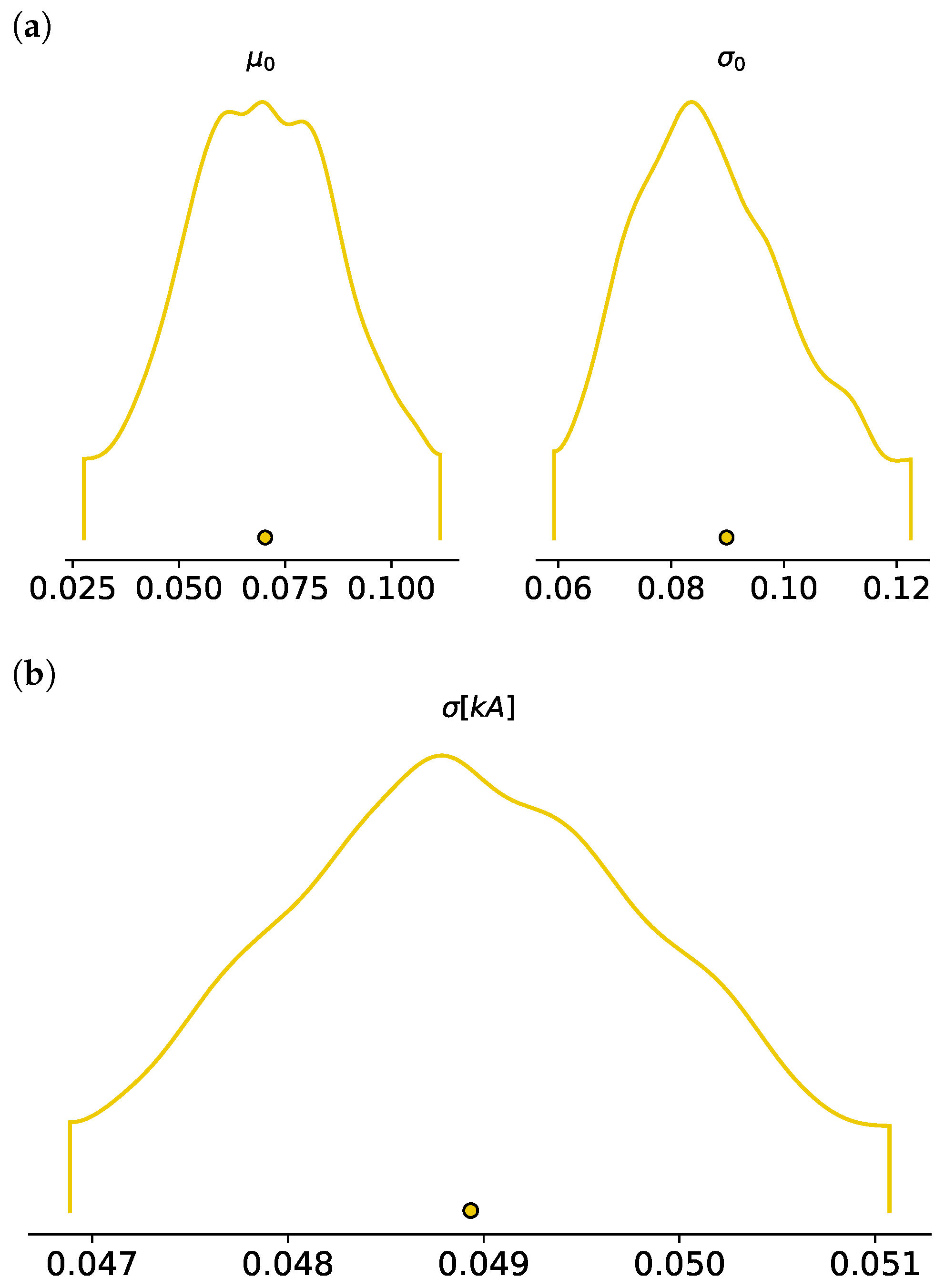
| Mean | sd | hdi_3% | hdi_97% | mcse_Mean | mcse_sd | ess_Bulk | ess_Tail | r_Hat | |
|---|---|---|---|---|---|---|---|---|---|
| 0.070 | 0.022 | 0.028 | 0.112 | 0.001 | 0.0 | 1686.0 | 1742.0 | 1.0 | |
| 0.090 | 0.018 | 0.059 | 0.123 | 0.000 | 0.0 | 1687.0 | 1599.0 | 1.0 | |
| 0.049 | 0.001 | 0.047 | 0.051 | 0.000 | 0.0 | 1689.0 | 2231.0 | 1.0 |
| Pole-to-Pole Faults | Pole-to-Ground Faults | |||||
|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | Min | Max | |
| Exp. no. | ||||||
| 0 | 8.947 | 8.868 | 9.028 | 3.738 | 3.727 | 3.751 |
| 1 | 2.531 | 2.485 | 2.575 | 4.732 | 4.712 | 4.752 |
| 2 | 1.795 | 1.775 | 1.817 | 4.460 | 4.436 | 4.481 |
| 3 | 4.183 | 4.156 | 4.208 | 2.772 | 2.766 | 2.777 |
| 4 | 2.590 | 2.579 | 2.602 | 2.645 | 2.639 | 2.650 |
| 5 | 2.632 | 2.620 | 2.645 | 4.359 | 4.349 | 4.369 |
| 6 | 2.432 | 2.394 | 2.467 | 3.290 | 3.282 | 3.300 |
| 7 | 3.642 | 3.618 | 3.662 | 8.290 | 8.230 | 8.347 |
| 8 | 3.198 | 3.141 | 3.260 | 3.570 | 3.560 | 3.580 |
| 9 | 2.255 | 2.222 | 2.290 | 5.212 | 5.184 | 5.236 |
| Mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
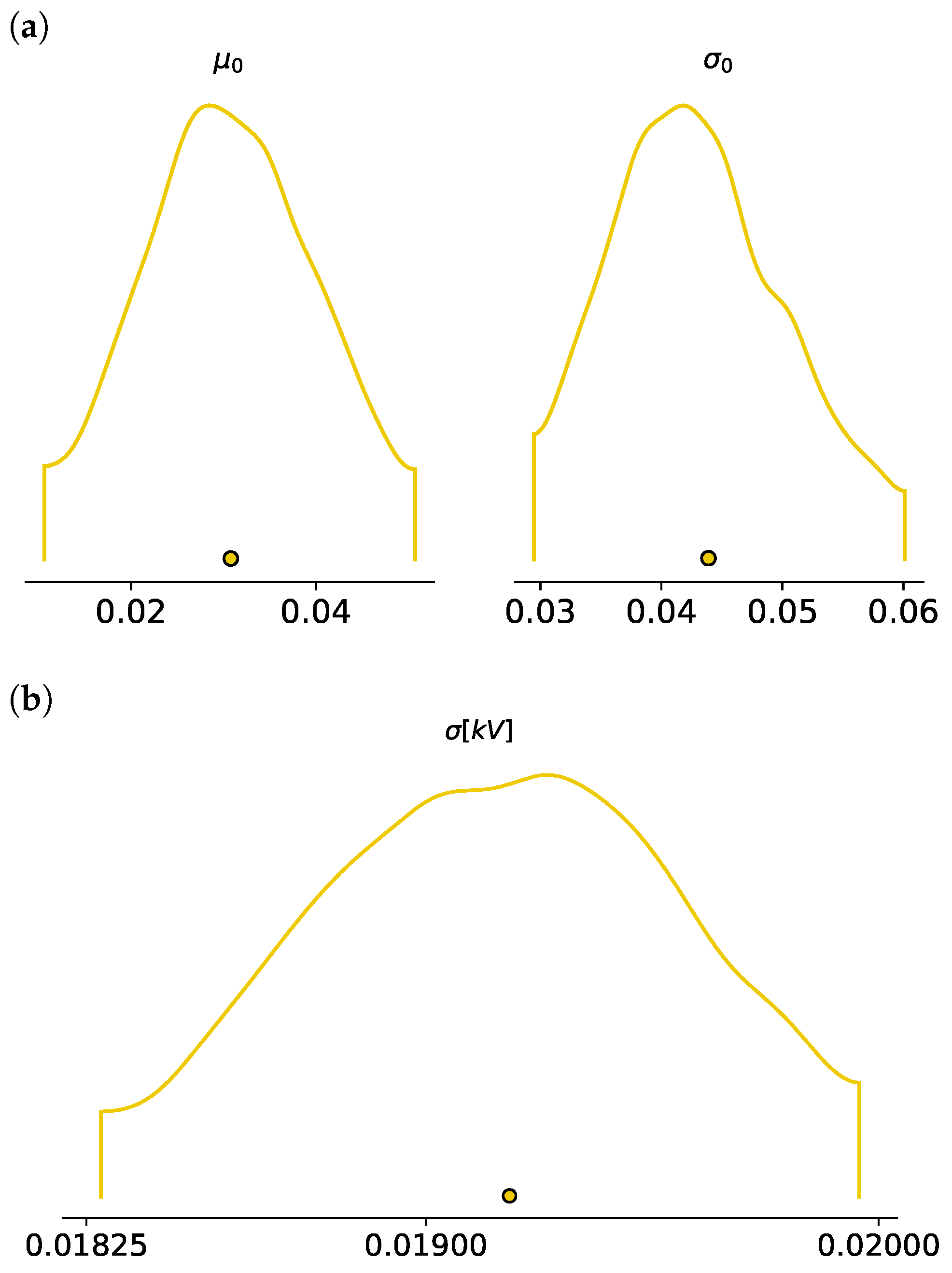
| 0.031 | 0.011 | 0.011 | 0.051 | 0.0 | 0.0 | 840.0 | 987.0 | 1.00 | |
| 0.044 | 0.009 | 0.029 | 0.060 | 0.0 | 0.0 | 742.0 | 877.0 | 1.00 | |
| 0.019 | 0.000 | 0.018 | 0.020 | 0.0 | 0.0 | 733.0 | 634.0 | 1.01 |
| Pole-to-Pole Faults | Pole-to-Ground Faults | |||||
|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | Min | Max | |
| Exp. no. | ||||||
| 0 | 9.176 | 5.036 | 1.934 | 3.672 | 3.553 | 3.802 |
| 1 | 4.282 | 3.818 | 4.818 | 6.690 | 6.360 | 7.041 |
| 2 | 2.489 | 1.813 | 3.540 | 2.596 | 2.510 | 2.673 |
| 3 | 1.124 | 9.160 | 1.398 | 2.265 | 2.193 | 2.342 |
| 4 | 7.260 | 6.172 | 8.566 | 4.809 | 4.596 | 5.037 |
| 5 | 1.881 | 1.744 | 2.029 | 1.104 | 1.032 | 1.202 |
| 6 | 1.163 | 1.091 | 1.236 | 2.081 | 1.905 | 2.279 |
| 7 | 5.456 | 3.664 | 8.499 | 3.052 | 2.903 | 3.206 |
| 8 | 6.295 | 5.348 | 7.457 | 5.398 | 5.131 | 5.675 |
| 9 | 3.252 | 2.331 | 5.029 | 3.930 | 3.789 | 4.080 |
| 10 | 1.521 | 6.879 | 3.795 | 3.035 | 2.923 | 3.148 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baranowski, J.; Grobler-Dębska, K.; Kucharska, E. Recognizing VSC DC Cable Fault Types Using Bayesian Functional Data Depth. Energies 2021, 14, 5893. https://doi.org/10.3390/en14185893
Baranowski J, Grobler-Dębska K, Kucharska E. Recognizing VSC DC Cable Fault Types Using Bayesian Functional Data Depth. Energies. 2021; 14(18):5893. https://doi.org/10.3390/en14185893
Chicago/Turabian StyleBaranowski, Jerzy, Katarzyna Grobler-Dębska, and Edyta Kucharska. 2021. "Recognizing VSC DC Cable Fault Types Using Bayesian Functional Data Depth" Energies 14, no. 18: 5893. https://doi.org/10.3390/en14185893
APA StyleBaranowski, J., Grobler-Dębska, K., & Kucharska, E. (2021). Recognizing VSC DC Cable Fault Types Using Bayesian Functional Data Depth. Energies, 14(18), 5893. https://doi.org/10.3390/en14185893







