A Comprehensive Review of Lithium-Ion Cell Temperature Estimation Techniques Applicable to Health-Conscious Fast Charging and Smart Battery Management Systems
Abstract
:1. Introduction
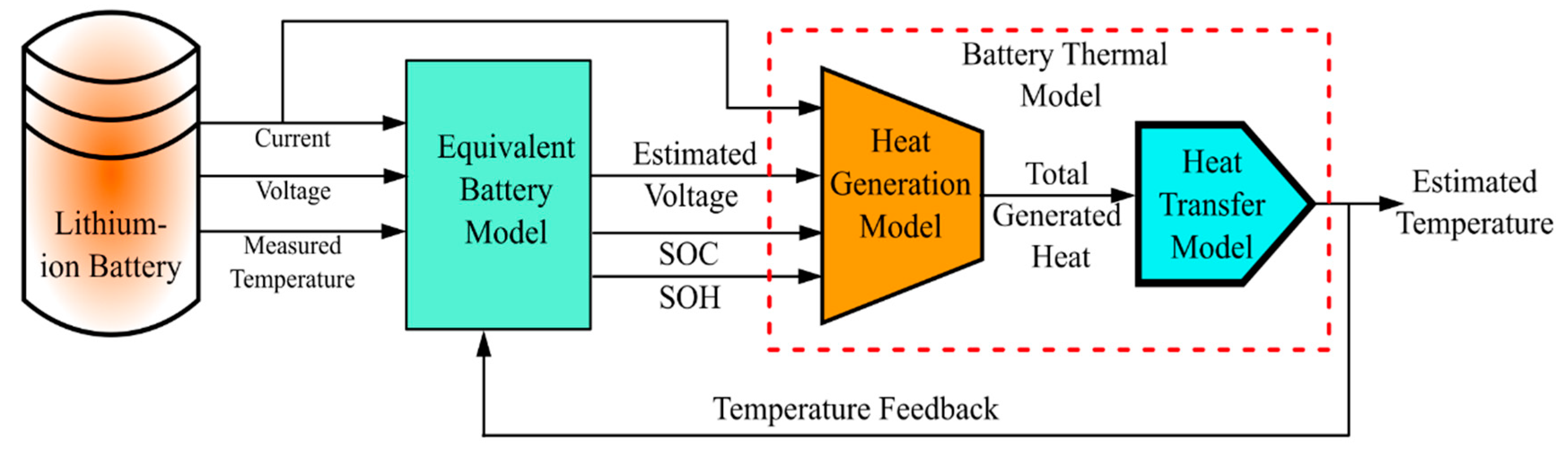
2. Generic Temperature Estimation Strategy
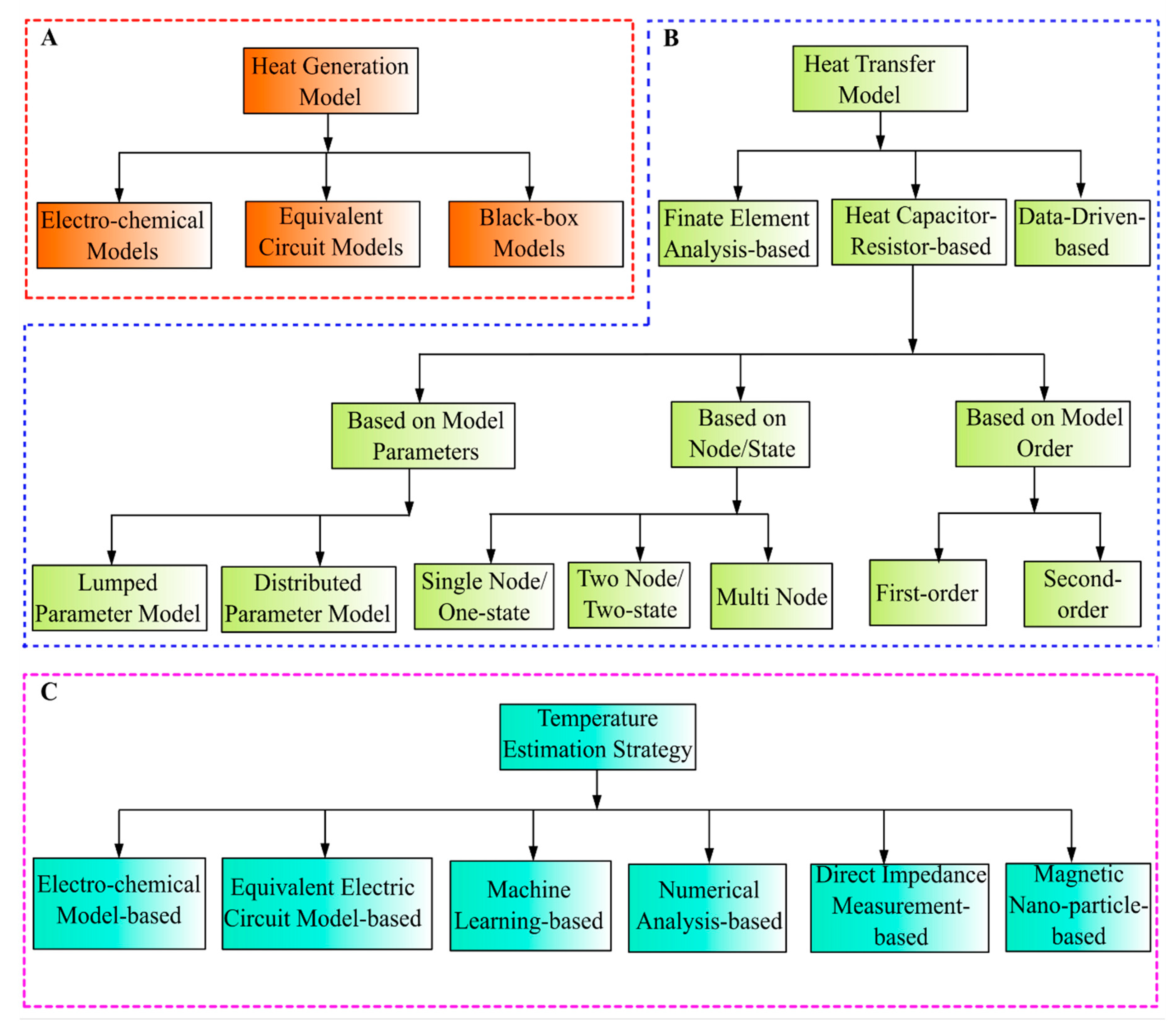
3. Classification of Temperature Estimation Strategies
4. Comprehensive Review of Temperature Estimation Strategies
4.1. Electrochemical Thermal Modelling-Based Temperature Estimation
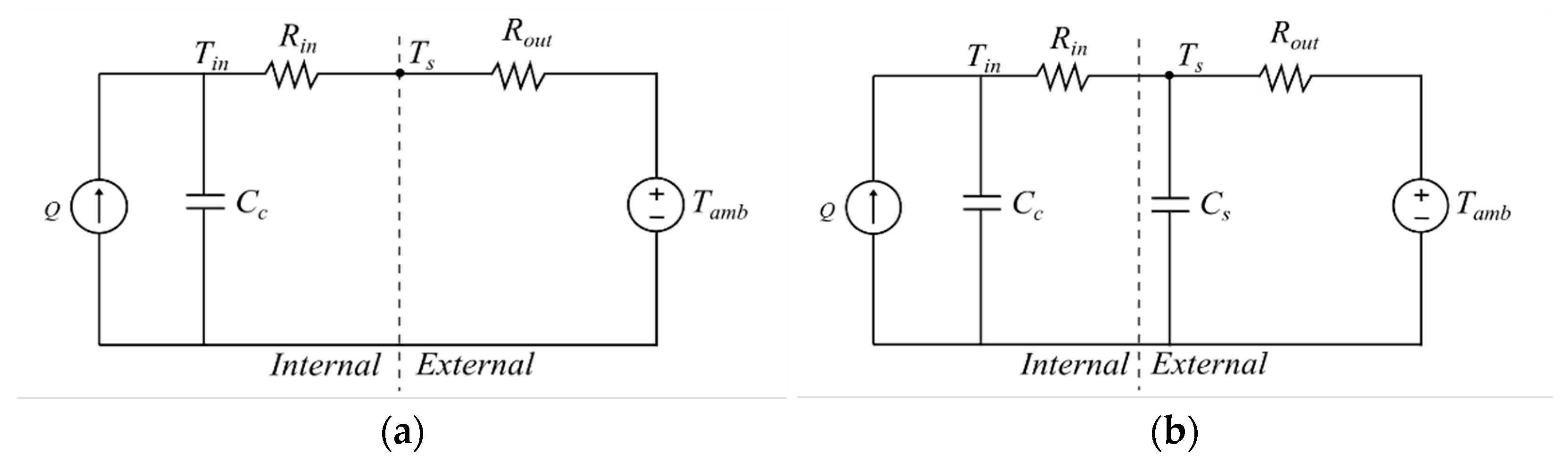
4.2. Equivalent Electric Circuit Model-Based Temperature Estimation
4.2.1. EECM-Based Cell Temperature Estimation
4.2.2. EECM-Based Temperature Estimation of LIB Pack
4.3. Numerical Analysis-Based Temperature Estimation
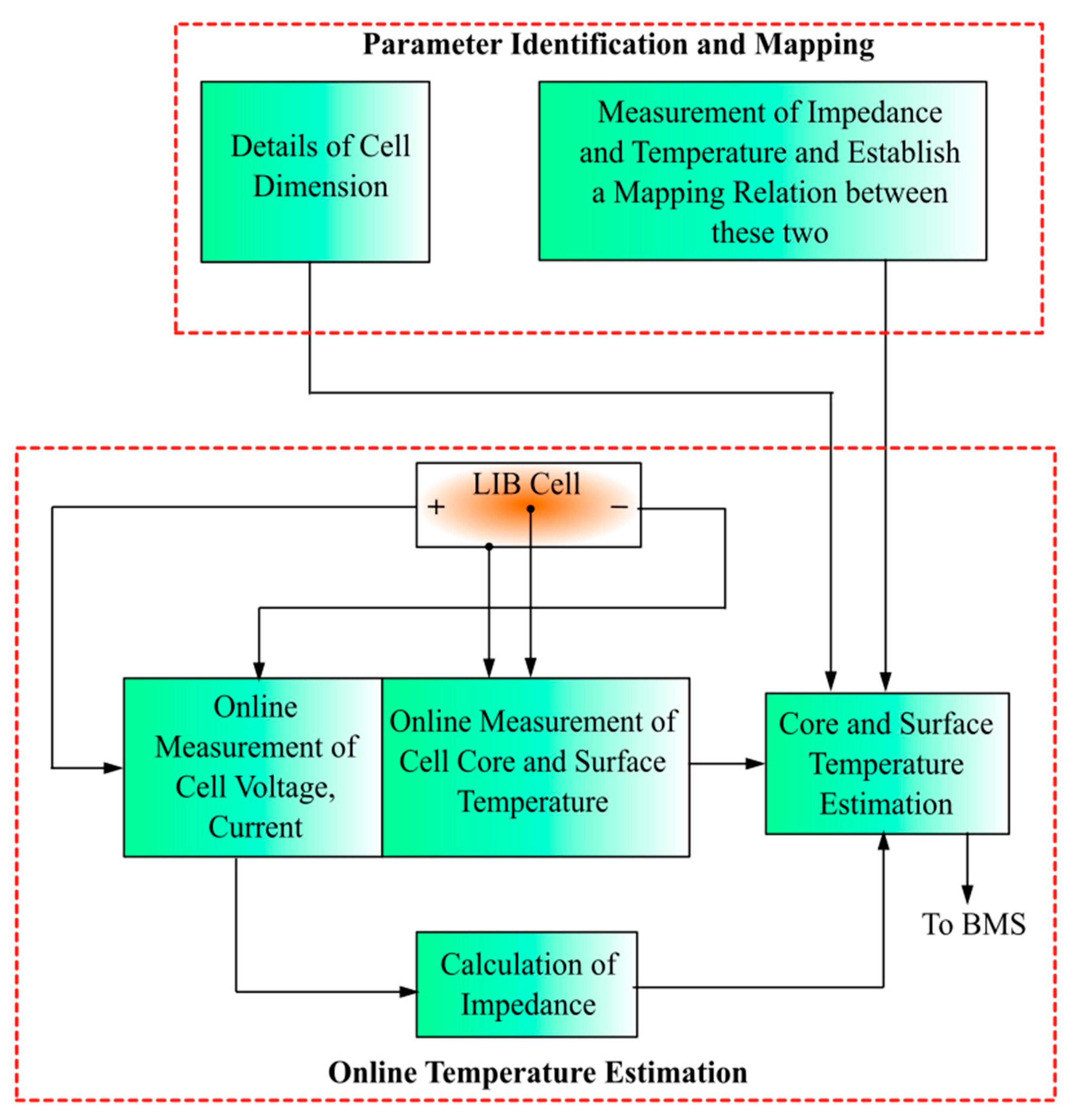
4.4. Direct Impedance Measurement-Based Temperature Estimation
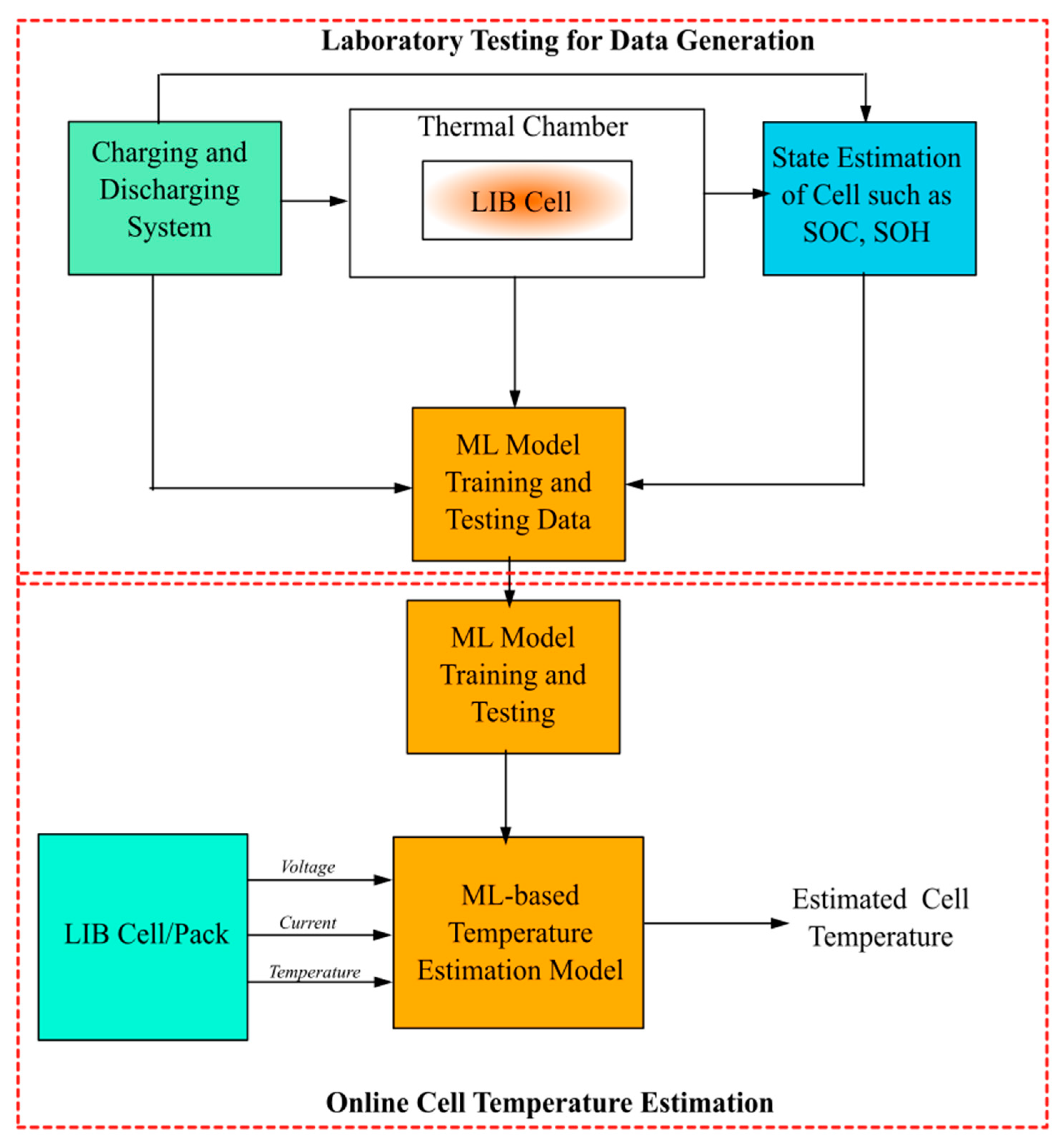
4.5. Machine Learning-Based Temperature Estimation
4.6. Magnetic Nanoparticles-Based Temperature Estimation
5. Discussion on Issues, Challenges and Future Research Recommendations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jilte, R.D.; Kumar, R.; Ma, L. Thermal performance of a novel confined flow Li-ion battery module. Appl. Therm. Eng. 2019, 146, 1–11. [Google Scholar] [CrossRef]
- Yang, X.-H.; Tan, S.-C.; Liu, J. Thermal management of li-ion battery with liquid metal. Energy Convers. Manag. 2016, 117, 577–585. [Google Scholar] [CrossRef]
- Richardson, R.R.; Ireland, P.T.; Howey, D. Battery internal temperature estimation by combined impedance and surface temperature measurement. J. Power Sources 2014, 265, 254–261. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wu, J.-T. Performance improvement of thermal management system of lithium-ion battery module on purely electric AUVs. Appl. Therm. Eng. 2019, 146, 74–84. [Google Scholar] [CrossRef]
- Surya, S.; Samanta, A.; Marcis, V.; Williamson, S.S. Smart core and surface temperature estimation techniques for health-conscious lithium-ion battery management systems: A model-to-model comparison. Preprints 2021, 1–21. [Google Scholar] [CrossRef]
- Tanim, T.R.; Rahn, C.D.; Wang, C.-Y. State of charge estimation of a lithium ion cell based on a temperature dependent and electrolyte enhanced single particle model. Energy 2015, 80, 731–739. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries. J. Power Sources 2017, 347, 1–13. [Google Scholar] [CrossRef]
- Zheng, F.; Jiang, J.; Sun, B.; Zhang, W.; Pecht, M. Temperature dependent power capability estimation of lithium-ion batteries for hybrid electric vehicles. Energy 2016, 113, 64–75. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S. Active cell balancing of lithium-ion battery pack using dual dc-dc converter and auxiliary lead-acid battery. J. Energy Storage 2021, 33, 102109. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S. Machine learning-based data-driven fault detection/diagnosis of lithium-ion battery: A critical review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. The low temperature performance of li-ion batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Mohan, S.; Kim, Y.; Stefanopoulou, A.G. Energy-conscious warm-up of li-ion cells from subzero temperatures. IEEE Trans. Ind. Electron. 2016, 63, 2954–2964. [Google Scholar] [CrossRef]
- Surya, S.; Marcis, V.; Williamson, S. Core temperature estimation for a lithium ion 18650 cell. Energies 2020, 14, 87. [Google Scholar] [CrossRef]
- Surya, S.; Mn, A. Effect of fast discharge of a battery on its core temperature. In Proceedings of the 2020 International Conference on Futuristic Technologies in Control Systems & Renewable Energy (ICFCR), Kerala, India, 23–24 September 2020. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; He, H.; Ding, G.; Cui, H.; Liu, L. Future smart battery and management: Advanced sensing from external to embedded multi-dimensional measurement. J. Power Sources 2021, 489, 229462. [Google Scholar] [CrossRef]
- Steinhorst, S.; Lukasiewycz, M.; Narayanaswamy, S.; Kauer, M.; Chakraborty, S. Smart cells for embedded battery management. In Proceedings of the 2014 IEEE International Conference on Cyber-Physical Systems, Networks, and Applications, Hong Kong, China, 25–26 August 2014. [Google Scholar]
- Huang, X.; Sui, X.; Stroe, D.-I.; Teodorescu, R. A review of management architectures and balancing strategies in smart batteries. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Fleming, J.; Amietszajew, T.; Charmet, J.; Roberts, A.J.; Greenwood, D.; Bhagat, R. The design and impact of In Situ and operando thermal sensing for smart energy storage. J. Energy Storage 2019, 22, 36–43. [Google Scholar] [CrossRef]
- Pan, Y.-W.; Hua, Y.; Zhou, S.; He, R.; Zhang, Y.; Yang, S.; Liu, X.; Lian, Y.; Yan, X.; Wu, B. A computational multi-node electro-thermal model for large prismatic lithium-ion batteries. J. Power Sources 2020, 459, 228070. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Pawlikowski, E.M.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J.E.E. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Ghalkhani, M.; Bahiraei, F.; Nazri, G.-A.; Saif, M. Electrochemical-thermal model of pouch-type lithium-ion batteries. Electrochim. Acta 2017, 247, 569–587. [Google Scholar] [CrossRef]
- Yang, X.-G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.-Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Chen, M.; Bai, F.; Song, W.; Lv, J.; Lin, S.; Feng, Z.; Li, Y.; Ding, Y. A multilayer electro-thermal model of pouch battery during normal discharge and internal short circuit process. Appl. Therm. Eng. 2017, 120, 506–516. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Diaz, L.B.; Patel, Y.; Zhang, T.; Offer, G.J. How to cool lithium ion batteries: Optimising cell design using a thermally coupled model. J. Electrochem. Soc. 2019, 166, A2849–A2859. [Google Scholar] [CrossRef]
- Damay, N.; Forgez, C.; Bichat, M.-P.; Friedrich, G. Thermal modeling of large prismatic LiFePO4/graphite battery. Coupled thermal and heat generation models for characterization and simulation. J. Power Sources 2017, 283, 37–45. [Google Scholar] [CrossRef]
- Allafi, W.; Zhang, C.; Uddin, K.; Worwood, D.; Dinh, T.Q.; Ormeno, P.A.; Li, K.; Marco, J. A lumped thermal model of lithium-ion battery cells considering radiative heat transfer. Appl. Therm. Eng. 2018, 143, 472–481. [Google Scholar] [CrossRef] [Green Version]
- Esmaeili, J.; Jannesari, H. Developing heat source term including heat generation at rest condition for lithium-ion battery pack by up scaling information from cell scale. Energy Convers. Manag. 2017, 139, 194–205. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Neural network based computational model for estimation of heat generation in LiFePO4 pouch cells of different nominal capacities. Comput. Chem. Eng. 2017, 101, 81–94. [Google Scholar] [CrossRef]
- Hu, X.; Liu, W.; Lin, X.; Xie, Y. A comparative study of control-oriented thermal models for cylindrical li-ion batteries. IEEE Trans. Transp. Electrif. 2019, 5, 1237–1253. [Google Scholar] [CrossRef]
- Xie, Y.; Li, W.; Hu, X.; Zou, C.; Feng, F.; Tang, X. Novel mesoscale electrothermal modeling for lithium-ion batteries. IEEE Trans. Power Electron. 2019, 35, 2595–2614. [Google Scholar] [CrossRef]
- Friesen, A.; Mönnighoff, X.; Börner, M.; Haetge, J.; Schappacher, F.M.; Winter, M. Influence of temperature on the aging behavior of 18650-type lithium ion cells: A comprehensive approach combining electrochemical characterization and post-mortem analysis. J. Power Sources 2017, 342, 88–97. [Google Scholar] [CrossRef]
- Fan, Y.; Bao, Y.; Ling, C.; Chu, Y.; Tan, X.; Yang, S. Experimental study on the thermal management performance of air cooling for high energy density cylindrical lithium-ion batteries. Appl. Therm. Eng. 2019, 155, 96–109. [Google Scholar] [CrossRef]
- Saw, L.H.; Poon, H.M.; Thiam, H.S.; Cai, Z.; Chong, W.T.; Pambudi, N.A.; King, Y.J. Novel thermal management system using mist cooling for lithium-ion battery packs. Appl. Energy 2018, 223, 146–158. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Yin, S.; Xu, J. Integrated computation model of lithium-ion battery subject to nail penetration. Appl. Energy 2016, 183, 278–289. [Google Scholar] [CrossRef] [Green Version]
- Doyle, M.; Fuller, T.F.; Newman, J.S. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Xiao, Y.; Fahimi, B. State-space based multi-nodes thermal model for lithium-ion battery. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Beijing, China, 31 August 2014. [Google Scholar]
- Tian, N.; Fang, H.; Wang, Y. 3-D Temperature field reconstruction for a lithium-ion battery pack: A distributed kalman filtering approach. IEEE Trans. Control. Syst. Technol. 2019, 27, 847–854. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Gao, W.; Wang, L.; Zhang, W. Online estimation of thermal parameters based on a reduced wide-temperature-range electro-thermal coupled model for lithium-ion batteries. J. Power Sources 2018, 396, 715–724. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal-electrochemical modeling of battery systems. J. Electrochem. Soc. 2000, 147, 2910–2922. [Google Scholar] [CrossRef]
- Kumaresan, K.; Sikha, G.; White, R.E. Thermal model for a li-ion cell. J. Electrochem. Soc. 2008, 155, A164–A171. [Google Scholar] [CrossRef]
- Forgez, C.; Do, D.V.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Dees, D.W.; Battaglia, V.S.; Bélanger, A. Electrochemical modeling of lithium polymer batteries. J. Power Sources 2002, 110, 310–320. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Siegel, J.; Stefanopoulou, A.G.; Li, Y.; Anderson, R.D.; Ding, Y.; Castanier, M. Online parameterization of lumped thermal dynamics in cylindrical lithium ion batteries for core temperature estimation and health monitoring. IEEE Trans. Control Syst. Technol. 2012, 21, 1745–1755. [Google Scholar] [CrossRef]
- Choi, J.W.; Aurbach, D. Promise and reality of post-lithium-ion batteries with high energy densities. Nat. Rev. Mater. 2016, 1, 16013. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Zhao, Y.; Tsui, K.-L.; Bae, S.J. A study of the relationship between coulombic efficiency and capacity degradation of commercial lithium-ion batteries. Energy 2018, 145, 486–495. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, X.; Ye, J.; Sun, Q.; Ping, P.; Sun, J. Thermal response of lithium-ion battery during charging and discharging under adiabatic conditions. J. Therm. Anal. Calorim. 2016, 124, 417–428. [Google Scholar] [CrossRef]
- Chen, Y. Heat transfer phenomena in lithium/polymer-electrolyte batteries for electric vehicle application. J. Electrochem. Soc. 1993, 140, 1833–1838. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation phenomena in lithium-ion-insertion cells. J. Electrochem. Soc. 1994, 141, 982–990. [Google Scholar] [CrossRef] [Green Version]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery: I discharge behavior of a single cell. J. Electrochem. Soc. 1995, 142, 3274–3281. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery: II temperature profiles in a cell stack. J. Electrochem. Soc. 1995, 142, 3282–3288. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Maleki, H.; Hong, J.; Selman, J. Thermal modeling and design considerations of lithium-ion batteries. J. Power Sources 1999, 83, 1–8. [Google Scholar] [CrossRef]
- Gomadam, P.M.; White, R.E.; Weidner, J.W. Modeling heat conduction in spiral geometries. J. Electrochem. Soc. 2003, 150, A1339–A1345. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J.W. Three-dimensional thermal modeling of lithium-polymer batteries under galvanostatic discharge and dynamic power profile. J. Electrochem. Soc. 1994, 141, 2947–2955. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Temperature rise in a battery module with constant heat generation. J. Electrochem. Soc. 1995, 142, 1054–1057. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Evans, J.W. Thermal analysis of lithium-ion batteries. J. Electrochem. Soc. 1996, 143, 2708–2712. [Google Scholar] [CrossRef]
- Rao, L.; Newman, J. Heat-generation rate and general energy balance for insertion battery systems. J. Electrochem. Soc. 1997, 144, 2697–2704. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Thomas, K.E.; Newman, J.; Darling, R.M. Mathematical modeling of lithium batteries. In Advances in Lithium-Ion Batteries; Springer: Berlin/Heidelberg, Germany, 2002; pp. 345–392. [Google Scholar]
- Van Schalkwijk, W.; Scrosati, B. Advances in lithium ion batteries introduction. In Advances in Lithium-Ion Batteries; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Smith, K.; Wang, C.-Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Amiruddin, S.; Farid, M.; Selman, J.R.; Al-Hallaj, S. Thermal management of li-ion battery with phase change material for electric scooters: Experimental validation. J. Power Sources 2005, 142, 345–353. [Google Scholar] [CrossRef]
- Fang, W.; Kwon, O.J.; Wang, C.-Y. Electrochemical-thermal modeling of automotive li-ion batteries and experimental validation using a three-electrode cell. Int. J. Energy Res. 2009, 34, 107–115. [Google Scholar] [CrossRef]
- Kim, U.S.; Yi, J.; Shin, C.B.; Han, T.; Park, S. Modelling the thermal behaviour of a lithium-ion battery during charge. J. Power Sources 2011, 196, 5115–5121. [Google Scholar] [CrossRef]
- Gerver, R.E.; Meyers, J.P. Three-dimensional modeling of electrochemical performance and heat generation of lithium-ion batteries in tabbed planar configurations. J. Electrochem. Soc. 2011, 158, A835–A843. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, X.-G.; Sun, F.; Wang, Z.; Wang, C.-Y. An online heat generation estimation method for lithium-ion batteries using dual-temperature measurements. Appl. Energy 2020, 272, 115262. [Google Scholar] [CrossRef]
- Wang, P.; Yang, L.; Wang, H.; Tartakovsky, D.; Onori, S. Temperature estimation from current and voltage measurements in lithium-ion battery systems. J. Energy Storage 2021, 34, 102133. [Google Scholar] [CrossRef]
- Marelli, S.; Corno, M. Model-based estimation of lithium concentrations and temperature in batteries using soft-constrained dual unscented kalman filtering. IEEE Trans. Control. Syst. Technol. 2021, 29, 926–933. [Google Scholar] [CrossRef]
- Mahamud, R.; Park, C. Reciprocating air flow for li-ion battery thermal management to improve temperature uniformity. J. Power Sources 2011, 196, 5685–5696. [Google Scholar] [CrossRef]
- Park, C.; Jaura, A.K. Dynamic Thermal Model of Li-Ion Battery for Predictive Behavior in Hybrid and Fuel Cell Vehicles; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Chen, L.; Hu, M.; Cao, K.; Li, S.; Su, Z.; Jin, G.; Fu, C. Core temperature estimation based on electro-thermal model of lithium-ion batteries. Int. J. Energy Res. 2020, 44, 5320–5333. [Google Scholar] [CrossRef]
- Maleki, H.; Shamsuri, A.K. Thermal analysis and modeling of a notebook computer battery. J. Power Sources 2003, 115, 131–136. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Li, D.; Yang, L. Identification of spatial temperature gradient in large format lithium battery using a multilayer thermal model. Int. J. Energy Res. 2019, 44, 282–297. [Google Scholar] [CrossRef]
- Lin, X.; Stefanopoulou, A.G.; Perez, H.E.; Siegel, J.B.; Li, Y.; Anderson, R.D. Quadruple adaptive observer of the core temperature in cylindrical li-ion batteries and their health monitoring. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012. [Google Scholar] [CrossRef]
- Lin, X.; Fu, H.; Perez, H.E.; Siege, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. Parameterization and observability analysis of scalable battery clusters for onboard thermal management. Oil Gas Sci. Technol. 2013, 68, 165–178. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wei, G.; Pei, L.; Lu, R.; Song, K.; Wu, C.; Zhu, C. Online internal temperature estimation for lithium-ion batteries based on kalman filter. Energies 2015, 8, 4400–4415. [Google Scholar] [CrossRef] [Green Version]
- Dai, H.; Zhu, L.; Zhu, J.; Wei, X.; Sun, Z. Adaptive kalman filtering based internal temperature estimation with an equivalent electrical network thermal model for hard-cased batteries. J. Power Sources 2015, 293, 351–365. [Google Scholar] [CrossRef]
- Doughty, D.H.; Butler, P.C.; Jungst, R.G.; Roth, E. Lithium battery thermal models. J. Power Sources 2002, 110, 357–363. [Google Scholar] [CrossRef]
- Xie, Y.; Li, W.; Hu, X.; Lin, X.; Zhang, Y.; Dan, D.; Feng, F.; Liu, B.; Li, K. An enhanced online temperature estimation for lithium-ion batteries. IEEE Trans. Transp. Electrif. 2020, 6, 375–390. [Google Scholar] [CrossRef]
- Sun, L.; Sun, W.; You, F. Core temperature modelling and monitoring of lithium-ion battery in the presence of sensor bias. Appl. Energy 2020, 271, 115243. [Google Scholar] [CrossRef]
- Zhu, C.; Shang, Y.; Lu, F.; Jiang, Y.; Cheng, C.; Mi, C. Core temperature estimation for self-heating automotive lithium-ion batteries in cold climates. IEEE Trans. Ind. Inform. 2019, 16, 3366–3375. [Google Scholar] [CrossRef]
- Xiao, Y. Model-based virtual thermal sensors for lithium-ion battery in EV applications. IEEE Trans. Ind. Electron. 2014, 62, 3112–3122. [Google Scholar] [CrossRef]
- Ma, Y.; Cui, Y.; Mou, H.; Gao, J.; Chen, H. Core temperature estimation of lithium-ion battery for EVs using kalman filter. Appl. Therm. Eng. 2020, 168, 114816. [Google Scholar] [CrossRef]
- Ismail, N.H.F.; Toha, S.F.; Azubir, N.A.M.; Ishak, N.H.M.; Hassan, I.D.M.K.; Ibrahim, B.S.K. Simplified heat generation model for lithium ion battery used in electric vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2013, 53, 012014. [Google Scholar] [CrossRef]
- Jeon, D.H. Numerical modeling of lithium ion battery for predicting thermal behavior in a cylindrical cell. Curr. Appl. Phys. 2014, 14, 196–205. [Google Scholar] [CrossRef]
- Baba, N.; Yoshida, H.; Nagaoka, M.; Okuda, C.; Kawauchi, S. Numerical simulation of thermal behavior of lithium-ion secondary batteries using the enhanced single particle model. J. Power Sources 2014, 252, 214–228. [Google Scholar] [CrossRef]
- Du, S.; Jia, M.; Cheng, Y.; Tang, Y.; Zhang, H.; Ai, L.; Zhang, K.; Lai, Y. Study on the thermal behaviors of power lithium iron phosphate (LFP) aluminum-laminated battery with different tab configurations. Int. J. Therm. Sci. 2015, 89, 327–336. [Google Scholar] [CrossRef]
- Yi, J.; Lee, J.; Shin, C.B.; Han, T.; Park, S. Modeling of the transient behaviors of a lithium-ion battery during dynamic cycling. J. Power Sources 2015, 277, 379–386. [Google Scholar] [CrossRef]
- Fleckenstein, M.; Bohlen, O.; Roscher, M.A.; Bäker, B. Current density and state of charge inhomogeneities in li-ion battery cells with LiFePO4 as cathode material due to temperature gradients. J. Power Sources 2011, 196, 4769–4778. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Ramadass, P.; Zhang, J.Z. Analysis of internal short-circuit in a lithium ion cell. J. Power Sources 2009, 194, 550–557. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Wu, B.; Huang, J.; Nie, Z.; Sun, Y.; An, F.; Wu, N. Examining temporal and spatial variations of internal temperature in large-format laminated battery with embedded thermocouples. J. Power Sources 2013, 241, 536–553. [Google Scholar] [CrossRef]
- Mutyala, M.S.K.; Zhao, J.; Li, J.; Pan, H.; Yuan, C.; Li, X. In Situ temperature measurement in lithium ion battery by transferable flexible thin film thermocouples. J. Power Sources 2014, 260, 43–49. [Google Scholar] [CrossRef]
- Srinivasan, R.; Carkhuff, B.G.; Butler, M.H.; Baisden, A.C. Instantaneous measurement of the internal temperature in lithium-ion rechargeable cells. Electrochim. Acta 2011, 56, 6198–6204. [Google Scholar] [CrossRef]
- Srinivasan, R. Monitoring dynamic thermal behavior of the carbon anode in a lithium-ion cell using a four-probe technique. J. Power Sources 2012, 198, 351–358. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Arnold, S.; Loges, A.; Werner, D.; Wetzel, T.; Ivers-Tiffée, E. Measurement of the internal cell temperature via. impedance: Evaluation and application of a new method. J. Power Sources 2013, 243, 110–117. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G. The effect of thermal gradients on the performance of lithium-ion batteries. J. Power Sources 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Brandon, N.; Mitcheson, P.; Yufit, V.; Howey, D.; Offer, G. Battery Monitoring in Electric Vehicles, Hybrid Electric Vehicles and Other Applications. U.S. Patent 2,013,022,915,6A1, 8 May 2013. [Google Scholar]
- Richardson, R.R.; Howey, D.A. Sensorless battery internal temperature estimation using a kalman filter with impedance measurement. IEEE Trans. Sustain. Energy 2015, 6, 1190–1199. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Sun, Z.; Wei, X.; Dai, H. A new lithium-ion battery internal temperature on-line estimate method based on electrochemical impedance spectroscopy measurement. J. Power Sources 2015, 274, 990–1004. [Google Scholar] [CrossRef]
- Debert, M.; Colin, G.; Bloch, G.; Chamaillard, Y. An observer looks at the cell temperature in automotive battery packs. Control Eng. Pract. 2013, 21, 1035–1042. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, J.; Zhang, L. State-of-health estimation for lithium-ion batteries based on the multi-island genetic algorithm and the gaussian process regression. IEEE Access 2017, 5, 21286–21295. [Google Scholar] [CrossRef]
- Hande, A. Internal battery temperature estimation using series battery resistance measurements during cold temperatures. J. Power Sources 2006, 158, 1039–1046. [Google Scholar] [CrossRef]
- Howey, D.; Mitcheson, P.D.; Yufit, V.; Offer, G.; Brandon, N.P. Online measurement of battery impedance using motor controller excitation. IEEE Trans. Veh. Technol. 2014, 63, 2557–2566. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H. A Spatiotemporal estimation method for temperature distribution in lithium-ion batteries. IEEE Trans. Ind. Inform. 2014, 10, 2300–2307. [Google Scholar] [CrossRef]
- Khelif, R.; Chebel-Morello, B.; Malinowski, S.; Laajili, E.; Fnaiech, F.; Zerhouni, N. Direct remaining useful life estimation based on support vector regression. IEEE Trans. Ind. Electron. 2017, 64, 2276–2285. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Corbetta, M.; Giglio, M.; Cadini, F. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks. J. Power Sources 2017, 344, 128–140. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Guo, Y.; Zhang, L. Data-driven hybrid internal temperature estimation approach for battery thermal management. Complexity 2018, 2018, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Zhong, J. Comparison of noninvasive and remote temperature estimation employing magnetic nanoparticles in DC and AC applied fields. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012. [Google Scholar]
- Zhong, J.; Dieckhoff, J.; Schilling, M.; Ludwig, F. Influence of static magnetic field strength on the temperature resolution of a magnetic nanoparticle thermometer. J. Appl. Phys. 2016, 120, 143902. [Google Scholar] [CrossRef]
- Yoshida, T.; Enpuku, K. Simulation and quantitative clarification of ac susceptibility of magnetic fluid in nonlinear brownian relaxation region. Jpn. J. Appl. Phys. 2009, 48, 127002. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, W.; Du, Z.; De Morais, P.C.; Xiang, Q.; Xie, Q. A noninvasive, remote and precise method for temperature and concentration estimation using magnetic nanoparticles. Nanotechnology 2012, 23, 075703. [Google Scholar] [CrossRef]
- Zou, D.; Li, M.; Wang, D.; Li, N.; Su, R.; Zhang, P.; Gan, Y.; Cheng, J. Temperature estimation of lithium-ion battery based on an improved magnetic nanoparticle thermometer. IEEE Access 2020, 8, 135491–135498. [Google Scholar] [CrossRef]
| Reference | Types of Models | Important Note |
|---|---|---|
| Thomas and Newman [60] | One-dimensional electrochemical model | Not used for temperature estimation |
| Doyle–Fuller–Newmann model [37,61] | Pseudo-two-dimensional (P2D) model | Not used for temperature estimation but several other researchers used |
| Al Hallaj et al. [53] | A transient one-dimensional thermal model with lumped parameters | Detailed information of electrodes, electrolytes and separator were considered in heat generation model |
| Fang et al. [64]. | Lumped parameter electrochemical-thermal-coupled model | Can estimate one or two average temperatures, performance of individual electrode at various operating temperatures, constant current and pulsing conditions characteristic were considered, experimentally validated |
| Gu and Wang [41] | Thermal energy generation model, multiphase micro-macroscopic electrochemical model | Temperature-dependent physicochemical properties and thermal behaviors under various charging conditions were considered. Capable of predicting the average cell temperature as well as the temperature distribution inside a cell, volume-averaging technique, numerical simulations |
| Kumaresan et al. [42] | One-dimensional thermal model | Thermal dependence of various parameters in the model on different discharge profiles was assessed, validated using experimental and simulation results |
| Kim et al. [65] | Two-dimensional modelling + Finite element method (FEM) | Able to provide temperature distribution based on potential and current density distribution, MATLAB, validated using experimental and simulation results |
| Gerver et al. [66] | A multi-dimensional electrochemical thermal model | Thermal properties of each cell layer are considered, experimentally validated |
| Wang et al. [68] | High-fidelity electrochemical model + onboard measurements + dual ensemble Kalman filter (DEKF) | Wide range of C-rates during the charging/discharging period, MATLAB, validated using experimental and simulation results |
| Marelli and Corno [69] | Pseudo-2D electrochemical model and soft-constrained dual unscented Kalman filter (DUKF) | Can provide information on the spatial distribution of internal temperature, MATLAB Simulation |
| Smith et al. [62] | A one-dimensional electrochemical lumped thermal model | Adaptive to different drive-cycles, tested and validated with FUDS and HWFET drive cycles, experimentally validated |
| Reference | Types of Models | Important Note |
|---|---|---|
| Mahamud et al. [70] | Lumped Parameter heat capacitance–resistance thermal model | ANSYS (Ansys, Inc., Canonsburg, PA, USA) FLUENT Simulation, validated using Experimental and simulation results |
| Forgeze et al. [43] | Lumped Parameter, Single-State, First-order model | Entropy changes are considered, experimentally validated |
| Surya et al. [13] | Lumped Parameter, Two-State, Second-order model + Kalman Filter (KF) | SOC, Surface temperature variation, MATLAB Simulation |
| Lin et al. [74] | Lumped Parameter, Two-State, Second-order model | High current rate, varying temperature, SOC, experimental validation using electrochemical impedance spectroscopy data |
| Li and Yang [75] | Extended lumped parameter, Two-state, Second-order model + Forgetting factor Recursive Least Square (FFRLS) | Temperature variation, cell ageing, SOC, Heat transfer modes, ANSYS Multiphysics Simulation, validated using experimental and simulation results |
| Lin et al. [45,76] | Lumped parameter, Two-state model + Least square (LS) algorithm + Nonuniform forgetting factors (NUFF) | Cell ageing and uncertainties in practical operation, validated using experimental and simulation results |
| Lin et al. [77] | Lumped-parameter model + Closed-loop observer | Influence of overpotential entropy changes, validated using a simulation study |
| Sun et al. [78] | Lumped parameter, Second-order, Single state thermal model + KF | Influence of entropy changes and overpotential, surface and ambient temperature variation, charge/discharge current profile, MATLAB simulation and experimental validation |
| Dai et al. [79] | Lumped parameter, Second-order, Two-state model + JKF + LS algorithm | Initialization error and the possible time-varying external thermal resistance, validated using experimental data |
| Doughty et al. [80] and Park et al. [71] | Lumped parameter, Two-state model + Extended KF | Ambient temperature variation, SOC, validated using a simulation study |
| Chen et al. [72] | Lumped parameter, Two-state thermal model + Joint KF (JKF) | Constantly varying temperature, SOC, Surface thermal resistance, experimentally validated |
| Pan et al. [19] | Lumped Parameter, Second-order, multi-node model + particle-swarm algorithm | Battery geometry, charge/discharge profile, Comparison with an FEA model, experimentally validated |
| Xie et al. [81] | One-dimensional (radial) lumped parameter, Three node model + Dual KF (DKF). | Anisotropy of thermal conductivity, SOC, external temperature, FEM and Computational Fluid Dynamics (CFD), experimental validation |
| Sun et al. [82] | Lumped parameter, single-state model + Extended unscented KF (EUKF) | Sensor bias, Considered heat radiation from the surface, MATLAB simulation and experimental validation |
| Zhu et al. [83] | Lumped parameter, Two-state model + extended state observer (ESO) | Thermal impact of an adjacent cell, Model uncertainties and time-variant parameters, MATLAB simulation, validation and comparison using electrochemical impedance spectroscopy data |
| Surya and Mn [14] | Lumped parameter, Single-state thermal model + KF + Recursive Least Square (RLS) algorithm | Effect of fast-discharge, MATLAB Simulation |
| Xiao Y. [84] | EECM-based virtual thermal sensors (VTS) + KF | Environmental uncertainties were considered, validated using experimental and simulation results |
| Ma et al. [85] and Ismail et al. [86] | ROM of a LIB pack for a central temperature of LIB pack + Recursive least square (RLS) | Temperature, SOC, validated using experimental and simulation results |
| Reference | Types of Models | Important Note |
|---|---|---|
| Dong Hyup Jeon [87] | A transient thermoelectric model with a porous electrode model + finite element method (FEM) | Different driving cycles, COMSOL Multiphysics (COMSOL Inc., Stockholm, Sweden) simulation and Experimental validation |
| Baba et al. [88] | Enhanced single-particle model + FEM | Three-dimensional temperature distribution inside the cell, cell geometry, and current profile, experimentally validated |
| Du et al. [89] | Three-dimensional model + ECM based heat generation model + FEM | Different current profiles, temperature variation, COMSOL Multiphysics simulation and experimental validation |
| Yi et al. [90] | Transient thermoelectric model + FEM | Transient behaviors under dynamic driving cycle Experimentally validated |
| Fleckenstein et al. [91] | Three-dimensional model + FVM | Different current density and local SOC inhomogeneities at different cell layers, MATLAB (MathWorks, MA, USA) simulation and experimental validation |
| Reference | Types of Models | Important Note |
|---|---|---|
| Srinivasan et al. [95,96] | Direct measurement of electrochemical impedance | Experimental validation with EIS data |
| Schmidt et al. [97] | Direct measurement of electrochemical impedance | Temperature non-uniformity was not considered, experimentally validated |
| Richardson et al. [3] | Thermal-impedance model + EIS measurement at single frequency + surface temperature feedback | Independent of cell thermal properties, heat generation or thermal boundary conditions, experimental validation with EIS data |
| Richardson and Howey [100] | Online EIS measurement (impedance-temperature detection (ITD) + dual-extended Kalman filter (DEKF) | Unknown convection coefficient is considered, experimentally validated |
| Zhu et al. [101] | Impedance response matrix analysis, developed using EIS measurements | Influence of cell temperature, SOC and SOH on the impedance spectrum, experimental validation with EIS data |
| Reference | Types of Models | Important Note |
|---|---|---|
| Liu and Li [107] | EECM + neural network (NN)-based learning approach | Model-plant mismatch caused by spatial nonlinearity and other model uncertainties, NN-model was validated using experimental data |
| Sbarufatti et al. [109] | Neural networks + Support vector machines | Influence of temperature, charging/discharging current, Python (Python Software Foundation, Wilmington, DE, USA), NN and SVM-model were validated using experimental data |
| Liu et al. [110] | RBF neural network (RBNN) and the extended Kalman filter (EKF) | Impact of temperature on cell behavior, validated using simulation data |
| Feng et al. [111] | Electrochemical-thermal-neural-network (ETNN) + Unscented Kalman filter (UKF). | Wide temperature and large current conditions, Python, validated using experimental data |
| Strategy | Major Issues and Challenges | Future Research Recommendations |
|---|---|---|
| Electrochemical Model-based |
|
|
| Equivalent Electric Circuit (EECM) Model-based |
|
|
| Machine Learning (ML)-based |
|
|
| Numerical Model-based |
|
|
| Direct Impedance Measurement-based |
|
|
| Magnetic Nanoparticle-based |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samanta, A.; Williamson, S.S. A Comprehensive Review of Lithium-Ion Cell Temperature Estimation Techniques Applicable to Health-Conscious Fast Charging and Smart Battery Management Systems. Energies 2021, 14, 5960. https://doi.org/10.3390/en14185960
Samanta A, Williamson SS. A Comprehensive Review of Lithium-Ion Cell Temperature Estimation Techniques Applicable to Health-Conscious Fast Charging and Smart Battery Management Systems. Energies. 2021; 14(18):5960. https://doi.org/10.3390/en14185960
Chicago/Turabian StyleSamanta, Akash, and Sheldon S. Williamson. 2021. "A Comprehensive Review of Lithium-Ion Cell Temperature Estimation Techniques Applicable to Health-Conscious Fast Charging and Smart Battery Management Systems" Energies 14, no. 18: 5960. https://doi.org/10.3390/en14185960
APA StyleSamanta, A., & Williamson, S. S. (2021). A Comprehensive Review of Lithium-Ion Cell Temperature Estimation Techniques Applicable to Health-Conscious Fast Charging and Smart Battery Management Systems. Energies, 14(18), 5960. https://doi.org/10.3390/en14185960







