Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application
Abstract
1. Introduction
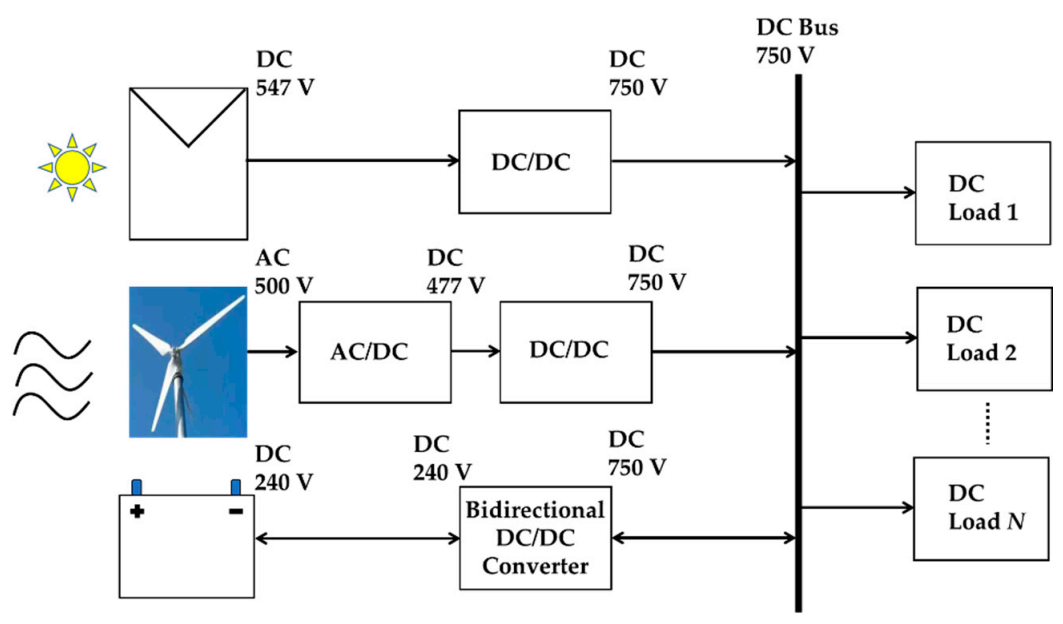
2. Materials and Methods
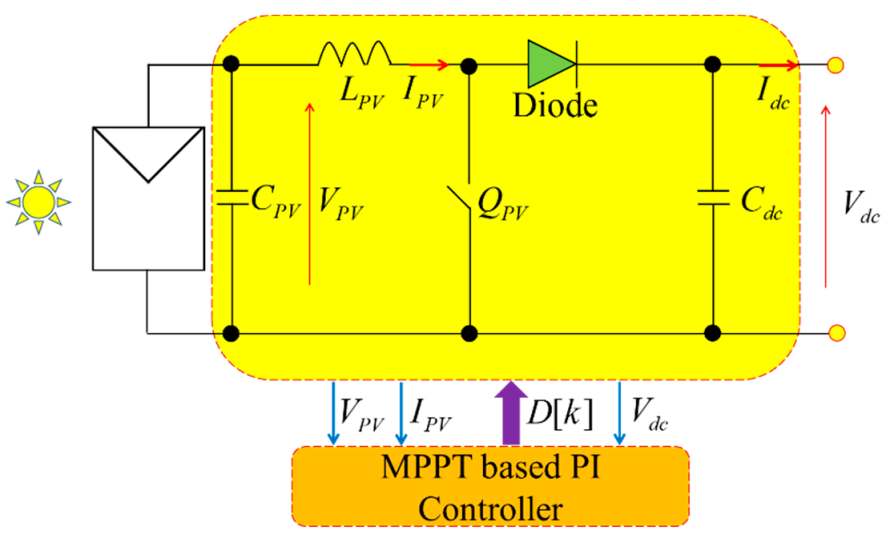
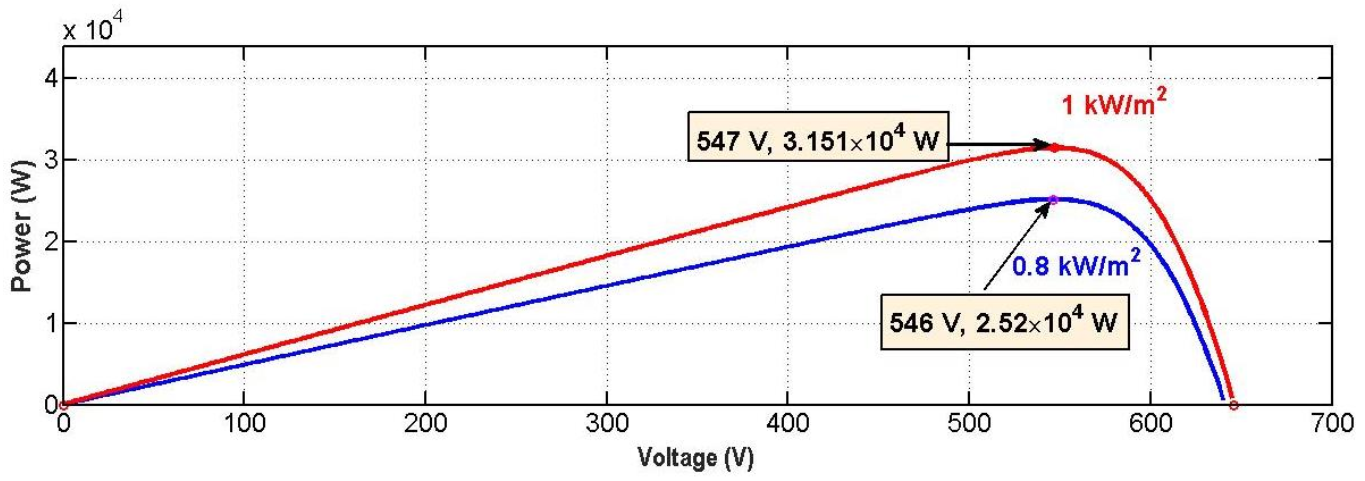
2.1. Solar PV Array Modelling
2.2. Wind Turbine Modeling
Modelling of Permanent Magnet Synchronous Generator
2.3. DC/DC Boost Converter
3. Maximum Power Point Tracking-Based Proportional and Integral Controller
3.1. Maximum Power Point Tracking Controller
3.2. Proportional Integral Controller
3.3. DC Bus Voltage Regulation Design for Solar PV
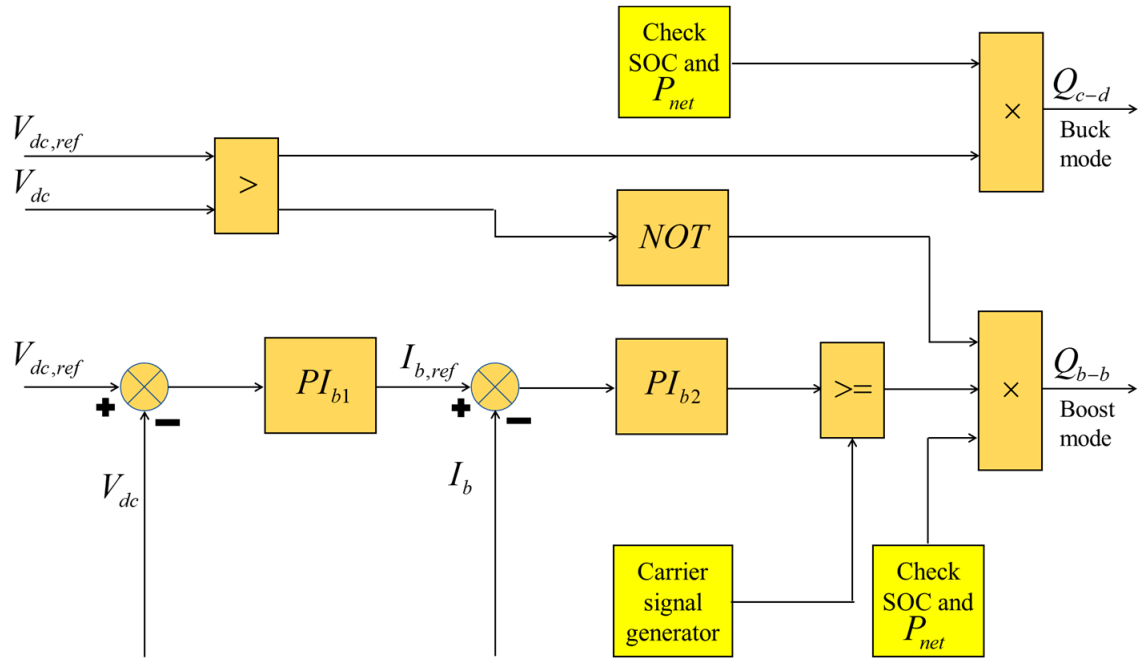
3.4. Solar PV with Battery Energy Storage System
Control of Battery Energy Storage System
3.5. DC Bus Voltage Regulation Design for Wind Generator
3.6. The Hybrid System of Solar-Wind with Battery Energy Storage System
4. Simulations and Results Discussions
4.1. Case 1 Constant Loading of the DC Microgrid
4.2. Case 2 Step-Load Increase in the DC Microgrid
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Values | Units |
|---|---|---|
| Max. power | 315 | W |
| Current at MPP | 5.76 | A |
| Voltage at MPP | 54.7 | V |
| Temperature coefficient of Voc | −0.27269 | %/°C |
| Open circuit voltage Voc | 64.6 | V |
| Short circuit current Isc | 6.14 | A |
| Current/temp. coefficient, Ki | 0.061745 | %/°C |
| Parameters | Values | Units |
|---|---|---|
| Boost converter for solar PV | ||
| Inductor LPV | 20 | mH |
| Capacitor Cd | 150 | µF |
| Resistive Load | 15 | Ω |
| Boost converter for wind system | ||
| Inductor Lw | 35 | mH |
| Buck–boost converter | ||
| Inductor Lb | 1 | mH |
| Parameters | Values | Units |
|---|---|---|
| Nominal Voltage, Vb | 240 | V |
| Rated Capacity | 248 | Ah |
| Parameters | Values | Units |
|---|---|---|
| Rated speed | 153 | rad/s |
| Armature resistance, Rs | 0.425 | Ω |
| Flux | 0.433 | Wb |
| Rated current | 12 | A |
| Stator inductance Ls | 8.4 | mH |
| Rated torque | 40 | Nm |
| Rated power | 6 | kW |
References
- Aslam, Z.; Li, H.; Hammerton, J.; Andrews, G.; Ross, A.; Lovett, J.C. Increasing access to electricity: An assessment of the energy and power generation potential from biomass waste residues in Tanzania. Energies 2021, 14, 1793. [Google Scholar] [CrossRef]
- Juma, M.; Msigwa, C.; Mwinyiwiwa, B.M.M. Solar PV based on maximum power point tracking embedded voltage regulation for micro-grid application. Int. J. Innov. Res. Adv. Eng. IJIRAE 2019, 6, 552–558. [Google Scholar]
- Oladigbolu, J.O.; Ramli, M.A.M.; Al-Turki, Y.A. Optimal design of a hybrid PV sola/micro-hydro/diesel/battery energy system for a remote rural village under tropical climate conditions. Electronics 2020, 9, 1491. [Google Scholar] [CrossRef]
- Hemeida, A.M.; El-Ahmar, M.H.; El-Sayed, A.M.; Hasanien, H.M.; Alkhalaf, S.; Esmail, M.F.C.; Senjyu, T. Optimum design of hybrid wind/PV energy system for remote area. Ain Shams Eng. J. 2019, 11, 11–23. [Google Scholar] [CrossRef]
- Alsadi, S.; Khatib, T. Photovoltaic power systems optimization research status: A review of criteria, constrains, models, techniques, and software tools. Appl. Sci. 2018, 8, 1761. [Google Scholar] [CrossRef]
- Singh, P.D.; Upadhaya, A.; Simte, M.; Singh, H.J. Design of an efficient microgrid system for a local area. Int. J. Electr. Eng. Technol. IJEET 2019, 10, 64–72. [Google Scholar] [CrossRef]
- Kinhal, V.; Katti, P.K. Rural electrification through solar and wind hybrid system: A self sustained grid free electric power source. Energy Procedia 2012, 14, 2081–2087. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F. Coordinated V-f and P-Q control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Petersen, L.; Iov, F.; Tarnowski, G.C. A model-based approach for stability assessment, control tuning and verification in off-grid hybrid power plants. Energies 2019, 13, 49. [Google Scholar] [CrossRef]
- Mwinyiwiwa, B.M.M.; Manyahi, M.J.; Gregory, N.; Kyaruzi, A.L. Conceptual synthesis of the multisource renewable energy-based micro grid. Int. Sch. Sci. Res. Innov. 2013, 7, 1687–1692. [Google Scholar]
- Tayab, U.B.; Mohd, A.R.; Leong, J.H.; Muhammad, K. A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- Mwinyiwiwa, B.M.M. DC bus voltage regulator for renewable energy based micro grid-application. Int. Sch. Sci. Res. Innov. 2013, 7, 1629–1633. [Google Scholar]
- Maher, E.N. Hybrid Power Systems Energy Management Based on Artificial Intelligence. Ph.D. Thesis, Manchester Metropolitan University, Manchester, UK, 2013. [Google Scholar]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Artificial intelligence based MPPT techniques for solar power system: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1043–1059. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-microgrid energy management systems: Architecture, communication, and scheduling strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Moreira, C.L.; Madureira, A.G. Defining control strategies for micro grids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar] [CrossRef]
- He, T.; Li, S.; Wu, S.; Li, K. Small-signal stability analysis for power system frequency regulation with renewable energy participation. Hindawi Math. Probl. Eng. 2021, 2021, 5556062. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Hu, W.; Wang, Y.; Dong, L.; Zhang, J. Coordinated optimal operation of hydro–wind–solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Khatib, T.; Sabri, L. Grid impact assessment of centralized and decentralized photovoltaic-based distribution generation: A case study of power distribution network with high renewable energy penetration. Hindawi Math. Probl. Eng. 2021, 2021, 5430089. [Google Scholar] [CrossRef]
- Patarroyo-Montenegro, J.F.; Vasques-Plaza, J.D.; Andrade, F. A state-space model of an inverter-based microgrid for multivariable feedback control analysis and design. Energies 2020, 13, 3279. [Google Scholar] [CrossRef]
- Chauhan, P.J.; Reddy, B.D.; Bhandari, S.; Panda, S.K. Battery energy storage for seamless transitions of wind generator in standalone microgrid. IEEE Trans. Ind. Appl. 2019, 55, 69–77. [Google Scholar] [CrossRef]
- Madaci, B.; Chenni, R.; Kurt, E.; Hemsas, K. Design and control of a stand-alone hybrid power system. Int. J. Hydrogen Energy 2016, 41, 12485–12496. [Google Scholar] [CrossRef]
- Errami, Y.; Ouassaid, M.; Maaroufia, M. Control of a PMSG based wind energy generation system for power maximization and grid fault conditions. Energy Procedia 2013, 42, 220–229. [Google Scholar] [CrossRef]
- ELmorshedy, M.F.; Allam, S.M.; Ahmed, I.A.S.; Essam, M.R. Voltage and frequency control of a stand-alone wind-energy conversion system based on PMSG. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015. [Google Scholar] [CrossRef]
- Sahu, S.; Yadav, S.P. Dynamic modelling and control of PMSG based stand-alone wind energy conversion system. In Proceedings of the Recent Advances on Engineering, Technology and Computational Sciences (RAETCS), Allahabad, India, 6–8 February 2018; pp. 1–6. [Google Scholar]
- Tan, N.V.; Nam, N.B.; Hieu, N.H.; Hung, L.K.; Minh, Q.D.; Lam, L.H. A proposal for an MPPT algorithm based on the fluctuations of the PV output power, output voltage, and control duty cycle for improving the performance of PV systems in microgrid. Energies 2020, 13, 4326. [Google Scholar] [CrossRef]
- Zhu, Y.; Wen, H.; Chu, G.; Hu, Y.; Li, X.; Ma, J. High-performance photovoltaic constant power generation control with rapid maximum power point estimation. IEEE Trans. Ind. Appl. 2021, 57, 714–729. [Google Scholar] [CrossRef]
- Justo, J.J.; Mushi, A.T. Performance analysis of renewable energy resources in rural areas: Case study of solar energy. Tanzan. J. Eng. Technol. 2020, 39, 1–12. [Google Scholar] [CrossRef]
- Iqbal, M.M.; Islam, K. Design and simulation of a PV system with battery storage using bidirectional DC-DC converter using MATLAB/Simulink. Int. J. Sci. Technol. Res. 2017, 6, 403–410. [Google Scholar]
- Haque, M.E.; Muttaqi, K.M.; Negnevitsky, M. Control of a standalone variable speed wind turbine with a permanent magnet synchronous generator. In Proceedings of the IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–9. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; IEEE Press, John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dileep, S.K.; Annapurna, N.V.B. Power quality improvement in standalone battery integrated wind energy system. In Proceedings of the International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 642–647. [Google Scholar] [CrossRef]
- Mushi, A.; Nagai, S.; Obara, H.; Kawamura, A. Design for nonlinear reference deadbeat control for boost converter. In Proceedings of the 2017 IEEE International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017. [Google Scholar] [CrossRef]
- Mushi, A.; Nagai, S.; Obara, H.; Kawamura, A. Fast and robust nonlinear deadbeat current control for boost converter. IEEJ J. Ind. Appl. 2017, 6, 311–319. [Google Scholar] [CrossRef][Green Version]
- Mushi, A.T. Proposal of Nonlinear Deadbeat Control for Boost Converter and the Experimental Verification. Ph.D. Thesis, Yokohama National University, Yokohama, Japan, 2017. Available online: https://ci.nii.ac.jp/naid/500001044068 (accessed on 6 June 2021).
- Kewat, S.; Singh, B.; Hussain, I. Power management in PV-battery-hydro based standalone microgrid. IET Renew. Power Gener. 2018, 12, 391–398. [Google Scholar] [CrossRef]
- Masenge, I.H.; Mwasilu, F. Modeling and control of solar PV with battery energy storage for rural electrification. Tanzan. J. Eng. Technol. 2020, 39, 47–58. [Google Scholar] [CrossRef]
- Mushi, A.; Nozaki, T.; Kawamura, A. Proposal for faster disturbance rejection of boost DC-DC converter based on simplified current minor loop. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015. [Google Scholar] [CrossRef]
- Juma, M.; Msigwa, C.; Mwinyiwiwa, B.M.M. Solar PV based maximum power point tracking embedded DC voltage regulation incorporating battery. Lond. J. Eng. Res. Lond. J. Press 2019, 19, 31–37. [Google Scholar]
- Rajasekaran, R.; Usha Rani, P. Bidirectional DC-DC converter for microgrid in energy management system. Int. J. Electron. 2021, 108, 322–343. [Google Scholar] [CrossRef]
- de Aguiar, C.R.; Fuzato, G.H.F.; Machado, R.Q.; Guerrero, J.M. An adaptive power sharing control for management of DC microgrids powered by fuel cell and storage system. IEEE Trans. Ind. Electron. 2020, 67, 3726–3735. [Google Scholar] [CrossRef]
- Magdi, S.; Mahmoud, N.M.; Alyazidi, M.I. Adaptive intelligent techniques for microgrid control systems: A survey. Int. J. Electr. Power Energy Syst. 2017, 90, 292–305. [Google Scholar] [CrossRef]
- Muhammad, H.R. Power Electronics Circuit, Devices and Applications; Prentice-Hall, Inc.: London, UK, 1988. [Google Scholar]
- Rahimi, M. Modeling, control and stability analysis of grid-connected PMSG based wind turbine assisted with diode rectifier and boost converter. Int. J. Electr. Power Energy Syst. 2017, 93, 84–96. [Google Scholar] [CrossRef]
- Gilbert, M. Renewable and Efficient Electric Power Systems; John Wiley & Sons, Inc.: London, UK, 2004. [Google Scholar]










| Gain | Values |
|---|---|
| 0.5 | |
| 0.6 | |
| 0.5 | |
| 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juma, M.I.; Mwinyiwiwa, B.M.M.; Msigwa, C.J.; Mushi, A.T. Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application. Energies 2021, 14, 5994. https://doi.org/10.3390/en14185994
Juma MI, Mwinyiwiwa BMM, Msigwa CJ, Mushi AT. Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application. Energies. 2021; 14(18):5994. https://doi.org/10.3390/en14185994
Chicago/Turabian StyleJuma, Mwaka I., Bakari M. M. Mwinyiwiwa, Consalva J. Msigwa, and Aviti T. Mushi. 2021. "Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application" Energies 14, no. 18: 5994. https://doi.org/10.3390/en14185994
APA StyleJuma, M. I., Mwinyiwiwa, B. M. M., Msigwa, C. J., & Mushi, A. T. (2021). Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application. Energies, 14(18), 5994. https://doi.org/10.3390/en14185994





