Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter?
Abstract
:1. Introduction
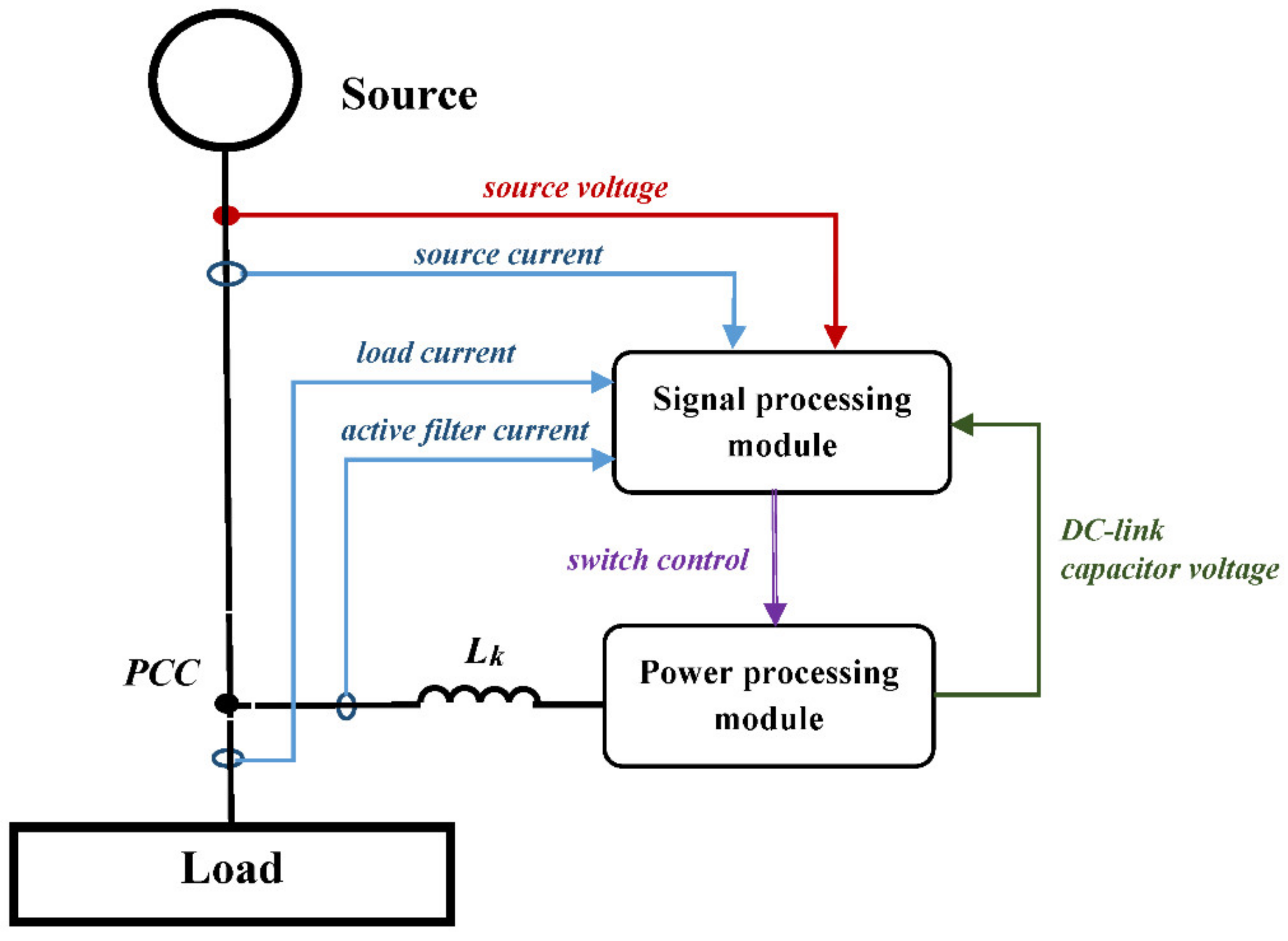
1.1. Measurement and Control Module (Signal Processing Module)
1.2. Active Filter with Reduced Number of Sensors
1.3. Indirect Current Control Technique
2. Active Filter Control with the Use of Equivalent Conductance Signal
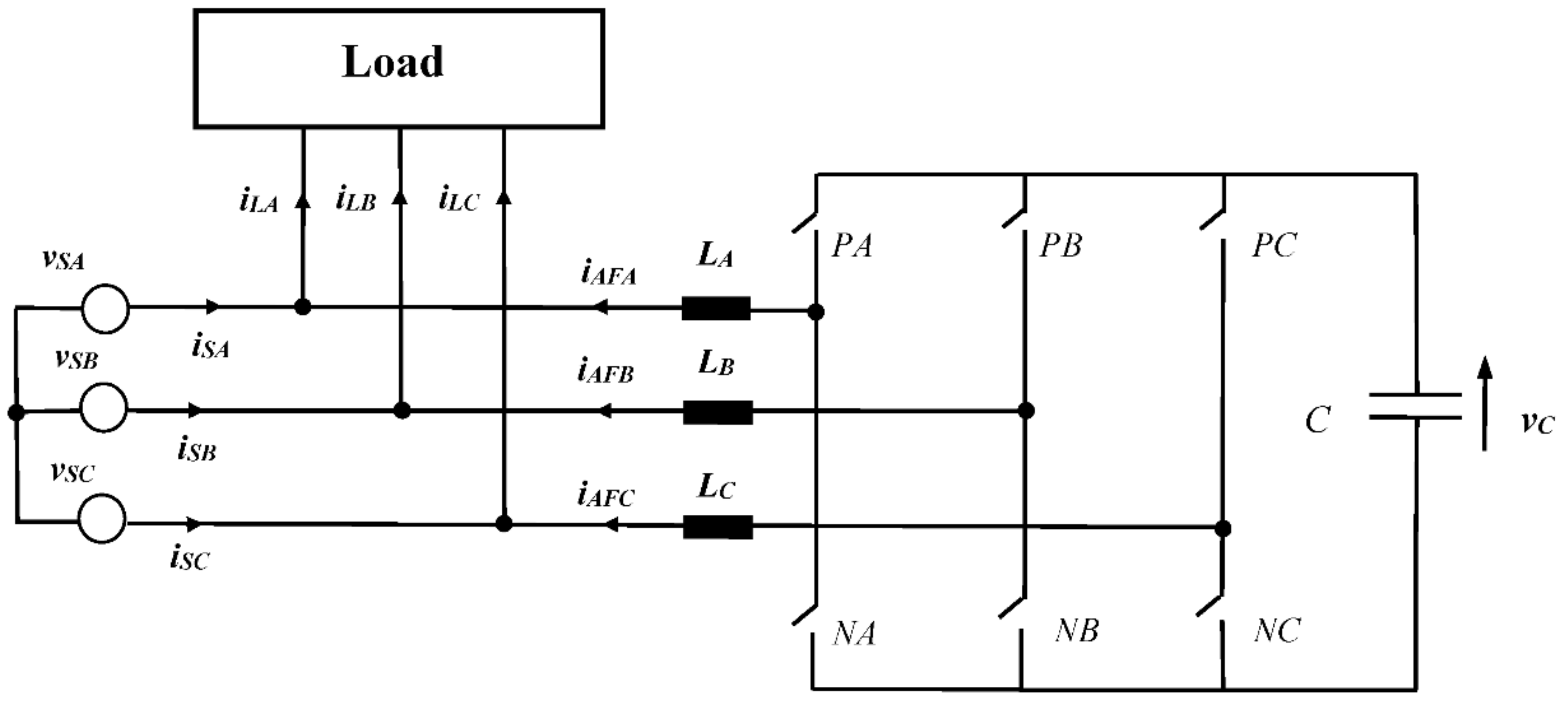
2.1. Basic Configuration of Shunt Active Filter
2.2. Load Equivalent Conductance Signal—Direct Control Technique Approach
3. Inertial Indirect Method of Current Reference Determination
3.1. Overall Form of the Equivalent Conductance Signal
- (1)
- Each change in magnitude of the load active power PL, and/or in energy loss PAF in the active filter circuitry, is transformed into the adequate change of magnitude of the conductance signal.
- (2)
- After each change of the load active power, and/or change of energy loss in the active filter circuitry, the conductance signal aims the steady state exponentially with a user-defined time Tst.
3.2. Energy Circulation in the Source-Active Filter-Load Circuitry
3.2.1. Buffering of Load Active Power Changes
3.2.2. Managing of In-Load Generated Power
3.3. Equivalent Conductance Signal for the Voltage-Source Inverter Based Active Filter
4. Current References Based on Continuous or Step Conductance Signal
4.1. Continuous Conductance Signal
4.2. Step Conductance Signal
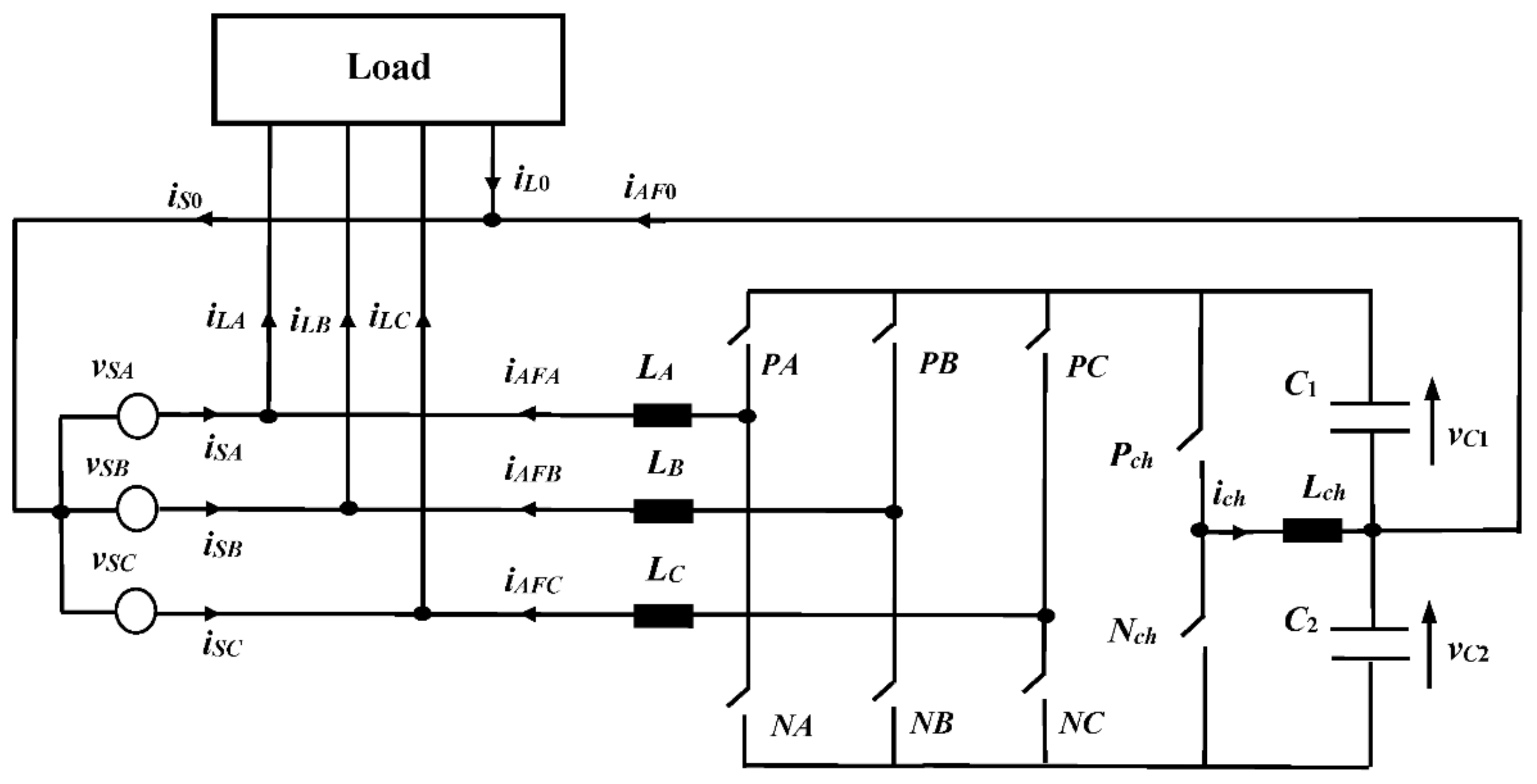
4.3. Conductance Signal for Three-Phase Four-Wire Active Filter
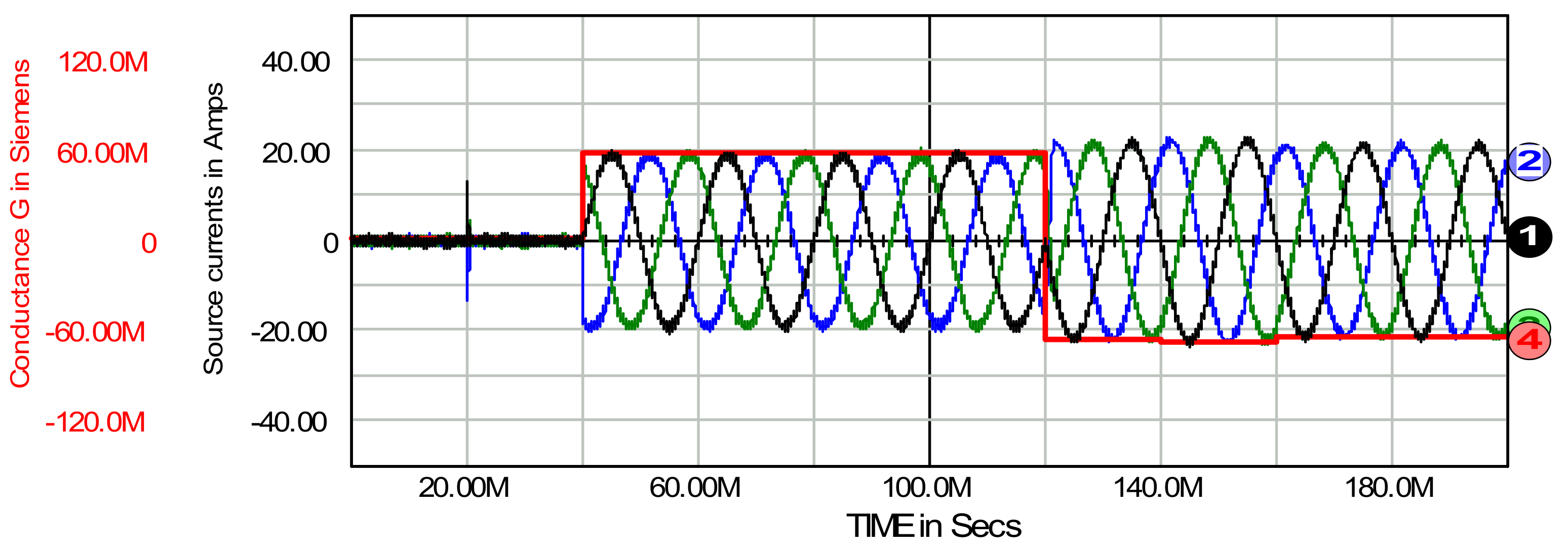
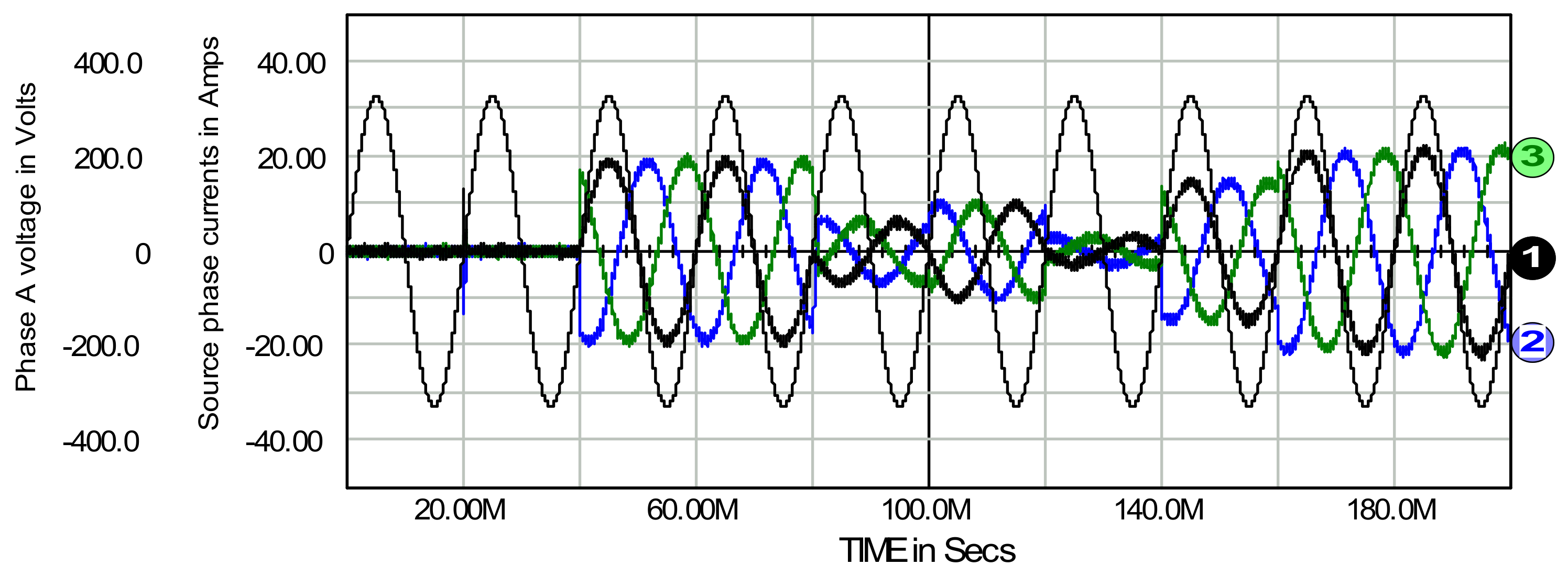
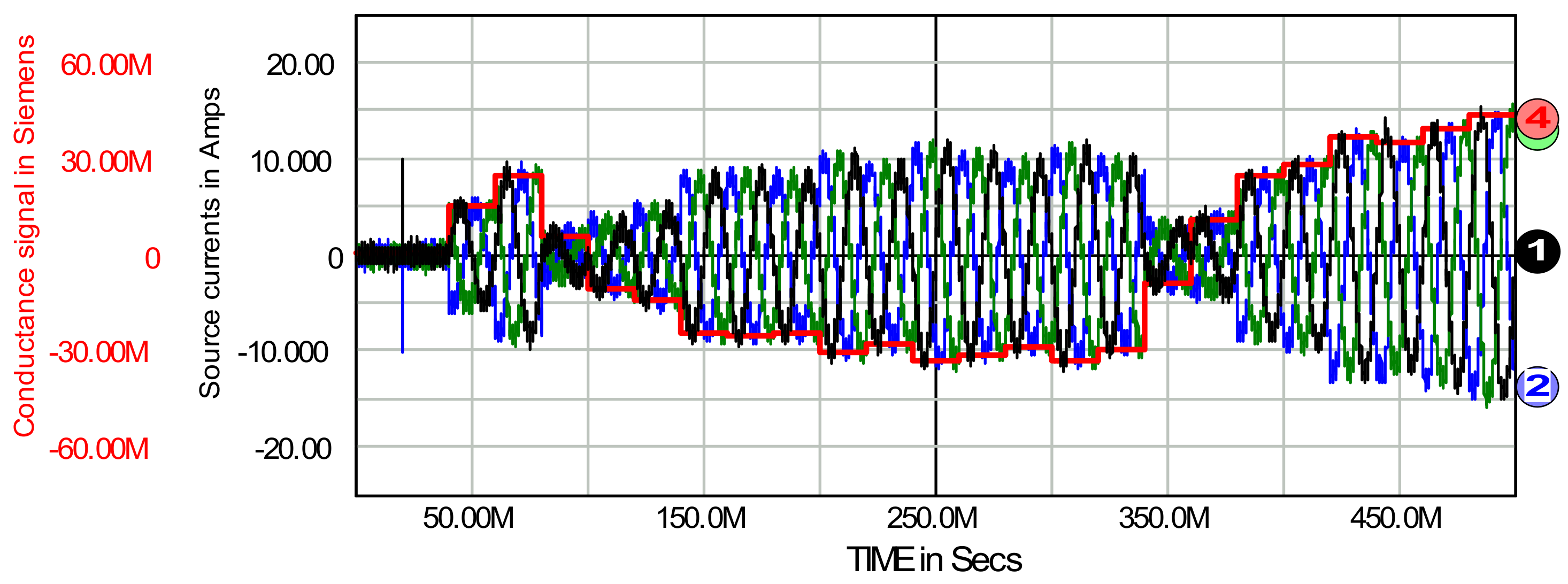
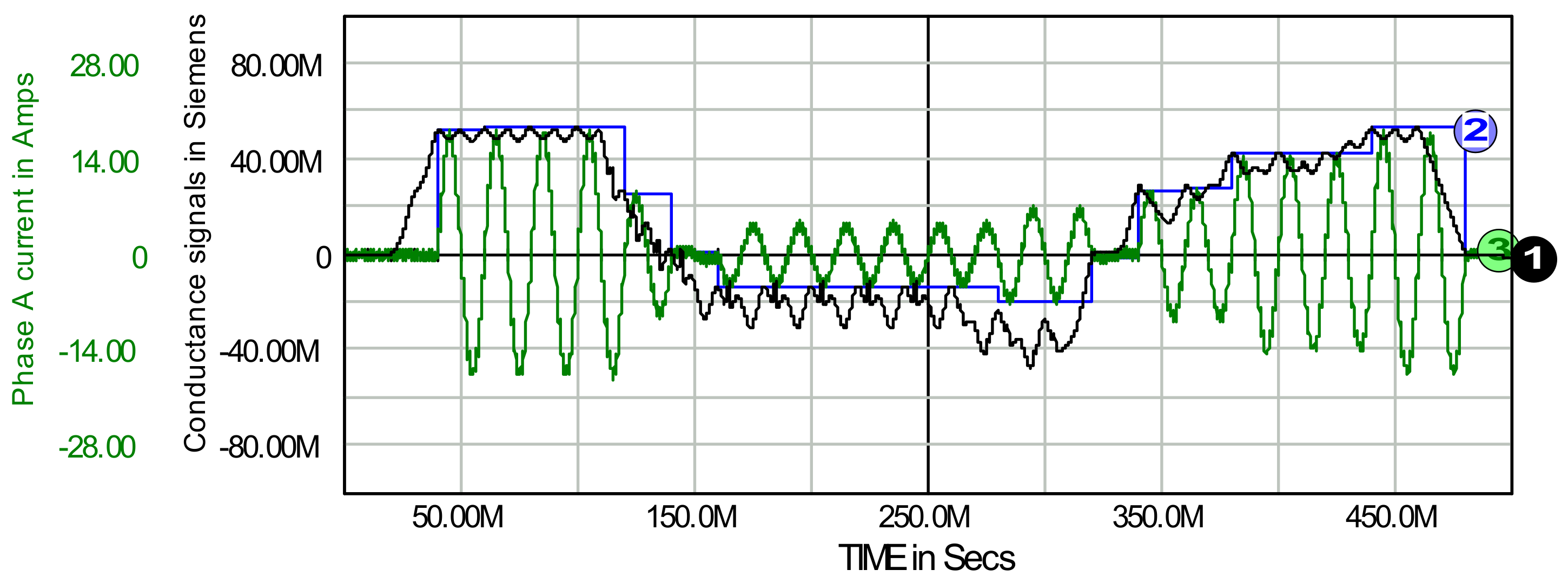
5. Verification of the Conductance Signal Control Method
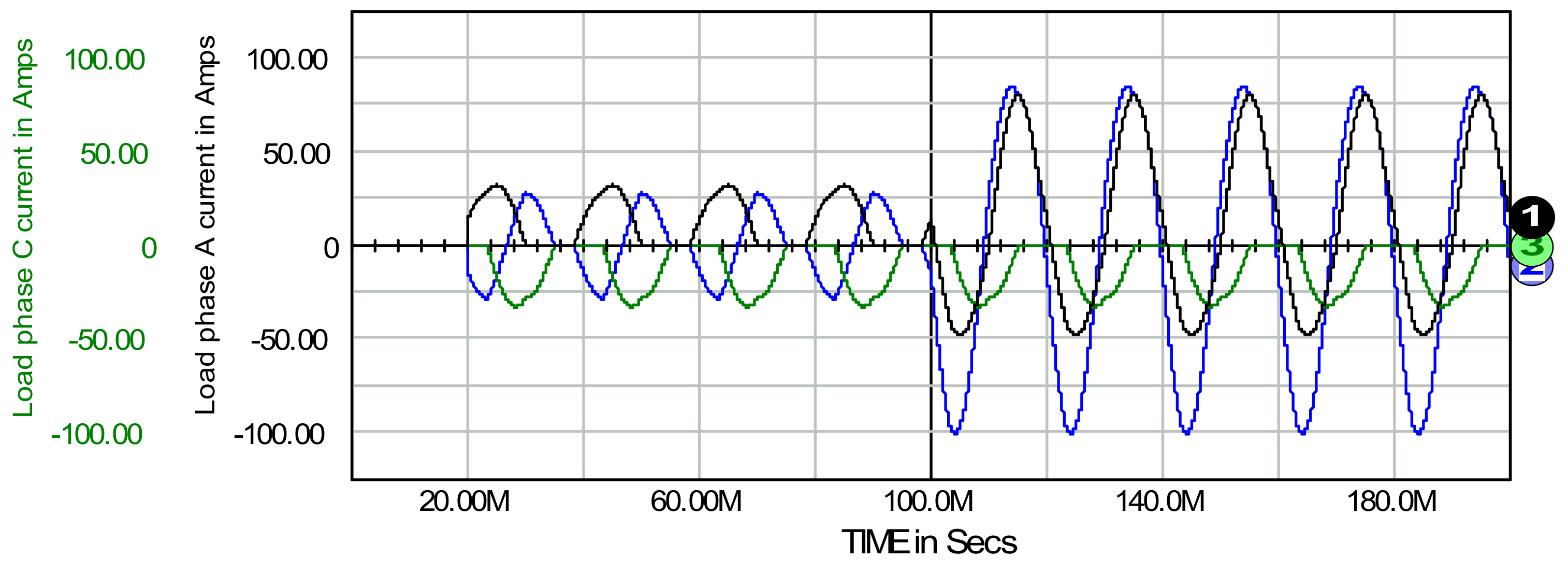
5.1. Basic Properties of the Filter Control Using the Conductance Signal
- Time period 20 ms–100 ms:
- phase A: 12.2 A mean, 17.6 A rms and 29% THD
- phase B: 0.0 A mean, 17.3 A rms and 37% THD
- phase C: −12.3 A mean, 17.7 A rms and 29% THD
- Time period 100 ms–200 ms:
- phase A: 12.2 A mean, 46.5 A rms and 29% THD
- phase B: 0.0 A mean, 66.5 A rms and 37% THD
- phase C: −12.2 A mean, 17.6 A rms and 29% THD
- Time period 40 ms–120 ms:
- phase A: −0.06 A mean, 13.4 A rms and 1.4% THD
- phase B: −0.03 A mean, 13.5 A rms and 1.9% THD
- phase C: 0.09 A mean, 13.5 A rms and 1.9% THD
- Time period 120 ms–200 ms:
- phase A: −0.02 A mean, 14.9 A rms and 1.4% THD
- phase B: 0.02 A mean, 14.9 A rms and 1.5% THD
- phase C: −0.02 A mean, 14.8 A rms and 1.2% THD
- source phase currents are practically sinusoidal waveforms of fundamental frequency,
- they are in phase with waveforms of respective phase voltages, and
- they are symmetrical.
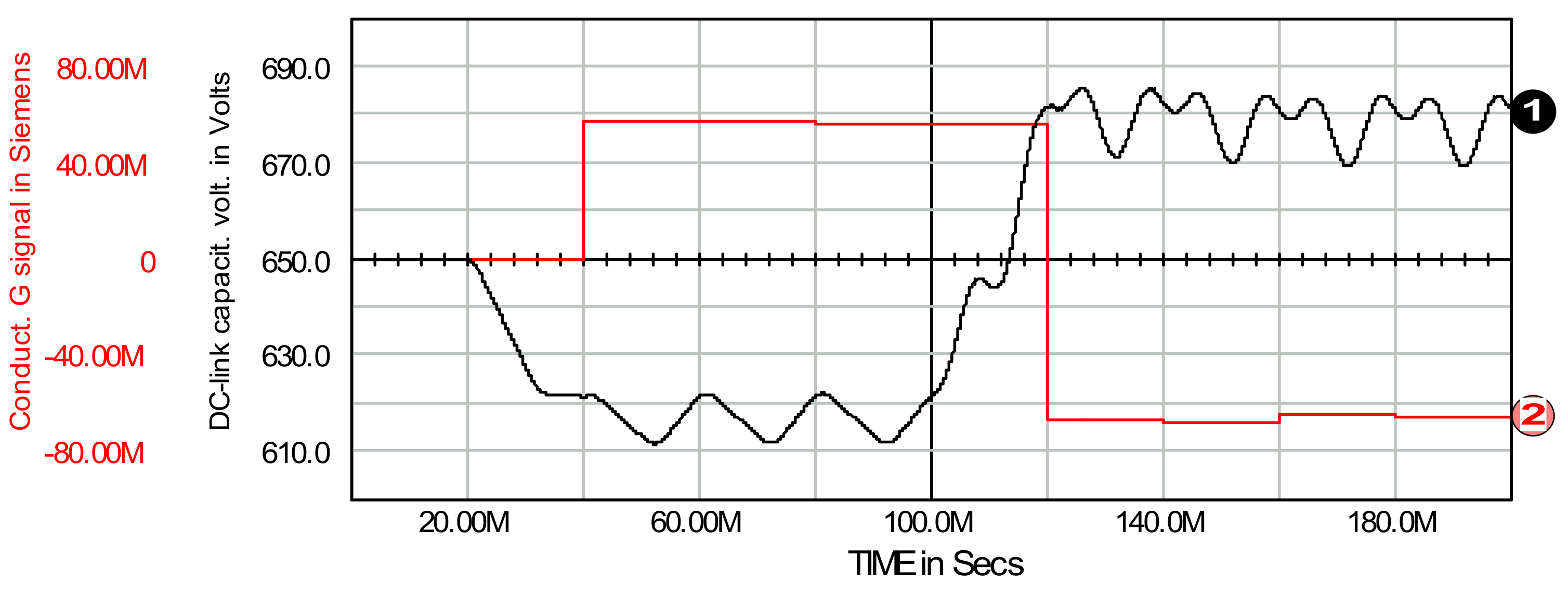
- Time period 40 ms–100 ms: G: mean 56.97 ms, st. dev. 0.22 ms; DC-link volt.: mean 617.0 V, pk-pk: 10.3 V
- Time period 120 ms–200 ms: G: mean −66.12 ms, st. dev. 1.37 ms; DC-link volt.: mean 679.8 V, pk-pk: 14.8 V
- energy changes in load active power are buffered by active filter;
- as assumed, the steady state is reached in one period T of supply source cycle after each change of load active power;
- in the steady state the conductance signal is practically constant and its mean indicates the actual magnitude of sum of load and active filter active powers: 9.1 kW (positive, consumed) and, simultaneously, −10.5 kW (negative, generated) for time periods 40 ms–100 ms and then 120 ms–200 ms, respectively;
- energy flow is bidirectional and is in clear relation to the DC-link capacitor voltage (with respect to its initial voltage VDCini, comp. (19) and (22));
- there is an excess of the active power generated in the generative part of the load in relation to the consumed active power in the load-and-active filter circuitry. The difference of both powers is transmitted to the supply source with unity power factor—in a balanced manner.
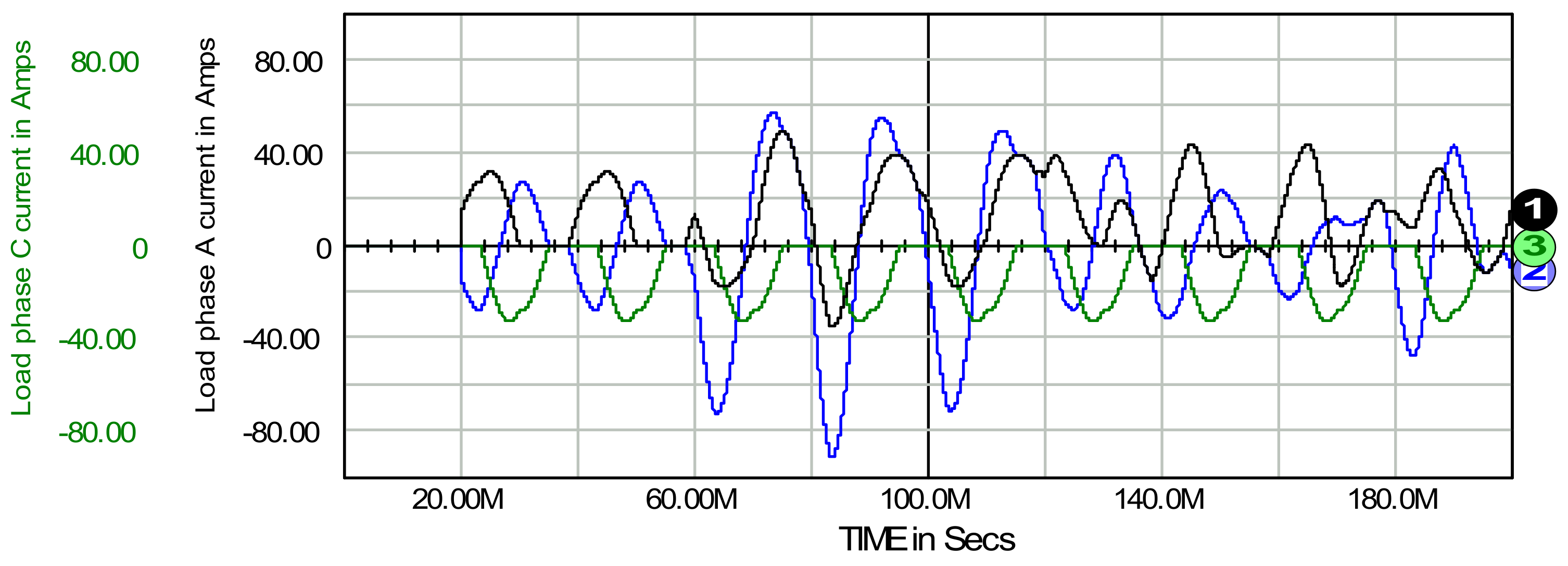
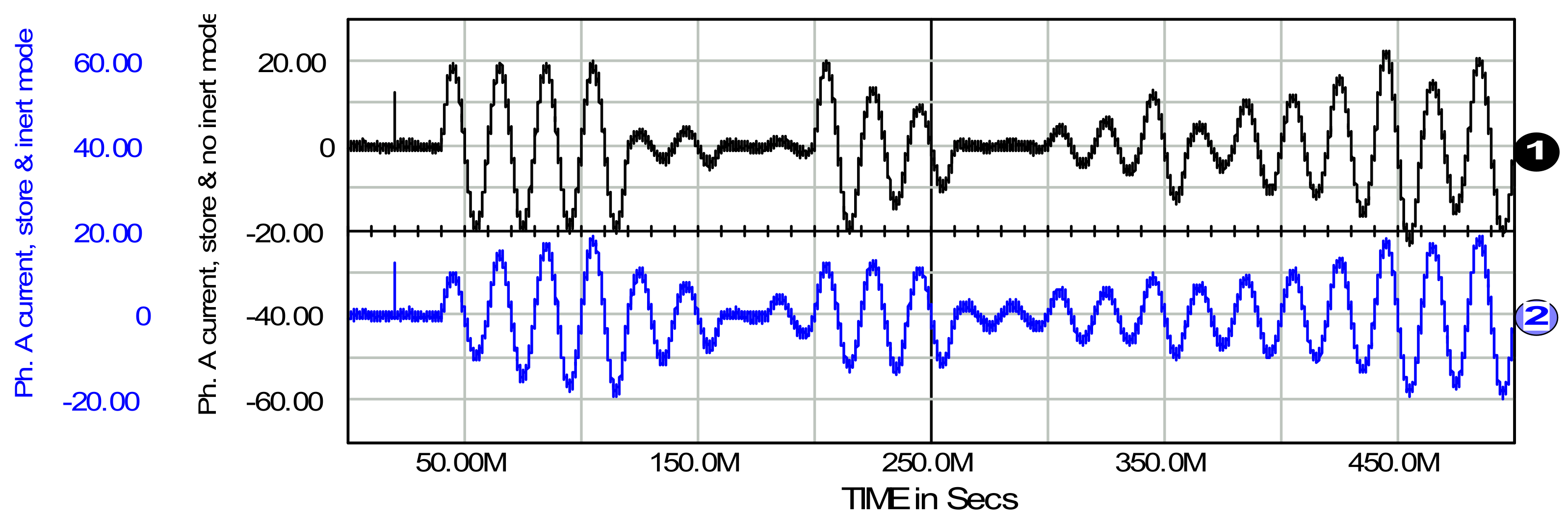
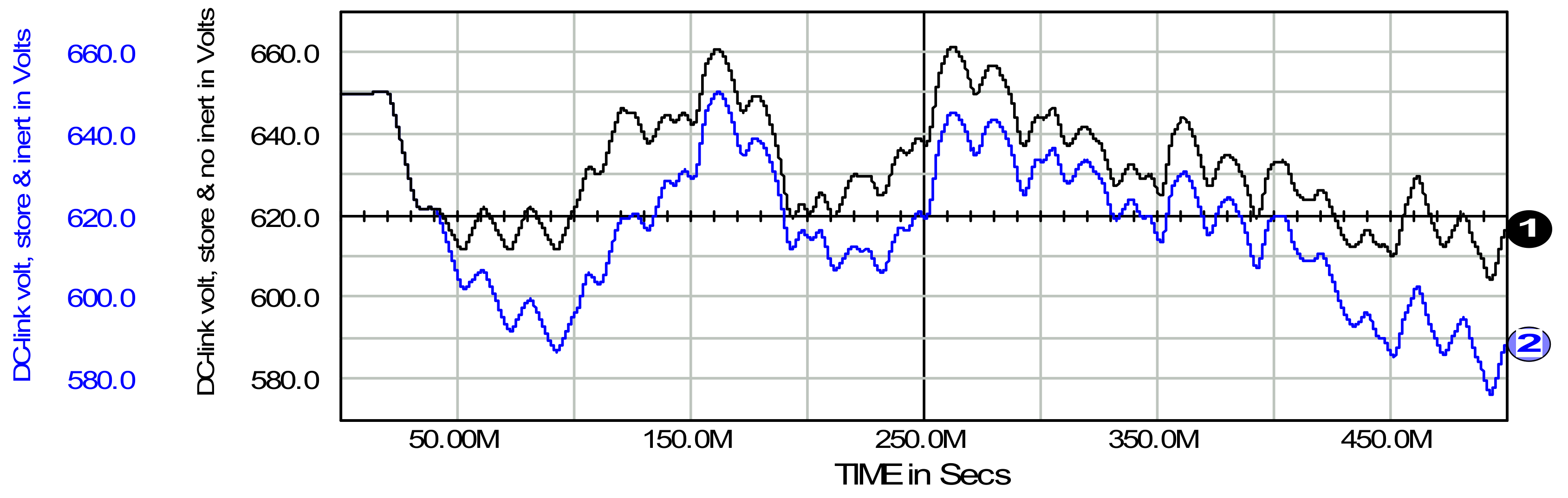
6. Transmit, Store, and Inertial Mode of Active Filter Operation
6.1. Transmit Mode of Active Filter Operation
- 13.5 A in time period 40 ms–80 ms (energy consumption),
- 4.5 A in 80 ms–100 ms (energy generation),
- 7.0 A (generation) in 100 ms–120 ms,
- 2.1 A (generation) in 120 ms–140 ms,
- 10.4 A (consumption) in 140 ms–160 ms,
- 15.1 A (consumption) in 160 ms–200 ms
- 23.4 A in 40 ms–80 ms,
- 7.8 A in 80 ms–100 ms,
- 12.1 A in 100 ms–120 ms,
- 3.6 A in 120 ms–140 ms,
- 18.0 A in 140 ms–160 ms,
- 26.2 A in 160 ms–200 ms
6.2. Store Mode of Active Filter Operation
- 13.5 A in 40 ms–80 ms,
- 11.2 A in 160 ms–180 ms,
- 15.5 A in 180 ms–200 ms
- 23.3 A in 40 ms–80 ms,
- 19.6 A in 160 ms–180 ms,
- 26.5 A in 180 ms–200 ms
6.3. Inertial Mode of Active Filter Operation
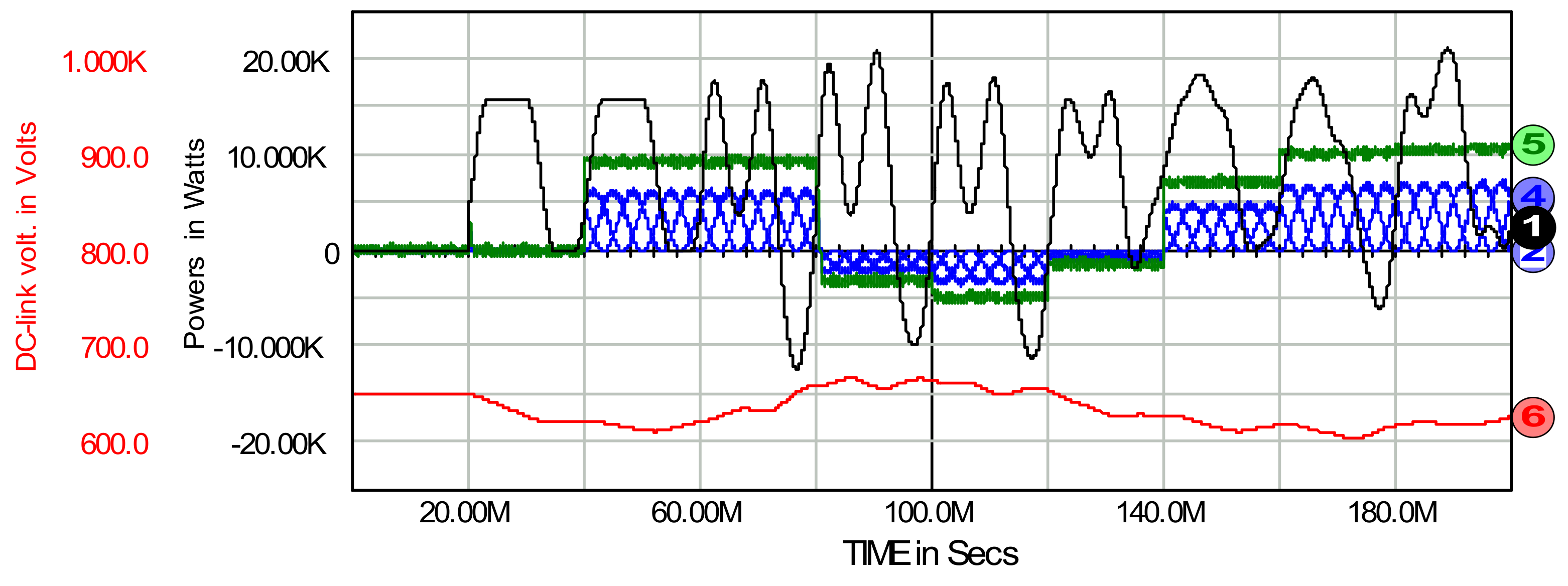
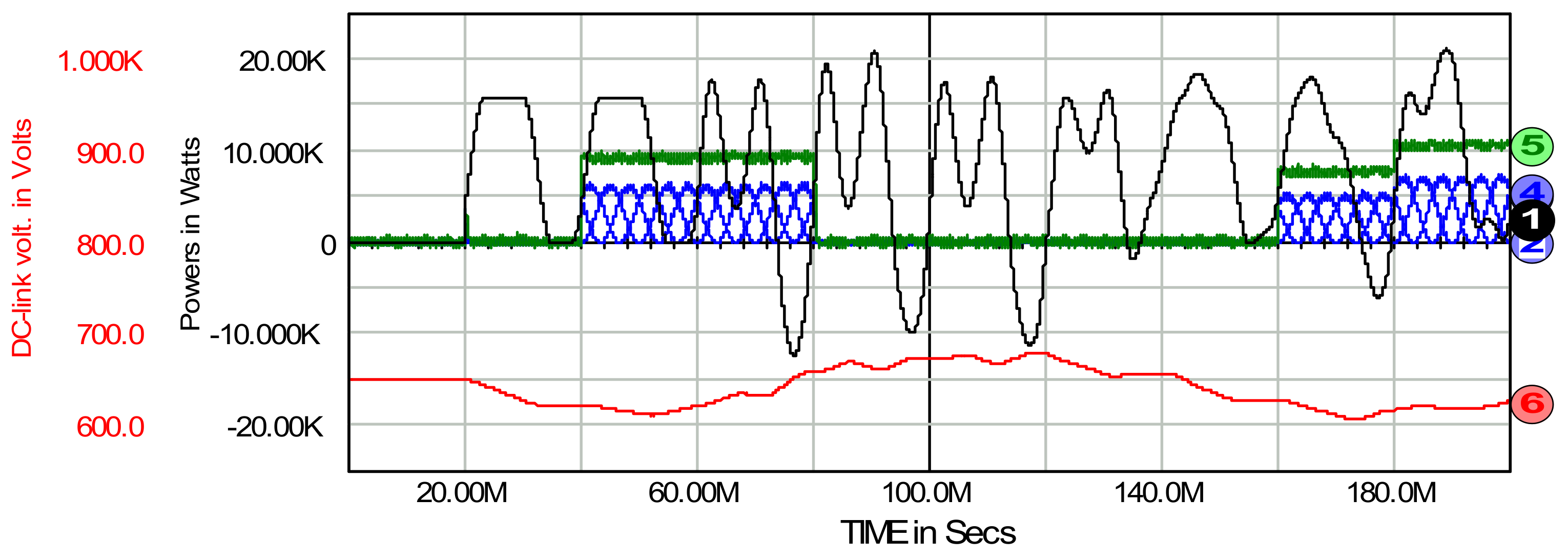
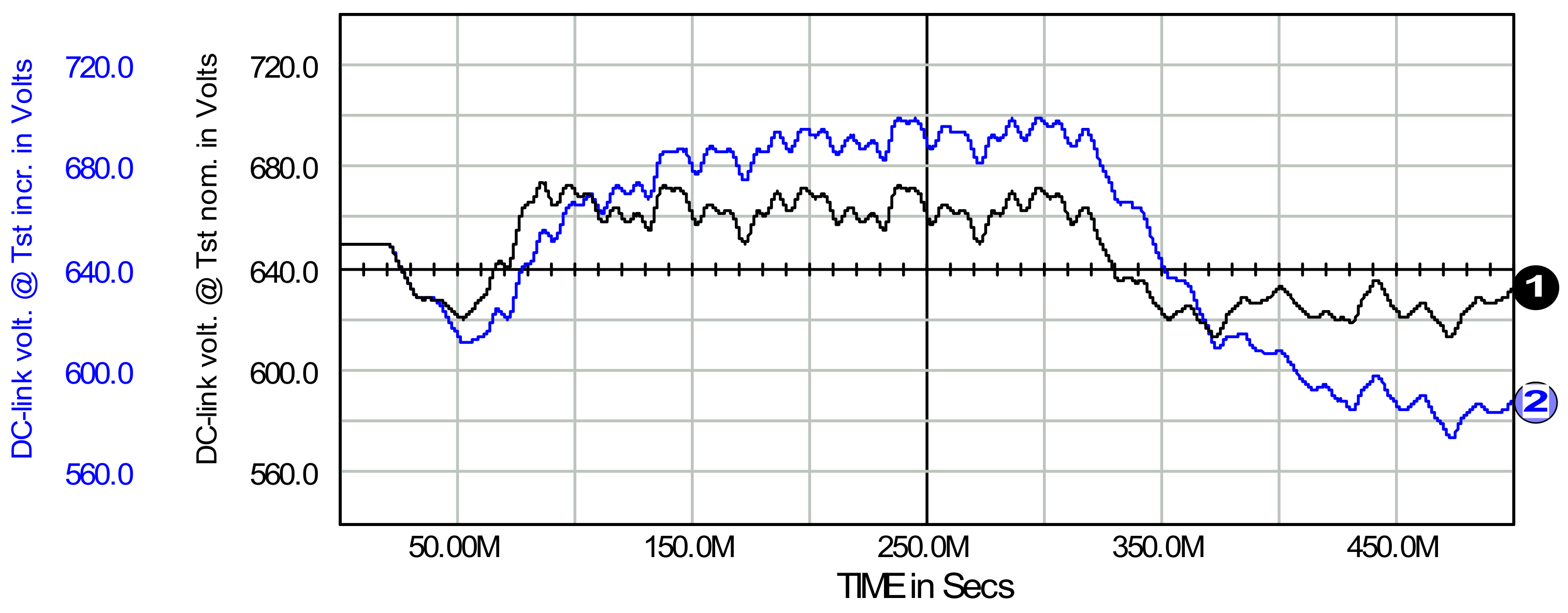
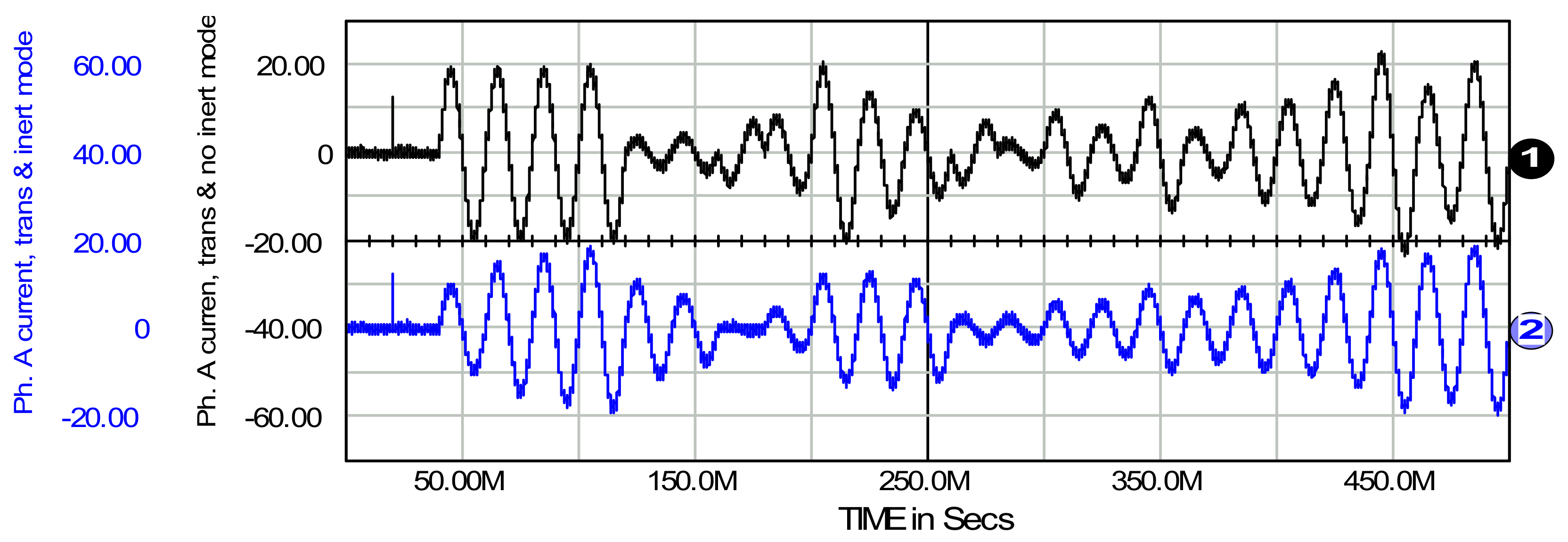
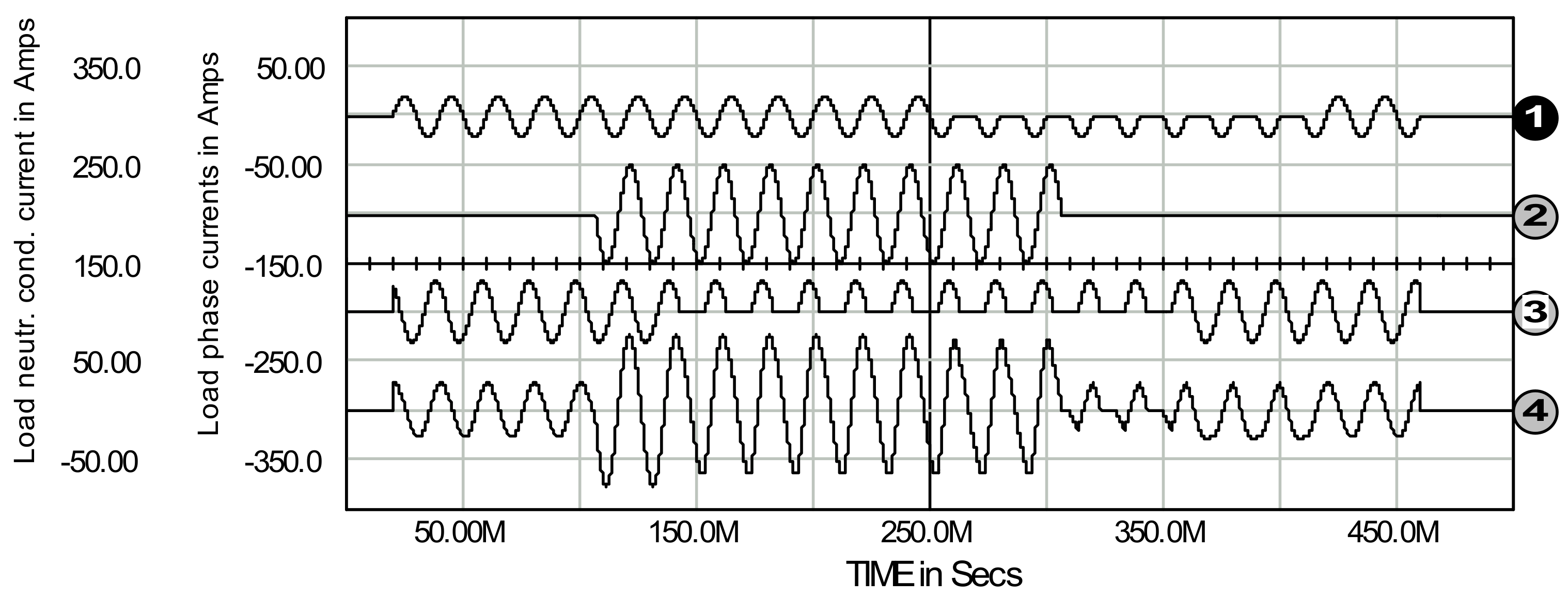
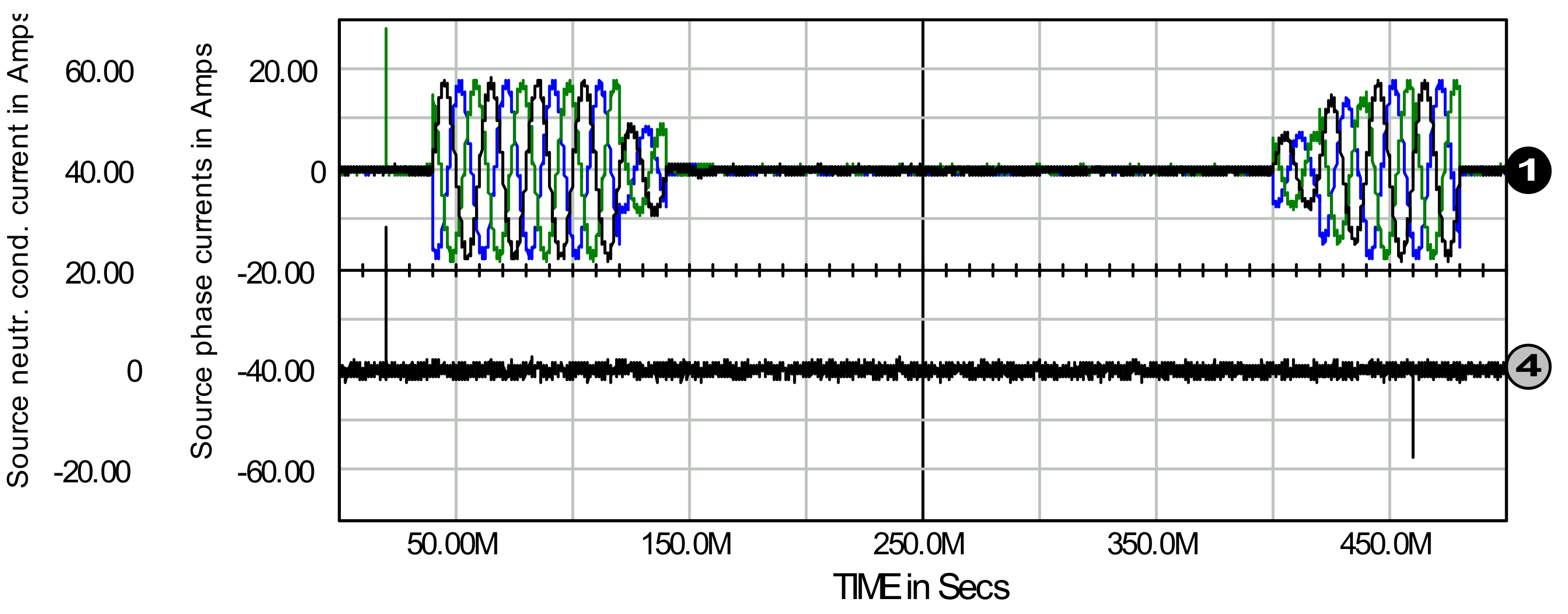
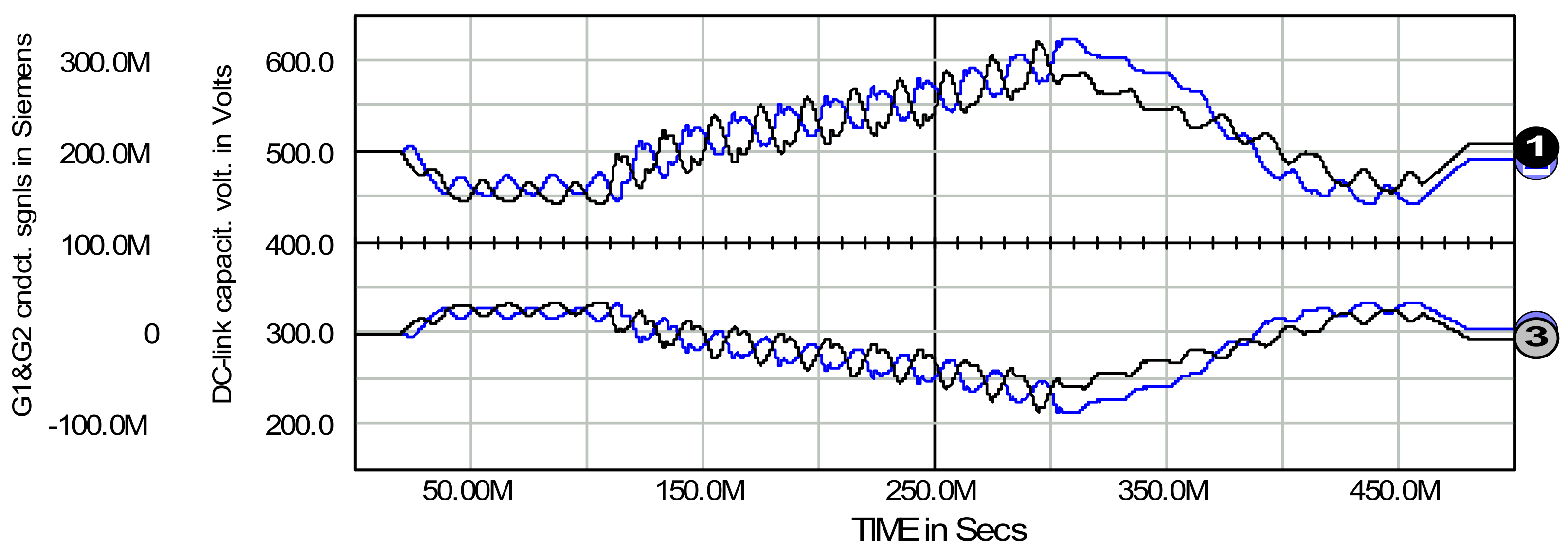
7. Passive and Generative Load on the AC and DC Side of the System
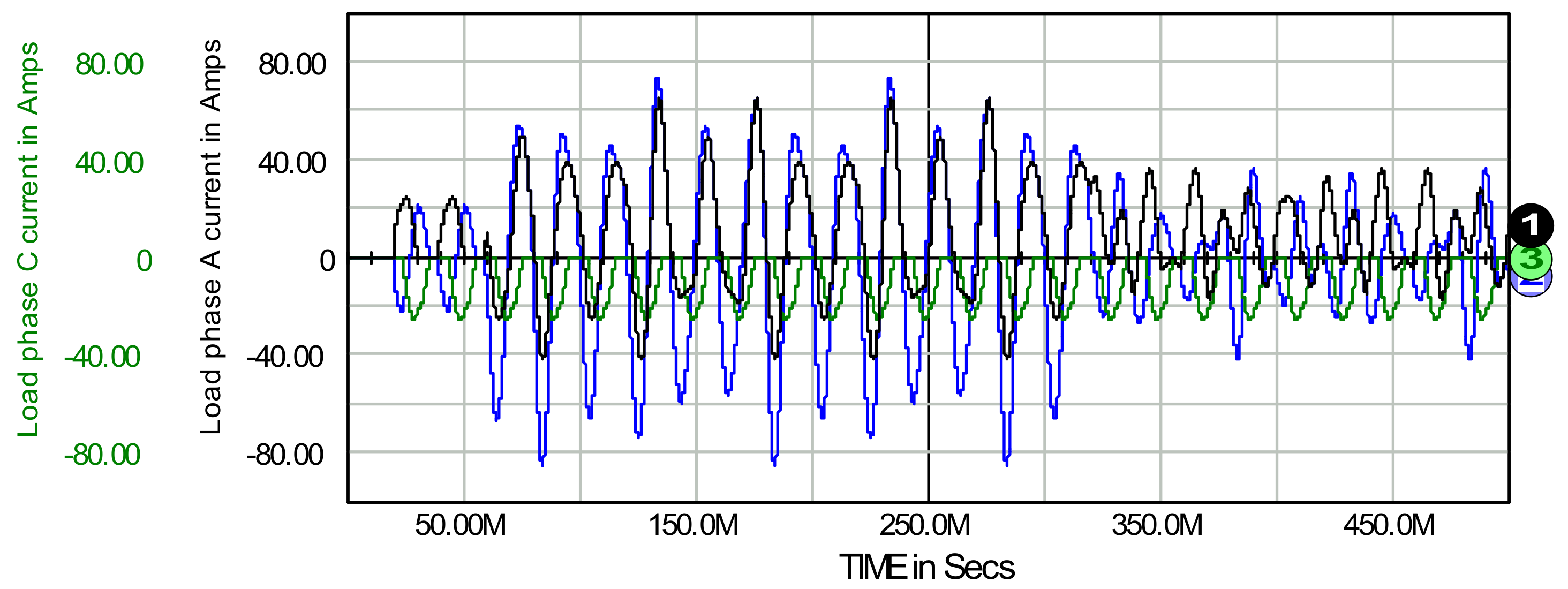
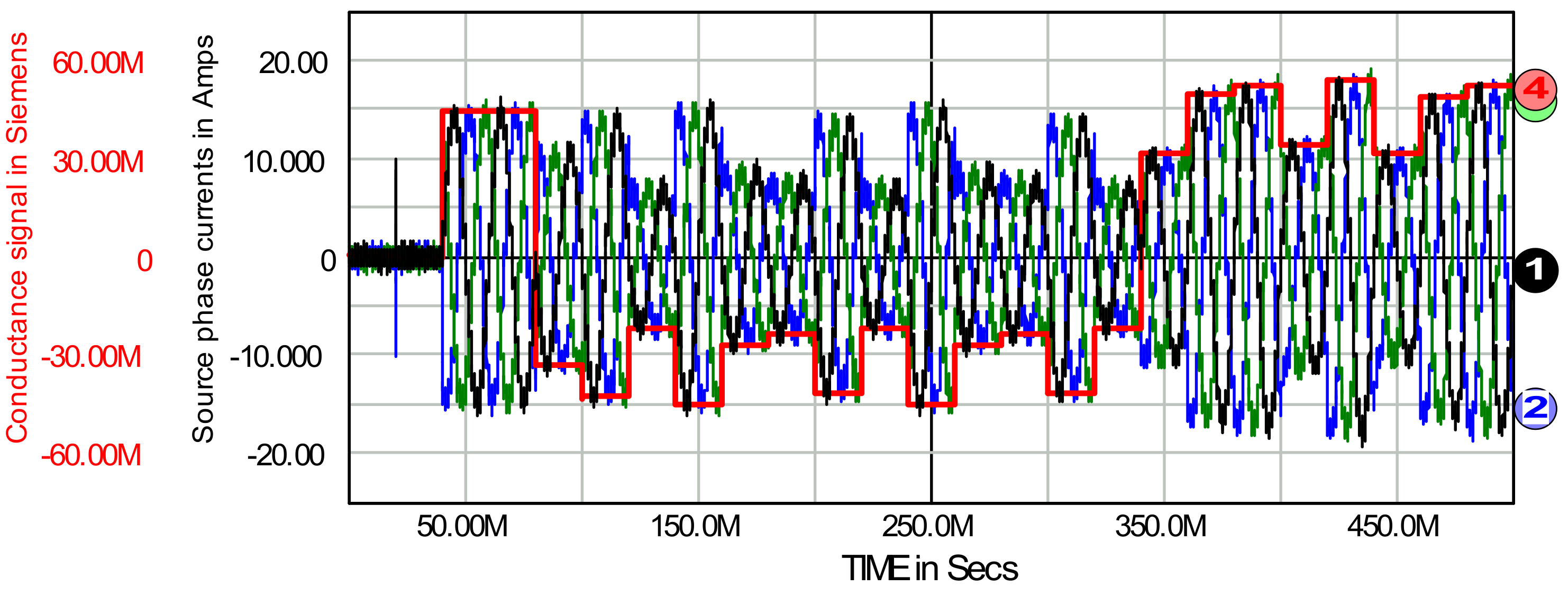
8. Three-Phase Four Wire Active Filter
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Green, T.C.; Marks, J.H. Control techniques for active power filters. IEEE Proc. Power Appl. 2005, 152, 369–381. [Google Scholar] [CrossRef] [Green Version]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Detection is key. Harmonic detection methods for active power filter applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chakraborty, C.; Bhattacharya, S. Shunt compensation. Reviewing traditional methods of reference current generation. IEEE Ind. Electron. Mag. 2009, 3, 38–49. [Google Scholar] [CrossRef]
- Khadkikar, V. Enhancing electric power quality using UPQC: A comprehensive overview. IEEE Trans. Power Electron. 2012, 27, 2284–2297. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Control algorithms for shunt active power filter for harmonics mitigation: A review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef] [Green Version]
- Briz, F.; Garcia, P.; Degner, M.W.; Diaz-Reigosa, D.; Guerrero, M. Dynamic behavior of current controllers for selective harmonic compensation in three-phase active power filters. IEEE Trans. Ind. Appl. 2013, 49, 1411–1420. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Li, N.R.; Cheng, Z.; Ni, R.; Zhang, Y. Selective harmonic compensation (SHC) PWM for grid interfacing high-power converters. IEEE Trans. Power Electron. 2014, 29, 1118–1127. [Google Scholar] [CrossRef]
- Singh, B.; Verma, V. Selective compensation of power-quality problems through active power filter by current decomposition. IEEE Trans. Power Del. 2008, 23, 792–799. [Google Scholar] [CrossRef]
- Orts-Grau, S.; Gimeno-Sales, F.J.; Segui-Chilet, S.; Abellen-Garcia, A.; Alcaniz-Fillol, M.; Masot-Periz, R. Selective compensation in four-wire electric systems based on a new equivalent conductance approach. IEEE Trans. Ind. Electron. 2009, 56, 2862–2874. [Google Scholar] [CrossRef]
- Alfonso-Gil, J.C.; Perez, E.; Arino, C.; Beltran, H. Optimization algorithm for selective compensation in shant active power filter. IEEE Trans. Ind. Electron. 2015, 62, 3351–3361. [Google Scholar]
- Bhowmik, S.; van Zyl, A.; Spee, R.; Enslin, J. Sensorless current control for active rectifiers. IEEE Trans. Ind. Appl. 1997, 33, 765–773. [Google Scholar] [CrossRef]
- Nedeljkovic, D.; Nemec, M.; Drobnic, K.; Ambrozic, V. Active power filter with a reduced number of current sensors. Electrotech. Rev. 2009, 76, 275–280. [Google Scholar]
- Angulo, M.; Ruiz-Caballero, D.A.; Lago, J.; Heldwein, M.L.; Mussa, S.A. Active power filter control strategy with implicit closed-loop current control and resonant controller. IEEE Ind. Electron. 2013, 60, 2721–2730. [Google Scholar] [CrossRef]
- Ketzer, M.B.; Jacobina, C.B. Sensorless control technique for PWM rectifiers with voltage disturbance rejection and adaptive power factor. IEEE Trans. Ind. Electron. 2015, 62, 1140–1151. [Google Scholar] [CrossRef]
- Ketzer, M.B.; Jacobina, C.B.; Lima, A.M.N. Shaping control strategies for active power filters. IET Power Electron. 2018, 11, 175–181. [Google Scholar] [CrossRef]
- Sharma, S.; Verma, V.; Behera, R. Real-time implementation of shunt active power filter with reduced sensors. IEEE Trans. Ind. Appl. 2020, 56, 1850–1861. [Google Scholar] [CrossRef]
- Fukuda, S.; Kanayama, T.; Muraoka, K. A current control method for active filters without detecting current harmonics. In Proceedings of the Fifth International Conference on Power Electronics and Drive Systems, 2003, PEDS 2003, Singapore, 17–20 November 2003; Volume 1, pp. 519–524. [Google Scholar]
- Ozdemir, E.; Ucar, M.; Kesler, M.; Kale, M. A simplified control algorithm for shunt active power filter without load and filter current measurement. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 2599–2604. [Google Scholar]
- Nedeljkovic, D.; Nemec, M.; Drobnic, K.; Ambrozic, V. Direct current control of active power filter without filter current measurement. In Proceedings of the 2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 11–13 June 2008; pp. 72–76. [Google Scholar]
- Ketzer, M.B.; Jacobina, C.B. Multivariable load current sensorless controller for universal active power filter. IET Power Electron. 2014, 7, 1777–1786. [Google Scholar] [CrossRef]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Ketzer, M.B.; Jacobina, C.B. Virtual flux sensorless control for shunt active power filters with quasi-resonant compensators. IEEE Trans. Power Electron. 2016, 31, 4818–4830. [Google Scholar] [CrossRef]
- Wojciechowski, D. Grid voltages sensorless control system of the PWM rectifier with active filtering function. In Proceedings of the IEEE Compatibility in Power Electronics, Gdynia, Poland, 6 January 2005; pp. 238–246. [Google Scholar]
- Choi, W.-H.; Lam, C.-S.; Wong, M.-C.; Han, Y.-D. Analysis of dc-link voltage controls in three-phase four-wire hybrid active power filters. IEEE Trans. Power Electron. 2013, 28, 2180–2191. [Google Scholar] [CrossRef]
- Lam, C.-S.; Choi, W.-H.; Wong, M.-C.; Han, Y.-D. Adaptive dc-link voltage controlled hybrid active power filters for reactive power compensation. IEEE Trans. Power Electron. 2012, 27, 1758–1772. [Google Scholar] [CrossRef]
- Tarkiainen, A.; Pollanen, R.; Niemela, M.; Pyrhonen, J. DC-link voltage effects on properties of a shunt active filter. In Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004. [Google Scholar]
- Longhui, W.; Fang, Z.; Pengbo, Z.; Hongyu, L.; Zhaoan, W. Study on the influence of supply-voltage fluctuation on shunt active power filter. IEEE Trans. Power Del. 2007, 22, 1743–1749. [Google Scholar] [CrossRef]
- Bitoleanu, A.; Popescu, M.; Dobriceanu, M.; Nastasoiu, F. DC-bus voltage optimum control of three-phase shunt active filtering system. In Proceedings of the 12th International Conference on Optimization of Electrical and Electronic Equipment, OPTIM 2010, Brasov, Romania, 20–22 May 2010. [Google Scholar]
- Sharma, S.; Verma, V. Modified control strategy for shunt active power filter with MRAS-based DC voltage estimation and load current sensor reduction. IEEE Trans. Ind. Appl. 2021, 57, 1652–1663. [Google Scholar] [CrossRef]
- Moreno, V.; Pigazo, A. Modified FBD method in active power filters to minimize the line current harmonics. IEEE Trans. Power Del. 2006, 22, 735–736. [Google Scholar] [CrossRef]
- Strzelecki, R.; Benysek, G.; Jarnut, M. Power quality conditioners with minimum number of current sensor requirement. Przegląd Elektrotechniczny (Electrotech. Rev.) 2008, 84, 295–298. [Google Scholar]
- Szromba, A.; Mysinski, W. Voltage-source-based conductance-signal controlled shunt active power filter. In Proceedings of the 2017 European Conference on Power Electronics and Applications, Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- Szromba, A. The Unified Power Quality Conditioner Control Method Based on the Equivalent Conductance Signals of the Compensated Load. Energies 2020, 13, 6298. [Google Scholar] [CrossRef]
- Fallah, M.; Modarresi, J.; Kojabadi, H.M.; Chang, L.; Guerrero, J.M. A modified indirect extraction method for a single-phase shunt active power filter with smaller DC-link capacitor size. Sustain. Energy Technol. Assess. 2021, 45, 101039. [Google Scholar]
- Dixon, J.W.; Ooi, B.T. Indirect current control of a unity power factor sinusoidal current boost type three-phase rectifier. IEEE Trans. Ind. Electr. 1988, 35, 508–515. [Google Scholar] [CrossRef]
- Nunez-Zuninga, T.; Pomilio, J. Shunt active power filter synthesizing resistive loads. IEEE Trans. Power Electron. 2002, 17, 273–278. [Google Scholar] [CrossRef]
- Hamadi, A.; Al-Haddad, K.; Lagace, P.; Chandra, A. Indirect current control techniques of three phase APF using fuzzy logic and proportional integral controller: Comparative analysis. In Proceedings of the 11th International Conference on Harmonics and Quality of Power, Lake Placid, NY, USA, 12–15 September 2004. [Google Scholar]
- Fei, J.; Li, T.; Zhang, S. Indirect current control of active power filter using novel sliding mode controller. In Proceedings of the IEEE 13th Workshop on Control and Modelling for Power Electronics, Kyoto, Japan, 10–13 June 2012. [Google Scholar]
- Ribeiro, R.; Azevedo, C.; Sousa, R. A robust adaptive control strategy of active power filters for power-factor correction, harmonic compensation, and balancing of nonlinear loads. IEEE Trans. Power Electron. 2012, 27, 718–730. [Google Scholar] [CrossRef]
- Trinh, Q.; Lee, H. An advanced current control strategy for three-phase shunt active power filter. IEEE Trans. Ind. Electron. 2012, 60, 5400–5410. [Google Scholar] [CrossRef]
- Ribeiro, R.; Rocha, T.; Sousa, R.; dos Santos, E.; Lima, A. A robust DC-link voltage control strategy to enhance the performance of shunt active power filters without harmonic detection schemes. IEEE Trans. Ind. Electron. 2014, 62, 803–813. [Google Scholar] [CrossRef]
- Wu, T.-F.; Chang, C.-H.; Lin, L.-C.; Yu, G.-R.; Chang, Y.-R. DC-bus voltage control with a three-phase bidirectional inverter for DC distribution systems. IEEE Trans. Power Electron. 2013, 28, 1890–1899. [Google Scholar] [CrossRef]
- Szromba, A. Shunt power electronic buffer as active filter and energy flow controller. Arch. Electr. Eng. 2013, 62, 55–75. [Google Scholar] [CrossRef] [Green Version]
- Grabowski, D.; Maciążek, M.; Pasko, M. Sizing of active power filters using some optimization strategies. COMPEL 2013, 32, 1326–1336. [Google Scholar] [CrossRef] [Green Version]
- Depenbrock, M.; Staudt, V. The FBD-method as tool for compensating non-active currents. In Proceedings of the 8th International Conference on Harmonics and Quality of Power, Athens, Greece, 14–16 October 1998; pp. 320–324. [Google Scholar]
- Fryze, S. Wirk-, Blind-, und Scheinleistung in Elektrischen Stromkreisen mit nichtsinusformigem Verlauf von Strom und Spannung. Elektrotechnische Z. 1932, 25, 33. [Google Scholar]
- Singh, B.; Chandra, A.; Al-Haddad, K. Performance comparision of two current control techniques applied to an active filter. In Proceedings of the 8th International Conference on Harmonics and Quality of Power, Athens, Greece, 14–16 October 1998; pp. 133–138. [Google Scholar]
- Herrera, R.; Salmeron, P.; Kim, H. Instantaneous reactive power theory applied to active power filter compensation: Different approaches, assessment, and experiment result. IEEE Trans. Ind. Electron. 2008, 55, 185–196. [Google Scholar] [CrossRef]
- Mishra, M.; Joshi, A.; Ghosh, A. Control schemes for equalization of capacitor voltages in neutral clamped shunt compensator. IEEE Trans. Power Del. 2003, 18, 538–544. [Google Scholar] [CrossRef] [Green Version]
- Montero, M.; Cadaval, E.; Gonzalves, F. Comparision of control strategies for shunt active power filters in three-phase four-wire systems. IEEE Trans. Power Electron. 2007, 22, 229–236. [Google Scholar] [CrossRef]
- Sozański, K. Improved shunt active power filters. Przegląd Elektrotechniczny (Electrotech. Rev.) 2008, 11, 290–294. [Google Scholar]
- Sozański, K.; Strzelecki, R.; Kempski, A. Digital control circuit for active power filter with modified instantaneous reactive power control algorithm. In Proceedings of the Power Electronics Specialists Conference PESC, Cairns, Australia, 23–27 June 2002; pp. 1031–1036. [Google Scholar]
- Urrea-Quintero, J.-H.; Munoz-Galeano, N.; Lopez-Lezama, J.M. Robust control of shunt active power filter: A dynamical model-based approach with verified controllability. Energies 2020, 13, 6253. [Google Scholar] [CrossRef]
- Intusoft. Better Design Through Simulation. Available online: www.intusoft.com (accessed on 16 September 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szromba, A. Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter? Energies 2021, 14, 6031. https://doi.org/10.3390/en14196031
Szromba A. Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter? Energies. 2021; 14(19):6031. https://doi.org/10.3390/en14196031
Chicago/Turabian StyleSzromba, Andrzej. 2021. "Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter?" Energies 14, no. 19: 6031. https://doi.org/10.3390/en14196031
APA StyleSzromba, A. (2021). Is It Possible to Obtain Benefits by Reducing the Contribution of the Digital Signal Processing Techniques to the Control of the Active Power Filter? Energies, 14(19), 6031. https://doi.org/10.3390/en14196031




