Energy Curtailment Scheduling MILP Formulation for an Islanded Microgrid with High Penetration of Renewable Energy
Abstract
:1. Introduction
2. Problem Formulation
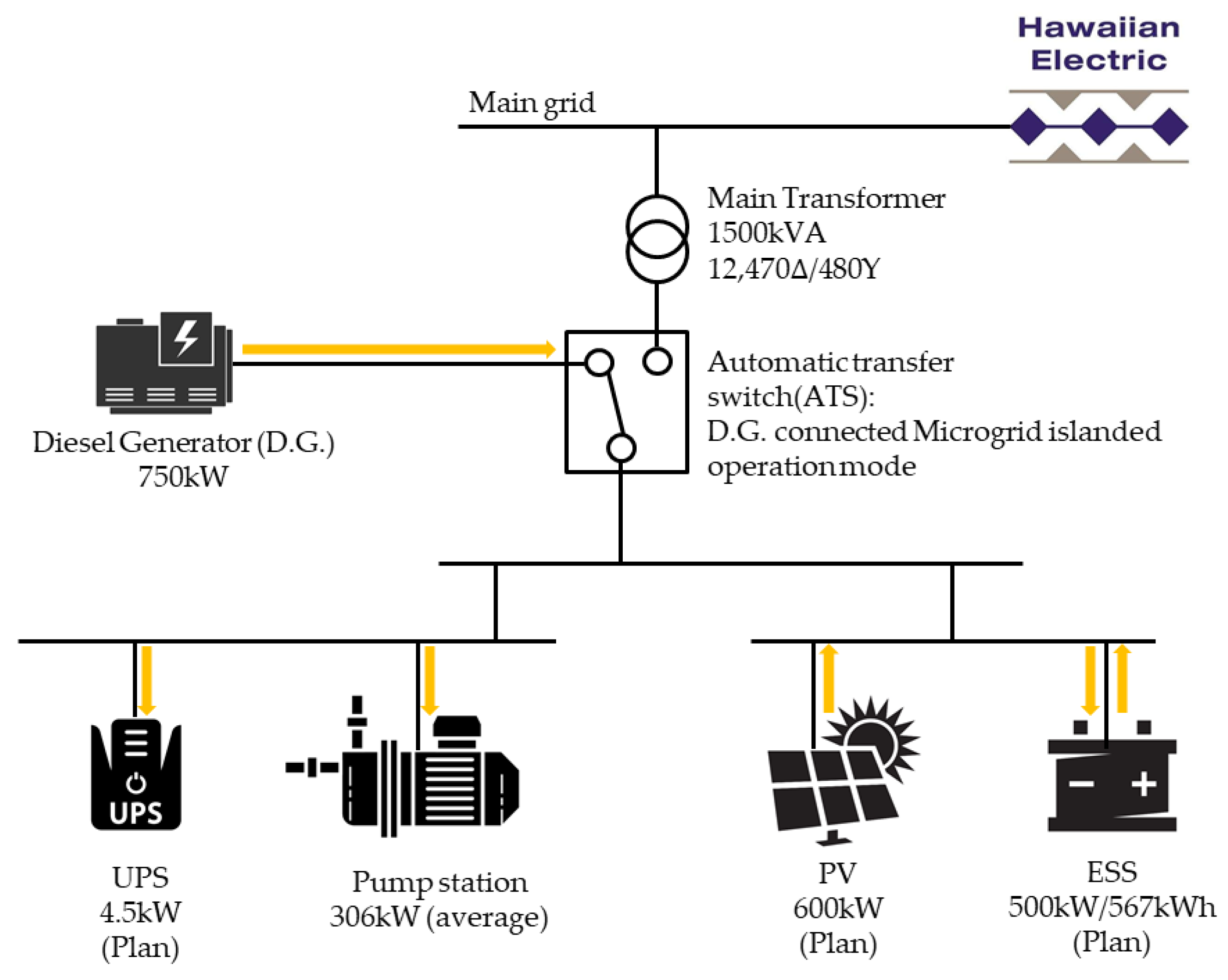
2.1. System Configuration
2.2. Formulation for MILP of Conventional Microgrid Scheduling
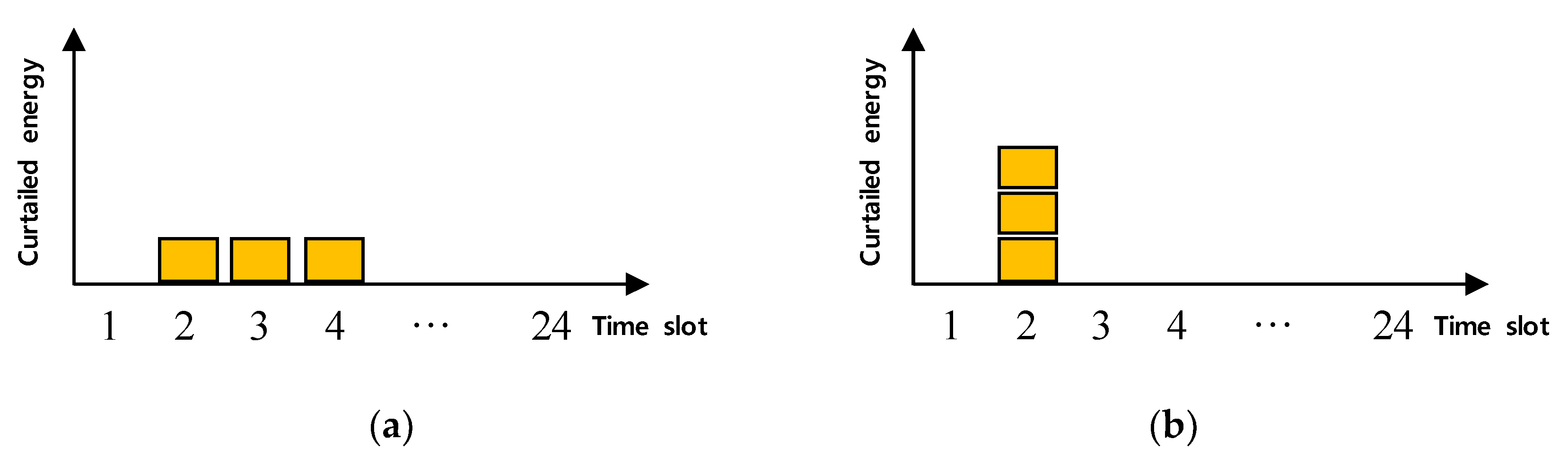
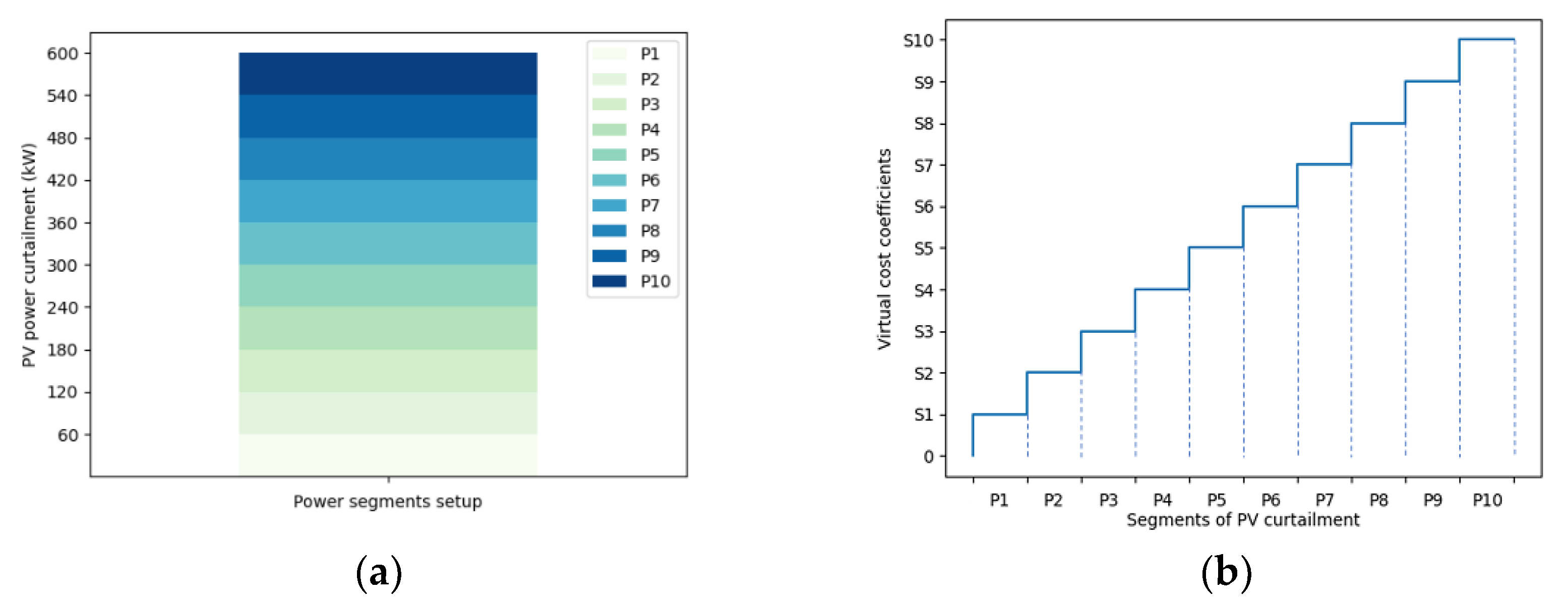
3. Curtailment Cost Gradation Method
4. Simulation Results and Discussion
4.1. Simulation Environment
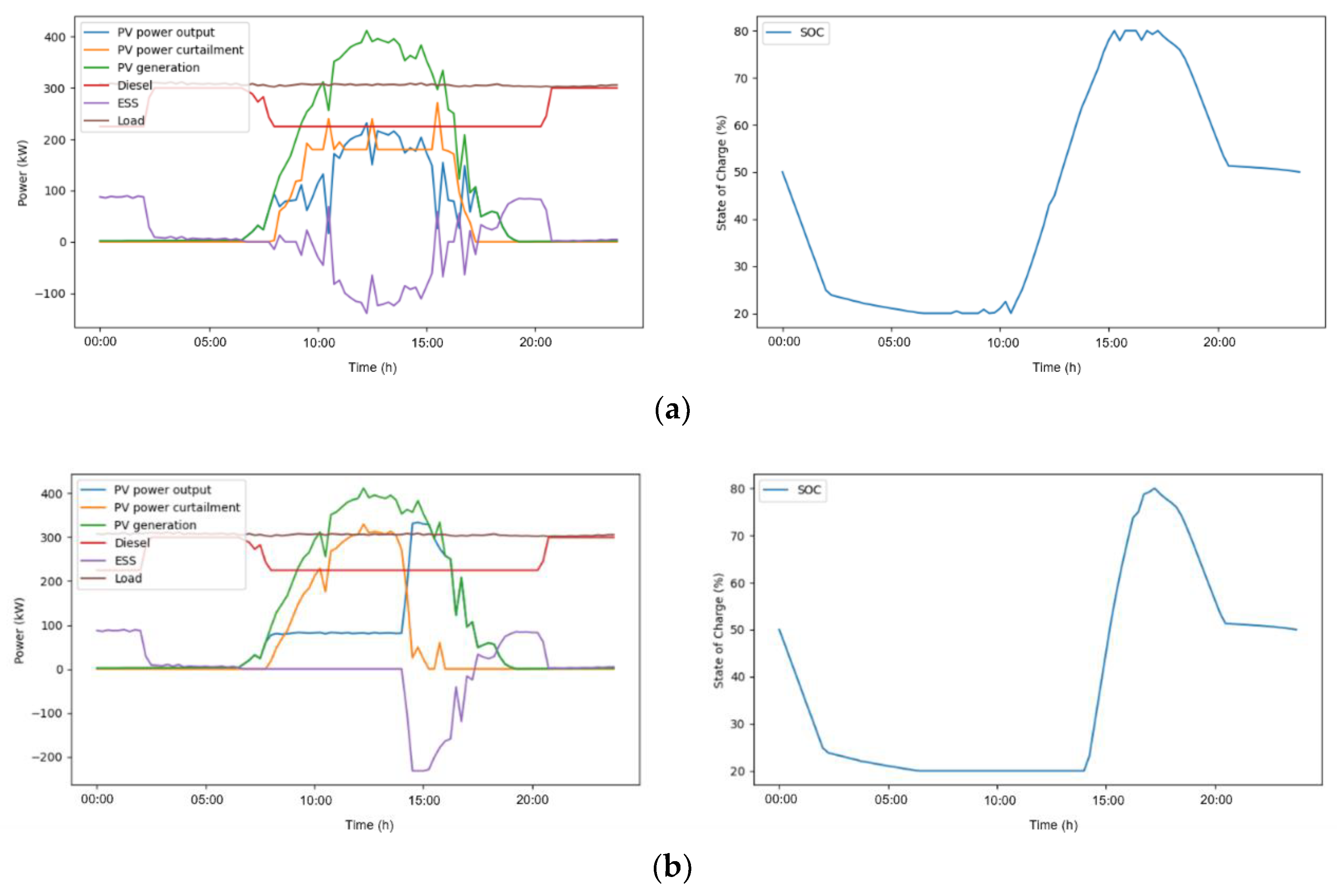
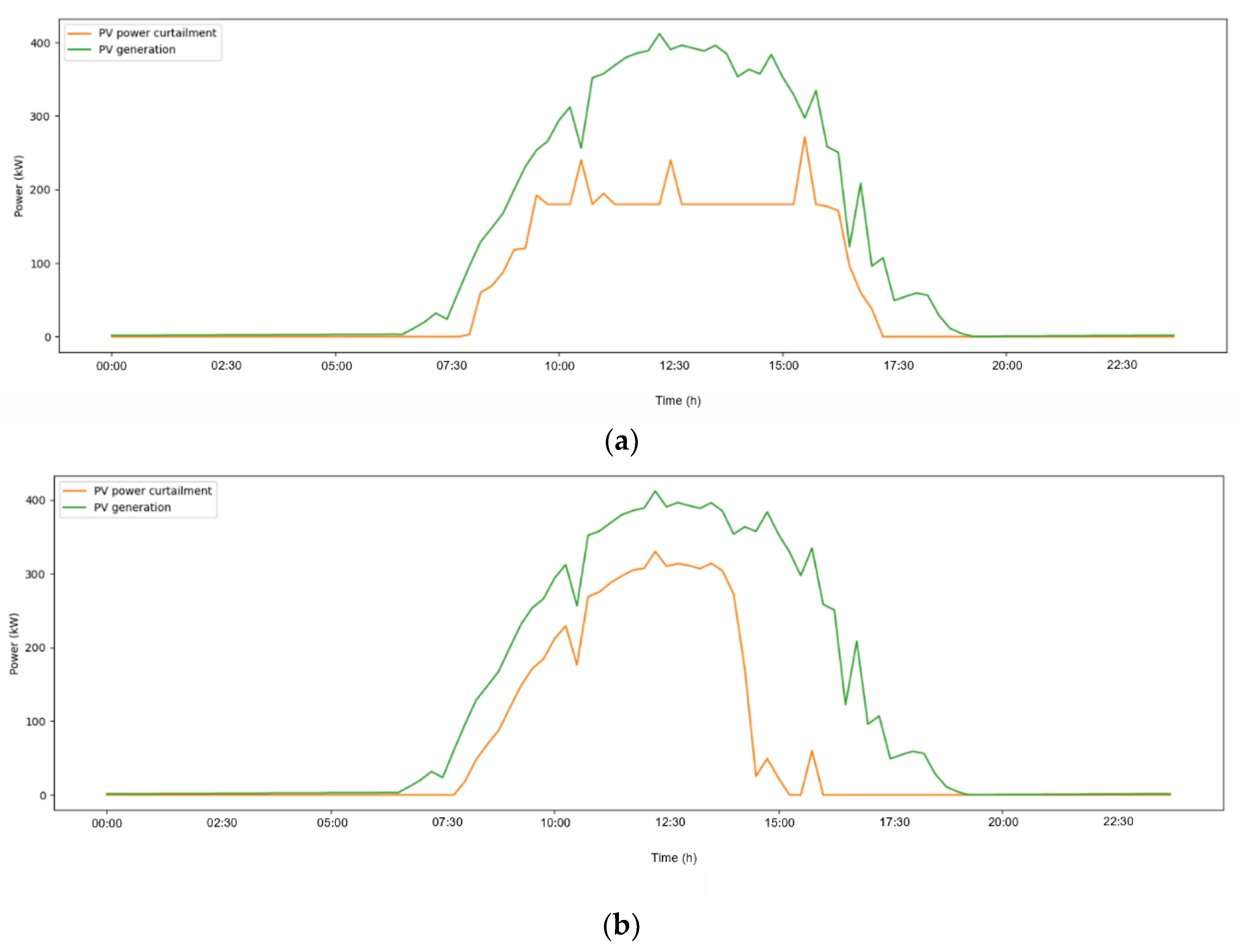
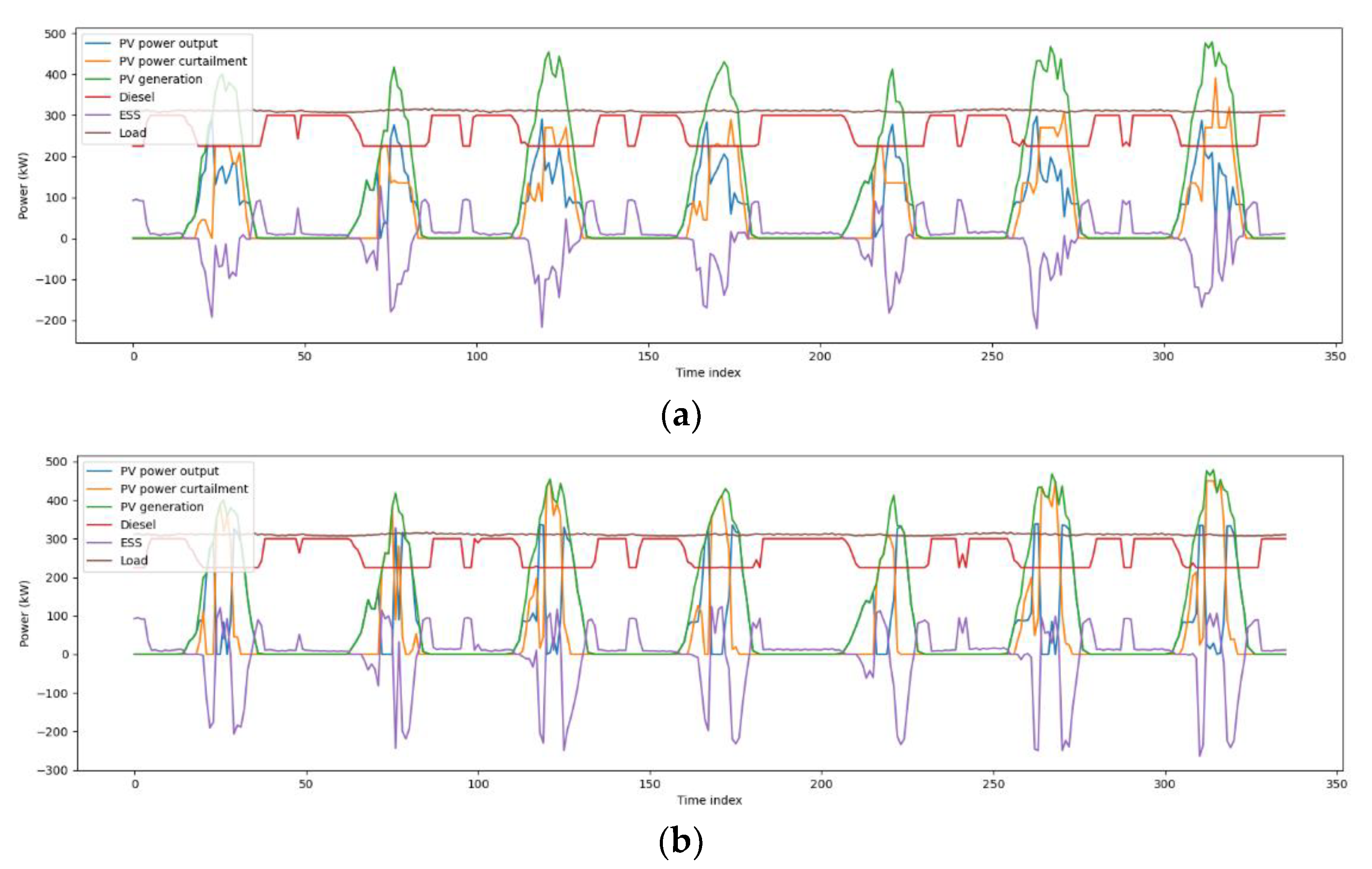
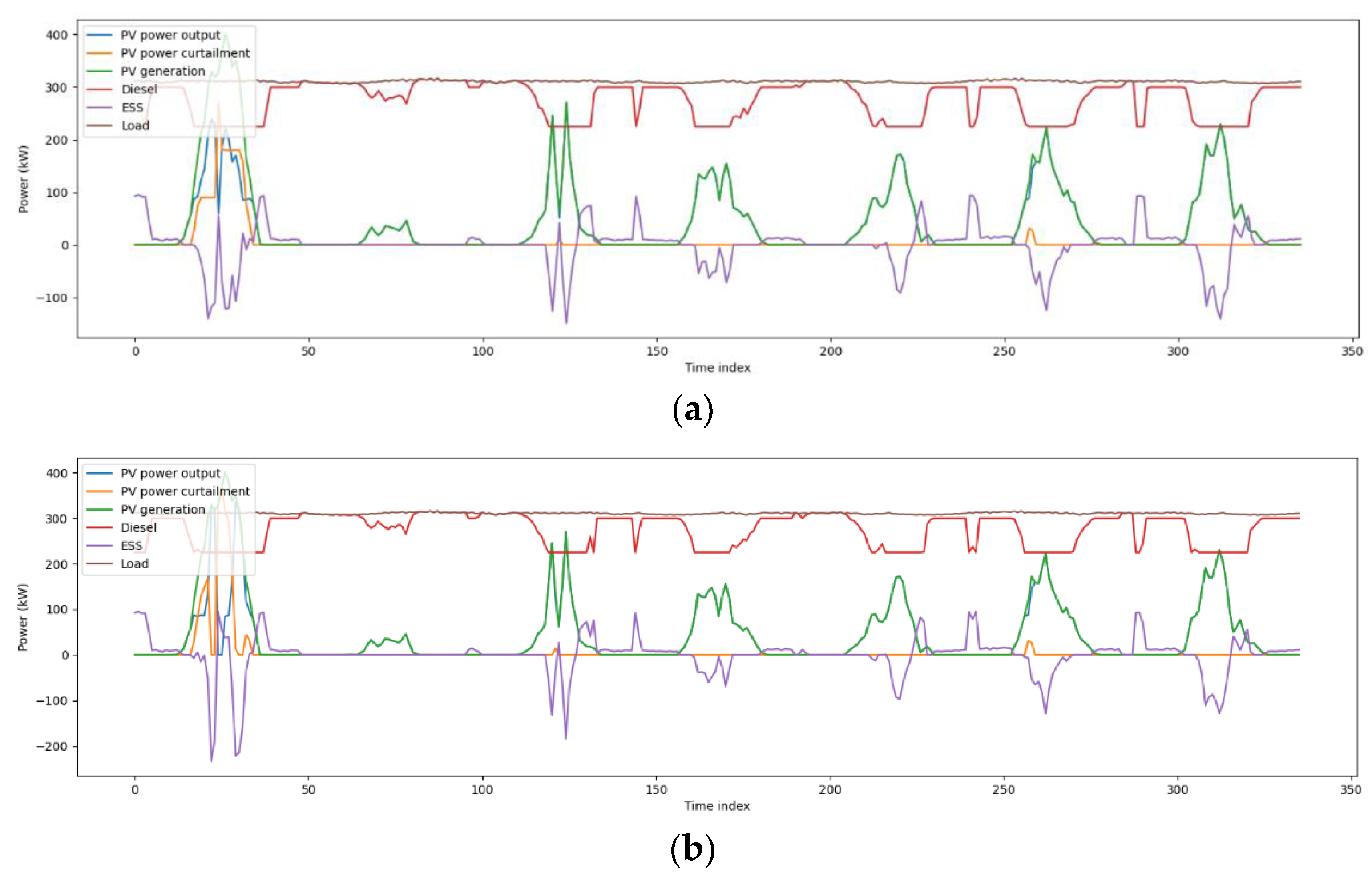
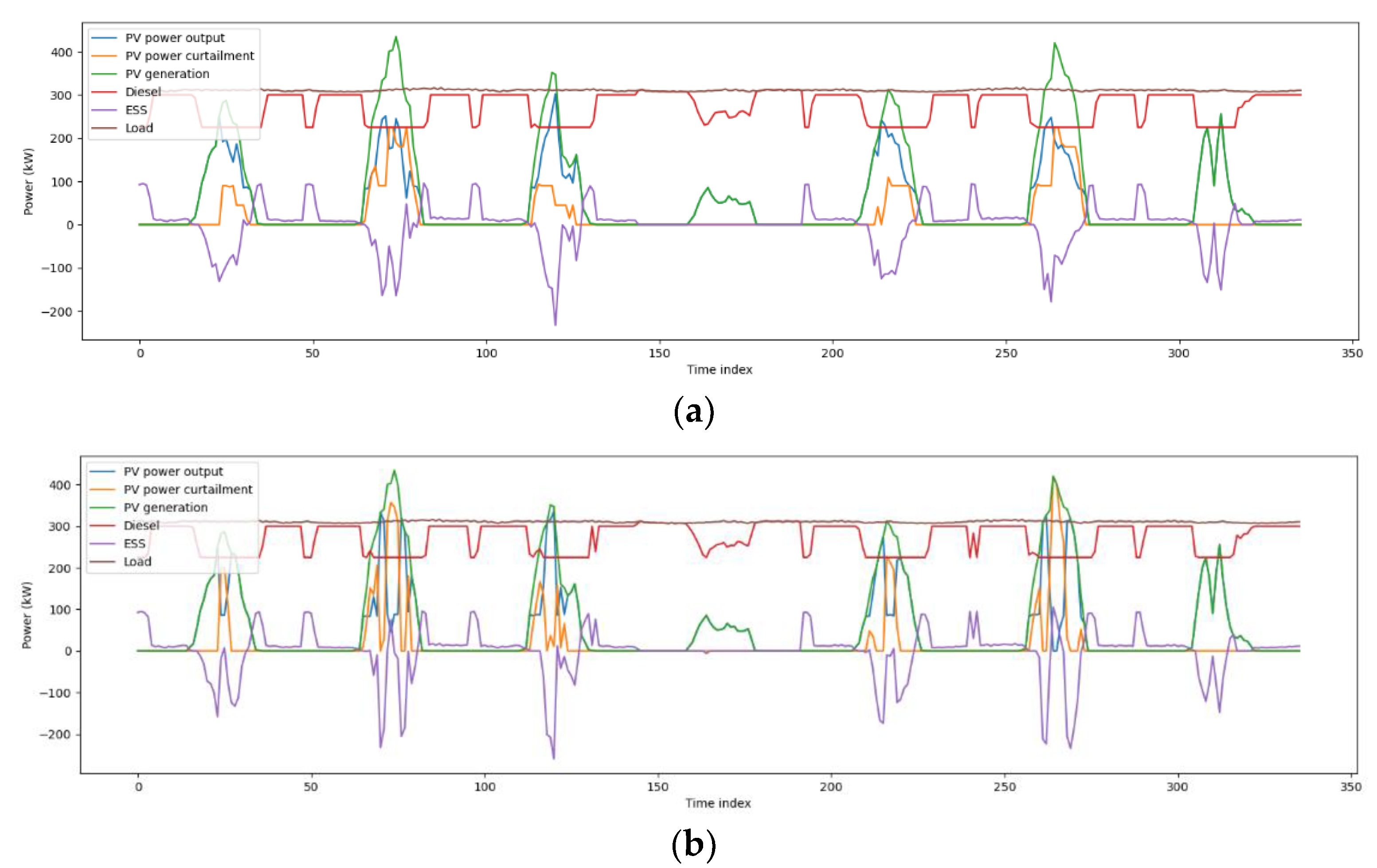
4.2. Single Day Simulation Results
4.3. Case Study and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclatures
| Index for operation time intervals | |
| Set of time periods | |
| Index for linearized diesel generation cost slop | |
| Set of diesel generation cost slopes | |
| Index for step curtailment cost slope | |
| Set of step curtailment cost slope | |
| Minimum/maximum output power of diesel generator | |
| Maximum output power of energy storage system (ESS) | |
| Minimum/maximum state of charge (SOC) of ESS | |
| Rating capacity of ESS | |
| Duration of each time interval | |
| Cost coefficients of diesel generator | |
| Slope rate of the diesel generation cost | |
| Cost coefficients of step curtailment | |
| Output power of diesel generator | |
| Discharge/charge output power of ESS | |
| Output power of photovoltaic (PV) generation system | |
| Load demand power | |
| Diesel generator ON/OFF status | |
| ESS discharging/charging status | |
| ESS discharging/charging status |
References
- Robert Rapier, Renewable Energy Growth Continues at a Blistering Pace, Forbes. 2 August 2020. Available online: https://www.forbes.com/sites/rrapier/2020/08/02/renewable-energy-growth-continues-at-a-blistering-pace/?sh=38b874c676b6 (accessed on 6 August 2021).
- IEA. Renewable Energy Market Update 2021; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/renewable-energy-market-update-2021 (accessed on 22 June 2021).
- Schermeyer, H.; Vergara, C.; Fichtner, W. Renewable energy curtailment: A case study on today’s and tomorrow’s congestion management. Energy Policy 2018, 112, 427–436. [Google Scholar] [CrossRef]
- Bird, L.; Cochran, J.; Wang, X. Wind and Solar Energy Curtailment: Experience and Practices in the United States; National Renewable Energy Laboratory: Denver, CO, USA, 2014. Available online: https://www.nrel.gov/docs/fy14osti/60983.pdf (accessed on 24 June 2021).
- Kim, R.-K.; Glick, M.B.; Olson, K.R.; Kim, Y.-S. MILP-PSO Combined Optimization Algorithm for an Islanded Microgrid Scheduling with Detailed Battery ESS Efficiency Model and Policy Considerations. Energies 2020, 13, 1898. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Aramburo, C.A.; Green, T.C.; Mugniot, N. Fuel Consumption Minimization of a Microgrid. IEEE Trans. Ind. Appl. 2005, 41, 673–681. [Google Scholar] [CrossRef] [Green Version]
- Khodaei, A. Microgrid Optimal Scheduling With Multi-Period Islanding Constraints. IEEE Trans. Power Syst. 2014, 29, 1383–1392. [Google Scholar] [CrossRef]
- Wen, Y.; Chung, C.Y.; Liu, X.; Che, L. Microgrid Dispatch With Frequency-Aware Islanding Constraints. IEEE Trans. Power Syst. 2019, 34, 2465–2468. [Google Scholar] [CrossRef]
- Kobauashi, D.; Masuta, T.; Ohtake, H. Coordinated operation scheduling method for BESS and thermal generators based on photovoltaic generation forecasts released every several hours. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017. [Google Scholar]
- Bandyopadhyay, S.; Kumar, P.; Arya, V. Planning curtailment of renewable generation in power grids. In Proceedings of the Proceedings of the International Conference on Automated Planning and Scheduling, London, UK, 12–17 June 2016. [Google Scholar]
- Su, X.; Masoum, M.A.S.; Wolfs, P.J. Optimal PV Inverter Reactive Power Control and Real Power Curtailment to Improve Performance of Unbalanced Four-Wire LV Distribution Networks. IEEE Trans. Sustain. Energy 2014, 5, 967–977. [Google Scholar] [CrossRef]
- Bitaraf, H.; Rahman, S. Reducing Curtailed Wind Energy Through Energy Storage and Demand Response. IEEE Trans. Sustain. Energy 2018, 9, 228–236. [Google Scholar] [CrossRef]
- Yi, J.; Lyons, P.F.; Davison, P.J.; Wang, P.; Taylor, P.C. Robust Scheduling Scheme for Energy Storage to Facilitate High Penetration of Renewables. IEEE Trans. Sustain. Energy 2016, 7, 797–807. [Google Scholar] [CrossRef]
- Albadi, M.; El-Saadany, E. Comparative study on impacts of wind profiles on thermal units scheduling costs. IET Renew. Power Gener. 2010, 5, 26–35. [Google Scholar] [CrossRef]
- Liu, G.; Starke, M.; Xiao, B.; Tomsovic, K. Robust optimisation-based microgrid scheduling with islanding constraints. IET Gener. Transm. Distrib. 2017, 11, 1820–1828. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; You, F. Bilayer Distributed Optimization for Robust Microgrid Dispatch With Coupled Individual-Collective Profits. IEEE Trans. Sustain. Energy 2021, 12, 1525–1538. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Xu, X.; Pan, G.; Liu, P.; Wu, Z.; Wang, L. A historical-correlation-driven robust optimization approach for microgrid dispatch. IEEE Trans. Smart Grid 2020, 12, 1135–1148. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Wi, Y.-M.; Joo, S.-K. Stochastic wind curtailment scheduling for mitigation of short-term variations in a power system with high wind power and electric vehicle. Appl. Sci. 2018, 8, 1684. [Google Scholar] [CrossRef] [Green Version]
- Hodge, B.-M.; Orwig, K.; Milligan, M. Examining Information Entropy Approaches as Wind Power Forecasting Performance Metrics; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Zhang, J.; Hodge, B.-M.; Florita, A.; Lu, S.; Hamann, H.F.; Banunarayanan, V. Metrics for Evaluating the Accuracy of Solar Power Forecasting; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Lyzwa, W.; Wierzbowski, M.; Olek, B. MILP formulation for energy mix optimization. IEEE Trans. Ind. Inform. 2015, 11, 1166–1178. [Google Scholar] [CrossRef]
- Jooshaki, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Lehtonen, M. MILP model of electricity distribution system expansion planning considering incentive reliability regulations. IEEE Trans. Power Syst. 2019, 34, 4300–4316. [Google Scholar] [CrossRef] [Green Version]
- Approximate Diesel Fuel Consumption Chart. Available online: https://www.generatorsource.com/Diesel_Fuel_Consumption.aspx (accessed on 8 September 2021).
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lee, H.-L.; Chun, Y.-H. Using piecewise linearization method to PCS input/output-efficiency curve for a stand-alone microgrid unit commitment. Energies 2018, 11, 2468. [Google Scholar] [CrossRef] [Green Version]
- Wouters, C.; Fraga, E.S.; James, A.M. An energy integrated, multi-microgrid, MILP (mixed-integer linear programming) approach for residential distributed energy system planning–a South Australian case-study. Energy 2015, 85, 30–44. [Google Scholar] [CrossRef] [Green Version]
- Park, K.-M.; Kim, J.-H.; Park, J.-Y.; Bang, S.-B. A Study on the Fire Risk of ESS through Fire Status and Field Investigation. Fire Sci. Eng. 2018, 32, 91–99. [Google Scholar] [CrossRef]
- Choi, S.; Min, S.-W. Optimal Scheduling and Operation of the ESS for Prosumer Market Environment in Grid-Connected Industrial Complex. IEEE Trans. Ind. Appl. 2018, 54, 1949–1957. [Google Scholar] [CrossRef]
- Cho, S.-M.; Kim, J.-S.; Kim, J.-C. Optimal Operation Parameter Estimation of Energy Storage for Frequency Regulation. Energies 2019, 12, 1782. [Google Scholar] [CrossRef] [Green Version]
- Goudarzi, A.; Li, Y.; Xiang, J. Efficient energy management of renewable resources in microgrids. In Renewable Energy Microgeneration Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 285–321. [Google Scholar]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. ETransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Shah, A.A.; Ahmed, K.; Han, X.; Saleem, A. A Novel Prediction Error Based Power Forecasting Scheme for Real PV System using PVUSA Model: A Grey Box Based Neural Network Approach. IEEE Access 2021, 9, 87196–87206. [Google Scholar] [CrossRef]



| Interval | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Slope rate (KRW/kWh) | 217.3 | 231.8 | 246.4 | 260.9 | 275.5 | 290.0 | 304.6 | 319.1 | 333.7 | 348.2 |
| Interval | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Curtailment cost coefficients | 1E-5 | 2E-5 | 3E-5 | 4E-5 | 5E-5 | 6E-5 | 7E-5 | 8E-5 | 9E-5 | 10E-5 |
| Time | Curtailment (kW) | Curtailment (kW) | |||
|---|---|---|---|---|---|
| Proposed Method | Conventional Method | Time | Proposed Method | Conventional Method | |
| 8:00 | 2 | 18 | 12:45 | 180 | 313 |
| 8:15 | 60 | 48 | 13:00 | 180 | 311 |
| 8:30 | 68 | 68 | 13:15 | 180 | 306 |
| 8:45 | 87 | 87 | 13:30 | 180 | 313 |
| 9:00 | 118 | 118 | 13:45 | 180 | 303 |
| 9:15 | 120 | 148 | 14:00 | 180 | 272 |
| 9:30 | 192 | 171 | 14:15 | 180 | 170 |
| 9:45 | 180 | 184 | 14:30 | 180 | 25 |
| 10:00 | 180 | 211 | 14:45 | 180 | 49 |
| 10:15 | 180 | 229 | 15:00 | 180 | 23 |
| 10:30 | 240 | 176 | 15:15 | 180 | 0 |
| 10:45 | 180 | 268 | 15:30 | 271 | 0 |
| 11:00 | 194 | 275 | 15:45 | 180 | 60 |
| 11:15 | 180 | 287 | 16:00 | 177 | 0 |
| 11:30 | 180 | 296 | 16:15 | 171 | 0 |
| 11:45 | 180 | 304 | 16:30 | 96 | 0 |
| 12:00 | 180 | 307 | 16:45 | 60 | 0 |
| 12:15 | 180 | 329 | 17:00 | 37 | 0 |
| 12:30 | 240 | 310 | 17:15 | 0 | 0 |
| Optimal Cost (KRW/Day) | Curtailment Standard Deviation | |
|---|---|---|
| Proposed method | 2,242,795 | 85.75 |
| Conventional method | 2,242,795 | 110.98 |
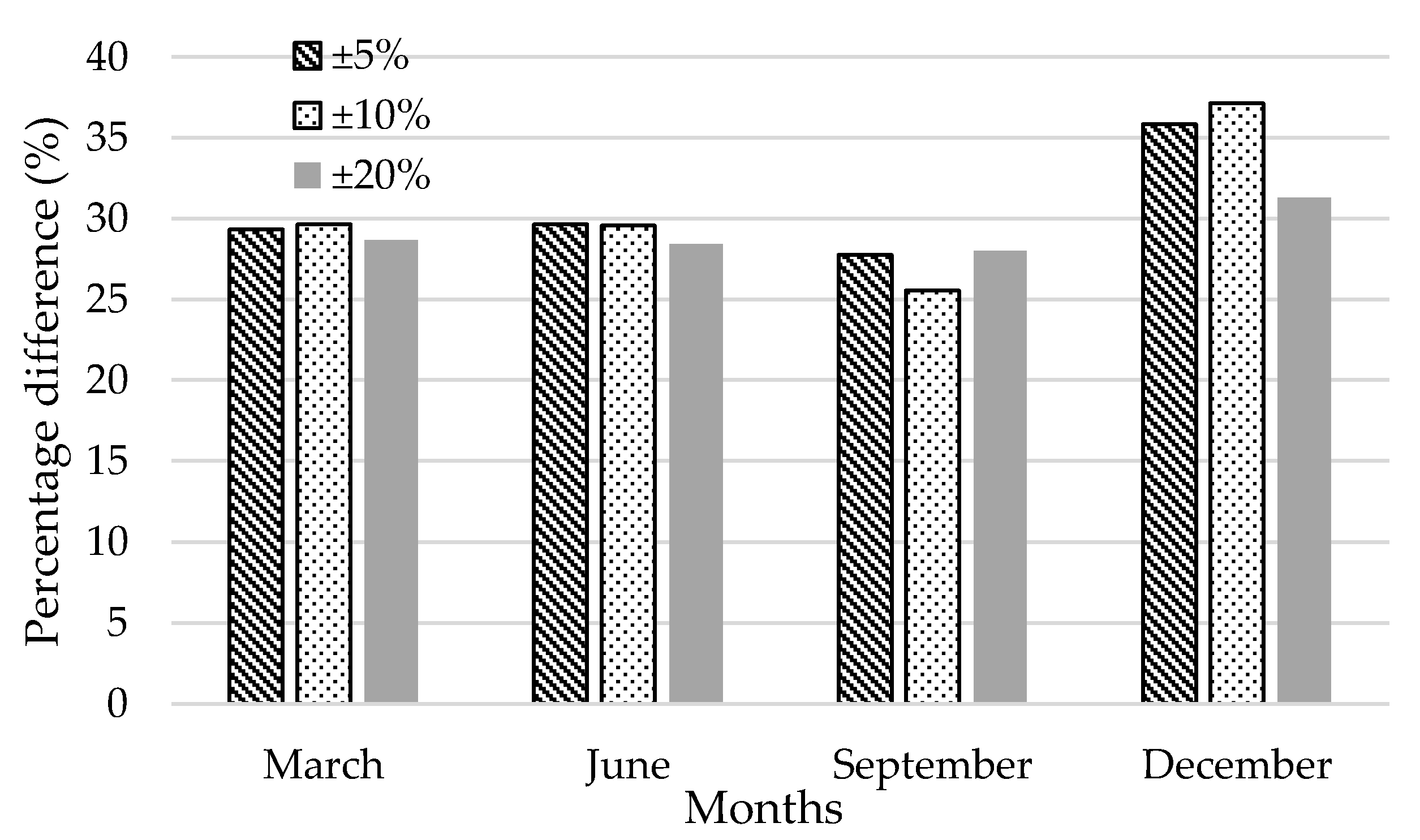
| Optimal Solution of Microgrid Operation Cost (KRW) | Curtailment Standard Deviation | ||||||
|---|---|---|---|---|---|---|---|
| ±5% | ±10% | ±20% | ±5% | ±10% | ±20% | ||
| March | Proposed method | 15,709,850.62 | 15,706,037.79 | 15,709,403.91 | 90.83 | 90.48 | 90.85 |
| Conventional method | 15,709,850.37 | 15,706,037.55 | 15,709,403.66 | 117.47 | 117.29 | 116.90 | |
| June | Proposed method | 15,720,649.01 | 15,727,001.9 | 15,733,890.35 | 76.06 | 75.84 | 74.44 |
| Conventional method | 15,720,648.84 | 15,727,001.77 | 15,733,890.18 | 98.61 | 98.27 | 95.59 | |
| September | Proposed method | 16,312,087.02 | 16,317,394.4 | 16,300,945.93 | 31.44 | 31.58 | 31.81 |
| Conventional method | 16,312,086.99 | 16,317,394.39 | 16,300,945.90 | 40.17 | 39.65 | 40.72 | |
| December | Proposed method | 16,111,120.14 | 16,108,491.3 | 16,124,666.02 | 46.61 | 46.49 | 45.50 |
| Conventional method | 16,111,120.08 | 16,108,491.19 | 16,124,665.97 | 63.31 | 63.75 | 59.73 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, W.-H.; Abunima, H.; Glick, M.B.; Kim, Y.-S. Energy Curtailment Scheduling MILP Formulation for an Islanded Microgrid with High Penetration of Renewable Energy. Energies 2021, 14, 6038. https://doi.org/10.3390/en14196038
Park W-H, Abunima H, Glick MB, Kim Y-S. Energy Curtailment Scheduling MILP Formulation for an Islanded Microgrid with High Penetration of Renewable Energy. Energies. 2021; 14(19):6038. https://doi.org/10.3390/en14196038
Chicago/Turabian StylePark, Woan-Ho, Hamza Abunima, Mark B. Glick, and Yun-Su Kim. 2021. "Energy Curtailment Scheduling MILP Formulation for an Islanded Microgrid with High Penetration of Renewable Energy" Energies 14, no. 19: 6038. https://doi.org/10.3390/en14196038
APA StylePark, W. -H., Abunima, H., Glick, M. B., & Kim, Y. -S. (2021). Energy Curtailment Scheduling MILP Formulation for an Islanded Microgrid with High Penetration of Renewable Energy. Energies, 14(19), 6038. https://doi.org/10.3390/en14196038







