A Review on the Thermal-Hydraulic Performance and Optimization of Compact Heat Exchangers
Abstract
:1. Introduction
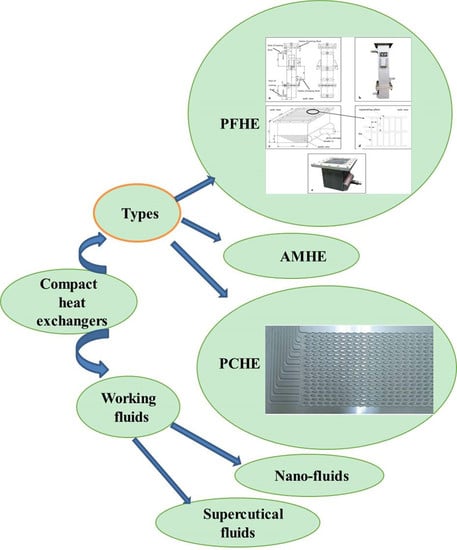
2. Main Types and Performance Optimization of Compact Heat Exchangers
2.1. Plate-Fin Heat Exchanger (PFHE)
2.2. Printed Circuit Heat Exchanger (PCHE)
2.2.1. PCHE with Straight Channels
2.2.2. PCHE with Zigzag Channels
2.2.3. PCHE with Wavy Channels
2.2.4. PCHE with S-Shaped Fin Channels
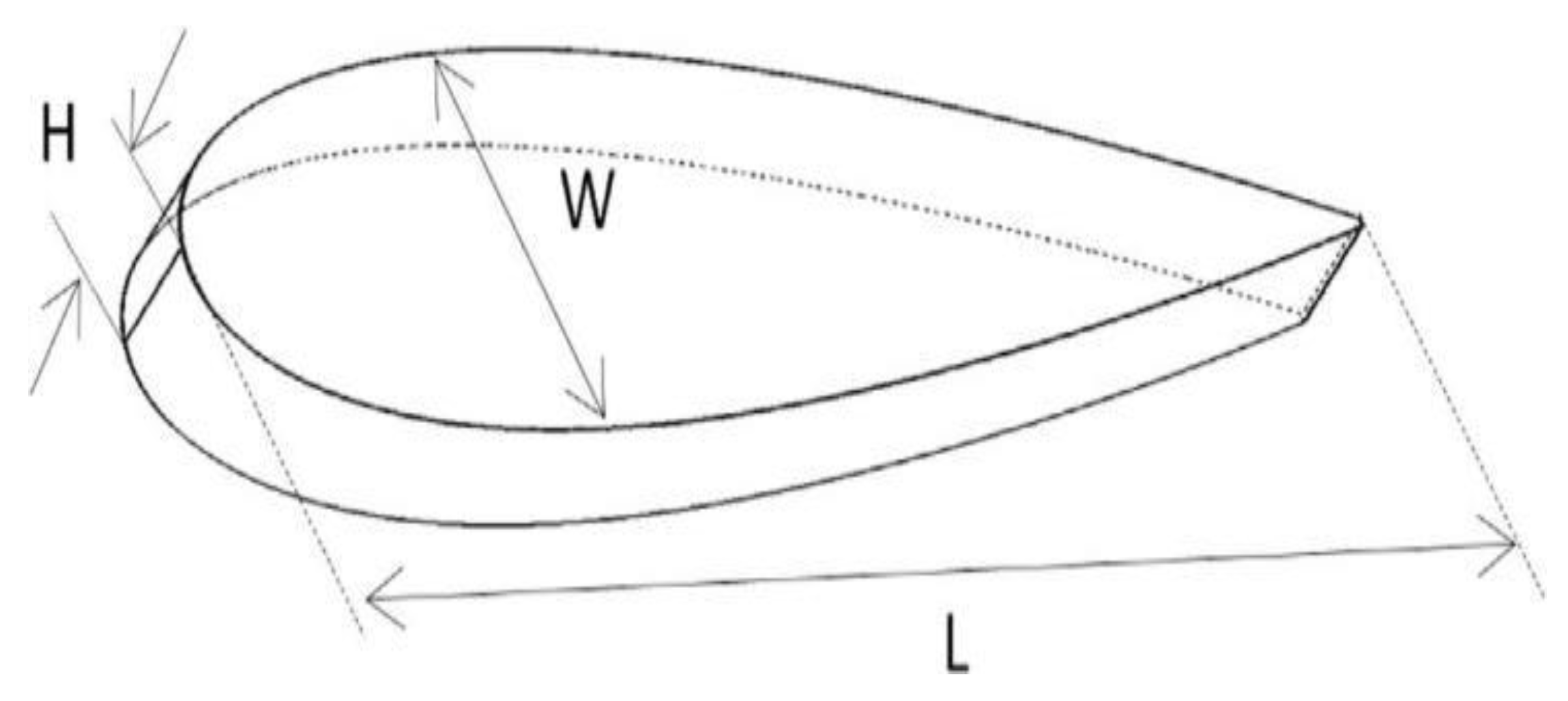
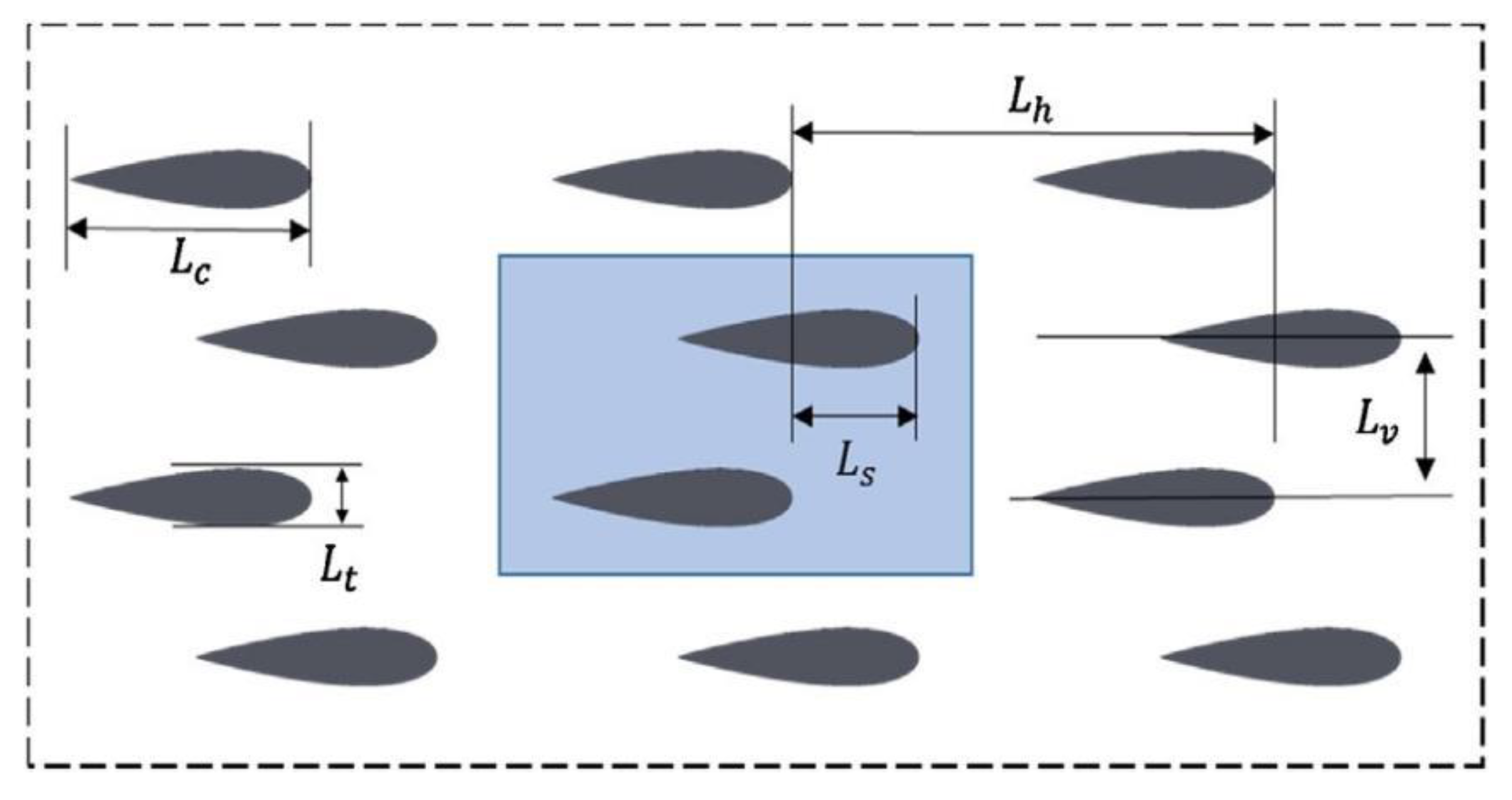
2.2.5. PCHE with Airfoil Fin Channels
2.3. Additive Manufacturing Heat Exchanger (AMHX)
3. Types of Fluid Working Medium in Compact Heat Exchanger
3.1. Nanofluid
3.2. Supercritical Fluid
3.2.1. Supercritical Carbon Dioxide (S-CO2)
3.2.2. Supercritical Helium and Supercritical Nitrogen
3.2.3. Supercritical Water
4. Performance Evaluation Indexes of Compact Heat Exchangers
5. Discussion and Suggestions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, M.; Zhao, P.; Wang, J.; Li, H.; Dai, Y. Conceptual design and parametric study of combined carbon dioxide/organic Rankine cycles. Appl. Therm. Eng. 2016, 103, 759–772. [Google Scholar] [CrossRef]
- Angelino, G. Carbon Dioxide Condensation Cycles for Power Production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.; Jang, C. Compatibility of candidate structural materials in high-temperature S-CO2 environment. In Proceedings of the Super-Critical CO2 Power Symposium, Pittsburgh, PA, USA, 9–10 September 2014. [Google Scholar]
- Schulenberg, T.; Wider, H.; Fütterer, M. Electricity production in nuclear power plants–Rankine vs. Brayton cycles. In Proceedings of the GLOBAL, New Orleans, LA, USA, 16–20 November 2003. [Google Scholar]
- Dostal, V.; Driscoll, M.J.; Hejzlar, P.; Todreas, N.E. A supercritical CO2 gas turbine power cycle for next-generation nuclear reactors. In Proceedings of the 10th International Conference on Nuclear Engineering, Arlington, VA, USA, 14–18 April 2002. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1998; pp. 17.1–17.2. [Google Scholar]
- Shah, R.K. Classification of heat exchangers. In Heat Exchangers: Thermal–Hydraulic Fundamentals and Design; Hemisphere Publishing: Washington, DC, USA, 1981; pp. 23–32. [Google Scholar]
- Hesselgreaves, J.E. Compact Heat Exchangers, Selection, Design and Operation; Pergamon: New York, NY, USA, 2001. [Google Scholar]
- DoE, U.S. A technology roadmap for generation IV nuclear energy systems. In Nuclear Energy Research Advisory Committee and the Generation IV International Forum; Doene: Berryville, VA, USA, 1 December 2002; pp. 48–52. [Google Scholar]
- Cheng, L.; Ribatski, G.; Thome, J.R. Analysis of supercritical CO2 cooling in macro- and micro-channels. Int. J. Refrig. 2008, 31, 1301–1316. [Google Scholar] [CrossRef]
- Cabeza, L.F.; de Gracia, A.; Fernández, A.I.; Farid, M. Supercritical CO2 as heat transfer fluid: A review. Appl. Therm. Eng. 2017, 125, 799–810. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Cai, W.; Wang, Y.; Liu, Y.; Li, Q.; Li, B. Review on the characteristics of flow and heat transfer in printed circuit heat exchangers. Appl. Therm. Eng. 2019, 153, 190–205. [Google Scholar] [CrossRef]
- Chai, L.; Tassou, S.A. A review of printed circuit heat exchangers for helium and supercritical CO2 Brayton cycles. Therm. Sci. Eng. Prog. 2020, 18, 100543. [Google Scholar] [CrossRef]
- Pandey, V.; Kumar, P.; Dutta, P. Thermo-hydraulic analysis of compact heat exchanger for a simple recuperated sCO2 Brayton cycle. Renew. Sustain. Energy Rev. 2020, 134, 110091. [Google Scholar] [CrossRef]
- Liu, G.; Huang, Y.; Wang, J.; Liu, R. A review on the thermal-hydraulic performance and optimization of printed circuit heat exchangers for supercritical CO2 in advanced nuclear power systems. Renew. Sustain. Energy Rev. 2020, 133, 110290. [Google Scholar] [CrossRef]
- Kwon, J.S.; Son, S.; Heo, J.Y.; Lee, J.I. Compact heat exchangers for supercritical CO2 power cycle application. Energy Convers. Manag. 2020, 209, 112666. [Google Scholar] [CrossRef]
- Ismail, L.S.; Velraj, R.; Ranganayakulu, C. Studies on pumping power in terms of pressure drop and heat transfer characteristics of compact plate-fin heat exchangers—A review. Renew. Sustain. Energy Rev. 2010, 14, 478–485. [Google Scholar] [CrossRef]
- Kays, W.M. The Basic Heat Transfer and Flow Friction Characteristics of Six Compact High-Performance Heat Transfer Surfaces. J. Eng. Power 1960, 82, 27–34. [Google Scholar] [CrossRef]
- Patankar, S.; Prakash, C. An analysis of the effect of plate thickness on laminar flow and heat transfer in interrupted-plate passages. Int. J. Heat Mass Transf. 1981, 24, 1801–1810. [Google Scholar] [CrossRef]
- Cur, N.; Sparrow, E.M. Measurements of developing and fully developed heat transfer coefficients along a periodically inter-rupted surface. Trans. ASME J. Heat Transf. 1979, 101, 211–216. [Google Scholar] [CrossRef]
- Kim, S.Y.; Paek, J.W.; Kang, B.H. Flow and Heat Transfer Correlations for Porous Fin in a Plate-Fin Heat Exchanger. J. Heat Transf. 2000, 122, 572–578. [Google Scholar] [CrossRef]
- Yan, W.-M.; Sheen, P.-J. Heat transfer and friction characteristics of fin-and-tube heat exchangers. Int. J. Heat Mass Transf. 2000, 43, 1651–1659. [Google Scholar] [CrossRef]
- Choi, J.M.; Kim, Y.; Lee, M. Air side heat transfer coefficients of discrete plate finned-tube heat exchangers with large fin pitch. Appl. Therm. Eng. 2010, 30, 174–180. [Google Scholar] [CrossRef]
- Han, H.; He, Y.-L.; Li, Y.-S.; Wang, Y.; Wu, M. A numerical study on compact enhanced fin-and-tube heat exchangers with oval and circular tube configurations. Int. J. Heat Mass Transf. 2013, 65, 686–695. [Google Scholar] [CrossRef]
- Okbaz, A.; Ali, P.; Ali, B.O. Experimental investigation of effect of different tube row-numbers, fin pitches and operating con-ditions on thermal and hydraulic performances of louvered and wavy finned heat exchangers. Int. J. Therm. Sci. 2020, 151, 106256. [Google Scholar] [CrossRef]
- Jeong, C.H.; Kim, H.R.; Ha, M.Y.; Son, S.W.; Lee, J.S.; Kim, P.Y. Numerical investigation of thermal enhancement of plate fin type heat exchanger with creases and holes in construction machinery. Appl. Therm. Eng. 2014, 62, 529–544. [Google Scholar] [CrossRef]
- Jiao, A.J.; Li, Y.Z.; Chen, C.Z. Experimental investigation on fluid flow maldistribution in plate-fin heat exchangers. Heat Transf. Eng. 2003, 24, 25–31. [Google Scholar]
- Zhang, Z.; Mehendale, S.; Tian, J.; Li, Y. Fluid Flow Distribution and Heat Transfer in Plate-Fin Heat Exchangers. Heat Transf. Eng. 2014, 36, 806–819. [Google Scholar] [CrossRef]
- Song, K.; Xi, Z.; Su, M.; Wang, L.; Wu, X.; Wang, L. Effect of geometric size of curved delta winglet vortex generators and tube pitch on heat transfer characteristics of fin-tube heat exchanger. Exp. Therm. Fluid Sci. 2017, 82, 8–18. [Google Scholar] [CrossRef]
- Song, K.; Tagawa, T. The optimal arrangement of vortex generators for best heat transfer enhancement in flat-tube-fin heat exchanger. Int. J. Therm. Sci. 2018, 132, 355–367. [Google Scholar] [CrossRef]
- Korzeń, A.; Taler, D. Modeling of transient response of a plate fin and tube heat exchanger. Int. J. Therm. Sci. 2015, 92, 188–198. [Google Scholar] [CrossRef]
- Taler, D. Mathematical modeling and control of plate fin and tube heat exchangers. Energy Convers. Manag. 2015, 96, 452–462. [Google Scholar] [CrossRef]
- Wen, J.; Yang, H.; Tong, X.; Li, K.; Wang, S.; Li, Y. Optimization investigation on configuration parameters of serrated fin in plate-fin heat exchanger using genetic algorithm. Int. J. Therm. Sci. 2016, 101, 116–125. [Google Scholar] [CrossRef]
- Blecich, P. Experimental investigation of the effects of airflow nonuniformity on performance of a fin-and-tube heat exchanger. Int. J. Refrig. 2015, 59, 65–74. [Google Scholar] [CrossRef]
- Yaïci, W.; Ghorab, M.; Entchev, E. 3D CFD study of the effect of inlet air flow maldistribution on plate-fin-tube heat exchanger design and thermal–hydraulic performance. Int. J. Heat Mass Transf. 2016, 101, 527–541. [Google Scholar] [CrossRef]
- Hassan, H.; Sajjad, S. Effect of flow maldistribution on the optimal design of a cross flow heat exchanger. Int. J. Therm. Sci. 2016, 109, 242–252. [Google Scholar]
- Dogan, B.; Altun, O.; Uğurlubilek, N.; Tosun, M.; Sarıçay, T.; Erbay, L.B.; Dogan, B. An experimental comparison of two multi-louvered fin heat exchangers with different numbers of fin rows. Appl. Therm. Eng. 2015, 91, 270–278. [Google Scholar] [CrossRef]
- Okbaz, A.; Cellek, M.S.; Pinarbasi, A.; Olcay, A.B. Computational investigation of heat transfer and pressure drop in a typical louver fin-and-tube heat exchanger for various louver angles and fin pitches. EPJ Web Conf. 2017, 143, 2084. [Google Scholar] [CrossRef] [Green Version]
- Ryu, K.; Lee, K.S. Generalized heat-transfer and fluid-flow correlations for corrugated louvered fins. Int. J. Heat Mass Transf. 2015, 83, 604–612. [Google Scholar] [CrossRef]
- Dezan, J.D.; Salviano, L.O.; Yanagihara, J.I. Interaction effects between parameters in a flat-tube louvered fin compact heat ex-changer with delta-winglets vortex generators. Appl. Therm. Eng. 2015, 91, 1092–1105. [Google Scholar] [CrossRef]
- Karthik, P.; Kumaresan, V.; Velraj, R. Fanning friction (f) and colburn (j) factors of a louvered fin and flat tube compact heat exchanger. Therm. Sci. 2017, 21, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Javaherdeh, K.; Vaisi, A.; Moosavi, R.; Esmaeilpour, M. Experimental and Numerical Investigations on Louvered Fin-and-Tube Heat Exchanger with Variable Geometrical Parameters. J. Therm. Sci. Eng. Appl. 2017, 9, 024501. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, Q.; Cheng, J.; Deng, J. Simulation investigation on inlet velocity profile and configuration parameters of louver fin. Appl. Therm. Eng. 2018, 138, 173–182. [Google Scholar] [CrossRef]
- Habibian, S.; Abolmaali, A.M.; Afshin, H. Numerical investigation of the effects of fin shape, antifreeze and nanoparticles on the performance of compact finned-tube heat exchangers for automobile radiator. Appl. Therm. Eng. 2018, 133, 248–260. [Google Scholar] [CrossRef]
- Gholami, A.; Mohammed, H.A.; Wahid, M.A.; Khiadani, M. Parametric design exploration of fin-and-oval tube compact heat ex-changers performance with a new type of corrugated fin patterns. Int. J. Therm. Sci. 2019, 144, 173–190. [Google Scholar] [CrossRef]
- Sadeghianjahromi, A.; Kheradmand, S.; Nemati, H.; Wang, C.-C. Optimization of the louver fin-and-tube heat exchangers-A parametric appoach. J. Enhanc. Heat Transf. 2020, 27, 289–312. [Google Scholar] [CrossRef]
- Damavandi, M.D.; Forouzanmehr, M.; Safikhani, H. Modeling and Pareto based multi-objective optimization of wavy fin-and-elliptical tube heat exchangers using CFD and NSGA-II algorithm. Appl. Therm. Eng. 2017, 111, 325–339. [Google Scholar] [CrossRef]
- Gholami, A.; Wahid, M.A.; Mohammed, H.A. Thermal–hydraulic performance of fin-and-oval tube compact heat exchangers with innovative design of corrugated fin patterns. Int. J. Heat Mass Transf. 2017, 106, 573–592. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Li, M.; Wang, S.; Li, X. Improved flow and heat transfer characteristics for heat exchanger by using a new humped wavy fin. Appl. Therm. Eng. 2017, 124, 510–520. [Google Scholar] [CrossRef]
- Lotfi, B.; Sundén, B.; Wang, Q. An investigation of the thermo-hydraulic performance of the smooth wavy fin-and-elliptical tube heat exchangers utilizing new type vortex generators. Appl. Energy 2016, 162, 1282–1302. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Zhang, J.; Mu, Y.; Tian, E.; Dan, D.; Zhang, X.; Tao, W. Experimental and numerical study and comparison of performance for wavy fin and a plain fin with radiantly arranged winglets around each tube in fin-and-tube heat exchangers. Appl. Therm. Eng. 2018, 133, 298–307. [Google Scholar] [CrossRef]
- Tang, L.; Du, X.; Pan, J.; Sundén, B. Air inlet angle influence on the air-side heat transfer and flow friction characteristics of a finned oval tube heat exchanger. Int. J. Heat Mass Transf. 2019, 145, 118702. [Google Scholar] [CrossRef]
- Abeykoon, C. Compact heat exchangers—Design and optimization with CFD. Int. J. Heat Mass Transf. 2019, 146, 118766. [Google Scholar] [CrossRef]
- Aasi, H.K.; Mishra, M. Experimental investigation and ANN modelling on thermo-hydraulic efficacy of cross-flow three-fluid plate-fin heat exchanger. Int. J. Therm. Sci. 2021, 164, 106870. [Google Scholar] [CrossRef]
- Unger, E.; Beyer, M.; Pietruske, H.; Szalinski, L.; Hampel, U. Air-side heat transfer and flow characteristics of additively manu-factured finned tubes in staggered arrangement. Int. J. Therm. Sci. 2021, 161, 106752. [Google Scholar] [CrossRef]
- Blecich, P.; Trp, A.; Lenic, K. Thermal performance analysis of fin-and-tube heat exchangers operating with airflow nonuni-formity. Int. J. Therm. Sci. 2021, 164, 106887. [Google Scholar] [CrossRef]
- Kruizenga, A.; Anderson, M.; Fatima, R.; Corradini, M.; Towne, A.; Ranjan, D. Heat Transfer of Supercritical Carbon Dioxide in Printed Circuit Heat Exchanger Geometries. J. Therm. Sci. Eng. Appl. 2011, 3, 031002. [Google Scholar] [CrossRef]
- Baek, S.; Kim, J.H.; Jeong, S.; Jung, J. Development of highly effective cryogenic printed circuit heat exchanger (PCHE) with low axial conduction. Cryogenics 2012, 52, 366–374. [Google Scholar] [CrossRef]
- Mylavarapu, S.K.; Sun, X.; Glosup, R.E.; Christensen, R.N.; Patterson, M. Thermal hydraulic performance testing of printed circuit heat exchangers in a high-temperature helium test facility. Appl. Therm. Eng. 2014, 65, 605–614. [Google Scholar] [CrossRef]
- Chu, W.-X.; Li, X.-H.; Ma, T.; Chen, Y.-T.; Wang, Q. Experimental investigation on SCO2-water heat transfer characteristics in a printed circuit heat exchanger with straight channels. Int. J. Heat Mass Transf. 2017, 113, 184–194. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, J.G.; Kim, T.H.; Kim, M.H.; Cha, J.-E.; Jo, H. Experimental study of a straight channel printed circuit heat exchanger on supercritical CO2 near the critical point with water cooling. Int. J. Heat Mass Transf. 2020, 150, 119364. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Sabharwall, P.; Kim, E.-S. Numerical study on crossflow printed circuit heat exchanger for advanced small modular reactors. Int. J. Heat Mass Transf. 2014, 70, 250–263. [Google Scholar] [CrossRef]
- Xiang, M.; Guo, J.; Huai, X.; Cui, X. Thermal analysis of supercritical pressure CO2 in horizontal tubes under cooling condition. J. Supercrit. Fluids 2017, 130, 389–398. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Peng, M.J.; Xia, G.L.; Cong, T.L. Numerical investigation on local heat transfer characteristics of S-CO2 in horizontal semicircular microtube. Appl. Therm. Eng. 2019, 154, 380–394. [Google Scholar] [CrossRef]
- Kim, J.H.; Baek, S.; Jeong, S.; Jung, J. Hydraulic performance of a microchannel PCHE. Appl. Therm. Eng. 2010, 30, 2157–2162. [Google Scholar] [CrossRef]
- Li, H.; Kruizenga, A.; Anderson, M.; Corradini, M.; Luo, Y.; Wang, H.; Li, H. Development of a new forced convection heat transfer correlation for CO2 in both heating and cooling modes at supercritical pressures. Int. J. Therm. Sci. 2011, 50, 2430–2442. [Google Scholar] [CrossRef]
- Kim, W.; Baik, Y.-J.; Jeon, S.; Jeon, D.; Byon, C. A mathematical correlation for predicting the thermal performance of cross, parallel, and counterflow PCHEs. Int. J. Heat Mass Transf. 2017, 106, 1294–1302. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Y.; Wang, J. Theoretical and numerical investigation on the fin effectiveness and the fin efficiency of printed circuit heat exchanger with straight channels. Int. J. Therm. Sci. 2018, 132, 558–566. [Google Scholar] [CrossRef]
- Zhang, G.-W.; Hu, P.; Chen, L.-X.; Liu, M.-H. Experimental and simulation investigation on heat transfer characteristics of in-tube supercritical CO2 cooling flow. Appl. Therm. Eng. 2018, 143, 1101–1113. [Google Scholar] [CrossRef]
- Zhao, Z.C.; Zhang, X.; Zhao, K.; Jiang, P.P.; Chen, Y.P. Numerical investigation on heat transfer and flow characteristics of super-critical nitrogen in a straight channel of printed circuit heat exchanger. Appl. Therm. Eng. 2017, 126, 717–729. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Zhang, L.; Yao, M.; Kruizenga, A.; Anderson, M. PDF-based modeling on the turbulent convection heat transfer of supercritical CO2 in the printed circuit heat exchangers for the supercritical CO2 Brayton cycle. Int. J. Heat Mass Transf. 2016, 98, 204–218. [Google Scholar] [CrossRef]
- Chu, W.-X.; Bennett, K.; Cheng, J.; Chen, Y.-T.; Wang, Q.-W. Numerical study on a novel hyperbolic inlet header in straight-channel printed circuit heat exchanger. Appl. Therm. Eng. 2018, 146, 805–814. [Google Scholar] [CrossRef]
- Ren, Z.; Zhao, Z.R.; Jiang, P.X.; Bo, H.L. Investigation on local convection heat transfer of supercritical CO2 during cooling in hori-zontal semicircular channels of printed circuit heat exchanger. Appl. Therm. Eng. 2019, 157, 113697. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Christensen, R.N.; Shi, S.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Experimental and numerical study of a printed circuit heat exchanger. Ann. Nucl. Energy 2016, 97, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Marchionni, M.; Chai, L.; Bianchi, G.; Tassou, S.A. Numerical modelling and transient analysis of a printed circuit heat exchanger used as recuperator for supercritical CO2 heat to power conversion systems. Appl. Therm. Eng. 2019, 161, 114190. [Google Scholar] [CrossRef]
- Meshram, A.; Jaiswal, A.K.; Khivsara, S.D.; Ortega, J.D.; Ho, C.; Bapat, R.; Dutta, P. Modeling and analysis of a printed circuit heat exchanger for supercritical CO2 power cycle applications. Appl. Therm. Eng. 2016, 109, 861–870. [Google Scholar] [CrossRef] [Green Version]
- Chai, L.; Tassou, S.A. Numerical study of the thermohydraulic performance of printed circuit heat exchangers for surpercritical CO2 Brayton cycle applications. Energy Procedia 2019, 161, 480–488. [Google Scholar] [CrossRef]
- Ma, T.; Li, M.-J.; Xu, J.-L.; Cao, F. Thermodynamic analysis and performance prediction on dynamic response characteristic of PCHE in 1000 MW S-CO2 coal fired power plant. Energy 2019, 175, 123–138. [Google Scholar] [CrossRef]
- Kwon, J.S.; Bae, S.J.; Heo, J.Y.; Lee, J.I. Development of accelerated PCHE off-design performance model for optimizing power system operation strategies in S-CO2 Brayton cycle. Appl. Therm. Eng. 2019, 159, 113845. [Google Scholar] [CrossRef]
- Jeon, S.; Baik, Y.-J.; Byon, C.; Kim, W. Thermal performance of heterogeneous PCHE for supercritical CO2 energy cycle. Int. J. Heat Mass Transf. 2016, 102, 867–876. [Google Scholar] [CrossRef]
- Aneesh, A.; Sharma, A.; Srivastava, A.; Vyas, K.; Chaudhuri, P. Thermal-hydraulic characteristics and performance of 3D straight channel based printed circuit heat exchanger. Appl. Therm. Eng. 2016, 98, 474–482. [Google Scholar] [CrossRef]
- Figley, J.; Sun, X.; Mylavarapu, S.K.; Hajek, B. Numerical study on thermal hydraulic performance of a Printed Circuit Heat Exchanger. Prog. Nucl. Energy 2013, 68, 89–96. [Google Scholar] [CrossRef]
- Tu, Y.; Zeng, Y. Flow and heat transfer characteristics study of supercritical CO2 in horizontal semicircular channel for cooling process. Case Stud. Therm. Eng. 2020, 21, 100691. [Google Scholar] [CrossRef]
- Cao, X.; Rao, Z.; Liao, S. Laminar convective heat transfer of supercritical CO2 in horizontal miniature circular and triangular tubes. Appl. Therm. Eng. 2011, 31, 2374–2384. [Google Scholar] [CrossRef]
- Khalesia, J.; Sarunacb, N.; Razzaghpanah, Z. Supercritical CO2 conjugate heat transfer and flow analysis in a rectangular microchannel subject to uniformly heated substrate wall. Therm. Sci. Eng. Pro. 2020, 19, 100596. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.; Huai, X.; Cui, X.; Cheng, K. Buoyancy effects on coupled heat transfer of supercritical pressure CO2 in horizontal semicircular channels. Int. J. Heat Mass Transf. 2019, 134, 437–449. [Google Scholar] [CrossRef]
- Nikitin, K.; Kato, Y.; Ngo, L. Printed circuit heat exchanger thermal–hydraulic performance in supercritical CO2 experimental loop. Int. J. Refrig. 2006, 29, 807–814. [Google Scholar] [CrossRef]
- Kim, I.H.; No, H.C.; Lee, J.I.; Jeon, B.G. Thermal hydraulic performance analysis of the printed circuit heat exchanger using a helium test facility and CFD simulations. Nucl. Eng. Des. 2009, 239, 2399–2408. [Google Scholar] [CrossRef]
- Kim, S.G.; Lee, Y.; Ahn, Y.; Lee, J.I. CFD aided approach to design printed circuit heat exchangers for supercritical CO2 Brayton cycle application. Ann. Nucl. Energy 2016, 92, 175–185. [Google Scholar] [CrossRef]
- Bennett, K.; Chen, Y.-T. Thermal-hydraulic correlations for zigzag-channel PCHEs covering a broad range of design parameters for estimating performance prior to modeling. Therm. Sci. Eng. Prog. 2019, 17, 100383. [Google Scholar] [CrossRef]
- Cheng, K.; Zhou, J.; Zhang, H.; Huai, X.; Guo, J. Experimental investigation of thermal-hydraulic characteristics of a printed circuit heat exchanger used as a pre-cooler for the supercritical CO2 Brayton cycle. Appl. Therm. Eng. 2020, 171, 115116. [Google Scholar] [CrossRef]
- Ma, T.; Li, L.; Xu, X.-Y.; Chen, Y.-T.; Wang, Q. Study on local thermal–hydraulic performance and optimization of zigzag-type printed circuit heat exchanger at high temperature. Energy Convers. Manag. 2015, 104, 55–66. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Christensen, R.N.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Pressure drop and heat transfer characteristics of a high-temperature printed circuit heat exchanger. Appl. Therm. Eng. 2016, 108, 1409–1417. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Sun, X.; Christensen, R.N. Thermal-hydraulic performance of printed circuit heat exchangers with zigzag flow channels. Int. J. Heat Mass Transf. 2018, 130, 356–367. [Google Scholar] [CrossRef]
- Kim, I.H.; No, H.C. Thermal hydraulic performance analysis of a printed circuit heat exchanger using a helium–water test loop and numerical simulations. Appl. Therm. Eng. 2011, 31, 4064–4073. [Google Scholar] [CrossRef]
- Yoon, S.J.; O’Brien, J.; Chen, M.H.; Sabharwall, P.; Sun, X.D. Development and validation of Nu and friction factor correlations for laminar flow in semi-circular zigzag channel of printed circuit heat exchanger. Appl. Therm. Eng. 2017, 123, 1327–1344. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Christensen, R.N.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Dynamic behavior of a high-temperature printed circuit heat exchanger: Numerical modeling and experimental investigation. Appl. Therm. Eng. 2018, 135, 246–256. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, K.-Y. Comparative study on performance of a zigzag printed circuit heat exchanger with various channel shapes and configurations. Heat Mass Transf. 2013, 49, 1021–1028. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, K.-Y. A Parametric Study of the Thermal-Hydraulic Performance of a Zigzag Printed Circuit Heat Exchanger. Heat Transf. Eng. 2014, 35, 1192–1200. [Google Scholar] [CrossRef]
- Kim, I.H.; Sun, X.D. CFD study and PCHE design for secondary heat exchangers with FLiNaK-Helium for SmAHTR. Nucl. Eng. Des. 2014, 270, 325–333. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.H. Thermal and hydraulic performance of SCO2 PCHE with different fin configurations. Appl. Therm. Eng. 2017, 127, 975–985. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.; Huai, X.; Cheng, K.; Cui, X. Studies on the thermal-hydraulic performance of zigzag channel with supercritical pressure CO2. J. Supercrit. Fluids 2019, 148, 104–115. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, K.-Y. Optimization of zigzag flow channels of a printed circuit heat exchanger for nuclear power plant application. J. Nucl. Sci. Technol. 2012, 49, 343–351. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Liese, E.; Zitney, S.E.; Bhattacharyya, D. Design and dynamic modeling of printed circuit heat exchangers for supercritical carbon dioxide Brayton power cycles. Appl. Energy 2018, 231, 1019–1032. [Google Scholar] [CrossRef]
- Lee, S.Y.; Park, B.G.; Chung, J.T. Numerical studies on thermal hydraulic performance of zigzag-type printed circuit heat exchanger with inserted straight channels. Appl. Therm. Eng. 2017, 123, 1434–1443. [Google Scholar] [CrossRef]
- Ma, T.; Pasquier, U.; Chen, Y.; Wang, Q. Numerical study on thermal-hydraulic performance of a two-sided etched zigzag-type high-temperature printed circuit heat exchanger. Energy Procedia 2017, 142, 3950–3955. [Google Scholar] [CrossRef]
- Li, X.-H.; Deng, T.-R.; Ma, T.; Ke, H.-B.; Wang, Q.-W. A new evaluation method for overall heat transfer performance of supercritical carbon dioxide in a printed circuit heat exchanger. Energy Convers. Manag. 2019, 193, 99–105. [Google Scholar] [CrossRef]
- Bennett, K.; Chen, Y.-T. A two-level Plackett-Burman non-geometric experimental design for main and two factor interaction sensitivity analysis of zigzag-channel PCHEs. Therm. Sci. Eng. Prog. 2019, 11, 167–194. [Google Scholar] [CrossRef]
- Bennett, K.; Chen, Y.-T. One-way coupled three-dimensional fluid-structure interaction analysis of zigzag-channel supercritical CO2 printed circuit heat exchangers. Nucl. Eng. Des. 2019, 358, 110434. [Google Scholar] [CrossRef]
- Baik, S.; Kim, S.G.; Lee, J.; Lee, J.I. Study on CO2—water printed circuit heat exchanger performance operating under various CO₂ phases for S-CO₂ power cycle application. Appl. Therm. Eng. 2017, 113, 1536–1546. [Google Scholar] [CrossRef]
- Baik, Y.-J.; Jeon, S.; Kim, B.; Jeon, D.; Byon, C. Heat transfer performance of wavy-channeled PCHEs and the effects of waviness factors. Int. J. Heat Mass Transf. 2017, 114, 809–815. [Google Scholar] [CrossRef]
- Khan, H.H.; Sharma, A.; Srivastava, A.; Chaudhuri, P. Thermal-hydraulic characteristics and performance of 3D wavy channel based printed circuit heat exchanger. Appl. Therm. Eng. 2015, 87, 519–528. [Google Scholar] [CrossRef]
- Sung, J.; Lee, J.Y. Effect of tangled channels on the heat transfer in a printed circuit heat exchanger. Int. J. Heat Mass Transf. 2017, 115, 647–656. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Yao, M.; Gao, W.; Zhang, Y.; Zhang, L. Investigation on the effects of narrowed channel cross-sections on the heat transfer performance of a wavy-channeled PCHE. Int. J. Heat Mass Transf. 2019, 135, 33–43. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Y.; Lu, M.; Wang, J.; Yan, X. Study on the Thermal-hydraulic Performance of Sinusoidal Channeled Printed Circuit Heat Exchanger. Energy Procedia 2019, 158, 5679–5684. [Google Scholar] [CrossRef]
- Cui, X.; Guo, J.; Huai, X.; Zhang, H.; Cheng, K.; Zhou, J. Numerical investigations on serpentine channel for supercritical CO2 recuperator. Energy 2019, 172, 517–530. [Google Scholar] [CrossRef]
- Aneesh, A.; Sharma, A.; Srivastava, A.; Chaudhury, P. Effects of wavy channel configurations on thermal-hydraulic characteristics of Printed Circuit Heat Exchanger (PCHE). Int. J. Heat Mass Transf. 2018, 118, 304–315. [Google Scholar] [CrossRef]
- Ngo, T.L.; Kato, Y.; Nikitin, K.; Tsuzuki, N. New printed circuit heat exchanger with S-shaped fins for hot water supplier. Exp. Therm. Fluid Sci. 2006, 30, 811–819. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Thermal-hydraulic analysis of sinusoidal fin-based printed circuit heat exchangers for supercritical CO2 Brayton cycle. Energy Convers. Manag. 2019, 193, 124–139. [Google Scholar] [CrossRef]
- Tsuzuki, N.; Kato, Y.; Ishiduka, T. High performance printed circuit heat exchanger. Appl. Therm. Eng. 2007, 27, 1702–1707. [Google Scholar] [CrossRef]
- Tsuzuki, N.; Kato, Y.; Nikitin, K.; Ishiduka, T. Advanced microchannel heat exchanger with S-shaped fins. J. Nucl. Sci. Technol. 2009, 46, 403–412. [Google Scholar] [CrossRef]
- Kim, D.E.; Kim, M.H.; Cha, J.E.; Kim, S.O. Numerical investigation on thermal–hydraulic performance of new printed circuit heat exchanger model. Nucl. Eng. Des. 2008, 238, 3269–3276. [Google Scholar] [CrossRef]
- Xu, X.; Ma, T.; Li, L.; Zeng, M.; Chen, Y.-T.; Huang, Y.; Wang, Q. Optimization of fin arrangement and channel configuration in an airfoil fin PCHE for supercritical CO2 cycle. Appl. Therm. Eng. 2014, 70, 867–875. [Google Scholar] [CrossRef]
- Kim, T.H.; Kwon, J.G.; Yoon, S.H.; Park, H.S.; Kim, M.H.; Cha, J.E. Numerical analysis of air-foil shaped fin performance in printed circuit heat exchanger in a supercritical carbon dioxide power cycle. Nucl. Eng. Des. 2015, 288, 110–118. [Google Scholar] [CrossRef]
- Ma, T.; Xin, F.; Li, L.; Xu, X.-Y.; Chen, Y.-T.; Wang, Q. Effect of fin-endwall fillet on thermal hydraulic performance of airfoil printed circuit heat exchanger. Appl. Therm. Eng. 2015, 89, 1087–1095. [Google Scholar] [CrossRef]
- Chu, W.-X.; Li, X.-H.; Ma, T.; Chen, Y.-T.; Wang, Q. Study on hydraulic and thermal performance of printed circuit heat transfer surface with distributed airfoil fins. Appl. Therm. Eng. 2017, 114, 1309–1318. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, L.; Huai, X.; Li, J.; Zhang, H.; Liu, Z. Comprehensive performance comparison of airfoil fin PCHEs with NACA 00XX series airfoil. Nucl. Eng. Des. 2017, 315, 42–50. [Google Scholar] [CrossRef]
- Cui, X.Y.; Guo, J.F.; Huai, X.L.; Cheng, K.Y.; Zhang, H.Y.; Xiang, M.R. Numerical study on novel airfoil fins for printed circuit heat exchanger using supercritical CO2. Int. J. Heat Mass Tran. 2018, 121, 354–366. [Google Scholar] [CrossRef]
- Pidapartia, S.R.; Andersonb, M.H.; Ranjan, D. Experimental investigation of thermal-hydraulic performance of discontinuous fin printed circuit heat exchangers for supercritical CO2 power cycles. Exp. Therm. Fluid Sci. 2019, 106, 119–129. [Google Scholar] [CrossRef]
- Fu, Q.; Ding, J.; Lao, J.; Wang, W.; Lu, J. Thermal-hydraulic performance of printed circuit heat exchanger with supercritical carbon dioxide airfoil fin passage and molten salt straight passage. Appl. Energy 2019, 247, 594–604. [Google Scholar] [CrossRef]
- Wang, W.-Q.; Qiu, Y.; He, Y.-L.; Shi, H.-Y. Experimental study on the heat transfer performance of a molten-salt printed circuit heat exchanger with airfoil fins for concentrating solar power. Int. J. Heat Mass Transf. 2019, 135, 837–846. [Google Scholar] [CrossRef]
- Shi, H.-Y.; Li, M.-J.; Wang, W.-Q.; Qiu, Y.; Tao, W.-Q. Heat transfer and friction of molten salt and supercritical CO2 flowing in an airfoil channel of a printed circuit heat exchanger. Int. J. Heat Mass Transf. 2020, 150, 119006. [Google Scholar] [CrossRef]
- Kwon, J.G.; Kim, T.H.; Park, H.S.; Cha, J.E.; Kim, M.H. Optimization of airfoil-type PCHE for the recuperator of small scale brayton cycle by cost-based objective function. Nucl. Eng. Des. 2016, 298, 192–200. [Google Scholar] [CrossRef]
- Bichnevicius, M.; Saltzman, D.; Lynch, S. Comparison of Louvered Plate-Fin Heat Exchangers Made via Additive Manufacturing; IMECE: Pittsburgh, PA, USA, 2018; p. 87941. [Google Scholar]
- Rasouli, E.; Subedi, S.; Montgomery, C.; Mande, C.W.; Stevens, M.; Narayanan, V.; Rollett, A.D. Design and performance characterization of an additively manufactured primary heat exchanger for sCO2 waste heat recovery cycles. In Proceedings of the 6th International Supercritical CO2 Power Cycles Symposium, Pittsburgh, PA, USA, 27–29 March 2018. [Google Scholar]
- Saltzman, D.; Bichnevicius, M.; Lynch, S.; Simpson, T.W.; Reutzel, E.; Dickman, C.; Martukanitz, R. Design and evaluation of an additively manufactured aircraft heat exchanger. Appl. Therm. Eng. 2018, 138, 254–263. [Google Scholar] [CrossRef]
- Moon, H.; Miljkovic, N.; King, W.P. High power density thermal energy storage using additively manufactured heat exchangers and phase change material. Int. J. Heat Mass Transf. 2020, 153, 119591. [Google Scholar] [CrossRef]
- Searle, M.; Black, J.; Straub, D.; Robey, E.; Yip, J.; Ramesh, S.; Roy, A.; Sabau, A.S.; Mollot, D. Heat transfer coefficients of additively manufactured tubes with internal pin fins for supercritical carbon dioxide cycle recuperators. Appl. Therm. Eng. 2020, 181, 116030. [Google Scholar] [CrossRef]
- Ho, J.Y.; Leong, K.; Wong, T. Additively-manufactured metallic porous lattice heat exchangers for air-side heat transfer enhancement. Int. J. Heat Mass Transf. 2020, 150, 119262. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Xu, J.C.; Ge, T.S.; Dai, Y.J.; Wang, R.Z. Design optimization and validation of high-performance heat exchangers using approximation assisted optimization and additive manufacturing. Sci. Technol. Built Environ. 2017, 23, 896–911. [Google Scholar]
- Cormier, Y.; Dupuis, P.; Farjam, A.; Corbeil, A.; Jodoin, B. Additive manufacturing of pyramidal pin fins: Height and fin density effects under forced convection. Int. J. Heat Mass Transf. 2014, 75, 235–244. [Google Scholar] [CrossRef]
- Kirsch, K.; Thole, K.A. Pressure loss and heat transfer performance for additively and conventionally manufactured pin fin arrays. Int. J. Heat Mass Transf. 2017, 108, 2502–2513. [Google Scholar] [CrossRef] [Green Version]
- Arie, M.A.; Shooshtari, A.H.; Tiwari, R.; Dessiatoun, S.V.; Ohadi, M.M.; Pearce, J. Experimental characterization of heat transfer in an additively manufactured polymer heat exchanger. Appl. Therm. Eng. 2016, 113, 575–584. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.; Andhare, R.S.; Shooshtari, A.; Ohadi, M. Development of an additive manufacturing-enabled compact manifold microchannel heat exchanger. Appl. Therm. Eng. 2018, 147, 781–788. [Google Scholar] [CrossRef]
- Greiciunas, E.; Borman, D.; Summers, J.; Smith, S.J. A numerical evaluation of next generation additive layer manufactured inter-layer channel heat exchanger. Appl. Therm. Eng. 2019, 162, 114304. [Google Scholar] [CrossRef]
- Wei, C.; Diaz, G.A.V.; Wang, K.; Li, P. 3D-printed tubes with complex internal fins for heat transfer enhancement—CFD analysis and performance evaluation. AIMS Energy 2020, 8, 27–47. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. Pro. ASME Int. Mech. Eng. Congress Expos. 1995, 66, 99–105. [Google Scholar]
- Hosseini, S.B.; Khoshkhoo, R.H.; Malabad, S.J. Experimental and numerical investigation on particle deposition in a compact heat exchanger. Appl. Therm. Eng. 2017, 115, 406–417. [Google Scholar] [CrossRef]
- Sohel, M.; Khaleduzzaman, S.; Saidur, R.; Hepbasli, A.; Sabri, M.F.M.; Mahbubul, I. An experimental investigation of heat transfer enhancement of a minichannel heat sink using Al2O3–H2O nanofluid. Int. J. Heat Mass Transf. 2014, 74, 164–172. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M. Influence of different design parameters and Al2O3 -water nanofluid flow on heat transfer and flow characteristics of sinusoidal-corrugated channels. Energy Convers. Manag. 2014, 88, 96–105. [Google Scholar] [CrossRef]
- Ray, D.; Das, D.K.; Vajjha, R.S. Experimental and numerical investigations of nanofluids performance in a compact minichannel plate heat exchanger. Int. J. Heat Mass Transf. 2014, 71, 732–746. [Google Scholar] [CrossRef]
- Gkountas, A.A.; Benos, L.T.; Nikas, K.-S.; Sarris, I.E. Heat transfer improvement by an Al2O3-water nanofluid coolant in printed-circuit heat exchangers of supercritical CO2 Brayton cycle. Therm. Sci. Eng. Prog. 2020, 20, 100694. [Google Scholar] [CrossRef]
- Gkountas, A.A.; Benos, L.T.; Sofiadis, G.N.; Sarris, I.E. A printed-circuit heat exchanger consideration by exploiting an Al2O3-water nanofluid: Effect of the nanoparticles interfacial layer on heat transfer. Therm. Sci. Eng. Prog. 2020, 22, 100818. [Google Scholar] [CrossRef]
- Chennu, R.; Veeredhi, V.R. Measurement of heat transfer coefficient and pressure drops in a compact heat exchanger with lance and offset fins for water based Al2O3 nano-fluids. Heat Mass Transf. 2019, 56, 257–267. [Google Scholar] [CrossRef]
- Stogiannis, I.; Mouza, A.; Paras, S. Efficacy of SiO2 nanofluids in a miniature plate heat exchanger with undulated surface. Int. J. Therm. Sci. 2015, 92, 230–238. [Google Scholar] [CrossRef]
- Ajeel, R.K.; Salim, W.-I.; Hasnan, K. Numerical investigations of heat transfer enhancement in a house shaped-corrugated channel: Combination of nanofluid and geometrical parameters. Therm. Sci. Eng. Prog. 2019, 17, 100376. [Google Scholar] [CrossRef]
- Khanlari, A.; Sözen, A.; Variyenli, H.I. Simulation and experimental analysis of heat transfer characteristics in the plate type heat exchangers using TiO2/water nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1343–1362. [Google Scholar] [CrossRef]
- Baba, M.S.; AVRaju, S.R.; Rao, M.B. Heat transfer enhancement and pressure drop of Fe3O4 -water nanofluid in a double tube counter flow heat exchanger with internal longitudinal fins. Case Stud. Therm. Eng. 2018, 12, 600–607. [Google Scholar] [CrossRef]
- Martínez, V.A.; Lozano-Steinmetz, F.; Vasco, D.A.; Zapata, P.A.; Chi-Duran, I.; Singh, D.P. Thermal characterization and stability analysis of aqueous ZnO-based nanofluids numerically implemented in microchannel heat sinks. Therm. Sci. Eng. Prog. 2021, 22, 100792. [Google Scholar] [CrossRef]
- Samruaisin, P.; Wongcharee, K.; Chuwattanakul, V.; Eiamsa-ard, S. Silver-water nanofuid fow and convective heat transfer in a micro-fin tube equipped with loose-fit twisted tapes. J. Therm. Anal. Calorim. 2020, 140, 2541–2554. [Google Scholar] [CrossRef]
- Manikandan, S.P.; Baskar, R. Heat transfer studies in compact heat exchanger using ZnO and TiO2 nanofluids in ethylene glycol/water. Chem. Ind. Chem. Eng. Q. 2018, 24, 309–318. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Pandya, N.; Pandya, B.; Joshi, A. Synthesis of metal-based nanofluids and their thermo-hydraulic performance in compact heat exchanger with multi-louvered fins working under laminar conditions. J. Therm. Anal. Calorim. 2019, 135, 2221–2235. [Google Scholar] [CrossRef]
- Ajeel, R.K.; Salim, W.-I.; Hasnan, K. Experimental and numerical investigations of convection heat transfer in corrugated channels using alumina nanofluid under a turbulent flow regime. Chem. Eng. Res. Des. 2019, 148, 202–217. [Google Scholar] [CrossRef]
- Abed, A.M.; Alghoul, M.; Sopian, K.; Mohammed, H.; Majdi, H.; Al-Shamani, A. Design characteristics of corrugated trapezoidal plate heat exchangers using nanofluids. Chem. Eng. Process. Process. Intensif. 2014, 87, 88–103. [Google Scholar] [CrossRef]
- Bezaatpour, M.; Rostamzadeh, H. Heat transfer enhancement of a fin-and-tube compact heat exchanger by employing magnetite ferrofluid flow and an external magnetic field. Appl. Therm. Eng. 2019, 164, 114462. [Google Scholar] [CrossRef]
- Dang, D.; Hihara, E. In-tube cooling heat transfer of supercritical carbon dioxide. Part 1. Experimental measurement. Int. J. Refrig. 2004, 27, 736–747. [Google Scholar] [CrossRef]
- Cai, H.-F.; Jiang, Y.-Y.; Wang, T.; Liang, S.-Q.; Zhu, Y.-M. Experimental investigation on convective heat transfer and pressure drop of supercritical CO2 and water in microtube heat exchangers. Int. J. Heat Mass Transf. 2020, 163, 120443. [Google Scholar] [CrossRef]
- Kruizenga, A.; Li, H.; Anderson, M.; Corradini, M. Supercritical Carbon Dioxide Heat Transfer in Horizontal Semicircular Channels. J. Heat Transf. 2012, 134, 081802. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, J.G.; Kim, M.H.; Cha, J.E.; Jo, H. Experimental investigation of buoyancy effects on local heat transfer of supercritical pressure CO2 in horizontal semicircular tube. Int. J. Heat Mass Transf. 2020, 164, 120496. [Google Scholar] [CrossRef]
- Gupta, S.; Saltanov, E.; Mokry, S.J.; Pioro, I.; Trevani, L.; McGillivray, D. Developing empirical heat-transfer correlations for supercritical CO2 flowing in vertical bare tubes. Nucl. Eng. Des. 2013, 261, 116–131. [Google Scholar] [CrossRef]
- Kim, E.D.; Kim, M.H. Experimental investigation of heat transfer in vertical upward and downward supercritical CO2 flow in a circular tube. Int. J. Heat Fluid Flow 2011, 32, 176–191. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Liu, B.; Zhao, C.-R.; Luo, F. Convection heat transfer of supercritical pressure carbon dioxide in a vertical micro tube from transition to turbulent flow regime. Int. J. Heat Mass Transf. 2012, 56, 741–749. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, T.J.; Drögemüller, P.; Yu, Q.H.; Ding, Y.L.; Li, Y.L. Enhancing deteriorated heat transfer of supercritical nitrogen in a vertical tube with wire matrix insert. Int. J. Heat Mass Tran. 2020, 162, 120358. [Google Scholar] [CrossRef]
- Cheng, H.; Ju, Y.; Fu, Y. Experimental and simulation investigation on heat transfer characteristics of supercritical nitrogen in a new rib tube of open rack vaporizer. Int. J. Refrig. 2019, 111, 103–112. [Google Scholar] [CrossRef]
- Basha, H.; Reddy, G.J.; Narayanan, N.S.V. Heat Transfer Characteristics of Nitrogen in Supercritical Region Using Redlich-Kwong Equation of State. Int. J. Chem. React. Eng. 2019, 17. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Shen, B.; Wang, R. Flow and heat transfer characteristics of supercritical nitrogen in a vertical mini-tube. Int. J. Therm. Sci. 2011, 50, 287–295. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Chen, X.; Ma, X.; Yang, S.; Li, S. Experimental and numerical investigation of thermal-hydraulic performance of supercritical nitrogen in airfoil fin printed circuit heat exchanger. Appl. Therm. Eng. 2019, 168, 114829. [Google Scholar] [CrossRef]
- Zhu, C.-Y.; Guo, Y.; Yang, H.-Q.; Ding, B.; Duan, X.-Y. Investigation of the flow and heat transfer characteristics of helium gas in printed circuit heat exchangers with asymmetrical airfoil fins. Appl. Therm. Eng. 2020, 186, 116478. [Google Scholar] [CrossRef]
- Wang, H.; Bi, Q.; Yang, Z.; Gang, W.; Hu, R. Experimental and numerical study on the enhanced effect of spiral spacer to heat transfer of supercritical pressure water in vertical annular channels. Appl. Therm. Eng. 2012, 48, 436–445. [Google Scholar] [CrossRef]
- Li, Z.; Lu, J.; Tang, G.; Liu, Q.; Wu, Y. Effects of rib geometries and property variations on heat transfer to supercritical water in internally ribbed tubes. Appl. Therm. Eng. 2015, 78, 303–314. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Bi, Q.; Wang, L. Experimental study of heat transfer and flow resistance of supercritical pressure water in a SCWR sub-channel. J. Supercrit. Fluids 2015, 100, 15–25. [Google Scholar] [CrossRef]
- Gang, W.; Pan, J.; Bi, Q.; Yang, Z.; Wang, H. Heat transfer characteristics of supercritical pressure water in vertical upward annuli. Nucl. Eng. Des. 2014, 273, 449–458. [Google Scholar] [CrossRef]
- Hu, Z.-X.; Liu, D.; Gu, H.-Y. Study on spacer-induced heat transfer deterioration of supercritical water in annular channel. Int. J. Heat Mass Transf. 2018, 125, 552–558. [Google Scholar] [CrossRef]
- Zhang, B.; Shan, J.; Jiang, J. Numerical analysis of supercritical water heat transfer in horizontal circular tube. Prog. Nucl. Energy 2010, 52, 678–684. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.; Gu, H.; Yang, Y.; Cheng, X. Experimental and numerical investigation of turbulent convective heat transfer deterioration of supercritical water in vertical tube. Nucl. Eng. Des. 2012, 248, 226–237. [Google Scholar] [CrossRef]
- Jaromin, M.; Anglart, H. A numerical study of heat transfer to supercritical water flowing upward in vertical tubes under normal and deteriorated conditions. Nucl. Eng. Des. 2013, 264, 61–70. [Google Scholar] [CrossRef]
- Wen, Q.; Gu, H. Numerical simulation of heat transfer deterioration phenomenon in supercritical water through vertical tube. Ann. Nucl. Energy 2010, 37, 1272–1280. [Google Scholar] [CrossRef]
- Lei, X.; Li, H.; Yu, S.; Chen, T. Numerical investigation on the mixed convection and heat transfer of supercritical water in horizontal tubes in the large specific heat region. Comput. Fluids 2012, 64, 127–140. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, M.; Feuerstein, F.; Liu, X. Prediction of heat transfer to supercritical water at different boundary conditions. Int. J. Heat Mass Transf. 2018, 131, 527–536. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Lu, J.; Zhang, D.; Zhang, H. Heat transfer to supercritical water in circular tubes with circumferentially non-uniform heating. Appl. Therm. Eng. 2014, 70, 190–200. [Google Scholar] [CrossRef]
- Bai, J.; Pan, J.; Wu, G.; Tang, L. Numerical investigation on the heat transfer of supercritical water in non-uniform heating tube. Int. J. Heat Mass Transf. 2019, 138, 1320–1332. [Google Scholar] [CrossRef]
- Wen, Q.; Gu, H. Numerical investigation of acceleration effect on heat transfer deterioration phenomenon in supercritical water. Prog. Nucl. Energy 2011, 53, 480–486. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, D.; Chen, G.; Xiao, F. Experimental investigation on heat transfer characteristics of smooth tube with downward flow. Int. J. Heat Mass Transf. 2014, 68, 669–676. [Google Scholar] [CrossRef]
- Wang, H.; Bi, Q.; Yang, Z.; Wang, L. Experimental and numerical investigation of heat transfer from a narrow annulus to supercritical pressure water. Ann. Nucl. Energy 2015, 80, 416–428. [Google Scholar] [CrossRef]
- Zhao, M.; Gu, H.; Cheng, X. Experimental study on heat transfer of supercritical water flowing downward in circular tubes. Ann. Nucl. Energy 2013, 63, 339–349. [Google Scholar] [CrossRef]
- Gang, W.; Bi, Q.; Yang, Z.; Wang, H.; Zhu, X.; Hao, H.; Leung, L. Experimental investigation of heat transfer for supercritical pressure water flowing in vertical annular channels. Nucl. Eng. Des. 2011, 241, 4045–4054. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, D.; Wang, S.; Wang, W.; Li, Y. Experimental and numerical analysis of heat transfer to water at supercritical pressures. Int. J. Heat Mass Transf. 2017, 108, 1676–1688. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Tang, G.; Zhang, D.; Lu, J. Comparison between heat transfer to supercritical water in a smooth tube and in an internally ribbed tube. Int. J. Heat Mass Transf. 2015, 84, 529–541. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Luo, Y.; Gu, H.; Shi, X.; Chen, T.; Laurien, E.; Zhu, Y. Experimental investigation on heat transfer from a heated rod with a helically wrapped wire inside a square vertical channel to water at supercritical pressures. Nucl. Eng. Des. 2009, 239, 2004–2012. [Google Scholar] [CrossRef]
- Yu, S.; Li, H.; Lei, X.; Feng, Y.; Zhang, Y.; He, H.; Wang, T. Influence of buoyancy on heat transfer to water flowing in horizontal tubes under supercritical pressure. Appl. Therm. Eng. 2013, 59, 380–388. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Guo, B.; Yu, S.; Zhang, Y.; Chen, T. Investigation of forced convection heat transfer of supercritical pressure water in a vertically upward internally ribbed tube. Nucl. Eng. Des. 2009, 239, 1956–1964. [Google Scholar] [CrossRef]
- Kao, M.-T.; Lee, M.; Ferng, Y.-M.; Chieng, C.-C. Heat transfer deterioration in a supercritical water channel. Nucl. Eng. Des. 2010, 240, 3321–3328. [Google Scholar] [CrossRef]
- Li, F.; Bai, B. A model of heat transfer coefficient for supercritical water considering the effect of heat transfer deterioration. Int. J. Heat Mass Transf. 2019, 133, 316–329. [Google Scholar] [CrossRef]
- Chen, L.; Liu, D.; Zhang, H.; Li, Q. Theoretical investigations on heat transfer to H2O/CO2 mixtures in supercritical region. Sci. China Ser. E Technol. Sci. 2020, 63, 1018–1024. [Google Scholar] [CrossRef]
- Jackson, J. Fluid flow and convective heat transfer to fluids at supercritical pressure. Nucl. Eng. Des. 2013, 264, 24–40. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, H.; Liu, D.; Li, S.; Li, Q. Experimental investigations on heat transfer to H2O/CO2 mixtures in supercritical region. Int. Commun. Heat Mass Transf. 2020, 116, 104706. [Google Scholar] [CrossRef]
- Mokry, S.; Pioro, I.; Farah, A.; King, K.; Gupta, S.; Peiman, W.; Kirillov, P. Development of supercritical water heat-transfer correlation for vertical bare tubes. Nucl. Eng. Des. 2011, 241, 1126–1136. [Google Scholar] [CrossRef]

| Authors | Research Method | Type | Research Work |
|---|---|---|---|
| Korzen & Taler [31] | Num & Exp | plain fin; oval tube | A method to establish a mathematical model of a tube-fin cross-flow heat exchanger is proposed and verified by experiments. |
| Taler [32] | Num & Exp | plain fin; circular tube | The proposed numerical simulation method based on the finite volume method and the integral average of tube exhaust temperature is suitable for the modeling of PFHE, and it is verified in the digital control system of automobile radiator. |
| Zhang et al. [28] | Exp | plain fin; circular tube | The effects of the single-phase and two-phase flow distribution of PFHE and the uneven flow distribution on heat transfer performance of PFHE are experimentally studied, and some improved perforated plate header structures are proposed. |
| Wen et al. [33] | Num | plain fin; circular tube | A hybrid genetic algorithm based on the Kriging response surface is presented, which is used to optimize the structure of zigzag fins of PFHE. |
| Blecich [34] | Exp | four-depth-row plain fin; tube with face split | The effect of the unevenness of the air flow on the thermal and hydraulic performance of PFHE is experimentally studied. The degree of efficiency drop and pressure drop increase depends on the degree of unevenness of the airflow and the orientation between the unevenness of the airflow and the pipe-side fluid circuit. |
| Yaïci et al. [35] | Num | plain fin; staggered circular tube | Using CFD simulations, the wind-side pressure transfer characteristics and geometric parameters of heat exchangers with different vertical tube spacing, horizontal tube spacing, and fin tube spacing are calculated and evaluated. |
| Hassan & Sajjad [36] | Num | plain fin; cross flow | Based on a multi-objective optimization algorithm, the cross-flow heat exchanger is optimized considering the influence of uneven flow distribution on both sides of the cold and hot. |
| Dogan et al. [37] | Exp | louvered fin-flat-tube type; double-row; triple-row | The research of PFHE was studied by experiment. NTU, effectiveness, j, f and volume goodness factor were considered. |
| Okbaz et al. [38] | Num | louver fin; double row tube | According to the louver angle, the fin spacing and Re, and the thermal hydraulic performance was studied, and the report was based on j and f |
| Ryu & Lee [39] | Num | corrugated louvered fin | Correlations developed can be applied not only to Fp/Lp < 1, but also to Fp/Lp > 1 when the range of Re is from 100 to 3000. |
| Dezan et al. [40] | Num | multi-louvered fin; delta-winglet vortex generators | Based on the combination of multi-louver wing and delta wing vortex generator, the influence of input parameters on heat transfer and pressure drop was studied. |
| Karthik et al. [41] | Num & Exp | louvered fin; air flow | Experiments on louver fins used as car radiators under different air flow rates showed that the f and j in the computational fluid dynamics analysis are in good agreement with the experimental data. The predicted value of the available correlation has a large deviation. |
| Javaherdeh et al. [42] | Num & Exp | louvered fin | The influence of louver angle and pitch on PFHE was studied. Besides louver number, the non-louvered inlet, exit fin length and re-direction of fluid flow were also considered. |
| Zuoqin et al. [43] | Num | Staggered fin; circular tube | The effect of louver fin configurations on heat transfer was investigated. |
| Habibian et al. [44] | Num | Louvered fin; Triangular & triangular vortex generator | Three fin models of shutters, triangular vortex generators and rectangular vortex generators have been established, and the performances of ordinary fins have been compared. |
| Gholami et al. [45] | Num | corrugated fin; oval tube | The effects of nine geometric factors, such as fin spacing, wing angle and groove angle of corrugated fins on performance of corrugated finned tubes in four rows of inline elliptical tube bundles were studied. |
| Sadeghianjahromi et al. [46] | Num | Louvered fin | The j and f are hardly affected by the pitch of fins, but reduce with the increase of the transverse and longitudinal tube spacing. Using the full factor method of maximum j and minimum f, the optimal angle of the blinds is about 20°. |
| Damavandi et al. [47] | Num | Wavy fin; Elliptical tube | Multi-objective optimization was carried out for the wavy fins and elliptical tube heat exchanger. |
| Gholami et al. [48] | Num | One-corrugated and three-corrugated fins; oval tube | The average Nu can be raised to 20.0% compared with the baseline case, meanwhile pressure drop can be reduced to 19.0%. |
| Zhang et al. [49] | Num & Exp | Humped and Triangular wavy fin | A new hump wave fin was proposed, and the flow and heat transfer characteristics of different hump radius (R = 0.3, 0.5, 0.7 and 0.9 mm) and Re (500 ≤ Re ≤ 5000) are studied. |
| Gholami et al. [45] | Num | Corrugated fin with one, two and three fluted domains; four-row inline oval tube bank | The corrugated section fins can significantly improve the heat transfer enhancement by changing the shape of the elliptical tube, the number of grooves and the different parameters of the groove area. |
| Lotfi et al. [50] | Num | smooth wavy fin; elliptical tube; rectangular trapezoidal winglet; angle rectangular winglet; curved angle rectangular winglet | Reducing the synergy angle is the main mechanism to improve thermal performance. According to the Re, VGs angle of attack, tube ellipticity ratio and wave fin height, a new correlation is proposed to estimate the average Nu, f and coordination angle. |
| Li et al. [51] | Num & Exp | plain fin with twelve VGs of delta winglets around each tube; circular wavy fin | Correlation of the Nu and f on the air side are achieved. Through internal analysis, the mechanism of thermal enhancement is revealed. |
| Tang et al. [52] | Num & Exp | plain-fin oval tube; Air inlet angle | The inlet angles of 45° and 90° correspond to the best thermal performance and the smallest pressure loss, respectively, while the inlet angle of 30° has the worst comprehensive performance. |
| Abeykoon [53] | Num | Design and optimization | This studies the theory of the design process of the heat exchanger, and then uses computational fluid dynamics to analyze and optimize its performance. Theoretical results and computational fluid dynamics results show that the difference in cooling performance of the thermal fluid is only 1.05%. Axial pressure drop is positively correlated with overall heat transfer coefficient and pumping power demand |
| Aasi et al. [54] | Exp | Plain rectangular fin; cross-flow; three-fluid; Artificial neural network | All four possible fluid arrangements for the cross-flow configuration are studied in detail. The ANN model is further used to predict the thermal-hydraulic efficiency of two inputs (Re and flow arrangement type) and four output performance parameters (j, f and efficiency ratio). |
| Unger et al. [55] | Exp | conventional circular plain fins (CPF); circular integrated pin fins (CIPF); serrated integrated pin fins (SIPF) | The thermal characteristics and flow characteristics of the traditional CPF, CIPF and CIPF with 1600-6600 Re in two rows and three rows were studied experimentally. This kind of heat exchanger enhances the thermal conductivity of the fin body and enhances the convective heat transfer capability on the air side through integrated pins and serrations. |
| Blecich et al. [56] | Exp | two fin-tube heat exchangers | A tube element method was developed under uneven air flow and verified by experiments. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, G.; Li, Z.; Zhang, F.; Liu, L.; E, J. A Review on the Thermal-Hydraulic Performance and Optimization of Compact Heat Exchangers. Energies 2021, 14, 6056. https://doi.org/10.3390/en14196056
Liao G, Li Z, Zhang F, Liu L, E J. A Review on the Thermal-Hydraulic Performance and Optimization of Compact Heat Exchangers. Energies. 2021; 14(19):6056. https://doi.org/10.3390/en14196056
Chicago/Turabian StyleLiao, Gaoliang, Zhizhou Li, Feng Zhang, Lijun Liu, and Jiaqiang E. 2021. "A Review on the Thermal-Hydraulic Performance and Optimization of Compact Heat Exchangers" Energies 14, no. 19: 6056. https://doi.org/10.3390/en14196056
APA StyleLiao, G., Li, Z., Zhang, F., Liu, L., & E, J. (2021). A Review on the Thermal-Hydraulic Performance and Optimization of Compact Heat Exchangers. Energies, 14(19), 6056. https://doi.org/10.3390/en14196056