Optimization of Electric Vehicles Based on Frank-Copula-GlueCVaR Combined Wind and Photovoltaic Output Scheduling Research

Abstract

Improving the efficiency of renewable energy and electricity utilization is an urgent problem for China under the objectives of carbon peaking and carbon neutralization. This paper proposes an optimization scheduling method of electric vehicles (EV) combined with wind and photovoltaic power based on the Frank-Copula-GlueCVaR. First, a joint output model based on copula theory was built to describe the correlation between wind and photovoltaic power output. Second, the Frank-Copula-GlueCVaR index was introduced in a novel way. Operators can now predetermine the future wind-photovoltaic joint output range based on this index and according to their risk preferences. Third, an optimal scheduling model aimed at reducing the group charging cost of EVs was proposed, thereby encouraging EV owners to participate in the demand response. Fourth, this paper: proposes the application of a Variant Roth–Serve algorithm; regards the EV group as a multi-intelligent group; and finds the Pareto optimal strategy of the EV group through continuous learning. Finally, case study results are shown to effectively absorb more renewable energy, reduce the consumption cost of the EV group, and suppress the load fluctuation of the whole EV group, which has a practical significance and theoretical value.

1. Introduction

Wind and photovoltaic power each play an important role in carbon neutralization. However, due to their intermittent and unstable characteristics, the expansion of wind and solar energies will jeopardize the stability of the power grid. On the demand side, electric vehicles (EVs) can serve both as energy consumers and energy storages [1]. Scientific charging and discharging scheduling of EVs can save charging costs for EV owners and mitigate the impact of uncoordinated EV charging on the distribution network. Therefore, the optimization of EV charging and discharging scheduling, considering the application of wind power and photovoltaics, has the potential to benefit both grid security and EV owners’ benefits. Therefore, accurate prediction of wind power, photovoltaic power, and the charging/discharging load of EVs is a contemporary research hot spot [2,3,4,5,6,7].

Many scholars have studied the impact of the combination of renewable energy and other distributed energy sources on modern power systems [8,9,10]. Zhang et al. have considered the uncertainties of wind power and photovoltaic power in a short-term optimal operation and have proposed a wind-solar-hydro hybrid system optimal scheduling model [11]. Han and Valizadeh have used the copula theory to apprehend the correlation of wind and photovoltaic energy output [12,13]. The binary normal and Archimedes copulas were applied, respectively. This paper proposes that the Frank copula is more suitable to predict wind power and photovoltaic output.

At the same time, uncoordinated EV charging patterns may lead to undesirable effects in power systems, such as higher peak loads and lower valley loads. Therefore, B Aluisio et al. [14,15,16,17,18] studied the optimization scheduling problem when EVs were connected to the grid. F Mwasilu et al. [19] comprehensively review and evaluate research on the interaction between EVs and smart grids, depicting future power system models with EV integration. Zhang K et al. [20] have proposed a decentralized valley-filling charging strategy, with the effectiveness of the model verified in a typical scene simulation in Beijing, China. With the increasing complexity of EV scheduling, there have been numerous attempts in the research to adopt model-free reinforcement learning (RL) methods. RL methods have good generalization and applicability to systems with unknown dynamics or that are affected by significant uncertainties. Sadeghianpourhamami N et al. [21,22,23,24,25,26] have also applied RL algorithms to the optimal scheduling of EVs. This paper applies the Variant Roth–Erev (RE) reinforcement learning algorithm. Compared to the RL algorithm applied in the previous paper, the Variant RE algorithm is simple in theory, more suitable for the actual situation, and has a shorter calculation time, thus can be used for day-ahead optimization scheduling.

In addition, because there are many factors that affect the charging/discharging power of EVs, various factors should be included in the optimal scheduling of the power system with EV integration. C.L. Guo et al. [27] have proposed an analysis model to analyze the overall value of EVs, an analysis model to evaluate the pollution reduction degree of photovoltaic power generation, and a model to transfer the inherent savings of wind power to off-peak charging loads without considering the optimal scheduling of charging and discharging of EVs. When Bin Zhang et al. [28] used reinforcement learning to optimize the scheduling of EV charge and discharge, the cost of the system operator was considered, but the interests of EV owners were not considered. Therefore, it is difficult to schedule EV owners to participate in the scheduling.

This paper applied a reinforcement learning algorithm and considered the interests of EV owners to build an EV charge and discharge optimization scheduling model with wind power and photovoltaic combined contribution.

The contributions of this paper may be summarized as follows:

(1)

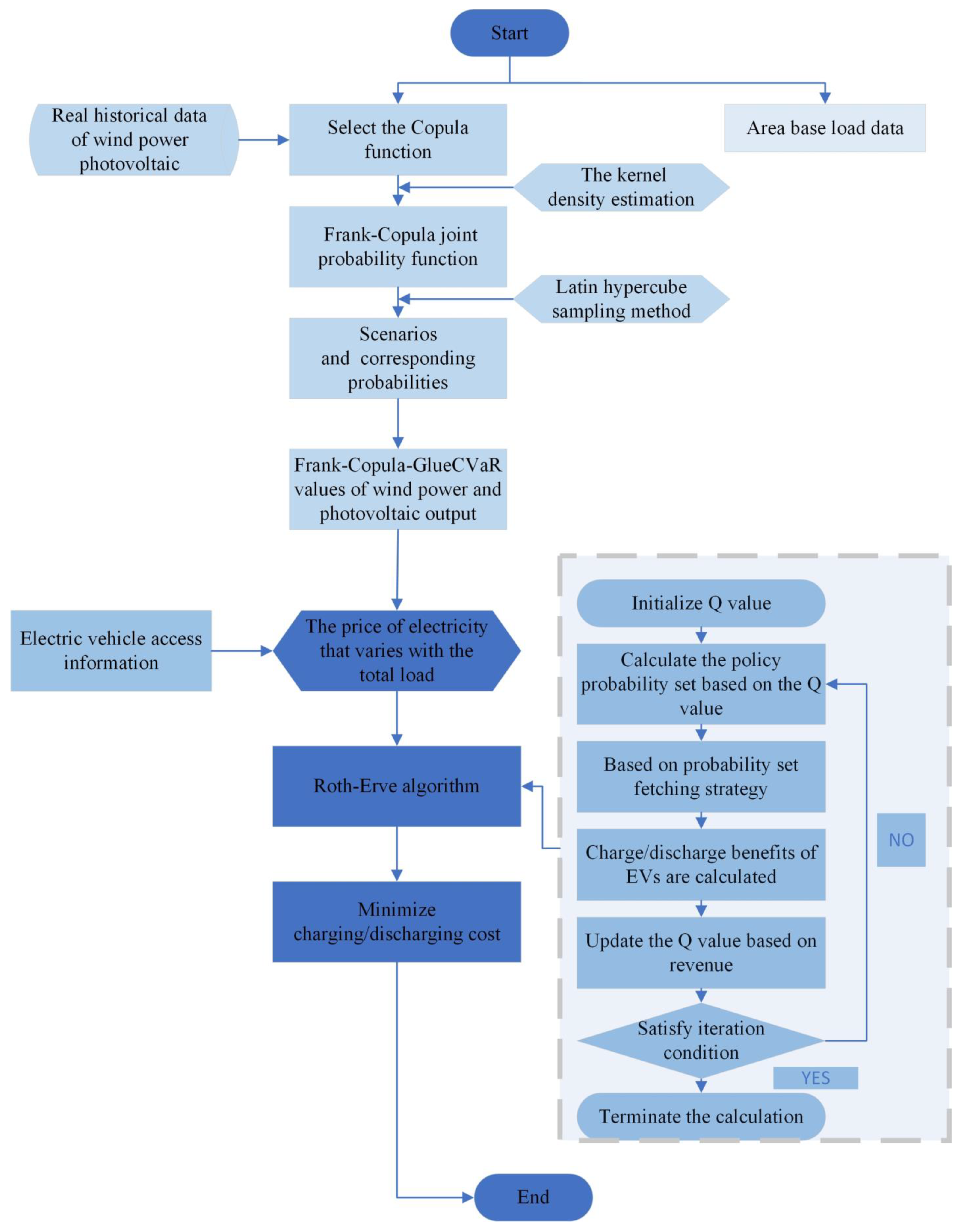
The Variant GlueCVaR risk measurement tool is proposed. The advantages of the Variant GlueCVaR are the ability to measure the risk or benefit of two related variables, the replacement of the defective VaR term in the original GlueVaR, and the ability to be effectively applied to the multivariate state.

(2)

The Frank copula function is applied to model the correlation of wind power and photovoltaic output, thus proposing the Frank-Copula-GlueCVaR index. The index can select the output value according to the risk preferences of decision makers, and can meet the different risk preferences of aggregators in different operation centers.

(3)

The Variant Roth-Erve algorithm is used to optimize the scheduling of EVs. Compared with the original Roth-Erve algorithm, the Variant Roth–Serve algorithm can further contribute to non-positive revenue, which is more suitable for the research of swarm optimization scheduling of EVs.

The remainder of the paper is organized as follows: Section 2 introduces basic theories and output models of the optimal scheduling; Section 3 describes in detail the mathematical models of each part of the system, as well as the influencing factors of the model, the optimization subjective, and their constraints; in Section 4, the application of Variant Roth–Erev reinforcement learning to the optimization of EVs is presented; Section 5 conducts an in-depth analysis and discussion on the simulation results, including sensitivity analysis, comparative analysis, scenario analysis, and carbon tax policy analysis; finally, Section 6 offers conclusions. As shown in Figure 1.

The case study presented in this paper demonstrates that the proposed index may be more effectively applied to aggregators with different preferences and that the effectiveness of the proposed algorithm is concurrently verified.

2. The Output Model of Optimal Scheduling

2.1. Related Basic Theories

2.1.1. Copula Theory

In this paper, the copula theory is used to model the correlation between wind and photovoltaic output. The copula is derived from Sklar’s theorem, which was proposed by Sklar in 1959. Sklar’s theorem is defined as follows [29]:

Let $H$ be the joint distribution function of the random variable $(X_1,X_2,\dots ,X_d)$, and $F_1,F_2,\dots ,F_d$ is the edge cumulative distribution function. There is a copula function $C(•)$ that:

$$H(x_1,x_2,\dots x_d)=C(F_1(x_1),F_2(x_2),\dots ,F_d(x_d))$$

(1)

The copula function can be obtained by using the inverse function of the joint distribution function and marginal distribution.

$$C(u_1,u_2,\dots u_n)=F(F_1^{-1}(u_1),F_2^{-1}(u_2),\dots ,F_n^{-1}(u_n))$$

(2)

As stated by Sklar’s theorem, any multivariate joint distribution can be written in terms of N univariate marginal distribution functions and a copula function. Therefore, the joint distribution modeling can be carried out from two aspects: edge distribution modeling and correlation structure modeling, so as to separate the correlation information and use the copula function for in-depth study.

2.1.2. Variant GlueCVaR Theory

The value at risk (VaR) and condition value at risk (CVaR) are used as measures to assess risks and calculate returns. VaR at level $\alpha$ is the $\alpha -$ quantile of a random VaRiable $X$ (which is called loss or benefit).

$$Va{R}_{\alpha }(X)=\inf \left\{x\right|F_X(x)\ge \alpha \}$$

(3)

where $F_X(\cdot )$ is the cumulative distribution function of $X$, and $0\le \alpha \le 1$ is the confidence level. However, VaR is not a coherent risk measure. In view of this problem, scholars have proposed the condition value at risk (CVaR) shown in Equation (4).

$$CVa{R}_{\alpha }(X)=\frac{1}{1-\alpha }{\displaystyle {\int }_{\alpha }^{1}Va{R}_{\kappa }(X)d\kappa }$$

(4)

CVaR is the mathematical expectation beyond VaR. CVaR can satisfy the nature of the risk consistency measurement. Meanwhile, CVaR can quantify the risk potential beyond VaR. Therefore, it has better control of tail risk.

Jaume et al. [30] proposed the GlueVaR theory in 2013, with risk as a measure of multiple risk preferences.

$$GlueVaR(X)={\omega }_{1}CVa{R}_{\beta }(X)+{\omega }_{2}CVa{R}_{\alpha }(X)+{\omega }_{3}Va{R}_{\alpha }(X)$$

(5)

$${\omega }_1+{\omega }_2+{\omega }_3=1$$

(6)

where $\alpha$ and $\beta$ are the confidence levels that satisfy $0\le \alpha <\beta \le 1$.

However, the GlueVaR shown in Equation (5) has two defects. First, GlueVaR only applies to one random variable, X, and thus cannot satisfy the case of multivariables. Second, terms in GlueVaR have VaR, but VaR is not a coherent risk measure. Aiming at these two problems, this paper proposes a new risk measurement tool defined as follows:

Definition 1. (Variant GlueCVaR)

For two correlated random variables X and Y, the following equation can be obtained:

$$GlueCVaR(X)={\omega }_{1}CVa{R}_{\alpha }(G(X,Y))+{\omega }_{2}CVa{R}_{\alpha }(X)+{\omega }_{3}CVa{R}_{\alpha }(Y)$$

(7)

$${\omega }_1+{\omega }_2+{\omega }_3=1$$

(8)

where$G(X,Y)$means the joint random variable of X and Y.$\alpha$is the confidence level that satisfies$0\le \alpha \le 1$.

2.2. Related Basic Theories

The joint distribution function in GlueCVaR should be characterized according to the historical data of wind and photovoltaic power in a certain area. The joint distribution of wind and photovoltaic power output can be characterized by correlation structure modeling and marginal distribution modeling.

The copula function is an efficient tool for describing the correlations between two variables. Different types of copula functions have different accuracy in describing tail correlations, so appropriate copula functions should be selected for describing different application scenarios. Among the commonly applied copula functions, Frank copula is fat-tailed. Moreover, the Frank copula can characterize the positive and negative correlations. These characteristics render the Frank copula appropriate to characterize the correlation between wind and photovoltaic power outputs.

The Frank copula belongs to Archimedean copulas, of which the copula distribution function can be generated by a generator. The Frank copula generator is $\phi (t)=-\ln (e^{-\theta t}-1)/(e^{-\theta t}-1)$, $\theta \in (-\infty ,+\infty )\backslash \left\{0\right\}$. The corresponding copula distribution function is:

$$c(u_1,u_2)=-\frac{1}{\theta }\log (1+\frac{(e^{-\theta u_1}-1)(e^{-\theta u_2}-1)}{e^{-\theta }-1})$$

(9)

where $\theta$ is the relevant parameter, and $u_1$, $u_2$ are the variables.

In this paper, the marginal distribution is obtained by a kernel density estimation based on historical data. Marginal distribution modeling and correlation modeling constitute the joint distribution of wind and photovoltaic power output. The specific steps are introduced as follows and are intuitively shown in Figure 2.

(1) Obtain marginal distribution of wind and photovoltaic power outputs. Based on $n$ days of historical wind and photovoltaic output data (sampling period is 1 h), the probability density of wind and photovoltaic output within each hour is established by using the following kernel density estimation method:

$$f_{h,t}(u_1(t))=\frac{1}{nh}{\displaystyle \sum _{d=1}^{n}K(\frac{u_1(t)-U_1(d,t)}{h})}$$

(10)

$$f_{h,t}(u_2(t))=\frac{1}{nh}{\displaystyle \sum _{d=1}^{n}K(\frac{u_2(t)-U_2(d,t)}{h})}$$

(11)

where $h$ is window width, and $U_1(d,t)$, $U_2(d,t)$ are, respectively, the wind power output and photovoltaic output at time $t$ on the $n$ h day. $K(•)$ is the kernel function.

(2) Obtain correlated power output of wind and photovoltaic. According to the Frank copula function, the joint probability density function of wind and photovoltaic output is specifically expressed as follows:

$$f(u_1,u_2)=\frac{-\theta (e^{-\theta }-1)e^{-\theta (u_1+u_2)}f(u_1)f(u_2)}{{[(e^{-\theta }-1)+(e^{-\theta u_1}-1)(e^{-\theta u_2}-1)]}^2}$$

(12)

According to the joint probability density function of the wind and photovoltaic power output, sample through Latin hypercube sampling technology. The wind and photovoltaic power output in each hour can be obtained by an inverse transformation method.

(4) N groups of scenarios of wind power and photovoltaic power output are selected, and the occurrence probability of the corresponding scenario $\gamma$ is $p(\gamma )$.

(5) The Frank-Copula-GlueCVaR of wind and photovoltaic power output is established as follows:

$$GlueCVa{R}_{\alpha }={\omega }_{1}CVa{R}_{\alpha }+{\omega }_{2}CVa{R}_{\alpha ,wp}+{\omega }_{3}CVa{R}_{{}_{\alpha ,pv}}$$

(13)

$$CVa{R}_{\alpha }=\min \{{\beta }_0+\frac{1}{1-\alpha }{\displaystyle \sum _{\gamma =1}^N{p}_{\gamma ,o}\cdot p(\gamma )}\}$$

(14)

$$CVa{R}_{\alpha ,wp}=\min \{{\beta }_{wp}+\frac{1}{1-\alpha }{\displaystyle \sum _{\gamma =1}^N{p}_{\gamma ,wp}\cdot p(\gamma )}\}$$

(15)

$$CVa{R}_{{}_{\alpha ,pv}}=\min \{{\beta }_{pv}+\frac{1}{1-\alpha }{\displaystyle \sum _{\gamma =1}^N{p}_{\gamma ,pv}\cdot p(\gamma )}\}$$

(16)

$${\omega }_1+{\omega }_2+{\omega }_3=1$$

(17)

Equations (14)–(16) represent the CVaR of the correlated wind-photovoltaic power output, the CVaR of wind power, and the CVaR of photovoltaic power output at confidence level $\alpha$, respectively. $p_{\gamma ,0}$, $p_{\gamma ,wp}$, and $p_{\gamma ,pv}$ are the power outputs of correlated wind and photovoltaic, wind power output, and photovoltaic output under scenario $\gamma$, respectively. $p(\gamma )$ is the probability of scenario $\gamma$. $GlueCVa{R}_{\alpha }$ means that the probability of the combined output of wind power is $1-\alpha$, not less than $GlueCVa{R}_{\alpha }$. That is, as long as the probability is within the risk acceptance range of decision makers, the wind power output can be considered as $GlueCVa{R}_{\alpha }$.

3. Modeling

3.1. Pricing Mechanism of EV Charging

In this paper, an aggregator in an operation center develops a real-time charging/discharging pricing mechanism for EVs. In this pricing mechanism, the price of electricity fluctuates according to load fluctuations, and the electricity price is a rising convex function of the total load [31,32,33]. In the proposed model, the combined output of wind-photovoltaic is taken into account, so that the function of determining electricity price is changed in response, and the relationship between electricity price and total load is shown in Equation (18). When the total load is lower than the given load value $L_0$, the charge/discharge price of EVs will be charged according to the standard price ${\rho }_0$, as shown in Equation (19).

$$\rho (t)=\{\begin{array}{c}\rho (L(t))\\ {\rho }_0\end{array}\begin{array}{c},\\ ,\end{array}\begin{array}{c}L(t)\ge L_0\\ L(t)<L_0\end{array}$$

(18)

$${\rho }_0=\rho (L_0)$$

(19)

$$L(t)={\displaystyle \sum _{i=1}^{N_l}{P}_{EV}(l,t)+P_{base}}(t)-GlueCVa{R}_{\alpha }(t)$$

(20)

In this paper, the total load is shown in (20). $P_{EV}(l,t)$ is the load of the $l$-th EV at time $t$; When $P_{EV}(l,t)$ is positive, the EV is charging; when $P_{EV}(l,t)$ is negative, the EV is discharging; when $P_{EV}(l,t)$ is zero, the EV is not charging or discharging. $P_{base}(t)$ is the regional base load at time $t$, which may include residential power consumption, commercial power consumption, and industrial power consumption, with different scopes according to different selected areas.

3.2. Objective Function

When an EV charges, it will receive information from the aggregator’s operation center. The information includes the following:

$$V=\{SO{C}_{in},SO{C}_{end},t_{in},t_{out},E_{type}\}$$

(21)

$$E_{type}=\{E_Q,P_C,P_D,{\eta }_C,{\eta }_D\}$$

(22)

where $SO{C}_{in}$ and $SO{C}_{end}$ represent the state of charge (SOC) of an EV when it connects to the grid and the SOC it must reach when it is disconnected, respectively. $t_{in}$ and $t_{out}$ are the times an EV starts and finishes charging, respectively. $E_{type}$ is the type of an EV. $E_{type}$ includes the EV charging and discharging power ($P_C,P_D$), EV charging and discharging efficiency (${\eta }_C,{\eta }_D$), and EV battery capacity ($E_Q$).

The purpose of this study is to minimize the charging cost of EVs, considering the combined contribution of wind power and photovoltaic power, so as to stimulate the active participation of EV owners in the demand response.

Therefore, the objective function of the model is set as the minimum charging cost of all EVs, as shown in Equation (23).

$$\min C={\displaystyle \sum _{l=1}^{N_l}{C}_l}$$

(23)

$$\min C_l={\displaystyle \sum _{t=t_{in}(l)}^{t_{out}(l)}(P_{EV}(l,t)\rho (t)\cdot \mathsf{\Delta }t+a_{loss}|P_{EV}(l,t){|}^2+b_{loss}|P_{EV}(l,t)|+c_{loss})}$$

(24)

$$P_{EV}(l,t)=\frac{1}{2}\cdot (I_0(l,t)(P_C(l){\eta }_C(l)-P_D(l){\eta }_D(l))+I_0{(l,t)}^2(P_C(l){\eta }_C(l)+P_D(l){\eta }_D(l)))$$

(25)

$$I_0(l,t)=\{-1,0,1\}$$

(26)

where $C_l$ is the charging cost of EV $l$, and $a_{loss}$, $b_{loss}$, and $c_{loss}$ are the charging and discharging loss coefficients of an EV. $I_0(l,t)$ is the charging strategy of EV $l$ at time t.

3.3. Constraints

EV charging and discharging need to meet the following constraints to satisfy the traveling requirements of EV owners so that EV owners are willing to participate in the demand response:

$$SO{C}_{in}(l)+{\displaystyle \sum _{t=t_{in}(l)}^{t_{out}(l)}{P}_{EV}(l,t)\mathsf{\Delta }t}/E_Q\ge SO{C}_{end}(l)$$

(27)

$$0\le SOC(l,t)\le 1$$

(28)

Equation (27) ensures that the SOC of an EV reaches the expected value when the EV drives away and that it does not affect the travel of EV owners. Equation (28) ensures that the SOC of each EV at any moment shall not be lower than the minimum value 0 or greater than the maximum value 1.

4. Optimal Scheduling of Electric Vehicles Based on Variant Roth–Erev Reinforcement Learning

As can be seen from Equation (24) in Section 3, the solution of the model is complex. Moreover, this is only for one EV. When the cost of all EVs is the lowest, the difficulty in solving the problem will be further increased. Therefore, this paper proposes the application of reinforcement learning to solve this problem.

In this paper, each EV is regarded as an agent, and the optimal scheduling of the EV group in the region can be regarded as a multi-agent system. Traditional optimization models cannot deal with a situation where multiple agents are simultaneously involved. The Roth–Erev (RE) algorithm provides a solution to this problem. Compared with the RE algorithm, the variant Roth–Erev (VAR) algorithm can handle cases where the net income is zero and the tendency value is negative. Moreover, a VRE algorithm can solve the problem of optimal scheduling of multi-agents. Therefore, this paper uses a VRE algorithm to optimize the charging and discharging scheduling of EVs.

The variables in the iteration process of the VRE algorithm are shown as follows:

$$\{a_l(d),q_l(d),p_l(d),{\pi }_l(d)\}, a_l(d)\in S_l$$

(29)

where $d$ is number of iterations. $a_l$ is the action taken by agent $l$ in the $d$-th iteration, which comes from the action set $S_l$. $S_l$ contains all possible actions of agent $l$. $q_l(d)$ is the propensity value of agent $l$ in $d$-th iteration, which is called the Q value. The Q value is used to calculate the action probability value $p_l(d)$. ${\pi }_l(d)$ is the benefit from each action, as defined by Equation (30):

$${\pi }_l(\cdot )=C_s(l)-C_l(\cdot )$$

(30)

$$C_s(l)\ge C_l(\cdot ),l=1,2,\dots ,N_l$$

(31)

where $C_s(l)$ shown in Equation (31) is set as general standard cost, which increases as the cost of EVs decreases. $C_s(l)$ is the incentive for EV owners to participate in demand response strategy; the charge/discharge cost of EV $l$ not participating in demand response can be used as the standard value. In addition, times of iteration, or the convergence threshold, can be set as the condition to terminate the learning process.

The VRE algorithm continuously updates $q_l(d)$ and $p_l(d)$ values in the iteration. In the iteration process, the probability of an action to bring more benefits will be more likely to be selected. Therefore, the optimization of each agent in a specific environment can be achieved.

Updates of $q_l(d)$ and $p_l(d)$ values are, respectively, calculated by Equations (32) and (33):

$$q_l(d+1)=\{\begin{array}{c}(1-r)q_l(d)+(1-ep)\cdot {\pi }_l(d)\begin{array}{cc},& a_l(d+1)=a_l(d)\end{array}\\ (1-r)q_l(d)+\frac{q_l(d)}{N-1}\cdot ep\begin{array}{cc},& a_l(d+1)\ne a_l(d)\end{array}\end{array}$$

(32)

$$p_l(d+1)=\exp (\frac{q_l(d+1)}{CP})/({\displaystyle \sum _{i=1}^N\frac{q_i(d+1)}{CP}})$$

(33)

where $r$ is the forgetting parameter, which means that the agent is more inclined to be affected by the recent actions in the learning process, while the influence of the longer actions on the next step is gradually weakened. $ep$ is an experimental parameter. A conservative agent chooses a smaller $ep$ value, which means that it is less inclined to choose a new action. An agent with a risk preference has a higher $ep$ value, indicating a greater tendency to choose unexplored new actions.

$CP$ is the Boltzmann cooling parameter. Equation (33) demonstrates that this parameter directly affects the relationship between the propensity value $q_l(d)$ and the probability value $p_l(d)$. The selection of the $CP$ value is one of the key points of the study. The appropriate $CP$ value can quickly learn the optimal decision, while the inappropriate $CP$ value may lead to the failure of the learning algorithm.

Figure 3 shows a flowchart for the EV scheduling method. First, the combined wind-photovoltaic output value is determined through the Frank-Copula-GlueCVaR index. Then, in the background of the combined contribution of wind-photovoltaic power, and considering the base load within the region, the grid connection optimization scheduling problem of EVs is studied. Finally, because the solution to this problem is too complex, this paper proposes applying a VRE reinforcement learning algorithm to learn the Pareto optimal strategy of group charging and discharging of EVs.

5. Case Study

5.1. Data Analysis

This paper collects the sales of EVs in Beijing from January to May 2020. The top four best-selling EV models were selected, as in the case analysis. Their battery parameters and market share are shown in Figure 4 and

Table 1. The type of EV.

Name	The Sales Ratio	$\mathbf{Battery} \mathbf{Capacity} (\mathbf{kw}\times \mathbf{h})$	$\mathbf{Charge}/\mathbf{Discharge} \mathbf{Power} \left(\mathbf{kw}\right)$
HG MINI	49%	13.9	1.6
T 3	26%	55	5.5
T Y	13%	77	7.7
Han EV	12%	76.9	9.6

, respectively.

As shown in Figure 4 and Table 1, the HongGuang Mini is currently the top-selling EV sold in Beijing. While its battery capacity is not high, its advantage lies in the small model, which is convenient for shuttles within cities. Tesla model 3 and Tesla model Y, as veteran brands in the EV industry, are relatively ahead in sales. BYD’s Han range of EV was close behind.

The daily driving habits of EVs are randomly generated based on data from [34,35] the Department of Transportation in 2001. The data have reference value and accords with the general habit of urban residents.

The Frank copula is used to predict the PV output of wind power, and the predicted values in different scenarios are given. Aggregators are equivalent to fund managers in the financial field. According to their risk preferences, aggregators give predicted values a risk confidence degree. Different risk confidence degrees determine different GlueCVaR index values, as is shown in Figure 5.

The 24 h data distribution of the GlueCVaR is shown in Figure 5. As is shown in Figure 5, for a GlueCVaR with six different confidence degrees, the lower is the confidence degree, the higher the value of the GlueCVaR; at the same time, the security is also lower. The manager can choose the right degree of confidence according to their risk preferences.

5.2. Case Result Analysis

In the case result analysis, the GlueCVaR with a confidence of 90% was selected as the predicted value of scenic output. This means that there is a 90% probability that the combined landscape output is not less than the GlueCVaR value. As is shown in Figure 6, it is the output force of wind power output and combined output. The GlueCVaR is the actual joint output for reference on the second day, while the green marked is the CVaR value of joint output when the confidence is 90%. Although it has a certain reference value, it is still not as safe as the GlueCVaR value.

As is shown in Figure 7, the charging and discharging costs of EVs optimized by the variant RE algorithms for scheduling proposed in this paper are compared with the charging costs of EVs participating in disordered charging. The point where a negative value appears is the actual income earned by the EV by participating in the optimization scheduling model. As is shown in

Table 2. Cost comparison.

Classification	Disorder Cost (Yuan)	VRE Cost (Yuan)	Savings Rate (%)
Total cost	774.0504796	150.636386	0.805392038
Average cost	7.740504796	1.50636386	0.805392038

, the optimal scheduling model can save an average of 80% of the cost of each vehicle owner.

It can be intuitively derived from Figure 8 that the optimized scheduling proposed in this paper can smooth the impact of group grid connection of EVs on the distribution network.

Table 3. Load comparison.

Classification	VRE Load (kwh)	Disorder Load (kwh)	Flat Rate (%)
variance	31.73568	90.1875	0.648114
Standard deviation	5.633443	9.49671	0.406801

presents the load variance and standard deviation based on VRE optimization and the load variance and standard deviation of disordered charging, respectively. As is shown in the table, the flat rate of the load exceeds 50%.

6. Conclusions

China has put forward a dual carbon target that is achieved by improving the utilization of renewable energy, increasing the use of electricity, and reducing greenhouse gas emissions. Renewable energy has intermittency, uncertainty, and other characteristics that endanger the safety and stability of the power grid. Therefore, the prediction of renewable energy output is key to improving the utilization rate of renewable energy.

In this paper, Frank-Copula-GlueCVaR values are proposed to determine the combined output of wind power and photovoltaic power. Decision makers choose different confidence degrees according to their own risk preferences and select corresponding Frank-Copula-GlueCVaR values. Under the background of wind power and photovoltaic combined grid connection, aggregators encourage EVs to participate in optimal scheduling by changing the electricity price so to reduce the impact of group charging and discharging of EVs on the grid. This paper proposes an optimal charging and discharging scheduling model for price EVs based on reinforcement learning variant RE algorithms. According to the case analysis, the cost of EVs is reduced by 80% through the optimization scheduling model proposed in this paper, while the variance and standard deviation of the load are reduced by 64% and 40%, respectively.

The case analysis proposed in this paper is limited by the small number of electric cars and tries not to bring down the demand side load fluctuations. In the future, computational speed, increased EV use, and an increase in the number and the improvement of the algorithms will allow for a more optimal dispatch of EV charging and discharging concentration calculation, including to a broader range of scheduling to damp demand side load fluctuations.

Unfortunately, this article does not compare other algorithms. In future studies, the proposed method and the improved particle swarm optimization (PSO) algorithm, column constraints generation algorithm, and other reinforcement learning algorithms will compare and analyze so to work out the most applicable and WP–PV–EV joint optimization scheduling algorithm.