Abstract
The dramatic deregulatory reforms in US electricity markets increased competition, resulting in more complex prices compared to other commodities. This paper aims to investigate and compare the overall and time-varying multifractality and efficiency of four major US electricity regions: Mass Hub, Mid C, Palo Verde, and PJM West. Multifractal detrended fluctuation analysis (MFDFA) is employed to better quantify the intensity of self-similarity. Large daily data from 2001 to 2021 are taken in order to make a more conclusive analysis. The four electricity market returns showed strong multifractal features with PJM West having the highest multifractality (corresponding to lowest efficiency) and Mass Hub having the lowest multifractality (i.e., highest efficiency). Moreover, all series exhibited mean reverting (anti-persistent) behavior in the overall time period. The findings of MFDFA rolling window suggest Palo Verde as the most volatile index, while a significant upward trend in the efficiency of Mass Hub and PJM West is observed after the first quarter of 2014. The novel findings have important implications for policymakers, regulatory authorities, and decision makers to forecast electricity prices better and control efficiency.
1. Introduction
For decades, the electricity industry has undergone drastic reforms in the United States (US) [1]. After World War II, this industry was regarded as a natural monopoly and was regulated as a state-owned utility [2]. In the 1990s, the industry was revolutionized from a natural monopoly to a free market through a wave of major regulatory reforms. Competition was injected into power generation and distribution segments of the system only [3,4]. The idea behind reforming the electricity market was to provide consumers with more choice so that the market would be driven by their preferences. For example, a consumer may choose an electricity retailer that uses ‘green’ sources such as solar, hydro, wind, etc., while another may choose the lowest cost provider irrespective of their sources [5]. Currently, most parts of the US feature open markets for new electricity generators, free trade between (giant) consumers and producers, and competitive pricing formation. Transmission services, on the other hand, are separate from generation and distribution segments and remained a monopoly under regulation due to their characteristics. Therefore, the transmission sector has been unable to attract the necessary investment due to its lack of development incentives [6].
Electricity reforms have not progressed uniformly in all US states. Some states continue to have a natural monopoly in electricity production, while others have been deregulated [5]. Under both regimes i.e., regulated and deregulated, the regulator producer is still in charge of production, but there is competition in the electricity supply. In deregulated states, electricity is distributed to suppliers who then sell it in a competitive market, while in regulated states, power is supplied directly to the consumers. Producers, distributers, and major industrial consumers who are more able to forecast electricity prices may change their consumption/supply strategies to outperform the competition in terms of cost and benefit. Furthermore, electricity prices absorb all the shocks of supply and demand. This results in spikes that exacerbate volatility because there are no electricity stockpiles to buffer shocks [7]. Hence, both producers and suppliers require better forecasts on both the demand and supply sides of the business model under both regimes. Now, the challenge is to develop strong forecasting models that accurately forecast demand and allow producers to determine the optimal output levels.
One major challenge in forecasting demand and supply is that electricity prices frequently present autocorrelation, heteroscedasticity, and nonlinearity [8]. Hence, assessment should be done using an accurate forecasting model [9,10,11]. Several studies combine mathematical approaches with artificial intelligence to predict electricity prices better (see [12] for a detailed review), as these methods have the potential to examine the complex inter-relationships between inputs and outputs. For example, Lin, Gow [13] proposed an Enhanced Radial Basis Function Network (ERBFN) by combining the Radial Basis Function Network (RBFN) and Orthogonal Experimental Design (OED) to forecast electricity market prices in order to minimize the price volatility risk. Keles et al. [14] present the forecasting methodology based on artificial neuronal networks (ANN) and find it well fitting for electricity prices with lowest possible errors. Agrawal et al. [15], on the other hand, employ New England electricity market data to introduce a novel forecasting model primarily centered on relevance vector machine (RVM). Luo and Weng [16] propose a more precise forecasting method by diversifying data sources such as highly correlated power data.
Electricity consumption is known to be influenced by the weather (wind speed, temperature, precipitation, and so on) as well as business activities (peaks, weekdays, weekends, holidays, etc.) [12]. Global climate change and the production burdens on old infrastructure also impact the supply and demand sides [5]. As a result, these characteristics lead to complex, highly volatile price dynamics which are not observed so much in other commodity markets [17], such as showing seasonality at different frequencies i.e., daily, weekly, annually, and sudden short-lived and generally unanticipated price spikes [18]. These complex characteristics make multifractality a particularly interesting way to look at the market efficiency of an electricity time series.
The concept of market efficiency has its roots in the efficient market hypothesis (EMH) of Fama [19], which plays an important role in modern financial economics. According to EMH, all available information is incorporated in the prices of efficient financial markets, which makes them impossible to predict as they behave randomly. Therefore, investors are unable to earn abnormal profits through arbitrage opportunities. However, due to external events of market friction and noisy traders, financial market prices fluctuate from their fair market values [20]. Empirically, it is shown that EMH fails to explain many irregularities/complexities of financial market time series. These irregularities include nonlinearity, long-range dependence [21,22,23], fat tails [24,25], volatility clustering [26], chaos [27], asymmetry [28], and self-similarity [29]. Mandelbrot [30] names these irregular structures as ‘fractals’ and introduced the concept of multifractality. Then, Peters [31] used the theory of fractals to propose the fractal market hypothesis (FMH), which strongly rejected the EMH. According to Peters [31], fractional Brownian motion produces more accurate financial market projections since it accounts for some well-proven irregularities.
Previous studies employed various multifractal econometric approaches such as wavelet transform modulus maxima, entropy methods, and others, but these studies found spurious indications of multifractality [32]. The Hurst [33] Rescaled Range method (R/S), on the other hand, has gained significance in the past two decades. However, it produces significant errors if time series are not stationary and have short-term memory. Then, Lo [34] developed a revised version of R/S to address its flaws and to account for short-term dependencies. These approaches appear to be best suited to examining long dependence correlation for stationary time series only [35]. Considering this fact, Kantelhardt et al. [36] proposed the multifractal detrended fluctuation analysis (MFDFA), which is an extension of the mono-fractal DFA [37]. As financial time series possess multifractal characteristics, using the single scaling exponent of the DFA to examine financial time series could produce spurious results [38,39,40,41]. Therefore, the MFDFA is stronger and performs better than the above-mentioned methods. MFDFA can explore the dynamics of market efficiency, long memory properties, degree of persistency, and the forecasting of financial markets. Hence, this approach can reliably characterize the multifractality of non-linear financial time series.
Researchers have applied MFDFA in a variety of financial time series such as stock markets [42,43,44,45], foreign exchanges [46,47], cryptocurrency market [48,49], gold [50], futures market [51,52], green bonds [53], and the carbon emission trading market [54]. For example, Aslam et al. [43] used MFDFA to examine the multifractal characteristics of MSCI in emerging Asian markets. The findings revealed the highest multifractality levels for India and Malaysia, while the Chinese and South Korean markets showed the lowest multifractality. Diniz-Maganini et al. [47] find that currencies which follow a Free Float regime have low multifractality i.e., higher efficiency than those currencies that follow a Managed Float regime. Telli and Chen [50] apply MFDFA and find the different multifractal characteristics of bitcoin return series from gold. More recently, there has been a significant increase in research examining the multifractality of financial markets during COVID-19. For instance, Choi [55] employed MFDFA to examine the multifractality of various sectors in US markets during COVID-19. The findings reveal the lowest levels of efficiency in the utilities sector, while the consumer discretionary sector has the highest efficiency. Aslam et al. [46] notice a significant decrease in forex markets’ efficiency during COVID-19. Aslam et al. [44] study the impact of COVID-19 on the markets of Central Eastern Europe and find a significant fluctuation in persistence behavior during the pandemic.
Various studies quantify/rank efficiency after examining MFDFA through the Magnitude of Long-Memory index (MLM) also known as Market Deficiency Measure (MDM) [56]. MLM ensures the robustness of the results and has become a significant tool for regulators and policymakers. For example, Li et al. [57] used this MLM measure to quantify the efficiency of six foreign exchange markets and found Chinese Renminbi (CNY) currency to be the most inefficient. Shahzad et al. [58] also employed this metric to examine clean energy indices. Recently, it has also been used to quantify the efficiency of financial markets during COVID-19 [28,48,49].
Considering the fact that electricity time series are non-linear and complex, compared to other commodities, this paper contributes to the literature on the efficiency and forecasting of the electricity market in three main ways, which are summed up as follows. Firstly, it provides the inner dynamics of efficiency through the multifractality of US electricity indices i.e., Mass Hub, Mid C, Palo Verde, and PJM West. To do so, we employ MFDFA [36], which makes it possible to quantify the multiple scaling exponents within each financial time series. This method allows us to assess the long memory, persistency, predictability, and informational efficiency in non-linear financial markets. Secondly, we quantify the multifractality of electricity indices through the MLM measure to rank the efficiency and ensure the robustness of the results. Thirdly, this study provides the first evidence of a rolling MFDFA approach to investigate further the evolution of complexity parameters i.e., and MLM of electricity indices. This approach has been extensively adopted in the literature, enabling us to capture the entire historical evolution of persistency and efficiency dynamics. For example, Guo et al. [52] used rolling MFDFA to analyze the dynamic efficiency of China’s copper futures market, Zhu and Bao [20] used it for exchange-traded funds (ETFs) and Aloui et al. [35] employed it for European credit market sectors.
2. Data and Descriptive Statistics
This study is based on examining the efficiency through multifractality of US electricity indices. Currently, electricity products are being traded at over two dozen delivery points and hubs in North America. Intercontinental Exchange (ICE) is a leading over-the-counter (OTC) trading platform for “day ahead” or prompt electricity markets of North America. The electricity indices selected for study are Mass Hub, Mid C, Palo Verde, and PJM West, which are sourced from the website of US Energy Information Administration (EIA). These indices are derived directly from the transactions executed on the ICE platform and constructed using the following formula:
where is the volumetric weighted average index price, and are the price and volume of a single transaction, while denotes the total volume of every qualified transaction.
The indices are based on the largest electricity utilization areas of the US and have enough data availability i.e., between 2001 and 2021, which allows us to make a conclusive analysis of multifractal behavior. Mass hub distributes power all over New England, Mid C hub supplies electricity to Columbia for the Northwest region, and Palo Verde is supplied throughout the Southwest region. Lastly, PJM West provides electricity to Indiana, Illinois, Delaware, Maryland, Ohio, Kentucky, Michigan, North Carolina, New Jersey, Virginia, West Virginia, Tennessee, Pennsylvania, and the District of Columbia. Table 1 presents the names, symbols, time periods, and the total number of observations of the indices. For analysis, the daily returns of prices are calculated by:

Table 1.
Description of indices, symbols, and data range.
The daily logarithmic returns plots of these US electricity indices are presented in Figure 1. Table 2 indicates the descriptive statistics of returns and shows negative average returns in all series. The highest average loss (about 0.01%) is observed for PJM West, whereas the lowest average loss (around 0.15%) is noted for MIDC Hub. However, MIDC Hub has the highest maximum return of 439% in a single day, while Mass Hub has the highest loss of 110%. As shown in Figure 1, MIDC Hub is the most volatile index, followed by Mass Hub, PJM West, and Palo Verde. Skewness values are non-zero i.e., negative for all the sample series with the exception of Mass Hub. For kurtosis, all series demonstrate sharp peak characteristics, indicating the presence of fat tails. Hence, these electricity indices have significant deviations from normal distribution, implying the presence of multifractality, which could be created by non-Gaussian distribution such as fat tails [59].
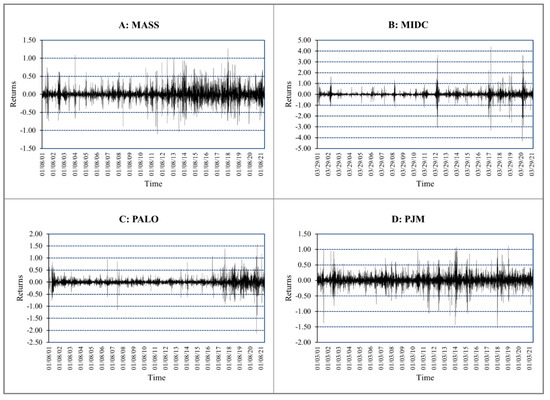
Figure 1.
Daily fluctuations in log returns of electricity indices.

Table 2.
Descriptive statistics.
3. Methodology
For many years, MFDFA [36] has been frequently employed for multifractal non-stationary financial time series. Thus, a brief explanation of it has been provided here.
Assume a finite length financial time series of where is the number of observations. The five following steps are required to complete this method:
- The profile value of is determined.where
- The profile is divided into equal time scale length of numerous non-overlapping components. As a result, the total number of components becomes . However, if is not a multiple of the time scale , a similar backward process is repeated to cover the full sample. After this, a total of are obtained, which is followed by calculating the local trend s for each of the segments by the kth-order polynomial fit.
- Ordinary Least Square (OLS) is employed within each component to fit the sample appropriately, and then, the local trend is estimated for each component. In this study, the fitting polynomial for each component is denoted as .with
To estimate the variance, we apply:
The linear polynomial fitting is demonstrated here. In practice, linear , quadratic , and cubic or those polynomials that have high orders can be applied when needed in order to fit the sample series. In this study, is used as the order, and it should not be set too high to avoid overfitting the sample series. To obtain the optimal order of , the findings for different s should also be compared.
- 4.
- The fluctuation function of order is estimated for all components through:
The fluctuation function is obtained for
Steps 2 to 4 are repeated for various time scales in order to examine how is affected by different on .
- 5.
- The log–log plots of vs. are analyzed at different levels. The generalized Hurst exponent [33] is specified by Equation (7) if a long-range power law correlation is present in sample series.
The Hurst exponent identifies the features of multifractality of financial time series through the speed of local fluctuation growth with increasing scale . A strong reliance of on is observed when series have multifractality, such as when large and small fluctuations scale differently. However, in the case of mono-fractal series, is constant for every . Since the scaling behavior of the variances is the same for all the components, the averaging in Equation (7) produces the same scaling behavior for all values of . There is a significant dependence of on if large and small fluctuations scale differently. In case of positive , the components with larger variances (i.e., large deviations from the corresponding fit) dominate the average . Hence, for positive , depicts the scaling behavior of the segments with larger fluctuations. On the contrary, the segments with small variance dominate the average for negative . Thus, describes the scaling behavior of the segments with small fluctuations for negative values of .
The value of represents the range of and indicates the degree of multifractality of a given time series. The higher the range of , the stronger the multifractality [60] but lower the strength of market efficiency because of fat-tailed behavior and long-range autocorrelation properties. Since multifractal properties are negatively correlated with market efficiency, the wider the multiple spectrum, the less efficient the market will be [61]. The fluctuation associated with shows a random walk at , which is persistent at and anti-persistent at .
The scaling exponent is defined as follows:
The singularity strength and the singularity spectrum are examined through Legendre transform and are calculated by the following equations:
Here, is also known as the Holder exponent and is used to characterize the singularity of the time series, where represents the derivative of with respect to . Whereas defines the fractal dimension generated by all points with the same singularity exponent and is a single, peaked, bell-shaped fractal spectrum. In other words, the singularity spectrum describes the multifractal measure in terms of interlaced sets with singularity force , while is the dimension of the contour subset characterized by . For mono-fractal series, the uniqueness of the spectrum generates a single point, while for multifractal series, the uniqueness of the spectrum is generated by a downward concave function, whose degree of multifractality is evaluated by . The width of the multifractal spectrum is calculated by taking the difference between maximum and minimum probability; i.e., and . If the width is small, the time series has higher efficiency and lower heterogeneity [62].
The selection of scale is important when investigating multifractality. However, there is some uncertainty regarding the maximum and minimum values of [63]. For instance, Zhang et al. [64] and Liu et al. [65] stated that the range generally achieves the requirements. However, Kantelhardt and Koscielny-Bunde [66] indicated that a narrower range of from to could be used to avoid a possible distortion of results by the so-called “freezing phenomenon” linked to the fat tails of time series. Therefore, in this study, we restrict to with a step size of 1.
Lastly, the methods of Wang et al. [56] and Wang et al. [67] are employed to quantify the level of inefficiency by calculating the market deficiency measure or the index of Magnitude of Long Memory (MLM). According to MLM, a market is efficient if all of its fluctuations follow a random walk behavior. This means that s related to different s are equal to 0.5. The MLM measure is defined as:
If large fluctuations and small fluctuations follow a random walk process, the market is qualified as efficient, and the MLM measure reaches zero. Whereas greater MLM values show weaker market efficiency and smaller MLM values show stronger market efficiency.
4. Results and Discussion
The MFDFA’s empirical results for the US electricity market indices are presented in this section. For all series, the log-log graphs of the fluctuation function vs. time scale , the slopes of generalized Hurst exponent, Renyi exponent , and the multifractal spectrum are presented in Figure 2. The fitted lines for all series are observed in the log-log graphs for the fluctuation functions and scales, which is picked up for . As for slopes of in Figure 2, the fitted lines that correspond to the generalized Hurst exponent evidently depend on . This declining pattern of and its dependency for scaling exponent imply the presence of multifractal structures. The plots of the Renyi exponent presented in Figure 2 are non-linear for all electricity indices. Finally, the presence of multifractality is proven by the multifractal spectrum , which is a single humped shape.
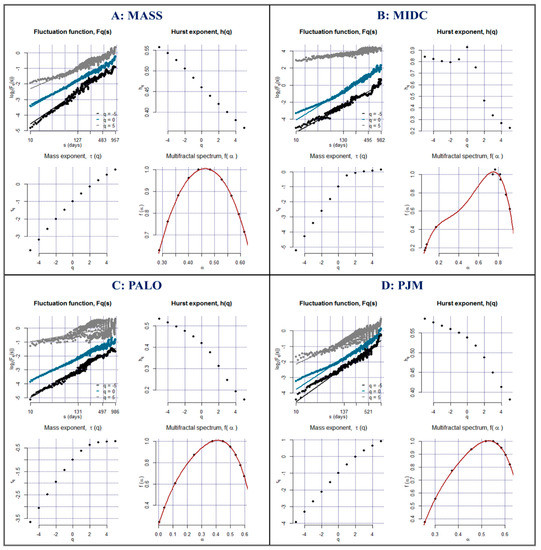
Figure 2.
The Multifractal detrended fluctuation analysis (MFDFA) findings of electricity indices. The Fluctuation functions for are displayed at the top left. The top right shows the Generalized Hurst exponent for each . The Mass exponent, , is presented at the bottom left, and the bottom right shows the Multifractal spectrum. The market’s codes are presented in Table 1.
Table 3 presents the results of for the range of to where a negative signifies small price fluctuations and a positive relates to large price fluctuations. It is well acknowledged that a market is said to be multifractal if fluctuates with from ; otherwise, it is mono fractal. As shown in Table 3, the values for the returns vary significantly with from , signaling that the electricity market indices are multifractal. For example, the findings for Mass Hub show that achieves a maximum of 0.40 at ; then, it falls to 0.24 at and finally to 0.10 at . The fact that the generalized Hurst exponent is decreasing supports its dependency on , implying the presence of multifractality in Mass Hub’s time fluctuations. Similar patterns and findings are found for the remaining electricity indices.

Table 3.
Generalized Hurst exponents ranging from q = −5 to q = 5.
The range or width of is examined through over the range which reveals the strength of multifractality. Larger values of are associated with higher multifractal patterns and lower efficiency levels shown by the sample series under analysis. Table 4 shows the findings of the width of . The greatest width of the generalized Hurst exponent is noted for PJM West () followed by Palo Verde () and MIDC Hub (). Mass hub, on the other hand, has the lowest level of multifractality, with a of 0.50. Hence, the findings reveal Mass Hub to be highly efficient, while PJM West is the least efficient index of them all. Similar results are confirmed in Figure 2, which presents the plots of the multifractal spectrum for all electricity market indices. PJM West has a very large width (), suggesting high multifractality levels compared to all electricity indices. The rationale behind the higher complexity of PJM is its bigger size than Mass Hub and other US electricity markets [68]. It serves more than 65 million people in 13 mid-Atlantic states and is the world’s largest competitive wholesale power market by load [69]. On other hand, Mass Hub only provides electricity to around 7 million consumers in six US states known as New England.

Table 4.
Results of efficiency.
Now, the classical Hurst exponent at is employed to examine the persistence of sample series, which is a key indicator of multifractal characteristics. For all electricity indices, the classical Hurst exponent values are less than , indicating anti-persistent behavior or negative autocorrelation. This means that any negative or positive change in one period will probably be followed by an opposite positive or negative change in the next period. Electricity prices have been found in the literature to be neither persistent nor random, but rather a mean-reverting (anti-persistent) process [70,71]. More recently, Kristjanpoller and Minutolo [5] found anti-persistent behavior while examining the multifractal cross-correlation through R/S of US electricity indices with WTI and natural gas.
For the robustness of results, the efficiency of electricity indices is further ranked according to the MLM measure. Higher MLM values are associated with greater market deficiency. In Table 4, the MLM results show PJM West to be most inefficient, with an MLM value of 0.34, whereas Mass Hub is the least inefficient, as indicated by the lowest MLM value of 0.25.
We now use a rolling window approach to examine the dynamic Hurst exponent and MLM to look at time-varying changes in the market efficiency of electricity indices. This method has been widely used to investigate the dynamic features of financial time series and to identify the potential repercussions of exogenous events [72]. Previous literature has discussed the importance of choosing the right length of rolling window. Zhang et al. (2018) argue that if the length of the rolling window is too large, the scaling exponents’ evolution gets smoother, and the significant trends are easier to spot. However, the impact of such events on short-term market dynamics is covered. The estimated parameters due to economic cycling and seasonal factors might lose their locality and be unable to illustrate the evolution of short-term events. Conversely, in the case of too short a length, some short-term parameters may experience significant fluctuations, making it difficult to find the trend [73]. Therefore, we use Zhao and Cui [74]’s rolling window setting of 1500 days as the window length because of the large sample size. To begin, the first 1500 days from the start of returns are taken to obtain the Hurst exponent and MLM. Then, the window is moved forward by dropping the first observation and adding another at the end. This process is repeated until the series is completed. A sequence of Hurst exponent and MLM is obtained by looping over a range of dates across the entire data set, as shown in Figure 3 and Figure 4.
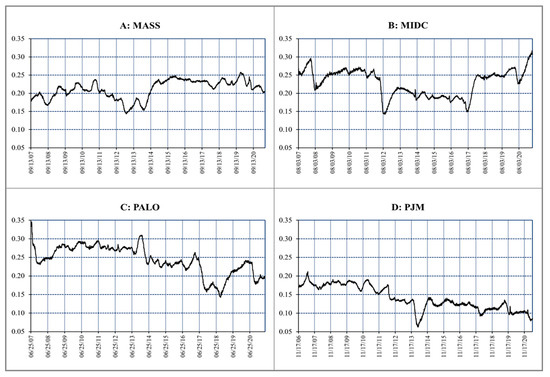
Figure 3.
Dynamic Hurst exponents evolution for electricity indices (q = 2, and window = 1500).
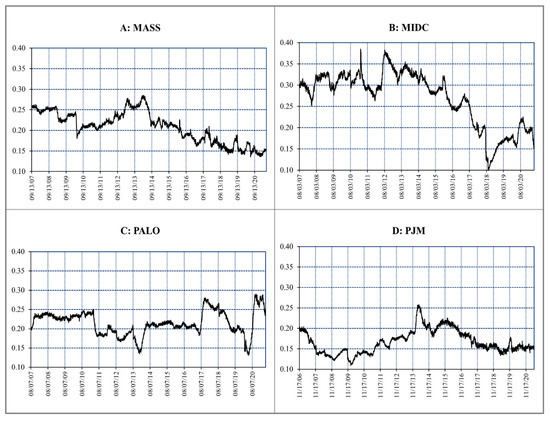
Figure 4.
Dynamic evolution of multifractality degree for electricity indices (, and ).
Figure 3 shows that the exponent lines never move up from 0.5 for all electricity indices throughout the time period. This indicates anti-persistent behavior (negative autocorrelation) during the whole sample. Figure 4 plots the results of the indices’ market inefficiency using the MLM measure. Looking at the graphs, we can see that all return series show rich multifractal degrees, but the highest is in Palo Verde. After the first quarter of 2014, MLM shows a downward trend for Mass Hub (New England) and PJM West, indicating an upward trend of market efficiency. According to the 2021 Regional Electricity Outlook report by ISO New England, a winter reliability program was designed in 2014 to keep the power grid reliable during periods of fuel insecurity. It happened because the region’s fuel delivery and energy security issues were highlighted by a brutal winter cold snap. For MIDC Hub, a significant improvement in efficiency is observed after the fourth quarter of 2012 with a maximum in 2018. The highest efficiency around the third quarter of 2018 could be due to the fact that electricity prices in the western US reached their highest levels since 2008. According to EIA [75], these high prices are the result of record high temperatures, which led to a relatively high demand for electricity. However, Palo Verde shows different behavior regarding market inefficiency, where the highest MLM values are found in 2017 and 2020, indicating the lowest efficiency. Electricity sales in the US declined by 80 billion kilowatt hours (kWh) in 2017, which is the largest drop since the economic recession in 2009. According to EIA [76], this major drop in sales is due to weather variations, which may have resulted in the highest inefficiency of Palo Verde in 2017. However, we found no significant impact of the recent COVID-19 pandemic on the degree of market efficiency for all electricity indices. On 11th March 2011, the Tohuku earthquake and tsunami struck Japan and sparked the Fukushima nuclear crisis. Woo et al. [77] document that the impact of that crisis is international and could have a significant effect on electricity markets, at least in the short term, as shutting down a nuclear plant reduces supply in the electricity market, which leads to a high market price. Figure 3 indicates a significant decrease in efficiency in electricity markets overall, especially Mass Hub and PJM West after 11 March 2011. Moreover, the overall electricity prices were high from 2012 to 2013, which were driven largely by an increase in spot natural gas prices [78]. However, due to regional supply and demand issues, the percentage increases in electricity prices were higher in MIDC and Mass Hub. MIDC is often among the least expensive in the regions because of the regional concentration of hydroelectric generation. According to EIA, the spring in MIDC region in 2013 was drier than the prior two springs, which kept prices higher. This could be attributed to the significant decrease in the inefficiency of MIDC from 2012 to 2013, as depicted in Figure 3. The cold weather put a strain on the already stressed natural gas pipeline infrastructure in New England. This resulted in electricity prices spikes in 2013, which might be the reason for the inefficiency spikes of Mass Hub during this period.
5. Conclusions
The electricity market in the United States has undergone major deregulatory reforms since the 1990s, aiming to increase competition and benefit consumers. This rising competitiveness altered the price dynamics, resulting in an unavoidable increase in pricing volatility [7,79]. At the same time, electricity prices incorporate all the supply/demand shocks, which leads to highly complex characteristics i.e., autocorrelation, heteroscedasticity, nonlinearity, etc. [8]. In this context, the focus is on examining the efficiency dynamics of US electricity markets, using multifractality to test these complex characteristics. To do so, we used MFDFA [36] to find the generalized Hurst exponent and the Renyi exponent . The four major electricity indices i.e., Mass Hub, Mid C, Palo Verde, and PJM West were studied. The roughly 20 years of data from 2001 to 2021 is a sufficient period to test its multifractality.
The findings of this study confirm a significance presence of multifractal behavior in all the US electricity markets studied. However, the strength of multifractality ( varies, with PJM West having the highest and Mass Hub having the lowest. As multifractality is the indicator of market efficiency, the most efficient market is Mass Hub, while PJM is seen to be least efficient. The MLM measure, which is a useful tool to quantify the efficiency of financial markets, further confirms the findings. Moreover, all electricity indices at exhibit anti-persistent (mean reverting) behavior. We employ an MFDFA rolling window approach to investigate the dynamic feature of persistency and efficiency through the classical Hurst exponent and MLM measure. The findings confirm anti-persistent behavior for all series over time as well. All electricity market indices show significant multifractal patterns over time with Palo Verde’s being the most volatile of all. Specifically, we found an upward trend in the efficiency of Mass Hub and PJM West after the first quarter of 2014.
Several factors and variables may have an impact on the multifractality and efficiency of financial markets. For example, Rizvi et al. [80] found liquidity and speculative bubble problems, Chung and Hrazdil [81] discovered that a positive link between liquidity and arbitrage activity leads to increased efficiency, and more recently, Al-Yahyaee et al. [82] found efficiency to be positively linked with liquidity and negatively with volatility. Furthermore, herding behavior [60], temporal correlation [83], volatility predictability [84], crash predictability [84,85], complexity of markets [86], and inefficient market structures [67,72,87] may also impact the multifractality of financial markets. Most importantly, government reforms [56], financial liberalization [60], economic freedom, and competitive financial intermediaries [88] are also positively linked with market efficiency and decrease multifractality.
This study provides novel findings for regulatory authorities, policymakers, and decision makers at the government and corporate levels. The significant multifractal behavior of the US electricity market implies the existence of dependency and inefficiency. These inefficiencies could be linked to the market’s predictability and imperfections, which in return lead to attaining abnormal returns [89]. Hence, regulators and policymakers should confirm transparency requirements to improve public access to information, which leads to reducing inefficiency. These findings may also be used by governments to decide on future deregulation of other possible natural monopolies, such as the electricity transmission sector. Additionally, the findings are useful for institutional investors who invest or trade in electricity market activities or energy stocks. This will help them to develop portfolios for better decision-making processes and risk management strategies, as according to previous studies, the width of the multiple spectrum is an indicator of future price fluctuations [84,90]. Therefore, these findings may also potentially help consumers who could see better electricity prices as producers and retailers are more able to match forecasts with demand. Future research should compare the efficiency and multifractality of the US electricity market with countries that have deregulated their electricity market and those that are still monopolistic. This research can also be extended by looking at the possible factors that may affect the multifractality of electricity markets.
Author Contributions
Conceptualization, H.A., F.A. and P.F.; Data curation, H.A., F.A. and P.F.; Formal analysis, H.A. and P.F.; Funding acquisition, F.A.; Writing—original draft, H.A., F.A. and P.F.; Writing—review and editing, H.A., F.A. and P.F. All authors have read and agreed to the published version of the manuscript.
Funding
Paulo Ferreira acknowledges the financial support of Fundação para a Ciência e a Tecnologia (grants UIDB/05064/2020 and UIDB/04007/2020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available at the website of US Energy Information Administration (EIA).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brehm, P.A.; Zhang, Y. The efficiency and environmental impacts of market organization: Evidence from the Texas electricity market. Energy Econ. 2021, 101, 105359. [Google Scholar] [CrossRef]
- Dertinger, A.; Hirth, L. Reforming the electric power industry in developing economies evidence on efficiency and electricity access outcomes. Energy Policy 2020, 139, 111348. [Google Scholar] [CrossRef]
- Borenstein, S.; Bushnell, J. The US Electricity Industry after 20 Years of Restructuring. Annu. Rev. Econ. 2015, 7, 437–463. [Google Scholar] [CrossRef]
- Rosellón, J.; Myslíková, Z.; Zenón, E. Incentives for transmission investment in the PJM electricity market: FTRs or regulation (or both?). Util. Policy 2011, 19, 3–13. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Asymmetric multi-fractal cross-correlations of the price of electricity in the US with crude oil and the natural gas. Phys. A Stat. Mech. Appl. 2021, 572, 125830. [Google Scholar] [CrossRef]
- Joskow, P.L. Lessons Learned from Electricity Market Liberalization. Energy J. 2008, 29. [Google Scholar] [CrossRef]
- Dias, J.G.; Ramos, S.B. Heterogeneous price dynamics in U.S. regional electricity markets. Energy Econ. 2014, 46, 453–463. [Google Scholar] [CrossRef]
- Heydari, A.; Nezhad, M.M.; Pirshayan, E.; Garcia, D.A.; Keynia, F.; De Santoli, L. Short-term electricity price and load forecasting in isolated power grids based on composite neural network and gravitational search optimization algorithm. Appl. Energy 2020, 277, 115503. [Google Scholar] [CrossRef]
- Uniejewski, B.; Weron, R. Efficient Forecasting of Electricity Spot Prices with Expert and LASSO Models. Energies 2018, 11, 2039. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Wu, C.-P. Day-Ahead Electricity Price Forecasting Using a Hybrid Principal Component Analysis Network. Energies 2012, 5, 4711–4725. [Google Scholar] [CrossRef]
- Lin, X.; Yu, H.; Wang, M.; Li, C.; Wang, Z.; Tang, Y. Electricity Consumption Forecast of High-Rise Office Buildings Based on the Long Short-Term Memory Method. Energies 2021, 14, 4785. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Lin, W.-M.; Gow, H.-J.; Tsai, M.-T. An enhanced radial basis function network for short-term electricity price forecasting. Appl. Energy 2010, 87, 3226–3234. [Google Scholar] [CrossRef]
- Keles, D.; Scelle, J.; Paraschiv, F.; Fichtner, W. Extended forecast methods for day-ahead electricity spot prices applying artificial neural networks. Appl. Energy 2016, 162, 218–230. [Google Scholar] [CrossRef]
- Agrawal, R.K.; Muchahary, F.; Tripathi, M.M. Ensemble of relevance vector machines and boosted trees for electricity price forecasting. Appl. Energy 2019, 250, 540–548. [Google Scholar] [CrossRef]
- Luo, S.; Weng, Y. A two-stage supervised learning approach for electricity price forecasting by leveraging different data sources. Appl. Energy 2019, 242, 1497–1512. [Google Scholar] [CrossRef]
- Matsumoto, T.; Yamada, Y. Simultaneous hedging strategy for price and volume risks in electricity businesses using energy and weather derivatives. Energy Econ. 2021, 95, 105101. [Google Scholar] [CrossRef]
- Nakajima, T.; Toyoshima, Y. Examination of the Spillover Effects among Natural Gas and Wholesale Electricity Markets Using Their Futures with Different Maturities and Spot Prices. Energies 2020, 13, 1533. [Google Scholar] [CrossRef]
- Fama, E. Efficient market hypothesis: A review of theory and empirical work. J. Financ. 1970, 25, 28–30. [Google Scholar] [CrossRef]
- Zhu, X.; Bao, S. Multifractality, efficiency and cross-correlations analysis of the American ETF market: Evidence from SPY, DIA and QQQ. Phys. A Stat. Mech. Appl. 2019, 533, 121942. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Lahmiri, S.; Uddin, G.S.; Bekiros, S. Nonlinear dynamics of equity, currency and commodity markets in the aftermath of the global financial crisis. Chaos Solitons Fractals 2017, 103, 342–346. [Google Scholar] [CrossRef]
- Yang, Y.-H.; Shao, Y.-H.; Shao, H.-L.; Stanley, H.E. Revisiting the weak-form efficiency of the EUR/CHF exchange rate market: Evidence from episodes of different Swiss franc regimes. Phys. A Stat. Mech. Appl. 2019, 523, 734–746. [Google Scholar] [CrossRef]
- Aloui, C.; Mabrouk, S. Value-at-risk estimations of energy commodities via long-memory, asymmetry and fat-tailed GARCH models. Energy Policy 2010, 38, 2326–2339. [Google Scholar] [CrossRef]
- Herrera, R.; Rodriguez, A.; Pino, G. Modeling and forecasting extreme commodity prices: A Markov-Switching based extreme value model. Energy Econ. 2017, 63, 129–143. [Google Scholar] [CrossRef]
- Oh, G.; Kim, S.; Eom, C. Long-term memory and volatility clustering in high-frequency price changes. Phys. A Stat. Mech. Appl. 2008, 387, 1247–1254. [Google Scholar] [CrossRef]
- Adrangi, B.; Chatrath, A.; Dhanda, K.K.; Raffiee, K. Chaos in oil prices? Evidence from futures markets. Energy Econ. 2001, 23, 405–425. [Google Scholar] [CrossRef]
- Naeem, M.A.; Bouri, E.; Peng, Z.; Shahzad, S.J.H.; Vo, X.V. Asymmetric efficiency of cryptocurrencies during COVID19. Phys. A Stat. Mech. Appl. 2021, 565, 125562. [Google Scholar] [CrossRef]
- He, L.-Y.; Chen, S.-P. Multifractal Detrended Cross-Correlation Analysis of agricultural futures markets. Chaos Solitons Fractals 2011, 44, 355–361. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Variation of Some Other Speculative Prices. J. Bus. 1967, 40, 393. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market. Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 24. [Google Scholar]
- Mensi, W.; Tiwari, A.K.; Al-Yahyaee, K.H. An analysis of the weak form efficiency, multifractality and long memory of global, regional and European stock markets. Q. Rev. Econ. Financ. 2019, 72, 168–177. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Lo, A.W. Long-Term Memory in Stock Market Prices. Econom. J. Econom. Soc. 1991, 59, 1279. [Google Scholar] [CrossRef]
- Aloui, C.; Shahzad, S.J.H.; Jammazi, R. Dynamic efficiency of European credit sectors: A rolling-window multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2018, 506, 337–349. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Fisher, A.J.; Calvet, L.E.; Mandelbrot, B.B. Multifractality of Deutschemark/US Dollar Exchange Rates; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Pasquini, M.; Serva, M. Multiscale behaviour of volatility autocorrelations in a financial market. Econ. Lett. 1999, 65, 275–279. [Google Scholar] [CrossRef][Green Version]
- Kwapien, J.; Oswiecimka, P.; Drożdż, S. Components of multifractality in high-frequency stock returns. Phys. A Stat. Mech. Appl. 2005, 350, 466–474. [Google Scholar] [CrossRef]
- Oświe, P.; Kwapień, J.; Drożdż, S. Multifractality in the stock market: Price increments versus waiting times. Phys. A Stat. Mech. Appl. 2005, 347, 626–638. [Google Scholar] [CrossRef]
- Aslam, F.; Mohti, W.; Ferreira, P. Evidence of Intraday Multifractality in European Stock Markets during the Recent Coronavirus (COVID-19) Outbreak. Int. J. Financ. Stud. 2020, 8, 31. [Google Scholar] [CrossRef]
- Aslam, F.; Latif, S.; Ferreira, P. Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis. Symmetry 2020, 12, 1157. [Google Scholar] [CrossRef]
- Aslam, F.; Nogueiro, F.; Brasil, M.; Ferreira, P.; Mughal, K.S.; Bashir, B.; Latif, S. The footprints of COVID-19 on Central Eastern European stock markets: An intraday analysis. Post-Communist Econ. 2020, 33, 751–769. [Google Scholar] [CrossRef]
- Maganini, N.D.; Filho, A.C.S.; Lima, F.G. Investigation of multifractality in the Brazilian stock market. Phys. A Stat. Mech. Appl. 2018, 497, 258–271. [Google Scholar] [CrossRef]
- Aslam, F.; Aziz, S.; Nguyen, D.K.; Mughal, K.S.; Khan, M. On the efficiency of foreign exchange markets in times of the COVID-19 pandemic. Technol. Forecast. Soc. Chang. 2020, 161, 120261. [Google Scholar] [CrossRef] [PubMed]
- Diniz-Maganini, N.; Rasheed, A.A.; Sheng, H.H. Exchange rate regimes and price efficiency: Empirical examination of the impact of financial crisis. J. Int. Financ. Mark. Inst. Money 2021, 73, 101361. [Google Scholar] [CrossRef]
- Kakinaka, S.; Umeno, K. Cryptocurrency market efficiency in short- and long-term horizons during COVID-19: An asymmetric multifractal analysis approach. Financ. Res. Lett. 2021, 102319. [Google Scholar] [CrossRef]
- Mnif, E.; Jarboui, A.; Mouakhar, K. How the cryptocurrency market has performed during COVID 19? A multifractal analysis. Financ. Res. Lett. 2020, 36, 101647. [Google Scholar] [CrossRef]
- Telli, Ş.; Chen, H. Multifractal behavior in return and volatility series of Bitcoin and gold in comparison. Chaos Solitons Fractals 2020, 139, 109994. [Google Scholar] [CrossRef]
- Fernandes, L.H.; de Araújo, F.H.; Silva, I.E. The (in)efficiency of NYMEX energy futures: A multifractal analysis. Phys. A Stat. Mech. Appl. 2020, 556, 124783. [Google Scholar] [CrossRef]
- Guo, Y.; Yao, S.; Cheng, H.; Zhu, W. China’s copper futures market efficiency analysis: Based on nonlinear Granger causality and multifractal methods. Resour. Policy 2020, 68, 101716. [Google Scholar] [CrossRef]
- Mensi, W.; Vo, X.V.; Kang, S.H. Upside-Downside Multifractality and Efficiency of Green Bonds: The Roles of Global Factors and COVID-19. Financ. Res. Lett. 2021, 101995. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Kim, N.-W.; Choi, K.-H.; Yoon, S.-M. Analysis of the Informational Efficiency of the EU Carbon Emission Trading Market: Asymmetric MF-DFA Approach. Energies 2020, 13, 2171. [Google Scholar] [CrossRef]
- Choi, S.-Y. Analysis of stock market efficiency during crisis periods in the US stock market: Differences between the global financial crisis and COVID-19 pandemic. Phys. A Stat. Mech. Appl. 2021, 574, 125988. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Gu, R. Analysis of efficiency for Shenzhen stock market based on multifractal detrended fluctuation analysis. Int. Rev. Financ. Anal. 2009, 18, 271–276. [Google Scholar] [CrossRef]
- Li, J.; Lu, X.; Jiang, W.; Petrova, V.S. Multifractal Cross-correlations between foreign exchange rates and interest rate spreads. Phys. A Stat. Mech. Appl. 2021, 574, 125983. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Bouri, E.; Kayani, G.M.; Nasir, R.M.; Kristoufek, L. Are clean energy stocks efficient? Asymmetric multifractal scaling behaviour. Phys. A Stat. Mech. Appl. 2020, 550, 124519. [Google Scholar] [CrossRef]
- He, L.-Y.; Chen, S.-P. Are crude oil markets multifractal? Evidence from MF-DFA and MF-SSA perspectives. Phys. A Stat. Mech. Appl. 2010, 389, 3218–3229. [Google Scholar] [CrossRef]
- Cajueiro, D.; Gogas, P.; Tabak, B.M. Does financial market liberalization increase the degree of market efficiency? The case of the Athens stock exchange. Int. Rev. Financ. Anal. 2009, 18, 50–57. [Google Scholar] [CrossRef]
- Caraiani, P. Evidence of Multifractality from Emerging European Stock Markets. PLoS ONE 2012, 7, e40693. [Google Scholar] [CrossRef]
- Zunino, L.; Tabak, B.; Figliola, A.; Pérez, D.; Garavaglia, M.; Rosso, O. A multifractal approach for stock market inefficiency. Phys. A Stat. Mech. Appl. 2008, 387, 6558–6566. [Google Scholar] [CrossRef]
- Zhan, C.; Liang, C.; Zhao, L.; Zhang, Y.; Cheng, L.; Jiang, S.; Xing, L. Multifractal characteristics analysis of daily reference evapotranspiration in different climate zones of China. Phys. A Stat. Mech. Appl. 2021, 583, 126273. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Qiu, L.; Zhang, B.; Sun, Y.; Gui, Z.; Zhang, Q. A modified multifractal detrended fluctuation analysis (MFDFA) approach for multifractal analysis of precipitation in dongting lake basin, China. Water 2019, 11, 891. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Zhang, X. Multiscale multifractal analysis on air traffic flow time series: A single airport departure flight case. Phys. A Stat. Mech. Appl. 2020, 545, 123585. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Wu, C. Cross-correlations between Chinese A-share and B-share markets. Phys. A Stat. Mech. Appl. 2010, 389, 5468–5478. [Google Scholar] [CrossRef]
- Mujeeb, S.; Javaid, N. ESAENARX and DE-RELM: Novel schemes for big data predictive analytics of electricity load and price. Sustain. Cities Soc. 2019, 51, 101642. [Google Scholar] [CrossRef]
- Lavin, L.; Murphy, S.; Sergi, B.; Apt, J. Dynamic operating reserve procurement improves scarcity pricing in PJM. Energy Policy 2020, 147, 111857. [Google Scholar] [CrossRef]
- Weron, R. Energy price risk management. Phys. A Stat. Mech. Appl. 2000, 285, 127–134. [Google Scholar] [CrossRef]
- Weron, R.; Przybyłowicz, B. Hurst analysis of electricity price dynamics. Phys. A Stat. Mech. Appl. 2000, 283, 462–468. [Google Scholar] [CrossRef]
- Cajueiro, D.O.; Tabak, B.M. Testing for time-varying long-range dependence in volatility for emerging markets. Phys. A Stat. Mech. Appl. 2005, 346, 577–588. [Google Scholar] [CrossRef]
- Liu, L.; Wan, J. A study of correlations between crude oil spot and futures markets: A rolling sample test. Phys. A Stat. Mech. Appl. 2011, 390, 3754–3766. [Google Scholar] [CrossRef]
- Zhao, R.; Cui, Y. Dynamic Cross-Correlations Analysis on Economic Policy Uncertainty and US Dollar Exchange Rate: AMF-DCCA Perspective. Discret. Dyn. Nat. Soc. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- EIA. Summer Average Wholesale Electricity Prices in Western U.S. Were Highest since 2008. 2018. Available online: https://www.eia.gov/todayinenergy/detail.php?id=37112 (accessed on 10 September 2021).
- EIA. In 2017, U.S. Electricity Sales Fell by the Greatest Amount since the Recession. 2018. Available online: https://www.eia.gov/todayinenergy/detail.php?id=35612 (accessed on 10 September 2021).
- Woo, C.K.; Ho, T.; Zarnikau, J.; Olson, A.; Jones, R.; Chait, M.; Horowitz, I.; Wang, J. Electricity-market price and nuclear power plant shutdown: Evidence from California. Energy Policy 2014, 73, 234–244. [Google Scholar] [CrossRef]
- EIA. New England and Pacific Northwest Had Largest Power Price Increases in 2013. 2014. Available online: https://www.eia.gov/todayinenergy/detail.php?id=14511 (accessed on 10 September 2021).
- Assereto, M.; Byrne, J. The Implications of Policy Uncertainty on Solar Photovoltaic Investment. Energies 2020, 13, 6233. [Google Scholar] [CrossRef]
- Rizvi, S.A.R.; Arshad, S.; Alam, N. A tripartite inquiry into volatility-efficiency-integration nexus—Case of emerging markets. Emerg. Mark. Rev. 2018, 34, 143–161. [Google Scholar] [CrossRef]
- Chung, D.; Hrazdil, K. Liquidity and market efficiency: A large sample study. J. Bank. Financ. 2010, 34, 2346–2357. [Google Scholar] [CrossRef]
- Al-Yahyaee, K.H.; Mensi, W.; Ko, H.-U.; Yoon, S.-M.; Kang, S.H. Why cryptocurrency markets are inefficient: The impact of liquidity and volatility. N. Am. J. Econ. Financ. 2020, 52, 101168. [Google Scholar] [CrossRef]
- Green, E.; Hanan, W.; Heffernan, D. The origins of multifractality in financial time series and the effect of extreme events. Eur. Phys. J. B 2014, 87, 1–9. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, D. Multifractal analysis of SSEC in Chinese stock market: A different empirical result from Heng Seng index. Phys. A Stat. Mech. Appl. 2005, 355, 497–508. [Google Scholar] [CrossRef]
- Grech, D.; Pamuła, G. The local Hurst exponent of the financial time series in the vicinity of crashes on the Polish stock exchange market. Phys. A Stat. Mech. Appl. 2008, 387, 4299–4308. [Google Scholar] [CrossRef]
- Kumar, S.; Deo, N. Multifractal properties of the Indian financial market. Phys. A Stat. Mech. Appl. 2009, 388, 1593–1602. [Google Scholar] [CrossRef]
- Tabak, B.; Cajueiro, D. Are the crude oil markets becoming weakly efficient over time? A test for time-varying long-range dependence in prices and volatility. Energy Econ. 2007, 29, 28–36. [Google Scholar] [CrossRef]
- Dewandaru, G.; Rizvi, S.A.R.; Bacha, O.I.; Masih, M. What factors explain stock market retardation in Islamic Countries. Emerg. Mark. Rev. 2014, 19, 106–127. [Google Scholar] [CrossRef]
- Dragotă, V.; Ţilică, E.V. Market efficiency of the Post Communist East European stock markets. Cent. Eur. J. Oper. Res. 2014, 22, 307–337. [Google Scholar] [CrossRef]
- Su, Z.-Y.; Wang, Y.-T. An Investigation into the Multifractal Characteristics of the TAIEX Stock Exchange Index in Taiwan. J. Korean Phys. Soc. 2009, 54, 1385–1394. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).