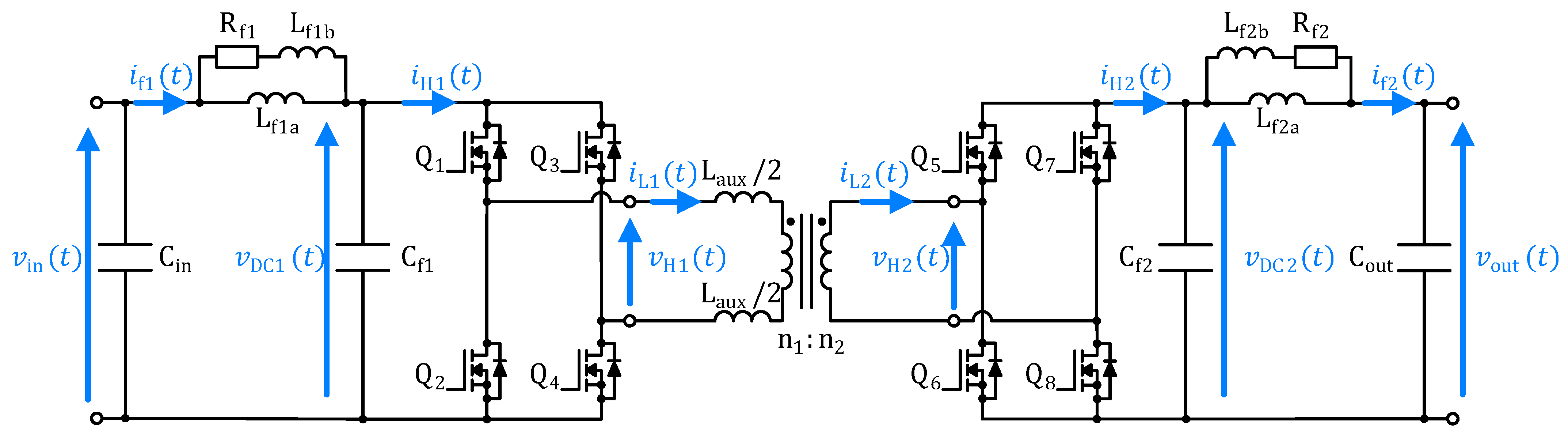
2.1. Modulation Scheme
The solution described here is based on some particular variant of the SPS modulation, i.e., the Double-Sided Single Phase Shift (DSSPS) modulation. The steady-state characteristics of this modulation scheme are the same as for the classical SPS modulation [
15]. Both H-bridges are controlled with a constant duty ratio of 50% and the converter is controlled by means of the phase shift
between them. Here, the phase shift
is expressed in unit of normalized time, which is relative to the switching period:
where
is normalized time;
t is absolute time (s);
is switching period (s). With such a definition, the value of
corresponds to an angular phase shift of
.
As derived in [
15], with such a modulation scheme the value of phase shift
should be limited to the range of
. An average output current (i.e., averaged over one switching period) can be then expressed as:
where the subscript
denotes the average value;
is the base current (A),
is the equivalent circuit inductance (H);
is the transformer turns ratio;
and
are the number of turns at the primary and secondary transformer sides.
Equation (2), which describes a relationship between the control variable
and average output current, is nonlinear. This function is strictly monotonic in the feasible control variable range (i.e.,
) and because of that it can be inverted. Hence, the phase shift value providing a reference value of the average output current can be calculated as:
where the subscript
denotes the reference value. The Equation (6) describes a control law used in the proposed solution (see current the control loop described in
Section 2.2), which provides a linear relationship between the reference output current value
and its average value in steady-state.
The DSSPS modulation scheme differs from the classical SPS algorithm during dynamic converter operation. According to the SPS modulation described in [
15] the primary-side AC voltage waveform remains stationary in time, whereas only the secondary-side voltage waveform is being shifted accordingly during the phase shift transition. On the other hand, the double-sided variant used in this paper assumes that both primary- and secondary-side voltage waveforms are shifted symmetrically to the center of the switching period [
13].
It is a well-known fact that usage of the same modulation scheme in steady-state and for dynamic operation introduces a so-called transient DC-bias current in transformer windings [
13]. This undesired current component deteriorates system performance in means of efficiency and dynamic performance, i.e., settling time after the phase shift transition. In order to avoid it, the modulation scheme used here is complemented with the Dual Rising Edge Shift (DRES) algorithm [
13], which allows to cancel the transient DC-bias current component. It is accomplished by an appropriate time shift of the rising edges for both primary- and secondary-side AC voltage waveforms. Equations allowing to calculate the time instants of consecutive switching operations are rewritten here for the readers’ convenience:
where
is a correction time;
is a change of phase shift value between the current and the previous switching cycle; and
k is a number of the switching cycle, in which the calculated control values are applied.
The function of the used modulation scheme during the transition of the phase shift value is demonstrated in
Figure 2. In the first switching cycle, the phase shift value equals
and in the second cycle it changes to
. AC voltage waveforms generated by both bridges are shown in
Figure 2a,b. The first plot presents an operation of the basis DSSPS modulation without additional corrective shift of the rising edges during transient operation, i.e., the corrective time
in Equations (7) and (8) is set to zero. On the second plot, the rising voltage edges are appropriately shifted by an amount of
, which is indicated with red arrows.
Transformer current waveforms are shown in
Figure 2c. The steady-state waveform (solid black line) describes the current signal shape, which should be expected during a static converter operation. It can be clearly seen that it exhibits a discontinuity, which is a reason for the DC-bias occurrence (for a more detailed explanation please refer to [
13]). It can also be observed that the current signal obtained using the basis DSSPS modulation (dashed red line) is shifted relative to the target steady-state waveform (an amount of this offset is called the DC-bias). Applying the DRES correction algorithm causes the resulting current waveform (solid red line) to converge to the steady-state one. This algorithm is designed in such a way that the transient state lasts no longer than half of the switching cycle [
13]. It assures that the waveforms of the transformer currents
and
, as well as the DC-side bridge currents
and
are the same as in the steady-state in the second half of each switching cycle (even during dynamic converter operation). This is a very important feature of this modulation scheme, which plays a fundamental role in the presented closed loop control system.
2.2. Current Control Loop
Schematic of the proposed current control loop is shown in
Figure 3. The control algorithm is realized in a discrete-time domain in a microcontroller. The controlled variable is the filter current at the converter’s output (see
in
Figure 1). It is sampled with a frequency equal to the switching frequency
. Hence, there exists a time delay of one sample in the control loop (represented as the
block in
Figure 3).
The applied phase shift value does not change during a control cycle, which was modeled as a Zero Order Hold (ZOH) element. The reference phase shift value is calculated based on the reference average value for the secondary-side bridge output current . The calculation is carried out according to Equation (6), which allows compensating for the non-linear static characteristic of the plant (see Equation (2)).
The signal
plays the role of the control variable and it is calculated by a discrete-time equivalent of the linear PI controller with limited output. For discretization, the bilinear transform was used [
16]. Choosing the appropriate limitation values for the controller output requires a special attention. On the one hand, the
signal should be limited in such a way, that calculation of the ’static inverse function’ (Equation (6)) gives a real number, i.e., the value under the square root must not be negative. Hence, the maximal value for the average output current in the
k-th control cycle equals:
On the other hand, it is not the case that the output current of DAB should always be limited to the maximally achievable value. In general, there may be a need to additionally limit the current according to specification of the device. Hence, the authors propose to evaluate the Equation (13) in each control cycle and use this value as the controller output limitation only then, if it results in an absolute value lower than the maximal current due to the converter’s specification:
where
is the actual maximal controller output limitation;
is the actual minimal controller output limitation;
is the maximal output current value according to the converter’s specification (A). The same limitation values are used for the voltage controller described in the next section.
It should be emphasized that the value
is not only a pure mathematical limitation, but it also describes an absolute maximal current, which can be achieved at the DAB output in steady-state [
15]. It is important to point out that the only variable in Equation (13) which can change over time is the input bridge DC voltage
. It means that the achievable output current range is proportional to the input voltage so it can dynamically change.
In the case of the discrete-time control systems, it is normally the case that the control loop as a whole is a mixed-domain system. It means that a control algorithm is realized in the discrete-time domain, whereas the plant is a physical circuit, which is a continuous-time system. In order to tune the parameters of the controller, the dynamics of the control loop should be modeled using an equivalent transfer function in either the z (discrete-time) or s (continuous-time) domain.
The dynamic model presented here is created in the continuous-time domain. It is based on an observation that dynamics of the core DAB circuit (i.e., the relationship between the controller output and average current at the DC side of the secondary-side bridge) can be approximated with a time delay. It should be emphasized that it is possible only because of the used modulation scheme with DRES compensation (see
Section 2.1) and the static inverse function (Equation (6)). It greatly reduces the complexity of system modeling in comparison with the state-of-the-art solution, i.e., the small-signal averaging technique.
The proposed approximation is going to be explained based on simulation results, which were obtained with a numerical converter model created in PLECS software [
17] (the DAB parameters are listed in
Table A1). The results are shown in
Figure 4. In the simulated scenario output signal of the controller (black), there is a step function which changes value from 0 A to 15 A at the beginning of the second control cycle presented on the plot, i.e., at
. The phase shift needed to achieve the average current value of 15 A in the steady-state is calculated with Equation (6) but it is applied first during the third control cycle, i.e.,
, because of the unity sample delay due to the discrete-time control realization. Hence, the current at the DC side of the secondary-side bridge (gray) remains unchanged during the first and second control cycles. As already mentioned in
Section 2.1, thanks to the DRES algorithm, the transient process lasts only for the first half of the control cycle, whereas in the second half of the cycle the current signal reaches a steady-state. The authors propose to approximate this current signal with its average value calculated in each half cycle (blue signal in
Figure 4). The dynamic relationship between the controller output signal (the reference value) and this averaged current signal (the result) can then be described as a time delay of 1.75 control periods. Such a delayed signal is shown in red in
Figure 4.
The dynamics of the filter current
depends on both the current transferred through the DAB converter
and output voltage
and can be described in the
s domain as follows [
11]:
where
is the transfer function of the low-pass current filter. Hence, the whole current control loop can be modeled according to the diagram shown in
Figure 5. Since the controller can directly influence only the current transferred through the core DAB circuit
, the output voltage signal
should be treated as a disturbance.
The control loop dynamics can then finally be described using the transfer functions as follows:
where
is the closed-loop system transfer function;
is the disturbance transfer function;
is the open-loop system transfer function;
is the transfer function of the controller;
is the proportional gain of the controller;
is the integral time of the controller (s);
is the transfer function of the controlled plant.
The proposed controller parameter tuning method is based on a notion of the gain margin [
18]:
where
is the complex frequency response of the transfer function
for which the gain margin is calculated;
is the gain margin cutoff frequency, i.e., a frequency resulting in phase lag of the frequency response equal to
(rad/s);
is the gain margin.
In the proposed tuning process the integral time is chosen arbitrary and then the proportional gain is calculated in such a way that the open-loop transfer function of the system (Equation (21)) exhibits the required gain margin value. The authors propose to choose the integral time of the controller in such a way that the decade containing the controller corner frequency (Equation (28)) is separated by at least one whole decade from the one containing the gain margin cutoff frequency (Equation (24)) calculated for a frequency response of the plant . In the next paragraphs, we explain why such a tuning rule was chosen.
Firstly, let us define how to calculate the proportional gain of the controller based on the chosen integral time and the requested gain margin value .
The calculation algorithm consists of two steps:
Step 1: Proportional gain of the controller is set to unity (
) and the integral time is set to the requested value (
). For such a case the Bode plots of the open-loop frequency response
are drawn. Based on that, the gain margin cutoff frequency
is determined according to Equation (24) and a gain margin for the unity gain is calculated as:
Step 2: Based on the calculated gain margin value it can be determined how to set the controller gain in order to achieve the requested gain margin of the open-loop system as follows:
Exemplary characteristics of the current control system tuned according to this procedure are shown in
Figure 6. A set of six characteristics for different input data values is presented. For each case, the requested gain margin value was exemplary chosen as
. On the other hand, the requested integral time values are varied between
s and
s. Bode plots for the amplitude and phase of the open-loop system frequency responses are shown in
Figure 6a,c respectively. The red solid lines represent the characteristics of the PI controller for different parameter values.
It is important to point out that the maximal phase lag which can be introduced by the controller equals
and varying of the integral time influences a frequency range where this phase lag is applied. Let us define the corner frequency of the PI controller as:
It is a very characteristic point, as it lies in the middle of the phase transition zone of the controller, i.e., between the phase lag values of and . It is important to observe that this transition zone has a width of approximately two decades at logarithmic frequency scale. It can then be approximately assumed that the controller introduces a phase lag of for frequencies lying one decade below the corner frequency and introduces no phase lag for frequencies lying one decade above this corner frequency.
It can also be observed that changing the integral time value in the descending direction introduces more phase lag to the open-loop system characteristics. As a result, the gain margin cutoff frequency values become slightly lower (see the white dots in
Figure 6c), but this influence is relatively small because of the steep phase characteristics of the plant in this frequency range introduced by the time delay element (see Equation (23)).
As the requested gain margin values are constant for all the six characteristics, the points indicating the gain margin on amplitude characteristics of the open-loop system must then lie relatively near to each other (see the white dots in
Figure 6a). It should also be emphasized that the PI controller exhibits amplifying features only in a limited frequency range, i.e., for frequencies lower than the corner frequency (Equation (28)). For frequencies higher than that threshold the controller gain is constant. As a result, shifting of the corner frequency of the controller into the higher values (and holding the constant gain margin value at the same time) allows to greatly increase the open-loop system gain in a pass-band of the control system. This effect can clearly be seen in
Figure 6a. Maximizing the gain of the open-loop system in the possibly wide frequency range is desirable [
19], as it brings frequency responses of the closed-loop system toward the unity and of the disturbance towards zero, which can be expressed mathematically as:
The positive effect that the rising of the controller corner frequency has on the closed-loop and disturbance characteristics of the system can be clearly observed by inspecting the amplitude frequency responses plotted in
Figure 6b,d. The bandwidth of the closed-loop system rises, as well as an attenuation of the disturbances in low-frequency range. Finally, this effect can also be observed in the step responses on the reference signal (
Figure 6e) and on the disturbance signal (
Figure 6f). These responses were determined using the ’step()’ function in MATLAB software [
20].
The above discussion allows to formulate a conclusion that for a given gain margin value, rising of the controller corner frequency has positive effects on system dynamics. On the other hand, at some point this effect saturates, as the controller phase lag equals in the whole relevant frequency range. The same applies to the amplitude characteristics of the open-loop system, as at some point the whole relevant part of these characteristics is amplified by the falling arm of the PI controller amplitude characteristics, and a further increase of the corner frequency has no relevant impact on the system behavior. It is then not important which exact value of the integral time is chosen, as long it assures that the relevant frequency band of the system lies meaningfully below the corner frequency of the controller. The already mentioned tuning rule (i.e., the controller corner frequency (Equation (28)) is separated by at least one whole decade from the one containing the gain margin cutoff frequency (Equation (24)) calculated for a frequency response of the plant ), which meets this requirement, since the transition zone of the controller ends approximately one decade below its corner frequency on the logarithmic frequency scale. In the presented case, the gain margin cutoff frequency calculated for the plant equals rad/s, i.e., it lies in the decade . According to the formulated rule of thumb the corner frequency should then not be smaller than rad/s (which corresponds to ).
Since there exist a rule on how to choose the integral time, the only parameter left to tune is the proportional gain of the controller. It can be chosen based on the requested gain margin value. This value should be chosen by a system designer based on the desirable characteristics of the reference step response. It can be done based on the system characteristics plotted in
Figure 7. There is again a set of six different characteristics, but this time the integral time of the controller is constant and set to the previously calculated value of
.
On the other hand, the requested gain margin is varied between the values of 2.25 and 3.50 (see the legend in
Figure 7c). Since the integral time is constant, varying of the controller gain has no influence on the phase characteristics of the open-loop system frequency response. However, it has an influence on the amplitude characteristics plotted in
Figure 7a. Changing of the gain margin value impacts the amplitude characteristics of the closed-loop system shown in
Figure 7b. This in turn changes a character of the step responses on the reference signal (see
Figure 7e). On the other hand, an impact on the disturbance rejection possibilities of the control system (see
Figure 7d,f) is not significant. A choice of the particular gain margin value should be made by the system designer based on his expertise. In the presented case, the authors propose to chose a value of
, which results in a possibly fast step response on the reference signal but without any overshoot (this value corresponds to the orange curves in
Figure 7). Nevertheless, the other value can be chosen too, if the designer desires a faster (lower gain margin) or less oscillatory (higher gain margin) character of the response.
To sum up, the final parameter values for the current controller presented in this paper are as follows:
2.3. Voltage Control Loop
For the voltage control purposes, an additional outer control loop was introduced to the control system. The schematic of the resulting control structure is shown in
Figure 8. The voltage controller regulates voltage
measured directly at the output capacitor (see
in
Figure 1). The voltage controller is realized in the same way as the current controller, i.e., it is a discrete-time equivalent of a linear PI controller with bounded output. The output signal of the voltage controller is the reference value of the output filter current
. This signal is a reference value for the inner current control loop. Its value is limited by the voltage controller to the feasible output current range in steady-state, i.e., it is limited to the same range as the current controller according to Equations (14) and (15).
In order to tune the parameters of the voltage controller, the dynamics of the control loop should be modeled first. This loop consists of the voltage controller and the inner control loop for the current and output capacitor (see the outer circuit schematic in
Figure 9).
The voltage controller can influence only the filter current signal (indirectly by setting the reference value of this current for the inner control loop). Hence, the load current signal should be treated as the disturbance for the voltage control system. The model of the voltage control loop should also contain the dynamics of the inner control loop for the current. These dynamics can be described using the closed-loop (Equation (19)) and disturbance (Equation (20)) transfer functions for the current control system. As the closed form analytical formulas for these functions are relatively complex, the authors decided to approximate them with the following equivalent functions for the simplicity:
where
is an approximation of the closed-loop transfer function for the current control system
;
is an approximation of the disturbance transfer function for the current control system
. The system poles exhibiting a slightly oscillating character were replaced by a series connection of the first order elements. It is a well-known technique that is used to simplify an analysis [
19]. The exact structure of the approximating transfer functions was found by inspection and the parameter values were found with an engineering approach, i.e., trial and error followed by a visual evaluation of the Bode plots of the original and approximating functions. Bode plots of the corresponding frequency responses are shown in
Figure 10. The original functions calculated for the current controller parameters (Equations (31)–(33)) according to equations (Equations (18)–(23)) are drawn with black color. The characteristics of the equivalent functions Equations (34) and (35) are drawn with orange color.
The block diagram illustrating the signal flow in the system is shown in
Figure 11a. The output voltage signal
is a result of integration of the capacitor current, i.e., (
). The filter current signal
is a sum of the current control loop responses on the reference signal (calculated by the voltage controller) and on the disturbance signal (output voltage). In order to describe the voltage control system dynamics using the standard notions of the plant, open-loop, closed-loop, and disturbance transfer functions [
18], this diagram should be converted to a different form. In the schematic shown in
Figure 11b the order of summation nodes was changed and the integration block was doubled to create an additional parallel path. The part marked with a dashed line can then be replaced with an equivalent transfer function
. It results in the final diagram shown in
Figure 11c, which can be described with the following transfer functions:
where
is the closed-loop system transfer function;
is the disturbance transfer function;
is the open-loop system transfer function;
is the transfer function of the controller;
is the proportional gain of the controller;
is the integral time of the controller (s);
is the transfer function of the controlled plant;
is the equivalent transfer function according to
Figure 11b.
The proposed tuning method for a voltage controller based on a notion of phase margin is defined as follows [
18]:
where
is the phase margin cutoff frequency (rad/s), i.e., a frequency for which the amplitude of the frequency response equals unity;
is the phase margin (
). The proposed method is designed in order to achieve a high control loop robustness.
Hence, for a given integral time value of the controller the proportional gain value is chosen in such a way that the phase margin calculated for the open-loop system frequency response is maximized.The calculation algorithm consists of three steps:
Step 1: Proportional gain of the controller is set to unity (
) and the integral time is set to the requested value (
). For such a case the Bode plots of the open-loop frequency response
are drawn. Based on that it is found for which frequency the phase of the drawn response is maximal:
Step 2: An aim of the algorithm is to find such a proportional gain value, that the phase margin cutoff frequency (Equation (43)) for the resulting open-loop system equals the value (Equation (45)), as it assures the possibly maximal phase margin value. In order to do so, an amplitude of the open-loop frequency response for the unity gain should be read from the drawn characteristic at the frequency (Equation (45)):
Step 3: Based on that, the proportional gain value can be calculated in such a way that the frequency response gain for the requested frequency equals unity, assuring that the phase margin calculation point lies exactly at the maximum of the phase characteristic:
which ends the calculation procedure.
When such an algorithm is applied, there is only one parameter of the controller to be tuned, i.e., the integral time value
(because the proportional gain value for the given value of integral time is determined by the above mentioned algorithm). Again, it is a decision of the designer which exact value to choose. It can be done based on system characteristics drawn for many different candidate values for the integral time, as exemplary illustrated in
Figure 12. The phase margin cutoff frequency points for each characteristic are marked with white dots at phase plots of the open-loop system frequency response (see
Figure 12c). It can be clearly seen that these points lie at frequencies of the possibly maximal phase margin values, as requested.
The final value of the integral time can be chosen based on the system step response on the disturbance signal and some common sense of the system robustness. The response on the reference signal step is of a lesser importance, as an overshoot can be eliminated with an additional pre-filter (as described later in this section) and the main task of the voltage regulatory system is to hold a constant output voltage value in various load conditions. The authors propose to choose an initial integral time value for the tuning, which provides a possibly fast attenuation of the disturbance step response with no overshoot. In the presented case it results in a value of
s, which corresponds to the orange curves in
Figure 12. As will be shown later in the course of this paper, the chosen value assures a proper behavior of a real control system in its linear operating range, but there are some negative effects occurring near the operational limits of the converter. The authors chose this integral time value as a starting point for the tuning of the experimental prototype with a full awareness of these issues. The reason is to demonstrate to the readers what can happen if the dynamics of this control loop is set to high. To sum up, the chosen set of the voltage controller parameters equals:
The last missing part of the proposed control system, is to add a pre-filter for the reference voltage signal. It allows to reduce an amount of overshoot in the reference step response of the system. After inspection of the closed-loop transfer function (Equation (37)) it appears that it exhibits only one zero, which equals to a zero of the controller (Equation (41)). The pre-filter was designed to compensate this zero. Hence, it has a stucture of a first order system with the time constant equal to the integral time of the voltage controller:
In order to finally validate the proposed dynamic models and parameter sets for both controllers, numerical models of the presented current and voltage control systems were created in PLECS software [
17]. The models contain all the parasitic elements listed in
Table A1 and allow to fully simulate the system dynamics, i.e., the results produced with these models can serve as a reference for the results obtained with the greatly simplified analytical models proposed in this paper. Hence, step responses on the reference and the disturbance signals were generated using the simulation models and then they were compared with those obtained with analytical ones. It should be emphasized that for this comparison both numerical and analytical models are supplemented with the pre-filter of the reference voltage signal (Equation (50)). It should also be mentioned that the control algorithm implemented in the simulation model is exactly the same as the one implemented in the laboratory prototype. However, stimulation of the control system was chosen in such a way that both controllers work in their linear operational region. The results are shown in
Figure 13.
The matching between the result obtained with both models is very good, especially taking into consideration the amount of simplifying assumptions made in the course of the analytical models derivation.