Electrofacies as a Tool for the Prediction of True Resistivity Using Advanced Statistical Methods—Case Study
Abstract
:1. Introduction
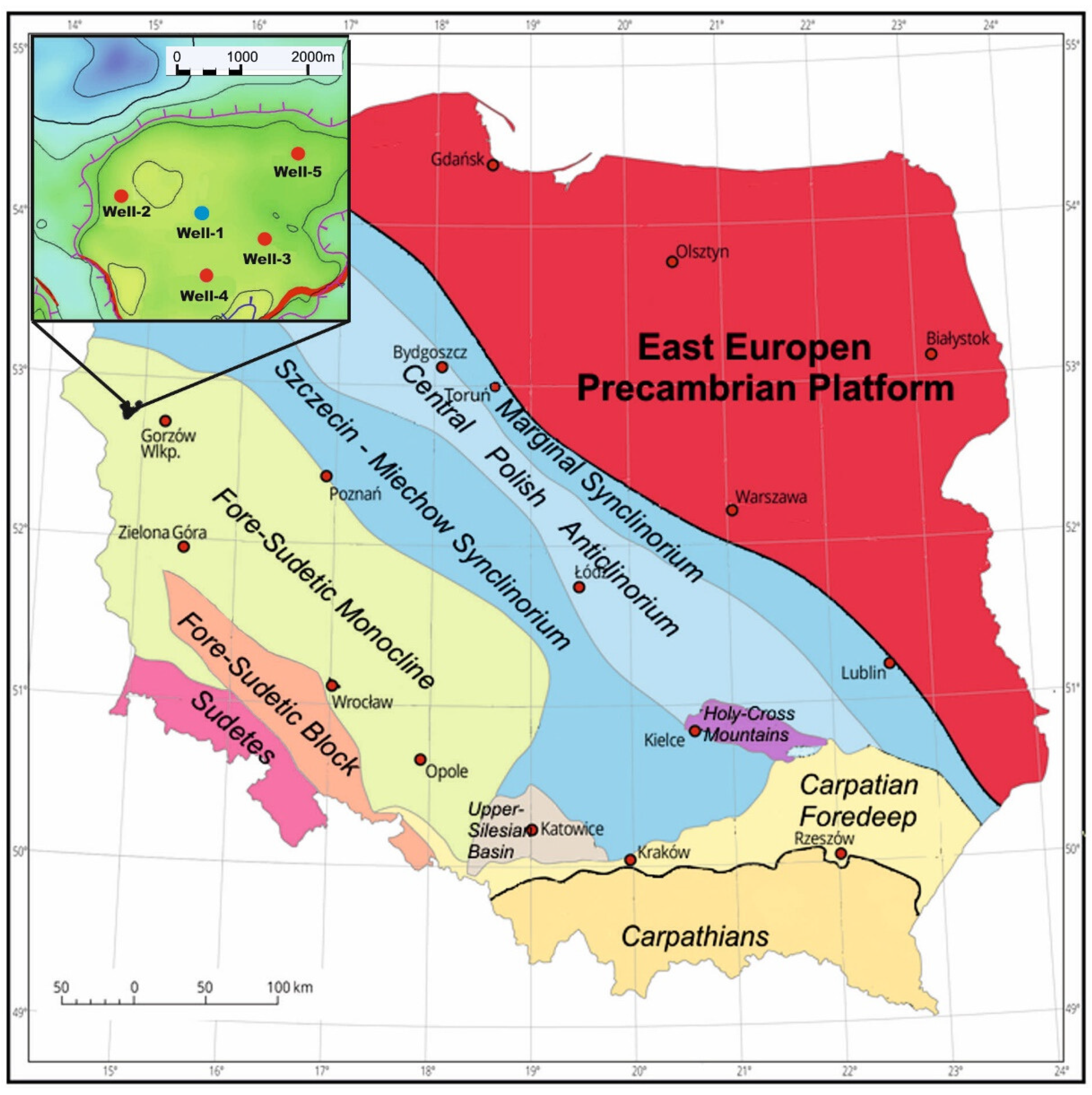
2. Materials and Methods
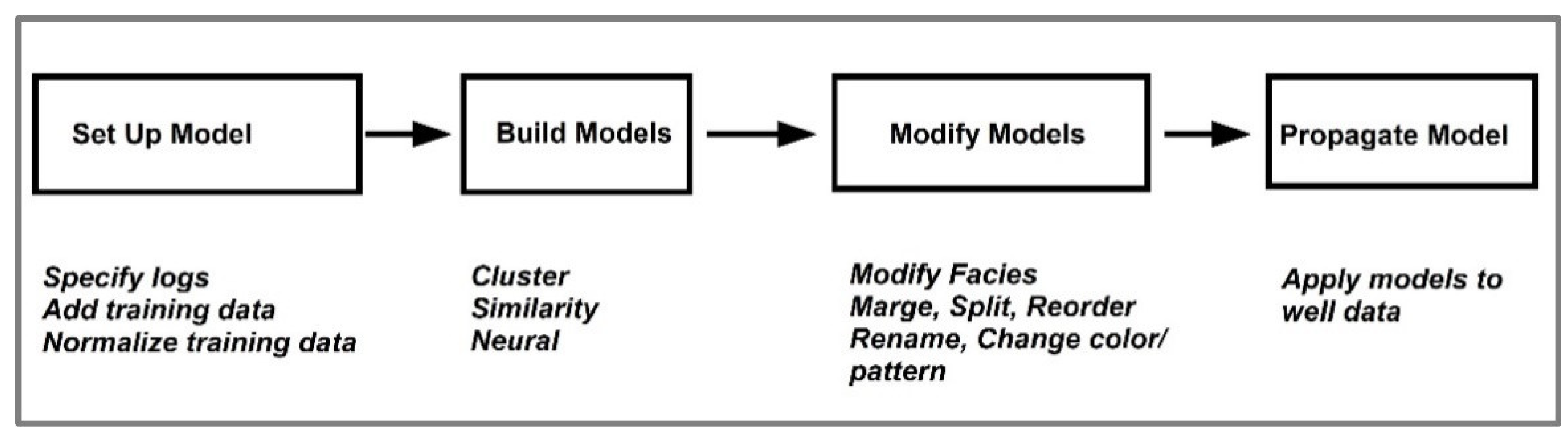
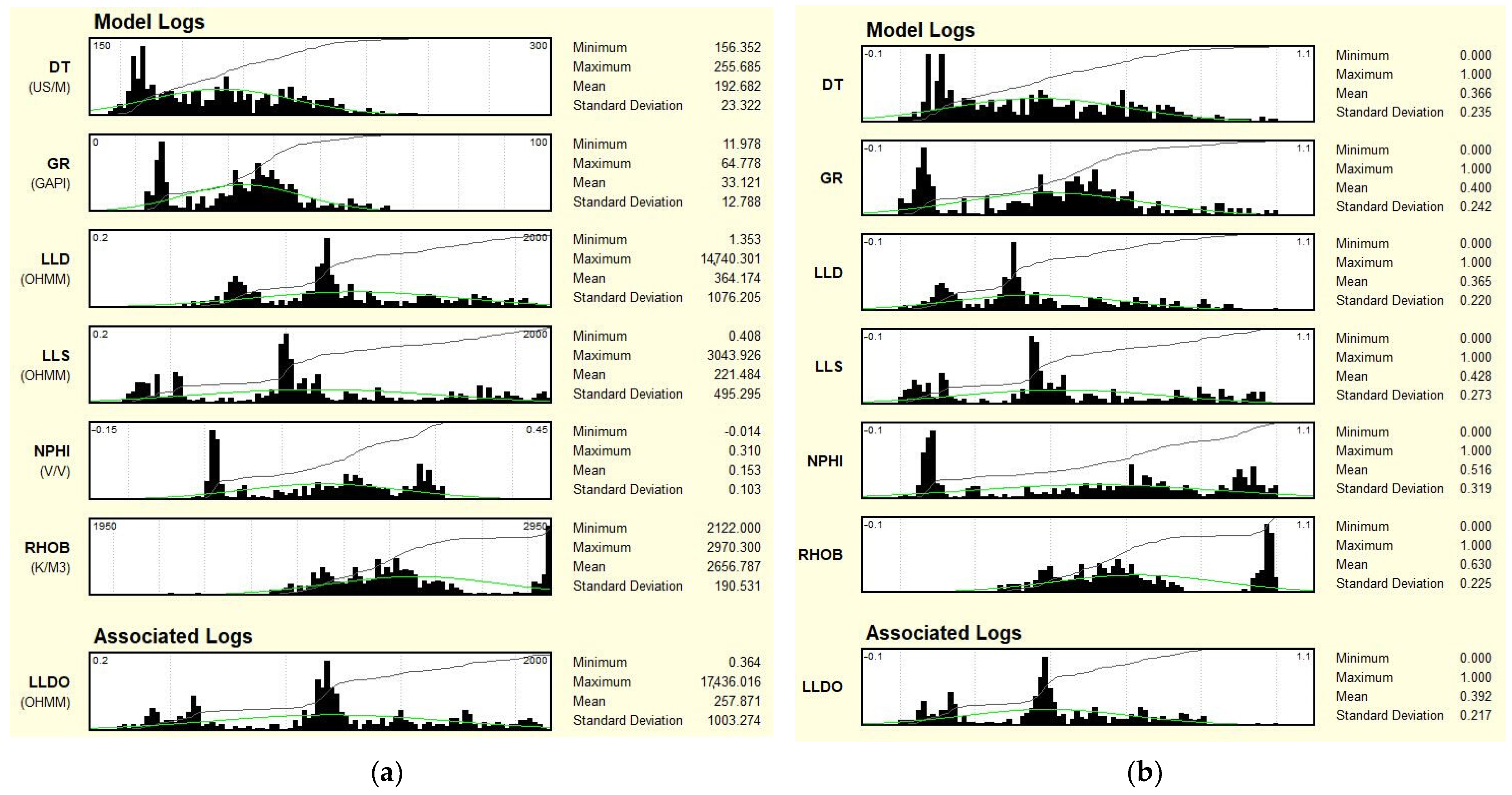
2.1. Electrofacies Calculation
- –
- cluster analysis—Multi-Resolution Graph-Based Clustering (MRGBC) [32], Self-Organizing Map (SOM), Dynamic Clustering, Ascendant Hierarchical Clustering (AHC);
- –
- similarity—Similarity Threshold Method (STM);
- –
2.2. True Resistivity Prediction (Rt_PRED/LLDO_PRED)
3. Results
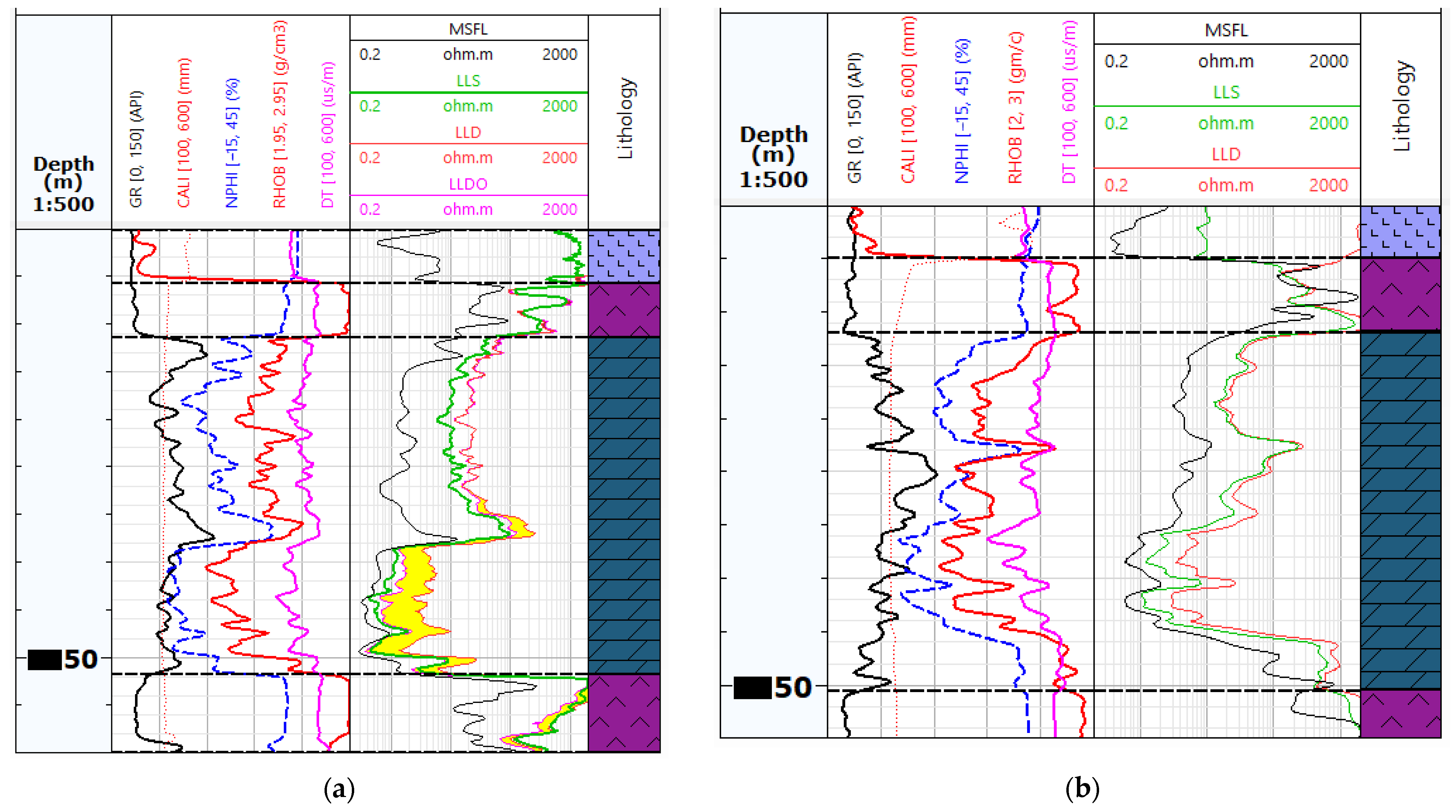
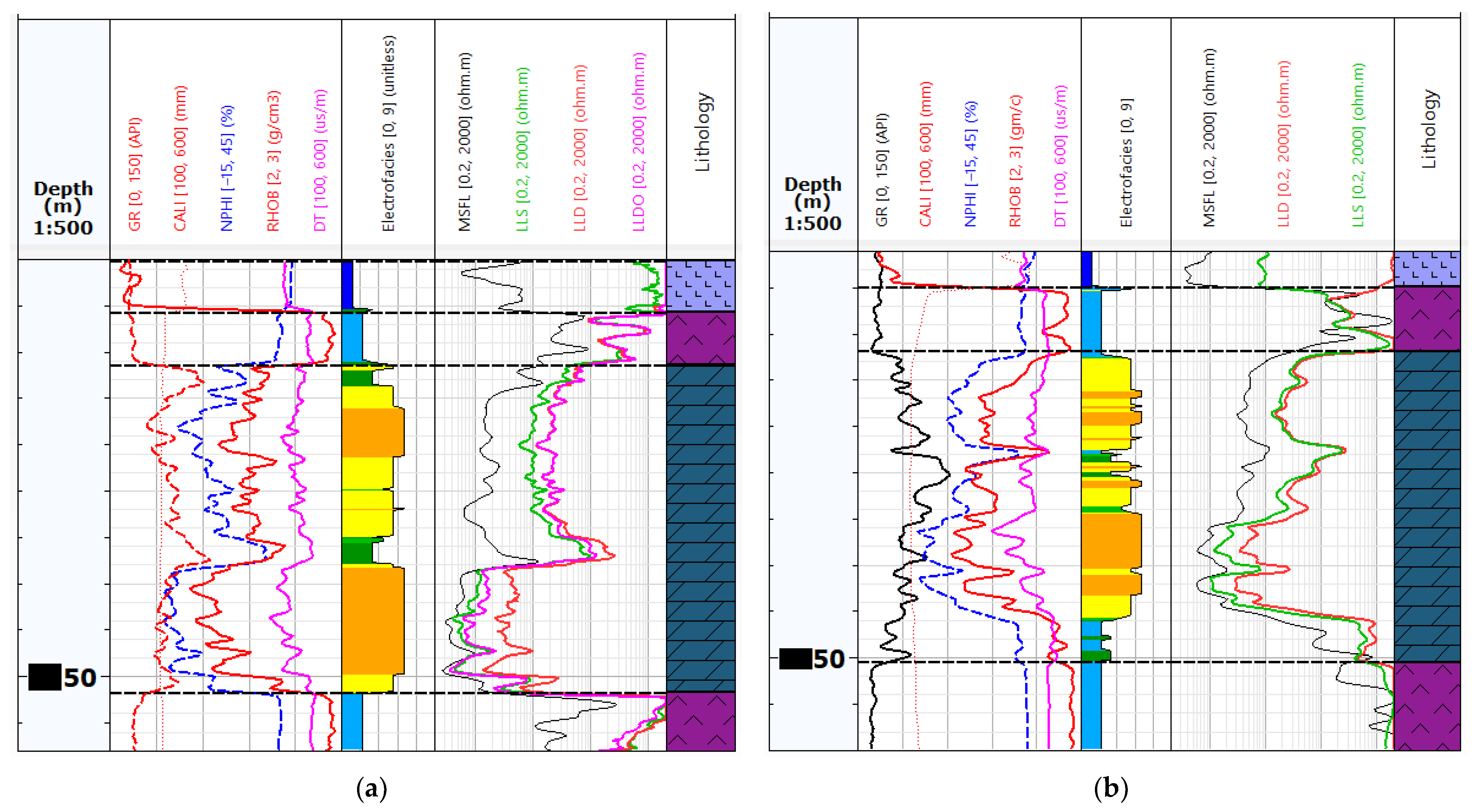
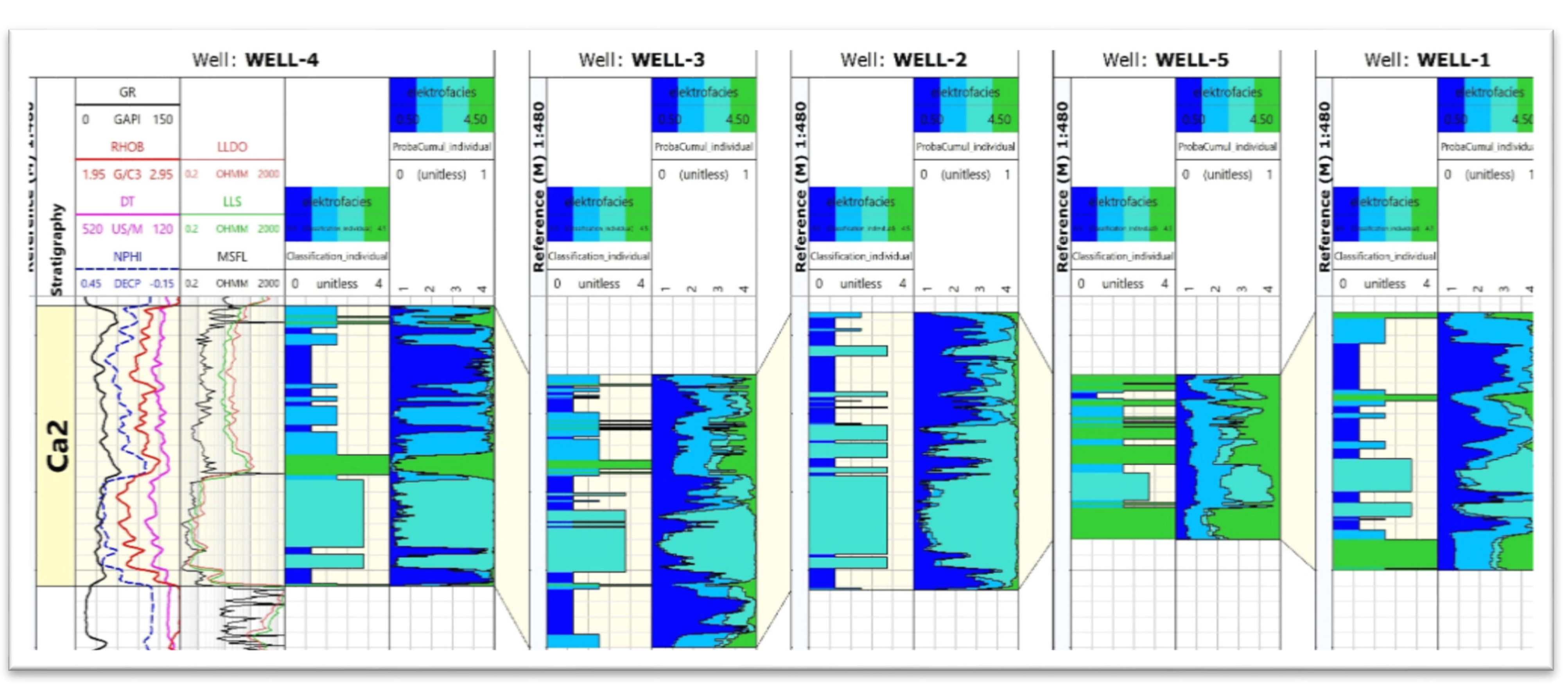
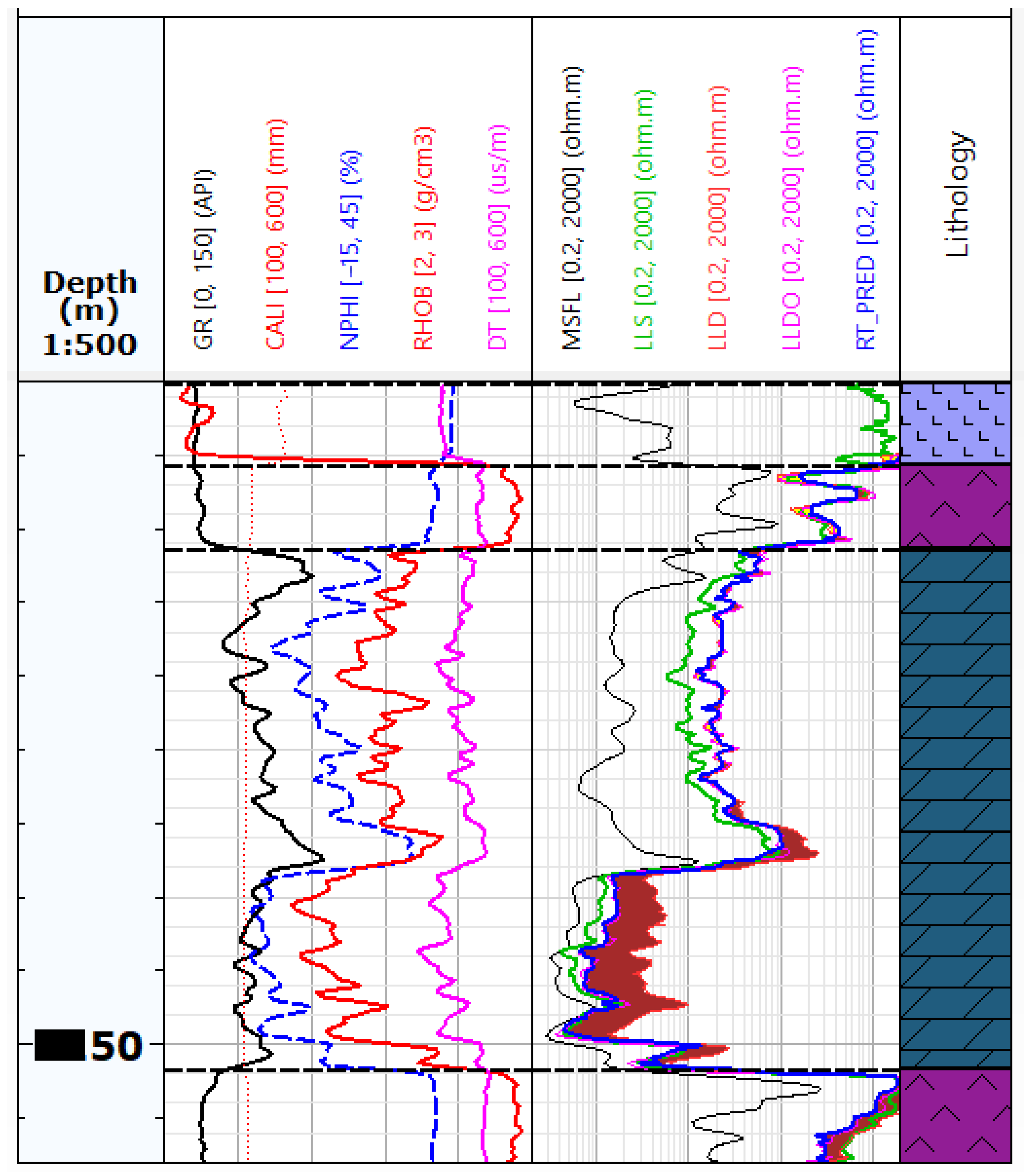
3.1. Electrofacies Calculation
- –
- electrofacies 1 (dark blue)—characterised by the lowest GR logs indication (average 13 API), average bulk density of 2.59 g/cc, average transit interval time 60 us/ft, and average neutron porosity on the order of 20%. It is characterised by high deep resistivity (10 ohmm) and a large filtration zone;
- –
- electrofacies 2 (medium blue)—characterised by relatively (in comparison to other groups) high GR logs indication (average 20 API), average bulk density of 2.62 g/cc, average transit interval time 57 us/ft, and medium average neutron porosity on the order of 15%. It is characterised by high deep resistivity (14 ohmm) and a large filtration zone;
- –
- electrofacies 3 (light blue)—characterised by low GR logs indication (average 14 API), the lowest average bulk density of 2.44 g/cc, average transit interval time 68 us/ft, and highest average neutron porosity on the order of 28%. It is characterised by relatively (in comparison to other groups) low deep resistivity (4 ohmm);
- –
- electrofacies 4 (green)—characterised by the highest GR logs indication (average 23 API), the highest average bulk density of 2.70 g/cc, the lowest average transit interval time 52 us/ft, and the lowest average neutron porosity on the order of 7%. It is characterised by high deep resistivity (17 ohmm) and a large filtration zone.
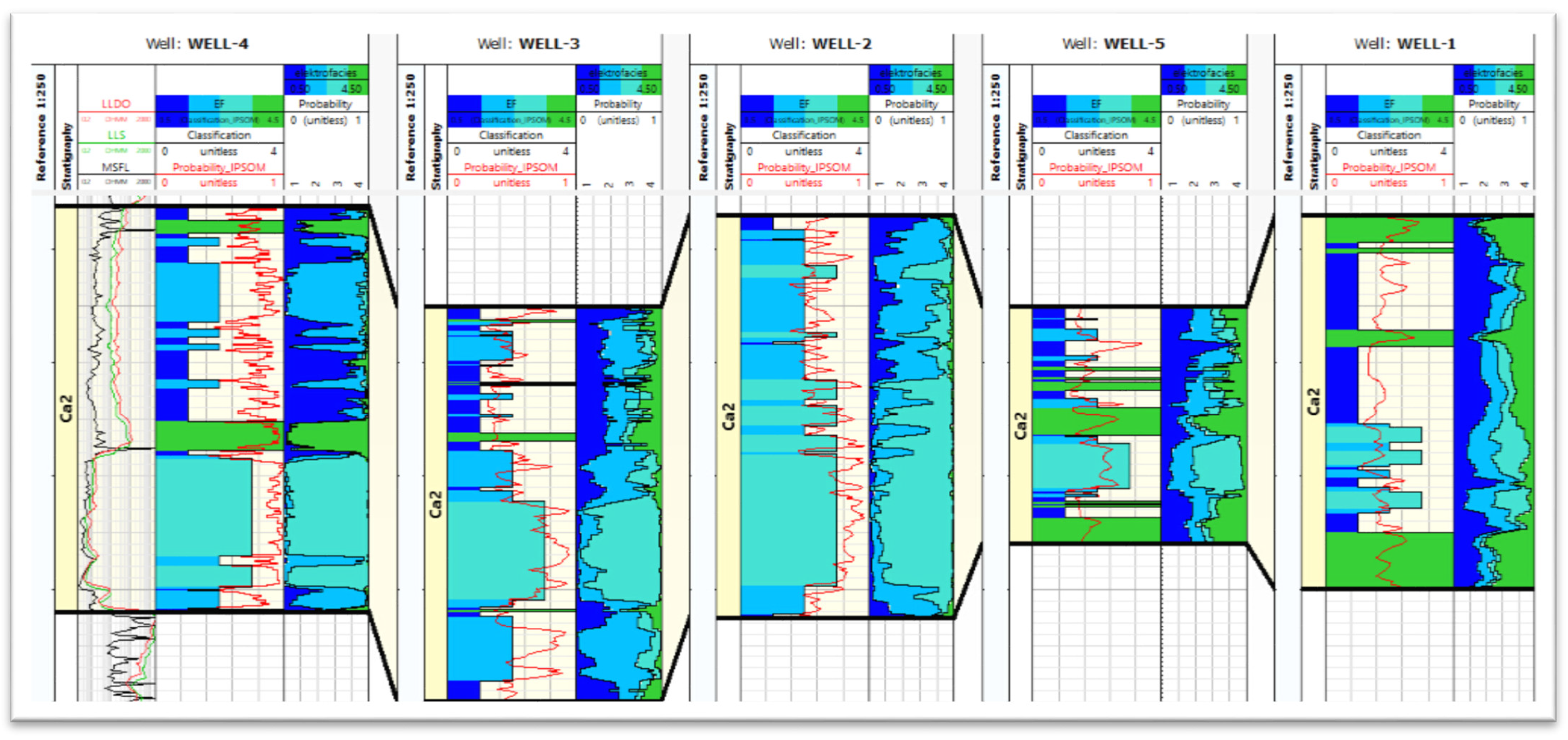
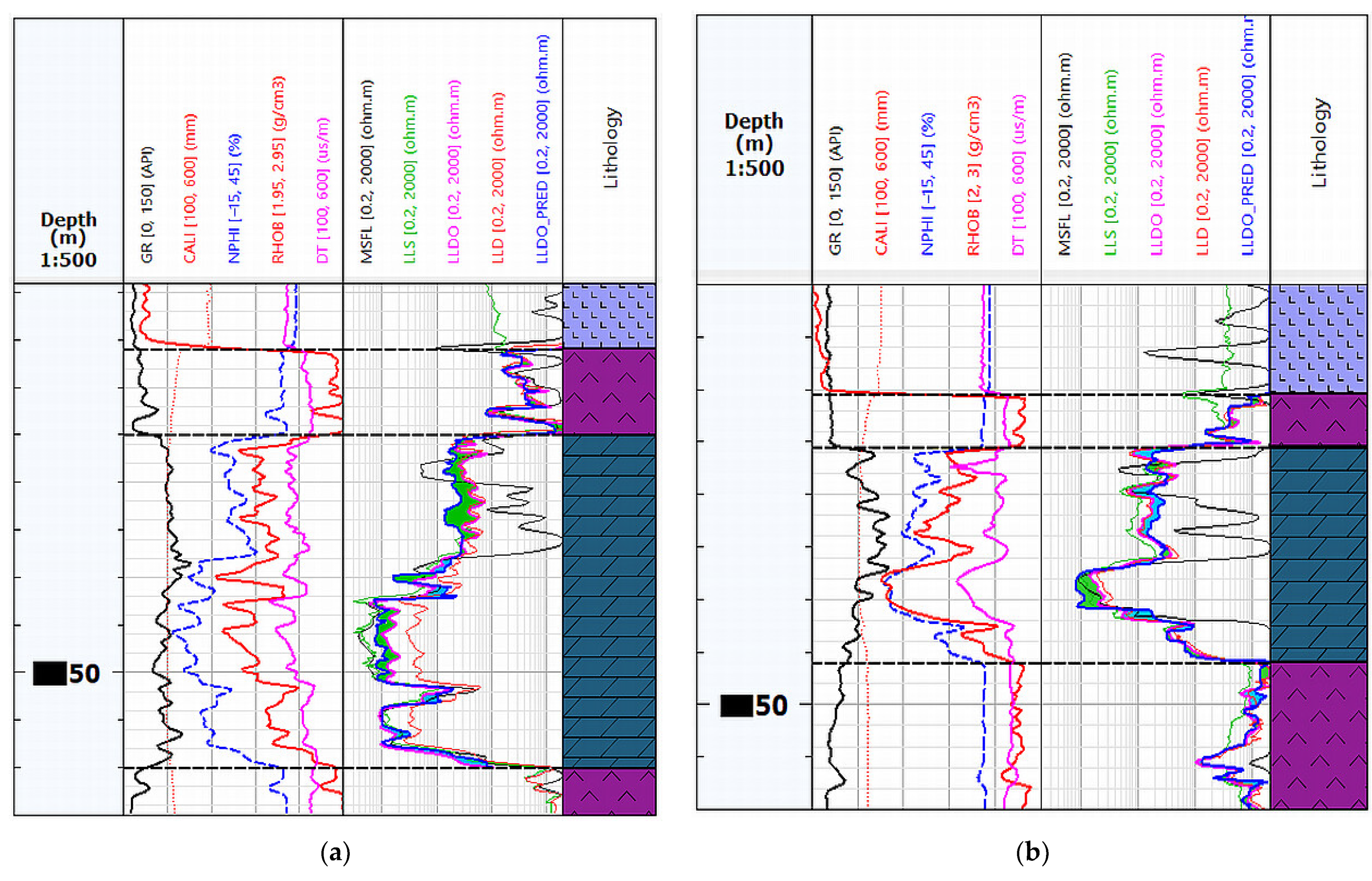
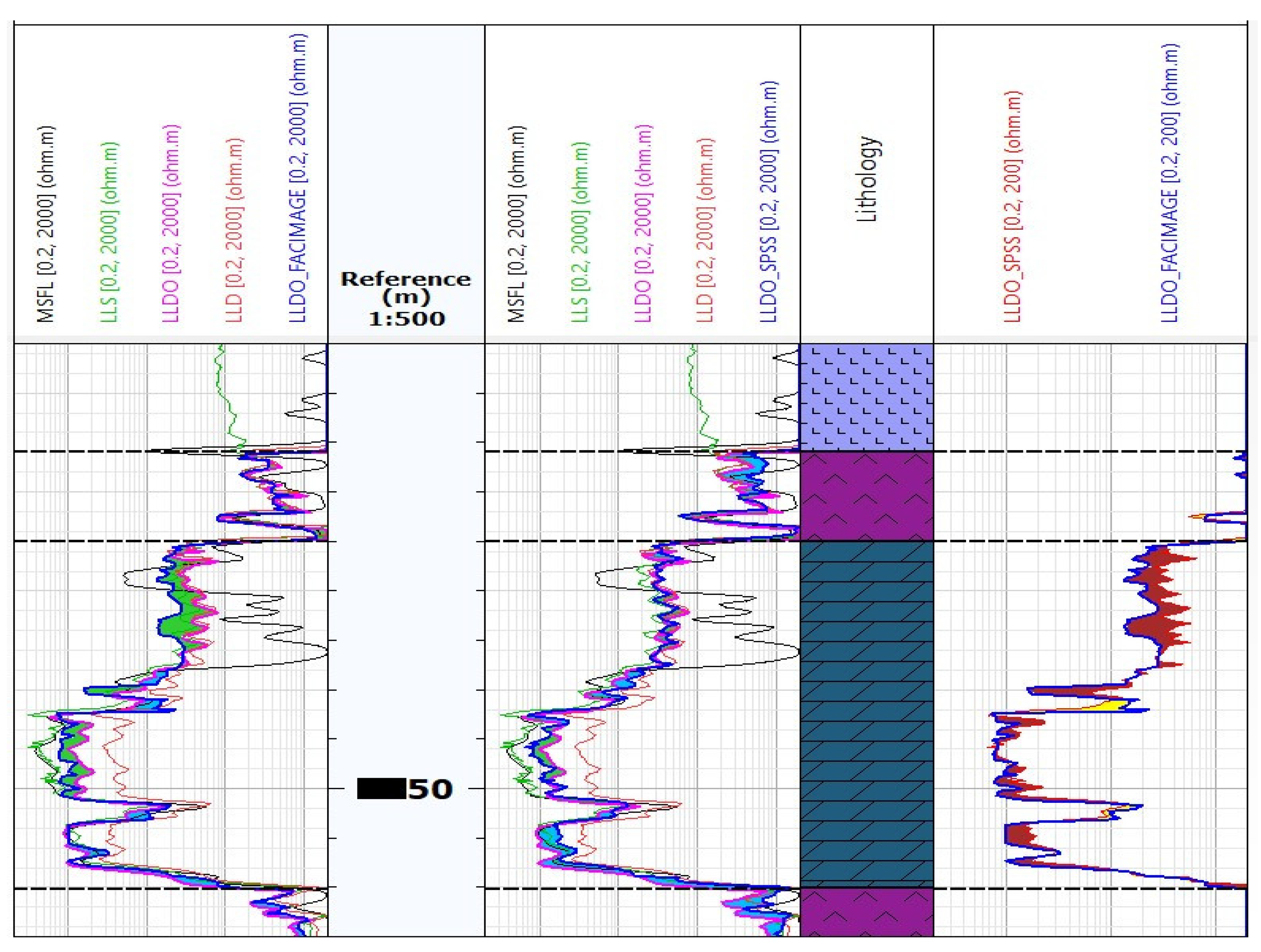
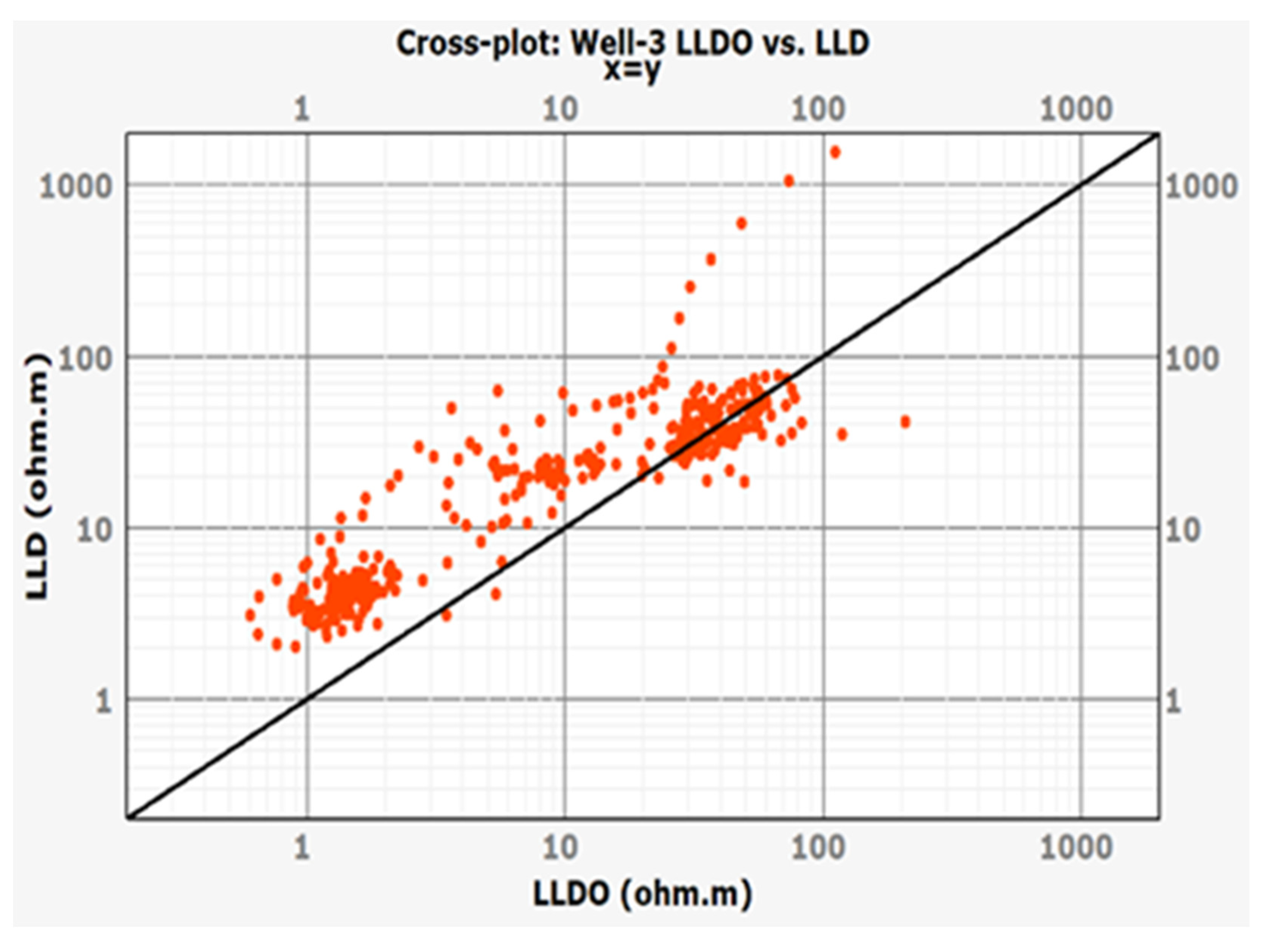
3.2. True Resistivity Prediction (Rt_PRED/LLDO_PRED)
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmitt, P.; Veronez, M.R.; Tognoli, F.M.W.; Todt, V.; Lopes, R.C.; Silva, C.A.U. Electrofacies Modelling and Lithological Classification of Coals and Mud-Bearing Fine-Grained Siliciclastic Rocks Based on Neural Networks. Earth Sci. Res. 2012, 2, 193. [Google Scholar] [CrossRef]
- Serra, O.; Abbott, H.T. The Contribution of Logging Data to Sedimentology and Stratigraphy. Soc. Pet. Eng. J. 1982, 22, 117–131. [Google Scholar] [CrossRef]
- SEG Wiki Dictionary: Electrofacies. Available online: https://wiki.seg.org/wiki/Dictionary:Electrofacies (accessed on 5 August 2021).
- Davis, J.C. Electrofacies in Reservoir Characterization. In Handbook of Mathematical Geosciences; Daya Sagar, B.S., Cheng, Q., Agterberg, F., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 211–223. ISBN 978-3-319-78998-9. [Google Scholar]
- Puskarczyk, E. Artificial Neural Networks as a Tool for Pattern Recognition and Electrofacies Analysis in Polish Palaeozoic Shale Gas Formations. Acta. Geophys. 2019, 67, 1991–2003. [Google Scholar] [CrossRef] [Green Version]
- Puskarczyk, E. Application of Multivariate Statistical Methods and Artificial Neural Network for Facies Analysis from Well Logs Data: An Example of Miocene Deposits. Energies 2020, 13, 1548. [Google Scholar] [CrossRef] [Green Version]
- Singh, S. Permeability Prediction Using Artificial Neural Network (ANN): A Case Study of Uinta Basin. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. SPE-99286-STU. [Google Scholar]
- Mohaghegh, S.; Balan, B.; Ameri, S. Permeability Determination From Well Log Data. SPE Form. Eval. 1997, 12, 170–174. [Google Scholar] [CrossRef]
- Huang, Z.; Shimeld, J.; Williamson, M.; Katsube, J. Permeability Prediction with Artificial Neural Network Modeling in the Venture Gas Field, Offshore Eastern Canada. Geophysics 1996, 61, 422–436. [Google Scholar] [CrossRef]
- Quadir, A.; Lewis, C.; Rau, R.-J. Generation of Pseudo-Synthetic Seismograms from Gamma-Ray Well Logs of Highly Radioactive Formations. Pure. Appl. Geophys. 2019, 176, 1579–1599. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.H.; Min, B.; Lim, J.; Lee, K. Generation of Synthetic Density Log Data Using Deep Learning Algorithm at the Golden Field in Alberta, Canada. Geofluids 2020, 2020, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Suau, J.; Grimaldi, P.; Poupon, A.; Souhaite, P. The Dual Laterolog-Rxo Tool. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, San Antonio, TX, USA, 8–11 October 1972. SPE-4018-MS. [Google Scholar]
- Trouiller, J.C.; Dubourg, I. A Better Deep Laterolog Compensated for Groningen and Reference Effects. In Proceedings of the SPWLA 35th Annual Logging Symposium, Tulsa, OK, USA, 19–22 June 1994. [Google Scholar]
- Nam, M.J.; Pardo, D.; Torres-Verdín, C. Assessment of Delaware and Groningen Effects on Dual-Laterolog Measurements with a Self-Adaptive Hp Finite-Element Method. Geophysics 2010, 75, F143–F149. [Google Scholar] [CrossRef]
- Andersen, B.I. Modeling and Inversion Methods for the Interpretation of Resistivity Logging Tool Response. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2001; pp. 149–151. [Google Scholar]
- Drahos, D.; Galsa, A. Modeling Groningen Effect on Deep Laterolog. Geosci. Eng. Vol. 2015, 46, 9–21. [Google Scholar]
- Woodhouse, R. The Laterolog Groningen Phantom Can Cost You Money. In Proceedings of the SPWLA 19th Annual Logging Symposium, El Paso, TX, USA, 13–16 June 1978. [Google Scholar]
- Lacour-Gayet, P. Method and Apparatus for Detecting an Anomaly in a Resistivity Measurement of an Earth Formation. U.S. Patent No. 4,335,35, 1982. [Google Scholar]
- Chemali, R.E.; Dirk, W.C. Method and Apparatus for Measuring Resistivity of an Earth Formation. U.S. Patent No. 4,646,026, 24 February 1987. [Google Scholar]
- Smits, J.W.; Dubourg, I.; Luling, M.G.; Minerbo, G.N.; Koelman, J.M.V.A.; Hoffman, L.J.B.; Lomas, A.T.; Oosten, R.K.V.D.; Schiet, M.J.; Dennis, R.N. Improved Resistivity Interpretation Utilizing a New Array Laterolog Tool and Associated Inversion Processing. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998. SPE-49328-MS. [Google Scholar]
- Lee, S.H.; Kharghoria, A.; Datta-Gupta, A. Electrofacies Characterization and Permeability Predictions in Complex Reservoirs. SPE Reserv. Eval. Eng. 2002, 5, 237–248. [Google Scholar] [CrossRef]
- Correia, G.G.; Schiozer, D.J. Reservoir Characterization Using Electrofacies Analysis in the Sandstone Reservoir of the Norne Field (Offshore Norway). Pet. Geosci. 2016, 22, 165–176. [Google Scholar] [CrossRef]
- Baudzis, S.; Jarzyna, J.A.; Puskarczyk, E. The Measurement and Interpretation Methodology of Resistivity Logs Affected by the Groningen Effect—A Polish Case Study. Geol. Geophys. Environ. 2020, 46, 35. [Google Scholar] [CrossRef]
- Jarzyna, J.A.; Baudzis, S.; Janowski, M.; Puskarczyk, E. Geothermal Resources Recognition and Characterization on the Basis of Well Logging and Petrophysical Laboratory Data, Polish Case Studies. Energies 2021, 14, 850. [Google Scholar] [CrossRef]
- Gorski, M.; Wojtkowiak, Z.; Radecki, S. Barnowko-Mostno-Buszewo (BMB); the Largest Crude Oil Deposit in Poland. Pet. Geosci. 1999, 5, 5–15. [Google Scholar] [CrossRef]
- Pikulski, L.; Wolnowski, T. Geological Analysis of the Main Dolomite Formations (Ca2) in Western Poland. In Proceedings of the AAPG/EAGE Internetional Research Conference, El Paso, TX, USA, 15 October 2000. [Google Scholar]
- Karnkowski, P. Oil and Gas Deposits in Poland; Geosynoptics Society “GEOS”: Cracow, Poland, 1999; ISBN 83-86695-01-3. [Google Scholar]
- Karnkowski, P.H. Permian Basin as a Main Exploration Target in Poland. Prz. Geol. 2007, 55, 1003–1015. [Google Scholar]
- Górski, M.; Król, E.; Kunicka-Górska, W.; Trela, M.; Urbańska, H. Wydzielanie pułapek węglowodorów w utworach poziomu dolomitu głównego poprzez rozpoznanie zmian litofacjalnych i strukturalnych na podstawie zintegrowanej interpretacji sejsmiki 3D i danych otworowych w rejonie Gorzowa. Prz. Geol. 1999, 47, 1080–1095. [Google Scholar]
- Krogulec, E.; Sawicka, K.; Zabłocki, S.; Falkowska, E. Mineralogy and Permeability of Gas and Oil Dolomite Reservoirs of the Zechstein Main Dolomite Basin in the Lubiatów Deposit (Poland). Energies 2020, 13, 6436. [Google Scholar] [CrossRef]
- Available online: Https://Www.Pdgm.Com/Products/Geolog/Facimage/ (accessed on 6 August 2021).
- Ye, S.-J.; Rabiller, P. A New Tool For Electro-Facies Analysis: Multi-Resolution Graph-Based Clustering. In Proceedings of the SPWLA 41st Annual Logging Symposium, Dallas, TX, USA, 4–7 June 2000. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-94463-0. [Google Scholar]
- Facimage Help, Paradigm/Emerson Geolog-Paradigm 20, Bulit in Manual Facimage 2020; Paradigm Ltd.: Brisbane, QLD, Australia, 2020.
- Kohonen, T. The Self-Organizing Map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Available online: https://Www.Ibm.Com/Analytics/Spss-Statistics-Software (accessed on 5 August 2021).
- Zhang, T.; Ramakrishnon, R.; Livny, M. BIRCH:An Efficient Data Clustering Method for Very Large Databases. In Proceedings of the ACM SIGMOD Conference on Management of Data, Montreal, QB, Canada, 1 June 1996; pp. 103–114. [Google Scholar]
- Chiu, T.; Fang, D.; Chen, J.; Wang, Y.; Jeris, C. A Robust and Scalable Clustering Algorithm for Mixed Type Attributes in Large Database Environment. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’01, San Francisco, CA, USA, 26–29 August 2001; pp. 263–268. [Google Scholar]
- Larose, D.T.; Larose, C.D. Discovering Knowledge in Data: An Introduction to Data Mining, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1-118-87357-1. [Google Scholar]
- Tian, Y.; Xu, H.; Zhang, X.-Y.; Wang, H.-J.; Guo, T.-C.; Zhang, L.-J.; Gong, X.-L. Multi-Resolution Graph-Based Clustering Analysis for Lithofacies Identification from Well Log Data: Case Study of Intraplatform Bank Gas Fields, Amu Darya Basin. Appl. Geophys. 2016, 13, 598–607. [Google Scholar] [CrossRef]
- Wu, H.; Wang, C.; Feng, Z.; Yuan, Y.; Wang, H.-F.; Xu, B.-S. Adaptive Multi-Resolution Graph-Based Clustering Algorithm for Electrofacies Analysis. Appl. Geophys. 2020, 17, 13–25. [Google Scholar] [CrossRef]
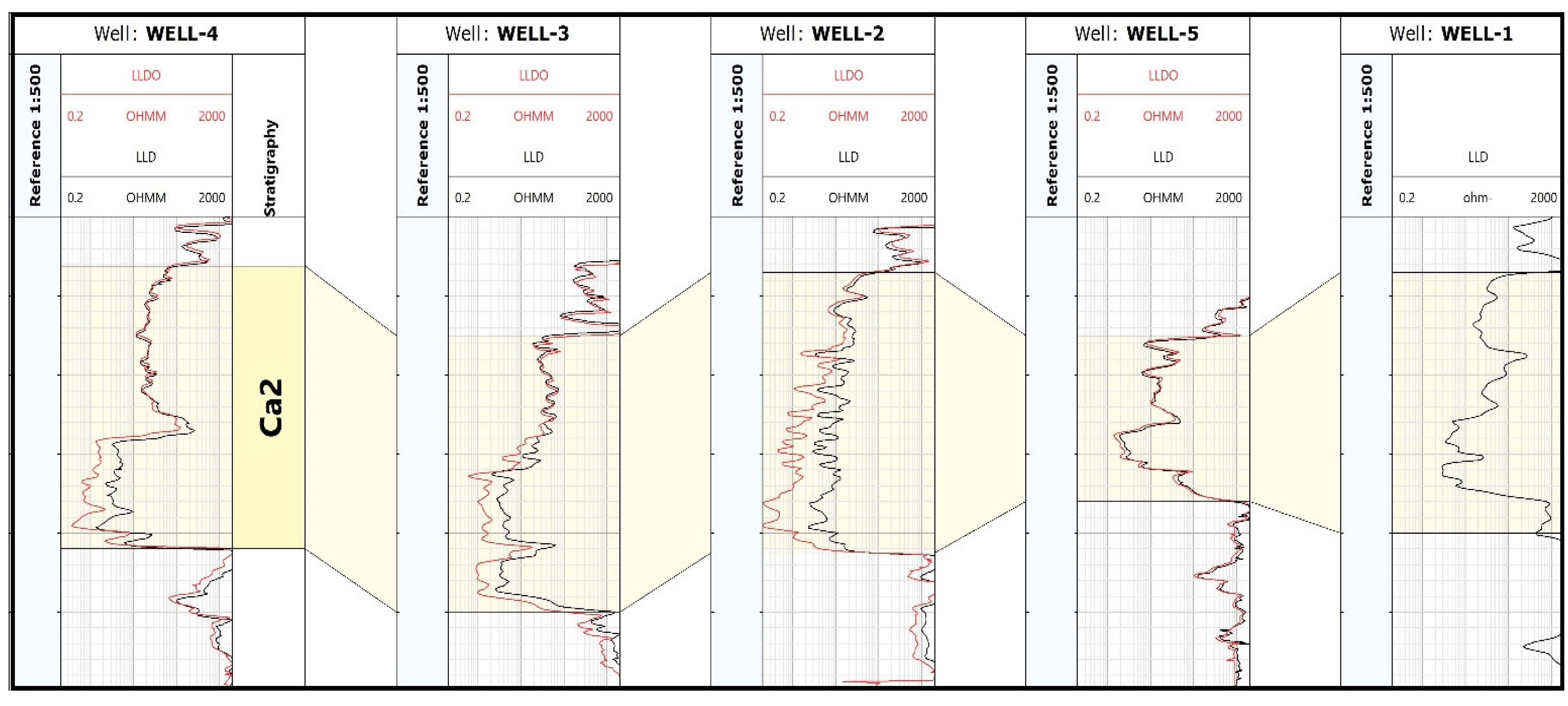

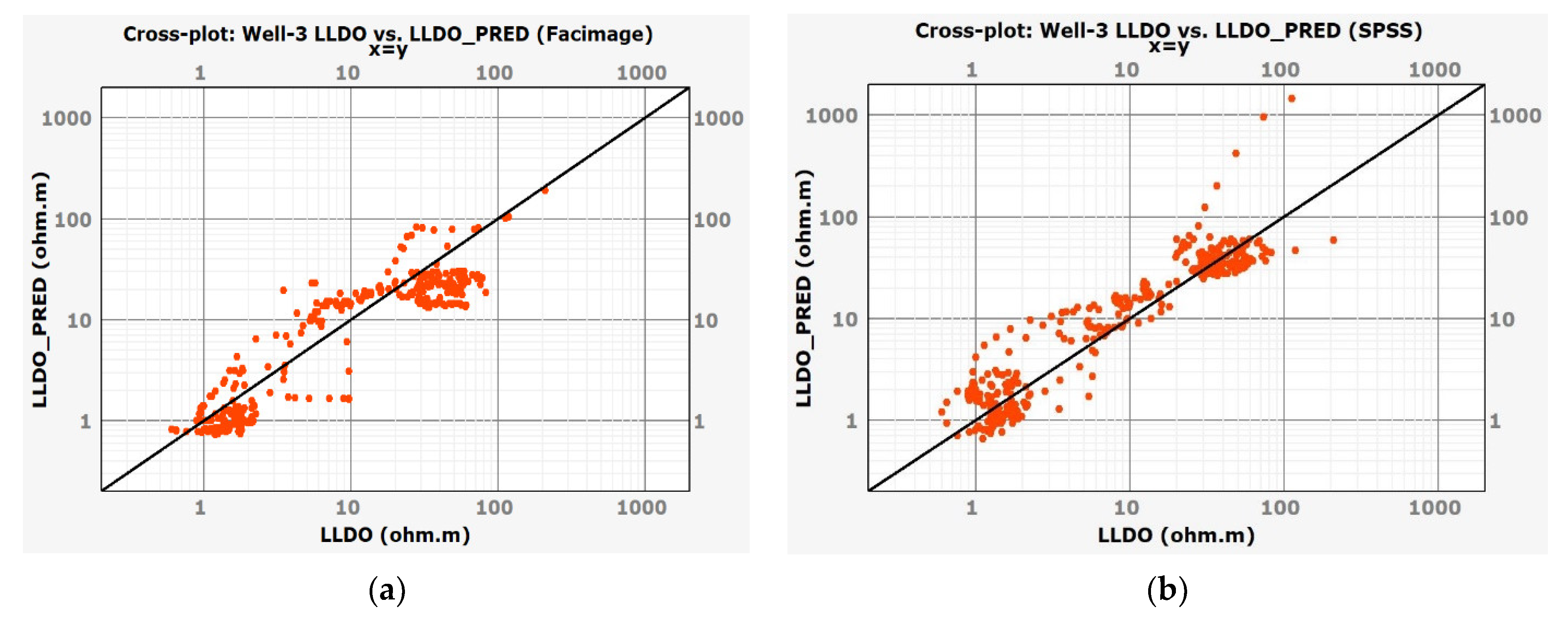
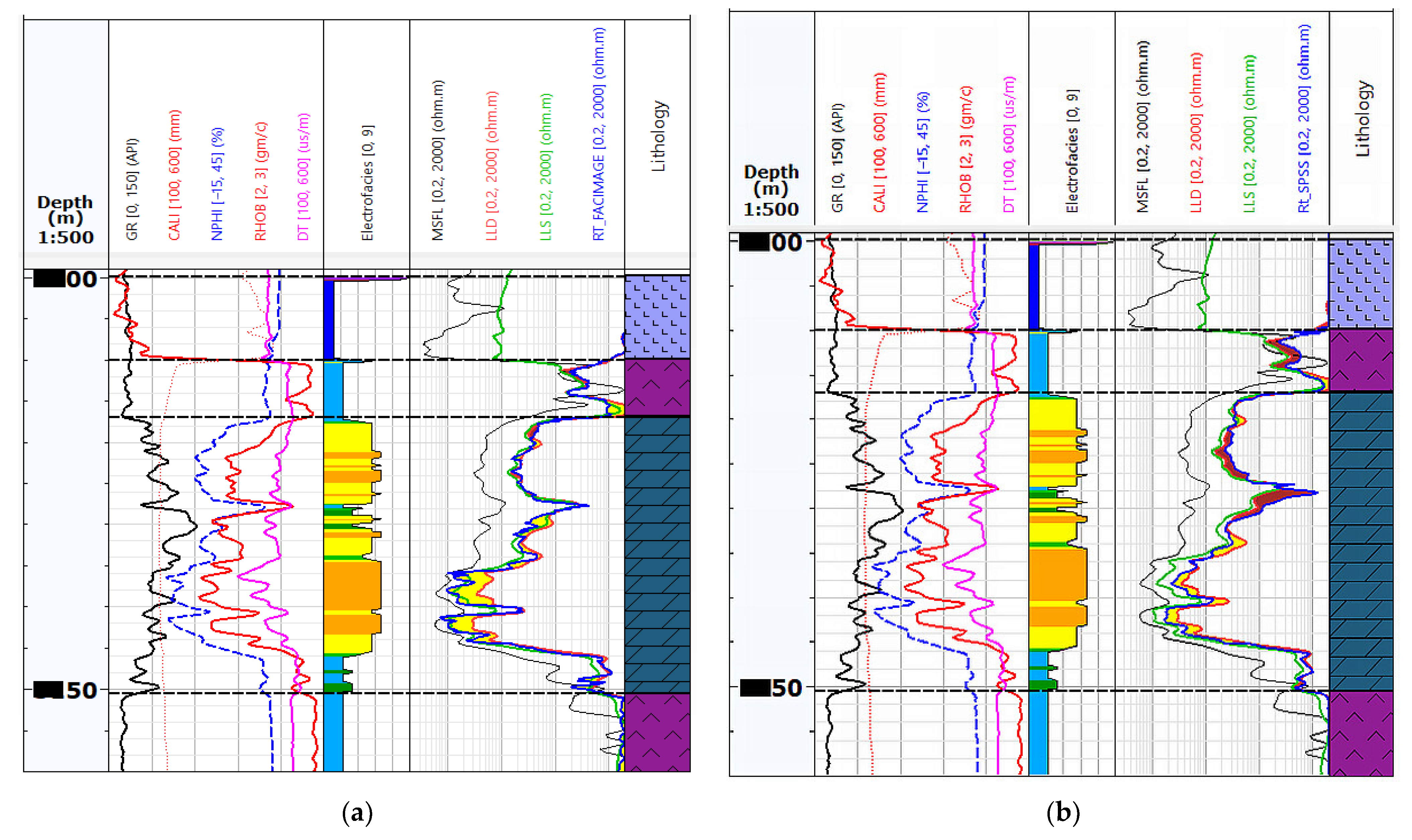
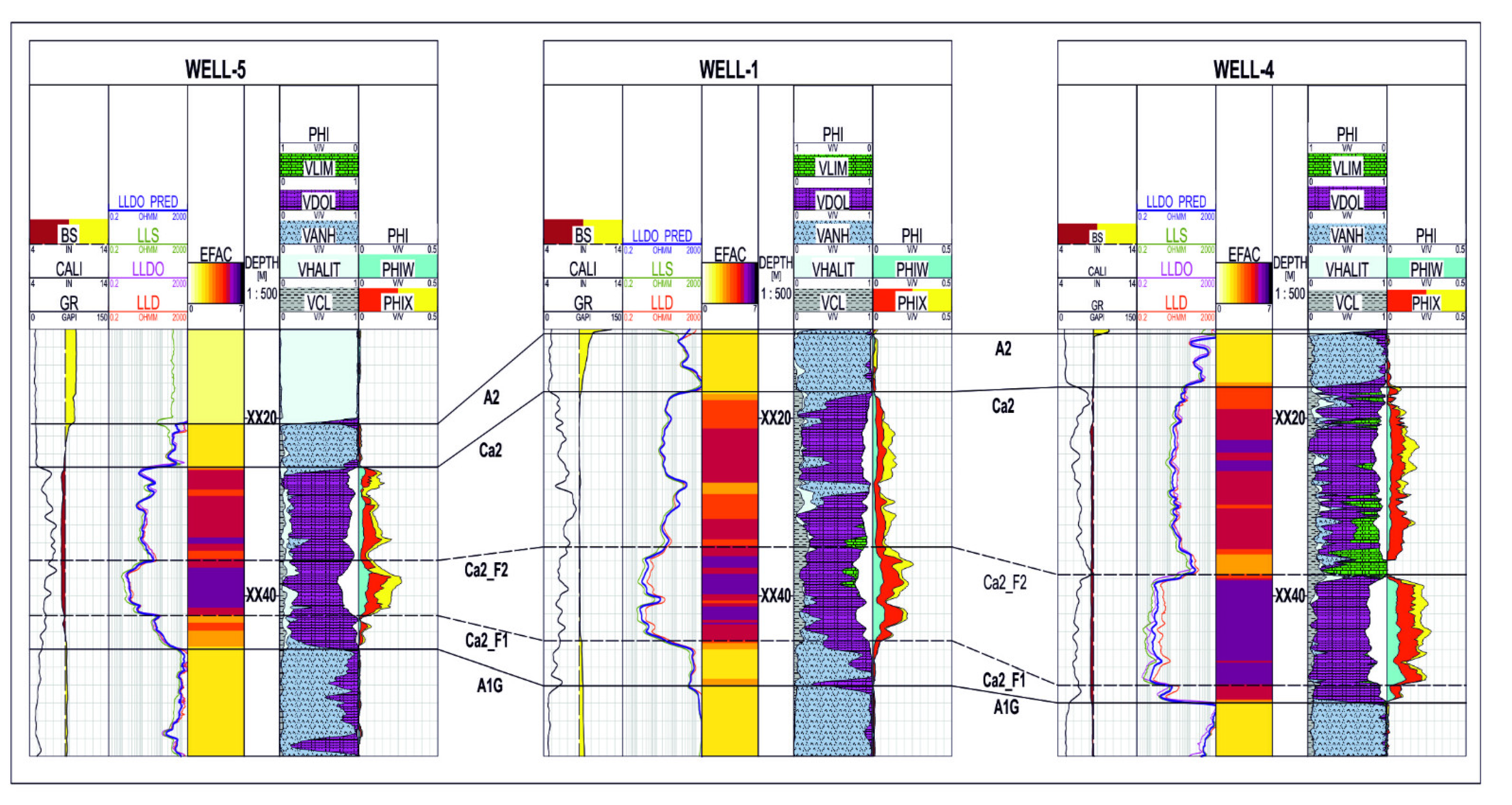
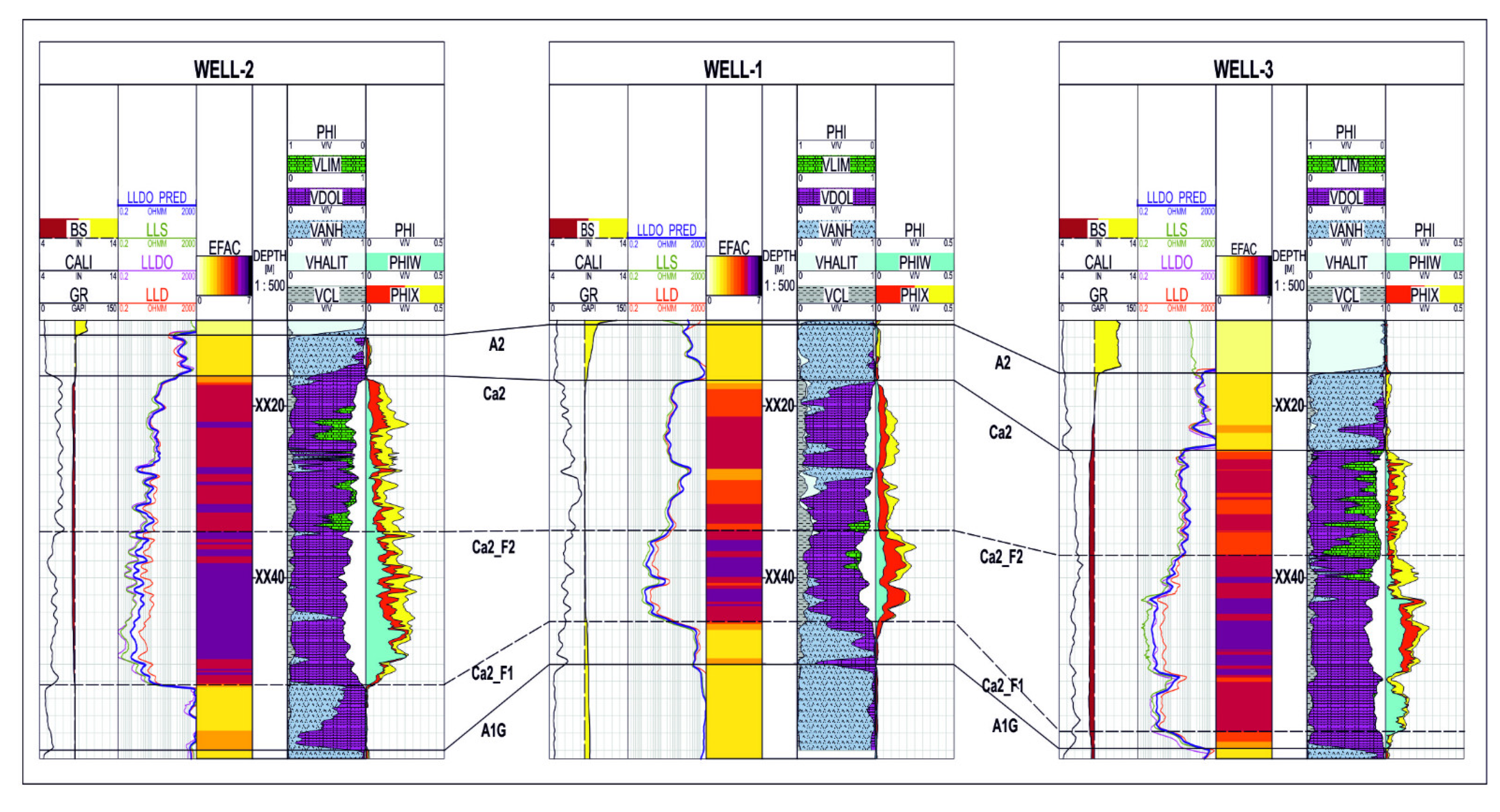
| Curve\Well | Well-1 | Well-2 | Well-3 | Well-4 | Well-5 |
|---|---|---|---|---|---|
| GR | Yes | Yes | Yes | Yes | Yes |
| LLS | Yes | Yes | Yes | Yes | Yes |
| LLD | Yes | Yes | Yes | Yes | Yes |
| LLDO | No | Yes | Yes | Yes | Yes |
| DT | Yes | Yes | Yes | Yes | Yes |
| CALI | Yes | Yes | Yes | Yes | Yes |
| RHOB | Yes | Yes | Yes | Yes | Yes |
| NPHI | Yes | Yes | Yes | Yes | Yes |
| Model | RMSE (log(LLDO)) | MAE (log(LLDO)) | RMSE (LLDO) | MAE (LLDO) |
|---|---|---|---|---|
| LLD | 0.4401 | 0.3602 | 102.4347 | 20.7308 |
| Facimage on Well-4 | 0.2723 | 0.2252 | 15.8028 | 9.3463 |
| IBM SPSS Statistics on Well-4 | 0.2882 | 0.2286 | 63.3347 | 18.8500 |
| IBM SPSS Statistics—mean of models built on Well-2, 4, and 5 | 0.2460 | 0.1837 | 89.8486 | 14.7368 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baudzis, S.; Karłowska-Pik, J.; Puskarczyk, E. Electrofacies as a Tool for the Prediction of True Resistivity Using Advanced Statistical Methods—Case Study. Energies 2021, 14, 6228. https://doi.org/10.3390/en14196228
Baudzis S, Karłowska-Pik J, Puskarczyk E. Electrofacies as a Tool for the Prediction of True Resistivity Using Advanced Statistical Methods—Case Study. Energies. 2021; 14(19):6228. https://doi.org/10.3390/en14196228
Chicago/Turabian StyleBaudzis, Stanisław, Joanna Karłowska-Pik, and Edyta Puskarczyk. 2021. "Electrofacies as a Tool for the Prediction of True Resistivity Using Advanced Statistical Methods—Case Study" Energies 14, no. 19: 6228. https://doi.org/10.3390/en14196228
APA StyleBaudzis, S., Karłowska-Pik, J., & Puskarczyk, E. (2021). Electrofacies as a Tool for the Prediction of True Resistivity Using Advanced Statistical Methods—Case Study. Energies, 14(19), 6228. https://doi.org/10.3390/en14196228






