Reliability-Based Robust Design Optimization of Lithium-Ion Battery Cells for Maximizing the Energy Density by Increasing Reliability and Robustness
Abstract
:1. Introduction
2. Electrochemical Numerical Analysis Model of LIB Cells
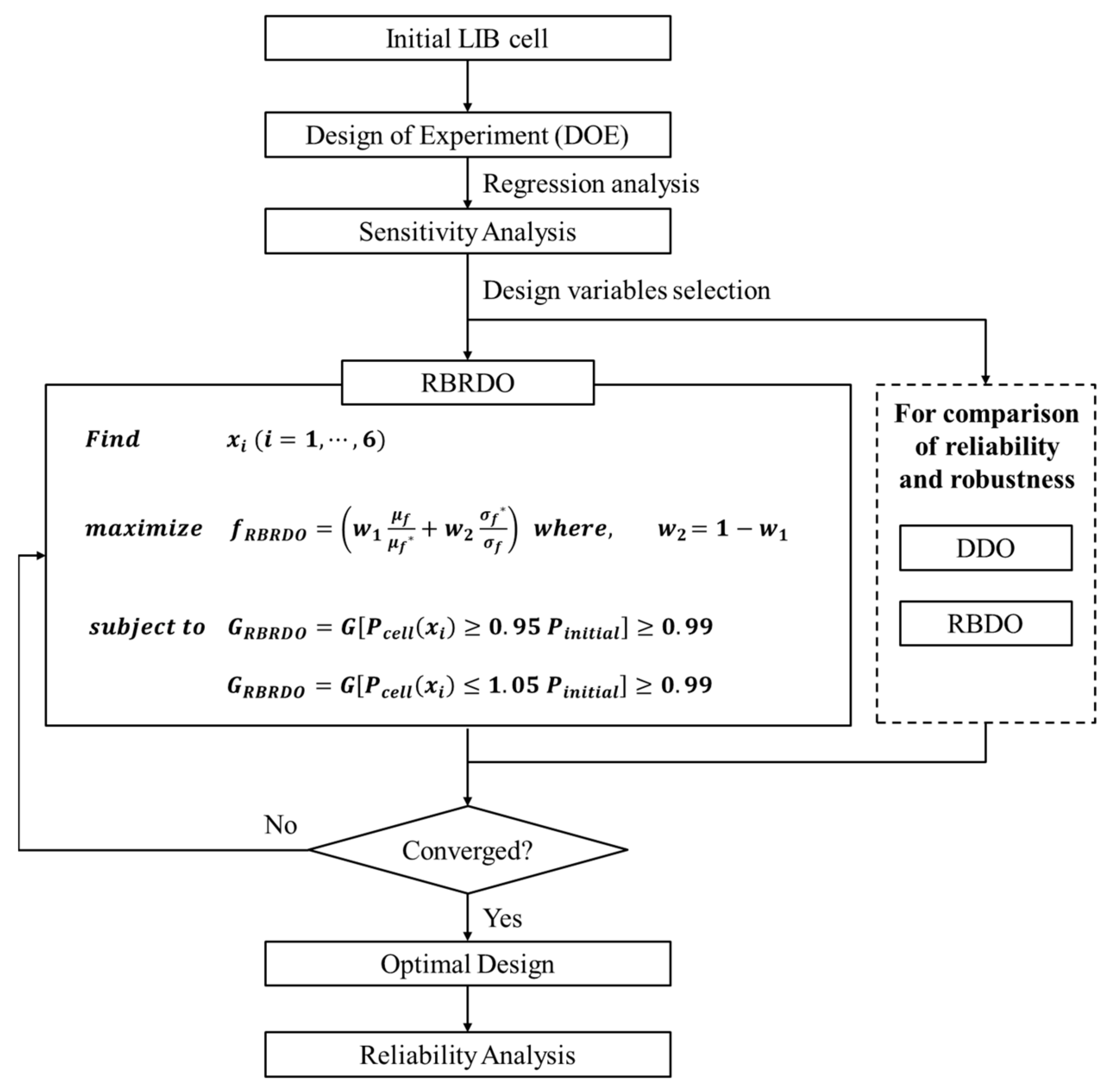
3. Reliability-Based Robust Design Optimization of LIB Cell
3.1. Variations in LIB Cell Performance due to Manufacturing Uncertainties
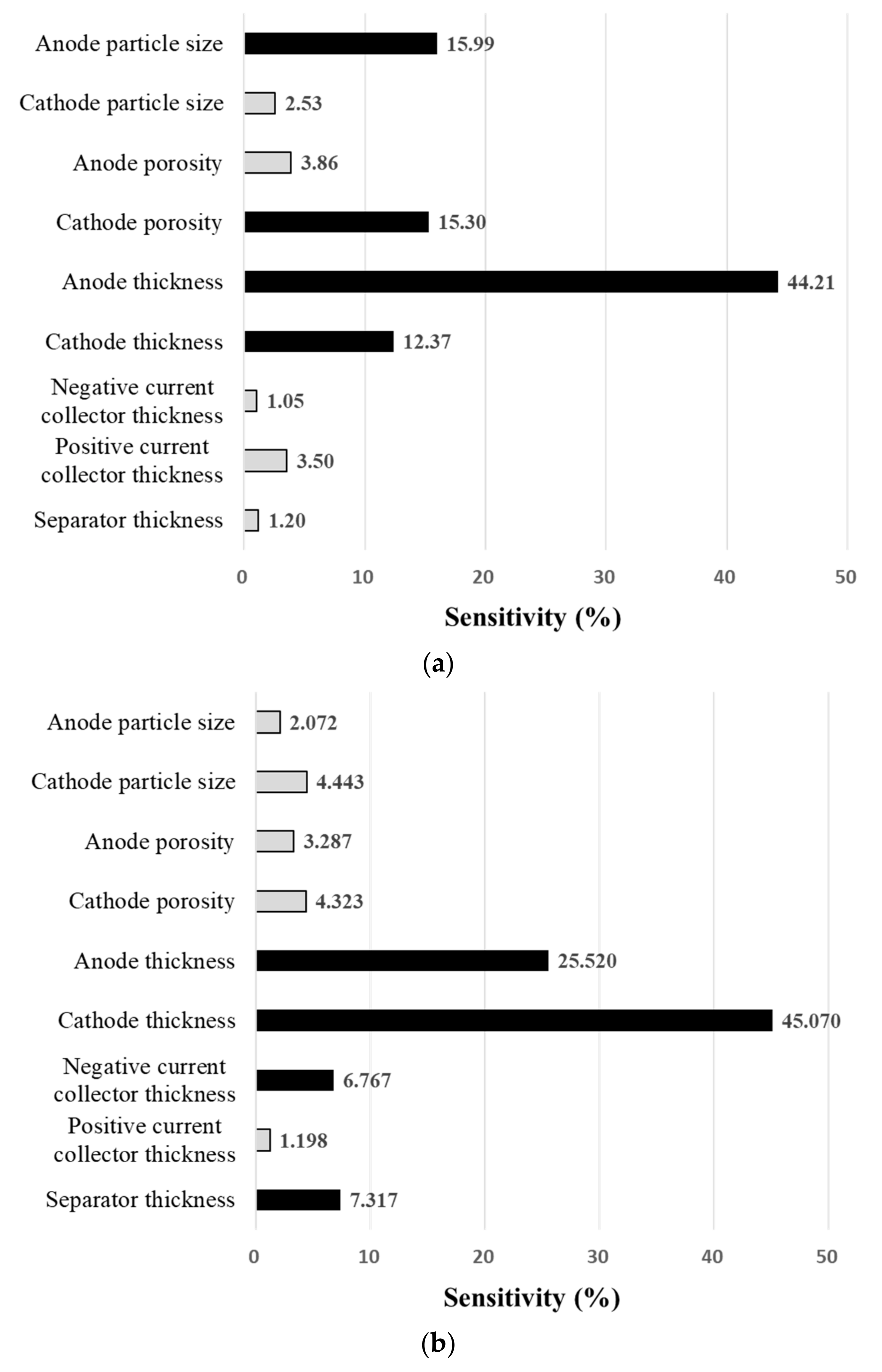
3.2. Sensitivity Analysis through DOE
3.3. Formulation of RBRDO
4. Discussion
4.1. RBRDO Results
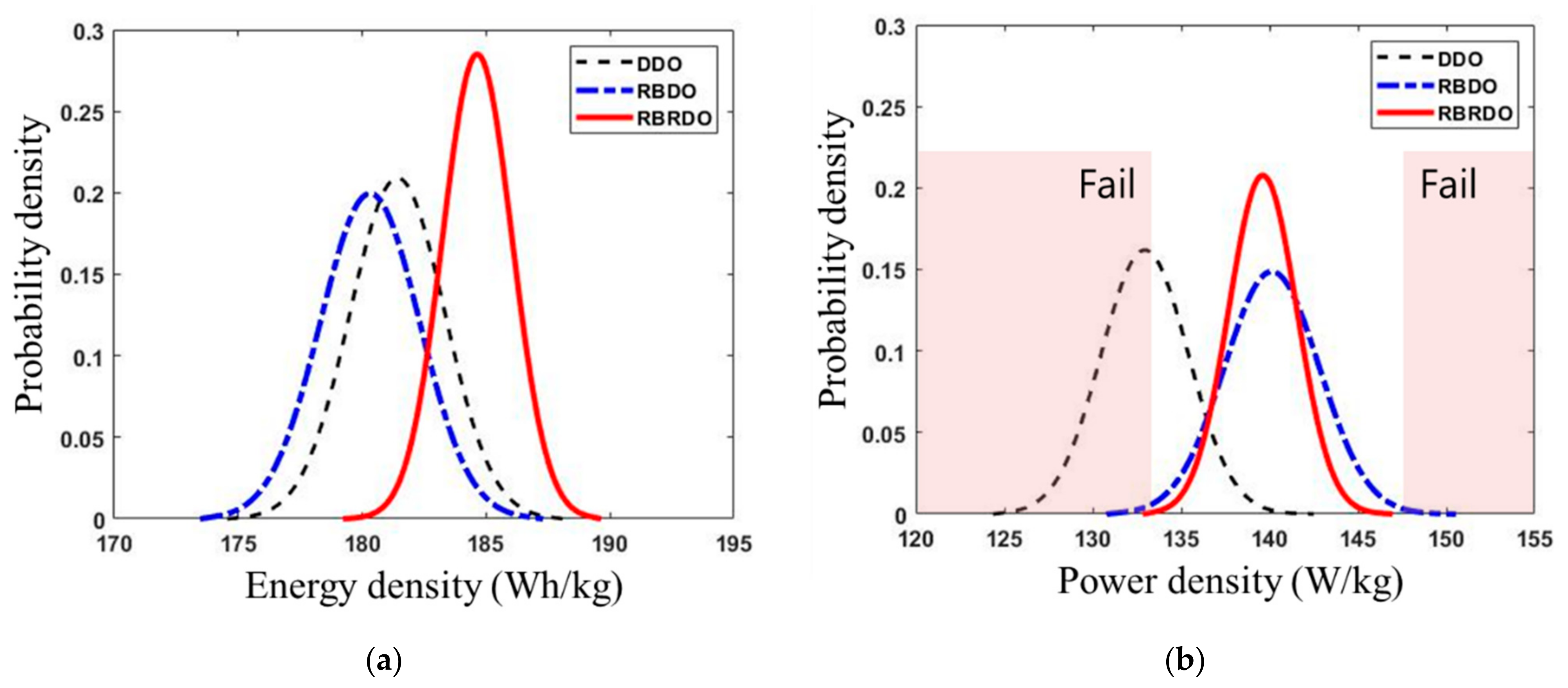
4.2. Comparison of Results from RBRDO with Those from DDO and RBDO
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of Symbols | |
| Energy density (Wh/kg) | |
| Power density (W/kg) | |
| Mass of cell (kg) | |
| Electric potential of cell | |
| Discharge current of cell | |
| Discharge time | |
| Design variable | |
| Mean of energy density | |
| Mean of initial energy density | |
| Standard deviation in energy density | |
| Standard deviation in initial energy density | |
| Weighting factor | |
| Objective function | |
| Constraint function | |
| Subscripts and superscripts | |
| Initial value | |
| Lithium-ion battery cell | |
References
- De, S.; Northrop, P.W.; Ramadesigan, V.; Subramanian, V.R. Model-based simultaneous optimization of multiple design parameters for lithium-ion batteries for maximization of energy density. J. Power Sources 2013, 227, 161–170. [Google Scholar] [CrossRef]
- Kim, C.-W.; Yang, H.-I.; Lee, K.-J.; Lee, D.-C. Metamodel-Based Optimization of a Lithium-Ion Battery Cell for Maximization of Energy Density with Evolutionary Algorithm. J. Electrochem. Soc. 2019, 166, A211–A216. [Google Scholar] [CrossRef]
- Kim, J.-S.; Lee, D.-C.; Lee, J.-J.; Kim, C.-W. Optimization for maximum specific energy density of a lithium-ion battery using progressive quadratic response surface method and design of experiments. Sci. Rep. 2020, 10, 15586. [Google Scholar] [CrossRef]
- Ahmed, W.; Hanif, A.; Kallu, K.D.; Kouzani, A.Z.; Ali, M.U.; Zafar, A. Photovoltaic Panels Classification Using Isolated and Transfer Learned Deep Neural Models Using Infrared Thermographic Images. Sensors 2021, 21, 5668. [Google Scholar] [CrossRef]
- Ali, M.U.; Saleem, S.; Masood, H.; Kallu, K.D.; Masud, M.; Alvi, M.J.; Zafar, A. Early hotspot detection in photovoltaic modules using color image descriptors: An infrared thermography study. Int. J. Energy Res. 2021. [Google Scholar] [CrossRef]
- Mannan, J.; Kamran, M.A.; Ali, M.U.; Mannan, M.M.N. Quintessential strategy to operate photovoltaic system coupled with dual battery storage and grid connection. Int. J. Energy Res. 2021. [Google Scholar] [CrossRef]
- Yuan, C.; Deng, Y.; Li, T.; Yang, F. Manufacturing energy analysis of lithium ion battery pack for electric vehicles. CIRP Ann. 2017, 66, 53–56. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Grundish, N.S.; Goodenough, J.B.; Chen, Y.; Guo, L.; Peng, Z.; Qi, X.; Yang, F.; Qie, L.; et al. The 2021 battery technology roadmap. J. Phys. D Appl. Phys. 2021, 54, 183001. [Google Scholar] [CrossRef]
- Pagliaro, M.; Meneguzzo, F. The driving power of the electron. J. Phys. Energy 2018, 1, 011001. [Google Scholar] [CrossRef]
- Jang, J.; Cho, S.-G.; Lee, S.-J.; Kim, K.-S.; Kim, J.-M.; Hong, J.-P.; Lee, T.H. Reliability-based robust design optimization with kernel density estimation for electric power steering motor considering manufacturing uncertainties. IEEE Trans. Magn. 2015, 51, 18–21. [Google Scholar] [CrossRef]
- Heimes, H.; Lienemann, C.; Kampker, A.; Locke, M. Battery Cell Production Process. 23 February 2019. Available online: https://www.researchgate.net/publication/330902286_Lithium-ion_Battery_Cell_Production_Process (accessed on 15 August 2021).
- Mohanty, D.; Li, J.; Born, R.; Maxey, L.C.; Dinwiddie, R.; Daniel, C.; Wood, D. Non-destructive evaluation of slot-die-coated lithium secondary battery electrodes by in-line laser caliper and IR thermography methods. Anal. Methods 2014, 6, 674–683. [Google Scholar] [CrossRef]
- DuBeshter, T.; Sinha, P.K.; Sakars, A.; Fly, G.W.; Jorne, J. Measurement of Tortuosity and Porosity of Porous Battery Electrodes. J. Electrochem. Soc. 2014, 161, A599–A605. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Modeling Parametric Uncertainty Using Polynomial Chaos Theory. ECS Trans. 2006, 3, 243–256. [Google Scholar] [CrossRef]
- Shin, D.; Poncino, M.; Macii, E.; Chang, N. A statistical model-based cell-to-cell variability management of Li-ion battery pack. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2015, 34, 252–265. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Ion transport restriction in mechanically strained separator membranes. J. Power Sources 2013, 226, 149–155. [Google Scholar] [CrossRef]
- Rumpf, K.; Rheinfeld, A.; Schindler, M.; Keil, J.; Schua, T.; Jossen, A. Influence of Cell-to-Cell Variations on the Inhomogeneity of Lithium-Ion Battery Modules. J. Electrochem. Soc. 2018, 165, A2587–A2607. [Google Scholar] [CrossRef]
- Barsukov, Y. Battery Cell Balancing: What to Balance and How; Texas Instruments: Dallas, TX, USA, 2005; pp. 1–8. Available online: http://focus.ti.com/download/trng/docs/seminar/Topic2-Battery Cell Balancing-What to Balance and How.pdf (accessed on 15 August 2021).
- Aizpuru, I.; Iraola, U.; Canales, J.M.; Unamuno, E.; Gil, I. Battery pack tests to detect unbalancing effects in series connected Li-ion cells. In Proceedings of the 4th International Conference on Clean Electrical Power: Renewable Energy Resources Impact, ICCEP 2013, Alghero, Italy, 11–13 June 2013; pp. 99–106. [Google Scholar] [CrossRef]
- Bentley, W.F. Cell balancing considerations for lithium-ion battery systems. In Proceedings of the Twelfth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 14–17 January 1997; pp. 223–226. [Google Scholar] [CrossRef]
- Ziegler, A.; Oeser, D.; Hein, T.; Montesinos-Miracle, D.; Ackva, A. Reducing Cell to Cell Variation of Lithium-Ion Battery Packs during Operation. IEEE Access 2021, 9, 24994–25001. [Google Scholar] [CrossRef]
- Khan, H.F.; Hanif, A.; Ali, M.U.; Zafar, A. A Lagrange multiplier and sigma point Kalman filter based fused methodology for online state of charge estimation of lithium-ion batteries. J. Energy Storage 2021, 41, 102843. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S. Active Cell Balancing of Lithium-Ion Battery Pack Using Dual DC-DC Converter and Auxiliary Lead-Acid Battery. J. Energy Storage 2021, 33, 102109. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J.S. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Srinivasan, V.; Newman, J. Design and optimization of a natural graphite/iron phosphate lithium-ion cell. J. Electrochem. Soc. 2004, 151, A1530–A1538. [Google Scholar] [CrossRef] [Green Version]
- Yoo, D.; Park, J.; Moon, J.; Kim, C. Reliability-Based Design Optimization for Reducing the Performance Failure and Maximizing the Specific Energy of Lithium-Ion Batteries Considering Manufacturing Uncertainty of Porous Electrodes. Energies 2021, 14, 6100. [Google Scholar] [CrossRef]
- Jang, G.U.; Kim, C.-W.; Bae, D.; Cho, Y.; Lee, J.-J.; Cho, S. Reliability-based robust design optimization for torque ripple reduction considering manufacturing uncertainty of interior permanent magnet synchronous motor. J. Mech. Sci. Technol. 2020, 34, 1249–1256. [Google Scholar] [CrossRef]
- Doh, J.; Yang, Q.; Raghavan, N. Reliability-based robust design optimization of polymer nanocomposites to enhance percolated electrical conductivity considering correlated input variables using multivariate distributions. Polymer 2020, 186, 122060. [Google Scholar] [CrossRef]
- Carneiro, G.D.N.; António, C.C. Reliability-based Robust Design Optimization with the Reliability Index Approach applied to composite laminate structures. Compos. Struct. 2019, 209, 844–855. [Google Scholar] [CrossRef]
- Lim, J.; Jang, Y.S.; Chang, H.S.; Park, J.C.; Lee, J. Role of multi-response principal component analysis in reliability-based robust design optimization: An application to commercial vehicle design. Struct. Multidiscip. Optim. 2018, 58, 785–796. [Google Scholar] [CrossRef]
- Xue, N.; Du, W.; Gupta, A.; Shyy, W.; Sastry, A.M.; Martins, J. Optimization of a Single Lithium-Ion Battery Cell with a Gradient-Based Algorithm. J. Electrochem. Soc. 2013, 160, A1071–A1078. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Wierzbicki, T.; Li, W. A review of safety-focused mechanical modeling of commercial lithium-ion batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Wang, Q.; Nakashima, T.; Lai, C.; Mutsuda, H.; Kanehira, T.; Konishi, Y.; Okuizumi, H. Modified Algorithms for Fast Construction of Optimal Latin-Hypercube Design. IEEE Access 2020, 8, 191644–191658. [Google Scholar] [CrossRef]
- PIDOTECH Inc. PIAnO User’s Manuals and Tutorials; PIDOTECH Inc.: Seoul, Korea, 2019. [Google Scholar]
- Du, X.; Chen, W. Sequential optimization and reliability assessment method for efficient probabilistic design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef] [Green Version]




| Parameters | Value | |||||
|---|---|---|---|---|---|---|
| Anode | Separator | Cathode | Negative Current Collector (Cu) | Positive Current Collector (Al) | Electrolyte | |
| Thickness () | 100 | 52 | 174 | 10 | 10 | - |
| Porosity | 0.357 | 0.46 | 0.444 | - | - | - |
| Particle size () | 12.5 | - | 8.5 | - | - | - |
| Density () | 2270 | 900 | 4140 | 8700 | 2700 | 1210 |
| Diffusivity () | - | - | - | |||
| Reaction rate constant | - | - | - | - | ||
| Electrical conductivity () | 100 | - | 3.8 | - | - | - |
| Initial concentration () | 22,055 | - | 4000 | - | - | 1000 |
| Maximum concentration () | 26,390 | - | 22,860 | - | - | - |
| Parameters | Mean | Standard Deviation | Distribution |
|---|---|---|---|
| Anode particle size (µm) | 12.5 | ±0.42 | Normal |
| Cathode particle size (µm) | 8.5 | ±0.447 | Normal |
| Anode porosity | 0.357 | ±0.013 | Normal |
| Cathode porosity | 0.444 | ±0.0025 | Normal |
| Anode thickness (µm) | 100 | ±1.27 | Normal |
| Cathode thickness (µm) | 174 | ±2.57 | Normal |
| Negative current collector thickness (µm) | 10 | ±0.76 | Normal |
| Positive current collector thickness (µm) | 10 | ±0.23 | Normal |
| Separator thickness (µm) | 52 | ±0.23 | Normal |
| Design Factors | Lower Bound | Upper Bound |
|---|---|---|
| Anode particle size (µm) | 0.2 | 20 |
| Cathode particle size (µm) | 0.5 | 50 |
| Anode porosity | 0.1 | 0.6 |
| Cathode porosity | 0.1 | 0.6 |
| Anode thickness (µm) | 40 | 250 |
| Cathode thickness (µm) | 40 | 250 |
| Negative current collector thickness (µm) | 10 | 15 |
| Positive current collector thickness (µm) | 10 | 25 |
| Separator thickness (µm) | 10 | 100 |
| Design Variables and Performance | Mean | Rate of Change (%) | |
|---|---|---|---|
| Initial Design | Optimal Design | ||
| Anode particle size (µm) | 12.5 | 0.653 | −94.8 |
| Cathode porosity | 0.444 | 0.100 | −77.5 |
| Anode thickness (µm) | 100 | 121 | +21.0 |
| Cathode thickness (µm) | 125 | 98.5 | +21.2 |
| Negative current collector thickness (µm) | 10 | 10.7 | +7.00 |
| Separator thickness (µm) | 52 | 51.8 | −0.39 |
| Energy density (Wh/kg) | 138.71 | 184.64 | +33.1 |
| Power density (W/kg) | 140.05 | 139.62 | −0.31 |
| Failure (%) | - | 0.60 | - |
| Optimal Design Methodology | ||||
|---|---|---|---|---|
| DDO | RBDO | RBRDO | ||
| Energy density (Wh/kg) | Mean | 181.424 | 180.3143 | 184.6439 |
| Standard deviation | 1.907481 | 1.999702 | 1.399288 | |
| Power density (W/kg) | Mean | 132.9427 | 140.1326 | 139.6208 |
| Standard deviation | 2.463361 | 2.683031 | 1.919787 | |
| Failure (%) | 55.80 | 1.0 | 0.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Yoo, D.; Moon, J.; Yoon, J.; Park, J.; Lee, S.; Lee, D.; Kim, C. Reliability-Based Robust Design Optimization of Lithium-Ion Battery Cells for Maximizing the Energy Density by Increasing Reliability and Robustness. Energies 2021, 14, 6236. https://doi.org/10.3390/en14196236
Park J, Yoo D, Moon J, Yoon J, Park J, Lee S, Lee D, Kim C. Reliability-Based Robust Design Optimization of Lithium-Ion Battery Cells for Maximizing the Energy Density by Increasing Reliability and Robustness. Energies. 2021; 14(19):6236. https://doi.org/10.3390/en14196236
Chicago/Turabian StylePark, Jinhwan, Donghyeon Yoo, Jaemin Moon, Janghyeok Yoon, Jungtae Park, Seungae Lee, Doohee Lee, and Changwan Kim. 2021. "Reliability-Based Robust Design Optimization of Lithium-Ion Battery Cells for Maximizing the Energy Density by Increasing Reliability and Robustness" Energies 14, no. 19: 6236. https://doi.org/10.3390/en14196236







