Regression Model-Based Flux Observer for IPMSM Sensorless Control with Wide Speed Range
Abstract
:1. Introduction
2. Dynamic Model of a IPMSM
3. Proposed Flux Observer
3.1. Nonlinear Observer Based on Regression Model
- It does not include uncertain information, such as rotor speed.
- It is easy to develop an observer using a nonlinear optimizing method, such as a gradient descent method.
- It is exponentially stable when the regressor vector is the PE condition [31].
3.2. New Linear Regression Form Derivation Processing
3.3. Adaptation Law Using Gradient Algorithm
3.4. Proposed Nonlinear Observer
4. Signal Injection Strategy
5. Simulation and Experimental Results
5.1. Simulation Results
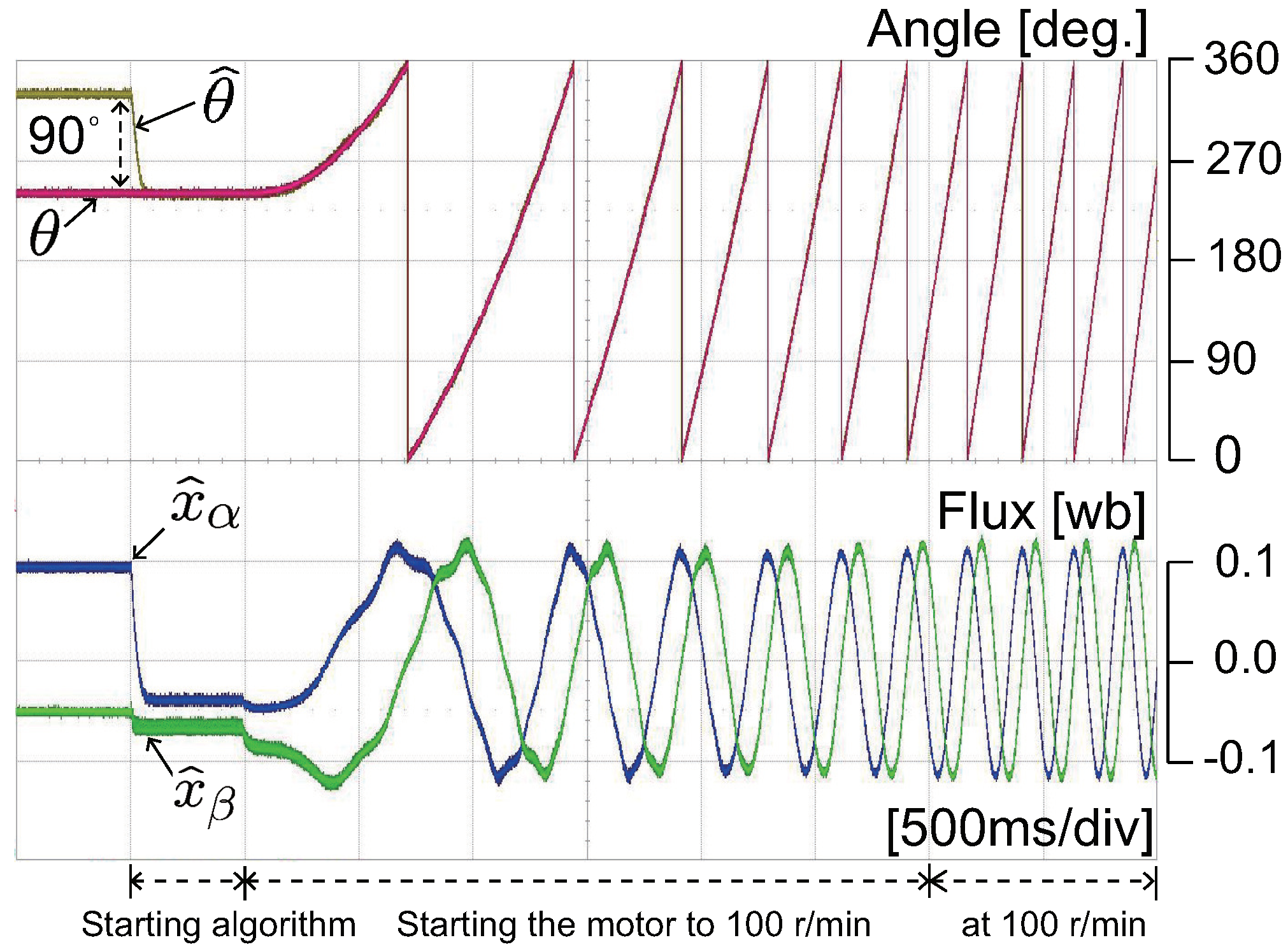
5.2. Experimental Results
6. Conclusions
Funding
Conflicts of Interest
Abbreviations
| Stationary axis reference frame quantities | |
| Synchronous axis reference frame quantities | |
| R | Resistance of stator winding |
| d-axis and q-axis inductance of stator winding | |
| d and q-axes stator flux linkage in the synchronous frame | |
| Stator winding resistance | |
| d and q-axes self-inductance | |
| Stator flux in the stationary frame | |
| Initial Stator flux | |
| Active flux in the stationary frame | |
| Rotor flux angle | |
| Estimation rotor flux angle error | |
| Electrical speed and mechanical speed | |
| Injection current magnitude | |
| Injection current frequency | |
| T | Shaft torque |
| Adaptation gain of observer | |
| Filter gain | |
| Differential operator | |
| PMSMs | Permanent-magnet synchronous motors |
| IPMSM | Interior permanent-magnet synchronous motor |
| SPMSM | Surface-mount PMSM |
| EMF | Electromotive force |
| PE | Persistence of excitation |
| FEM | Finite-element method |
| LPF | Low pass filter |
| BPF | Band-pass filter |
Appendix A. Linear Regression Derivation Process
Appendix B. Swapping Lemma
References
- Chen, S.; Zhang, X.; Wu, X.; Tan, G.; Chen, X. Sensorless Control for IPMSM Based on Adaptive Super-Twisting Sliding-Mode Observer and Improved Phase-Locked Loop. Energies 2019, 12, 1225. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Nondahl, T.; Schmidt, P.; Royak, S.; Harbaugh, M. Rotor Position Estimation for Synchronous Machines Based on Equivalent EMF. IEEE Trans. Ind. Appl. 2011, 47, 1310–1318. [Google Scholar]
- Bao, D.; Wu, H.; Wang, R.; Zhao, F.; Pan, X. Full-Order Sliding Mode Observer Based on Synchronous Frequency Tracking Filter for High-Speed Interior PMSM Sensorless Drives. Energies 2020, 13, 6511. [Google Scholar] [CrossRef]
- Usama, M.; Kim, J. Improved Self-Sensing Speed Control of IPMSM Drive Based on Cascaded Nonlinear Control. Energies 2021, 14, 2205. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, T.; Bao, Y.; Zhang, H.; Gerada, C. A Nonlinear Extended State Observer for Rotor Position and Speed Estimation for Sensorless IPMSM Drives. IEEE Tran. Power Electron. 2020, 35, 733–743. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, I.; Nam, K.; Yang, J.; Hwang, T. Sensorless Control of PMSM in a High-Speed Region Considering Iron Loss. IEEE Trans. Ind. Electron. 2015, 62, 6151–6159. [Google Scholar] [CrossRef]
- Hasegawa, M.; Hatta, H.; Matsui, K. Adaptive flux observer on stator frame and its design based on /spl gamma/-positive real problem for sensorless IPMSM drives. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, IECON 2005, Raleigh, NC, USA, 6–10 November 2005. [Google Scholar]
- Boldea, I.; Paicu, M.C.; Andreescu, G.D. Active Flux Concept for Motion-Sensorless Unified AC Drives. IEEE Trans. Power Electron. 2008, 23, 2612–2618. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Yang, K. High Frequency Square-Wave Voltage Injection Scheme-Based Position Sensorless Control of IPMSM in the Low- and Zero- Speed Range. Energies 2019, 12, 4776. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Yang, Z.; Lin, F. A Novel Strategy for Sensorless Control of IPMSM with Error Compensation Based on Rotating High Frequency Carrier Signal Injection. Energies 2020, 13, 1919. [Google Scholar] [CrossRef]
- Choi, J.; Nam, K. Wound Synchronous Machine Sensorless Control Based on Signal Injection into the Rotor Winding. Energies 2018, 11, 3278. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Yang, S.; Tu, J. Comparative Evaluation of a Permanent Magnet Machine Saliency-Based Drive with Sine-Wave and Square-Wave Voltage Injection. Energies 2018, 11, 2189. [Google Scholar] [CrossRef] [Green Version]
- Mubarok, M.S.; Liu, T.-H.; Tsai, C.-Y.; Wei, Z.-Y. A Wide-Adjustable Sensorless IPMSM Speed Drive Based on Current Deviation Detection under Space-Vector Modulation. Energies 2020, 13, 4431. [Google Scholar] [CrossRef]
- Foo, G.; Rahman, M.F. Sensorless Sliding-Mode MTPA Control of an IPM Synchronous Motor Drive Using a Sliding-Mode Observer and HF Signal Injection. IEEE Tran. Ind. Electron. 2010, 57, 1270–1278. [Google Scholar] [CrossRef]
- Andreescu, G.D.; Pitic, C.I.; Blaabjerg, F.; Boldea, I. Combined Flux Observer With Signal Injection Enhancement for Wide Speed Range Sensorless Direct Torque Control of IPMSM Drives. IEEE Trans. Energy Convers. 2008, 23, 393–402. [Google Scholar] [CrossRef]
- Barnard, F.J.W.; Villet, W.T.; Kamper, M.J. Hybrid Active-Flux and Arbitrary Injection Position Sensorless Control of Reluctance Synchronous Machines. IEEE Trans. Ind. Appl. 2015, 51, 3899–3906. [Google Scholar] [CrossRef]
- Silva, C.; Asher, G.M.; Sumner, M. Hybrid rotor position observer for wide speed-range sensorless PM motor drives including zero speed. IEEE Trans. Ind. Electron. 2006, 53, 373–378. [Google Scholar] [CrossRef]
- Yousefi-Talouki, A.; Pescetto, P.; Pellegrino, G.; Boldea, I. Combined Active Flux and High-Frequency Injection Methods for Sensorless Direct-Flux Vector Control of Synchronous Reluctance Machines. IEEE Trans. Power Electron. 2018, 33, 2447–2457. [Google Scholar] [CrossRef]
- Tuovinen, T.; Hinkkanen, M. Adaptive Full-Order Observer With High-Frequency Signal Injection for Synchronous Reluctance Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Preindl, M.; Sirouspour, S.; Emadi, A. Unified wide-speed sensorless scheme using nonlinear optimization for IPMSM drives. IEEE Trans. Power Electron. 2017, 32, 6308–6322. [Google Scholar] [CrossRef]
- Peng, F.; Yao, Y.; Wang, Z.; Huang, Y.; Yang, H.; Xie, B. Position Estimation Method of IPMSM in Full Speed Range by Simplified Quadratic Optimization. IEEE Access 2020, 8, 109964–109975. [Google Scholar] [CrossRef]
- Chen, J.; Chen, S.; Wu, X.; Tan, G.; Hao, J. A Super-Twisting Sliding-Mode Stator Flux Observer for Sensorless Direct Torque and Flux Control of IPMSM. Energies 2019, 12, 2564. [Google Scholar] [CrossRef] [Green Version]
- Ortega, R.; Praly, L.; Astolfi, A.; Lee, J.; Nam, K. Estimation of rotor position and speed of permanent magnet synchronous motors with guaranteed stability. IEEE Trans. Control Syst. Technol. 2011, 19, 601–614. [Google Scholar] [CrossRef]
- Dib, W.; Ortega, R.; Malaize, A.J. Sensorless control of permanent-magnet synchronous motor in automotive applications: Estimation of the angular position. In Proceedings of the IECON 2011—37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 728–733. [Google Scholar]
- Lee, J.; Hong, J.; Nam, K.; Ortega, R.; Praly, L.; Astolfi, A. Sensorless Control of Surface-Mount Permanent-Magnet Synchronous Motors Based on a Nonlinear Observer. IEEE Trans. Power Electron. 2010, 25, 290–297. [Google Scholar]
- Bobtsov, A.; Pyrkin, A.; Ortega, R.; Vukosavic, S.; Stankovic, A.M.; Panteley, E.V. A Robust Globally Convergent Postion Observer for the Permanent Magnet Synchronous Motor. Automatica 2015, 61, 47–54. [Google Scholar] [CrossRef]
- Bobtsov, A.; Pyrkin, A.; Ortega, R. A new approach for estimation of electrical parameters and flux observation of permanent magnet synchronous motors. Int. J. Adapt. Control Signal Process 2015, 30, 1434–1448. [Google Scholar] [CrossRef]
- Choi, J.; Nam, K.; Bobtsov, A.A.; Pyrkin, A.; Ortega, R. Robust Adaptive Sensorless Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2017, 30, 3989–3997. [Google Scholar] [CrossRef]
- Choi, J.; Nam, K.; Bobtsov, A.A.; Ortega, R. Sensorless Control of IPMSM Based on Regression Model. IEEE Trans. Power Electron. 2019, 34, 9191–9201. [Google Scholar] [CrossRef]
- Nam, K.H. AC Motor Control and Electric Vehicle Application; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781138712492. [Google Scholar]
- Ortega, R.; Praly, L.; Aranovskiy, S.; Yi, B.; Zhang, W. On dynamic regressor extension and mixing parameter estimators: Two Luenberger observers interpretations. Automatica 2018, 95, 548–551. [Google Scholar] [CrossRef]
- Sastry, S.; Bodson, M. Adaptive Control: Stability, Convergence and Robustness; Prentice-Hall: London, UK, 1989; ISBN 9780486482026. [Google Scholar]
- Jung, S.; Hong, J.; Nam, K. Current Minimizing Torque Control of the IPMSM Using Ferrari’s Method. IEEE Trans. Power Electron. 2013, 28, 5603–5617. [Google Scholar] [CrossRef]
- Seyyedzadeh, S.M.; Shoulaie, A. Accurate Modeling of the Nonlinear Characteristic of a Voltage Source Inverter for Better Performance in Near Zero Currents. IEEE Trans. Ind. Electron. 2019, 66, 71–78. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; Xu, X.; Sun, X.; Zhao, J. Rotor Position Estimation Approaches for Sensorless Control of Permanent Magnet Traction Motor in Electric Vehicles: A Review. World Electr. Veh. J. 2021, 12, 9. [Google Scholar] [CrossRef]
- Rashed, M.; MacConnell, P.F.A.; Stronach, A.F.; Acarnley, P. Sensorless Indirect-Rotor-Field-Orientation Speed Control of a Permanent-Magnet Synchronous Motor With Stator-Resistance Estimation. IEEE Trans. Ind. Electron. 2007, 54, 1664–1675. [Google Scholar] [CrossRef]












| Term | Previous Regression Model [29] | Proposed Regression Model |
|---|---|---|
| Regression Form | (14) | |
| Known variable | (18) | |
| Known vector (Regressor vector) | (29) | |
| Disturbance (Non- Vanishing) | (13) | |
| Disturbance (Vanishing) | ||
| Regressor vector at standstill | (30) | |
| Injection method | q-axis signal injection | -axis signal injection |
| Lissajous of regressor vector (with signal injection) | <Signal injection method to q-axis current>  | <Signal injection method to -axis current>  |
| Zero-speed operation under load | Impossible | Possible |
| Required parameters | R, , and | R, , , and |
| Parameter | Value |
|---|---|
| Rated output power | 1.3 kW |
| Rated torque | 6.25 Nm |
| Rated speed () | 2000 r/min |
| Rated current | 8.7 Arms |
| Numbers of poles (P) | 6 poles |
| PM flux linkage constant () | 0.11 Wb |
| d axis inductance () | 6.25 mH |
| q axis inductance () | 8.68 mH |
| Stator resistance (R) | 0.39 |
| Filter gain () | 2500 |
| Adaptation gain () | 1.0 |
| Injection current reference amplitude () | 1.5 A |
| Injection signal frequency () | 2500 rad/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J. Regression Model-Based Flux Observer for IPMSM Sensorless Control with Wide Speed Range. Energies 2021, 14, 6249. https://doi.org/10.3390/en14196249
Choi J. Regression Model-Based Flux Observer for IPMSM Sensorless Control with Wide Speed Range. Energies. 2021; 14(19):6249. https://doi.org/10.3390/en14196249
Chicago/Turabian StyleChoi, Jongwon. 2021. "Regression Model-Based Flux Observer for IPMSM Sensorless Control with Wide Speed Range" Energies 14, no. 19: 6249. https://doi.org/10.3390/en14196249





