Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors
Abstract
:1. Introduction
2. Methods
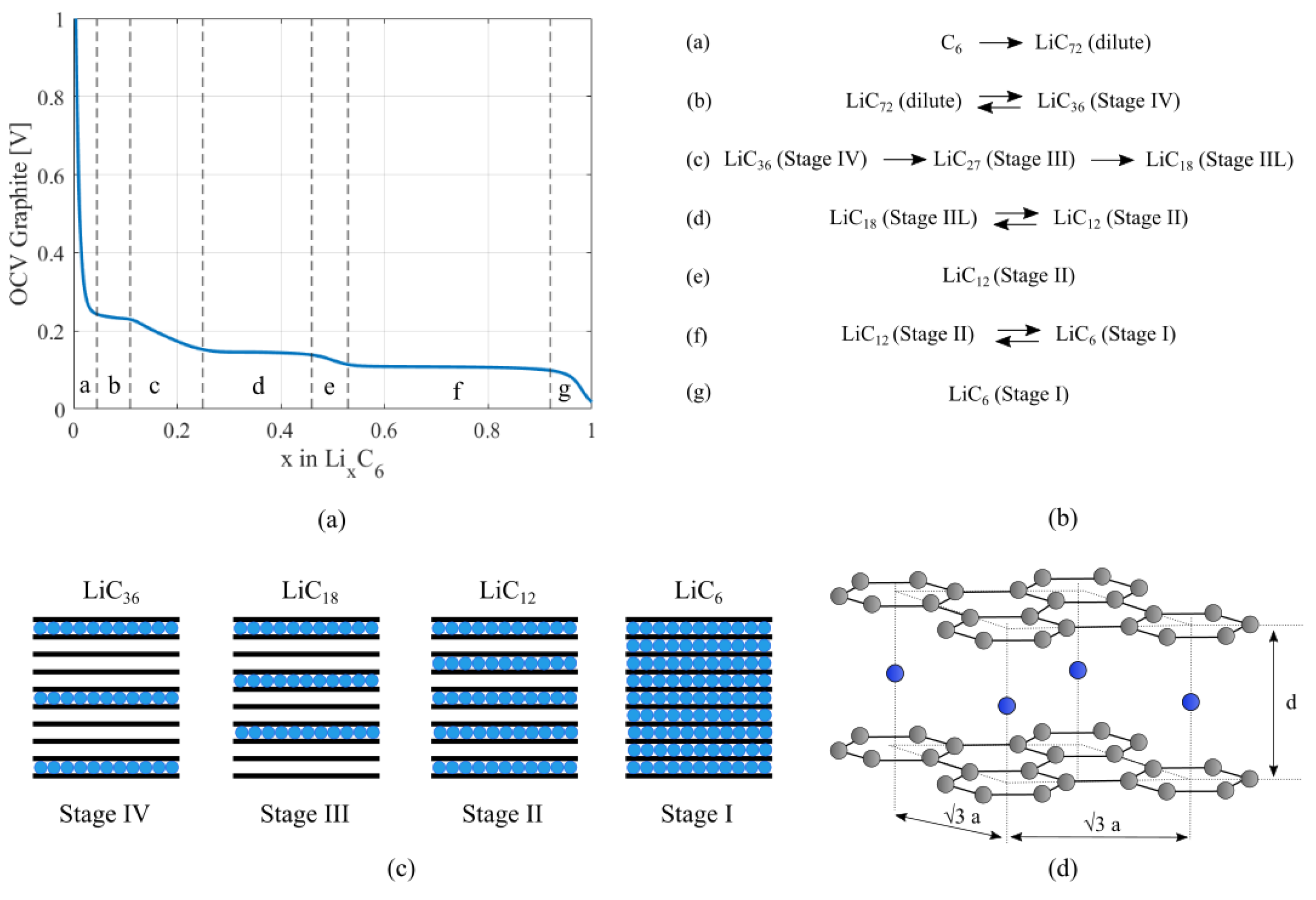
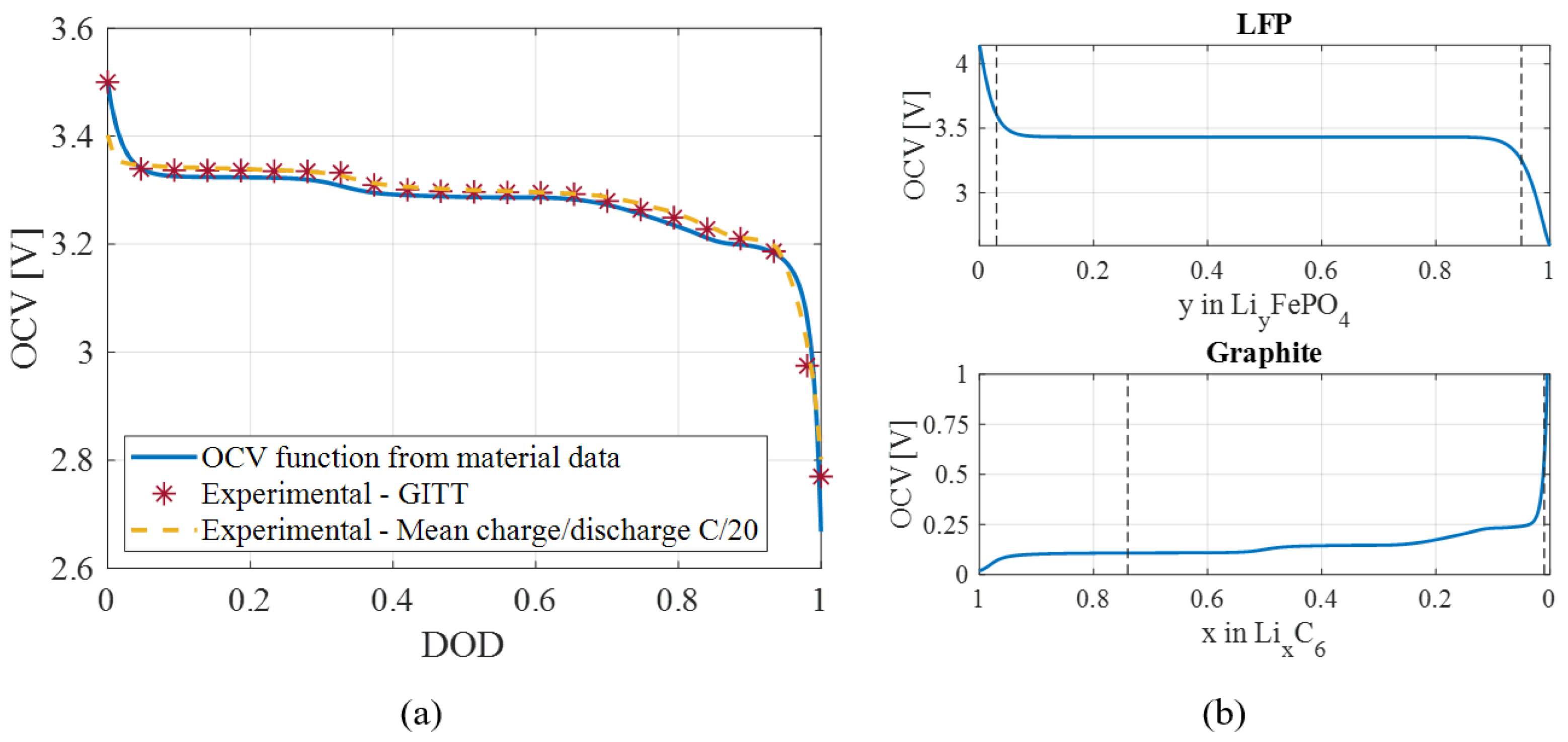
2.1. Crystal Structure of Active Materials
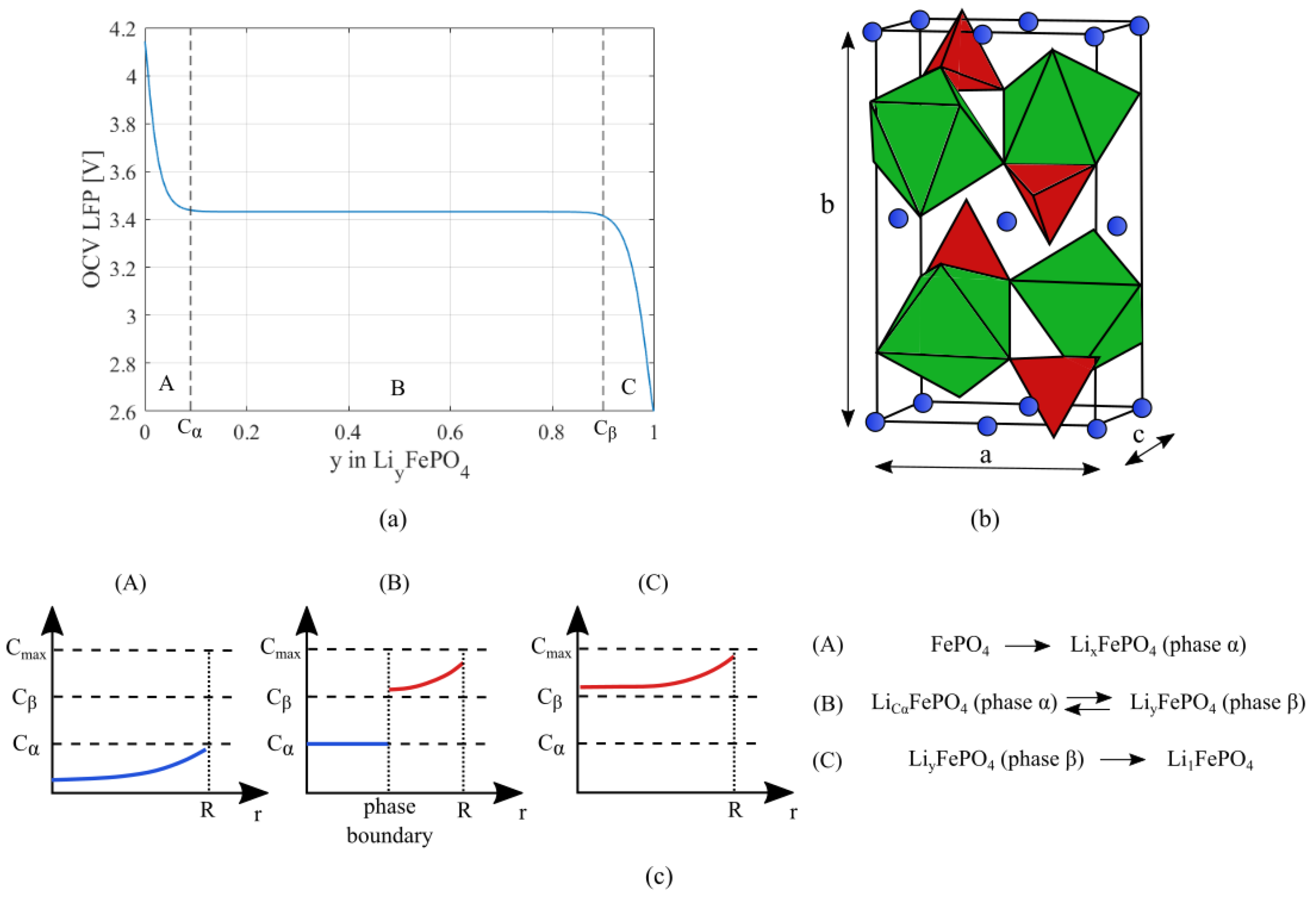
2.2. Mechanical Model
3. Experimental Set-Up
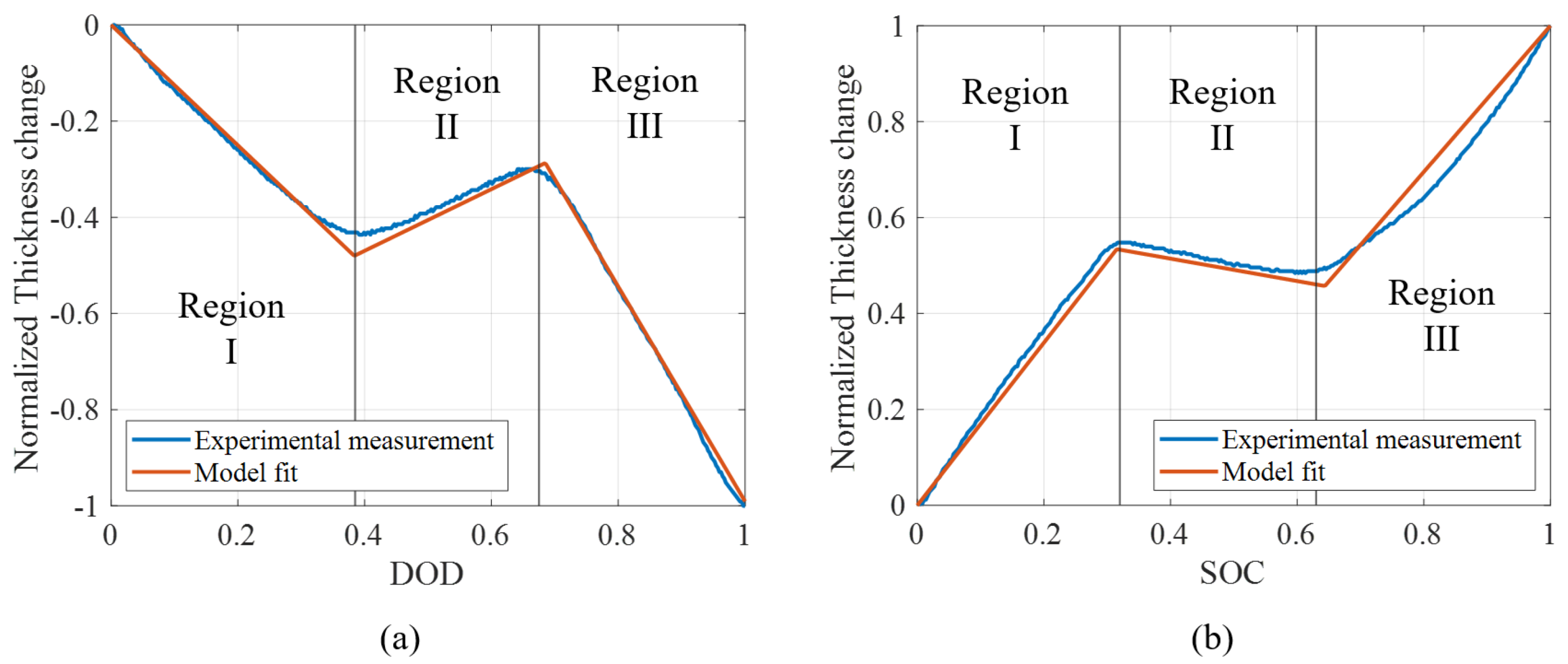
4. Results and Discussion
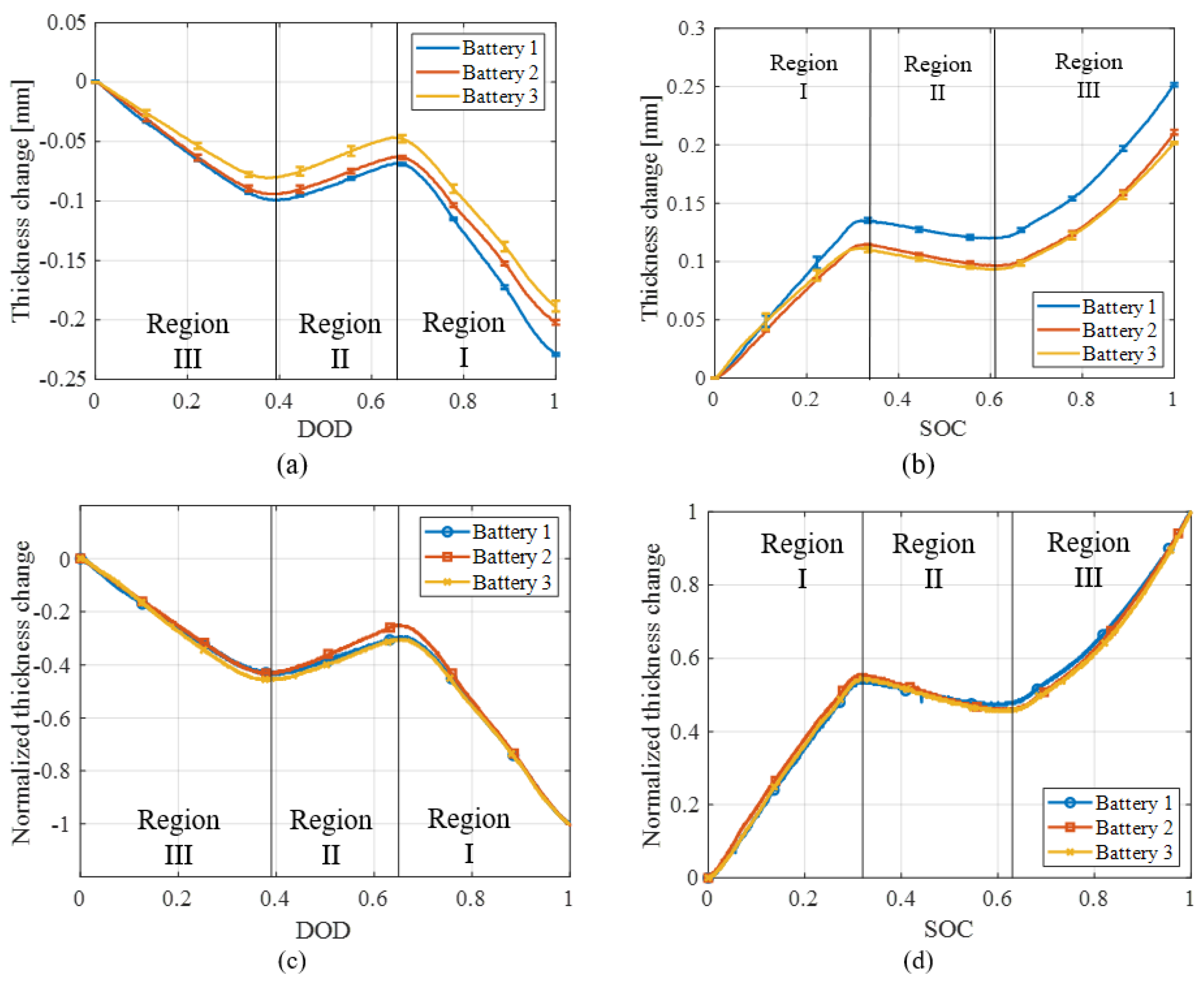
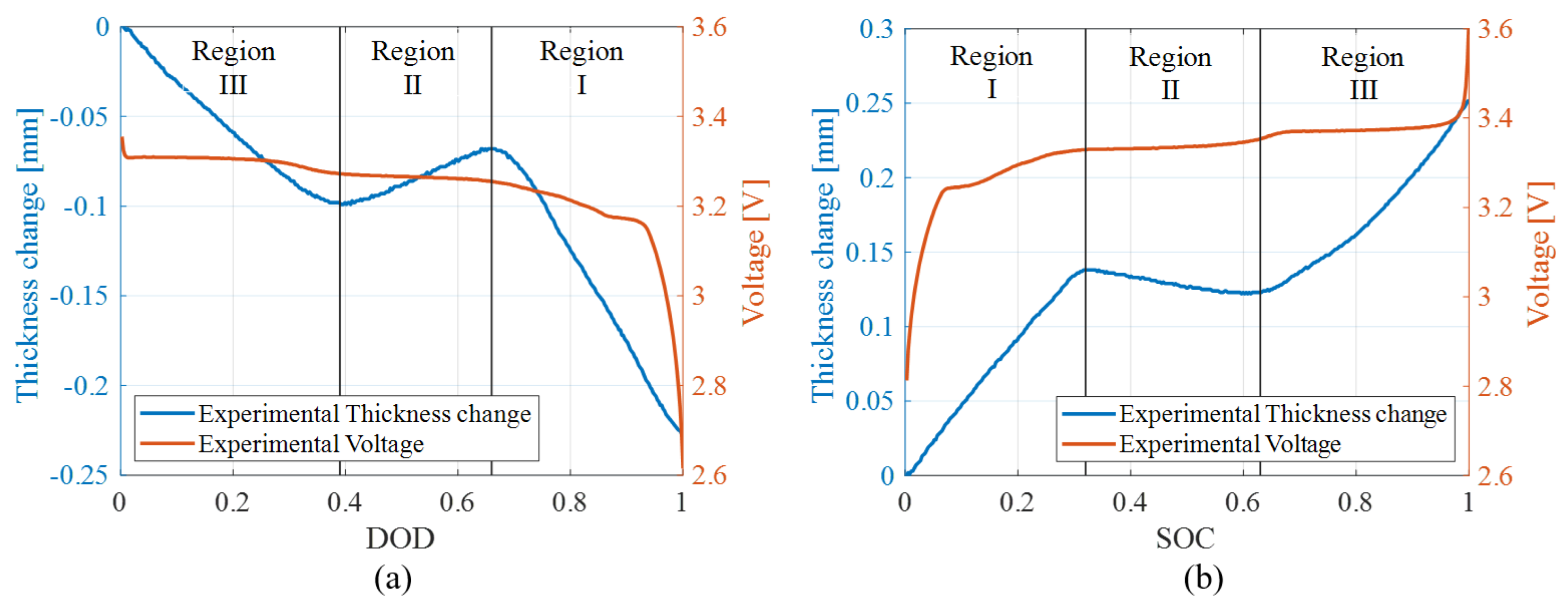
4.1. Swelling Measurements
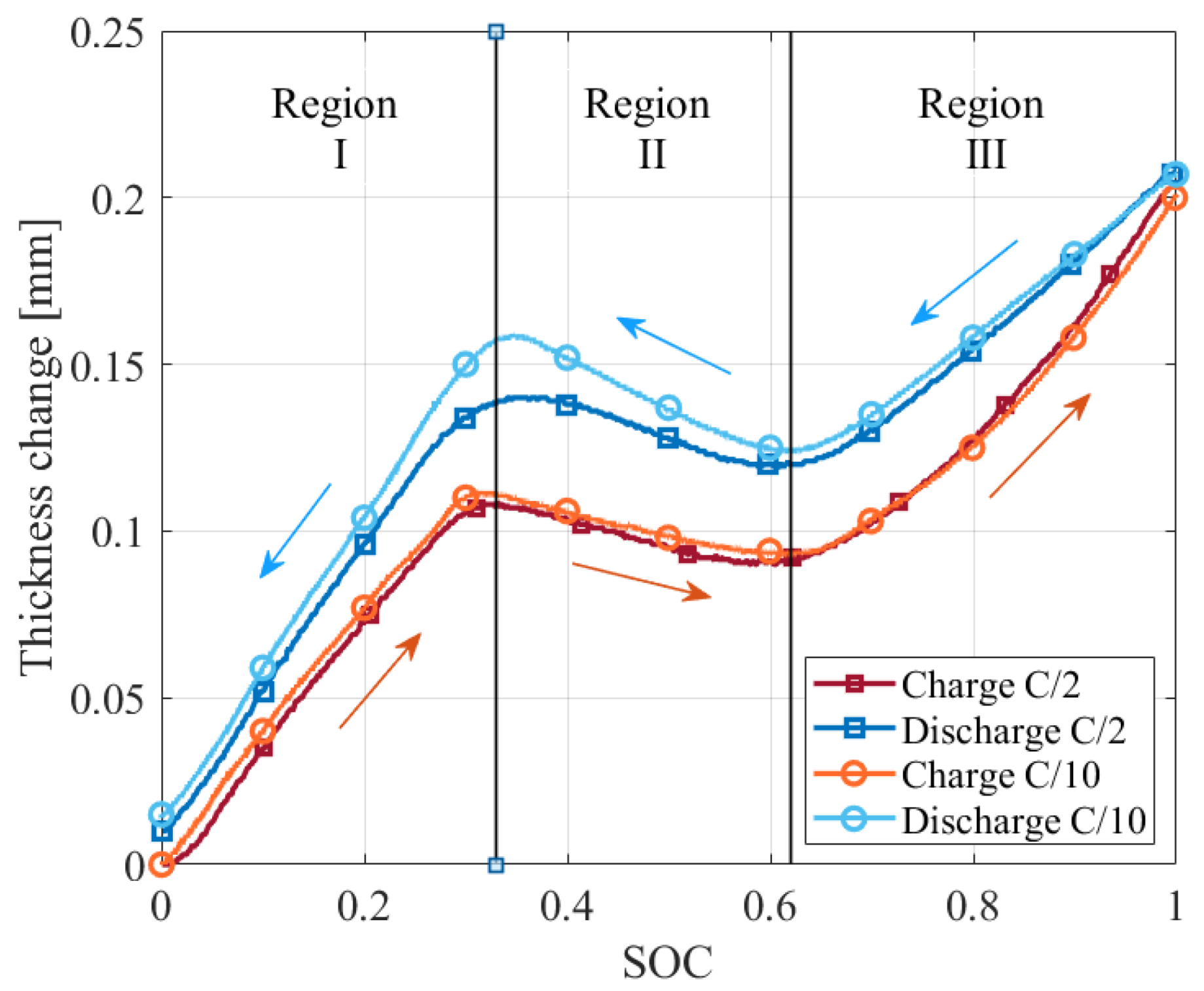
4.1.1. Hysteresis
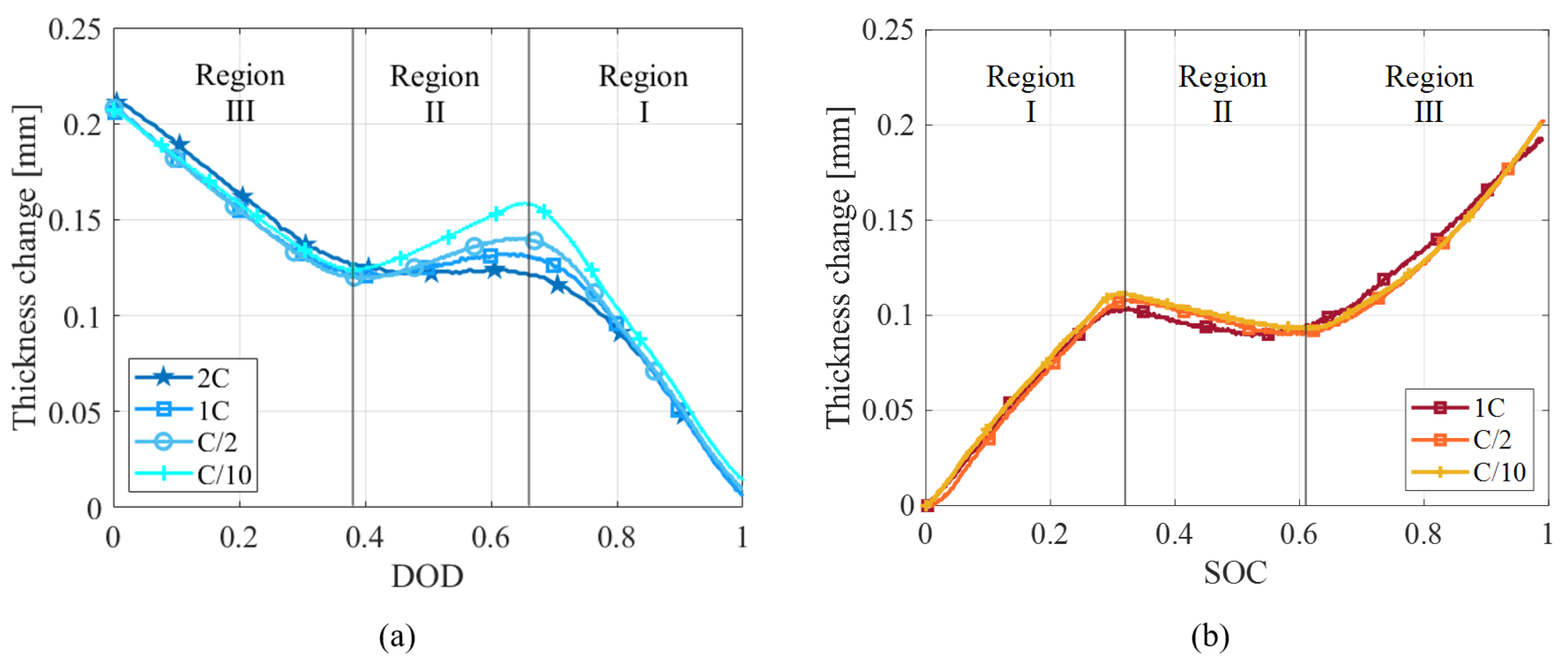
4.1.2. Current Rate Dependence
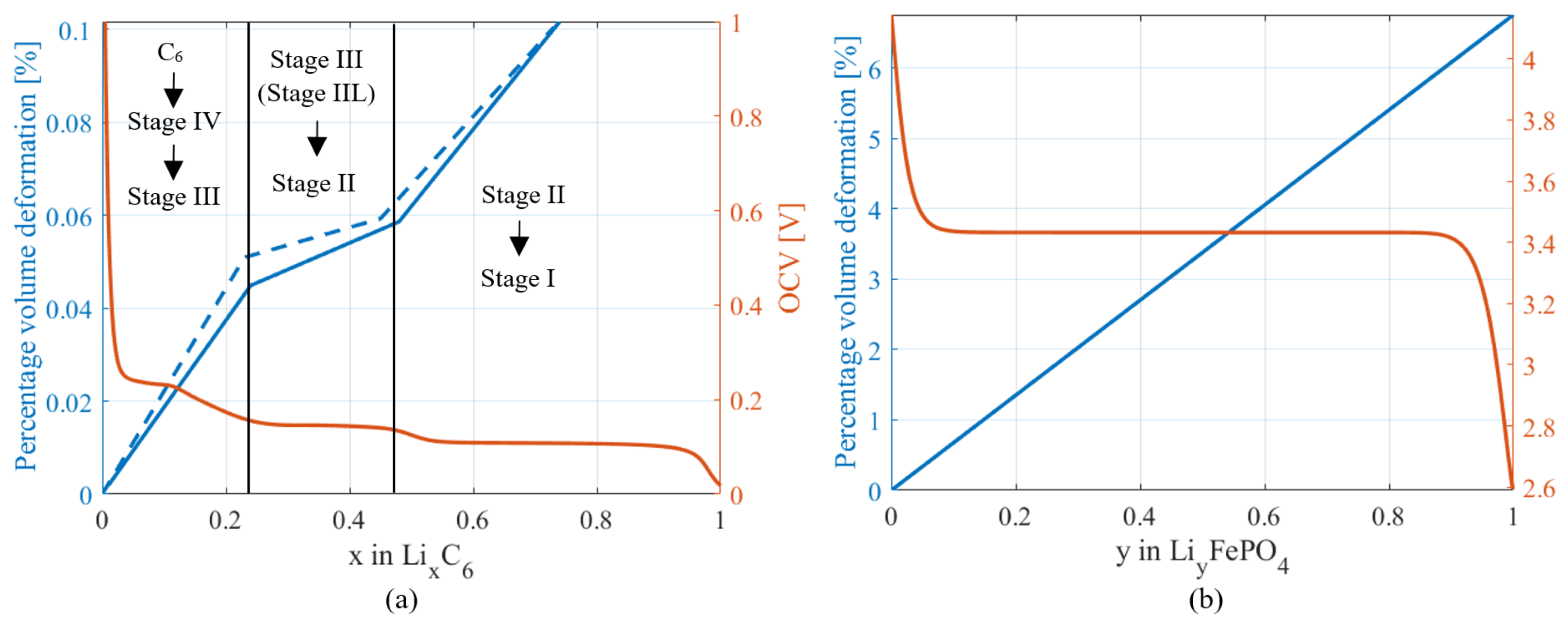
4.2. Model
4.2.1. Parameters Identification
4.2.2. Comparison of Model with Experimental Measurements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Somà, A.; Bruzzese, F.; Mocera, F.; Viglietti, E. Hybridization factor and performance of hybrid electric telehandler vehicle. IEEE Trans. Ind. Appl. 2016, 52, 5130–5138. [Google Scholar] [CrossRef]
- Mocera, F.; Vergori, E.; Somà, A. Battery performance analysis for working vehicle applications. IEEE Trans. Ind. Appl. 2019, 56, 644–653. [Google Scholar] [CrossRef]
- Mocera, F.; Somà, A. Analysis of a Parallel Hybrid Electric Tractor for Agricultural Applications. Energies 2020, 13, 3055. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F.; Somà, A. Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies 2020, 13, 1717. [Google Scholar] [CrossRef] [Green Version]
- Mocera, F.; Somà, A.; Clerici, D. Study of aging mechanisms in lithium-ion batteries for working vehicle applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–8. [Google Scholar]
- Clerici, D.; Mocera, F.; Somà, A. Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries. Energies 2021, 14, 134. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F. Micro-scale modeling of Lithium-ion battery. Mater. Sci. Eng. 2021, 1038, 012007. [Google Scholar] [CrossRef]
- Vergori, E.; Yu, Y. Monitoring of Li-ion cells with distributed fibre optic sensors. Procedia Struct. Integr. 2019, 24, 233–239. [Google Scholar] [CrossRef]
- Koyama, Y.; Chin, T.E.; Rhyner, U.; Holman, R.K.; Hall, S.R.; Chiang, Y.M. Harnessing the actuation potential of solid-state intercalation compounds. Adv. Funct. Mater. 2006, 16, 492–498. [Google Scholar] [CrossRef]
- Koerver, R.; Zhang, W.; de Biasi, L.; Schweidler, S.; Kondrakov, A.O.; Kolling, S.; Brezesinski, T.; Hartmann, P.; Zeier, W.G.; Janek, J. Chemo-mechanical expansion of lithium electrode materials–on the route to mechanically optimized all-solid-state batteries. Energy Environ. Sci. 2018, 11, 2142–2158. [Google Scholar] [CrossRef]
- Popp, H.; Koller, M.; Jahn, M.; Bergmann, A. Mechanical methods for state determination of Lithium-Ion secondary batteries: A review. J. Energy Storage 2020, 32, 101859. [Google Scholar] [CrossRef]
- Cheng, X.; Pecht, M. In situ stress measurement techniques on li-ion battery electrodes: A review. Energies 2017, 10, 591. [Google Scholar] [CrossRef]
- Mohan, S.; Kim, Y.; Siegel, J.B.; Samad, N.A.; Stefanopoulou, A.G. A phenomenological model of bulk force in a li-ion battery pack and its application to state of charge estimation. J. Electrochem. Soc. 2014, 161, A2222. [Google Scholar] [CrossRef] [Green Version]
- Samad, N.A.; Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G. Battery capacity fading estimation using a force-based incremental capacity analysis. J. Electrochem. Soc. 2016, 163, A1584. [Google Scholar] [CrossRef] [Green Version]
- Figueroa-Santos, M.A.; Siegel, J.B.; Stefanopoulou, A.G. Leveraging Cell Expansion Sensing in State of Charge Estimation: Practical Considerations. Energies 2020, 13, 2653. [Google Scholar] [CrossRef]
- Plotnikov, Y.; Karp, J.; Knobloch, A.; Kapusta, C.; Lin, D. Eddy current sensor for in situ monitoring of swelling of Li-ion prismatic cells. AIP Conf. Proc. 2015, 1650, 434–442. [Google Scholar]
- Peng, J.; Zhou, X.; Jia, S.; Jin, Y.; Xu, S.; Chen, J. High precision strain monitoring for lithium ion batteries based on fiber Bragg grating sensors. J. Power Sources 2019, 433, 226692. [Google Scholar] [CrossRef]
- Oh, K.Y.; Siegel, J.B.; Secondo, L.; Kim, S.U.; Samad, N.A.; Qin, J.; Anderson, D.; Garikipati, K.; Knobloch, A.; Epureanu, B.I.; et al. Rate dependence of swelling in lithium-ion cells. J. Power Sources 2014, 267, 197–202. [Google Scholar] [CrossRef]
- Bauer, M.; Wachtler, M.; Stöwe, H.; Persson, J.V.; Danzer, M.A. Understanding the dilation and dilation relaxation behavior of graphite-based lithium-ion cells. J. Power Sources 2016, 317, 93–102. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Siegel, J.B.; Stefanopoulou, A.G. Towards better estimability of electrode-specific state of health: Decoding the cell expansion. J. Power Sources 2019, 427, 101–111. [Google Scholar] [CrossRef]
- Mohtat, P.; Lee, S.; Sulzer, V.; Siegel, J.B.; Stefanopoulou, A.G. Differential Expansion and Voltage Model for Li-ion Batteries at Practical Charging Rates. J. Electrochem. Soc. 2020, 167, 110561. [Google Scholar] [CrossRef]
- Willenberg, L.K.; Dechent, P.; Fuchs, G.; Sauer, D.U.; Figgemeier, E. High-precision monitoring of volume change of commercial lithium-ion batteries by using strain gauges. Sustainability 2020, 12, 557. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, M.; Novais, S.; Ding, M.S.; Ferreira, M.S.; Koch, S.; Passerini, S.; Pinto, J.L. Internal strain and temperature discrimination with optical fiber hybrid sensors in Li-ion batteries. J. Power Sources 2019, 410, 1–9. [Google Scholar] [CrossRef]
- Ganguli, A.; Saha, B.; Raghavan, A.; Kiesel, P.; Arakaki, K.; Schuh, A.; Schwartz, J.; Hegyi, A.; Sommer, L.W.; Lochbaum, A.; et al. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 2: Internal cell signals and utility for state estimation. J. Power Sources 2017, 341, 474–482. [Google Scholar] [CrossRef] [Green Version]
- Jones, E.; Silberstein, M.; White, S.R.; Sottos, N.R. In situ measurements of strains in composite battery electrodes during electrochemical cycling. Exp. Mech. 2014, 54, 971–985. [Google Scholar] [CrossRef]
- Yu, Y.; Vergori, E.; Worwood, D.; Tripathy, Y.; Guo, Y.; Somá, A.; Greenwood, D.; Marco, J. Distributed thermal monitoring of lithium ion batteries with optical fibre sensors. J. Energy Storage 2021, 39, 102560. [Google Scholar] [CrossRef]
- Bitzer, B.; Gruhle, A. A new method for detecting lithium plating by measuring the cell thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Schmitt, J.; Kraft, B.; Schmidt, J.P.; Meir, B.; Elian, K.; Ensling, D.; Keser, G.; Jossen, A. Measurement of gas pressure inside large-format prismatic lithium-ion cells during operation and cycle aging. J. Power Sources 2020, 478, 228661. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 2006, 10, 293–319. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Modeling of a commercial graphite/LiFePO4 cell. J. Electrochem. Soc. 2011, 158, A562. [Google Scholar] [CrossRef]
- Bohn, E.; Eckl, T.; Kamlah, M.; McMeeking, R. A model for lithium diffusion and stress generation in an intercalation storage particle with phase change. J. Electrochem. Soc. 2013, 160, A1638. [Google Scholar] [CrossRef]
- Asenbauer, J.; Eisenmann, T.; Kuenzel, M.; Kazzazi, A.; Chen, Z.; Bresser, D. The success story of graphite as a lithium-ion anode material–fundamentals, remaining challenges, and recent developments including silicon (oxide) composites. Sustain. Energy Fuels 2020, 4, 5387–5416. [Google Scholar] [CrossRef]
- Didier, C.; Pang, W.K.; Guo, Z.; Schmid, S.; Peterson, V.K. Phase Evolution and Intermittent Disorder in Electrochemically Lithiated Graphite Determined Using in Operando Neutron Diffraction. Chem. Mater. 2020, 32, 2518–2531. [Google Scholar] [CrossRef]
- Mercer, M.P.; Peng, C.; Soares, C.; Hoster, H.E.; Kramer, D. Voltage hysteresis during lithiation/delithiation of graphite associated with meta-stable carbon stackings. J. Mater. Chem. 2021, 9, 492–504. [Google Scholar] [CrossRef]
- Taminato, S.; Yonemura, M.; Shiotani, S.; Kamiyama, T.; Torii, S.; Nagao, M.; Ishikawa, Y.; Mori, K.; Fukunaga, T.; Onodera, Y.; et al. Real-time observations of lithium battery reactions—operando neutron diffraction analysis during practical operation. Sci. Rep. 2016, 6, 28843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, K.P.; Okasinski, J.S.; Kalaga, K.; Shkrob, I.A.; Abraham, D.P. Quantifying lithium concentration gradients in the graphite electrode of Li-ion cells using operando energy dispersive X-ray diffraction. Energy Environ. Sci. 2019, 12, 656–665. [Google Scholar] [CrossRef] [Green Version]
- Senyshyn, A.; Dolotko, O.; Mühlbauer, M.; Nikolowski, K.; Fuess, H.; Ehrenberg, H. Lithium intercalation into graphitic carbons revisited: Experimental evidence for twisted bilayer behavior. J. Electrochem. Soc. 2013, 160, A3198. [Google Scholar] [CrossRef]
- Zhou, H. Two-phase transition of Li-intercalation compounds in Li-ion batteries. Mater. Today 2014, 17, 451–463. [Google Scholar]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 1997, 144, 1188. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Dubarry, M.; Somerville, L.; McGordon, A.; Jennings, P.; Bloom, I. A comparison of methodologies for the non-invasive characterisation of commercial Li-ion cells. Prog. Energy Combust. Sci. 2019, 72, 1–31. [Google Scholar] [CrossRef]
- Fath, J.P.; Dragicevic, D.; Bittel, L.; Nuhic, A.; Sieg, J.; Hahn, S.; Alsheimer, L.; Spier, B.; Wetzel, T. Quantification of aging mechanisms and inhomogeneity in cycled lithium-ion cells by differential voltage analysis. J. Energy Storage 2019, 25, 100813. [Google Scholar] [CrossRef]
- Lewerenz, M.; Marongiu, A.; Warnecke, A.; Sauer, D.U. Differential voltage analysis as a tool for analyzing inhomogeneous aging: A case study for LiFePO4| Graphite cylindrical cells. J. Power Sources 2017, 368, 57–67. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Zheng, H.; Li, J.; Song, X.; Liu, G.; Battaglia, V.S. A comprehensive understanding of electrode thickness effects on the electrochemical performances of Li-ion battery cathodes. Electrochim. Acta 2012, 71, 258–265. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Ma, F. Cathode Chemistries and Electrode Parameters Affecting the Fast Charging Performance of Li-Ion Batteries. J. Electrochem. Energy Convers. Storage 2020, 17, 021111. [Google Scholar] [CrossRef]
- Yagci, M.C.; Behmann, R.; Daubert, V.; Braun, J.A.; Velten, D.; Bessler, W.G. Electrical and Structural Characterization of Large-Format Lithium Iron Phosphate Cells Used in Home-Storage Systems. Energy Technol. 2021, 9, 2000911. [Google Scholar] [CrossRef]


| Material | Phase | Lithiation Index | Lattice Parameters [Å] | Volume [Å] | Volume Deformation [%] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Graphite | x | d | ||||||||
| 0.00 (0.00 ÷ 0.16) | 4.268 | 3.355 | 158.76 () | 0% | ||||||
| Stage IV/III | 0.16 (0.00 ÷ 0.42) | 4.282 | 3.511 | 167.22 | 5.33% | |||||
| Stage IIL | 0.24 (0.14 ÷ 0.45) | 4.282 | 3.519 | 167.61 | 5.53% | |||||
| Stage II | 0.48 (0.24 ÷ 0.80) | 4.287 | 3.509 | 167.55 | 5.57% | |||||
| Stage I | 1.00 (0.48 ÷ 1.00) | 4.305 | 3.706 | 178.44 | 12.4% | |||||
| LFP | y | a | b | c | ||||||
| 0 (0 ÷ 0.9) | 5.79 | 9.82 | 4.79 | 272.36 () | 0% | |||||
| 1 (0.1 ÷ 1) | 6.01 | 10.33 | 4.69 | 291.39 | 6.53% | |||||
| Material | Stoichiometric Limits | OCV Function | |
|---|---|---|---|
| Graphite | |||
| 0.01 | 0.73 | ||
| LFP | |||
| 0.03 | 0.96 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerici, D.; Mocera, F.; Somà, A. Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors. Energies 2021, 14, 6281. https://doi.org/10.3390/en14196281
Clerici D, Mocera F, Somà A. Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors. Energies. 2021; 14(19):6281. https://doi.org/10.3390/en14196281
Chicago/Turabian StyleClerici, Davide, Francesco Mocera, and Aurelio Somà. 2021. "Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors" Energies 14, no. 19: 6281. https://doi.org/10.3390/en14196281
APA StyleClerici, D., Mocera, F., & Somà, A. (2021). Experimental Characterization of Lithium-Ion Cell Strain Using Laser Sensors. Energies, 14(19), 6281. https://doi.org/10.3390/en14196281









