1. Introduction
The spread of non-linear loads in residential and industrial environments in recent years has had a considerable impact on electrical distribution grids since such loads cause harmonic distortions in current and/or voltage waveforms and imbalance in polyphase systems. Thus, the classical power theory, whose definitions apply exclusively to purely sinusoidal waveforms, has become inadequate to deal with the current and future scenarios.
Therefore, modern power theories have been proposed with the purpose of correctly analyze linear and non-linear loads, as proposed by Budeanu [
1], Fryze [
1], Buchholz [
2], Depenbrock [
2], Akagi [
3], and Tenti [
4]. Although Budeanu and Fryze developed contributions to single-phase systems, they noticed power portions linked to harmonic components, making compensation difficult. Buchholz extended Fryze’s theory to polyphase systems. From the works of Fryze and Buchholz, Depenbrock presented the first attempt to decompose current parcels in polyphase systems; however, their variables have no physical meaning. Akagi’s theory is based on the Clarke transform and was developed for three-phase systems in general. Such theory does not present a physical meaning to each portion of power or current; conversely, it can be very efficient to compensations with active power filters. The Conservative Power Theory (CPT) presented by Tenti, Matavelli, and Paredes [
4], the focus of this work, proposes current decomposition in different quantities that contain specific physical meaning and can be applied to the obtainment of power and energy. This allows to correctly characterize loads and makes it possible to compensate the undesirable components of current.
The application of a power theory capable of dealing with distorted currents and voltages is significant; through more accurate power measurements and the detection of harmful electric current components, it is possible to perform corrective actions that assist in the efficient performance of the electrical system.
The CPT definitions can be used in shunt active power filters (SAPF) applications for any electrical systems, including in three-wire two-phase systems [
5] and four-wire three-phase systems [
6]. Ref. [
7] proposes the application of a single-phase asymmetrical cascaded H-bridge multilevel inverter (ACHMI) in microgrids with non-linear loads, where the CPT is used to generate current references for the mitigation of disturbances.
The CPT is also used to compensate the distortion current and the reactive current of a single-phase system [
8]. The used converter of a photovoltaic power generation system connected to the grid also acts as a shunt active filter using current portions obtained through the CPT. In Ref. [
9], CPT is used for the same purpose as [
8], but in a three-phase system. Ref. [
10] proposes the application of CPT to identify and quantify different current references for disturbance mitigation through a grid-connected wind turbine system converter.
Besides that, CPT can be applied in load-sharing strategies between converters of a microgrid. Ref. [
11] proposes an application of four-arm converters in a microgrid with a distributed communication network, where the theory is used to identify harmonic and unbalance components. Through the control algorithm and the communication network, it is possible to feed the converters with distortion and unbalance components requested by the loads, according to the capacity of each converter, avoiding the overload of one or more converters.
A load-sharing strategy based on a decision algorithm among two distributed energy sources connected to the grid was proposed in [
12], where the CPT is applied to decompose the current into portions serving as a reference for the control system.
CPT definitions can be used to generate current references to be compensated by grid-connected multifunction inverters (MFGTIs) [
13]. Ref. [
13] proposes a platform composed of a control center and inverters with communication capability. The centralized control can send and receive data from the inverters remotely, allowing the microgrid operator to define and adjust inverter parameters indicating their functionality in each situation. The control center can send the distortion current and/or reactive current references to the inverters to carry out the compensation, which enables cooperation between the converters and between these and the passive compensators present in the network.
Ref. [
14] proposes a “multi-master-slave” control strategy in an isolated microgrid where the current reference of the “slave” converter units is generated from the load currents. “Master” and “slave” converters are connected to a common bus, where the “slaves” inject their available energy to locally compensate for unwanted current components originating from non-linear and/or unbalanced local loads, and the “master” units share the remaining charge with distant groups.
Ref. [
15] proposes the usage of load compliance factors calculated through CPT and the application of the pattern recognition method (K-Nearest Neighbor) to determine the most suitable compensators to improve the power factor and reduce losses on the network.
Refs. [
16,
17] used some of the modern power theories to analyze the error of the reactive power obtained from digital power meters and the power theories. In Ref. [
16], there is no mention of sampling rate, and in [
17] the authors adopted a 250 kHz sampling rate. The work in [
18] used a sampling rate of 6 kHz to better reproduce the 25th harmonics of the load current. Ref. [
19] proposes a three-phase power meter based in Fourier analysis. These papers do not focus on how the chosen sampling rate could affect the measurement errors. Additionally, the higher is the sampling rate, greater is the number of harmonics included in the calculus [
20], and less error is achieved but without proper analysis.
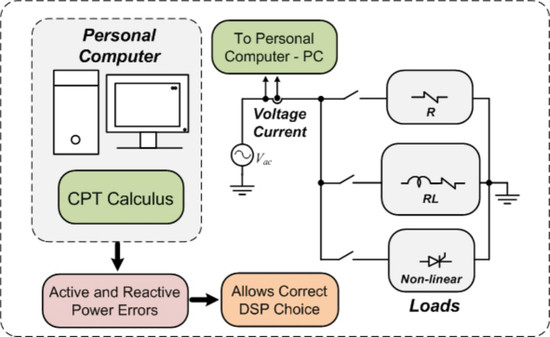
For the application of CPT in digital systems, it is necessary to define the sampling rate that will be used to perform the mathematical calculus. Based on this fact, this article assesses the influence of the sampling rate on the measurements of active power and reactive power with definitions based on CPT. The authors would like to highlight that this analysis is very important since it influences the choice of the most suitable microprocessor for the implementation of CPT. It is the first article in the literature that deals with the analysis of the sampling rate impact on the CPT measurements and, thus, its archival value.
This article is summarized as follows. In
Section 2, the theoretical background of CPT is presented and the experimental arrangement is described. In
Section 3, the obtained results are presented and discussed. Finally,
Section 4 concludes the work.
4. Conclusions
This article presented as the main contribution the analysis of the sampling rate as an influence factor in electrical power measurements based on the Conservative Power Theory.
It was observed, by means of statistical analysis, that the reactive power mean error is inversely proportional to the sampling frequency, since the CPT uses the impartial integral, which in the discrete domain accumulates certain amount of error depending on the sampling rate. On the other hand, it was also confirmed that the sampling rate influences are neglectable for active power measurements.
The present study contributes with the valuable information of the sampling frequency for which the error added to the reactive power can be considered acceptable. This information becomes decisive when the intention of digital implementation is in question, and it can assist in the choice of an appropriate device for the implementation.
In summary, it is possible to conclude that, although CPT has great potential for power calculations, it demands favorable processing and memory resources, since the sample rate must be adequate to avoid accuracy errors in the reactive power.
Based on the literature review, the CPT has notorious capability of dealing with distorted currents and, consequently, adds new power quantities resulted from these phenomena. For these situations, the sampling rate can influence the distorted power measurements both for the errors associated with the reactive portion and for the harmonics of higher order present in the signals of voltages and currents.
Despite the importance of the tests of accuracy performed in this paper and the relevant information about the minimal sampling rate to minimize errors, it is noted that the study must be complemented with tests of hypotheses on the values of standard deviation aiming to conclude about the precision reached with the measurement results.