Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil
Abstract
:1. Introduction
- Enhancing the FRT capability of a WECS using a non-conventional method; high-temperature SC of solenoidal structure;
- Introducing a new application for an FOPI controller in WECS;
- Adopting two new optimization techniques; HS and GWO to determine the optimum design of the proposed high-temperature SC and the FOPI control parameters;
- Presenting a comparison of HS and GWO techniques and the PSO to highlight the effectiveness of the employed methods.
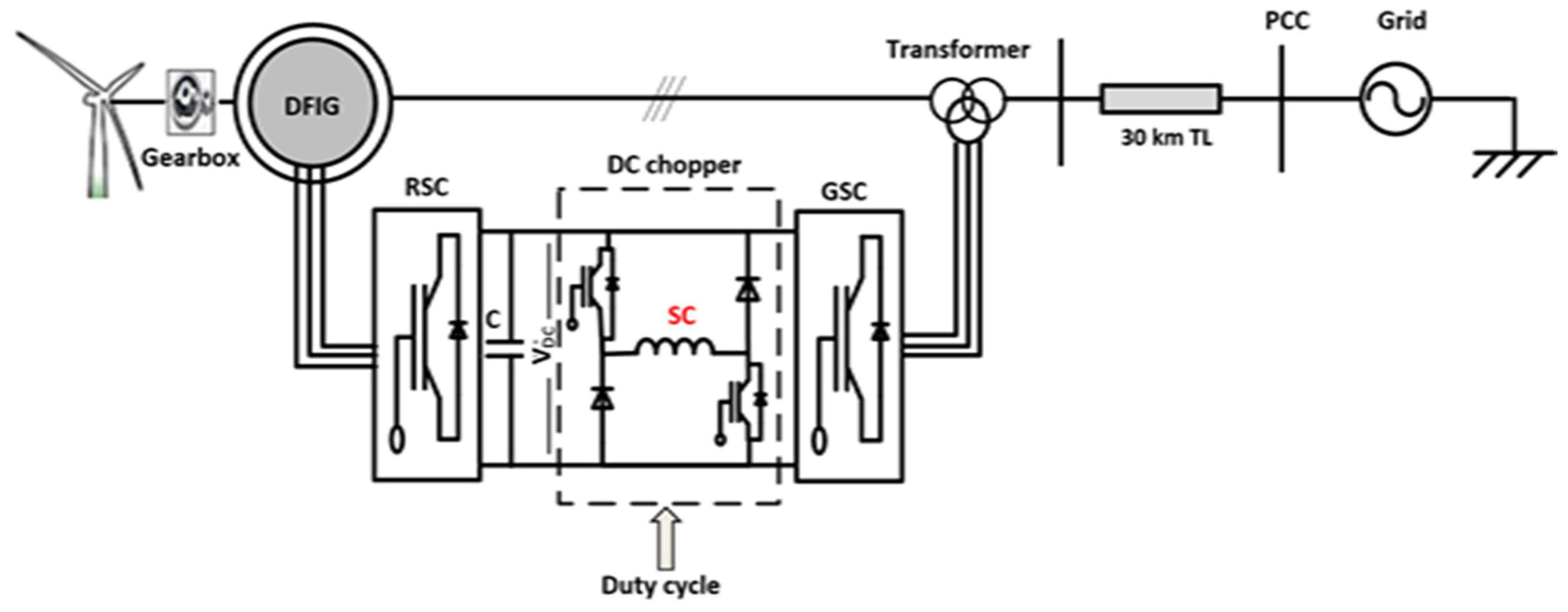
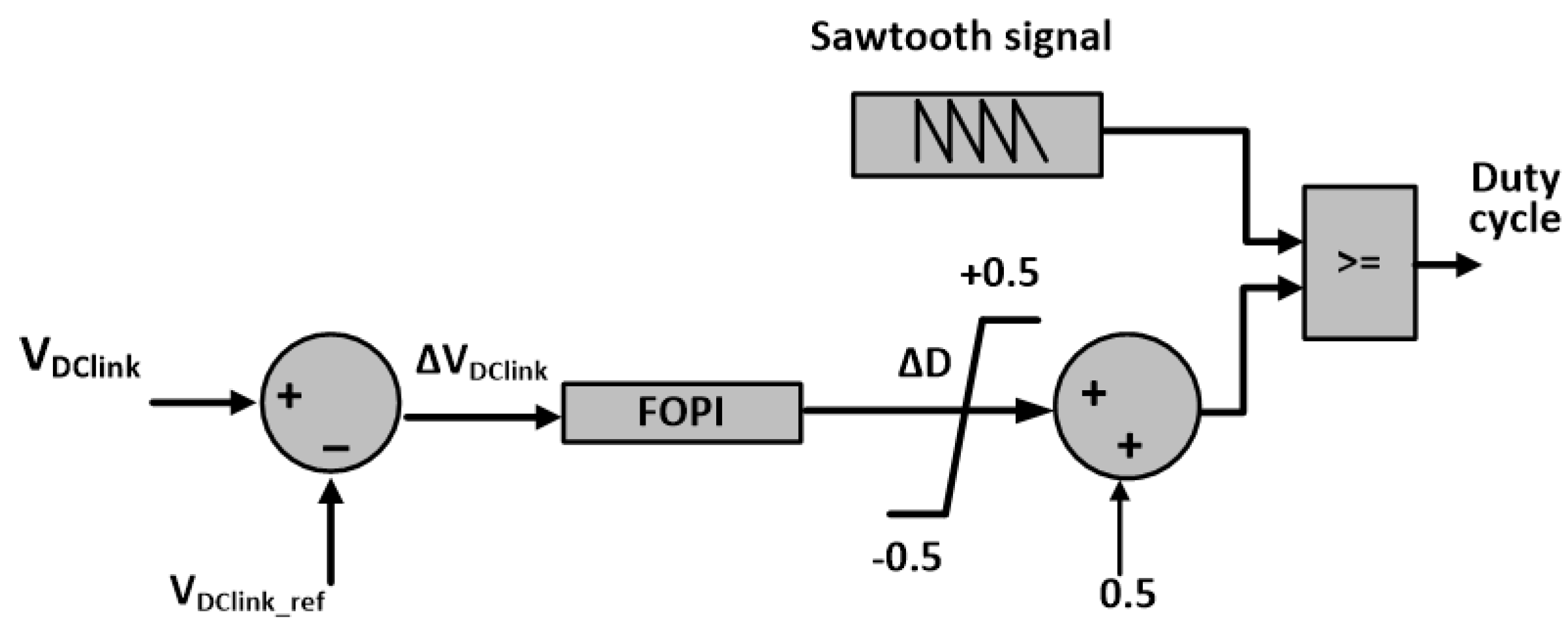
2. System under Study and Proposed Controller
3. Evolutionary Computing Techniques
- (i)
- Play any pitch concord as of the memory;
- (ii)
- Play any neighboring pitches of the pitch HS as of the memory;
- (iii)
- Play irregular pitch from the conceivable pitch.
4. Results and Discussions
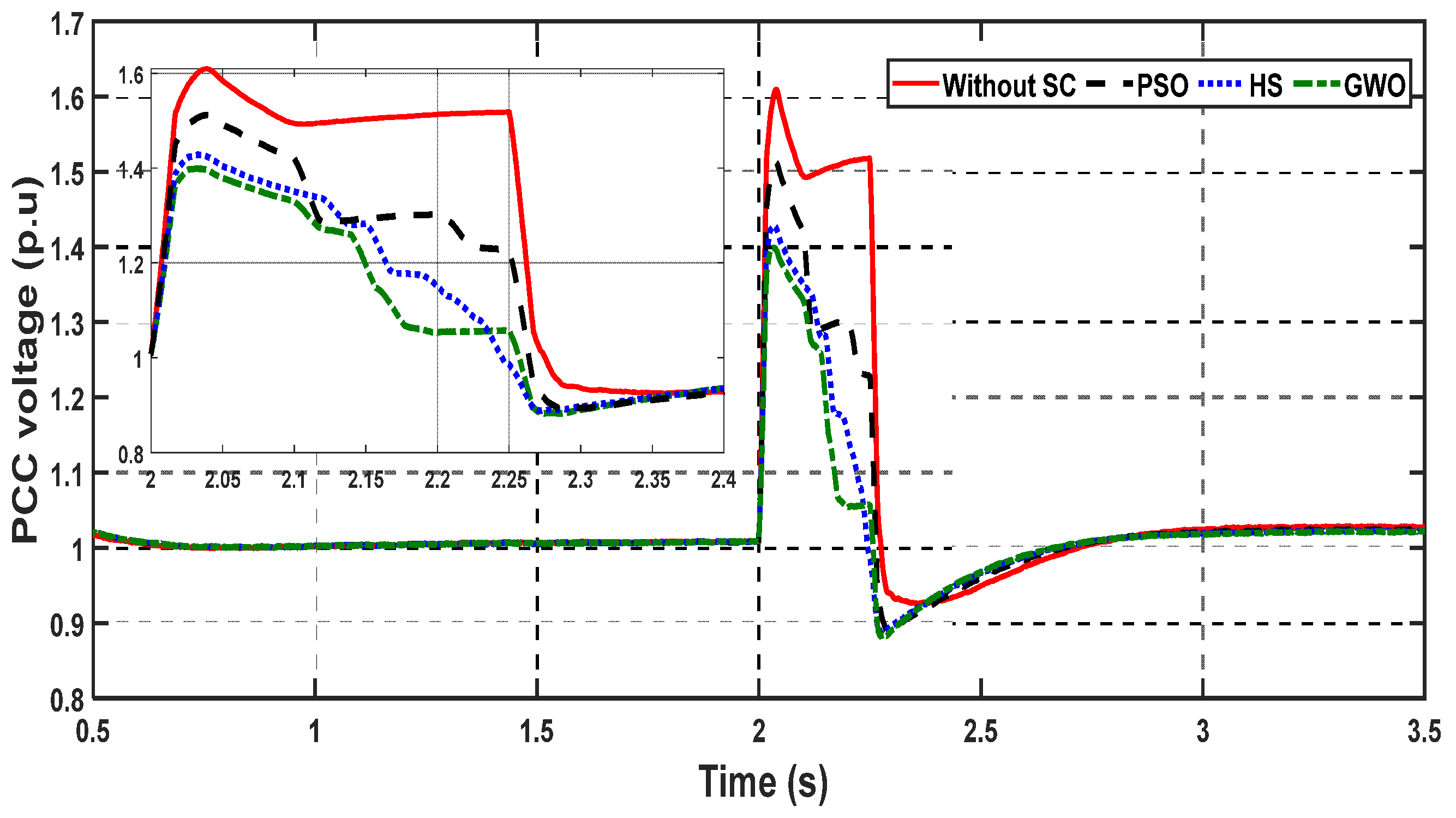
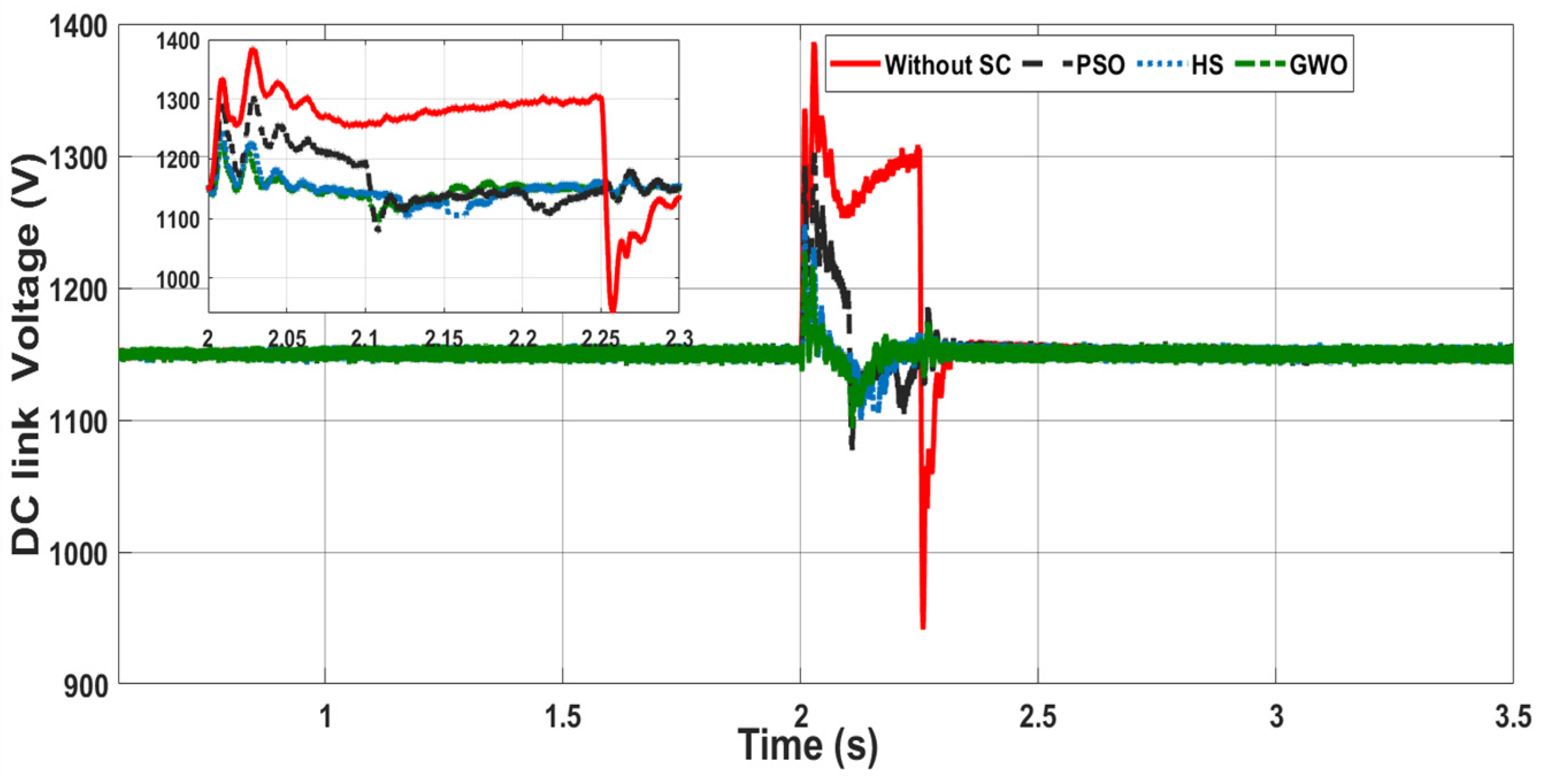
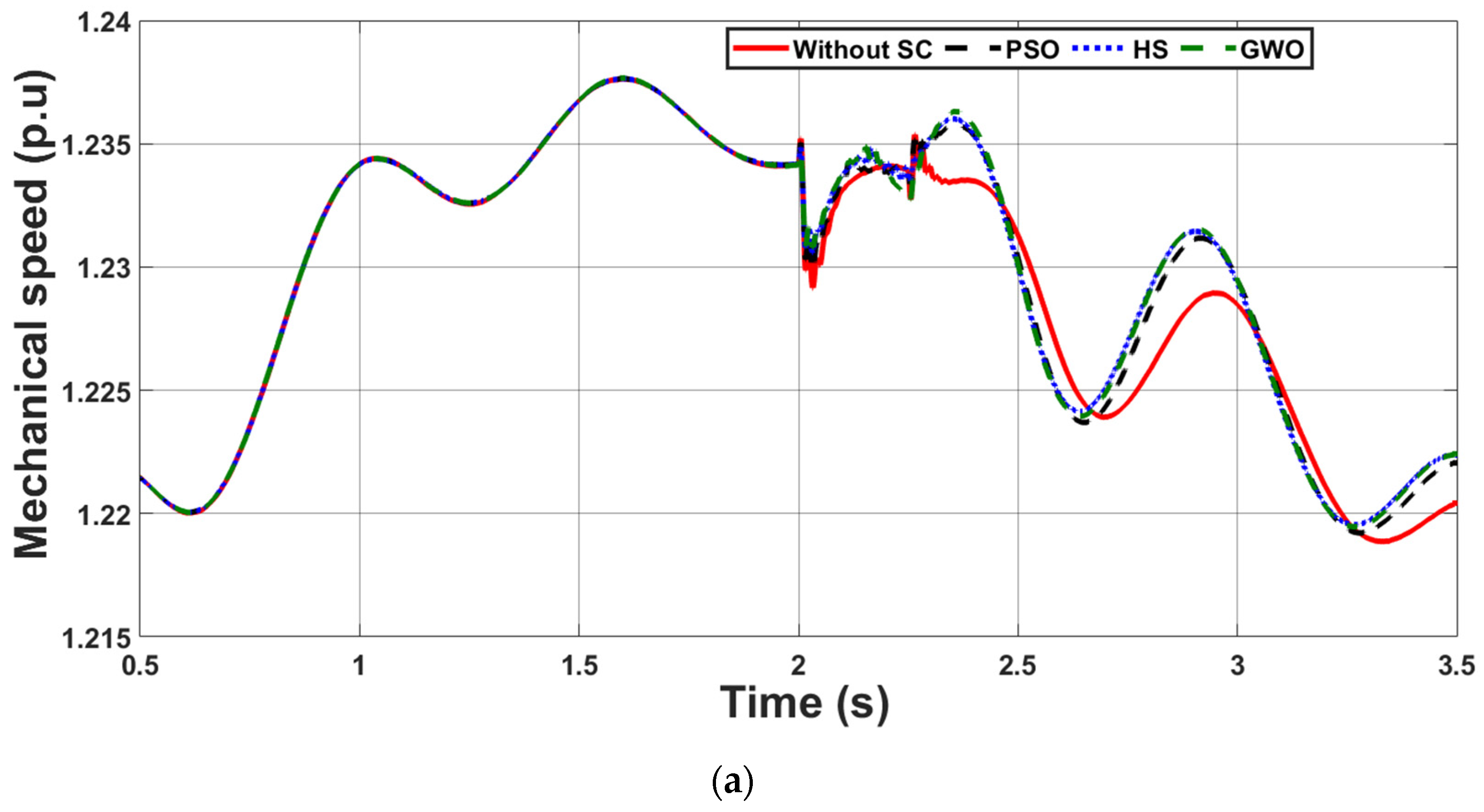
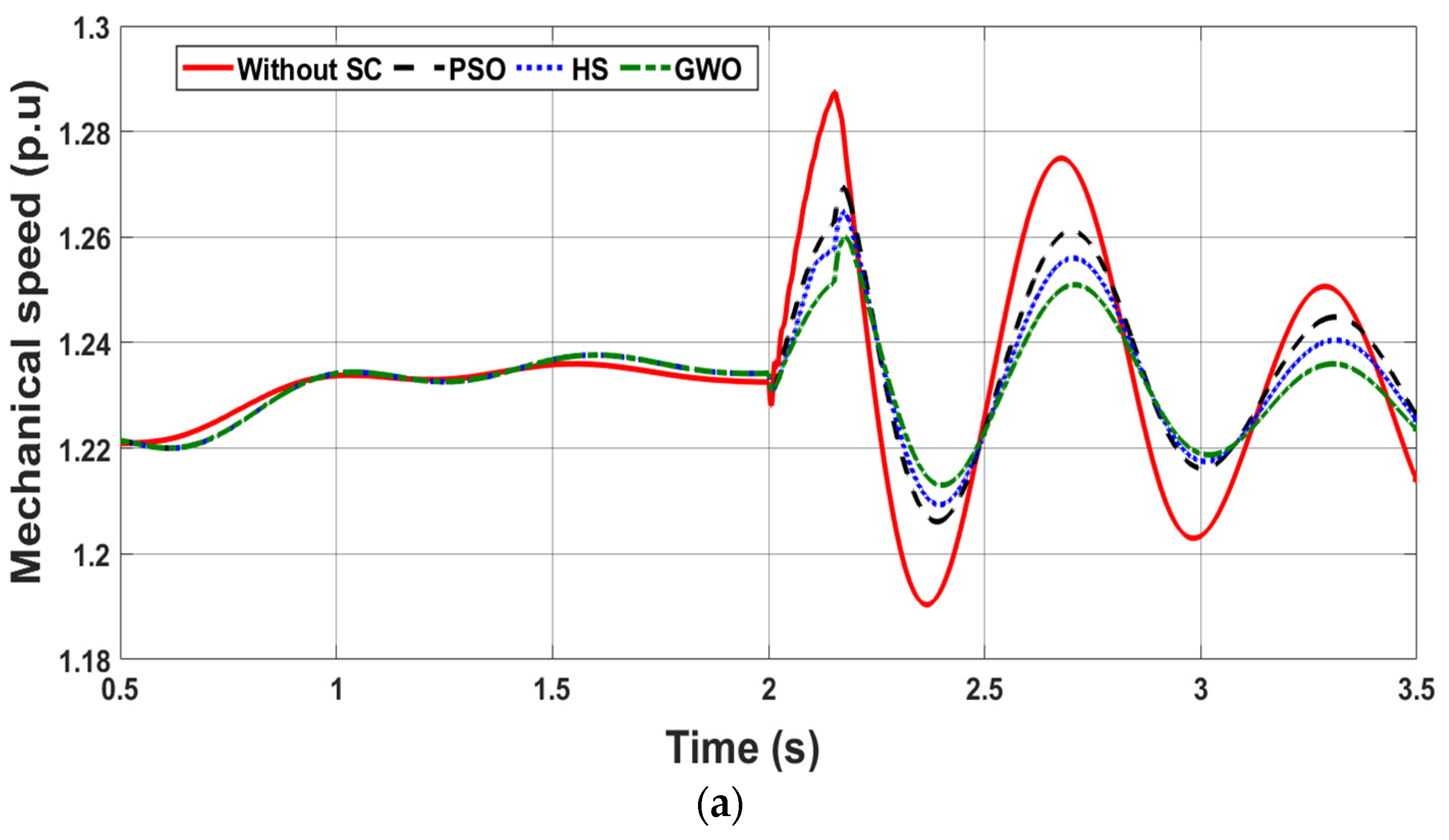
4.1. Case Study 1: Voltage Swell
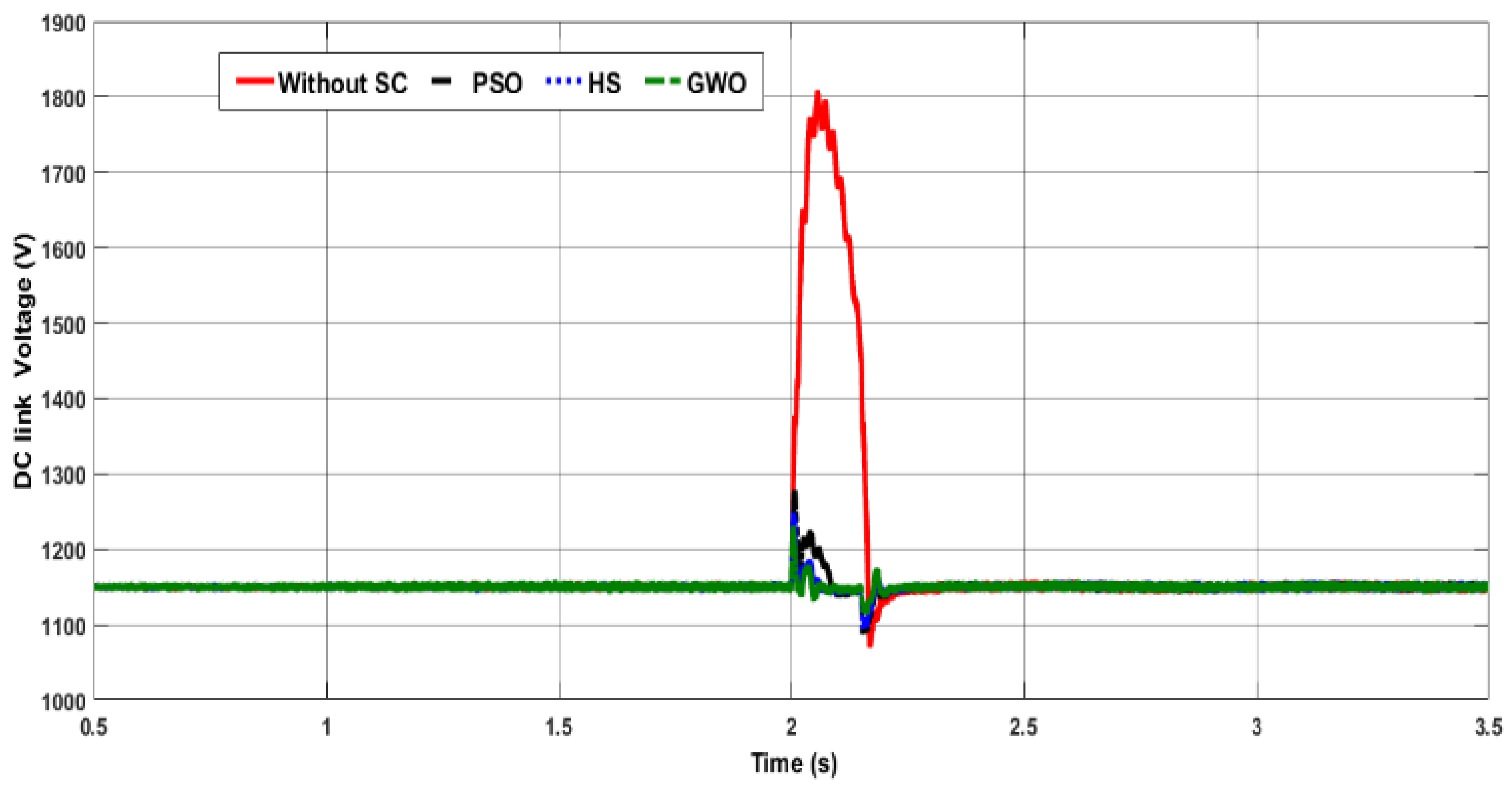
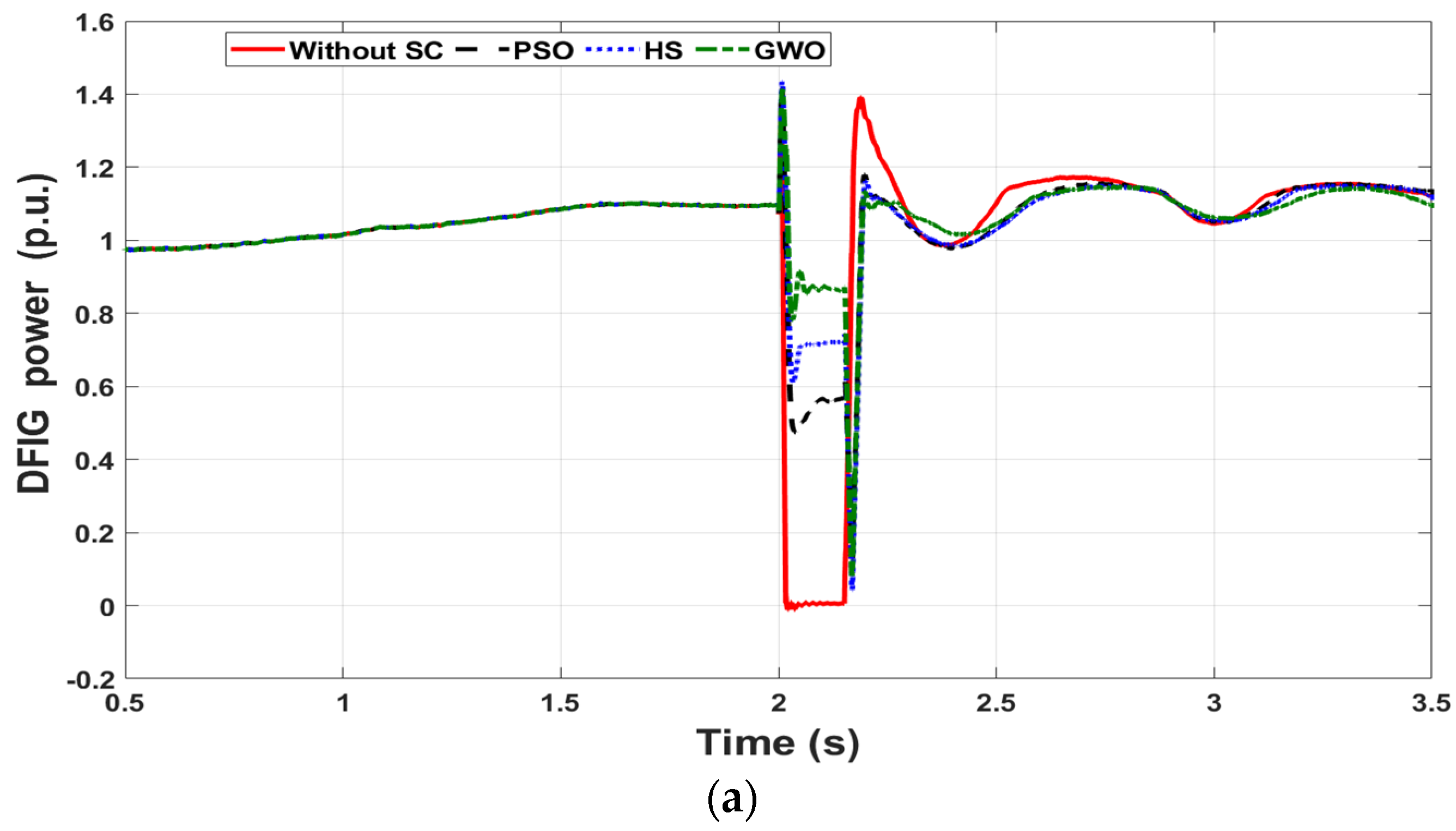
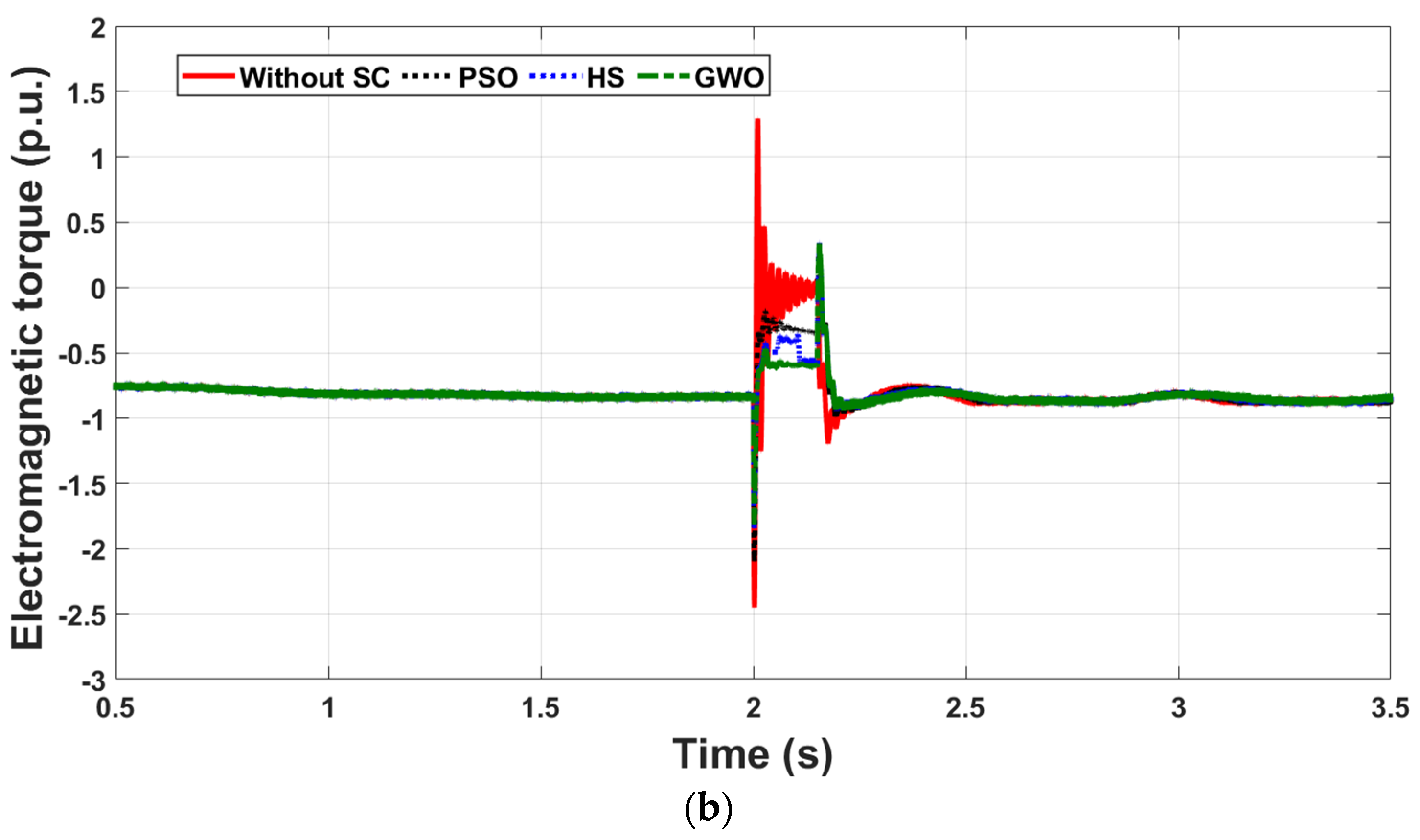
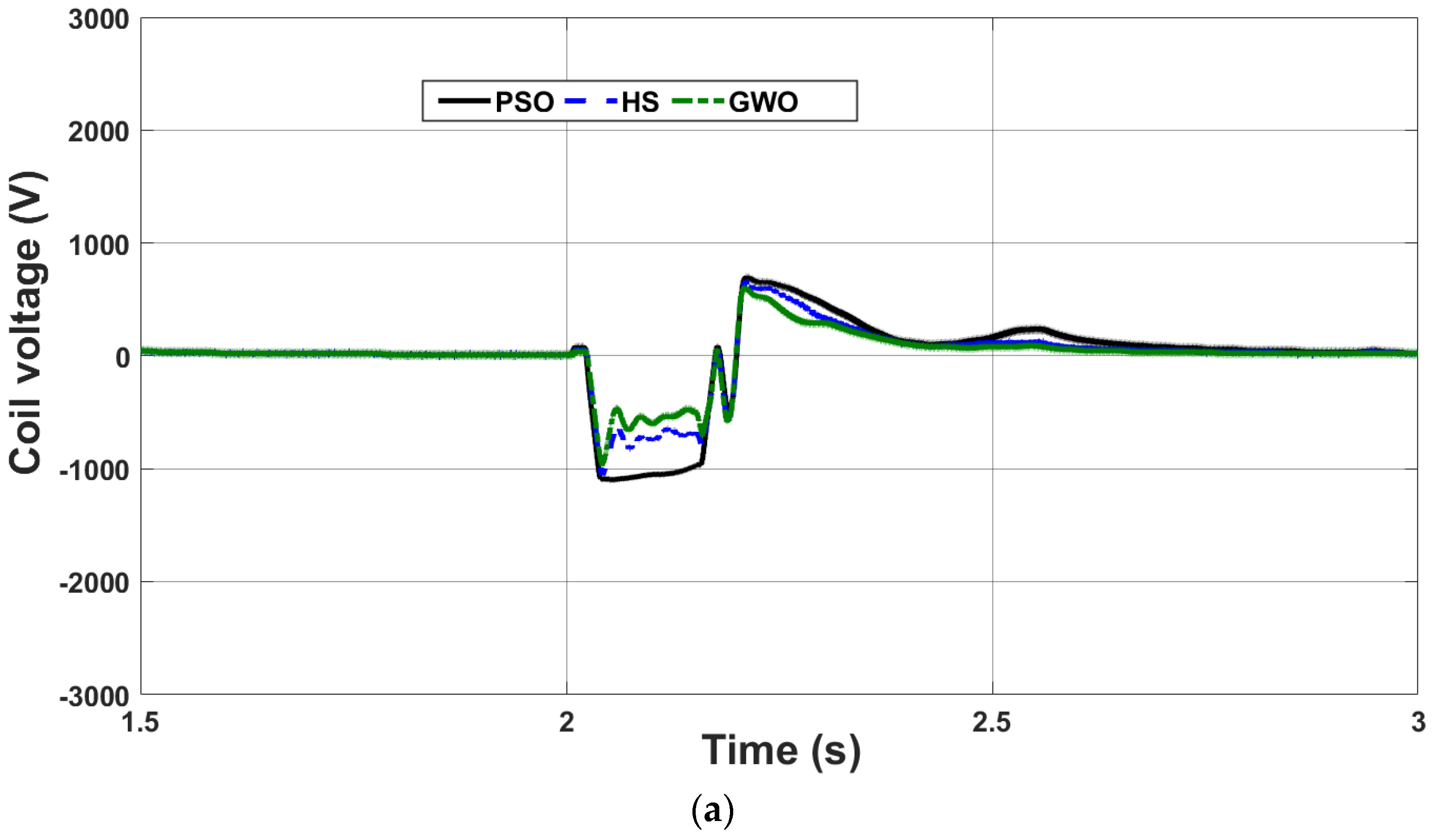
4.2. Case Study 2: Three-Phase Short Circuit Fault
5. Cost Analysis
6. Conclusions
- GWO featured superior optimization ability to HS and the conventional PSO techniques;
- Although a minimum SC size was obtained using GWO, the two case studies investigated in this paper demonstrated that the performance of the DFIG-WECS with parameters calculated by GWO was the best among the other two techniques. This was attributed to the adequate tuning and proper calculation of the FOPI control parameters;
- The proposed method can be used for new and existing WECS installations to enhance the FRT capability of the DFIG during fault and disturbance events;
- Although the cost of high-temperature superconductors was more affordable than low-temperature superconductors, the cost was still relatively high due to the cryogenic system. With the rapid advancement in superconducting materials, several applications of SC in power systems will be seen in the very near future.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value |
|---|---|
| Rated power | 1.5 MW |
| Rated voltage | 575 V |
| Rated frequency | 60 Hz |
| Stator resistance | 0.0045 Ω |
| Stator inductance | 0.0357 H |
| Rotor resistance | 0.0032 Ω |
| Rotor inductance | 0.033 H |
| Mutual inductance | 0.575 H |
| Length, km. | R, Ω/km | L, H/km | C, F/km |
|---|---|---|---|
| 30 | 0.1153 | 1.05 × 10−3 | 11.33 × 10−9 |
References
- Yunus, A.M.S.; Abu-Siada, A.; Masoum, M.A.S. Improving Dynamic Performance of Wind Energy Conversion System using Fuzzy-Based Hysteresis Current Controlled SMES. IET Power Electron. 2012, 5, 1305–1314. [Google Scholar] [CrossRef] [Green Version]
- Yunus, A.M.S.; Abu-Siada, A.; Masoum, M.A.S. Improvement of LVRT Capability of Variable Speed Wind Turbine Generators Using SMES Unit. In Proceedings of the IEEE Innovation Smart Grid Technologies Conference, Perth, WA, USA, 13–16 November 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Ding, Y.; Singh, C.; Goel, L.; Østergaard, J.; Wang, P. Short-term and medium-term reliability evaluation for power systems with high penetration of wind power. IEEE Trans. Sustain. Energy 2014, 5, 896–906. [Google Scholar] [CrossRef]
- Nordel Connection Code Wind Turbines. Available online: https://www.wind-energy-the-facts.org/grid-codes-and-essential-requirements-for-wind-power-plants.html (accessed on 15 January 2007).
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Jadhav, H.T.; Roy, R. A comprehensive review on the grid integration of doubly fed induction generator. Int. J. Elect. Power Energy Syst. 2013, 49, 8–18. [Google Scholar] [CrossRef]
- Semen, S.; Niiranen, J.; Kanerva, S.; Arkkio, A.; Saitz, J. Performance study of a doubly fed wind-power induction generator under network disturbance. IEEE Trans. Energy Convers. 2006, 21, 883–890. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Abu-Siada, A.; Elnaggar, M. Application of Superconductors to Improve the Performance of DFIG-based WECS. IEEE Access J. 2019, 7, 103760–103769. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Alenany, A.; Abu-Siada, A. Enhancing the performance of wind energy conversion systems using unified power flow controller. IET Gener. Transm. Distrib. 2020, 14, 1922–1929. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Sabiha, N.A. Ferroresonance Overvoltage Mitigation using STATCOM for Grid-Connected Wind Energy Conversion Systems. J. Mod. Power Syst. Clean Energy 2020. [Google Scholar] [CrossRef]
- Mossad, M.I. Model Reference Adaptive Control of STATCOM for Grid-Integration of Wind Energy Systems. IET Electr. Power Appl. J. 2018. [Google Scholar] [CrossRef]
- Wessels, C.; Gebhardt, F.; Fuchs, F.W. Fault ride-through of a DFIG wind turbine using a dynamic voltage restorer during symmetrical and asymmetrical grid faults. IEEE Trans. Power Electron. 2011, 26, 807–815. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Xiao, L.; Dai, S. Enhancing low-voltage ride-through capability and smoothing output power of DFIG with a superconducting fault-current limiter-magnetic energy storage system. IEEE Trans. Energy Convers. 2012, 27, 277–295. [Google Scholar] [CrossRef]
- Rahim, A.H.M.A.; Nowicki, E.P. Supercapacitor energy system for fault-ride through of a DFIG wind generation system. Energy Convers. Manag. 2012, 52, 96–102. [Google Scholar] [CrossRef]
- Yunus, M.S.; Abu-Siada, A.; Mosaad, M.I.; Albalawi, H.; Aljohani, M.; Jin, J.X. Application of SMES Technology in Improving the Performance of a DFIG-WECS Connected to a Weak Grid. IEEE Access 2021, 9, 124541–124548. [Google Scholar] [CrossRef]
- Viola, J.; Angel, L.; Sebastian, J.M. Design and robust performance evaluation of a fractional order PID controller applied to a DC motor. IEEE/CAA J. Autom. Sin. 2017, 4, 304–314. [Google Scholar] [CrossRef]
- Zhong, J.; Li, L. Tuning Fractional-Order PIλDμ Controllers for a Solid-Core Magnetic Bearing System. IEEE Trans. Control. Syst. Technol. 2015, 23, 1648–1656. [Google Scholar] [CrossRef]
- Pullaguram, D.; Mishra, S.; Senroy, N.; Mukherjee, M. Design and Tuning of Robust Fractional Order Controller for Autonomous Microgrid VSC System. IEEE Trans. Ind. Appl. 2018, 54, 91–101. [Google Scholar] [CrossRef]
- El-Naggar, M.F.; Mosaad, M.I.; Hasanien, H.M.; AbdulFattah, T.A.; Bendary, A.F. Elephant herding algorithm-based optimal PI controller for LVRT enhancement of wind energy conversion systems. Ain Shams Eng. J. 2021, 12, 599–608. [Google Scholar] [CrossRef]
- Ngamroo, I. Optimization of SMES-FCL for Augmenting FRT Performance and Smoothing Output Power of Grid-Connected DFIG Wind Turbine. IEEE Trans. Appl. Supercond. 2016, 26, 7. [Google Scholar] [CrossRef]
- Karaipoom, T.; Ngamroo, I. Optimal superconducting coil integrated into DFIG wind turbine for fault ride through capability enhancement and output power fluctuation suppression. IEEE Trans. Sustain. Energy 2015, 6, 1. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Ramadan, H.S. Power Quality Enhancement of Grid Connected Fuel Cell Using Evolutionary Computing Techniques. Int. J. Hydrogen Energy 2018. [Google Scholar] [CrossRef]
- Sahu, P.R.; Hota, P.K.; Panda, S. Modifieded whale optimization algorithm for fractional-order multi-input SSSC-based controller design. Optim. Control Appl. Methods 2018, 39, 1802–1817. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, X.; Yu, T.; Shu, H.; Fang, Z. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Convers. Manag. 2017, 133, 427–443. [Google Scholar] [CrossRef]
- Gaing, Z. A Particle Swarm Optimization Approach for Optimum Design of PID Controller in AVR System. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef] [Green Version]
- el Metwally, M.M.; el Emary, A.A.; el Bendary, F.M.; Mosaad, M.I. Optimal Power Flow Using Evolutionary Programming Techniques. In Proceedings of the International Middle East Power System Conference MEPCON, Aswan, Egypt, 12–15 March 2008; pp. 260–264. [Google Scholar]
- Abu-Siada, A.; Mosaad, M.I.; Kim, D.W.; El-Naggar, M.F. Estimating Power Transformer High frequency Model Parameters using Frequency Response Analysis. IEEE Trans. Power Deliv. 2020, 35, 1267. [Google Scholar] [CrossRef]
- Manjarresa, D.; Landa-Torres, I.; Gil-Lope, S.; DelSer, J.; Bilbaob, M.N.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- Alhejji, A.; Mosaad, M.I. Performance enhancement of grid-connected PV systems using adaptive reference PI controller. Ain Shams Eng. J. 2020. [Google Scholar] [CrossRef]
- Geleta, D.K.; Manshahia, M.S.; Vasant, P.; Banik, A. Grey wolf optimizer for optimal sizing of hybrid wind and solar renewable energy system. Comput. Intell. 2020, 1–30. [Google Scholar] [CrossRef]
- Yunus, A.; Abu-Siada, A.; Masoum, M. Application of SMES unit to improve DFIG power dispatch and dynamic performance during intermittent misfire and fire-through faults. IEEE Trans. Appl. Supercond. 2013, 23, 5701712. [Google Scholar] [CrossRef]
- Nomura, S.; Shintomi, T.; Akita, S.; Nitta, T.; Shimada, R.; Meguro, S. Technical and cost evaluation on SMES for electric power compensation. IEEE Trans. Appl. Supercon. 2010, 20, 1373–1378. [Google Scholar] [CrossRef]
- Snider, E.; Dasenbrock-Gammon, N.; McBride, R. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature 2020, 586, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L. Electromagnetic force distribution and deformation homogeneity of electromagnetic tube expansion with a new concave coil structure. IEEE Access 2019, 7, 117107–117114. [Google Scholar] [CrossRef]
- Yunus, A.M.S.; Abu-Siada, A.; Masoum, M.A.S. Effects of SMES on the dynamic behaviors of type D-Wind Turbine Generator-Grid connected during short circuit. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Kim, D.; Abu-Siada, A.; Sutinjo, A. State-of-the-Art Literature Review of WPT: Current Limitations and Solutions on IPT. Electr. Power Syst. Res. 2018, 154, 493–502. [Google Scholar] [CrossRef]









| Method | SC Design Parameters | FOPI Parameters | |||
|---|---|---|---|---|---|
| LSC (H) | Isco (kA) | Kp | Ki | λ | |
| PSO | 0.2 | 3.24 | 0.7 | 1.1 | 0.85 |
| HS | 0.198 | 0.323 | 1.2 | 0.95 | 0.56 |
| GWO | 0.19 | 0.321 | 0.95 | 1.02 | 0.82 |
| Criteria | PCC Voltage | DC-Link Voltage | ||||
|---|---|---|---|---|---|---|
| PSO | HS | GWO | PSO | HS | GWO | |
| Overshooting% | +15 −55 | +14 −45 | +13.25 −40 | 10.8 −5.2 | 8.5 −4.7 | 7.2 −2.78 |
| Settling time (s) | 0.27 | 0.27 | 0.27 | 0.23 | 0.195 | 0.19 |
| Steady state error% | 1.6 | 1.2 | 0.9 | 0.437 | 0.435 | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosaad, M.I.; Abu-Siada, A.; Ismaiel, M.M.; Albalawi, H.; Fahmy, A. Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil. Energies 2021, 14, 6319. https://doi.org/10.3390/en14196319
Mosaad MI, Abu-Siada A, Ismaiel MM, Albalawi H, Fahmy A. Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil. Energies. 2021; 14(19):6319. https://doi.org/10.3390/en14196319
Chicago/Turabian StyleMosaad, Mohamed I., Ahmed Abu-Siada, Mohamed M. Ismaiel, Hani Albalawi, and Ahmed Fahmy. 2021. "Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil" Energies 14, no. 19: 6319. https://doi.org/10.3390/en14196319
APA StyleMosaad, M. I., Abu-Siada, A., Ismaiel, M. M., Albalawi, H., & Fahmy, A. (2021). Enhancing the Fault Ride-through Capability of a DFIG-WECS Using a High-Temperature Superconducting Coil. Energies, 14(19), 6319. https://doi.org/10.3390/en14196319








