Multifrequency Impedance Tomography System for Research on Environmental and Thermal Processes

Abstract

The possibility for spatial and temporal monitoring of environmental, chemical or thermal processes is of high importance for their better understanding thus control and optimization. Therefore, measurement methods that enable such opportunities might be especially valuable for researchers and process engineers. For this reason, in this paper the novel Electrical Impedance Tomography system is proposed that enables the visualization of the processes in which the electrical conductivity of material is changing. The proposed EIT system is based mostly on general purpose equipment. It consists of three laboratory-grade devices: a signal generator, a switching device and a data acquisition card for voltage measurement. In addition to those devices, the current source was constructed to complete the system. The EIT system was designed to have the ability of sourcing the current of frequency up to 250 kHz. A set of validation experiments were carried out to verify the EIT system accuracy. The validation tests consisted of object detection, distinguishing between objects of different conductivity, multifrequency imaging and visualization of slow-changing processes. The obtained results were also compared with the numerical simulations. The proposed system was proven to have the ability of correct imaging of irregularity inside the area of the sensor.

1. Introduction

Research on processes in environmental studies, chemical engineering or industrial technology optimization is focused on spatial and temporal changeability of certain properties of the matter inside the specified region of interest. Applied measurement techniques should be precise yet non-invasive (or at least non-intrusive) to minimize the negative interaction with the process. The development in the field of measurement methods over past decades has brought a number of techniques like magnetic resonance imaging (MRI), tomography, thermal imaging, ultrasonic methods, etc. [1]. One of such group of methods is electrical tomography. The word ‘tomography’ is used for all visualization methods that use measurements performed at the border of the examined object to provide the information about spatial distribution of certain properties within this object [2]. Opposite to hard field tomography, that uses ionizing radiation, electrical methods are safe and not that expensive. The ‘modalities’ of the electrical tomography might be used depending on electrical properties of the examined material. Such modalities are:

• Electrical Impedance Tomography (EIT)—the distribution of electrical conductivity is determined within the examined object [3]. In this modality also impedance spectroscopy might be introduced [4].
• Electrical Capacitance Tomography (ECT)—allows to determine the permittivity distribution in an area filled with dielectric material [5,6].
• Magnetic Induction Tomography (MIT)—may be used to determine the permeability distribution inside the examined object [7].

Electrical Impedance Tomography is a non-intrusive method of imaging of the spatial distribution of electrical conductivity inside the area of the sensor. Generally speaking, in the EIT method a set of measurements is taken from the electrodes placed on the internal surface of the sensor that surrounds the object of interest. Stimulation signal from the current source is injected through selected electrodes using a particular injection pattern. The most common are adjacent pattern (electrodes: 1-2, 2-3, 3-4 and so on) and opposite pattern (electrodes: 1-9, 2-10, 3-11 and so on, for 16-electrodes sensor). During stimulation of the selected electrode pair the voltage measurements are taken from the rest of the electrodes. Next the sourcing electrodes are switched to another pair in a circular manner and the measurements are repeated until the measurement set is completed. Eventually, the image that represents distribution of conductivity is reconstructed using one of the algorithms for solving of the inverse problem [3,8]. The EIT method suffers from several limitations of its applicability. The main one is that material inside the sensor must conduct the electricity. The minimal conductivity limit is different between systems as it is mainly connected with current source ability to drive the different load. In some of the EIT systems that problem was overcome with the use of voltage source. The applications of the EIT method in different domains were widely described, e.g., [3,8]; some of the most common examples are also described in the paragraphs below.

In recent years, the EIT has been proven to be a reliable research method. Originating from the clinical trials in early 1980s, the EIT method has spread over different branches of science [3]. Additionally, in the industrial applications this method is becoming more popular [8]. Most of the processes in which the electrical properties (conductivity, permittivity) of the material is changing might be monitored by the use of EIT. Such processes may include, e.g., [2,3,8]: mixing procedures, chemical and biochemical reactions, moisture and pollution transport, multiphase flow, etc. Estimating both real and imaginary components of the complex conductivity and their dependence on frequency enables further possibilities for process monitoring [9,10,11].

A number of research efforts have been undertaken to estimate a spatial distribution of moisture content in a certain material. In the paper [12], the EIT method was applied for characterizing the moisture transport in concrete and other cement-based materials. Similarly, Rymarczyk et al. [13] have analyzed the use of the EIT method for estimation of the moisture transport in the walls of buildings. This research was focused on comparison of the machine learning algorithm of image reconstruction with the classical Gauss–Newton. A few papers showed the use of EIT for assessment of the moisture content in material for optimization of drying process, e.g., [14]. The results described in the paper showed a satisfactory ability to localize an insufficiently dried part of the material which might be useful for process control. The research has also proved usefulness of the multifrequency excitation and impedance spectroscopy for analysis of plant-based tissue. The use of complex conductivity for tomographic imaging is not a new idea [11,15], however, it gains popularity as it can give spectral information about the region of interest [16]. The in-depth review of the impedance spectroscopy use in the EIT is given in [4]. It is noteworthy that a lot of the above-mentioned processes are relatively slow thus the EIT imaging rate is not a crucial parameter. Another important field of research where tomographic methods are widely applied is multiphase flow. Depending on electrical properties of the transported material, as well as the carrier medium, different modalities might be applied. The majority of papers report the use of ECT, e.g., [17,18]. Still, application of EIT in this field is not unusual. In the paper [19], the authors proposed the EMT/EIT system for multiphase flow monitoring which is characterized by very high imaging rate (up to 1000 frames per second). They also described a comparison between two different methods of electrode location: on the inner surface of the pipe (galvanically coupled) and on the outer surface (capacitively coupled). A similar situation exists in a field of mixing or separation processes—the material inside the object of interest determines the modality to be used. The use of EIT for continuous monitoring of oil/water separator is demonstrated in [20]. The authors showed that electrical tomography is an effective tool especially for optimizing start-up and operation of the separator. Impedance tomography is also convenient for monitoring saline/sand dual-phase flow what was described in, e.g., [21]. In this research, the EIT system was used as a flowmeter, moreover, it was able to measure the solid concentration as well. Additionally, some chemical processes have been reported to be studied using EIT [2]. In the paper [22], the author described an exemplary case of using the EIT for monitoring a chemical reactor with a 3D EIT sensor. One of the most important, from the environmental point of view, might be carbon dioxide absorption that was studied, e.g., in paper [23]. The authors found the important relationship between impedance and frequency that may be used for the process optimization. It confirms that the use of impedance spectroscopy may augment the possibility for the use of the EIT method [11,24]. There is little research reporting the results of EIT use for, e.g., pollutant transport or temperature field reconstruction. It might be concluded that, despite the large number of studies that have been undertaken, a number of processes, in which the EIT may show its usefulness, have been left untouched. One of the reasons for this situation might be difficult availability of EIT devices for researchers.

Beginning in the early stage of the EIT development, the tomography systems have been built primarily by the researchers themselves. Although nowadays there are a few companies on the market that are producing the EIT appliances, still a lot of research is conducted using purpose-built apparatus. The EIT is considered to be a ‘low-cost’ method [8] especially in comparison with, e.g., CT scanners. However, in research applications, especially at their early stages, such an expense might not be always justifiable. Moreover, the commercial EIT systems do not always guarantee the flexibility of device adjustment that is necessary in a research area. Company like, e.g., Sciospec (Bennewitz, DE) [25] are offering EIT systems that are suitable for research purposes. Starting from 16-electrodes, single frequency systems up to 256-electrodes devices with impedance analyzer built-in. Probably the most recognizable manufacturer in this area is ITS Ltd. (Manchester, UK) [26]. The company provides several types of EIT and ECT devices which are mostly designed for industrial purposes. Other example might be Process Tomography Ltd. (Cheshire, UK) [27] which is mostly focused on delivery capacitance tomography systems. According to aforesaid company websites, the starting prices are approximately EUR 20,000–30,000, which is triple the cost of the system proposed in this paper.

As has been said, many research teams create their own EIT system. In the monography [3], one can find the historical background of EIT. Additionally, the authors of paper [28] reviewed several early years EIT systems, designed mainly for clinical and industrial studies. One of the earliest examples of such a system might be the 32-electrode EIT device described in [29]. Contrary to commonly used current sourcing, the authors proved the possibility of utilizing the voltage source instead. For the application characterized by high resistivity of the material inside the EIT sensor, it is virtually impossible to build a current source that would have output impedance high enough. The use of voltage sourcing for study on such materials seems to be more appropriate [14]. In the middle of the 1990s a few multifrequency EIT systems appeared. The first attempts to use impedance spectroscopy with the EIT were performed in clinical research. The example of such an EIT device is described in [30]. The authors developed and validated the multifrequency EIT system intended for research on biological tissues. The system was based partially on a few building blocks which were available on the market: a waveform generator, a digital I/O card and a DAQ card. However, most of signal conditioning circuit was built by the researchers themselves. The reported system allows for 16–32 channels measurement in the frequency range 1 kHz–1 MHz. Several EIT devices have been developed since then. Most of them were focused on increasing the speed of imaging. For this purpose, those systems were fully designed and built by the research teams. The examples might be the KHU Mark1 [31] and its further improved version KHU Mark2 [32]. The system was able to reach 100 frames-per-second (fps) with the frequency bandwidth 10 Hz–500 kHz. Those systems involve parallel signal processing and measurement for the increase of the imaging rate. The ‘state-of-the-art’ systems that have been made recently are based on FPGA (field-programmable gate array). This partially simplifies the circuit and enables the faster data acquisition. The example system of that kind is described in paper [33]. Instead of commonly used sinusoidal excitation, the authors introduced two other sourcing methods. For speed up the measurements they proposed the use of chirp signal (a sinusoidal wave that increases in frequency linearly over time) or the use of multisinusoidal signal, based on Fourier series. The FPGA-based EIT device might also be built with general purpose modules that are available on the market as shown in paper [34]. Using the National Instruments FPGA CompactRIO controller with several I/O cards and complementing the system with the own designed signal conditioning board, the researchers constructed the EIT system with ability of 1953 fps imaging rate. Current development in the field of programmable microcontrollers brought progress of ‘low-cost’ EIT appliances. The use of developers’ boards like Arduino or Raspberry PI makes the build of EIT device easier and cheaper, however, the quality of the imaging mostly depends on the quality of a signal conditioning circuit which has to be carefully designed anyway [16,35]. The majority of the above-mention systems are characterized by high complexity as they were designed for high speed imaging. On the other hand, a lot of valuable research results might be achieved using EIT devices that are focused mostly on accuracy rather than the speed.

For the aforesaid reasons, the main aim of this research was to develop and validate the EIT system based on general purpose laboratory equipment. This kind of instrument is commonly used in most research laboratories and they are also not very expensive. Furthermore, as those devices are designed to be used for accurate measurements, they are characterized by very low uncertainty as well as the high noise immunity. In order to enable the possibility for impedance spectroscopy, the proposed solution allows for multifrequency current injection and measurement of both real and imaginary components of complex impedance. Although there are a few examples of EIT systems based on general purpose devices [36,37], these systems are intended to be used in specific areas of the research, thus they are not as versatile as the proposed solution. Therefore, the primary novelty of the proposed EIT system is that the system provides functionality and quality of imaging similar to the commercial systems (excluding imaging rate) with the use of general purpose, inexpensive, laboratory equipment.

2. Materials and Methods

2.1. The Principle of the EIT Imaging

In the cross-section of a sensor the conductivity distribution may be determined based on the measured voltage in a two-step process. The aim of the first step is to solve the forward problem, leading to calculation of the transformation matrix of the measurement system. This stage is based on the Laplace equation (Equation (1)) which describes the distribution of electrical potential V in the area with the studied material of conductivity σ.

$$\nabla ·\sigma \nabla V=0$$

(1)

For a given measurement system, the solution of Equation (1) is generally carried out with Finite Elements Method. Introducing v as the vector of potentials measured on the electrodes leads to the designation of the transformation matrix T, that satisfies Equation (2):

$$v=\mathrm{T}·\sigma$$

(2)

Reconstruction of the conductivity image is the second stage of the analysis of acquired data. The image is constructed by solving the inverse problem defined by Equation (3):

$$\sigma ={\mathrm{T}}^{-1}·v$$

(3)

As the T matrix is not a square one, therefore, it is not possible to apply conventional methods for calculation of the inverse matrix. This problem has resulted in a number of algorithms for image reconstruction, approximating the solution of the inverse problem. Starting from linear methods (e.g., Linear Back-Projection) through nonlinear and iterative methods (e.g., Gauss–Newton) [3,8,38], the approach to the inverse problem has evolved into a dozen modern algorithms that utilize so-called artificial intelligence methods. In the paper [39], one can find a review of almost 70 papers describing novel methods for image reconstruction.

As the inverse problem is ill-conditioned, the solution may not be unique thus the distribution of the analyzed properties in the area of the sensor might not be correctly reflected. The feasibility of the accurate imaging and the expected quality of the image should by then verified using numerical simulation. The use of dedicated software, e.g., EIDORS (Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software) [40,41], allows both the simulation examination of the EIT system and the reconstruction of images based on experimental data.

Considering the use of the impedance spectroscopy, the conductivity in Equation (1) has to be substituted by the complex admittivity γ of the material inside the sensor (Equation (4)):

$$\gamma =\sigma +j\omega \epsilon$$

(4)

This in turn enables the opportunity to enhance the EIT system with the ability to create a set of images depicting frequency-dependent relations for both real component (conductivity σ) and imaginary component (permittivity ε) of the complex admittivity [4].

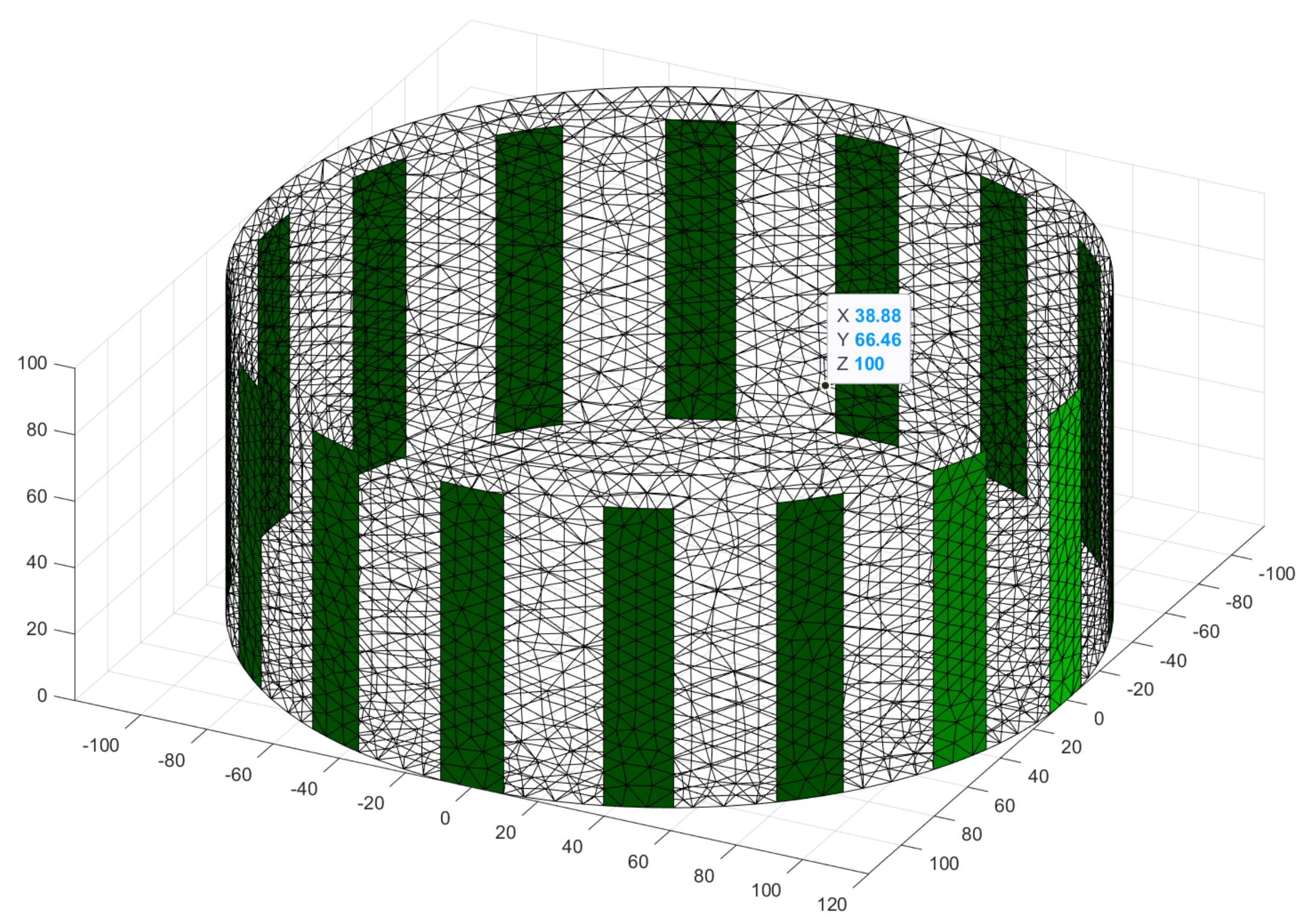
2.2. The EIT System Build

The basic block diagram of the EIT system is not very complicated, however, the quality of the devices is crucial for the imaging reliability. For this reason, the use of laboratory-grade general purpose instruments may contribute to the opportunity to build a high quality impedance tomography appliance. In general, most of EIT systems consist of four building blocks: a signal generator, a voltage controlled current source (VCCS), a switching unit and a voltage measurement device. In the proposed EIT system, three of them are general purpose instruments:

• arbitrary waveform signal generator (Keysight 33511B),
• switching device (Keysight 34972A),
• DAQ card (NI PCIe-6351).

All of them may be replaced with devices of similar functionalities. The block diagram of the proposed EIT system is presented in the picture (Figure 1). All the devices are controlled through the PC (omitted in the picture).

The arbitrary waveform generator applied for this research is Keysight 33511B [42], however, virtually any laboratory signal generator is suitable for this function. Moreover, a DAQ card, described further, also has a signal generation ability thus the signal generator does not need to be a separate part of the system, which might reduce the overall cost of the system at the cost of slightly more programming effort. It was decided to use the arbitrary waveform generator for its ability to generate not only simple sinusoidal signal but also more complex signal, e.g., based on Fourier series, that allows for simultaneous multifrequency excitation for the purpose of further research. Signal from generator controls the current source but it states the reference signal for measured voltage processing as well.

The Keysight 34972A [43] is the general purpose data acquisition mainframe that can be equipped with up to three signal switching cards. For the purpose of signal sourcing, two 8 × 4 matrix switch cards (Keysight 34904A) were chosen while for voltage measurement a multiplexer card (Keysight 34901A) was used. All the switching cards are based on relays, the switching speed of which is much slower than semiconductor-based multiplexers. On the other hand, relay-based switching devices have very low contact resistance. The product manual reports 1MHz bandwidth of the switching cards, therefore, they are not limiting the overall bandwidth of the system. The use of a matrix switch for the sourcing signal provides flexibility of selection of the current pattern. Several current injection patterns may be applied: adjacent, opposite and dual-electrode pair (current injection through two independently selected pair of electrodes). The switching hardware and above-mentioned flexibility limit the number of electrodes to 16. However, if the opposite current injection pattern is used together with measurement electrodes voltage in reference to the ground, up to 32 channels might be utilized using the same hardware. For the purpose of reduction of connection influence on measurement accuracy, a four-wires method was applied—separate cables were used for the current signal injection and for voltage measurement. It is worth mentioning that the switching system itself may also work with LCR meter or impedance analyzer providing an alternative method for impedance spectroscopy in the area of the sensor. Besides the above-mentioned Keysight unit, there are other brands on the market that provide similar devices, e.g., Keithley or National Instruments.

Probably the most essential part of the EIT system that demands careful selection is a DAQ card. The voltage signals acquired from each electrode are in the order of millivolts while the measurement of differential voltage between consecutive electrodes is vital for imaging quality. A lot of EIT systems described in literature, e.g., [16,31], are based on 12 bit ADC (analog-to-digital converter) limiting distinguishability of the voltage signals to 4096 states. In order to increase the resolution of voltage measurements for this system, a 16 bit DAQ card was chosen. Another important parameter of the DAQ card is the sampling rate which, according to the Nyquist sampling theorem, limits the overall bandwidth of the system. The applied DAQ card (National Instruments PCIe-6351+ [44]) is a 16 bit card with a sampling rate up to 1.25 MHz (if one channel is used) or 1.00 MHz divided by the number of channels (if multiple channels are used). Assuming that for the measurement of both real and imaginary components of the voltage an additional reference sinusoidal signal is necessary to be measured (as the components are calculated programmatically), the frequency bandwidth for the whole system is limited to 250 kHz. It is remarkable that calculations of the complex voltage components might be realized also in a hardware manner (e.g., using a lock-in amplifier [45] or another demodulation circuit). In such a situation, total bandwidth of the system will be much wider.

The only part of the EIT system that was built especially for this research is the current source. Although there are commercially available VCCS (e.g., Stanford Research CS580) on the market they are not as common as the other above-mentioned devices. Additionally, they are also rather expensive. In this research the current source was built based on improved Howland circuit instead [46]. It is a well known circuit that only consists of a few electronic parts which, if carefully selected, provide a simple yet reliable bidirectional current source. The quality of the build and proper adjustment of the VCCS is primarily connected with output impedance of the current source. Ideally, the output impedance should be infinite, however, due to imperfect properties of the electronic parts the output impedance significantly decreases with the increase of frequency. In this research, the current source was built around the LT1222 operational amplifier [47] for its high bandwidth and the ability to drive also the capacitive load. The improved Howland circuit demands also the use of four resistors that have matched resistance. Introducing an additional trimming resistor, it is possible to match the resistors to 0.01% [46].

All the above-mentioned devices are mounted in the 19′’ rack case that provides additional shielding. The signal generator and switching device are connected to the PC with the Ethernet interface while the DAQ card is the internal device controlled by the PCIe bus for fast data acquisition. The EIT system is controlled using PC and the Matlab (MathWorks, Natick, USA) software. It provides reliable interfacing for instruments control (Instrument Control Toolbox) as well as DAQ operation and data storage (Data Acquisition Toolbox). Moreover, Matlab is also a framework for commonly used EIT image reconstruction software EIDORS [40]. The EIT sensor (Figure 2) was built in the form of a circular vessel of diameter 240 mm using polycarbonate pipe. Sixteen electrodes made of 19 mm wide self-adhesive tinned copper foil were circumferentially arranged inside the vessel.

2.3. Data Processing and Image Reconstruction

In this research, an adjacent current injection pattern was applied. This means that in each single projection, current is injected through neighbouring pairs of electrodes (e.g., 1-2, 2-3, 3-4, etc.) and the voltage differences between adjacent electrodes are being measured. In the subsequent projection, the next sourcing electrode pair is enabled and the voltage measurement is repeated. Thus, for the 16-electrode sensor the measurement set consists of 256 voltage measurements (assuming that voltage is also measured on electrodes injecting current). Each measured voltage signal is in the form of sinusoidal waveform (Equation (5)):

$$u_m\left(t\right)=U_m\sin \left(\omega t+{\phi }_m\right)$$

(5)

where U_m stands for amplitude of measured voltage, ω is the angular frequency and ϕ_m is the phase of the signal. As the frequency of voltage signal is known only the amplitude and phase needs to be extracted from the sampled waveform. For this purpose, an additional reference waveform U_r is logged simultaneously (Equation (6)):

$$u_r\left(t\right)=U_r\sin \left(\omega t+{\phi }_r\right)$$

(6)

Both waveforms are sampled with a sampling rate up to 500 kHz. The method of introducing a reference sinusoid is widely used in the lock-in amplifiers [45], however, it might be adopted to be used in software version as well [48]. Even if in this research only the real component of conductivity was reconstructed, such a data processing method allows for imaginary component reconstruction too. Assuming the frequency of both signals is equal and the initial phase of reference signal is zero, multiplication of the acquired signals leads to (Equation (7)):

$$u_m\left(t\right)·u_r\left(t\right)=\frac{1}{2}{U}_m{U}_r\left[\cos \left({\phi }_m\right)-cos\left(2\omega t+{\phi }_m\right)\right]$$

(7)

The frequency-dependent component in the brackets in Equation (7) has the zero average value so after averaging over integer number of periods it disappears. From Equation (7), the ‘in-phase’ component can be derived (Equation (8)):

$$\mathrm{I}=\frac{1}{2}{U}_m{U}_r\cos \left({\phi }_m\right)$$

(8)

Repeating the above calculations with the reference signal shifted by the angle of π/2, the ‘quadrature’ component might be derived (Equation (9)):

$$\mathrm{Q}=\frac{1}{2}{U}_m{U}_r\sin \left({\phi }_m\right)$$

(9)

Finally, amplitude and phase of the signal can be obtained from (Equations (10) and (11)):

$$U_m=\sqrt{I^2+Q^2}$$

(10)

$${\phi }_m=\arctan \left(\frac{Q}{I}\right)$$

(11)

Reconstruction of the conductivity image requires the foresaid set of measured voltages. Nevertheless, the algorithm chosen for solving of the inverse problem should also be carefully selected as it determines the quality of the images. A number of algorithms have been developed since the EIT gained popularity. Several of them are implemented in the EIDORS software which helps to apply the EIT. In this research, the NOSER algorithm [38] was adopted, however, the comparison with well-established Gauss–Newton method was also performed.

2.4. Description of the Validation Method

Similarly to other research methods, the EIT needs to be thoroughly validated. For this purpose, four experimental investigations were carried out. The trials were focused on:

• correct detection of the material inside the area of the sensor,
• distinguishing between conductive and non-conductive material,
• detection of material characterized by frequency-dependent conductivity,
• visualization of the temporal progress of the selected process.

Except the last one, all the experiments were carried out for the EIT sensor filled with tap water of conductivity 0.04 S/m at 20 °C. This conductivity was measured using EXTECH EC400 m. In the last trial, the sensor was filled with sand soaked with tap water. It was decided not to introduce any quantitative indicators that would describe the quality of the imaging at this stage of the research.

Electrical tomography methods are known for the low imaging resolution [8]. For this reason, a verification of feasibility of proper objects detection is essential. Moreover, the limited resolution might undesirably influence the distinguishability of objects located in close neighborhood. In the first experiment, three polypropylene pipes, of diameter 32 mm, were arranged in three manners with different distances between pipes. The results were compared with numerical simulation for every arrangement of the material. In this research, a limit for the distance between pipes that does not affect the distinguishability was indicated.

As the EIT method is based on conductivity mapping, it should be able to distinguish between conductive and non-conductive material inside the area of the sensor. During the second experimental research two objects were inserted into the sensor: a polypropylene pipe and an aluminum rod of diameters 32 and 50 mm, respectively. The electrical conductivity of polypropylene is much lower than the background conductivity (tap water) while the conductivity of aluminum is significantly greater, therefore, an image of high contrast might be expected. The obtained results were compared with numerical simulations as well.

One of the cases in which the use of multifrequency tomography might be useful is monitoring of the processes that involve biological material, e.g., food processing or biological wastewater treatment. According to the Hayden model [49], the most of biological tissues are characterized by frequency-dependent conductivity. For low frequency of the current, excitation the conductivity of the material is relatively low whereas with the increase of frequency it significantly raises. An exemplary study of such a relationship was shown in paper [14] for the drying process of chokeberry (Aronia Melanocarpa). The purpose of the third stage of experimental research was to verify the ability of the EIT system to detect a biological material with current excitation for several different values of frequency. The biological material used for the experiment was carrot root of diameter approximately 30 mm. According to [50], fresh, unprocessed carrot is characterized by conductivity slightly lower (for low frequency) than tap water used in this research. Therefore, the reconstructed image should show the carrot root to be less conductive than background. On the other hand, with the increase of frequency, the conductivity of carrot increases, consequently the reconstructed image should be opposite. The experiment was carried for one location of the carrot root and six different frequencies of current excitation: 1, 10, 15, 20, 25 and 50 kHz.

Even if the proposed EIT system is far slower in comparison with systems based on semiconductor multiplexers, it still might be a valuable tool for monitoring of the temporal progress of certain processes. Such processes may include most situations where spatial distribution of electrical conductivity is changing over time—excluding processes which are too fast to be monitored using the described method. The exemplary processes might be pollutant migration, heat transfer or drying procedures. In the last experimental research, the pollutant migration dynamics was investigated. To ensure the process was not too fast, the research was carried out in the sensor that was filled with sand soaked with tap water. During the experiment, the 1% saline was injected into the sand bed through vertical distributor. The distributor was made of plastic pipe of diameter 5 mm with perforation at the one side of the sidewall. Therefore, the injected saline was flowing in the specified direction (towards the center of the sensor). The saline was injected by the following portions: 5 mL every 120 s for 10 min then injection was stopped and dilution of the saline was monitored over time.

3. Results and Discussion

3.1. Comparison of Selected Algorithms for the Image Reconstruction

Quality of the conductivity imaging depends on several factors. Besides the EIT measurement devices, also the impact of sensor geometry: size and number of electrodes as well as the precision of electrodes placement should be noticed. Another important component to be chosen is the algorithm for image reconstruction. In this research, the NOSER algorithm was applied. This algorithm is known for overestimating the size of detected objects [38]. However, in comparison with another well-established algorithm, the Gauss–Newton method, the NOSER algorithm has shown better fitting to real position and size estimation of detected objects (Figure 3). Both methods are characterized by correct placement of the detected objects but the separation between objects is better with the NOSER method. Moreover, using this method estimated size of the objects is closer to the real value. As the comparison between many other algorithms was not the aim of this research, it was decided to apply the NOSER algorithm for further validation experiments.

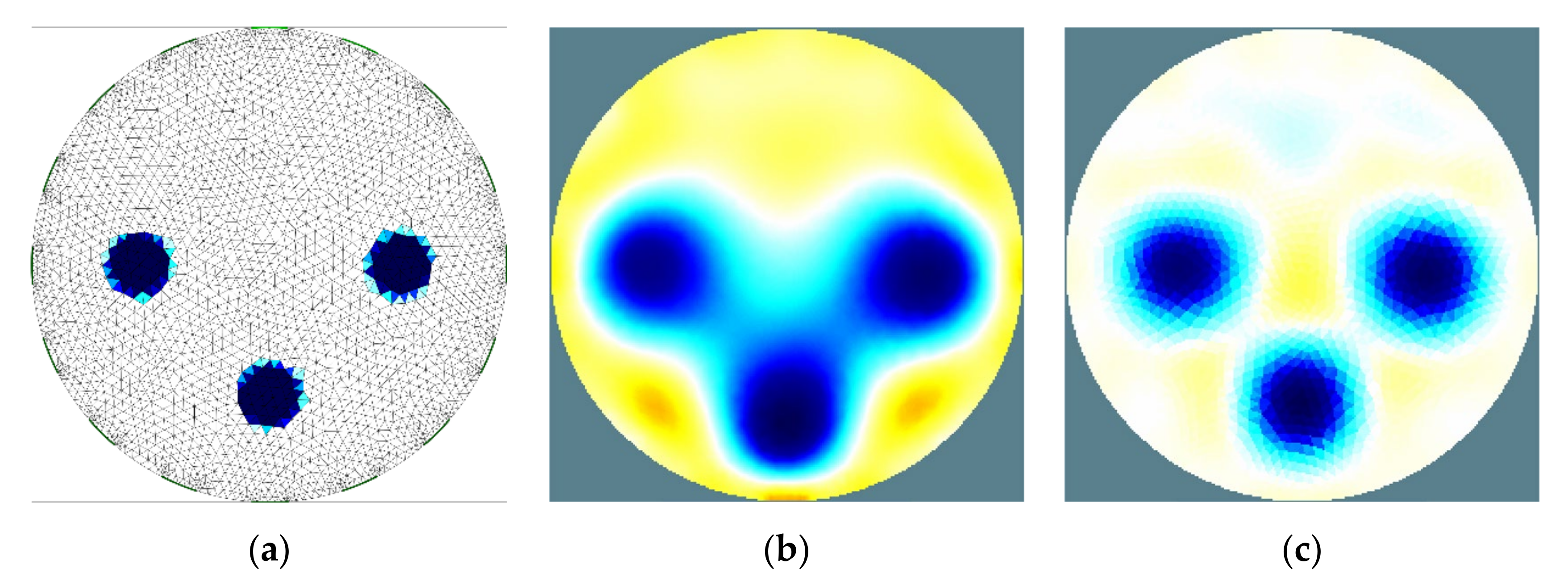
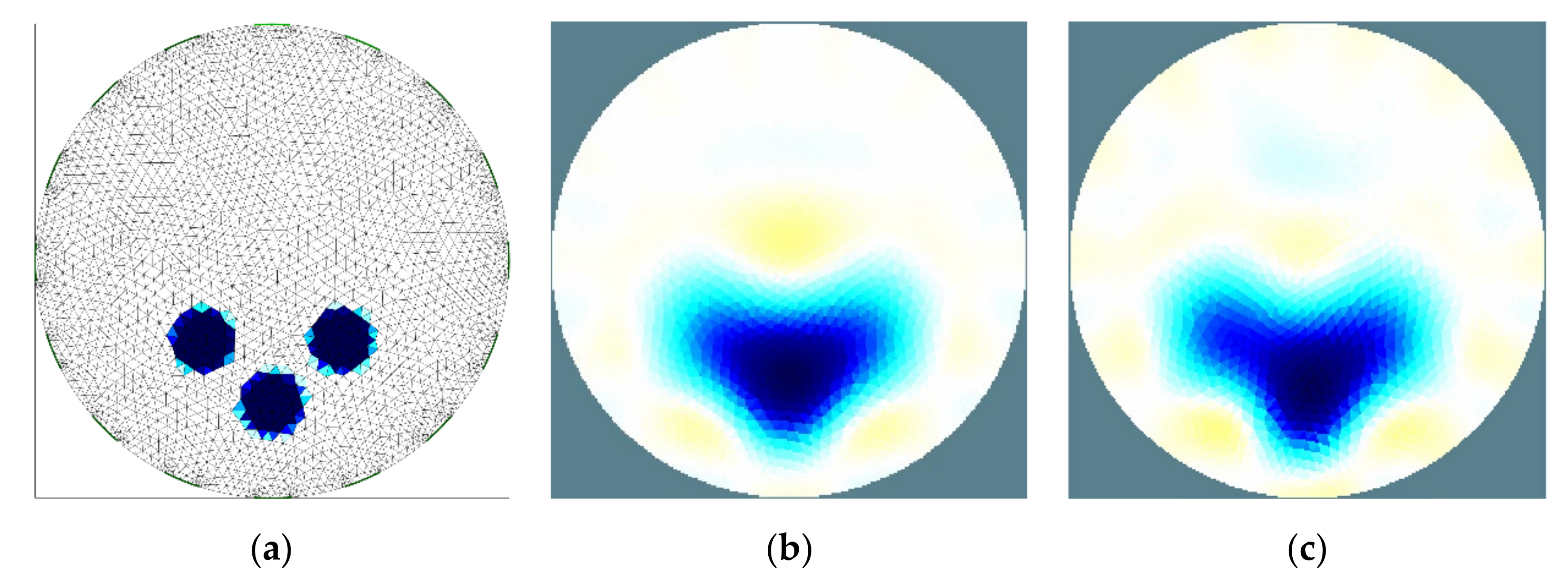
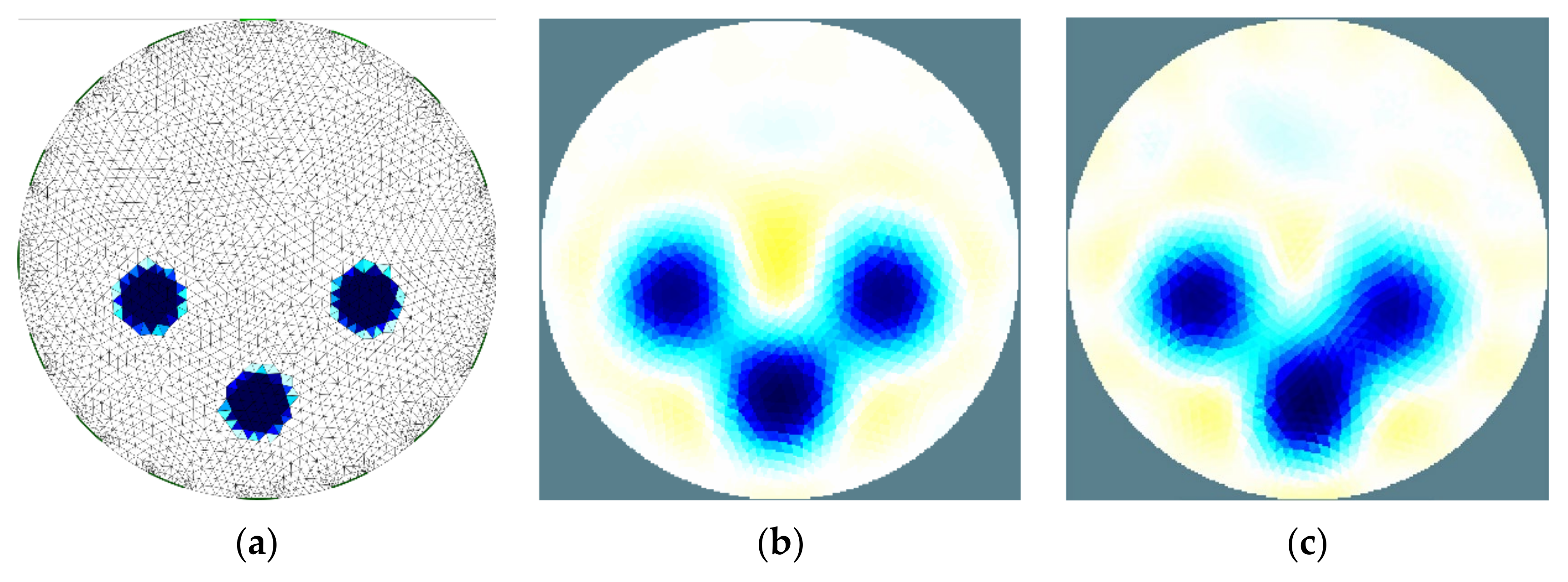
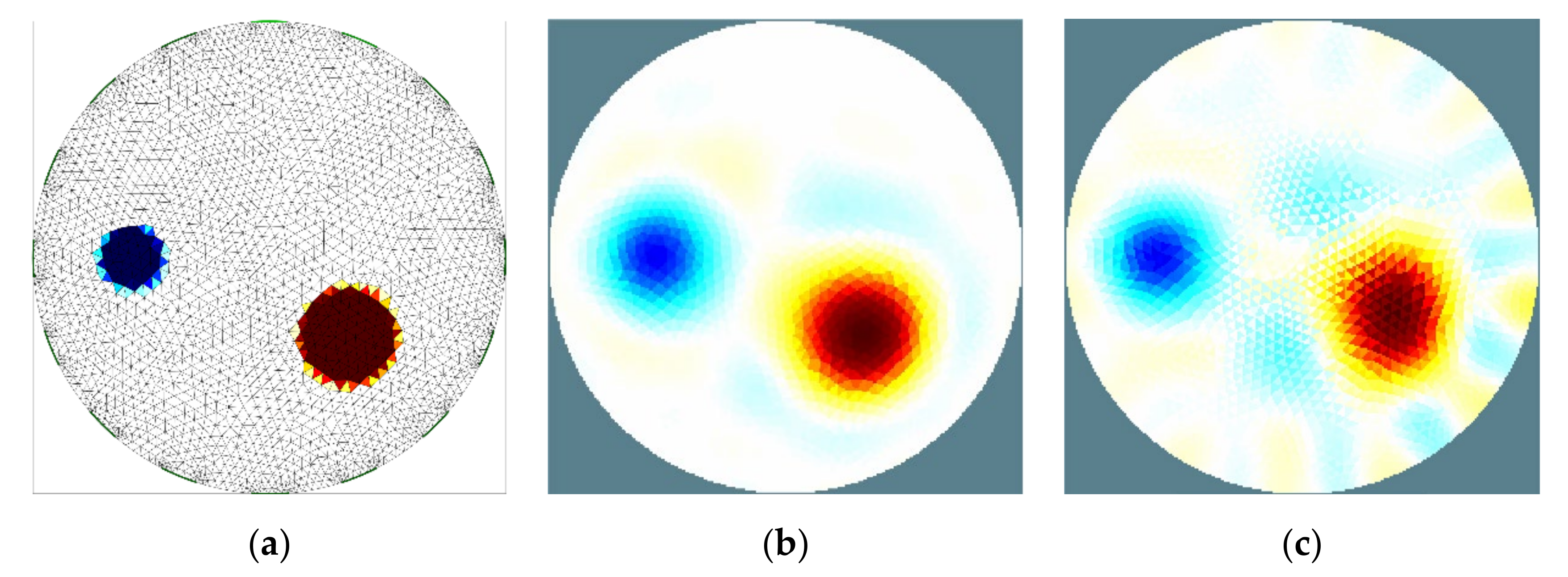
3.2. Analysis of the Object Detection

Exact detection of the object position as well as the separation of each element is the most important feature of every imaging technique. Position of the circular object may be described by location of its center. Taking into account this criterion, all cases presented below (Figure 4, Figure 5 and Figure 6) are characterized by correct object detection. Simulation results showed that even if centers of the objects may be detected correctly, the size of the object is overestimated. As foresaid, it is a known feature of the NOSER algorithm. It is likely that further image processing might prevent from this effect to some extent.

In the first case (Figure 4), the distance between objects is large enough for proper separation, thus in the reconstructed images all the objects are identified with the highest possible precision. The comparison between images based on simulated and measured data shows close similarity that proves the correct operation of the EIT system. Moreover, it also verifies the correctness of the sensor assembly and the electrodes placement.

During the experiment, the distance between objects was decreased to the value of 10 mm (between sidewalls of the objects). This case is illustrated in the picture (Figure 5). In the situation of too close objects, it is impossible to distinguish between each object in the reconstructed image. It was found that the limit distance between objects that ensures its proper separation was similar to object diameter—that is approximately 14% of sensor diameter (Figure 6). In the picture one can observe an asymmetry of image reconstructed on the basis of measured data. It is likely that the reason of that irregularity was minor lack of precision during objects placement. The obtained limit value depends mostly on geometry of the sensor and the electrodes than the EIT device itself.

3.3. Distinguishability between Conductive and Non-Conductive Objects

The results of this experiment are shown in the picture (Figure 7). Comparison between images based on simulated and measured data shows that the polypropylene pipe is detected correctly. Both position of its center and size of the non-conductive object is estimated with the same precision as in the simulation. The aluminum rod is not detected with the same level of accuracy. One can observe the kind of blurriness at the border of the rod which makes it difficult to estimate the position and the size of the rod. It is likely that the reason for this effect is the presence of a thin layer of material of conductivity lower than the object itself on the surface of the aluminum rod. As the main aim of this experiment is to attest the capability of distinguishing between objects of different conductivity, the obtained result satisfies the expectations.

3.4. Multifrequency Detection of the Biological Material

As mentioned in Section 2.4, unprocessed carrot is characterized by conductance slightly lower (if measured at low frequency) than tap water used in this research. For this reason, if frequency of excitation current is relatively low (1–10 kHz) the reconstructed images show the area of lower conductivity in the position where carrot was placed (Figure 8a,b).

According to the Hayden model [49], the conductivity of most of the biological tissues increases with the increase of frequency, therefore, the appearance of a higher conductivity area might be expected above a certain frequency. In the reconstructed images, obtained for frequencies 25 and 50 kHz (Figure 8e,f), this effect might be observed. However, for a certain frequency range, the results are not that obvious. In the pictures (Figure 8c,d for 15 and 20 kHz, respectively) the images are shown in which the detected object is reconstructed as split area of conductive and non-conductive materials. The explanation for this effect is likely to be an inhomogeneity in the carrot root. According to the obtained results, the EIT system has proven its ability for multifrequency imaging. Additionally, the use of multifrequency excitation seems to be a promising method for applying the proposed EIT system into the research investigations. Especially extending its ability with widening the frequency bandwidth and applying the imaginary component of the conductivity will be subject of further research and development of the system.

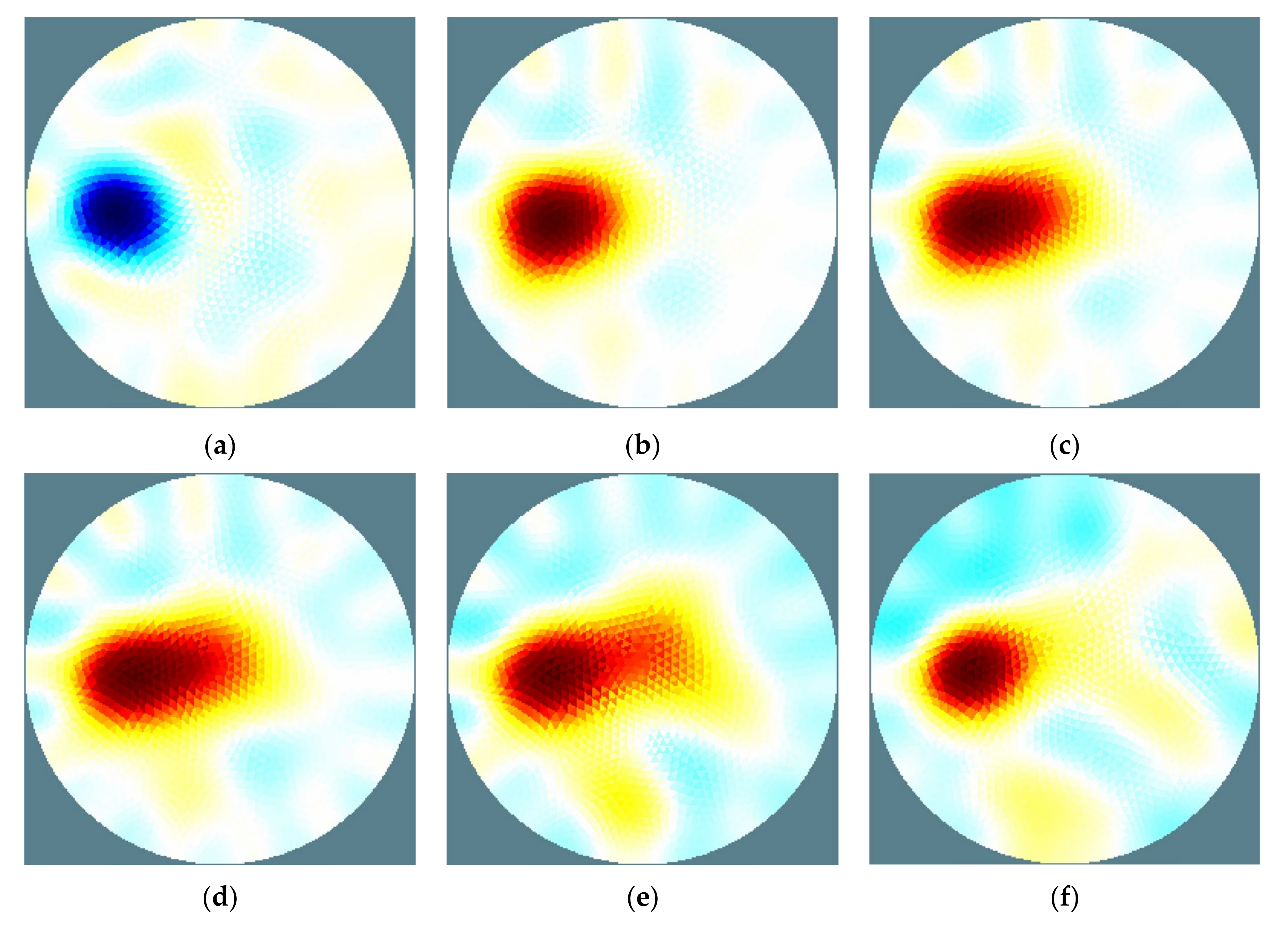
3.5. Visualization of the Pollutant Migration in the Sand Bed

The ability of proposed EIT system for monitoring of the dynamics of any process is limited for its low imaging rate. Depending on applied settings, acquiring a complete measurement set for reconstruction of single image takes at least 60 s. Still, there are a lot of processes that may be monitored with an even longer sampling period. The example chosen process—a migration of pollutant in a fixed sand bed—was selected for basic examination of the EIT system dynamic abilities. As the real propagation of the pollutant was not monitored nor simulated in another way, the evaluation of the reconstructed images in this experiment is based on general prediction of the process evolution. Consequently, it can be a qualitative assessment only. In the picture (Figure 9), a few images are presented that illustrate the process evolution.

The distributor itself has lower conductivity than background, thus before injection it is shown in the reconstructed image as non-conductive area (Figure 9a). Once the first portion of saline was injected through the distributor, the conductivity in its surrounding became higher than background (Figure 9b). Further injections spread the saline in the direction toward the center of the area which is visualized correctly (Figure 9c,d). After the injections were stopped, the saline was diluting thus its concentration decreased but the area of higher conductivity increased (Figure 9e). Eventually, the saline in higher concentration existed only inside the distributor and its close surrounding (Figure 9f).

4. Conclusions

In the paper, the EIT system based on general purpose laboratory equipment was proposed. The use of laboratory-grade devices like signal generator, switching mainframe and DAQ card enables the possibility to build the EIT system at a reasonable cost, yet of high quality of imaging.

The proposed EIT system was proven by the experimental validation to be useful research apparatus for monitoring of the selected processes. The obtained results showed the ability for precise estimation of position and size of the objects inside the sensor. It was found that if the distance between objects is greater than 14% of the sensor diameter, they are separated correctly. Otherwise, for a closer distance between objects, they are merged to a certain extent in the reconstructed image. Additionally, distinguishing between objects of higher and lower conductivity can be considered correct. Although the minor blurriness around the object of higher conductivity may be observed, overall rating of the image reconstruction is good based on comparison with the numerical simulation. The experimental validation of multifrequency imaging of biological material has given mostly the results predictable by the Hayden model. However, two of them were ambiguous, thus this subject should be further investigated. The last stage of validation showed that even if the proposed EIT system is not characterized by high imaging rate, its usefulness for monitoring of the certain processes might have been considered proven. It is noteworthy that the quality of obtained images is dependent not only on the EIT electronics itself. The precision of EIT sensor built as well as the proper selection of the image reconstruction algorithm are on the same level of importance.

The main drawback of the proposed EIT system, which might be important for certain studies, is low imaging rate. As the switching cards in the proposed system are built from electromechanical relays, its switching speed is far lower than semiconductor-based multiplexers used in most of the EIT systems. It was found that the acquisition of a full measurement set for a single image is at least 60 s. Certainly, it limits the possibilities for use of this EIT system to monitoring the stationary states of the processes or for monitoring the dynamics of slow-changing processes. From the certain point of view, the necessity of building the VCCS using several electronic parts might be treated as another disadvantage of the described system. However, the improved Howland circuit is characterized by simplicity, thus its assembly is not very demanding.

During the validation experiments, a few features of the EIT system revealed to be important for further research. As the most valuable aspect of proposed system is its ability for multifrequency imaging, the bandwidth of the system should be extended. Currently, the frequency is limited to 250 kHz. However, if the demodulation circuit will be added to the system, the detection of the in-phase and quadrature components might be realized in hardware, a manner that in turn allows for bandwidth increase up to 1 MHz (frequency limit for switching cards). Unfortunately, it will require a VCCS upgrade as its output impedance might be insufficient for such a frequency range. Additionally, a promising development of proposed EIT system would be the imaging of both real and imaginary components of complex conductivity. Although the EIT system is prepared for this ability, it has not been validated yet.